实验二:窄带高斯随机过程的产生讲解
随机信号实验-高斯过程的产生

随机信号实验 --高斯过程的产生赵骏一、实验目的掌握产生具有一定相关性的高斯过程的方法。
二、实验内容(1)产生协方差函数为()ταστ-=e C 2,0>α的高斯过程。
(2)分析其概率密度函数错误!未指定书签。
、均值、方差、相关函数和功率谱。
三、实验仪器和设备(1)计算机一台。
(2)Matlab 软件。
四、实验原理一般情况下,认为所要进行仿真的随机过程都满足平稳性和各态历经性。
严格的说,产生的随机序列并非是随机过程的样本函数,但是可以近似地认为是一个样本函数。
仿真协方差函数为ταστ-=e C 2)(的高斯过程的方法如下:1.产生N 个均值为0,方差为1并且相互独立的高斯分布随机数n x 。
2.根据递推公式n n n x e y e y ατατσ211----+=计算出一组随机数n y ,其中初值为0y ,采样间隔是τ。
3.如果要仿真的随机信号数学期望不为0,将数学期望加到随机数上,就可以得到对应均值和方差的随机过程或随机序列的一个样本,生成随机序列样本函数。
4.估计随机信号的期望和方差分别为∑-=∧=1)(1N n X n x N m ,210)(1∑-=∧∧⎥⎦⎤⎢⎣⎡-=N n X X m n x N D 。
5.计算产生的随机过程的自相关函数为∑--=∧+=10)()(1)(τττN n n x n x NR 。
6.计算产生的随机过程的功率谱密度为221)(1)(1)(ωωωX Ne n x NS N n nj X ==∑-=-∧。
7.利用自相关函数傅立叶变换计算随机信号的理论功率谱密度和估计值进行比较。
理论方法计算功率谱密度为ττωωτd e R S j X X ⎰∞∞--=)()(。
五、实验步骤与结果记录(1)高斯过程的产生按照实验原理中所描述的产生高斯过程的步骤,编写实验程序如下:clc,clear N=250; alp=1; sig=1; delt=1; a=1;mm=zeros(1,N); x1=rand(1,N); x2=rand(1,N);x3=a.*sqrt(-2*log(x1)).*cos(2*pi*x2)+mm; %产生随高斯分布的随机数 y(1)=sig*x3(1);for n=2:N %产生高斯过程一个样本 y(n)=exp(-alp)*y(n-1)+sig*sqrt(1-exp(-2*alp*delt))*x3(n); end i=1:N; plot(i,y); hold on ;plot(i,mm,'-'); title('高斯过程样本函数')运行程序后得到如图1所示的高斯过程的样本函数。
第6章 窄带随机过程
xˆ
2
(
t
)dt
x
2
(t
)dt
lim 1 T xˆ 2 (t)dt lim 1 T x 2 (t)dt
T 2T T
T 2T T
上 海 大 学 通 信 学 院
上 海 大 学 通 信 学 院
3
2016/10/28
上
海 三、窄带随机过程的性质
大
学
通 问题:若已知Z(t)的功率谱密度 GZ ( ) 或统计特性RZ ( ) 信 (讨论平稳窄带过程),则其B(t)和 (t ) 或X(t) 和Y (t)
性质4.
RX
(
)
1
0 GZ ()cos[( 0 ) ]d
性质5. RX ( ) RY ( )
性质6.
RXY
(
)
1
0 GZ ()sin[( 0 ) ]d
性质7. RY X ( ) RXY ( ), RXY ( ) RXY ( )
上
海
大 学
性质8. RXY (0) E[X(t)Y(t)] 0, RY X (0) 0
(
f
),奇函数
由此可知:时域实信号正、负频域的频谱可互求。
1
2016/10/28
上
海 大
从有效利用信号的角度出发,实信号负频域部分是冗余
学 的,所以只要保留正频域的频谱,记为 S ( f ),即可。
通
信 学
若只取正频域频谱
S ( f ),则
S
(
f
)
S (
f
),即S ( f ) 不满
院 足共轭对称性,且 S ( f ) 时域复信号。
s( t )
h( t )
窄带过程产生及随机信号功率谱仿真

一、模拟产生一个窄带随机过程。
首先产生两个相互独立的随机过程Ac(t)和As(t),用两个正交载波进行调制得到窄带过程。
绘出其波形、相关函数及功率谱(1000数据点)。
(陈超然)程序代码:clear all;clc;N=1000;X1 =0.2*randn(1,N);X2 =0.2*randn(1,N);fs=200;t =-0.5:1/N:(0.5-1/N);A=[1 -0.9];B=1;Xc=filter(B,A,X1);Xs=filter(B,A,X2);for n=1:NY(n)=Xc(n)*cos(2*pi*fs*t(n))- Xs(n)*sin(2*pi*fs*t(n));end[R,lags]= xcorr(Y,N);%计算序列的自相关NFFT=2^nextpow2(N); %求得最接近总点数的2^n,这里是1024Pxx=abs(fft(R,NFFT)/N); %对自相关函数进行fft变换f=fs*linspace(0,1,NFFT);figure(1)n=1:N;plot(t(n),Y(n));title('输出波形');figure(2)plot(lags,R);title('自相关函数');figure(3);plot(f,Pxx);%绘制功率谱曲线title('功率谱密度');运行结果输出波形相关函数功率谱密度二、如果信号X(t)的表达式为:X (t) = sin c(100t) cos(2p *200t)1、绘出信号及其幅度频谱曲线;2、当中心频率向左搬移f0=200Hz时,求出其低通等效信号,并绘出其幅度频谱、信号的同相、正交分量及包络;3、当中心频率向左搬移f0=100Hz时,求出其低通等效信号,并绘出其幅度频谱、信号的同相、正交分量及包络。
(郭静)程序代码:clcclearN=512;fs=N/0.5;%%%%%%%%%%%%%%%%%%%%%%%%%信号的产生及可视化%%%%%%%%%%%%%%%%%%%%%%%%%%t=-0.25:0.5/N:(0.25-0.5/N);for n=1:NX(n)=sinc(100*t(n))*cos(2*pi*200*t(n));h_t(n)=1/(pi*t(n));endn=1:N;figure(1)plot(t(n),X(n));grid;axis([-0.15 0.15 -1 1]);title('信号曲线');Xw=abs(fft(X,N)); %fft变化,除以信号的点数看原信号的幅值f=fs*linspace(0,1,N);%频率轴的产生figure(2)plot(f,Xw)title('信号幅频曲线') axis([0 1024 0 6])运行结果-0.1-0.050.050.10.15-1-0.8-0.6-0.4-0.200.20.40.60.81信号曲线01002003004005006007008009001000123456信号幅频特性%%%%%%%%%%%%%%%%%%%%%%%%%频率左移100%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for n=1:NXc_1(n)=sinc(100*t(n))*cos(2*pi*100*t(n)); %信号频率左移100Ac_1(n)=sinc(100*t(n));endAs_1=hilbert(Ac_1); %信号的hilbert变换for n=1:NXs_1(n)=As_1(n)*sin(2*pi*100*t(n));endX_hil_1=hilbert(Xc_1);X_1_hil_fft=abs(fft(X_hil_1,N)); %信号的fft变换for n=1:NX_1_enve(n)=sqrt(Ac_1(n)^2+As_1(n)^2); %求信号的包络endfigure(3)subplot(221)plot(f,X_1_hil_fft)axis([0 512 0 12]);title('信号频率左移100hilbert变换的频谱')subplot(222)plot(t,Xc_1)title('f0=100低通等效同相分量')axis([-0.15 0.15 -0.6 1]);subplot(223)plot(t,Xs_1)axis([-0.15 0.15 -0.6 1]);title('f0=100低通等效正交分量')subplot(224)plot(t,X_1_enve)axis([-0.15 0.15 0 1.5]);title('f0=100低通等效包络')运行结果:%%%%%%%%%%%%%%%%%%%%%%%%%信号频率左移200%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for n=1:NXc_2(n)=sinc(100*t(n))*cos(2*pi*0*t(n));Ac_2(n)=sinc(100*t(n)); endAs_2=hilbert(Ac_2); for n=1:NXs_2(n)=As_2(n)*sin(2*pi*0*t(n)); endX_hil_2=hilbert(Xc_2);X_2_hil_fft=abs(fft(Xc_2,N)); for n=1:NX_2_enve(n)=sqrt(Ac_2(n)^2+As_2(n)^2); end figure(4) subplot(221) plot(f,X_2_hil_fft) axis([0 512 0 12]);title('信号频率左移200hilbert 变换的频谱') subplot(222) plot(t,Xc_2)title('f0=200低通等效同相分量') axis([-0.15 0.15 -0.6 1]); subplot(223) plot(t,Xs_2)axis([-0.15 0.15 -0.6 1]); title('f0=200低通等效正交分量') subplot(224) plot(t,X_2_enve)hilbert 变换后信号左移100的频谱f0=100低通等效同相分量f0=100低通等效正交分量f0=100低通等效包络axis([-0.15 0.15 0 1.5]); title('f0=200低通等效包络')运行结果:hilbert 变换后信号左移200的频谱f0=200低通等效同相分量f0=200低通等效正交分量f0=200低通等效包络。
第5章-窄带随机过程

第五章 窄带随机过程5.1 窄带随机过程的概念1. 通信工程中的信号频率在通信工程中,如雷达、广播、电视等信号,在传输中信号有相对固定的信号频率。
对于有相对固定频率的信号,其数学表达方法的研究是非常重要的。
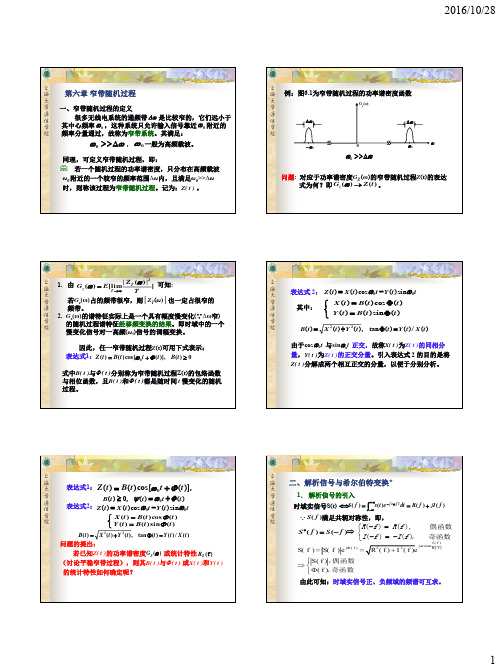
2. 窄带随机过程(1) 带通随机过程的定义若随机过程)(t X 的谱密度满足:⎩⎨⎧∆<-=其它0)()(0ωωωωωS S X 则称)(t X 为带通过程。
带通过程的谱密度的图解如下图。
(2) 窄通随机过程的定义若)(t X 为带通过程,且0ωω<<∆,即中心频率过大于谱宽,则称)(t X 为窄通随机过程。
3. 窄带随机过程的解析表达方法之一:莱斯表示法(1)窄带随机过程的莱斯表示定理:任何一个实窄带随机过程)(t X 都可表示为下式:)sin()()cos()()(00t t b t t a t X ωω-=证明:略。
注:证明过程要用到一种重要的数学变换――希尔伯特变换,此变换需掌握。
(2) )(t a 、)(t b 的性质 ①)(t a 、)(t b 都是实随机过程。
②0))(())((==t b E t a E . 。
③)(t a 与)(t b 各自广义平稳,联合平稳,且:)()(ττb a R R =。
④))(())(())((222t X E t b E t a E ==,由此可得方差22b a σσ=。
⑤0)0(=ab R ,这说明)(t a 与)(t b 在同一时刻正交。
⑥)()(ωωb a S S =。
4. 窄带随机过程的解析表达方法之二:准正弦振荡表示法定理:实窄带随机过程)(t X 都可表示为下式:))(cos()()(0t t t A t X Φ+=ω证明:由莱斯表示法有:)()()(22t b t a t A +=, )()()(t a t b arctgt =Φ )(t A 与)(t Φ都是慢变化的随机过程。
慢变化是指)(t A 与)(t Φ随时间变化比)cos(0t ω随时间的变化要缓慢得多。
六.窄带随机过程

(2)
ˆ x(t ) 的希尔伯特变换为 x(t )
ˆ H [ x(t )] x(t )
两次希尔伯特变换相当于连续两次 900 相移,结果 正好是 1800反相
9 2013-7-21
1.2 希尔伯特变换性质(3)
(3)
y(t ) v(t ) * x(t ) 的希尔伯特变换为
ˆ ˆ ˆ y (t ) v (t ) * x (t ) v (t ) * x (t )
1 x (t ) d
反变换
ˆ x( ) ˆ x(t ) H [ x(t )] d t ˆ 1 x(t ) d
1
1
ˆ 1 x(t ) d
5
2013-7-21
CZ1Z2 E (Z1 mZ1 )* (Z2 mZ2 )
15 2013-7-21
1.3 复随机过程
若X与Y分别是实随机变量,定义
Z (t ) X (t ) jY (t )
为复随机变量 均值: 方差:
mZ (t ) mX (t ) jmY (t )
DZ (t ) DX (t ) DY (t )
H ( )
一个典型的确定性窄带信号可表示为 窄带系统
白噪声
X (t )
Y (t )
x 系统示意图 或宽带噪声 ( t ) a ( t ) cos[ 0 t ( t )]
x(t ) y(t ) a(t ) ——幅度调制或包络调制信号
窄带噪声
0
窄带系统传递函数
(t ) ——相位调制信号
1.1 希尔伯特变换
窄带随机过程的模拟与分析

实验报告实验题目:窄带随机过程的模拟窄带随机过程的模拟一、实验目的(1)了解具有任意功率谱(低频)的正态随机过程的模拟; (2)了解窄带随机过程的模拟方法。
二、实验原理(1)任意功率谱的正态随机过程的模拟假定需要产生一个持续时间为d T 的高斯随机过程的一个样本()X t ,要求功率谱满足()X G f 。
为此,可以先将()X t 进行周期延拓,得到一个周期信号,然后对周期信号进行傅里叶级数展开。
即0201()()j f k k k dXt X e f T π∞=-∞==∑由于傅里叶级数是k X 的线性组合,所以,如果k X 是零均值的高斯随机变量,那么()X t 也是零均值高斯过程,如果{}()Xt 是两两正交的序列,则周期信号的功率谱为线谱。
即 2220()()(())kk k X k G f g f kf gE X δ∞=-∞=- =∑通过选择k g 就可以得到期望的功率谱。
假定()X G f 是带限的,即()0()X G f f B = >那么,{}2k g 只有有限项,共21M +项,与此对应的傅里叶级数也是21M +项。
因此,只需产生21M +个互相正交的零均值高斯随机变量{}11,,,,M M M M X X X X --+- 。
然后据此构造时域样本函数即可,有02()[]()Mj f k i t k k MX i X i t X e π∆=-=∆=∑其中t ∆为任意小的时间间隔。
(2)窄带随机过程的模拟对于窄带系统,当系统输入白噪声或宽带噪声时,输出可以表示为0()()cos[()]Y t A t t t ω=+Φ其中0ω为中心频率,()A t 和()t Φ是满变化的随机过程,对上式展开得00()()cos ()sin c s Y t A t t A t t ωω=-其中,()()cos (),()()sin ()c s A t A t t A t A t t =Φ=Φ,是慢变化的随机过程,分别称为窄带随机过程的同向分量和正交分量。
6.窄带随机过程的产生 - 随机信号分析实验报告

计算机与信息工程学院综合性实验报告一、实验目的1、基于随机过程的莱斯表达式产生窄带随机过程。
2、掌握窄带随机过程的特性,包括均值(数学期望)、方差、概率密度函数、相关函数及功率谱密度等。
3、掌握窄带随机过程的分析方法。
二、实验仪器或设备1、一台计算机2、MATLAB r2013a 三、实验内容及实验原理基于随机过程的莱斯表达式00()()cos ()sin y t a t t b t t ωω=- (3.1)实验过程框图如下:理想低通滤波器如图所示:图1 理想低通滤波器()20AH ∆ω⎧ω≤⎪ω=⎨⎪⎩其它(3.2) 设白噪声的物理谱0=X G N ω(),则系统输出的物理谱为 220=()=20Y X N AG H G ∆ω⎧0≤ω≤⎪ωωω⎨⎪⎩()()其它(3.3) 输出的自相关函数为:01()()cos 2Y Y R G d τωωτωπ∞=⎰ /221cos 2N A d ωωτωπ∆=⎰ (3.4) 20sin 242N A ωτωωτπ∆∆=⋅∆ 可知输出的自相关函数()Y R τ是一个振荡函数。
计算高斯白噪声x(t)、限带白噪声()a t 、()b t 及窄带随机过程()y t 的均值,并绘出随机过程各个随机过程的自相关函数,功率谱密度图形。
四、MATLAB 实验程序function random(p,R,C) %产生一个p 个点的随机过程%--------------------------高斯窄带随机过程代码--------------------------% n=1:p;w=linspace(-pi,pi,p); wn=1/2*pi*R*C;[b,a]=butter(1,wn,'low'); %产生低通滤波器Xt=randn(1,p); %产生p 个点均值为0方差为1的随机数,即高斯白噪声 at=filter(b,a,Xt); %让高斯白噪声通过低通滤波器y_at=at.*cos(w.*n); %产生随机过程a(t)y_bt=at.*sin(w.*n); %产生随机过程b(t)yt=y_at-y_bt; %产生一个p个点的高斯窄带随机过程subplot(211)plot(yt)title('高斯窄带随机过程y(t)')subplot(212)pdf_ft=ksdensity(yt) ;plot(pdf_ft)title('y(t)的概率密度图')disp('均值如下')E_Xt=mean(y_at)E_at=mean(y_at)E_bt=mean(y_bt)E_ft=mean(yt)%-----------------------自相关函数代码如下--------------------------% figure(2)R_Xt=xcorr(Xt); %高斯白噪声X(t)的自相关函数R_at=xcorr(at); %限带白噪声的自相关函数R_y_at=xcorr(y_at); %随机过程a(t).coswt的自相关函数R_y_bt=xcorr(y_bt); %随机过程b(t).coswt的自相关函数R_ft=xcorr(yt);subplot(2,2,1);plot(R_Xt);title('高斯白噪声的自相关函数R_Xt'); %并绘制图形subplot(2,2,2)plot(R_at);title('限带白噪声的自相关函数R_a_bx'); %并绘制图形subplot(2,2,3)plot(R_y_bt);title('随机过程b(t)的自相关函数R_y_bt');subplot(2,2,4)plot(R_ft);title('高斯窄带随机过程y(t)的自相关函数R_yt');%------------------------功率谱密度代码如下---------------------------% figure(3)subplot(1,2,1)periodogram(Xt);title('高斯白噪声功率谱密度S_Xt');subplot(1,2,2)periodogram(at);title('限带白噪声功率谱密度S_a_bt');figure(4)subplot(3,1,1)periodogram(y_at);title('随机过程a(t).coswt概率密度概率密度S_y_at');subplot(3,1,2)periodogram(y_bt);title('随机过程b(t).sinwt功率谱密度S_y_bt');subplot(3,1,3);periodogram(yt);title('高斯窄带随机过程y(t)的功率谱密度S_yt');五、实验结果将上述random 函数放在Path 中后,在Commaod Window 中输入:random(1000,10,0.001)时,输出结果如下:01002003004005006007008009001000-0.50.5高斯窄带随机过程y(t)0102030405060708090100246y(t)的概率密度图0500100015002000-50005001000高斯白噪声的自相关函数R X t 0500100015002000-101020限带白噪声的自相关函数R ab x 0500100015002000-50510随机过程b(t)的自相关函数R yb t 0500100015002000-101020高斯窄带随机过程y(t)的自相关函数R y t00.51-40-30-20-10010Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯白噪声功率谱密度S X t 00.51-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )限带白噪声功率谱密度S ab t0.10.20.30.40.50.60.70.80.91-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程a(t).coswt 概率密度概率密度S ya t00.10.20.30.40.50.60.70.80.91-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程b(t).sinwt 功率谱密度S yb t0.10.20.30.40.50.60.70.80.91-50-40-30-20-10Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯窄带随机过程y(t)的功率谱密度S y t在Commaod Window 中输出的结果如下:E_Xt = 0.0020 E_at= 0.0020 E_bt= -0.0020 E_ft = 0.0040六、实验结果分析:1、由于高斯白噪声Xt是标准正态的,所以均值趋近于零,而at,bt是由Xt通过一个线性系统(低通滤波器)得到的,所以输出均值不变,仍为零,从程序运行结果可以看出,Xt,at,bt均值都趋近于零。
第12讲_窄带随机过程2

窄带信号通过窄带系统窄带信号通过窄带系统窄带信号的低通表示方法Xω(A中除载波频率之外的所有信息,称为)窄带信号通过窄带系统窄带系统的表示方法H(H窄带信号通过窄带系统窄带信号通过窄带系统的计算方法例已知,,且,。
窄带信号通过窄带系统()0()cos x t m t t =ωr t ()0cos ,00,t t Th t <<⎧=⎨⎩ω其他02T >>πω()h t 求()解法1:T=∗()()()r t x t h t +∞−∞=−∫()()x t h d τττ=−−∫000()cos ()cos Tm t t d τωτωττ=−+−−∫∫000011()cos ()cos (2)22T Tm t td m t t d τωττωττ1t d =−u t τt =−2u t τ=∫cos ()t m u du ω++∫1()cos u tm udu ω窄带信号通过窄带系统解法2:先求等效基带信号T先求等效带信号()=0()cos x t m t tω()()()=+=000()cos sin j t xt m t t jm t t m t e ωωω ()()0()j t L x t xt e m t ω−== 再求系统的等效低通表示=−−0()[()()]cos h t U t U t T tω=−−=−−0j t h ω +⎡⎤⎣⎦00()[()()]cos sin [()()]t U t U t T t j t U t U t T e ωω窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性窄带随机过程的统计特性表示形式1()()cos ()C A t A t t =Φ()()sin ()S A t A t t =Φ00ˆ()()cos ()sin C A t X t t X t t ωω=+00ˆ()()sin ()cos S A t X t t X t t ωω=−+A t A t 表示形式1:表示形式2:30和都是实随机过程()C ()S 如果,则,由此有[()][()]0C S E A t E A t ==[()]0E X t =ˆ[()]0E Xt =窄带随机过程的统计特性()A t ,+τ窄带随机过程的统计特性A t()+τ,t窄带随机过程的统计特性A t()窄带随机过程的统计特性GG2ωG窄带随机过程的统计特性A t()窄带随机过程的统计特性对零值的窄带平稳随机过程对于零均值的窄带平稳随机过程同相分量和正交分量均为零均值的平稳随机过程同相分量和正交分量的自相关函数相同,且方差均等于窄带随机过程的方差同相分量和正交分量联合平稳,且互相关函数为奇函数联合平稳关函数为奇函数36窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布由于窄带正态随机过程包络和相位的分布ˆ由窄带正态随机过程包络和相位的分布()()cos ()=A t A t t ϕ窄带正态随机过程包络和相位的分布222⎪⎜⎟d 包络的一维概率密度为()()0,0,0==⎨⎝⎠⎪<⎩∫A A f A f A A ϕϕϕσσ分布41窄带正态随机过程包络和相位的分布相位的一维概率密度为窄带正态随机过程包络和相位的分布()cos ()A t a N t θ=+窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布窄带正态随机过程包络和相位的分布作业。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本科实验报告实验名称:窄带高斯随机过程的产生一、实验目的熟悉窄带随机过程的定义,了解窄带随机过程产生的原理与方法,最后估计实验产生的窄带随机过程的功率谱;掌握具有指定功率谱的随机过程产生方法,并以此产生窄带随机过程。
二、实验原理(一)窄带随机过程的产生原理窄带随机过程可以表示为下面的准正弦振荡的形式:cos X t A t ωτϕτ0()=()[+()]或者表示为同相分量与正交分量的合成:00cos sin c s X t A t t A t t ωω()=()-()其中c A t ()与s A t ()均为低频变化的随机过程,可以通过模拟其分布及功率谱特性来实现窄带随机过程的产生。
(二)用频域法模拟任意随机过程模拟一个时长为d T 的高斯随机过程的一个样本函数()X t , 要求功率谱密度满足指定的形式,先将()X t 进行周期性延拓,并做DFS()0201()j k k f kdX e f T X t π∞∞=-==∑若k X 是零均值的高斯随机变量,那么()X t 也是零均值的高斯随机过程。
若{}k X 是两两正交的序列()2220()(())k k k k X g f k G f E X f g δ=-∞∞=-=∑即可以控制k g 得到期望的功率谱。
假定()(0)X G f B f =>,即()X G f 带限,则{}2k g 为有限项,对应的DFS系数{}k X 也为21M +项0()B M f ⎡⎤=⎢⎥⎣⎦,因此只需产生21M +个相互正交的零均值高斯随机变量{}101,,,,,,M M M M X X X X X --+-,其方差为22()k kE X g =。
2k g 应与()0X G kf 成比例,即()20X k G g kf β=,则有()()220()MMMBX XBMk kk k MMk G f G kf df E X g β=-=-=--===∑∑⎰∑即()()BX B MXMk G f G df kf β=--=⎰∑ 产生步骤: i. 根据要求的时长d T 确定01d f T = ,根据功率谱的带宽确定0B M f = ii. 计算系数βiii.产生21M +个独立的高斯随机变量,()0(0,)(,1,,0,,1~,)k X N k M X M G M M kf β=--+-iv.构建时域样本函数[]()02()Mf k Mj i t k k X X i i t X e π∆=-=∆=∑(三)用时域滤波法模拟任意随机过程功率谱为1的白噪声通过线性系统,输出的是服从高斯分布的,且输出的功率谱为()()2X G f H f =,因此要产生功率谱为()X G f 的有色高斯噪声,只需设计一个滤波器即可,该滤波器的传递函数应满足()()X H f G f =三、实验内容模拟产生一段时长5ms 的窄带高斯随机过程()X t 的样本函数。
假定c A t ()与s A t ()的功率谱密度均为41()()1(/)c s G f G f f f ==+∆,其中f ∆为功率谱密度的3dB 带宽。
按照频域法或时域滤波器法分别产生时长为5ms 的低通过程c A t ()和s A t (),然后按图示合成()X t ,其中01000/()f Hz π=。
分别画出模拟产生的c A t ()、s A t ()和()X t 的波形。
1. 零均值高斯随机序列的产生产生一段5ms 的零均值高斯随机过程的两个样本()(),c s A t A t ,其功率谱密度要求为()411(/)Xf G f f =+∆ (1)利用频域法产生()c A t 根据时长5d T ms =,可确定01200df Hz T '== 1f kHz ∆=是功率谱密度的3dB 带宽,取6B f =∆,则030BM f =='计算系数()()60006043043000011(/1000)199.9811(/1000)6200BXB MM k X k G f df df f G kf k β=-=---+===+∑∑⎰⎰ 产生21M +个独立的高斯随机变量,4(0,)(30,29,,29,30)1(200/1~000)k X N k k β=--+构建时域样本函数[](3022003)0j t k k i k X i X e π∆=-=∑(2)利用时域滤波法产生()s A t滤波器的传递函数()()411(/)X H f G f f f ==+∆有色高斯的功率谱密度为()44/43/4/43/41()1(/)()()()()j j X j j f f f f f e f f e f f e f G f f e ππππ--∆==+∆-∆-∆-∆-∆,前两个极点与()H f 有关,后两个极点与()H f *有关,故滤波器的传递函数为()2/43/4()()()j j H f f f f e f f e ππ∆=-∆-∆ 做傅立叶反变换得系统的冲激响应为()0002cos t t e h t ωωω-=-式中02f ωπ=∆,输入为白噪声()W t ,则输出为有色高斯过程()()(t)X h W t t =*对()0002cos t t e h t ωωω-=-进行采样离散,采样频率为410s f Hz =,得离散序列()0/002cos /s n f s n n h e f ωωω-=-则()000-2cos snf nn sn H z ez f ωωω∞--=∞=-∑,这将涉及到IIR 滤波器的设计,过程比较繁琐,考虑到()(),c s A t A t 信号的一致性,这里仍然采取频域法2. 将()(),c s A t A t 调制后合成()X t根据题意()00()cos2()sin 2c s X A t f t t A t f t ππ=-,其中01000/f π= 故由仿真可得结果程序如下:%窄带随机过程的产生 clc;clear;%设置参数fc=1000/pi; %信号的载波频率 dt=1e-5; %采样间隔 Td=5e-3; %信号时长 df=1e3; %3dB 带宽B = 6*df;fo=1/Td; %中心频率点M=floor(B*Td); %傅里叶级数系数长度 m=[-M:M];I=sqrt(-1); %虚数i%% 频域法的功率谱密度图 Ac(t) x= 0:0.01:10 ;psd=1./(1+x.^4); %功率谱密度的函数表达式power=2*df*sum(psd)*0.01; %功率绝对大小 ∑-B~B Gx() s=1./(1+((m*fo)/df).^4); %以fo 为单位,s 即为各个离散点处功率谱密度函数的值 beta=power/sum(s); %系数βs=beta*s; %s=∑Gx(kfo),而所需的 ,故beta*s 即为所要的功率谱密度%原功率谱密度函数图 -8000Hz - 8000Hz f=[-8:0.01:8]*df;psd0=1./(1+(f/df).^4);%作图显示subplot 211;stem(m*fo,s/fo,'b'); %点线图,横轴为频率,以fo为单位值,纵轴为功率谱相对值hold on;plot(f,psd0,'r'); %连续的功率谱密度axis([-8*df 8*df 0 1.2]);xlabel('frequency (Hz)');ylabel('PSD');title('\fontsize{18}\sl频域法离散采样后的功率谱密度与原功率谱密度');legend('频域法的功率谱密度','原功率谱密度');%生成时域信号对应的傅立叶变换z0=randn(1); z0=z0*sqrt(s(M+1));zplus=sqrt(s(M+2:2*M+1)/2).*(randn(1,M)+I*randn(1,M));zminus=conj(fliplr(zplus));z=[zminus z0 zplus];%做反傅立叶变换,求出时域信号,即窄带随机过程频域法高斯有色信号X(t) Ac(t)t = 0:dt:Td; %时长5msAc=zeros(1,length(t));for m=-M:MAc=Ac+z(m+M+1)*exp(I*2*pi*m*fo*t);end;hold on;subplot 212;plot(t*1000,real(Ac),'b');xlabel('t (msec)');ylabel('Ac(t)');title('\fontsize{18}\sl频域法产生的Ac(t)');%% 时域滤波法的功率谱密度图As(t)T = 0.005; % 时域长度5msfs = 1e5; % 采样频率10kHzn = round(T*fs)+1; %采样点数t = linspace(0,T,n);W = randn(1,n); % 高斯白噪声% plot(W);w0 = sqrt(2)*pi*df;h = -2 * w0 * exp( -w0*t ) .* cos( w0*t );Y = conv(W,h);As = T*Y(1:n);%生成时域信号对应的傅立叶变换z0=randn(1); z0=z0*sqrt(s(M+1));zplus=sqrt(s(M+2:2*M+1)/2).*(randn(1,M)+I*randn(1,M));zminus=conj(fliplr(zplus));z=[zminus z0 zplus];%做反傅立叶变换,求出时域信号,即窄带随机过程频域法高斯有色信号X(t) Ac(t)t = 0:dt:Td; %时长5msAs=zeros(1,length(t));for m=-M:MAs=As+z(m+M+1)*exp(I*2*pi*m*fo*t);end;figuresubplot 211plot(t,As)xlabel('t (msec)');ylabel('As(t)');title('\fontsize{18}\sl时域滤波法产生的As(t)');%% Ac(t) As(t) 调制合成%合成信号X(t)t=0:dt:Td;X = Ac.*cos(2*pi*fc*t*1000) - As .*sin(2*pi*fc*t*1000 );figure;subplot 211;plot(t*1000,real(X),'b');xlabel('t (msec)');ylabel('X(t)');title('\fontsize{18}\sl 合成信号X(t)'); %定义图名。
