语音信号盲分离—ICA算法
基于负熵最大的FastICA语音信号分离算法

实现信号盲分离功能。并将其成功应用于运用信号分选过程中,最终复原语音时域波形,完成信号分选任务。仿真实
验中,详细讨论了该方法在不同信噪比以及不同源信号数目情况下的分选能力,证明了方法的有效性和优越性。
关键词:负熵,语音信号,数目估计,盲分离,循环相关
中图分类号:TN91
文献标识码:A
DOI:10.3969/j.issn.1002-0640.2017.08.023
·101·
(总第 42-1402)源自火力与指挥控制2017 年 第 8 期
混合模型,提出了一种基于时频分析的盲信号分离 算法,并通过仿真实验验证了该算法的优越性;文 献[5]中,Mukai R提出了一种基于移动语音的实时 分离算法,提高了分离算法的实时性,放宽了算法 的应用范围;文献[6]中,Fevotte C 等人提出了一种 基于对角化的语音分离算法;还有一些研究机构致 力于语音信号盲分离算法的硬件实现[7],在此不再 赘述。
收稿日期:2016-06-17
修回日期:2016-09-15
* 基金项目:陕西省 2017 年军民融合研究基金(17JMR26);渭南市科研发展计划项目(2015KYJ-2-6);渭南师范学院理工类科
研基金资助项目(16YKS010)
作者简介:同晓荣(1972- ),男,陕西白水人,副教授。研究方向:嵌入式系统、信号处理和计算机应用技术。
断涌现出新的成果,主要集中在语音信号模型的建 立与优化、分离算法的优化与改进两方面。文献[3] 中,Smith D 等人对语音信号的模型构建进行了分 析,提出 了稀疏分解(Sparse Decomposition,SD)模 型 , 计 算 声 场 分 析 (Computational Auditory Scene Analysis,CASA) 模型以及自回归 - 基频(AR-F0) 模型;文献[4]中,王卫华等人针对语音信号的卷积
盲源信号分离的有理函数ica法

盲源信号分离的有理函数ICA法目录摘要 (I)Abstract (II)1 绪论 (1)1.1课题研究的背景及意义 (1)1.2国内外研究现状及发展趋势 (2)1.3论文的主要研究内容和结构安排 (5)2独立成分分析的基本理论及算法 (7)2.1独立成分分析的数学模型 (7)2.2 约束条件 (8)2.3 预处理 (9)2.4 独立成分分析的基本估计方法 (10)2.4.1 极大化非高斯性的估计方法 (10)2.4.2 极大似然估计方法 (13)2.4.3 极小化互信息估计方法 (13)2.4.4 优化算法 (14)3 有理函数ICA法 (16)3.1 Infomax算法 (16)3.2 扩展Infomax算法 (19)3.3 有理函数ICA法的理论基础 (21)3.4 有理函数ICA法 (24)3.5 FastICA算法 (25)3.5.1 应用有理函数的FsatICA算法 (27)4 数值实验 (28)4.1 算法的评价准则 (28)4.2 有理函数ICA法和扩展Infomax算法的比较 (29)4.3 应用有理函数的FastICA算法的实验 (36)结论 (38)参考文献 (40)攻读硕士学位期间发表学术论文情况 (44)致谢 (45)- IV - (46)1 绪论1.1 课题研究的背景及意义盲源信号分离指的是仅根据观测的混合信号,分离出各个原始的信号,其中最具有代表性的例子就是“鸡尾酒会”问题。
在鸡尾酒会上,有每个人的说话声,嘈杂的音乐声等,在不同的位置放置一些麦克风来记录这些声音,那么每个麦克风记录的声音就是不同的声音的混合(图1.1)。
在事先不知道声音来源和麦克风具体位置的情况下,仅仅根据麦克风收到的混合声音分离出需要的声音就是一种盲源信号分离问题。
图1.1 鸡尾酒会示意图Fig. 1.1 Cocktail party这里的“盲”既表示未知源信号又表示源信号的混合方式是不确定且未知。
基于负熵最大的FastICA语音信号分离算法

基于负熵最大的FastICA语音信号分离算法同晓荣【摘要】语音信号分离是现代信号处理的热点问题,针对未知信号源个数的情况,提出一种基于负熵最大的FastICA(Fast Independent Component Algorithm)语音信号盲分离算法,有效解决了源信号数目估计、语音信号分离及复原等问题.改进的算法增加了源信号数目估计环节,放宽了算法适用条件,即在源信号数目未知的情况下,也能够实现信号盲分离功能.并将其成功应用于运用信号分选过程中,最终复原语音时域波形,完成信号分选任务.仿真实验中,详细讨论了该方法在不同信噪比以及不同源信号数目情况下的分选能力,证明了方法的有效性和优越性.%Speech signal separation is a hot topic in modern signal processing problems,aiming at the condition of the number of unknown source,a kind of separation algorithm based on negative entropy maximum fast independent component the correlation algorithm is proposed in this paper,this algorithm can effectively solve the problem of unknown-number of source signals. The improved algorithm increases a link of number estimation of speech signal,and it relaxed algorithm applicable conditions,namely,in the case of a number of unknown source signals,also can realize blind signal separation function. The proposed method has successful applied in the process of the use of signal sorting,the time domain waveform signal sorting task. This algorithm is discussed in detail in different SNR and number of cases of different source signal separation ability,to prove the validity of the method and superiority in simulation experiments.【期刊名称】《火力与指挥控制》【年(卷),期】2017(042)008【总页数】5页(P101-104,110)【关键词】负熵;语音信号;数目估计;盲分离;循环相关【作者】同晓荣【作者单位】渭南师范学院网络安全与信息化学院,陕西渭南 714099【正文语种】中文【中图分类】TN91语音信号盲分离最早起源于“鸡尾酒会”问题[1],其实质为“多通道盲解卷积”,即从麦克风阵列观测的卷积混合信号中分离出具有价值的源语音信号[2]。
PCA与ICA相结合的语音信号盲分离

C m u r n i ei d p lai s o p t gn r g n A pi t n 计算机工程与应用 eE e na c o
@数 据 库 、 号 与信 息处 理@ 信
P A与 I A相结合的语音信号盲 分离 C C
王玉静 , 于凤 芹
WA NGY j g Y e g i ui , UFn q n n
lrt o f ce t t x a h e aain e e t tn ad t es lt n e p r n eut h w a ep o o e ai c e in r stesp rt f c a d r ,h i ai x e me t s l s o t t h r p s d y i mai o s mu o i r s h t
盲源分离(ICA)

Infomax 法的判据:在给定合适的 gi(Yi)后,使输出 r = [r1,r2,…,
rM]的总熵量H(r)极大。
和互信息极小化准则等价
gi 可采用某些单调增长函数 (如: sigmoid 函数、tanh(• )等) , 只是信源的pdf 需要一律是超高斯型,或一律是亚高斯型。
三、分离算法
源信号的各分量具有单位方差。
三、分离算法
(一)目标函数 采用基于独立性测度的分离准则。
非高斯最大化准则
互信息极小化准则
信息极大化 极大似然准则
三、分离算法
(1)非高斯最大化准则 根据大数定理,多个相互独立的随机变量之和趋向于高斯分布。因此, 分离信号的非高斯性可以作为衡量是否成功分离的准则。常用的非高
为亚高斯分布。
三、分离算法
负熵:信息论中的“熵” 是随机变量的随机性越大,熵就越大,高斯 变量是所有等方差的随机变量中熵最大的。负熵是任意随机变量与高 斯随机变量之间的相对熵,定义如下:
J[p(y)]值越大表示它距离高斯分布越远,可用来作为非高斯性的度量。
三、分离算法
(2)互信息极小化准则(Minimization of Mutual Information, MMI) 当 y中各分量统计独立时,互信息 I ( y ) =0,互信息定义如下:
基于负熵的, 提取多个源信号的固定点算法步骤如下:
四、仿真结果
四、仿真结果
源信号只含一个随机噪声分离后得到的波形图
源信号含两个随机噪声分离后得到的波形图
在同一个ICA系统中,信号的非高斯性 越强,分离出来的信号越接近源信号, 分离效果越好;反之,分离效果越差。
次序不确定性
五、问题
基于Fast-ICA的盲信号分离的研究与实现

基于Fast-ICA的盲信号分离的研究与实现作者:徐丽琴来源:《科技视界》 2014年第30期徐丽琴(西安邮电大学电子工程学院,陕西西安 710121)【摘要】本文介绍一种典型的ICA算法——Fast-ICA算法的基本原理及其在瞬时混合语音信号盲分离中的应用与实现,通过对三路随机混合语音信号进行的分离实验,说明了Fast-ICA算法可以用于分离超高斯语音信号,且具有较快的收敛速度,证明了其在瞬时混合盲语音信号分离中的现实有效性。
【关键词】盲源分离;独立分量分析;Fast-ICA0 引言盲源分离是指在源信号和传输信道参数均未知的情况下,根据源信号的统计特性,仅由观测信号来恢复或分离出源信号。
这里“盲”有两重含义:第一,信号源是未知的;第二,传输信道也是未知的。
盲源分离是当前信号处理领域的一个研究热点,在语音信号处理、数字图像处理、生物医学信号处理等领域有着非常广阔和诱人的应用前景。
独立成分分析[1],即ICA,是一种应用很广泛的技术,其目的是寻找一个变换矩阵,使得变换后的各输出分量之间尽可能相互统计独立,是目前实现盲源分离的一种最主要的方法。
1 ICA数学模型假设N个统计独立的源信号经过线性瞬时混合被M个传感器接收,则每个观测信号是这N 个信号的一个线性组合。
下面的方程对于线性时不变瞬时混合函数成立:3 Fast-ICA算法Fast—ICA算法是Hyvarinen从熵最优化方法推导出一种算法[2],其思路是通过随机梯度法调节分离矩阵W来达到优化目的,在该算法的每次迭代中,采样数据是成批使用的,算法是并行分布的,且计算简单,需要的内存少,速度很快,又称为定点法算法。
对于单个信号的提取,Fast—ICA算法的代价函数定义为:需要注意的是,在每次迭代完后都要对分离矩阵进行归一化处理,这样做的目的是为了增强算法的稳定性。
对于多个独立分量的分离,可以重复上述过程一个一个提取独立分离,每提出一个分量后要从混合信号中减去这一独立分量,如此重复,直至所有的独立分量全部分离出来为止。
基于稀疏编码和ICA的带噪混叠语音盲分离
( I 1 2 利 用 最 大 似 然 估 计 法 ( ai m L eho 一 ) , M x u i lod m ki
Et ao , L ) sm t n M E 可由带噪信号 y得到 i i
*国家 自然科 学肇金 资助项 目(07 15 ; 6520 ) 高等学校博士学科点专项科研 基金资助项 目( o200 207 N .0542 1 ) 收稿 日期 :08—1 20 0—0 8
16 3
第 4期
杜
军 :基 于稀疏 编码和 IA的带 噪混 叠语音盲分离 C
第 2 卷 3
( 是列矢 量) W 为该神经元 网络权值矩 阵 , 网络 中只有少 数的一些 神经元权 值起主 要作用 . s s, … . ] 在该 设 =[ , 为该
一
些神经元权值起主要的作用… . 后来 H v i n对稀疏编码 的应用从 整体上进行 了系统 的分析 . y ̄n e 稀疏编码 的关
键 问题就是要找到一 个神经元 网络矩阵 , 一 使信号经 过该矩 阵转换后得 到 的分量 具有稀 疏分布 . 疏编码 作为一 』稀 种稀疏神经元 网络表征方法可 以有效的用于去除 噪声 . 这种稀 疏表 征可 以借 助于 IA特 征提取来 得到 , C 实际也
=
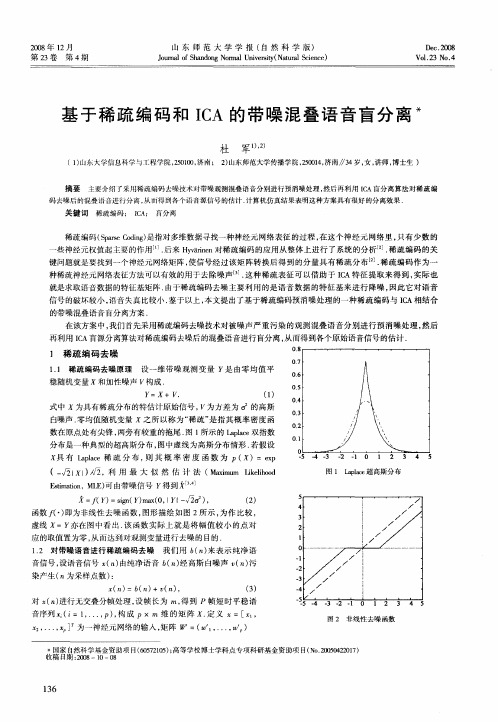
图 1 Lpae al 超高斯分布 c
厂 Y =s n r m x0 f 一 2 ) ( ) i ( ) a( , yf √ , g
() 2
/
/
函数 厂 ・即为非线性去 噪 函数 , () 图形描 绘如 图 2 示 , 所 为作 比较 ,
虚线 X=Y亦在图 中看 出 . 函数 实 际上 就是 将幅值 较小 的点对 该
ica算法分离信号的代码中文解释

ICA算法是一种用于分离混合信号的计算机算法。
它是一种盲源分离方法,可以在不知道混合信号的确切成分的情况下,将混合信号解耦为原始信号。
ICA算法在信号处理、机器学习、神经科学和医学图像处理等领域有着广泛的应用。
在介绍ICA算法的代码实现之前,让我们先来理解一下ICA算法是如何工作的。
ICA算法的核心思想是找到一个转换矩阵,使得混合信号经过这个转换后能够被分离成相互独立的原始信号。
ICA算法的目标是找到一个矩阵,使得原始信号经过这个矩阵的线性变换后,各个维度上的信号能够相互独立。
这个转换矩阵可以通过最大化信号的非高斯性来进行估计,从而实现信号的盲分离。
现在让我们来看一下ICA算法的代码实现。
以下是一个简单的Python代码示例,用于演示如何使用sklearn库中的FastICA模块来实现ICA算法的信号分离。
# 导入所需的库import numpy as npfrom sklearn.decomposition import FastICAimport soundfile as sf# 读取混合信号数据data, sr = sf.read('mixed_signal.wav')# 初始化FastICA模型ica = FastICA(n_components=3)# 对混合信号进行ICA分离S_ = ica.fit_transform(data)# 计算混合矩阵A_ = ica.mixing_# 保存分离后的信号for i in range(3):sf.write('separated_signal_{}.wav'.format(i), S_[:, i], sr)在这段代码中,首先我们使用soundfile库来读取混合信号的数据。
我们初始化FastICA模型,并通过fit_transform方法对混合信号进行分离,得到分离后的信号数据。
我们将分离后的信号保存为.wav文件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究现状简介
线性瞬时混合信号
较早进行盲源分离方法研究的是jutten和Herault,1986年,他们提出了一种盲源分 离方法,该方法基于反馈神经网络,通过选取奇次的非线性函数构成Hebb训练,从 而达到盲源分离的目的。但该方法不能完成多于两个源信号的分离,非线性函数的 选取具有随意性,并且缺乏理论解释。 1991年,Juttcn, Herault以及Comon和Sorouchyari在杂志Signal Processing上发表了 关于盲信号分离的三篇经典文章,标志着盲源分离问题研究的重大进展.他们不仅提 出了盲源分离中著名的H-J学习算法,而且设计了专门的CMOS集成芯片来实现他们 的算法。H-J方法后来由Jutten和Herault、Comon, Cichocki和Moszczynski以及其他研 究者解释并发展。Tong和liu分析了盲源分离的可分离性和不确定,并给出了一类基 于高阶统计量的矩阵代数分方法。 1993年,Cardoso提出了基于高阶统计的联合对角化盲源分离方法,并应用于波 束形成。
(2)如果源信号具有时序结构,则其有非零的时序相关数,从而可以降低对统计 独立性的限制条件,用二阶统计量方法(SOS)就足以估计混合矩阵和源信号。这种 (SOS)方法不允许分离功率谱形状相同或i.id(独立同分布)的源信号。 (3)第三种方法即采用非平稳性(Ns)和二阶统计量(SOS)。由于源信号主要随时间 有不同的变化,就可以考虑利用二阶非平稳性。Matsuoka等人首先考虑了非平稳性, 并证‘明在盲源分离中可以应用简单的解相关技术。与其他方法相比,基于非平稳 性信息的方法能够分离具有相同功率谱形状的有色高斯源,然而,却不能够分离具 有相同非平稳特性的源信号。
研究现状简介
1995年,Bell和Sejnowsk基于信息理论,通过最大化输出非线性节点的熵,得出 一种最大信息(Informatian Maximization,简记Infomax)传输的准则函数,并由此导出 一种自适应盲源分离和盲反卷积方法,当该方法中非线性函数的选取逼近源信号的 概率分布时,可以较好地恢复出源信号。该算法虽有其局限性,但在分离线性混合 的语音信号方面非常有效。 1997年,Hyvarinen等基于源信号非高斯性测度,给出一类定点训练算法(fixedpoint),该类算法可以提取单个具有正或负峰度的源信号。 1999年,Lee、 Girolami和Sejnowski将信息最大化原则的独立分量分析作了进一 步的扩展,实现了超高斯源信号和亚高斯源信号的盲源分离,这个方法选取两个不 同的非线性函数分别实现超高斯信号和亚高斯信号的盲源分离。但是这个方法只局 限于实现标准的独立分量分析,不能解决当源信号维数大于混合信号维数时的盲源 分离向题,也不能实现具有噪音的独立分量分析。
语音信号盲分离 —ICA算法
主要内容
背景介绍 研究现状介绍 盲分离的概念、方法和准则
ICA算法 语音信号盲分离实例
Fast
背景介绍
语音信号的分离近年来成为信号处理领域的一个研究热点,它在电话会议、助 听器及便携设备、机器的语音识别方面有很多的应用与影响。而盲信号处理的方法 常被用于语音分离中去,“盲”是指没有关于源信号本身以及传输信道的知识,盲 分离的理论基础是独立分量分析(ICA),其可以广泛的被应用于通信、图像、语音、 生物医学、雷达、地震、声纳等多种类型信号的处理。盲分离技术可以用于消除不 需要的干扰以增加语音质量。 语音分离使得助听器有更强大的处理功能,使得接收信号分离出尽可能接近原 始的语音。更适合于语音编码和基音检测。特别是在混合语音信号进行编码方面, 传统的单通道方法处理起来十分困难,而混合语音可以看作多路语音信号的线性组 合,其每一路语音信号都可视为独立分量,这正好与ICA的假设相符。语音识别。机 器的语音识别能力远不及人类,尤其是在有噪音和干扰的背景下。 这时作为语音识 别的前端处理,盲语音分离可以很好的去除干扰,不论是加性噪声还是其他不感兴 趣的语音,这就大大增强了机器的识别率。
盲分离的概念、方法和准则
盲源分离的基本方法
(4)第四种方法运用了信号的不同多样性,典型的是时域多样性、频域多样性(谱 或时间相干性”)或者时频域多样性,更一般的,即联合空间一时间一频率(STF)多样 性。
BSS和ICA的区别与关系
自从 BSS 和 ICA 的概念产生以来,人们几乎是不加区分地使用这两个概念。但 是,如果深入研究 BSS 和ICA 的基本原理和作用对象,两者之间的区别和联系是显 而易见的。 Comon 对 ICA 给出了较严格的定义:对于观测信号矢量,存在一个线性变换, 使得观测信号在线性变换下各分量的统计独立性最大化。这一过程称之为 ICA 过程。
盲源分离的目的就是在源信号s和混合系统A均未知的情况下,仅由观测数据向量x通 过调整分离系统W,使得输出y是源信号s的估计,即:
y W x s
盲分离的概念、方法和准则
盲源分离的基本方法
盲源分离包含了线性瞬时混合和卷积混合两种盲源分离问题。解决盲源分离问题 的重要方法一独立分量分析(Independent Component Analysis,ICA)通常以线性瞬时混 合为模型,而盲解卷积则是一种更为实际的盲源分离问题,其混合模型是一种卷积混 合,线性卷积混合模型比较接近实际,这是因为: (1)实际中每一个源信号不会同时到达所有的传感器,每一个传感器对不同的源延 时不同,延时值的大小取决于传感器与源信号间的相对位置以及信号的传播速度; (2)源信号到达传感器是经过多途传播的,即多径效应。假设信号是线性组合的, 则从传感器观测到的信号是源信号各种延时值的线性组合。解决此类问题的盲信号处 理方法就是盲解卷积。特别地,ICA方法也可被用于盲解卷积或盲均衡。此外,盲信 号处理还包括许多重要内容,例如非线性BSS或非线性ICA问题、盲多用户检测以及 盲波束形成等等。
1994年,Krob和Benidir研究了利用高阶统计量解决多项式结构的非线性混合问题。 1995年,Deco和Brauer研究了一个基于Volume-Conserving结构的非线性变换的盲 源分离。 1997年,Yang、Amari和Cichocki基于对于源信号各分量统计独立的假设,利用 两层感知器网络结构得出基于最大熵( Minimum Entropy,简记ME)和最小互信息思 想(Minimum Mutual information,简记MMI )的代价函数,并提出了反向学习算法, 当合理选择非线性函数时该算法可以分离出一些特定非线性混合的源信号。
BSS考察的是在什么条件下可以使全局矩阵实现广义对角化,而不去衡量输出信 号的统计独立性是否达到最大化。因此BSS并不一定要求源信号是统计独立的。例如 AMUSE、GED算法只要求源信号具有统计不相关性。如果源信号是统计独立的,那 么BSS的输出信号也一定是统计独立的,这时BSS和ICA等价。 从作用对象看,ICA除了可以用于多源信号的分离外,还可以用于其它多维数据 的分析,例如图像的特征提取、经济数据分析等。而BSS不仅仅局限于瞬时混合信号 的分离,还包括实际应用中更重要的卷积混合信号的分离。 可以说ICA是实现BSS的一种方法,而BSS是ICA的一个具体的应用。
研究现状简介
1998年,Taleb、Jutten 和 Olympieff 提出了一种非线性混合信号盲源分 离算法,该算法基于熵,对于分离某些盲混合信号具有良好性能。
2001年,Valpola、Honkela 和 Karhunen提出了贝叶斯集合学习算法 (Bayesian Ensemble Learning Algorithm ),该算法采用多层感知器神经元网络 (MLP ),能够对非线性静态和动态过程实现盲源分离。Tan和Wang提出了基 于遗传算法( Genetic Algorithm)的盲源分离方法,该算法利用遗传算法使信 号非线性混合度最小化,然后对去除非线性后的数据进行线性分离,从而实 现盲源分离。与传统的梯度算法相比,基于遗传算法的盲源分离方法有着更 快的收敛速度和稳定性,能够在全局范围内寻找最优解。Tan、Wang和 Zurada提出了径向基网络算法(Radial Basis Function Network Algorithm),使 用径向基函数神经网络来逼近非线性混合的逆映射实现盲源分离。
盲分离的概念、方法和准则
盲分离的目标准则
根据源信号不同的特征,盲源分离的实现方法有很多,但它们的原理可以归纳 为以下四种准则:
(1)独立分量分析(Independent Component Analysis, ICA):当假设源信号各分量间 彼此统计独立,且没有时间结构时,在某一分离准则下通过对神经网络权值的反馈 调整,使得变换后信号的不同分量之间的相依性最小,也即输出达到尽可能的独立。 这种方法对多于一个高斯分布的源信号不适用(因为高斯信号的线性叠加仍是高斯信 号),这是近年来盲源分离的主要解决方法。
与此对应,可以给出BSS的如下定义:对于观测信号矢量,存在线性变换w,使 得全局矩阵G的各行及各列中只有一个非零元素(不妨称之为广义对角矩阵),即 G=PD。其中P为置换阵;D为对角阵,从而实现信号分离。
盲分离的概念、方法和准则
BSS和ICA的区别与联系
ICA的目的是通过线性变换使得观测信号的各个分量的统计独立性最大化。通常 用输出信号的互信息、熵等作为统计独立性的量度,如基于信息论的Informax 算法、 Amari 的自然梯度算法等。如果源信号之间具有统计独立性,那么可以通过ICA实现 信号的分离。
盲分离的概念、方法和准则
盲源分离的基本方法
尽管有许多不同的盲源分离算法可用,但它们的原理却都可以归纳为如图所示 的以下四个方法:
相互独立、 非高斯、 ICA
非稳态、 时变方差
时序结构、 线性可预测
时频、谱和 空间多样性
盲分离的概念、方法和准则
盲源分离的基本函数来衡量信号独立性和非高斯性或者稀疏性。 当假信号具有统计独立性,且没有时间结构时,高阶统计量方法是求解盲源分离问 题的基段(间接或直接的),这种方法对多于一个高斯分布的源信号不适用。
