北京市山谷学校数学几何图形初步(培优篇)(Word版 含解析)
七年级上册数学 几何图形初步(培优篇)(Word版 含解析)

一、初一数学几何模型部分解答题压轴题精选(难)1.已知,,点E是直线AC上一个动点(不与A,C重合),点F是BC边上一个定点,过点E作,交直线AB于点D,连接BE,过点F作,交直线AC于点G.(1)如图①,当点E在线段AC上时,求证:.(2)在(1)的条件下,判断这三个角的度数和是否为一个定值?如果是,求出这个值,如果不是,说明理由.(3)如图②,当点E在线段AC的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.(4)当点E在线段CA的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出之间的关系.【答案】(1)解:∵∴∵∴∴(2)解:这三个角的度数和为一个定值,是过点G作交BE于点H∴∵∴∴∴即(3)解:过点G作交BE于点H∴∵∴∴∴即故的关系仍成立(4)不成立| ∠EGF-∠DEC+∠BFG=180°【解析】【解答】解:(4)过点G作交BE于点H∴∠DEC=∠EGH∵∴∴∠HGF+∠BFG=180°∵∠HGF=∠EGF-∠EGH∴∠HGF=∠EGF-∠DEC∴∠EGF-∠DEC+∠BFG=180°∴(2)中的关系不成立,∠EGF、∠DEC、∠BFG之间关系为:∠EGF-∠DEC+∠BFG=180°故答案为:不成立,∠EGF-∠DEC+∠BFG=180°【分析】(1)根据两条直线平行,内错角相等,得出;两条直线平行,同位角相等,得出,即可证明.(2)过点G作交BE于点H,根据平行线性质定理,,,即可得到答案.(3)过点G作交BE于点H,得到,因为,所以,得到,即可求解.(4)过点G作交BE于点H,得∠DEC=∠EGH,因为,所以,推得∠HGF+∠BFG=180°,即可求解.2.(1)问题发现:如图 1,已知点 F,G 分别在直线 AB,CD 上,且 AB∥CD,若∠BFE=40°,∠CGE=130°,则∠GEF 的度数为________;(2)拓展探究:∠GEF,∠BFE,∠CGE 之间有怎样的数量关系?写出结论并给出证明;答:∠GEF=▲ .证明:过点 E 作 EH∥AB,∴∠FEH=∠BFE(▲),∵AB∥CD,EH∥AB,(辅助线的作法)∴EH∥CD(▲),∴∠HEG=180°-∠CGE(▲),∴∠FEG=∠HFG+∠FEH=▲ .(3)深入探究:如图 2,∠BFE 的平分线 FQ 所在直线与∠CGE 的平分线相交于点 P,试探究∠GPQ 与∠GEF 之间的数量关系,请直接写出你的结论.【答案】(1)90°(2)解:∠GEF=∠BFE+180°−∠CGE,证明:过点 E 作 EH∥AB,∴∠FEH=∠BFE(两直线平行,内错角相等),∵AB∥CD,EH∥AB,(辅助线的作法)∴EH∥CD(平行线的迁移性),∴∠HEG=180°-∠CGE(两直线平行,同旁内角互补),∴∠FEG=∠HFG+∠FEH=∠BFE+180°−∠CGE ,故答案为:∠BFE+180°−∠CGE;两直线平行,内错角相等;平行线的迁移性;两直线平行,同旁内角互补;∠BFE+180°−∠CGE;(3)解:∠GPQ+∠GEF=90°,理由是:如图2,∵FQ平分∠BFE,GP平分∠CGE,∴∠BFQ=∠BFE,∠CGP=∠CGE,在△PMF中,∠GPQ=∠GMF−∠PFM=∠CGP−∠BFQ,∴∠GPQ+∠GEF=∠CGE− ∠BFE+∠GEF= ×180°=90°.即∠GPQ+∠GEF=90°.【解析】【解答】(1)解:如图1,过E作EH∥AB,∵AB∥CD,∴AB∥CD∥EH,∴∠HEF=∠BFE=40°,∠HEG+∠CGE=180°,∵∠CGE=130°,∴∠HEG=50°,∴∠GEF=∠HEF+∠HEG=40°+50°=90°;故答案为:90°;【分析】(1)如图1,过E作EH∥AB,根据平行线的性质可得∠HEF=∠BFE=40 ,∠HEG=50 ,相加可得结论;(2)由①知:∠HEF=∠BFE,∠HEG+∠CGE=180°,则∠HEG=180°−∠CGE,两式相加可得∠GEF=∠BFE+180°−∠CGE;(3)如图2,根据角平分线的定义得:∠BFQ=∠BFE,∠CGP=∠CGE,由三角形的外角的性质得:∠GPQ=∠GMF−∠PFM=∠CGP−∠BFQ,计算∠GPQ+∠GEF并结合②的结论可得结果.3.问题情境1:如图1,AB∥CD,P是ABCD内部一点,P在BD的右侧,探究∠B,∠P,∠D之间的关系?小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠B,∠P,∠D之间满足____关系。
北京市山谷学校数学全等三角形(培优篇)(Word版 含解析)

北京市山谷学校数学全等三角形(培优篇)(Word 版 含解析)一、八年级数学轴对称三角形填空题(难)1.如图,在四边形ABCD 中,BC CD = ,对角线BD 平分ADC ∠,连接AC ,2ACB DBC ∠=∠,若4AB =,10BD =,则ABC S =_________________.【答案】10【解析】【分析】由等腰三角形的性质和角平分线的性质可推出AD ∥BC ,然后根据平行线的性质和已知条件可推出CA=CD ,可得CB=CA=CD ,过点C 作CE ⊥BD 于点E ,CF ⊥AB 于点F ,如图,根据等腰三角形的性质和已知条件可得DE 的长和BCF CDE ∠=∠,然后即可根据AAS 证明△BCF ≌△CDE ,可得CF=DE ,再根据三角形的面积公式计算即得结果.【详解】解:∵BC CD =,∴∠CBD =∠CDB ,∵BD 平分ADC ∠,∴∠ADB =∠CDB ,∴∠CBD =∠ADB ,∴AD ∥BC ,∴∠CAD =∠ACB ,∵2ACB DBC ∠=∠,2ADC BDC ∠=∠,∠CBD =∠CDB ,∴ACB ADC ∠=∠,∴CAD ADC ∠=∠,∴CA=CD ,∴CB=CA=CD ,过点C 作CE ⊥BD 于点E ,CF ⊥AB 于点F ,如图,则152DE BD ==,12BCF ACB ∠=∠, ∵12BDC ADC ∠=∠,ACB ADC ∠=∠,∴BCF CDE ∠=∠, 在△BCF 和△CDE 中,∵BCF CDE ∠=∠,∠BFC =∠CED =90°,CB=CD ,∴△BCF ≌△CDE (AAS ),∴CF=DE =5,∴11451022ABC S AB CF =⋅=⨯⨯=. 故答案为:10.【点睛】本题考查了等腰三角形的判定和性质、平行线的判定和性质、角平分线的定义以及全等三角形的判定和性质等知识,涉及的知识点多、综合性强、具有一定的难度,正确添加辅助线、熟练掌握上述知识是解题的关键.2.△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=6.现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF 运动过程中,若△AEM能构成等腰三角形,则BE的长为______.【答案】363【解析】【分析】分若AE=AM 则∠AME=∠AEM=45°;若AE=EM;若MA=ME 则∠MAE=∠AEM=45°三种情况讨论解答即可;【详解】解:①若AE=AM 则∠AME=∠AEM=45°∵∠C=45°∴∠AME=∠C又∵∠AME>∠C∴这种情况不成立;②若AE=EM∵∠B=∠AEM=45°∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°∴∠BAE=∠MEC在△ABE和△ECM中,B BAE CEN AE EIIC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△ECM (AAS ),∴CE =AB =6,∵AC =BC =2AB =23,∴BE =23﹣6;③若MA =ME 则∠MAE =∠AEM =45°∵∠BAC =90°,∴∠BAE =45°∴AE 平分∠BAC∵AB =AC ,∴BE =12BC =3. 故答案为23﹣6或3.【点睛】本题考查了等腰三角形的判定,掌握分类讨论的数学思想是解答本题的关键.3.如图,在01A BA △中,20B ∠=︒,01A B A B =,在1A B 上取点C ,延长01A A 到2A ,使得121A A AC =;在2A C 上取一点D ,延长12A A 到3A ,使得232A A A D =;…,按此做法进行下去,第n 个等腰三角形的底角n A ∠的度数为__________.【答案】11()802n -︒⋅.【解析】 【分析】 先根据等腰三角形的性质求出∠BA 1 A 0的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律即可得出第n 个等腰三角形的底角∠A n 的度数.【详解】解:∵在△A 0BA 1中,∠B=20°,A 0B=A 1B ,∴∠BA 1 A 0= 1801802022B ︒︒︒-∠-= =80°, ∵A 1A 2=A 1C ,∠BA 1 A 0是△A 1A 2C 的外角,∴∠CA 2A 1= 108022BA A ︒∠= =40°; 同理可得,∠DA 3A 2=20°,∠EA 4A 3=10°,∴第n 个等腰三角形的底角∠A n = 11()802n -︒⋅.【点睛】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA 2A 1,∠DA 3A 2及∠EA 4A 3的度数,找出规律是解答此题的关键.4.等腰三角形顶角为30°,腰长是4cm ,则三角形的面积为__________【答案】4【解析】如图,根据30°角所对直角边等于斜边的一半的性质,可由等腰三角形的顶角为30°,腰长是4cm ,可求得BD=12AB =4×12=2,因此此三角形的面积为:S=12AC•BD=12×4×2=8×12=4(cm 2).故答案是:4.5.如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于E ,交AC 于F ,过点O 作OD AC ⊥于D 下列结论:①EF BE CF =+;②点O 到ABC ∆各边的距离相等;③1902BOC A ∠=+∠;④设OD m =,AE AF n +=,则AEF S mn ∆=;⑤1()2AD AB AC BC =+-.其中正确的结论是.__________.【答案】①②③⑤【解析】【分析】由在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC =90°+12∠A 正确;由平行线的性质和角平分线的定义得出△BEO 和△CFO 是等腰三角形得出EF =BE +CF 故①正确;由角平分线的性质得出点O 到△ABC 各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD =m ,AE +AF =n ,则S △AEF =12mn ,故④错误,根据HL 证明△AMO ≌△ADO 得到AM =AD ,同理可证BM =BN ,CD =CN ,变形即可得到⑤正确.【详解】 ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =12∠ABC ,∠OCB =12∠ACB ,∠A +∠ABC +∠ACB =180°,∴∠OBC +∠OCB =90°﹣12∠A ,∴∠BOC =180°﹣(∠OBC +∠OCB )=90°+12∠A ;故③正确; ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴∠OBC =∠OBE ,∠OCB =∠OCF . ∵EF ∥BC ,∴∠OBC =∠EOB ,∠OCB =∠FOC ,∴∠EOB =∠OBE ,∠FOC =∠OCF ,∴BE =OE ,CF =OF ,∴EF =OE +OF =BE +CF ,故①正确;过点O 作OM ⊥AB 于M ,作ON ⊥BC 于N ,连接OA .∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴ON =OD =OM =m ,∴S △AEF =S △AOE +S △AOF =12AE •OM +12AF •OD =12OD •(AE +AF )=12mn ;故④错误; ∵在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O ,∴点O 到△ABC 各边的距离相等,故②正确;∵AO =AO ,MO =DO ,∴△AMO ≌△ADO (HL ),∴AM =AD ;同理可证:BM =BN ,CD =CN .∵AM +BM =AB ,AD +CD =AC ,BN +CN =BC ,∴AD =12(AB +AC ﹣BC )故⑤正确. 故答案为:①②③⑤.【点睛】本题考查了角平分线的定义与性质,等腰三角形的判定与性质.此题难度适中,解题的关键是注意数形结合思想的应用.6.如图,在Rt ABC △中,AC BC =,D 是线段AB 上一个动点,把ACD 沿直线CD 折叠,点A 落在同一平面内的A '处,当A D '平行于Rt ABC △的直角边时,ADC ∠的大小为________.【答案】112.5︒或67.5︒【解析】【分析】当A D '平行于Rt ABC △的直角边时,有两种情况,一是当A D BC '时,二是当A D AC '时,两种情况根据折叠的性质及等腰三角形的性质进行角度的计算即可.【详解】 如图1,当点D 在线段AB 上,且A DBC '时,45A DB B '∠=∠=︒, 45180ADC A DC '∴∠+∠-=︒︒,解得112.5A DC ADC '∠=∠=︒.图1如图2,当A D AC '时,45A DB A '∠=∠=︒,45180ADC A DC '∴∠+∠+=︒︒,解得67.5A DC ADC '∠=∠=︒.图2【点睛】本题考查了翻折变换的性质,等腰直角三角形的性质,掌握折叠的性质是解题关键.7.如图,在△ABC 中,AB=AC ,∠BAC=120°,D 为BC 上一点,DA ⊥AC ,AD=24 cm ,则BC 的长________cm .【答案】72【解析】【分析】按照等腰三角形的性质、角的和差以及含30°直角三角形的性质进行解答即可.【详解】解:∵AB=AC ,∠BAC=120°∴∠B=∠C=30°∵DA ⊥AC ,AD=24 cm∴DC=2AD=48cm ,∵∠BAC=120°,DA ⊥AC∴∠BAD=∠BAC-90°=30°∴∠B=∠BAD∴BD=AD=24cm∴BC=BD+DC=72cm故答案为72.【点睛】本题考查了腰三角形的性质、角的和差以及含30°直角三角形的性质,其中灵活运用含30°直角三角形的性质是解答本题的关键.8.如图,在△ABC 中,P ,Q 分别是BC ,AC 上的点,PR ⊥AB ,PS ⊥AC ,垂足分别是R ,S ,若AQ PQ =,PR PS =,那么下面四个结论:①AS AR =;②QP //AR ;③△BRP ≌△QSP ;④BRQS ,其中一定正确的是(填写编号)_____________.【答案】①,②【解析】【分析】连接AP ,根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS ,根据等腰三角形性质推出∠QAP=∠QPA ,推出∠QPA=∠BAP ,根据平行线判定推出QP ∥AB 即可;在Rt △BRP 和Rt △QSP 中,只有PR=PS .无法判断△BRP ≌△QSP 也无法证明BRQS .【详解】解:连接AP①∵PR ⊥AB ,PS ⊥AC ,PR=PS ,∴点P 在∠BAC 的平分线上,∠ARP=∠ASP=90°,∴∠SAP=∠RAP ,在Rt △ARP 和Rt △ASP 中,由勾股定理得:AR 2=AP 2-PR 2,AS 2=AP 2-PS 2,∵AP=AP ,PR=PS ,∴AR=AS ,∴①正确;②∵AQ=QP ,∴∠QAP=∠QPA ,∵∠QAP=∠BAP ,∴∠QPA=∠BAP ,∴QP ∥AR ,∴②正确;③在Rt △BRP 和Rt △QSP 中,只有PR=PS ,不满足三角形全等的条件,故③④错误;故答案为:①②.【点睛】本题主要考查了角平分线的性质与勾股定理的应用,熟练掌握根据垂直与相等得出点在角平分线上是解题的关键.9.已知如图,每个小正方形的边长都是1231,,, ....A A A 都在格点上,123345567,, ....A A A A A A A A A 都是斜边在x 轴上,且斜边长分别为2,4,6,.的等腰直角三角形.若123A A A △的三个顶点坐标为()()()1232,0,1,1,0,0A A A -,则依图中规律,则19A 的坐标为 ___________【答案】()8,0-【解析】【分析】根据相邻的两个三角形有一个公共点,列出与三角形的个数与顶点的个数的关系式,再求出A 19所在的三角形,并求出斜边长.然后根据第奇数个三角形,关于直线x=1对称,第偶数个三角形关于直线x=2对称,求出OA 19,写出坐标即可.【详解】解:设到第n 个三角形顶点的个数为y则y=2n+1,当2n+1=19时,n=9,∴A 19是第9个三角形的最后一个顶点,∵等腰直角三角形的斜边长分别为2,4,6....∴第9个等腰直角三角形的斜边长为2×9=18,由图可知,第奇数个三角形在x 轴下方,关于直线x=1对称,∴OA 19=9-1=8,∴19A 的坐标为()8,0-故答案是()8,0-【点睛】本题考查点的坐标变化规律,根据顶点个数与三角形的关系,判断出点A 19所在的三角形是解题关键10.在下列结论中:①有三个角是60︒的三角形是等边三角形;②有一个外角是120︒的等腰三角形是等边三角形;③有一个角是60︒,且是轴对称的三角形是等边三角形;④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形.其中正确的是__________.【答案】①②③④【解析】【分析】依据等边三角形的定义,含有一个600角的等腰三角形是等边三角形判断即可.【详解】有三个角是600的三角形是等边三角形,故①正确;外角是1200时,邻补角为600,即有一个内角是600的等腰三角形是等边三角形,故②正确;轴对称的三角形是等腰三角形,且含有一个600角,因此是等边三角形,故③正确;一腰上的高也是中线,故底边等于腰长,所以此三角形是等边三角形,故④正确.故此题正确的是①②③④.【点睛】此题考查等边三角形的判定方法,熟记方法才能熟练运用.二、八年级数学轴对称三角形选择题(难)11.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .2B .2C .32D .不能确定【答案】B【解析】已知,如图,P 为等边三角形内任意一点,PD 、PE 、PF 分别是点P 到边AB 、BC 、AC 的距离,连接AP 、BP 、CP ,过点A 作AH ⊥BC 于点H ,已知等边三角形的边长为3,可求得高线AH S △ABC =12BC •AH =12AB •PD+12BC•PE +12AC •PF ,所以12×3×AH =12×3×PD +12×3×PE +12×3×PF ,即可得PD +PE +PF =AH P 到三角形三边B.点睛:本题考查了等边三角形的性质,根据三角形的面积求点P 到三边的距离之和等于等边三角形的高是解题的关键,作出图形更形象直观.12.如图,ABC ,分别以AB 、AC 为边作等边三角形ABD 与等边三角形ACE ,连接BE 、CD ,BE 的延长线与CD 交于点F ,连接AF ,有以下四个结论:①BE CD =;②FA 平分EFC ∠;③FE FD =;④FE FC FA +=.其中一定正确的结论有()A .1B .2C .3D .4【答案】C【解析】【分析】 根据等边三角形的性质证出△BAE ≌△DAC ,可得BE =CD ,从而得出①正确;过A 作AM ⊥BF 于M ,过A 作AN ⊥DC 于N ,由△BAE ≌△DAC 得出∠BEA =∠ACD ,由等角的补角相等得出∠AEM =∠CAN ,由AAS 可证△AME ≌△ANC ,得到AM =AN ,由角平分线的判定定理得到FA 平分∠EFC ,从而得出②正确;在FA 上截取FG ,使FG =FE ,根据全等三角形的判定与性质得出△AGE ≌△CFE ,可得AG =CF ,即可求得AF =CF +EF ,从而得出④正确;根据CF +EF =AF ,CF +DF =CD ,得出CD ≠AF ,从而得出FE ≠FD ,即可得出③错误.【详解】∵△ABD 和△ACE 是等边三角形,∴∠BAD =∠EAC =60°,AE =AC =EC .∵∠BAE +∠DAE =60°,∠CAD +∠DAE =60°,∴∠BAE =∠DAC ,在△BAE 和△DAC 中,∵AB AD BAE DAC AE AC =⎧⎪∠=∠⎨⎪=⎩,∴△BAE ≌△DAC (SAS ),∴BE =CD ,①正确;过A作AM⊥BF于M,过A作AN⊥DC于N,如图1.∵△BAE≌△DAC,∴∠BEA=∠ACD,∴∠AEM=∠ACN.∵AM⊥BF,AN⊥DC,∴∠AME=∠ANC.在△AME和△ANC中,∵∠AEM=∠CAN,∠AME=∠ANC,AE=AC,∴△AME≌△ANC,∴AM=AN.∵AM⊥BF,AN⊥DC,AM=AN,FA平分∠EFC,②正确;在FA上截取FG,使FG=FE,如图2.∵∠BEA=∠ACD,∠BEA+∠AEF=180°,∴∠AEF+∠ACD=180°,∴∠EAC+∠EFC=180°.∵∠EAC=60°,∴∠EFC=120°.∵FA平分∠EFC,∴∠EFA=∠CFA=60°.∵EF=FG,∠EFA=60°,∴△EFG是等边三角形,∴EF=EG.∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,∴∠AEG=∠CEF,在△AGE和△CFE中,∵AE ACAEG CEFEG EF=⎧⎪∠=∠⎨⎪=⎩,∴△AGE≌△CFE(SAS),∴AG=CF.∵AF=AG+FG,∴AF=CF+EF,④正确;∵CF+EF=AF,CF+DF=CD,CD≠AF,∴FE≠FD,③错误,∴正确的结论有3个.故选C.【点睛】本题考查了等边三角形的判定与性质以及全等三角形的判定与性质,正确作辅助线是解答本题的关键.13.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3 B.4 C.5 D.6【答案】B【解析】【分析】首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为32以及BC=12,可得DE=8,利用中位线定理可求出PQ.【详解】∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=12DE=4.故选:B.【点睛】本题考查了三角形的中位线定理和等腰三角形的性质和判定,解答本题的关键是判断出△BAE 、△CAD 是等腰三角形,利用等腰三角形的性质确定PQ 是△ADE 的中位线.14.如图,在ABC ∆中,120BAC ︒∠=,点,E F 分别是ABC ∆的边AB 、AC 的中点,边BC 分别与DE 、DF 相交于点,H G ,且,DE AB DF AC ⊥⊥,连接AD 、AG 、AH ,现在下列四个结论:①60EDF ︒∠=,②AD 平分GAH ∠,③B ADF ∠=∠,④GD GH =.则其中正确的结论有( ).A .1个B .2个C .3个D .4个【答案】A【解析】【分析】利用,DE AB DF AC ⊥⊥及四边形的内角和即可得到①正确;;根据三角形内角和与线段的垂直平分线性质得到∠BAH+∠GAC=60︒,无条件证明∠GAD=∠HAD,故②错误;由等量代换得B ADF ∠≠∠,故③错误;利用三角形的内角和与对顶角相等得到GD GH ≠,故④错误.【详解】∵,DE AB DF AC ⊥⊥,∴∠DEA=∠DFA=90︒,∵120BAC ︒∠=,∴∠EDF=360︒-∠DEA-∠DFA-∠BAC=60︒,故①正确;∵120BAC ︒∠=,∴∠B+∠C=60︒,∵点,E F 分别是ABC ∆的边AB 、AC 的中点,,DE AB DF AC ⊥⊥, ∴BH=AH ,AG=CG ,∴∠BAH=∠B ,∠GAC=∠C ,∴∠BAH+∠GAC=60︒,∵无条件证明∠GAD=∠HAD,∴AD 不一定平分GAH ∠,故②错误;∵∠ADF+∠DAF=90︒,∠B=∠BAH,90BAH DAF ∠+∠≠,∴B ADF ∠≠∠,故③错误;∵90B BHE ∠+∠=,30B ∠≠ ,∴ 60BHE ∠≠,∴60DHG ∠≠,∴DHG HDG ∠≠∠,∴GD GH ≠,故④错误,故选:A.【点睛】此题考查线段的垂直平分线的性质,利用三角形的内角和,四边形的内角和求角度,利用对顶角相等,等角对等边推导边的关系.15.如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE 、BD 相交于点 O ,AE 、BD 分别交 CD 、CE 于 M 、N ,连接 MN 、OC ,则下列所给的结论中:①AE =BD ;②CM =CN ;③MN ∥AB ;④∠AOB =120º;⑤OC 平分∠AOB .其中结论正确的个数是( )A .2B .3C .4D .5【答案】D【解析】【分析】 由题意易证:△ACE ≅△DCB ,进而可得AE =BD ;由△ACE ≅△DCB ,可得∠CAE=∠CDB ,从而△ACM ≅△DCN ,可得:CM =CN ;易证△MCN 是等边三角形,可得∠MNC=∠BCE , 即MN ∥AB ;由∠CAE=∠CDB ,∠AMC=∠DMO ,得∠ACM=∠DOM=60°,即∠AOB =120º;作CG ⊥AE ,CH ⊥BD ,易证CG =CH ,即:OC 平分∠AOB .【详解】∵△ACD 和△BCE 都是等边三角形,∴AC=DC ,CE=CB ,∠ACE=∠DCB=120°,∴△ACE ≅△DCB(SAS)∴AE =BD ,∴①正确;∵△ACE ≅△DCB ,∴∠CAE=∠CDB ,∵△ACD 和△BCE 都是等边三角形,∴∠ACD=∠BCE=∠DCE=60°,AC=DC ,在△ACM 和△DCN 中,∵60CAE CDB AC DCACD DCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△ACM ≅△DCN (ASA ),∴CM =CN ,∴②正确;∵CM =CN ,∠DCE=60°,∴△MCN 是等边三角形,∴∠MNC=60°,∴∠MNC=∠BCE ,∴MN ∥AB ,∴③正确;∵△ACE ≅△DCB ,∴∠CAE=∠CDB ,∵∠AMC=∠DMO ,∴180°-∠CAE-∠AMC=180°-∠CDB-∠DMO ,即:∠ACM=∠DOM=60°,∴∠AOB =120º,∴④正确;作CG ⊥AE ,CH ⊥BD ,垂足分别为点G ,点H ,如图,在△ACG 和△DCH 中,∵90?AMC DHC CAE CDB AC DC ∠=∠=⎧⎪∠=∠⎨⎪=⎩∴△ACG ≅△DCH (AAS ),∴CG =CH ,∴OC 平分∠AOB ,∴⑤正确.故选D.【点睛】本题主要考查全等三角形的判定定理和性质定理,等边三角形的性质定理以及角平分线性质定理的逆定理,添加合适的辅助线,是解题的关键.16.如图,△ABC、△CDE都是等腰三角形,且CA=CB, CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确的是()A.①②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】①根据全等三角形的判定定理得到△ACD≌△BCE(SAS),由全等三角形的性质得到AD=BE;故①正确;②设CD与BE交于F,根据全等三角形的性质得到∠ADC=∠BEC,得到∠DOE=∠DCE=α,根据平角的定义得到∠BOD=180°-∠DOE=180°-α,故②正确;③根据全等三角形的性质得到∠CAD=∠CBE,AD=BE,AC=BC根据线段的中点的定义得到AM=BN,根据全等三角形的性质得到CM=CN,∠ACM=∠BCN,得到∠MCN=α,推出△MNC不一定是等边三角形,故③不符合题意;④过C作CG⊥BE于G,CH⊥AD于H,根据全等三角形的性质得到CH=CG,根据角平分线的判定定理即可得到OC平分∠AOE,故④正确.【详解】解:①∵CA=CB,CD=CE,∠ACB=∠DCE=α,∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,在△ACD和△BCE中AC BCACD BCECD CE⎪∠⎪⎩∠⎧⎨===∴△ACD≌△BCE(SAS),∴AD=BE;故①正确;②设CD与BE交于F,∵△ACD≌△BCE,∴∠ADC=∠BEC,∵∠CFE=∠DFO,∴∠DOE=∠DCE=α,∴∠BOD=180°-∠DOE=180°-α,故②正确;③∵△ACD≌△BCE,∴∠CAD=∠CBE,AD=BE,AC=BC又∵点M、N分别是线段AD、BE的中点,∴AM=12AD,BN=12BE,∴AM=BN,在△ACM和△BCN中AC BCCAM CBNAM BN⎪∠⎪⎩∠⎧⎨===∴△ACM≌△BCN(SAS),∴CM=CN,∠ACM=∠BCN,又∠ACB=α,∴∠ACM+∠MCB=α,∴∠BCN+∠MCB=α,∴∠MCN=α,∴△MNC不一定是等边三角形,故③不符合题意;④过C作CG⊥BE于G,CH⊥AD于H,∴∠CHD=∠ECG=90°,∵∠CEG=∠CDH,CE=CD,∴△CGE≌△CHD(AAS),∴CH=CG,∴OC平分∠AOE,故④正确,故选:B.【点睛】本题综合考查了全等三角形的性质和判定,三角形的内角和定理,等边三角形的性质和判定等知识点的应用,解此题的关键是根据性质进行推理,此题综合性比较强,有一定的代表性.17.在平面直角坐标系中,等腰△ABC的顶点A、B的坐标分别为(1,0)、(2,3),若顶点C 落在坐标轴上,则符合条件的点C有( )个.A.9 B.7 C.8 D.6【答案】C【解析】【分析】要使△ABC 是等腰三角形,可分三种情况(①若CA =CB ,②若BC =BA ,③若AC =AB )讨论,通过画图就可解决问题.【详解】①若CA =CB ,则点C 在AB 的垂直平分线上.∵A (1,0),B (2,3),∴AB 的垂直平分线与坐标轴有2个交点C 1,C 2.②若BC =BA ,则以点B 为圆心,BA 为半径画圆,与坐标轴有3个交点(A 点除外)C 3,C 4,C 5;③若AC =AB ,则以点A 为圆心,AB 为半径画圆,与坐标轴有4个交点C 6,C 7,C 8,C 9.而C 8(0,-3)与A 、B 在同一直线上,不能构成三角形,故此时满足条件的点有3个.综上所述:符合条件的点C 的个数有8个.故选C .【点睛】本题考查了等腰三角形的判定、垂直平分线的性质的逆定理等知识,还考查了动手操作的能力,运用分类讨论的思想是解答本题的关键.18.已知:如图,ABC ∆、CDE ∆都是等腰三角形,且CA CB =,CD CE =,ACB DCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=-;③CMN ∆是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是( )A .①②③B .①②④C .①③④D .①②③④【答案】B【解析】【分析】 ①根据∠ACB=∠D CE 求出∠ACD=∠BCE,证出ACD BCE ≅△△即可得出结论,故可判断; ②根据全等求出∠CAD=∠CBE,根据三角形外角定理得∠DOB=∠OBA+∠BAO,通过等角代换能够得到∠DOB=∠CBA+∠BAC,根据三角形内角和定理即可求出∠CBA+∠BAC,即可求出∠DOB ,故可判断;③根据已知条件可求出AM=BN,根据SAS 可求出CAM CBN ≅,推出CM=CN ,∠ACM=∠BCN,然后可求出∠MCN=∠ACB=α,故可判断CMN ∆的形状;④在AD 上取一点P 使得DP=EO,连接CP ,根据ACD BCE ≅△△,可求出∠CEO=∠CDP ,根据SAS 可求出 CEO CDP ≅,可得∠COE=∠CPD,CP=CO,进而得到 ∠COP=∠COE ,故可判断.【详解】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,又∵CA=CB,CD=CE ,∴ACD BCE ≅△△(SAS),∴AD=BE,故①正确;②正确,理由如下:由①知,ACD BCE ≅△△,∴∠CAD=∠CBE,∵∠DOB 为ABO 的外角,∴∠DOB=∠OBA+∠BAO=∠EBC+∠CBA+∠BAO=∠DAC+∠BAO+∠CBA=∠CBA+∠BAC, ∵∠CBA+∠BAC+∠ACB=180°,∠ACB=α,∴∠CBA+∠BAC=180°-α,即∠DOB=180°-α,故②正确;③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM=12AD,BN= 12BE, 又∵由①知,AD=BE,∴AM=BN,又∵∠CAD=∠CBE,CA=CB,∴CAM CBN ≅(SAS), ∴CM=CN ,∠ACM=∠BCN,∴∠MCN=∠MCB+∠CBN=∠MCB+∠ACM=∠ACB=α,∴MCN △为等腰三角形且∠MCN=α,∴MCN △不是等边三角形,故③错误;④正确,理由如下:如图所示,在AD 上取一点P 使得DP=EO,连接CP ,由①知,ACD BCE ≅△△,∴∠CEO=∠CDP ,又∵CE=CD,EO=DP ,∴CEO CDP ≅(SAS),∴∠COE=∠CPD,CP=CO,∴∠CPO=∠COP ,∴∠COP=∠COE,即OC 平分∠AOE,故④正确;故答案为:B.【点睛】本题考查了三角形全等的判定和性质,三角形内角和定理和外角定理,等边三角形的判定,根据已知条件作出正确的辅助线,找出全等三角形是解题的关键.19.如图,O 是正三角形ABC 内一点,OA=3,OB=4,OC=5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′,下列结论:①△BO′A 可以由△BOC 绕点B 逆时针旋转60°得到;②点O 与O ′的距离为4;③∠AOB=150°;④S 四边形AOBO′=6+33;⑤S△AOC+S△AOB=6+934.其中正确的结论是()A.①②③⑤B.①③④C.②③④⑤D.①②⑤【答案】A【解析】试题解析:由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,又∵OB=O′B,AB=BC,∴△BO′A≌△BOC,又∵∠OBO′=60°,∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;如图①,连接OO′,∵OB=O′B,且∠OBO′=60°,∴△OBO′是等边三角形,∴OO′=OB=4.故结论②正确;∵△BO′A≌△BOC,∴O′A=5.在△AOO′中,三边长为3,4,5,这是一组勾股数,∴△AOO′是直角三角形,∠AOO′=90°,∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,故结论③正确;S四边形AOBO′=S△AOO′+S△OBO′=12×3×4+34×423故结论④错误;如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形, 则S △AOC +S △AOB =S 四边形AOCO″=S △COO″+S △AOO″=12×3×4+3×32=6+93, 故结论⑤正确.综上所述,正确的结论为:①②③⑤.故选A .20.如图,ABC △中,60BAC ∠=︒,ABC ∠、ACB ∠的平分线交于E ,D 是AE 延长线上一点,且120BDC ∠=︒.下列结论:①120BEC ∠=︒;②DB DE =;③2BDE BCE ∠=∠.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】 分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC ∠=︒,∴18060120ABC ACB ∠+∠=︒-︒=︒,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴12EBC ABC ∠=∠,12ECB ACB ∠=∠, ∴11()1206022EBC ECB ABC ACB ∠+∠=∠+∠=⨯︒=︒, ∴180()18060120BEC EBC ECB ∠=︒-∠+∠=︒-︒=︒, 故①正确.如图,过点D 作DF AB ⊥于F ,DG AC ⊥的延长线于G ,∵BE 、CE 分别为ABC ∠、ACB ∠的平分线,∴AD 为BAC ∠的平分线, ∴DF DG =,∴36090260120FDG ∠=︒-︒⨯-︒=︒,又∵120BDC ∠=︒,∴120BDF CDF ∠+∠=︒,120CDG CDF ∠+∠=︒.∴BDF CDG ∠=∠,∵在BDF 和CDG △中,90BFD CGD DF DGBDF CDG ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩, ∴BDF ≌()CDG ASA ,∴DB CD =,∴1(180120)302DBC ∠=︒-︒=︒, ∴30DBC DBC CBE CBE ∠=∠+∠=︒+∠,∵BE 平分ABC ∠,AE 平分BAC ∠,∴ABE CBE ∠=∠,1302BAE BAC ∠=∠=︒, 根据三角形的外角性质, 30DEB ABE BAE ABE ∠=∠+∠=∠+︒,∴DEB DBE ∠=∠,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE ∠=∠,故③正确,综上所述,正确结论有①②③,故选:D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.。
北京市山谷学校数学全等三角形(培优篇)(Word版 含解析)

一、八年级数学全等三角形解答题压轴题(难)1.(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=12∠BAD,上述结论是否仍然成立,并说明理由;(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O 之间夹角∠EOF=70°,试求此时两舰艇之间的距离.(4)能力提高:如图4,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,试求出MN的长.【答案】(1)EF=BE+FD;(2)EF=BE+FD仍然成立;(3)210;(4)MN10.【解析】试题分析:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;(2)延长FD到点G,使DG=BE,连接AG,证明△ABE≌△AD G,再证△AEF≌△AGF,得EF=FG,即可得到答案;(3)连接EF,延长AE,BF相交于点C,根据探索延伸可得EF=AE+FB,即可计算出EF的长度;(4)在△ABC外侧作∠CAD=∠BAM,截取AD=A M,连接CD,DN,证明△ACD≌△ABM,得到CD=BM,再证MN=ND,则求出ND的长度,即可得到答案.解:(1)由△AEF≌△AGF,得EF=GF,又由BE=DG,得EF=GF=DF+DG=DF+BE;(2)EF=BE+FD仍然成立.证明:如答图1,延长FD到点G,使DG=BE,连接AG,∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,∴∠B=∠ADG,在△ABE与△ADG中,AB=AD,∠B=∠ADG,BE=DG,∴△ABE≌△ADG.∴AE=AG,∠BAE=∠DAG.又∵∠EAF=12∠BAD,∴∠F AG=∠F AD+∠DAG=∠F AD+∠BAE=∠BAD-∠EAF=∠BAD-12∠BAD=12∠BAD,∴∠EAF=∠GAF.在△AEF与△AGF中,AE=AG,∠EAF=∠GAF,AF=AF,∴△AEF≌△AGF.∴EF=FG.又∵FG=DG+DF=BE+DF.∴EF=BE+FD.(3)如答图2,连接EF,延长AE,BF相交于点C,在四边形AOBC中,∵∠AOB=30°+90°+20°=140°,∠FOE=70°=12∠AOB,又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,∴结论EF=AE+FB成立.∴EF=AE+FB=1.5×(60+80)=210(海里).答:此时两舰艇之间的距离为210海里;(4)如答图3,在△ABC外侧作∠CAD=∠BAM,截取AD=AM,连接CD,DN,在△ACD与△ABM中,AC=AB,∠CAD=∠BAM,AD=AM,则△ACD≌△ABM,∴CD=BM=1,∠ACD=∠ABM=45°,∵∠NAD=∠NAC+∠CAD=∠NAC+∠BAM=∠BAC-∠MAN=45°,∴∠MAD=∠MAN+∠NAD=90°=2∠NAD,又∵AM=AD,∠NCD+∠MAD=(∠ACD+∠ACB)+90°=180°,∴对于四边形AMCD符合探索延伸,则ND=MN,∵∠NCD=90°,CD=1,CN=3,∴MN=ND=10.2.在四边形ABCD 中,E 为BC 边中点.(Ⅰ)已知:如图,若AE 平分∠BAD,∠AED=90°,点F 为AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD(Ⅱ)已知:如图,若AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点F,G 均为AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+12BC+CD.【答案】(Ⅰ)(1)证明见解析;(2)证明见解析;(Ⅱ)(1)证明见解析;(2)证明见解析.【解析】【分析】(Ⅰ)(1)运用SAS 证明△ABE ≌AFE 即可;(2)由(1)得出∠AEB=∠AEF ,BE=EF ,再证明△DEF ≌△DEC (SAS ),得出DF=DC ,即可得出结论;(Ⅱ)(1)同(Ⅰ)(1)得△ABE ≌△AFE (SAS ),△DGE ≌△DCE (SAS ),由全等三角形的性质得出BE=FE ,∠AEB=∠AEF ,CE=GE ,∠CED=∠GED ,进而证明△EFG 是等边三角形;(2)由△EFG 是等边三角形得出GF=EE=BE=12BC ,即可得出结论. 【详解】(Ⅰ)(1)∵AE 平分∠BAD ,∴∠BAE=∠FAE ,在△ABE 和△AFE 中, AB AF BAE FAE AE AE ⎪∠⎪⎩∠⎧⎨===,∴△ABE ≌△AFE (SAS ),(2)∵△ABE ≌△AFE ,∴∠AEB=∠AEF ,BE=EF ,∵E 为BC 的中点,∴BE=CE ,∴FE=CE ,∵∠AED=∠AEF+∠DEF=90°,∴∠AEB+∠DEC=90°,∴∠DEF=∠DEC ,在△DEF 和△DEC 中,FE CE DEF DEC DE DE ⎪∠⎪⎩∠⎧⎨===,∴△DEF ≌△DEC (SAS ),∴DF=DC ,∵AD=AF+DF ,∴AD=AB+CD ;(Ⅱ)(1)∵E 为BC 的中点,∴BE=CE=12BC , 同(Ⅰ)(1)得:△ABE ≌△AFE (SAS ),△DEG ≌△DEC (SAS ),∴BE=FE,∠AEB=∠AEF,CE=GE,∠CED=∠GED,∵BE=CE,∴FE=GE,∵∠AED=120°,∠AEB+∠CED=180°-120°=60°,∴∠AEF+∠GED=60°,∴∠GEF=60°,∴△EFG是等边三角形,(2)∵△EFG是等边三角形,∴GF=EF=BE=12 BC,∵AD=AF+FG+GD,∴AD=AB+CD+12 BC.【点睛】本题考查了全等三角形的判定与性质、等边三角形的判定与性质等知识;熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.3.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.(1)求证:BG=CF;(2)请你判断BE+CF与EF的大小关系,并说明理由.【答案】(1)详见解析;(2)BE+CF>EF,证明详见解析【解析】【分析】(1)先利用ASA判定△BGD CFD,从而得出BG=CF;(2)利用全等的性质可得GD=FD,再有DE⊥GF,从而得到EG=EF,两边之和大于第三边从而得出BE+CF>EF.【详解】解:(1)∵BG∥AC,∴∠DBG=∠DCF.∵D为BC的中点,∴BD=CD又∵∠BDG=∠CDF,在△BGD与△CFD中,∵DBG DCFBD CDBDG CDF∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BGD≌△CFD(ASA).∴BG=CF.(2)BE+CF>EF.∵△BGD≌△CFD,∴GD=FD,BG=CF.又∵DE⊥FG,∴EG=EF(垂直平分线到线段端点的距离相等).∴在△EBG中,BE+BG>EG,即BE+CF>EF.【点睛】本题考查了三角形全等的判定和性质,要注意判定三角形全等的一般方法有:SSS、SAS、AAS、ASA、HL.4.如图,在ABC∆中,90C∠=︒,4cmAC BC==,点D是斜边AB的中点.点E 从点B出发以1cm/s的速度向点C运动,点F同时从点C出发以一定的速度沿射线CA 方向运动,规定当点E到终点C时停止运动.设运动的时间为x秒,连接DE、DF.(1)填空:ABCS∆=______2cm;(2)当1x=且点F运动的速度也是1cm/s时,求证:DE DF=;(3)若动点F以3cm/s的速度沿射线CA方向运动,在点E、点F运动过程中,如果存在某个时间x,使得ADF∆的面积是BDE∆面积的两倍,请你求出时间x的值.【答案】(1)8;(2)见解析;(3)45或4.【解析】【分析】(1)直接可求△ABC的面积;(2)连接CD,根据等腰直角三角形的性质可求:∠A=∠B=∠ACD=∠DCB=45°,即BD=CD,且BE=CF,即可证△CDF≌△BDE,可得DE=DF;(3)分△ADF的面积是△BDE的面积的两倍和△BDE与△ADF的面积的2倍两种情况讨论,根据题意列出方程可求x的值.【详解】解:(1)∵S△ABC=12⨯AC×BC∴S△ABC=12×4×4=8(cm2)故答案为:8(2)如图:连接CD∵AC=BC,D是AB中点∴CD平分∠ACB又∵∠ACB=90°∴∠A=∠B=∠ACD=∠DCB=45°∴CD=BD依题意得:BE=CF∴在△CDF与△BDE中BE CFB DCABD CD=⎧⎪∠=∠⎨⎪=⎩∴△CDF≌△BDE(SAS)∴DE=DF(3)如图:过点D作DM⊥BC于点M,DN⊥AC于点N,∵AD=BD,∠A=∠B=45°,∠AND=∠DMB=90°∴△ADN≌△BDM(AAS)∴DN=DM当S△ADF=2S△BDE.∴12×AF×DN=2×12×BE×DM∴|4-3x|=2x∴x1=4,x2=4 5综上所述:x=45或4【点睛】本题考查了动点问题的函数图象,全等三角形的性质和判定,利用分类思想解决问题是本题的关键.5.已知△ABC中,AB=AC,点P是AB上一动点,点Q是AC的延长线上一动点,且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同,PQ与BC相交于点D,若AB=82,BC=16.(1)如图1,当点P为AB的中点时,求CD的长;(2)如图②,过点P作直线BC的垂线,垂足为E,当点P、Q在移动的过程中,设BE+CD=λ,λ是否为常数?若是请求出λ的值,若不是请说明理由.【答案】(1)4;(2)8【解析】【分析】(1)过P点作PF∥AC交BC于F,由点P和点Q同时出发,且速度相同,得出BP=CQ,根据PF∥AQ,可知∠PFB=∠ACB,∠DPF=∠CQD,则可得出∠B=∠PFB,证出BP=PF,得出PF=CQ,由AAS证明△PFD≌△QCD,得出,再证出F是BC的中点,即可得出结果;(2)过点P作PF∥AC交BC于F,易知△PBF为等腰三角形,可得BE=12BF,由(1)证明方法可得△PFD≌△QCD 则有CD=12CF,即可得出BE+CD=8.【详解】解:(1)如图①,过P点作PF∥AC交BC于F,∵点P 和点Q 同时出发,且速度相同,∴BP=CQ ,∵PF ∥AQ ,∴∠PFB=∠ACB ,∠DPF=∠CQD ,又∵AB=AC ,∴∠B=∠ACB ,∴∠B=∠PFB ,∴BP=PF ,∴PF=CQ ,又∠PDF=∠QDC ,∴△PFD ≌△QCD ,∴DF=CD=12CF , 又因P 是AB 的中点,PF ∥AQ , ∴F 是BC 的中点,即FC=12BC=8, ∴CD=12CF=4; (2)8BE CD λ+==为定值.如图②,点P 在线段AB 上,过点P 作PF ∥AC 交BC 于F ,易知△PBF 为等腰三角形,∵PE ⊥BF∴BE=12BF ∵易得△PFD ≌△QCD∴CD=12CF ∴()111182222BE CD BF CF BF CF BC λ+==+=+== 【点睛】 此题考查了等腰三角形的性质,全等三角形的判断与性质,熟悉相关性质定理是解题的关键.6.如图①,在ABC 中,90BAC ∠=︒,AB AC =,AE 是过A 点的一条直线,且B 、C 在AE 的异侧,BD AE ⊥于D ,CE AE ⊥于E .(1)求证:BD DE CE =+.(2)若将直线AE 绕点A 旋转到图②的位置时(BD CE <),其余条件不变,问BD 与DE 、CE 的关系如何?请予以证明.【答案】(1)见解析;(2)BD=DE-CE ,理由见解析.【解析】【分析】(1)根据已知利用AAS 判定△ABD ≌△CAE 从而得到BD=AE ,AD=CE ,因为AE=AD+DE ,所以BD=DE+CE ;(2)根据已知利用AAS 判定△ABD ≌△CAE 从而得到BD=AE ,AD=CE ,因为AD+AE=BD+CE ,所以BD=DE-CE .【详解】解:(1)∵∠BAC=90°,BD ⊥AE ,CE ⊥AE ,∴∠BDA=∠AEC=90°,∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°∴∠ABD=∠CAE ,∵AB=AC ,在△ABD 和△CAE 中,BDA AEC ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE (AAS ),∴BD=AE ,AD=CE ,∵AE=AD+DE ,∴BD=DE+CE ;(2)BD与DE、CE的数量关系是BD=DE-CE,理由如下:∵∠BAC=90°,BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∴∠ABD+∠DAB=∠DAB+∠CAE,∴∠ABD=∠CAE,∵AB=AC,在△ABD和△CAE中,BDA AECABD CAEAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∴AD+AE=BD+CE,∵DE=BD+CE,∴BD=DE-CE.【点睛】此题主要考查全等三角形的判定和性质,常用的判定方法有SSS,SAS,AAS,HL等.这种类型的题目经常考到,要注意掌握.7.如图,在ABC∆中,903,7C AC BC∠=︒==,,点D是BC边上的动点,连接AD,以AD为斜边在AD的下方作等腰直角三角形ADE.(1)填空:ABC∆的面积等于;(2)连接CE,求证:CE是ACB∠的平分线;(3)点O在BC边上,且1CO=,当D从点O出发运动至点B停止时,求点E相应的运动路程.【答案】(1)212;(2)证明见解析;(3)32【解析】【分析】(1)根据直角三角形的面积计算公式直接计算可得;(2)如图所示作出辅助线,证明△AEM≌△DEN(AAS),得到ME=NE,即可利用角平分线的判定证明;(3)由(2)可知点E在∠ACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=1()2AC CD +,根据CD 的长度计算出CE 的长度即可.【详解】 解:(1)903, 7C AC BC ∠=︒==,∴112137222ABC S AC BC =⨯=⨯⨯=, 故答案为:212 (2)连接CE ,过点E 作EM ⊥AC 于点M ,作EN ⊥BC 于点N ,∴∠EMA=∠END=90°,又∵∠ACB=90°,∴∠MEN=90°,∴∠MED+∠DEN=90°,∵△ADE 是等腰直角三角形∴∠AED=90°,AE=DE∴∠AEM+∠MED=90°,∴∠AEM=∠DEN∴在△AEM 与△DEN 中,∠EMA=∠END=90°,∠AEM=∠DEN ,AE=DE∴△AEM ≌△DEN (AAS )∴ME=NE∴点E 在∠ACB 的平分线上,即CE 是ACB ∠的平分线(3)由(2)可知,点E 在∠ACB 的平分线上,∴当点D 向点B 运动时,点E 的路径为一条直线,∵△AEM ≌△DEN∴AM=DN ,即AC-CM=CN-CD在Rt △CME 与Rt △CNE 中,CE=CE ,ME=NE ,∴Rt △CME ≌Rt △CNE (HL )∴CM=CN∴CN=1() 2AC CD+,又∵∠MCE=∠NCE=45°,∠CME=90°,∴CE=22()2CN AC CD=+,当AC=3,CD=CO=1时,CE=2(31)22 2+=当AC=3,CD=CB=7时,CE=2(37)52 2+=∴点E的运动路程为:522232-=,【点睛】本题考查了全等三角形的综合证明题,涉及角平分线的判定,几何中动点问题,全等三角形的性质与判定,解题的关键是综合运用上述知识点.8.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:△DEF是等边三角形.【答案】(1)见解析;(2)成立,理由见解析;(3)见解析【解析】【分析】(1)因为DE=DA+AE ,故通过证BDA AEC ≅△△,得出DA=EC ,AE=BD ,从而证得DE=BD+CE.(2)成立,仍然通过证明BDA AEC ≅△△,得出BD=AE ,AD=CE ,所以DE=DA+AE=EC+BD.(3)由BDA AEC ≅△△得BD=AE ,=BDA AEC ∠∠,ABF 与ACF 均等边三角形,得==60BA AC ︒∠F ∠F ,FB=FA ,所以=BA BA AC AC ∠F +∠D ∠F +∠E ,即FBD FAB ≅∠∠,所以BDF AEF ≅△△,所以FD=FE ,BFD AFE ≅∠∠,再根据=60BFD FA BFA =︒∠+∠D ∠,得=60AF FA =︒∠E +∠D ,即=60FE =︒∠D ,故DFE △是等边三角形.【详解】证明:(1)∵BD ⊥直线m ,CE ⊥直线m∴∠BDA =∠CEA=90°,∵∠BAC =90°∴∠BAD+∠CAE=90°,∵∠BAD+∠ABD=90°∴∠CAE=∠ABD ,又AB=AC ,∴△ADB ≌△CEA∴AE=BD ,AD=CE ,∴DE=AE+AD= BD+CE(2)∵∠BDA =∠BAC=α,∴∠DBA+∠BAD=∠BAD +∠CAE=180°—α∴∠DBA=∠CAE ,∵∠BDA=∠AEC=α,AB=AC∴△ADB≌△CEA,∴AE=BD,AD=CE∴DE=AE+AD=BD+CE(3)由(2)知,△ADB≌△CEA, BD=AE,∠DBA =∠CAE∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=60°∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE∵BF=AF,∴△DBF≌△EAF∴DF=EF,∠BFD=∠AFE∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°∴△DEF为等边三角形.【点睛】利用全等三角形的性质证线段相等是证两条线段相等的重要方法.9.如图1,已知CF是△ABC的外角∠ACE的角平分线,D为CF上一点,且DA=DB.(1)求证:∠ACB=∠ADB;(2)求证:AC+BC<2BD;(3)如图2,若∠ECF=60°,证明:AC=BC+CD.【答案】(1)详见解析;(2)详见解析;(3)详见解析.【解析】【分析】(1)过点D分别作AC,CE的垂线,垂足分别为M,N,证明Rt△DAM≌Rt△DBN,得出∠DAM=∠DBN ,则结论得证;(2)证明Rt △DMC ≌Rt △DNC ,可得CM=CN ,得出AC+BC=2BN ,又BN <BD ,则结论得证;(3)在AC 上取一点P ,使CP=CD ,连接DP ,可证明△ADP ≌△BDC ,得出AP=BC ,则结论可得出.【详解】(1)证明:过点D 分别作AC ,CE 的垂线,垂足分别为M ,N ,∵CF 是△ABC 的外角∠ACE 的角平分线,∴DM =DN ,在Rt △DAM 和Rt △DBN 中,DA DB DM DN =⎧⎨=⎩, ∴Rt △DAM ≌Rt △DBN (HL ),∴∠DAM =∠DBN ,∴∠ACB =∠ADB ;(2)证明:由(1)知DM =DN ,在Rt △DMC 和Rt △DNC 中,DC DC DM DN =⎧⎨=⎩, ∴Rt △DMC ≌Rt △DNC (HL ),∴CM =CN ,∴AC +BC =AM +CM +BC =AM +CN +BC =AM +BN ,又∵AM =BN ,∴AC +BC =2BN ,∵BN <BD ,∴AC +BC <2BD .(3)由(1)知∠CAD =∠CBD ,在AC 上取一点P ,使CP =CD ,连接DP ,∵∠ECF =60°,∠ACF =60°,∴△CDP 为等边三角形,∴DP =DC ,∠DPC =60°,∴∠APD =120°,∵∠ECF =60°,∴∠BCD =120°,在△ADP 和△BDC 中,APD BCD PAD CBD DA DB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADP ≌△BDC (AAS ),∴AP =BC ,∵AC =AP +CP ,∴AC =BC +CP ,∴AC =BC +CD .【点睛】本题是三角形综合题,考查了等边三角形的判定与性质,全等三角形的判定与性质,角平分线的性质等知识,解题的关键是灵活运用所学知识解决问题.10.在平面直角坐标系中,点A (0,5),B (12,0),在y 轴负半轴上取点E ,使OA =EO ,作∠CEF =∠AEB ,直线CO 交BA 的延长线于点D .(1)根据题意,可求得OE = ;(2)求证:△ADO≌△ECO;(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?【答案】(1)5;(2)见解析;(3)当两动点运动时间为72、174、10秒时,△OPM与△OQN全等【解析】【分析】(1)根据OA=OE即可解决问题.(2)根据ASA证明三角形全等即可解决问题.(2)设运动的时间为t秒,分三种情况讨论:当点P、Q分别在y轴、x轴上时;当点P、Q都在y轴上时;当点P在x轴上,Q在y轴时若二者都没有提前停止,当点Q提前停止时;列方程即可得到结论.【详解】(1)∵A(0,5),∴OE=OA=5,故答案为5.(2)如图1中,∵OE=OA,OB⊥AE,∴BA=BE,∴∠BAO=∠BEO,∵∠CEF=∠AEB,∴∠CEF=∠BAO,∴∠CEO=∠DAO,在△ADO与△ECO中,CE0DA0OA0ECOE AOD∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADO≌△ECO(ASA).(2)设运动的时间为t秒,当PO=QO时,易证△OPM≌△OQN.分三种情况讨论:①当点P、Q分别在y轴、x轴上时PO=QO得:5﹣t=12﹣3t,解得t=72(秒),②当点P、Q都在y轴上时PO=QO得:5﹣t=3t﹣12,解得t=174(秒),③当点P在x轴上,Q在y轴上时,若二者都没有提前停止,则PO=QO得:t﹣5=3t﹣12,解得t=72(秒)不合题意;当点Q运动到点E提前停止时,有t﹣5=5,解得t=10(秒),综上所述:当两动点运动时间为72、174、10秒时,△OPM与△OQN全等.【点睛】本题属于三角形综合题,考查了全等三角形的判定,坐标与图形的性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.。
北京市山谷学校七年级数学上册第四章《几何图形初步》知识点总结(含解析)

北京市山谷学校七年级数学上册第四章《几何图形初步》知识点总结(含解析)一、选择题1.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为()A.0 B.1 C.2 D.3B解析:B【分析】将图1折成正方体,然后判断出A、B在正方体中的位置关系,从而可得到AB之间的距离.【详解】解:将图1折成正方体后点A和点B为同一条棱的两个端点,得出AB=1,则小虫从点A沿着正方体的棱长爬行到点B的长度为1.故选B.【点睛】本题主要考查的是展开图折成几何体,判断出点A和点B在几何体中的位置是解题的关键.2.下面四个图形中,能判断∠1>∠2的是()A.B.C.D. D解析:D【分析】根据图象,利用排除法求解.【详解】A.∠1与∠2是对顶角,相等,故本选项错误;B.根据图象,∠1<∠2,故本选项错误;C.∠1是锐角,∠2是直角,∠1<∠2,故本选项错误;D.∠1是三角形的一个外角,所以∠1>∠2,故本选项正确.故选D.【点睛】本题考查了学生识图能力和三角形的外角性质.3.如图.∠AOB=∠COD,则( )A.∠1>∠2 B.∠1=∠2C.∠1<∠2 D.∠1与∠2的大小无法比较B解析:B【解析】∵∠AOB=∠COD,∴∠AOB-∠BOD=∠COD-∠BOD,∴∠1=∠2;故选B.【点睛】考查了角的大小比较,培养了学生的推理能力.4.如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠EOC,则下列四个结论正确的个数有()∠DOE=60°,∠BOE=13①∠BOD=30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.A.1个B.2个C.3个D.4个D解析:D【分析】根据题意首先计算出∠AOD的度数,再计算出∠AOE、∠EOC、∠BOE、∠BOD的度数,然后再分析即可.【详解】解:由题意设∠BOE=x,∠EOC=3x,∵∠DOE=60°,OD平分∠AOB,∴∠AOD=∠BOD =60°-x,根据题意得:2(60°-x)+4x=180°,解得x=30°,∴∠EOC=∠AOE=90°,∠BOE=30°,∴∠BOD=∠AOD=30°,故①正确;∵∠BOD=∠AOD=30°,∴射线OE平分∠AOC,故②正确;∵∠BOE=30°,∠AOB=60°,∠DOE=60°,∴∠AOB+∠BOE=90°,∠BOE+∠DOE=90°,∴图中与∠BOE互余的角有2个,故③正确;∵∠AOE=∠EOC=90°,∴∠AOE+∠EOC=180°,∵∠EOC=90°,∠DOB=30°,∠BOE=30°,∠AOD=30°,∴∠COD+∠AOD=180°,∠COD+∠BOD=180°,∠COD+∠BOE=180°,∠COB+∠AOB=180°,∠COB+∠DOE=180°,∴图中互补的角有6对,故④正确,正确的有4个,故选:D.【点睛】本题主要考查角平分线以及补角和余角,解答的关键是正确计算出图中各角的度数.5.如图∠AOC=∠BOD=90︒,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:图中小于平角的角有6个;丙:∠AOB+∠COD =90︒;丁:∠BOC+∠AOD = 180︒ .其中正确的结论有().A.4个B.3个C.2个D.1个B解析:B【分析】根据余角的性质,补角的性质,可得答案.【详解】解:甲∠AOB+∠BOC=∠BOC+∠COD=90°,∠AOB=∠COD,故甲正确;乙∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD,故乙正确;丙∠AOB=∠COD,故丙错误;丁:∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=180°,故丁正确;故选:B.【点睛】本题考查了余角、补角的定义和角的有关推理的应用,能正确进行推理是解此题的关键,难度适中.6.已知柱体的体积V=S•h,其中S表示柱体的底面面积,h表示柱体的高.现将矩形ABCD绕轴l旋转一周,则形成的几何体的体积等于()A .2 r h πB .22?r h πC .23?r h πD .24?r h π C解析:C【分析】 根据柱体的体积V=S•h ,求出形成的几何体的底面积,即可得出体积.【详解】∵柱体的体积V=S•h ,其中S 表示柱体的底面面积,h 表示柱体的高,现将矩形ABCD 绕轴l 旋转一周,∴柱体的底面圆环面积为:π(2r )2-πr 2=3πr 2,∴形成的几何体的体积等于:3πr 2h .故选:C .【点睛】此题考查圆柱体体积公式,根据已知得出柱体的底面面积是解题的关键.7.已知线段AB =6cm ,反向延长线段AB 到C ,使BC =83AB ,D 是BC 的中点,则线段AD 的长为____cmA .2B .3C .5D .6A解析:A【分析】由BC =83AB 可求出BC 的长,根据中点的定义可求出BD 的长,利用线段的和差关系求出AD 的长即可.【详解】∵BC =83AB ,AB=6cm , ∴BC=6×83=16cm , ∵D 是BC 的中点,∴BD=12BC=8cm , ∵反向延长线段AB 到C ,∴AD=BD-AB=8-6=2cm ,故选A.【点睛】本题考查了比较线段的长短,理解线段中点的概念,利用中点的性质转化线段之间的倍分关系是解题关键.8.如图,图中射线、线段、直线的条数分别为()A.5,5,1 B.3,3,2C.1,3,2 D.8,4,1D解析:D【分析】直线没有端点,射线有一个端点,线段有两个端点.【详解】以A点为端点的射线有2条,以B为端点的射线有3条,以C为端点的射线有2条,以D 为端点射线有1条,合计射线8条.线段:AB,BC,AC,BD ,合计4条.直线:AC,合计1条故本题 D.【点睛】直线没有端点,射线有一个端点,线段有两个端点.9.如图,从A地到C地,可供选择的方案是走水路、走陆路、走空中,从A地到B地有三条水路、两条陆路,从B地到C地有4条陆路可供选择,走空中,从A地不经B地直线到C地,则从A地到C地可供选择的方案有( )A.10种B.20种C.21种D.626种C解析:C【分析】本题只需分别数出A到B、B到C、A到C的条数,再进一步分析计算即可.【详解】观察图形,得:A到B有5条,B到C有4条,所以A到B到C有5×4=20条,A到C一条.所以从A地到C地可供选择的方案共21条.故选C.【点睛】解决本题的关键是能够有顺序地数出所有情况.10.如图,点O在直线AB上,图中小于180°的角共有()A.10个B.9个C.11个D.12个B 解析:B【解析】【分析】利用公式:()21n n-来计算即可.【详解】根据公式:()21n n-来计算,其中,n指从点O发出的射线的条数.图中角共有4+3+2+1=10个,根据题意要去掉平角,所以图中小于180°的角共有10−1=9个.故选B.【点睛】此题考查角的的定义,解题关键在于掌握其定义性质.二、填空题11.硬币在桌面上快速地转动时,看上去象球,这说明了_________________.面动成体【分析】本题是面动成体的原理在现实中的具体表现根据面动成体原理解答即可【详解】硬币在桌面上快速地转动时看上去象球这说明了面动成体故答案为面动成体【点睛】本题考查了点线面体掌握面动成体原理是解解析:面动成体【分析】本题是面动成体的原理在现实中的具体表现,根据面动成体原理解答即可.【详解】硬币在桌面上快速地转动时,看上去象球,这说明了面动成体,故答案为面动成体.【点睛】本题考查了点、线、面、体,掌握面动成体原理是解题的关键.12.如图是一个正方体的表面展开图,已知正方体的每个面上都是一个有理数,且相对面上的两个数互为倒数,那么代数式abc-的值是_________.【解析】【分析】将此正方体的表面展开图折叠成正方体观察abc 分别对应的值即可得出答案【详解】将图中所示图形折叠成正方体后a 与4相对应b 与2相对应c 与-1相对应∴∴【点睛】由平面图形的折叠及立体图形的 解析:34- 【解析】【分析】将此正方体的表面展开图折叠成正方体,观察a ,b ,c 分别对应的值,即可得出答案.【详解】将图中所示图形折叠成正方体后,a 与4相对应,b 与2相对应,c 与-1相对应, ∴1a 4=,1b 2=,c 1=- ∴3=-4a b c - 【点睛】由平面图形的折叠及立体图形的表面展开图的特点解题.13.如图所示,∠BOD =45°,那么不大于90°的角有___个,它们的度数之和是____.450°【分析】(1)∠AOE =90°故图中所有的角都是不大于90°的角;(2)将所有的角相加发现有的角相加等于∠EOA 即和为90°而有的角相加等于∠BOD 即和为45°将这样的角凑在一起计算即可求出解析:450°【分析】(1)∠AOE =90°,故图中所有的角都是不大于90°的角;(2)将所有的角相加,发现有的角相加等于∠EOA ,即和为90°,而有的角相加等于∠BOD ,即和为45°,将这样的角凑在一起计算,即可求出所有角的度数.【详解】不大于 90°的角有∠EOD ,∠EOC ,∠EOB ,∠EOA ,∠DOC ,∠DOB ,∠DOA ,∠COB ,∠COA ,∠BOA 共10个;它们的度数之和是(∠EOD +∠DOA)+(∠EOC +∠COA)+(∠ EOB +∠BOA)+[(∠DOC +∠COB)+∠DOB]+∠EOA =90°+90°+90°+(45°+45°)+90°=450°.故答案为10;450°.【点睛】此题主要考查角的表示与和差关系,解题的关键是熟知角的定义运算法则.14.科学知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面的这两个情景,请你做出判断.情景一:如图,从教学楼到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所.学数学知识来说明这个问题:_______________________________________________.情景二:农民兴修水利,开挖水渠,先在两端立桩拉线,然后沿线开挖,请你说出其中的道理:_______________________________________________________________________________ _.你赞同以上哪种做法,你认为应用科学知识为人类服务时应注意什么?情景一:两点之间线段最短;情景二:两点确定一条直线;赞同第二种应用科学知识为人类服务时应注意保护周边的环境等(合理即可)【解析】【分析】学校和图书馆两根立桩之间的路线可看做是一条线段接下来根据根据线解析:情景一:两点之间,线段最短;情景二:两点确定一条直线;赞同第二种,应用科学知识为人类服务时,应注意保护周边的环境等.(合理即可)【解析】【分析】学校和图书馆、两根立桩之间的路线可看做是一条线段,接下来,根据根据线段的性质来分析得出即可.【详解】第一个情景是根据两点之间线段最短的原理来做的,第二个是两点确定一条直线;我赞同第二种做法.我们利用科学的同时,必须注意保护我们周围赖以生存的生态环境.故答案为:两点之间线段最短;两点确定一条直线;我赞同第二种做法.我们利用科学的同时,必须注意保护我们周围赖以生存的生态环境.【点睛】此题考查两点之间线段最短的应用,两点确定一条直线,掌握线段的性质是解题的关键. 15.如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.若3AC=,1CP=,则线段PN的长为________.【解析】【分析】根据线段中点的性质计算即可CB的长结合图形根据线段中点的性质可得CN的长进而得出PN的长【详解】∵AP=AC+CPCP=1∴AP=3+1=4∵P为AB的中点∴AB=2AP=8∵CB=解析:3 2【解析】【分析】根据线段中点的性质计算即可CB 的长,结合图形、根据线段中点的性质可得CN 的长,进而得出PN 的长.【详解】∵AP=AC+CP ,CP=1,∴AP=3+1=4,∵P 为AB 的中点,∴AB=2AP=8,∵CB=AB-AC ,AC=3,∴CB=5,∵N 为CB 的中点,∴CN=12BC=52, ∴PN=CN-CP=32. 故答案为32. 【点睛】 本题考查的是两点间的距离的计算,掌握线段的中点的性质、灵活运用数形结合思想是解题的关键.16.填空:(1)8.76︒=________︒________'________'';(2)41348︒'''=________︒;(3)36000''=________'=________︒;(4)0.15︒=________'=________''.4536423600109540【分析】根据题意可知(1)(2)(3)(4)都是度分秒的计算由度化度分秒的运算法则整数的度数直接填入度数小数部分乘以60即可得到分分的小数部分乘以60得到秒;度分秒化 解析:45 36 4.23 600 10 9 540【分析】根据题意可知,(1)(2)(3)(4)都是度分秒的计算,由度化度分秒的运算法则,整数的度数直接填入,度数小数部分乘以60,即可得到分,分的小数部分乘以60得到秒;度分秒化度的运算法则为分别除以60,即可得到答案;【详解】解:(1)0.766045.6'⨯=,0.6'6036⨯="∴8.76845'36︒=︒";(2)48600.8'"÷=,'13.8600.23÷=︒∴'41348 4.23"︒=︒;(3)3600060600'"÷=,'6006010÷=︒∴'3600060010"==︒;(4)0.15609'︒⨯=,9'60540⨯="∴0.159540'︒==".故答案为(1)8,45,36;(2)4.23;(3)600,10;(4)9,540.【点睛】本题考查了度分秒之间的换算,解题的关键是掌握度分秒的运算法则.17.如图所示,第(1)个图有2个相同的小正方形,第(2)个图有6个相同的小正方形,第(3)个图有12个相同的小正方形,第(4)个图有20个相同的小正方形,……,按此规律,那么第(n )个图有________个相同的小正方形.n(n +1)【分析】通过观察可以发现每一个图形中正方形的个数等于图形序号乘以比序号大一的数根据此规律解答即可【详解】第(1)个图有2个相同的小正方形2=1×2第(2)个图有6个相同的小正方形6=2×解析:n(n +1)【分析】通过观察可以发现,每一个图形中正方形的个数等于图形序号乘以比序号大一的数,根据此规律解答即可.【详解】第(1)个图有2个相同的小正方形,2=1×2,第(2)个图有6个相同的小正方形,6=2×3,第(3)个图有12个相同的小正方形,12=3×4,第(4)个图有20个相同的小正方形,20=4×5,…,以此类推,第n 个图应有n(n +1)个相同的小正方形.【点睛】本题是对图形变化规律的考查,发现正方形的个数是两个连续整数的乘积是解题的关键,此类题目对同学们的能力要求较高,在平时的学习中要不断积累.18.若∠B 的余角为57.12°,则∠B=_____°_____’_____”5248【分析】根据互为余角列式再进行度分秒换算求出结果【详解】5712°=根据题意得:∠B=90°-=-==故答案为【点睛】本题考查余角的定义正确进行角度的计算是解题的关键解析:52 48【分析】根据互为余角列式,再进行度分秒换算,求出结果.【详解】57.12°='''57712︒根据题意得:∠B=90°-'''57712︒='''895960︒-'''57712︒=()8957︒-()'597-''(60-12) ='''325248︒故答案为'''325248︒.本题考查余角的定义,正确进行角度的计算是解题的关键.19.如图,90AOC BOD ∠=∠=︒,70AOB ∠=︒,在∠AOB 内画一条射线OP 得到的图中有m 对互余的角,其中AOP x ∠=︒,且满足050x <<,则m =_______.3或4或6【分析】分三种情况下:①∠AOP =35°②∠AOP =20°③0<x <50中的其余角根据互余的定义找出图中互余的角即可求解【详解】①∠AOP =∠AOB=35°时∠BOP=35°∴互余的角有∠解析:3或4或6【分析】分三种情况下:①∠AOP =35°,②∠AOP =20°,③0<x <50中的其余角,根据互余的定义找出图中互余的角即可求解.【详解】①∠AOP =12∠AOB =35°时,∠BOP=35° ∴互余的角有∠AOP 与∠COP ,∠BOP 与∠COP ,∠AOB 与∠COB ,∠COD 与∠COB ,一共4对;②∠AOP =90°-∠AOB =20°时,∴互余的角有∠AOP 与∠COP ,∠AOP 与∠AOB ,∠AOP 与∠COD ,∠COD 与∠COB ,∠AOB 与∠COB ,∠COP 与∠COB ,一共6对;③0<x <50中35°与20°的其余角,互余的角有∠AOP 与∠COP ,∠AOB 与∠COB ,∠COD 与∠COB ,一共3对.则m =3或4或6.故答案为:3或4或6.【点睛】本题考查了余角和补角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.20.一个几何体,从不同方向看到的图形如图所示.拼成这个几何体的小正方体的个数为______.6【分析】根据从不同方位看到的图形的形状可知该几何体有2列2行底面有4个小正方体摆成大正方体上面至少2个小正方体放在靠前面的2个小正方体上面由此解答【详解】由题图可知该几何体第一层有4个小正方体第二【分析】根据从不同方位看到的图形的形状可知,该几何体有2列2行,底面有4个小正方体摆成大正方体,上面至少2个小正方体,放在靠前面的2个小正方体上面.由此解答.【详解】由题图可知,该几何体第一层有4个小正方体,第二层有2个小正方体,所以拼成这个几何体的小正方体的个数为6.故答案为:6.【点睛】本题主要考查从不同方向观察物体和几何体,关键注重培养学生的空间想象能力.三、解答题21.如图,点C 是AB 的中点,D ,E 分别是线段AC ,CB 上的点,且AD =23AC ,DE =35AB ,若AB =24 cm ,求线段CE 的长.解析:CE =10.4cm .【分析】根据中点的定义,可得AC 、BC 的长,然后根据题已知求解CD 、DE 的长,再代入CE=DE-CD 即可.【详解】∵AC=BC=12AB=12cm ,CD=13AC=4cm ,DE=35AB=14.4cm , ∴CE=DE ﹣CD=10.4cm. 22.射线OA ,OB ,OC ,OD ,OE 有公共端点O .(1)若OA 与OE 在同一直线上,如图(1),试写出图中小于平角的角.(2)如图(2),若108AOC ︒∠=,(072)COE n n ︒∠=<<,OB 平分AOE ∠,OD平分COE ∠,求BOD ∠的度数.解析:(1)AOD ∠,AOC ∠,AOB ∠,∠BOE ,BOD ∠,BOC ∠,COE ∠,COD ∠,DOE ∠;(2)54︒【分析】(1)根据角的定义即可解决;(2)利用角平分线的性质即可得出∠BOD=12∠AOC+12∠COE ,进而求出即可. 【详解】 (1)题图(1)中小于平角的角有AOD ∠,AOC ∠,AOB ∠,∠BOE ,BOD ∠,BOC ∠,COE ∠,COD ∠,DOE ∠.(2)因为OB 平分AOE ∠,OD 平分COE ∠,108AOC ︒∠=,(072)COE n n ︒∠=<<,所以1111()2222BOD BOE DOE AOE COE AOE COE AOC ∠=∠-∠=∠-∠=∠-∠=∠. 因为108AOC ∠=︒,所以54BOD ∠=︒【点睛】本题考查了角的平分线的定义和角的有关计算,本题中将所有锐角的和转化成与∠AOE 、∠BOD 和∠BOD 的关系是解题的关键,23.如图,已知点C 为线段AB 上一点,15cm AC =,35CB AC =,D ,E 分别为线段AC ,AB 的中点,求线段DE 的长.解析:5cm【分析】根据线段的中点定义即可求解.【详解】解:因为15cm AC =,35CB AC =, 所以3159(cm)5CB =⨯=, 所以15924(cm)AB =+=.因为D ,E 分别为线段AC ,AB 的中点,所以112cm 2AE BE AB ===,17.5cm 2DC AD AC ===. 所以127.5 4.5(cm)DE AE AD =-=-=. 【点睛】本题考查了两点间的距离,解决本题的关键是利用线段的中点定义.24.如图,已知∠AOB=90°,∠EOF=60°,OE 平分∠AOB ,OF 平分∠BOC ,求∠AOC 和∠COB 的度数.解析:120°,30°【分析】先根据角平分线,求得∠BOE 的度数,再根据角的和差关系,求得BOF ∠的度数,最后根据角平分线,求得BOC ∠、AOC ∠的度数.【详解】∵OE 平分∠AOB ,∠AOB=90°∴∠BOE=∠AOB =45°又∵∠EOF=60°∴∠BOF=∠EOF -∠BOE= 15°又∵OF 平分∠BOC∴∠BOC=2∠BOF=30°∴∠AOC=∠AOB +∠BOC=120°故∠AOC=120°,∠COB=30°.【点睛】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.注意:也可以根据AOC ∠的度数是EOF ∠度数的2倍进行求解.25.如图,平面上有四个点A 、B 、C 、D ,根据下列语句画图.(1)画直线AB 、CD 交于E 点;(2)画线段AC 、BD 交于点F ;(3)连接E 、F 交BC 于点G ;(4)连接AD ,并将其反向延长;(5)作射线BC .解析:见解析.【分析】(1)连接AB 、CD 并向两方无限延长即可得到直线AB 、CD ;交点处标点E ;(2)连接AC 、BD 可得线段AC 、BD ,交点处标点F ;(3)连接AD 并从D 向A 方向延长即可;(4)连接BC,并且以B为端点向BC方向延长.【详解】解:所求如图所示:.【点睛】本题考查的是直线、射线、线段的定义及性质,解答此题的关键是熟知以下知识,即直线向两方无限延伸;射线向一方无限延伸;线段有两个端点画出图形即可.26.如图,在数轴上有A,B两点,点A在点B的左侧.已知点B对应的数为2,点A对应的数为a.(1)若a=﹣1,则线段AB的长为;(2)若点C到原点的距离为3,且在点A的左侧,BC﹣AC=4,求a的值.解析:(1)3;(2)﹣2【分析】(1)根据点A、B表示的数利用两点间的距离公式即可求出AB的长度;(2)设点C表示的数为c,则|c|=3,即c=±3,根据BC﹣AC=4列方程即可得到结论.【详解】(1)AB=2﹣a=2﹣(﹣1)=3,故答案为:3;(2)∵点C到原点的距离为3,∴设点C表示的数为c,则|c|=3,即c=±3,∵点A在点B的左侧,点C在点A的左侧,且点B表示的数为2,∴点C表示的数为﹣3,∵BC﹣AC=4,∴2﹣(﹣3)﹣[a﹣(﹣3)]=4,解得a=﹣2.【点睛】本题主要考查数轴上两点之间的距离,解此题的关键在于熟练掌握其知识点.27.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;(2)若图中的正方形边长为5cm ,长方形的长为8cm ,请计算修正后所折叠而成的长方体的表面积和体积.解析:(1)多余一个正方形,图形见解析;(2)表面积为:210cm 2;体积为:200cm 3.【分析】(1)根据长方体的展开图判断出多余一个正方形;(2)根据表面积=四个长方形的面积+两个正方形的面积,体积=底面积×高分别列式计算即可得解.【详解】解:(1)多余一个正方形,如图所示:(2)表面积为:225285450160210()cm ⨯+⨯⨯=+=,体积为:2358200()cm ⨯=【点睛】本题考查了几何体的展开图以及长方体的表面积、体积的求法,熟练掌握长方体的展开图是解题的关键.28.已知直线l 上有三点A 、B 、C ,AB=3,AC=2,点M 是AC 的中点.(1)根据条件,画出图形;(2)求线段BM 的长.解析:(1)见解析;(2)2或4.【分析】(1)分C 点在线段AB 上和C 点在BA 的延长线上两种情况画出图形即可;(2)利用(1)中所画图形,根据中点的定义及线段的和差故选,分别求出MB 的长即可.【详解】(1)点C 的位置有两种:当点C 在线段AB 上时,如图①所示:当点C 在BA 的延长线上时,如图②所示:(2)∵点M是AC的中点,AC=2,∴AM=CM=12AC=1,如图①所示,当点C在线段AB上时,∵AB=AM+MB,AB=3,∴MB=AB-AM=2.如图②所示:当点C在BA的延长线上时,MB=AM+AB=4.综上所述:MB的长为2或4.【点睛】本题主要考查中点的定义及线段之间的和差关系,灵活运用分类讨论的思想是解题关键.。
北京市山谷学校数学 二次函数(培优篇)(Word版 含解析)

北京市山谷学校数学二次函数(培优篇)(Word版含解析)一、初三数学二次函数易错题压轴题(难)1.已知,抛物线y=-12x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.(1)直接填写抛物线的解析式________;(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.求证:MN∥y轴;(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG •CH 为定值.【答案】(1)2122y x x=-++;(2)见详解;(3)见详解.【解析】【分析】(1)把点C、D代入y=-12x2 +bx+c求解即可;(2)分别设PM、PC的解析式,由于PM、PC与抛物线的交点分别为:M、N.,分别求出M、N的代数式即可求解;(3)先设G、H的坐标,列出QG、GH的解析式,得出与抛物线的交点D、E的横坐标,再列出直线AE的解析式,算出它与抛物线横坐标的交点方程.运用韦达定理即可求证.【详解】详解:(1)∵y=-12x2 +bx+c过点C(0,2),点Q(2,2),∴2122222b cc⎧-⨯++⎪⎨⎪=⎩=,解得:12b c =⎧⎨=⎩. ∴y=-12x 2+x+2; (2) 设直线PM 的解析式为:y=mx ,直线PC 的解析式为:y=kx+2 由22122y kx y x x =+⎧⎪⎨=-++⎪⎩得12x 2+(k-1)x=0, 解得:120,22x x k ==-,x p =22p x k =- 由21=22y mx y x x =⎧⎪⎨-++⎪⎩得12x 2+(m-1)x-2=0, ∴124b x x a⋅=-=- 即x p•x m =-4,∴x m =4p x -=21k -. 由24y kx y x =+⎧⎨=+⎩得x N =21k -=x M , ∴MN ∥y 轴.(3)设G (0,m ),H (0,n ).设直线QG 的解析式为y kx m =+,将点()2,2Q 代入y kx m =+得22k m =+22m k -∴= ∴直线QG 的解析式为22m y x m -=+ 同理可求直线QH 的解析式为22n y x n -=+; 由222122m y x m y x x -⎧=+⎪⎪⎨⎪=-++⎪⎩得221=222m x m x x -+-++ 解得:122,2x x m ==-2D x m ∴=-同理,2E x n =-设直线AE 的解析式为:y=kx+4, 由24122y kx y x x =+⎧⎪⎨=-++⎪⎩, 得12x 2-(k-1)x+2=0 124b x x a∴⋅=-= 即x D x E =4, 即(m-2)•(n-2)=4∴CG•CH=(2-m )•(2-n )=4.2.在平面直角坐标系中,将函数2263,(y x mx m x m m =--≥为常数)的图象记为G . (1)当1m =-时,设图象G 上一点(),1P a ,求a 的值;(2)设图象G 的最低点为(),o o F x y ,求o y 的最大值;(3)当图象G 与x 轴有两个交点时,设右边交点的横坐标为2,x 则2x 的取值范围是 ;(4)设1112,,2,16816A m B m ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭,当图象G 与线段AB 没有公共点时,直接写出m 的取值范围. 【答案】(1)0a =或3a =-;(2)118;(3)21136x -<<-;(4)18m <-或116m >- 【解析】【分析】(1)将m=-1代入解析式,然后将点P 坐标代入解析式,从而求得a 的值;(2)分m >0和m ≤0两种情况,结合二次函数性质求最值;(3)结合二次函数与x 轴交点及对称轴的性质确定取值范围;(4)结合一元二次方程根与系数的关系确定取值范围.【详解】解:(1)当1m =-时,()22613y x x x =++≥ 把(),1P a 代入,得22611a a ++=解得0a =或3a =-(2)当0m >时,,(3)F m m -此时,0o y m =-<当0m ≤时,2223926=2()22y x mx m x m m m =----- ∴239,22F m m m ⎛⎫-- ⎪⎝⎭此时,229911=()22918m m m ---++ ∴0y 的最大值118= 综上所述,0y 的最大值为118(3)由题意可知:当图象G 与x 轴有两个交点时,m >0 当抛物线顶点在x 轴上时,22=4(6)42()=0b ac m m -=--⨯⨯-△解得:m=0(舍去)或29m =- 由题意可知抛物线的对称轴为直线x=32m 且x ≥3m ∴当图象G 与x 轴有两个交点时,设右边交点的横坐标为x 2,则x 2的取值范围是21136x -<<- (4)18m <-或116m >- 【点睛】本题属于二次函数综合题,考查了二次函数的性质,不等式等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会用转化的思想思考问题,属于中考压轴题.3.如图,直线l :y =﹣3x +3与x 轴,y 轴分别相交于A 、B 两点,抛物线y =﹣x 2+2x +b 经过点B .(1)该抛物线的函数解析式;(2)已知点M 是抛物线上的一个动点,并且点M 在第一象限内,连接AM 、BM ,设点M 的横坐标为m ,△ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值; (3)在(2)的条件下,当S 取得最大值时,动点M 相应的位置记为点M '.①写出点M '的坐标;②将直线l 绕点A 按顺时针方向旋转得到直线l ',当直线l ′与直线AM '重合时停止旋转,在旋转过程中,直线l '与线段BM '交于点C ,设点B ,M '到直线l '的距离分别为d 1,d 2,当d 1+d 2最大时,求直线l '旋转的角度(即∠BAC 的度数).【答案】(1)2y x 2x 3=-++;(2)21525228S m ⎛⎫=--+ ⎪⎝⎭ ,258;(3)①57,24M ⎛⎫' ⎪⎝⎭;②45° 【解析】【分析】(1)利用直线l 的解析式求出B 点坐标,再把B 点坐标代入二次函数解析式即可求出b 的值.(2)设M 的坐标为(m ,﹣m 2+2m +3),然后根据面积关系将△ABM 的面积进行转化. (3)①由(2)可知m =52,代入二次函数解析式即可求出纵坐标的值. ②可将求d 1+d 2最大值转化为求AC 的最小值.【详解】(1)令x=0代入y=﹣3x+3,∴y=3,∴B(0,3),把B(0,3)代入y=﹣x2+2x+b并解得:b=3,∴二次函数解析式为:y=﹣x2+2x+3.(2)令y=0代入y=﹣x2+2x+3,∴0=﹣x2+2x+3,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为-1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=﹣3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M的坐标为(m,﹣m2+2m+3),∴S=S四边形OAMB﹣S△AOB=S△OBM+S△OAM﹣S△AOB=12×m×3+12×1×(-m2+2m+3)-12×1×3=﹣12(m﹣52)2+258,∴当m=52时,S取得最大值258.(3)①由(2)可知:M′的坐标为(52,74).②设直线l′为直线l旋转任意角度的一条线段,过点M′作直线l1∥l′,过点B作BF⊥l1于点F,根据题意知:d 1+d 2=BF ,此时只要求出BF 的最大值即可,∵∠BFM′=90︒,∴点F 在以BM′为直径的圆上,设直线AM′与该圆相交于点H ,∵点C 在线段BM′上,∴F 在优弧'BM H 上,∴当F 与M′重合时,BF 可取得最大值,此时BM′⊥l 1,∵A (1,0),B (0,3),M′(52,74), ∴由勾股定理可求得:AB 10,M′B 55M′A 85, 过点M′作M′G ⊥AB 于点G ,设BG =x ,∴由勾股定理可得:M′B 2﹣BG 2=M′A 2﹣AG 2,∴851610﹣x )2=12516﹣x 2, ∴x =5108, cos ∠M′BG ='BG BM =22,∠M′BG= 45︒ 此时图像如下所示,∵l 1∥l′,F 与M′重合,BF ⊥l 1∴∠B M′P=∠BCA =90︒,又∵∠M′BG=∠CBA= 45︒∴∠BAC =45︒.【点睛】本题主要考查了一次函数与二次函数的综合以及一次函数旋转求角度问题,正确掌握一次函数与二次函数性质及综合问题的解法是解题的关键.4.二次函数22(0)63m m y x x m m =-+>的图象交y 轴于点A ,顶点为P ,直线PA 与x 轴交于点B .(1)当m =1时,求顶点P 的坐标;(2)若点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上,且0b m ->,试求a 的取值范围;(3)在第一象限内,以AB 为边作正方形ABCD .①求点D 的坐标(用含m 的代数式表示);②若该二次函数的图象与正方形ABCD 的边CD 有公共点,请直接写出符合条件的整数m 的值.【答案】(1)P (2,13);(2)a 的取值范围为:a <0或a >4;(3)①D (m ,m +3); ②2,3,4.【解析】【分析】(1)把m =1代入二次函数22(0)63m m y x x m m =-+>解析式中,进而求顶点P 的坐标即可;(2)把点Q (a ,b )代入二次函数22(0)63m m y x x m m =-+>解析式中,根据0b m ->得到关于a 的一元二次不等式即一元一次不等式组,解出a 的取值范围即可; (3)①过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,求出二次函数与y 轴的交点A 的坐标,得到OA 的长,再根据待定系数法求出直线AP 的解析式,进而求出与x 轴的交点B 的坐标,得到OB 的长;通过证明△ADF ≌△ABO ,得到AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,求出点D 的坐标;②因为二次函数的图象与正方形ABCD 的边CD 有公共点,由①同理可得:C (m+3,3),分当x 等于点D 的横坐标时与当x 等于点C 的横坐标两种情况,进行讨论m 可能取的整数值即可.【详解】解:(1)当m =1时,二次函数为212163y x x =-+, ∴顶点P 的坐标为(2,13); (2)∵点Q (a ,b )在二次函数22(0)63m m y x x m m =-+>的图象上, ∴2263m m b a a m =-+, 即:2263m m b m a a -=- ∵0b m ->, ∴2263m m a a ->0, ∵m >0, ∴2263a a ->0, 解得:a <0或a >4,∴a 的取值范围为:a <0或a >4;(3)①如下图,过点D 作DE ⊥x 轴于点E ,过点A 作AF ⊥DE 于点F ,∵二次函数的解析式为2263m m y x x m =-+, ∴顶点P (2,3m ), 当x=0时,y=m ,∴点A (0,m ),∴OA=m ;设直线AP 的解析式为y=kx+b(k≠0),把点A (0,m ),点P (2,3m )代入,得: 23m b m k b =⎧⎪⎨=+⎪⎩, 解得:3m k b m⎧=-⎪⎨⎪=⎩,∴直线AP 的解析式为y=3m -x+m , 当y=0时,x=3,∴点B (3,0);∴OB=3;∵四边形ABCD 是正方形,∴AD=AB ,∠DAF+∠FAB=90°,且∠OAB+∠FAB =90°,∴∠DAF=∠OAB ,在△ADF 和△ABO 中,DAF OAB AFD AOB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADF ≌△ABO (AAS ),∴AF=OA=m ,DF=OB=3,DE=DF+EF= DF+OA=m+3,∴点D 的坐标为:(m ,m+3);②由①同理可得:C (m+3,3),∵二次函数的图象与正方形ABCD 的边CD 有公共点,∴当x =m 时,3y m ≤+,可得322363m m m m -+≤+,化简得:32418m m -≤. ∵0m >,∴2184m m m -≤,∴218(2)4m m--≤, 显然:m =1,2,3,4是上述不等式的解,当5m ≥时,2(2)45m --≥,18 3.6m ≤,此时,218(2)4m m-->, ∴符合条件的正整数m =1,2,3,4; 当x = m +3时,y ≥3,可得2(3)2(3)363m m m m m ++-+≥, ∵0m >,∴21823m m m ++≥,即218(1)2m m++≥, 显然:m =1不是上述不等式的解,当2m ≥时,2(1)211m ++≥,189m ≤,此时,218(1)2m m++>恒成立, ∴符合条件的正整数m =2,3,4;综上:符合条件的整数m 的值为2,3,4.【点睛】本题考查二次函数与几何问题的综合运用,熟练掌握二次函数的图象和性质、一次函数的图象和性质、正方形的性质是解题的关键.5.如图,在平面直角坐标系x O y 中,抛物线y = ax 2+ bx + c 经过A 、B 、C 三点,已知点A (-3,0),B (0,3),C (1,0).(1)求此抛物线的解析式;(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;(3)在直线x = -2上是否存在点M,使得∠MAC = 2∠MCA,若存在,求出M点坐标.若不存在,说明理由.【答案】(1)y=-x2-2x+3;(2)点(-32,154),△PDE的周长最大;(3)点M(-2,)或(-2,【解析】【分析】(1)将A、B、C三点代入,利用待定系数法求解析式;(2)根据坐标发现,△AOB是等腰直角三角形,故只需使得PD越大,则△PDE的周长越大.联立直线AB与抛物线的解析式可得交点P坐标;(3)作点A关于直线x=-2的对称点D,利用∠MAC = 2∠MCA可推导得MD=CD,进而求得ME的长度,从而得出M坐标【详解】解:(1)∵抛物线y=ax2+bx+c经过点A(-3,0),B(0,3),C(1,0),∴9303a b cca b c-+=⎧⎪=⎨⎪++=⎩,解得:123abc=-⎧⎪=-⎨⎪=⎩,所以,抛物线的解析式为y=-x2-2x+3;(2)∵A(-3,0),B(0,3),∴OA=OB=3,∴△AOB是等腰直角三角形,∴∠BAO=45°,∵PF⊥x轴,∴∠AEF=90°-45°=45°,又∵PD⊥AB,∴△PDE是等腰直角三角形,∴PD越大,△PDE的周长越大,易得直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,联立223y x my x x=+⎧⎨=--+⎩,消掉y得,x2+3x+m-3=0,当△=9-4(m-3)=0,即m=214时,直线与抛物线只有一个交点,PD最长,此时x=-32,y=154,∴点(-32,154),△PDE的周长最大;(3)设直线x=-2与x 轴交于点E ,作点A 关于直线x=-2的对称点D ,则D (-1,0),连接MA ,MD ,MC .∴MA=MD ,∠MAC=∠MDA=2∠MCA ,∴∠CMD=∠DCM ∴MD=CD=2 , ∴ME=3∴点M (-2,3)或(-2,-3).【点睛】本题是动点和最值的考查,在解决动点问题时,寻找出不变量来分析是解题关键,最值问题,通常利用对称来简化分析6.如图,抛物线y =ax 2+bx +2经过点A(−1,0),B(4,0),交y 轴于点C ;(1)求抛物线的解析式(用一般式表示);(2)点D 为y 轴右侧抛物线上一点,是否存在点D 使S △ABC =23S △ABD ?若存在,请求出点D 坐标;若不存在,请说明理由;(3)将直线BC 绕点B 顺时针旋转45°,与抛物线交于另一点E ,求BE 的长.【答案】(1)213222y x x =-++(2)存在,D (1,3)或(2,3)或(5,3-)(3)10【解析】【分析】 (1)由A 、B 的坐标,利用待定系数法可求得抛物线解析式;(2)由条件可求得点D 到x 轴的距离,即可求得D 点的纵坐标,代入抛物线解析式可求得D 点坐标;(3)由条件可证得BC ⊥AC ,设直线AC 和BE 交于点F ,过F 作FM ⊥x 轴于点M ,则可得BF=BC ,利用平行线分线段成比例可求得F 点的坐标,利用待定系数法可求得直线BE 解析式,联立直线BE 和抛物线解析式可求得E 点坐标,则可求得BE 的长.【详解】解:(1)∵抛物线y=ax 2+bx+2经过点A (-1,0),B (4,0),∴2016420a b a b -+=⎧⎨++=⎩,解得:1232a b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴抛物线解析式为:213222y x x =-++; (2)由题意可知C (0,2),A (-1,0),B (4,0),∴AB=5,OC=2,∴S △ABC =12AB•OC=12×5×2=5, ∵S △ABC =23S △ABD , ∴S △ABD =315522⨯=, 设D (x ,y ), ∴11155222AB y y •=⨯•=, 解得:3y =;当3y =时,2132322y x x =-++=, 解得:1x =或2x =,∴点D 的坐标为:(1,3)或(2,3);当3y =-时,2132322y x x =-++=-, 解得:5x =或2x =-(舍去),∴点D 的坐标为:(5,-3);综合上述,点D 的坐标为:(1,3)或(2,3)或(5,-3);(3)∵AO=1,OC=2,OB=4,AB=5,∴AC ==BC ==∴222AC BC AB +=,∴△ABC 为直角三角形,即BC ⊥AC ,如图,设直线AC 与直线BE 交于点F ,过F 作FM ⊥x 轴于点M ,由题意可知∠FBC=45°,∴∠CFB=45°, ∴25CF BC == ∴AO AC OM CF =,即1525OM = 解得:2OM =, ∴OC AC FM AF =,即2535FM = 解得:6FM =,∴点F 为(2,6),且B 为(4,0),设直线BE 解析式为y=kx+m ,则2640k m k m +=⎧⎨+=⎩,解得312k m =-⎧⎨=⎩, ∴直线BE 解析式为:312y x =-+;联立直线BE 和抛物线解析式可得:231213222y x y x x =-+⎧⎪⎨=-++⎪⎩, 解得:40x y =⎧⎨=⎩或53x y =⎧⎨=-⎩, ∴点E 坐标为:(5,3)-, ∴22(54)(3)10BE =-+-=【点睛】本题为二次函数的综合应用,涉及待定系数法、三角形面积、勾股定理及其逆定理、平行线分线段成比例、函数图象的交点、等腰直角三角形的性质、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中求得D 点的纵坐标是解题的关键,在(3)中由条件求得直线BE 的解析式是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,有一定的难度.7.如图,抛物线2(0)y ax bx c a=++≠与坐标轴的交点为()30A-,,()10B,,()0,3C-,抛物线的顶点为D.(1)求抛物线的解析式.(2)若E为第二象限内一点,且四边形ACBE为平行四边形,求直线CE的解析式.(3)P为抛物线上一动点,当PAB∆的面积是ABD∆的面积的3倍时,求点P的坐标.【答案】(1)223y x x=+-;(2)33y x=--;(3)点P的坐标为()5,12-或()3,12.【解析】【分析】(1)本题考查二次函数解析式的求法,可利用待定系数法,将点带入求解;(2)本题考查二次函数平行四边形存在性问题,可根据题干信息结合平行四边形性质确定动点位置,进一步利用待定系数法求解一次函数解析式;(3)本题考查二次函数与三角形面积问题,可先根据题干面积关系假设动点坐标,继而带入二次函数,列方程求解.【详解】(1)∵抛物线2y ax bx c=++与坐标轴的交点为()30A-,,()10B,,()0,3C-,∴9303a b ca b cc-+=⎧⎪++=⎨⎪=-⎩,解得123abc=⎧⎪=⎨⎪=-⎩∴抛物线的解析式为223y x x=+-.(2)如图,过点E作EH x⊥轴于点H,则由平行四边形的对称性可知1AH OB==,3EH OC==.∵3OA =,∴2OH =,∴点E 的坐标为()2,3-.∵点C 的坐标为()0,3-,∴设直线CE 的解析式为()30y kx k =-<将点()2,3E -代入,得233k --=,解得3k =-,∴直线CE 的解析式为33y x =--.(3)∵2223(1)4y x x x =+-=+-,∴抛物线的顶点为()1,4D --.∵PAB ∆的面积是ABD ∆的面积的3倍,∴设点P 为(),12t .将点(),12P t 代入抛物线的解析式223y x x =+-中, 得22312t t +-=,解得3t =或5t =-,故点P 的坐标为()5,12-或()3,12.【点睛】本题考查二次函数与几何的综合,利用待定系数法求解解析式时还可以假设交点式,几何图形存在性问题求解往往需要利用其性质,假设动点坐标,列方程求解.8.定义:函数l 与l '的图象关于y 轴对称,点(),0P t 是x 轴上一点,将函数l '的图象位于直线x t =左侧的部分,以x 轴为对称轴翻折,得到新的函数w 的图象,我们称函数w 是函数l 的对称折函数,函数w 的图象记作1F ,函数l 的图象位于直线x t =上以及右侧的部分记作2F ,图象1F 和2F 合起来记作图象F .例如:如图,函数l 的解析式为1y x =+,当1t =时,它的对称折函数w 的解析式为()11y x x =-<.(1)函数l 的解析式为21y x =-,当2t =-时,它的对称折函数w 的解析式为_______; (2)函数l 的解析式为1²12y x x =--,当42x -≤≤且0t =时,求图象F 上点的纵坐标的最大值和最小值;(3)函数l 的解析式为()2230y ax ax a a =--≠.若1a =,直线1y t =-与图象F 有两个公共点,求t 的取值范围.【答案】(1)()212y x x =+<-;(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩;图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-;(3)当3t =-,1t <≤,5t <<时,直线1y t =-与图象F 有两个公共点. 【解析】【分析】(1)根据对折函数的定义直接写出函数解析式即可;(2)先根据题意确定F 的解析式,然后根据二次函数的性质确定函数的最大值和最小值即可;(3)先求出当a=1时图像F 的解析式,然后分14t -=-、点(),1t t -落在223()y x x x t =--≥上和点(),1t t -落在()223y x x x t =--+<上三种情况解答,最后根据图像即可解答.【详解】解:(1)()212y x x =+<-(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩当4x =-时,3y =-,当1x =-时,32y =, 当1x =时,32y =-,当2x =时,1y =, ∴图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-. (3)当1a =时,图象F 的解析式为2223()23()y x x x t y x x x t ⎧=--≥⎨=--+<⎩∴该函数的最大值和最小值分别为4和-4;a :当14t -=-时,3t =-,∴当3t =-时直线1y t =-与图象F 有两个公共点;b :当点(),1t t -落在223()y x x x t =--≥上时,2123t t t -=--,解得13172t -=,23172t += c :当点(),1t t -落在()223y x x x t =--+<上时,2123t t t -=--+,解得34t =-(舍),41t =14t -=,∴55t =∴当31712t -<≤或31752t +<<时,直线1y t =-与图象F 有两个公共点; 综上所述:当3t =-,3171t -<≤,3175t +<<时,直线1y t =-与图象F 有两个公共点.【点睛】本题属于二次函数综合题,考查了“称折函数”的定义、二次函数的性质、解二元一次方程等知识,弄清题意、灵活运用所学知识是解答本题的关键.9.如图,在平面直角坐标系中,抛物线y =﹣12x 2+bx +c 与x 轴交于B ,C 两点,与y 轴交于点A ,直线y =﹣12x +2经过A ,C 两点,抛物线的对称轴与x 轴交于点D ,直线MN 与对称轴交于点G ,与抛物线交于M ,N 两点(点N 在对称轴右侧),且MN ∥x 轴,MN =7.(1)求此抛物线的解析式.(2)求点N 的坐标.(3)过点A 的直线与抛物线交于点F ,当tan ∠FAC =12时,求点F 的坐标. (4)过点D 作直线AC 的垂线,交AC 于点H ,交y 轴于点K ,连接CN ,△AHK 沿射线AC 以每秒1个单位长度的速度移动,移动过程中△AHK 与四边形DGNC 产生重叠,设重叠面积为S ,移动时间为t (0≤t 5S 与t 的函数关系式.【答案】(1)y =﹣12x 2+32x +2;(2)点N 的坐标为(5,-3);(3)点F 的坐标为:(3,2)或(173,﹣509);(4)25,049494t tS tt⎧⎛≤≤⎪⎪⎝⎭=-<≤+<≤.【解析】【分析】(1)点A、C的坐标分别为(0,2)、(4,0),将点A、C坐标代入抛物线表达式即可求解;(2)抛物线的对称轴为:x=32,点N的横坐标为:37522+=,即可求解;(3)分点F在直线AC下方、点F在直线AC的上方两种情况,分别求解即可;(4)分0≤t<t<t【详解】解:(1)直线y=﹣12x+2经过A,C两点,则点A、C的坐标分别为(0,2)、(4,0),则c=2,抛物线表达式为:y=﹣12x2+bx+2,将点C坐标代入上式并解得:b=32,故抛物线的表达式为:y=﹣12x2+32x+2…①;(2)抛物线的对称轴为:x=32,点N的横坐标为:375 22+=,故点N的坐标为(5,-3);(3)∵tan∠ACO=2142AOCO===tan∠FAC=12,即∠ACO=∠FAC,①当点F在直线AC下方时,设直线AF交x轴于点R,∵∠ACO=∠FAC,则AR=CR,设点R(r,0),则r2+4=(r﹣4)2,解得:r=32,即点R的坐标为:(32,0),将点R、A的坐标代入一次函数表达式:y=mx+n得:230 2nm n=⎧⎪⎨+=⎪⎩,解得:432mn⎧=-⎪⎨⎪=⎩,故直线AR的表达式为:y=﹣43x+2…②,联立①②并解得:x=173,故点F(173,﹣509);②当点F在直线AC的上方时,∵∠ACO=∠F′AC,∴AF′∥x轴,则点F′(3,2);综上,点F的坐标为:(3,2)或(173,﹣509);(4)如图2,设∠ACO=α,则tanα=12AOCO=,则sinα5,cosα5①当0≤t 35时(左侧图),设△AHK移动到△A′H′K′的位置时,直线H′K′分别交x轴于点T、交抛物线对称轴于点S,则∠DST =∠ACO =α,过点T 作TL ⊥KH ,则LT =HH ′=t ,∠LTD =∠ACO =α,则DT ='52co 5c s 2os L HH T t αα===,DS =tan DT α, S =S △DST =12⨯DT ×DS =254t ; 35<t 35时(右侧图), 同理可得:S =''DGS T S 梯形=12⨯DG ×(GS ′+DT ′)=12⨯3+55﹣323594-; 35<t 53594+; 综上,S =2535,023593535,(245435935(5)1044t t t t t t ⎧⎛≤≤⎪ ⎪⎝⎭⎪⎪⎨-<≤⎪⎪⎪+<≤⎪⎩. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、图形平移、图形的面积计算等,其中(3)、(4),要注意分类求解,避免遗漏.10.如图,经过原点的抛物线2y ax x b =-+与直线2y =交于A ,C 两点,其对称轴是直线2x =,抛物线与x 轴的另一个交点为D ,线段AC 与y 轴交于点B .(1)求抛物线的解析式,并写出点D 的坐标;(2)若点E 为线段BC 上一点,且2EC EA -=,点(0,)P t 为线段OB 上不与端点重合的动点,连接PE ,过点E 作直线PE 的垂线交x 轴于点F ,连接PF ,探究在P 点运动过程中,线段PE ,PF 有何数量关系?并证明所探究的结论;(3)设抛物线顶点为M ,求当t 为何值时,DMF ∆为等腰三角形?【答案】(1)214y x x =-;点D 的坐标为(4,0);(2)5PF PE =,理由见解析;(3)512t =或98t = 【解析】【分析】(1)先求出a 、b 的值,然后求出解析式,再求出点D 的坐标即可;(2)由题意,先求出点E 的坐标,然后证明Rt Rt PBE FHE ∆∆∽,得到2EF PE =,结合勾股定理,即可得到答案;(3)根据题意,可分为三种情况进行分析:FM FD =或DF DM =或FM MD =,分别求出三种情况的值即可.【详解】解:(1)∵抛物线2y ax x b =-+经过原点, ∴0b =.又抛物线的对称轴是直线2x =,∴122a --=,解得:14a =. ∴抛物线的解析式为:214y x x =-. 令2104y x x =-=, 解得:10x =,24x =.∴点D 的坐标为(4,0).(2)线段PE 、PF 的数量关系为:5PF PE =.证明:由抛物线的对称性得线段AC 的中点为(2,2)G ,如图①,AE EG GC +=,∴EG GC AE =-,∴EG EG EG GC AE EC EA +=+-=-,∵2EC EA -=,∴1EG =,∴(1,2)E ,过点E 作EH x ⊥轴于H ,则2EH OB ==.∵PE EF ⊥,∴90PEF ∠=︒,∵BE EH ⊥,∴90BEH ∠=︒.∴PEB HEF ∠=∠.在Rt PBE ∆与Rt FHE ∆中,∵PEB HEF ∠=∠,90EHF EBP ∠=∠=︒,∴Rt Rt PBE FHE ∆∆∽,∴12PE BE EF HE ==, ∴2EF PE =. 在Rt PEF ∆中,由勾股定理得:222222(2)5PF PE EF PE PE PE =+=+=,∴5PF PE =.(3)由2211(2)144y x x x =-=--, ∴顶点M 坐标为(2,1)-.若DMF ∆为等腰三角形,可能有三种情形:(I )若FM FD =.如图②所示:连接MG 交x 轴于点N ,则90MNF ∠=︒,∵(4,0)D ,∴2222125MD MN ND =+=+=. 设FM FD k ==,则2NF k =-.在Rt MNF ∆中,由勾股定理得:222NF MN MF +=,∴22(2)1k k -+=,解得:54k =, ∴54FM =,34NF =, ∴1MN =,即点M 的纵坐标为1-;令1y =-,则2114x x -=-, ∴2x =,即ON=2,∴OF=114, ∴11,04F ⎛⎫ ⎪⎝⎭. ∵(1,2)E ,∴1,2BE BP t ==-,∴221(2)PE t =+-,∴251(2)PF t =•+-,在Rt △OPF 中,由勾股定理,得222OP OF PF +=,∴22211()55(2)4t t +=+-, ∴98t =. (II )若DF DM =.如图③所示:此时5FD DM ==∴45OF =,∴(45,0)F ,由(I )知,PE =,PF =在Rt △OPF 中,由勾股定理,得222OP OF PF +=,∴222(455(2)t t +-=+-∴12t =. (III )若FM MD =.由抛物线对称性可知,此时点F 与原点O 重合.∵PE EF ⊥,点P 在直线AC 上方,与点P 在线段OB 上运动相矛盾,故此种情形不存在.【点睛】本题考查的是二次函数综合运用,涉及到相似三角形的判定和性质,一次函数的性质,等腰三角形的性质,全等三角形的判定和性质,以及勾股定理等知识,其中(3),要注意分类求解,避免遗漏.。
北京市山谷学校数学几何模型压轴题(培优篇)(Word版 含解析)

北京市山谷学校数学几何模型压轴题(培优篇)(Word 版 含解析)一、初三数学 旋转易错题压轴题(难)1.如图1,在Rt ABC △中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是_________,位置关系是_________;(2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4=AD ,10AB =,请直接写出PMN 面积的最大值.【答案】(1)PM PN =,PM PN ⊥;(2)等腰直角三角形,见解析;(3)492【解析】【分析】(1)由三角形中位线定理及平行的性质可得PN 与PM 等于DE 或CE 的一半,又△ABC 为等腰直角三角形,AD=AE ,所以得PN=PM ,且互相垂直;(2)由旋转可推出BAD CAE ∆∆≌,再利用PM 与PN 皆为中位线,得到PM=PN ,再利用角度间关系推导出垂直即可;(3)找到面积最大的位置作出图形,由(2)可知PM=PM ,且PM ⊥PN ,利用三角形面积公式求解即可.【详解】(1)PM PN =,PM PN ⊥;已知点M ,P ,N 分别为DE ,DC ,BC 的中点,根据三角形的中位线定理可得 12PM EC =,12PN BD =,//PM EC ,//PN BD 根据平行线性质可得DPM DCE ∠=∠,NPD ADC ∠=∠在Rt ABC ∆中,90A ∠=︒,AB AC =,AD AE =可得BD EC =,90DCE ADC ∠+∠=︒即得PM PN =,PM PN ⊥故答案为:PM PN =;PM PN ⊥.(2)等腰直角三角形,理由如下:由旋转可得BAD CAE ∠=∠,又AB AC =,AD AE =∴BAD CAE ∆∆≌∴BD CE =,ABD ACE ∠=∠,∵点M ,P 分别为DE ,DC 的中点∴PM 是DCE ∆的中位线∴12PM CE =,且//PM CE , 同理可证12PN BD =,且//PN BD ∴PM PN =,MPD ECD ∠=∠,PNC DBC ∠=∠,∴MPD ECD ACD ACE ACD ABD ∠=∠=∠+∠=∠+∠,DPN PNC PCN DBC PCN ∠=∠+∠=∠+∠,∴90MPN MPD DPN ACD ABD DBC PCN ABC ACB ∠=∠+∠=∠+∠+∠+∠=∠+∠=︒,即PMN ∆为等腰直角三角形.(3)把ADE ∆绕点A 旋转的如图的位置,此时1()72PN AD AB =+=,1()72PM AE AC =+= 且PN 、PM 的值最长,由(2)可知PM PN =,PM PN ⊥ 所以PMN ∆面积最大值为1497722⨯⨯=. 【点睛】本题主要考查三角形中位线的判定及性质、全等三角形的判定及性质、等腰直角三角形的判定及性质、旋转的性质等相关知识,解题关键在于找到图形中各角度之间的数量关系.2.(1)观察猜想如图(1),在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点.以点D为顶点作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG,则线段BG和AE的数量关系是_____;(2)拓展探究将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,则(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.(3)解决问题若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,直接写出AF的值.【答案】(1)BG=AE.(2)成立.如图②,连接AD.∵△ABC是等腰三直角角形,∠BAC=90°,点D是BC的中点.∴∠ADB=90°,且BD=AD.∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE,DG=DE.∴△BDG≌△ADE,∴BG=AE.…………………………………………7分(3)由(2)知,BG=AE,故当BG最大时,AE也最大.正方形DEFG绕点D逆时针方向旋转270°时,BG最大,如图③.若BC=DE=2,则AD=1,EF=2.在Rt△AEF中,AF2=AE2+EF2=(AD+DE)2+EF2=(1+2)2+22=13.∴AF=【解析】解:(1)BG=AE.(2)成立.如图②,连接AD.∵△ABC是等腰三直角角形,∠BAC=90°,点D是BC的中点.∴∠ADB=90°,且BD=AD.∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE,DG=DE.∴△BDG≌△ADE,∴BG=AE.(3)由(2)知,BG=AE,故当BG最大时,AE也最大.Z+X+X+K]因为正方形DEFG在绕点D旋转的过程中,G点运动的图形是以点D为圆心,DG为半径的圆,故当正方形DEFG旋转到G点位于BC的延长线上(即正方形DEFG绕点D逆时针方向旋转270°)时,BG最大,如图③.若BC=DE=2,则AD=1,EF=2.在Rt△AEF中,AF2=AE2+EF2=(AD+DE)2+EF2=(1+2)2+22=13.∴AF=.即在正方形DEFG旋转过程中,当AE为最大值时,AF=.3.阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE,(1)在图1中证明小胖的发现;借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).【答案】(1)证明见解析;(2)证明见解析;(3)∠EAF =12 m°.【解析】分析:(1)如图1中,欲证明BD=EC,只要证明△DAB≌△EAC即可;(2)如图2中,延长DC到E,使得DB=DE.首先证明△BDE是等边三角形,再证明△ABD≌△CBE即可解决问题;(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.想办法证明△AFE≌△AFG,可得∠EAF=∠FAG=12 m°.详(1)证明:如图1中,∵∠BAC=∠DAE ,∴∠DAB=∠EAC ,在△DAB 和△EAC 中,AD AE DAB EAC AB AC ⎧⎪∠∠⎨⎪⎩===, ∴△DAB ≌△EAC ,∴BD=EC .(2)证明:如图2中,延长DC 到E ,使得DB=DE.∵DB=DE ,∠BDC=60°,∴△BDE 是等边三角形,∴∠BD=BE ,∠DBE=∠ABC=60°,∴∠ABD=∠CBE ,∵AB=BC ,∴△ABD ≌△CBE ,∴AD=EC ,∴BD=DE=DC+CE=DC+AD .∴AD+CD=BD .(3)如图3中,将AE 绕点E 逆时针旋转m°得到AG ,连接CG 、EG 、EF 、FG ,延长ED 到M ,使得DM=DE ,连接FM 、CM .由(1)可知△EAB≌△GAC,∴∠1=∠2,BE=CG,∵BD=DC,∠BDE=∠CDM,DE=DM,∴△EDB≌△MDC,∴EM=CM=CG,∠EBC=∠MCD,∵∠EBC=∠ACF,∴∠MCD=∠ACF,∴∠FCM=∠ACB=∠ABC,∴∠1=3=∠2,∴∠FCG=∠ACB=∠MCF,∵CF=CF,CG=CM,∴△CFG≌△CFM,∴FG=FM,∵ED=DM,DF⊥EM,∴FE=FM=FG,∵AE=AG,AF=AF,∴△AFE≌△AFG,∴∠EAF=∠FAG=12 m°.点睛:本题考查几何变换综合题、旋转变换、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会利用“手拉手”图形中的全等三角形解决问题,学会构造“手拉手”模型,解决实际问题,属于中考压轴题.4.(1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.填空:线段AD,BE之间的关系为 .(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.(3)解决问题如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B 的位置的变化,直接写出PC 的范围.【答案】(1) AD=BE ,AD⊥BE.(2) AD=BE ,AD⊥BE.(3) 5-32≤PC≤5+32.【解析】【分析】(1)根据等腰三角形性质证△ACD ≌△BCE (SAS ),得AD=BE ,∠EBC=∠CAD ,延长BE 交AD 于点F ,由垂直定义得AD ⊥BE .(2)根据等腰三角形性质证△ACD ≌△BCE (SAS ),AD=BE ,∠CAD=∠CBE ,由垂直定义得∠OHB=90°,AD ⊥BE ;(3)作AE ⊥AP ,使得AE=PA ,则易证△APE ≌△ACP ,PC=BE ,当P 、E 、B 共线时,BE 最小,最小值=PB-PE ;当P 、E 、B 共线时,BE 最大,最大值=PB+PE ,故5-32≤BE≤5+32.【详解】(1)结论:AD=BE ,AD ⊥BE .理由:如图1中,∵△ACB 与△DCE 均为等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ACD=90°,在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩=== ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠EBC=∠CAD延长BE 交AD 于点F ,∵BC ⊥AD ,∴∠EBC+∠CEB=90°,∵∠CEB=AEF ,∴∠EAD+∠AEF=90°,∴∠AFE=90°,即AD⊥BE.∴AD=BE,AD⊥BE.故答案为AD=BE,AD⊥BE.(2)结论:AD=BE,AD⊥BE.理由:如图2中,设AD交BE于H,AD交BC于O.∵△ACB与△DCE均为等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∴ACD=∠BCE,在Rt△ACD和Rt△BCE中AC BCACD BCECD CE⎧⎪∠∠⎨⎪⎩===,∴△ACD≌△BCE(SAS),∴AD=BE,∠CAD=∠CBE,∵∠CAO+∠AOC=90°,∠AOC=∠BOH,∴∠BOH+∠OBH=90°,∴∠OHB=90°,∴AD⊥BE,∴AD=BE,AD⊥BE.(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,∴PC=BE,图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-32,图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+32,∴5-32≤BE≤5+32,即5-32≤PC≤5+32.【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.5.如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.①在旋转过程中,当∠OAG′是直角时,求α的度数;②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.【答案】(1)见解析;(2)①30°或150°,②AF'的长最大值为2 22 +315α=.【解析】【分析】(1)延长ED交AG于点H,易证△AOG≌△DOE,得到∠AGO=∠DEO,然后运用等量代换证明∠AHE=90°即可;(2)①在旋转过程中,∠OAG′成为直角有两种情况:α由0°增大到90°过程中,当∠OAG′=90°时,α=30°,α由90°增大到180°过程中,当∠OAG′=90°时,α=150°;②当旋转到A、O 2,此时α=315°.【详解】(1)如图1,延长ED交AG于点H,∵点O是正方形ABCD两对角线的交点,∴OA=OD,OA⊥OD,∵OG=OE,在△AOG和△DOE中,90OA ODAOG DOEOG OE=⎧⎪∠=∠=︒⎨⎪=⎩,∴△AOG≌△DOE,∴∠AGO=∠DEO,∵∠AGO+∠GAO=90°,∴∠GAO+∠DEO=90°,∴∠AHE=90°,即DE⊥AG;(2)①在旋转过程中,∠OAG′成为直角有两种情况:(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,∵OA=OD=12OG=12OG′,∴在Rt△OAG′中,sin∠AG′O=OAOG'=12,∴∠AG′O=30°,∵OA⊥OD,OA⊥AG′,∴OD∥AG′,∴∠DOG′=∠AG′O=30°∘,即α=30°;(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,同理可求∠BOG′=30°,∴α=180°−30°=150°.综上所述,当∠OAG′=90°时,α=30°或150°.②如图3,当旋转到A. O、F′在一条直线上时,AF′的长最大,∵正方形ABCD的边长为1,∴OA=OD=OC=OB=22,∵OG=2OD,∴2,∴OF′=2,∴AF′=AO+OF′=22+2,∵∠COE′=45°,∴此时α=315°.【点睛】本题考查的是正方形的性质、旋转变换的性质以及锐角三角函数的定义,掌握正方形的四条边相等、四个角相等,旋转变换的性质是解题的关键,注意特殊角的三角函数值的应用.6.已知△ABC是边长为4的等边三角形,边AB在射线OM上,且OA=6,点D是射线OM上的动点,当点D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.(1)如图1,求证:△CDE是等边三角形.(2)设OD=t,①当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE周长的最小值;若不存在,请说明理由.②求t为何值时,△DEB是直角三角形(直接写出结果即可).【答案】(1)见解析;(2)①见解析;②t=2或14.【解析】【分析】(1)由旋转的性质得到∠DCE=60°,DC=EC,即可得到结论;(2)①当6<t<10时,由旋转的性质得到BE=AD,于是得到C△DBE=BE+DB+DE=AB+DE=4+DE,根据等边三角形的性质得到DE=CD,由垂线段最短得到当CD⊥AB时,△BDE的周长最小,于是得到结论;②存在,当点D与点B重合时,D,B,E不能构成三角形;当0≤t<6时,由旋转的性质得到∠ABE=60°,∠BDE<60°,求得∠BED=90°,根据等边三角形的性质得到∠DEB=60°,求得∠CEB=30°,求得OD=OA-DA=6-4=2=t;当6<t<10时,此时不存在;当t>10时,由旋转的性质得到∠DBE=60°,求得∠BDE>60°,于是得到t=14.【详解】(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE,∴∠DCE=60°,DC=EC,∴△CDE是等边三角形;(2)①存在,当6<t<10时,由旋转的性质得,BE=AD,∴C△DBE=BE+DB+DE=AB+DE=4+DE,由(1)知,△CDE是等边三角形,∴DE=CD,∴C△DBE=CD+4,由垂线段最短可知,当CD⊥AB时,△BDE的周长最小,此时,CD=3,∴△BDE的最小周长=CD+4=3;②存在,∵当点D与点B重合时,D,B,E不能构成三角形,∴当点D与点B重合时,不符合题意;当0≤t<6时,由旋转可知,∠ABE=60°,∠BDE<60°,∴∠BED=90°,由(1)可知,△CDE是等边三角形,∴∠DEB=60°,∴∠CEB=30°,∵∠CEB=∠CDA,∴∠CDA=30°,∵∠CAB=60°,∴∠ACD=∠ADC=30°,∴DA=CA=4,∴OD=OA﹣DA=6﹣4=2,∴t=2;当6<t<10时,由∠DBE=120°>90°,∴此时不存在;当t>10时,由旋转的性质可知,∠DBE=60°,又由(1)知∠CDE=60°,∴∠BDE=∠CDE+∠BDC=60°+∠BDC,而∠BDC>0°,∴∠BDE>60°,∴只能∠BDE=90°,从而∠BCD=30°,∴BD=BC=4,∴OD=14,∴t=14,综上所述:当t=2或14时,以D、E、B为顶点的三角形是直角三角形.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,三角形周长的计算,直角三角形的判定,熟练掌握旋转的性质是解题的关键.7.如图,矩形OABC的顶点A在x轴正半轴上,顶点C在y轴正半轴上,点B的坐标为(4,m)(5≤m≤7),反比例函数y=16x(x>0)的图象交边AB于点D.(1)用m的代数式表示BD的长;(2)设点P在该函数图象上,且它的横坐标为m,连结PB,PD①记矩形OABC面积与△PBD面积之差为S,求当m为何值时,S取到最大值;②将点D绕点P逆时针旋转90°得到点E,当点E恰好落在x轴上时,求m的值.【答案】(1)BD=m﹣4(2)①m=7时,S取到最大值②m=5【解析】【分析】(1)先确定出点D横坐标为4,代入反比例函数解析式中求出点D横坐标,即可得出结论;(2)①先求出矩形OABC的面积和三角形PBD的面积得出S=﹣12(m﹣8)2+24,即可得出结论;②利用一线三直角判断出DG=PF,进而求出点P的坐标,即可得出结论.【详解】解:(1)∵四边形OABC是矩形,∴AB⊥x轴上,∵点B(4,m),∴点D的横坐标为4,∵点D在反比例函数y=16x上,∴D(4,4),∴BD=m﹣4;(2)①如图1,∵矩形OABC的顶点B的坐标为(4,m),∴S矩形OABC=4m,由(1)知,D(4,4),∴S△PBD=12(m﹣4)(m﹣4)=12(m﹣4)2,∴S=S矩形OABC﹣S△PBD=4m﹣12(m﹣4)2=﹣12(m﹣8)2+24,∴抛物线的对称轴为m=8,∵a<0,5≤m≤7,∴m=7时,S取到最大值;②如图2,过点P作PF⊥x轴于F,过点D作DG⊥FP交FP的延长线于G,∴∠DGP=∠PFE=90°,∴∠DPG+∠PDG=90°,由旋转知,PD=PE,∠DPE=90°,∴∠DPG+∠EPF=90°,∴∠PDG=∠EPF,∴△PDG≌△EPF(AAS),∴DG=PF,∵DG=AF=m﹣4,∴P(m,m﹣4),∵点P在反比例函数y=16x,∴m(m﹣4)=16,∴m=m=2﹣【点睛】此题是反比例函数综合题,主要考查了待定系数法,矩形的性质,三角形的面积公式,全等三角形的判定,构造出全等三角形是解本题的关键.8.在矩形ABCD 中,2AB =,1BC =,以点A 为旋转中心,逆时针旋转矩形ABCD ,旋转角为(0180)αα<<,得到矩形AEFG ,点B 、点C 、点D 的对应点分别为点E 、点F 、点G .()1如图①,当点E 落在DC 边上时,直写出线段EC 的长度为______;()2如图②,当点E 落在线段CF 上时,AE 与DC 相交于点H ,连接AC ,①求证:ACD ≌CAE ;②直接写出线段DH 的长度为______.()3如图③设点P 为边FG 的中点,连接PB ,PE ,在矩形ABCD 旋转过程中,BEP 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.【答案】(1)23;(2)①见解析;34②;(3)存在,PBE 的面积的最大值为21,理由见解析【解析】【分析】()1如图①中,在Rt ADE 中,利用勾股定理即可解决问题;()2①证明:如图②中,根据HL 即可证明ACD ≌CAE ;②如图②中,由ACD ≌CAE ,推出ACD CAE ∠∠=,推出AH HC =,设AH HC m ==,在Rt ADH 中,根据222AD DH AH +=,构建方程即可解决问题; ()3存在.如图③中,连接PA ,作BM PE ⊥交PE 的延长线于M.由题意:PF PC 1==,由AG EF 1==,G F 90∠∠==,推出PA PE ==PBE 1S PE BM 22=⋅⋅=,推出当BM 的值最大时,PBE 的面积最大,求出BM 的最大值即可解决问题;【详解】()1四边形ABCD 是矩形,AB CD 2∴==,BC AD 1==,D 90∠=,矩形AEFG 是由矩形ABCD 旋转得到,AE AB 2∴==,在Rt ADE 中,DE ==CE 2∴=,故答案为2.()2①当点E 落在线段CF 上,AEC ADC 90∠∠∴==,在Rt ADC 和Rt AEC 中,{AC CACD AE ==, Rt ACD ∴≌()Rt CAE HL ; ACD ②≌CAE ,ACD CAE ∠∠∴=,AH HC ∴=,设AH HC m ==,在Rt ADH 中,222AD DH AH +=,2221(2m)m ∴+-=,5m 4∴=, 53DH 244∴=-=,故答案为34;()3存在.理由如下:如图③中,连接PA,作BM PE⊥交PE的延长线于M,由题意:PF PC1==,AG EF1==,G F90∠∠==,PA PE2∴==,PBE 12S PE BM BM2∴=⋅⋅=,∴当BM的值最大时,PBE的面积最大,BM PB≤,PB AB PA≤+,PB22∴≤+,BM22∴≤+,BM∴的最大值为22+,PBE∴的面积的最大值为21+.【点睛】本题是四边形综合题,考查了矩形的性质,旋转变换,全等三角形的判定和性质,勾股定理,三角形的面积,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.二、初三数学圆易错题压轴题(难)9.如图,抛物线的对称轴为轴,且经过(0,0),()两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),(1)求的值;(2)求证:点P在运动过程中,⊙P始终与轴相交;(3)设⊙P与轴相交于M,N(<)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.【答案】(1)a=,b=c=0;(2)证明见解析;(3)P的纵坐标为0或4+2或4﹣2.【解析】试题分析:(1)根据题意得出二次函数一般形式进而将已知点代入求出a,b,c的值即可;(2)设P(x,y),表示出⊙P的半径r,进而与x2比较得出答案即可;(3)分别表示出AM,AN的长,进而分别利用当AM=AN时,当AM=MN时,当AN=MN 时,求出a的值,进而得出圆心P的纵坐标即可.试题解析:(1)∵抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,∴抛物线的一般式为:y=ax2,∴=a()2,解得:a=±,∵图象开口向上,∴a=,∴抛物线解析式为:y=x2,故a=,b=c=0;(2)设P(x,y),⊙P的半径r=,又∵y=x2,则r=,化简得:r=>x2,∴点P在运动过程中,⊙P始终与x轴相交;(3)设P(a,a2),∵PA=,作PH⊥MN于H,则PM=PN=,又∵PH=a2,则MH=NH==2,故MN=4,∴M(a﹣2,0),N(a+2,0),又∵A(0,2),∴AM=,AN=,当AM=AN时,=,解得:a=0,当AM=MN时,=4,解得:a=2±2(负数舍去),则a2=4+2;当AN=MN时,=4,解得:a=﹣2±2(负数舍去),则a2=4﹣2;综上所述,P的纵坐标为0或4+2或4﹣2.考点:二次函数综合题.10.已知圆O的半径长为2,点A、B、C为圆O上三点,弦BC=AO,点D为BC的中点,(1)如图,连接AC 、OD ,设∠OAC=α,请用α表示∠AOD ;(2)如图,当点B 为AC 的中点时,求点A 、D 之间的距离:(3)如果AD 的延长线与圆O 交于点E ,以O 为圆心,AD 为半径的圆与以BC 为直径的圆相切,求弦AE 的长.【答案】(1)1502AOD α∠=︒-;(2)7AD =;(3)331331or +- 【解析】【分析】(1)连接OB 、OC ,可证△OBC 是等边三角形,根据垂径定理可得∠DOC 等于30°,OA=OC 可得∠ACO=∠CAO=α,利用三角形的内角和定理即可表示出∠AOD 的值.(2)连接OB 、OC ,可证△OBC 是等边三角形,根据垂径定理可得∠DOB 等于30°,因为点D 为BC 的中点,则∠AOB=∠BOC=60°,所以∠AOD 等于90°,根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD 、AD 的长.(3)分两种情况讨论:两圆外切,两圆内切.先根据两圆相切时圆心距与两圆半径的关系,求出AD 的长,再过O 点作AE 的垂线,利用勾股定理列出方程即可求解.【详解】(1)如图1:连接OB 、OC.∵BC=AO∴OB=OC=BC∴△OBC 是等边三角形∴∠BOC=60°∵点D 是BC 的中点∴∠BOD=1302BOC ∠=︒ ∵OA=OC∴OAC OCA ∠=∠=α∴∠AOD=180°-α-α-30︒=150°-2α(2)如图2:连接OB 、OC 、OD.由(1)可得:△OBC 是等边三角形,∠BOD=1302BOC ∠=︒ ∵OB=2,∴OD=OB∙cos 30︒=3∵B 为AC 的中点, ∴∠AOB=∠BOC=60°∴∠AOD=90°根据勾股定理得:AD=227AO OD +=(3)①如图3.圆O 与圆D 相内切时:连接OB 、OC ,过O 点作OF ⊥AE∵BC 是直径,D 是BC 的中点∴以BC 为直径的圆的圆心为D 点由(2)可得:3D 的半径为1∴31设AF=x在Rt △AFO 和Rt △DOF 中,2222OA AF OD DF -=-即)2222331x x -=-- 解得:331x += ∴AE=3312AF +=②如图4.圆O 与圆D 相外切时:连接OB 、OC ,过O 点作OF ⊥AE∵BC 是直径,D 是BC 的中点∴以BC 为直径的圆的圆心为D 点由(2)可得:OD=3,圆D 的半径为1∴AD=31-在Rt △AFO 和Rt △DOF 中,2222OA AF OD DF -=-即()2222331x x -=--+解得:331x -= ∴AE=3312AF -=【点睛】本题主要考查圆的相关知识:垂径定理,圆与圆相切的条件,关键是能灵活运用垂径定理和勾股定理相结合思考问题,另外需注意圆相切要分内切与外切两种情况.11.在平面直角坐标系xOy中,⊙C的半径为r(r>1),点P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:过圆心C的任意直线CP与⊙C交于点A,B,若满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图点P为⊙C的一个“完美点”.(1)当⊙O的半径为2时①点M(32,0)⊙O的“完美点”,点(﹣3,﹣12)⊙O的“完美点”;(填“是”或者“不是”)②若⊙O的“完美点”P在直线y=34x上,求PO的长及点P的坐标;(2)设圆心C的坐标为(s,t),且在直线y=﹣2x+1上,⊙C半径为r,若y轴上存在⊙C的“完美点”,求t的取值范围.【答案】(1)①不是,是;②PO的长为1,点P的坐标为(45,35)或(﹣45,﹣35);(2)t的取值范围为﹣1≤t≤3.【解析】【分析】(1)①利用圆的“完美点”的定义直接判断即可得出结论.②先确定出满足圆的“完美点”的OP的长度,然后分情况讨论计算即可得出结论;(2)先判断出圆的“完美点”的轨迹,然后确定出取极值时OC与y轴的位置关系即可得出结论.【详解】解:(1)①∵点M(32,0),∴设⊙O与x轴的交点为A,B,∵⊙O的半径为2,∴取A(﹣2,0),B(2,0),∴|MA﹣MB|=|(32+2)﹣(2﹣32)|=3≠2,∴点M不是⊙O的“完美点”,同理:点(﹣3,﹣12)是⊙O的“完美点”.故答案为不是,是.②如图1,根据题意,|PA﹣PB|=2,∴|OP+2﹣(2﹣OP)|=2,∴OP=1.若点P在第一象限内,作PQ⊥x轴于点Q,∵点P在直线y=34x上,OP=1,∴43,55 OQ PQ==.∴P(43,55).若点P在第三象限内,根据对称性可知其坐标为(﹣45,﹣35).综上所述,PO的长为1,点P的坐标为(43,55)或(43,55--)).(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|=2,∴|CP+r﹣(r﹣CP)|=2.∴CP=1.∴对于任意的点P,满足CP=1,都有|CP+r﹣(r﹣CP)|=2,∴|PA﹣PB|=2,故此时点P为⊙C的“完美点”.因此,⊙C的“完美点”是以点C为圆心,1为半径的圆.设直线y=﹣2x+1与y轴交于点D,如图2,当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.设切点为E,连接CE,∵⊙C的圆心在直线y=﹣2x+1上,∴此直线和y轴,x轴的交点D(0,1),F(12,0),∴OF=12,OD=1,∵CE∥OF,∴△DOF∽△DEC,∴OD OF DE CE=,∴112 DE=,∴DE=2,∴OE=3,t的最大值为3,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.同理可得t的最小值为﹣1.综上所述,t的取值范围为﹣1≤t≤3.【点睛】此题是圆的综合题,主要考查了新定义,相似三角形的性质和判定,直线和圆的位置关系,解本题的关键是理解新定义的基础上,会用新定义,是一道比中等难度的中考常考题.12.已知:AB为⊙O直径,弦CD⊥AB,垂足为H,点E为⊙O上一点,AE BE=,BE与CD交于点F.(1)如图1,求证:BH =FH ;(2)如图2,过点F 作FG ⊥BE ,分别交AC 、AB 于点G 、N ,连接EG ,求证:EB =EG ; (3)如图3,在(2)的条件下,延长EG 交⊙O 于M ,连接CM 、BG ,若ON =1,△CMG 的面积为6,求线段BG 的长.【答案】(1)见解析;(2)见解析;(3)210 .【解析】【分析】(1)连接AE ,根据直径所对圆周角等于90°及弧与弦的关系即可得解;(2)根据题意,过点C 作CQ FG CS FB ⊥⊥,,连接CE BC 、,通过证明Rt CGQ Rt CBS ∆≅∆,CBE CGE ∆≅∆即可得解;(3)根据题意,过点G 作GT CD ⊥于T ,连接CN ,设CAB α∠=,证明()CMG CNG AAS ∆≅∆,再由面积法及勾股定理进行计算求解即可.【详解】解:(1)如下图,连接AE∵AB 为直径∴90AEB =︒∠∵AE BE =∴AE BE =∴45B ∠=︒又∵CD AB ⊥于H ∴45HFB ∠=︒∴HF HB =;(2)如下图,过点C 作CQ FG CS FB ⊥⊥,,连接CE BC 、AB 为直径,∴90ACB QCS ∠=∠=︒∴GCQ BCS ∠=∠∴()Rt CGQ Rt CBS AAS ∆≅∆∴CG CB =同理()CBE CGE SAS ∆≅∆∴EG EB =;(3)如下图,过点G 作GT CD ⊥于T ,连接CN设CAB α∠=由(2)知:CM CB =∴CM CB =∵HB HF =∴45HBF HFB ∠=∠=︒∵GF BE ⊥∴45NFH NH BH CN BC ∠=︒∴=∴=,,∴CM CB CN ==则:2MEB α∠=902AEG α∠=︒-∴45EAG EGA α∠=∠=︒+∴45M MGC α∠=∠=︒+∴()CMG CNG AAS ∆≅∆∵CMG ∆面积为6∴6CAN GAN S S -=设2122BH NH x OA OB x AN x ====+=+,,则()CGT BCH AAS ∆≅∆∴C BH x ==∴6AN CH AN TH ⋅-⋅=∴1(22)62x CT +⋅= 解得:2x =∵2BC BH BA =⋅∴2210BC =⨯,则25BC = ∴2210BG BC ==.【点睛】本题主要考查了圆和三角形的综合问题,熟练掌握圆及三角形的各项重要性质及判定方法是解决本题的关键.13.如图.在Rt ABC 中,90ACB ∠=︒,6AC =,10AB =,DE 是ABC 的中位线,连结BD ,点F 是边BC 上的一个动点,连结AF 交BD 于H ,交DE 于G .(1)当点F 是BC 的中点时,求DH BH的值及GH 的长 (2) 当四边形DCFH 与四边形BEGH 的面积相等时,求CF 的长:(3)如图2.以CF 为直径作O . ①当O 正好经过点H 时,求证:BD 是O 的切线: ②当DH BH的值满足什么条件时,O 与线段DE 有且只有一个交点.【答案】(1)12DH BH =,133GH =;(2)83CF =;(3)①见解析;②当32DH BH =或2514DH BH >时,O 与线段DE 有且只有一个交点. 【解析】【分析】(1)根据题意得H 为ABC 的重心,即可得DH BH的值,由重心和中位线的性质求得16=GH AF ,由勾股定理求得AF 的长,即可得GH 的长; (2)根据图中面积的关系得S 四边形DCFG =DEB S ,列出关系式求解即可得CF 的长;(3)根据O 与线段DE 有且只有一个交点,可分两类情况讨论:当O 与DE 相切时,求得DH BH 的值;当O 过点E ,此时是O 与线段DE 有两个交点的临界点,即可得出O 与线段DE 有且只有一个交点时DH BH 满足的条件. 【详解】解:(1)∵DE 是ABC 的中位线,∴,D E 分别是,AC AB 的中点,//DE BC ,又∵点F 是BC 的中点,∴BD 与AF 的交点H 是ABC 的重心,:1:2DH BH ∴=,即12DH BH =;:1:2=HF AH , ∴13=HF AF , 在ACF 中,D 为AC 中点,//DE BC ,则//DG CF ,∴DG 为ACF 的中位线,G 为AF 的中点,12∴=GF AF , 111236∴=-=-=GH GF HF AF AF AF , 在Rt ABC 中,90ACB ∠=︒,6AC =,10AB =,8BC ∴===, 则142==CF BC ,AF ∴=16∴=⨯=GH ; (2)∵四边形DCFH 与四边形BEGH 的面积相等,∴S 四边形DCFH +DGH S=S 四边形BEGH +DGH S , 即S 梯形DCFG =DEB S ,∵6AC =,8BC =,DE 是ABC 的中位线,∴3CD =,4DE =, ∵1143622=⋅⋅=⨯⨯=DEB S DE CD , 设2CF a =,∵DG 为ACF 的中位线, ∴12==DG CF a ,则S 梯形DCFG ()3(2)622+⋅==+=DG CF CD a a , 解得:43a =, 823∴==CF a ; (3)①证明:如图2,连结、CH OH ,CF 为O 的直径,O 经过点H ,90∴∠=︒FHC ,∴90∠=∠=︒AHC FHC ,AHC 为直角三角形,D 为AC 的中点,12∴==DH AC CD , ∠∠∴=DCH DHC .又OC OH =,∴∠=∠OCH OHC ,∴∠+=∠+OCH DCH OHC DHC ,即90∠=∠=︒DHO ACB ,∴BH BD ⊥,即BD 是O 的切线;②如图3-1,当O 与DE 相切时,O 与线段DE 有且只有一个交点,设O 的半径为r ,圆心O 到DE 的距离为d ,∴当r=d 时,O 与DE 相切, ∵//DE CF ,90ACB ∠=︒,3CD =,∴两平行线、DE CF 之间的距离为3CD =,∴3r =,则6CF =,1862,32=-=-===BF BC CF DG CF , 由//DE CF 得:DGH BFH ,32DH DG BH BF ∴==; 如图3-2,当O 经过点E 时,连接OE 、OG , 设O 的半径为r ,即==OE OC r ,∵G 为AF 的中点,O 为CF 的中点,∴//OG CD ,∴四边形COGD 为平行四边形,又∵90ACB ∠=︒,∴四边形COGD 为矩形,∴90∠=︒DGO ,则90∠=︒OGE ,OGE 为直角三角形,∴=3=OG CD ,==DG OC r ,则4=-=-GE DE DG r ,由勾股定理得:222+=OG GE OE ,即2223(4)+-=r r , 解得:258r =,则258==OE OC ,2524==CF r 257258,448∴=-=-===BF BC CF DG OC ,由//DE BC 得:DGH BFH ,252514874∴===DH DG BH BF, 则当2514DH BH >时,O 与线段DE 有且只有一个交点; 综上所述,当32DH BH =或2514DH BH >时,O 与线段DE 有且只有一个交点. 【点睛】本题属于圆综合题,考查了切线的性质与判定、中位线的性质等知识,解题的关键是灵活添加常用的辅助线,属于中考压轴题.14.如图①②,在平面直角坐标系中,边长为2的等边CDE ∆恰好与坐标系中的OAB ∆重合,现将CDE ∆绕边AB 的中点(G G 点也是DE 的中点),按顺时针方向旋转180︒到△1C DE 的位置.(1)求1C 点的坐标;(2)求经过三点O 、A 、1C 的抛物线的解析式;(3)如图③,G 是以AB 为直径的圆,过B 点作G 的切线与x 轴相交于点F ,求切线BF 的解析式;(4)抛物线上是否存在一点M ,使得:16:3AMF OAB S S ∆∆=.若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】(1)13)C ;(2)2323y x x =;(3)323y x =;(4)128383,M M ⎛⎛- ⎝⎭⎝⎭.【解析】【分析】(1)利用中心对称图形的性质和等边三角形的性质,可以求出.(2)运用待定系数法,代入二次函数解析式,即可求出.(3)借助切线的性质定理,直角三角形的性质,求出F ,B 的坐标即可求出解析式. (4)当M 在x 轴上方或下方,分两种情况讨论.【详解】解:(1)将等边CDE ∆绕边AB 的中点G 按顺时针方向旋转180︒到△1C DE , 则有,四边形'OAC B 是菱形,所以1C 的横坐标为3,根据等边CDE ∆的边长是2, 利用等边三角形的性质可得13)C ;(2)抛物线过原点(0,0)O ,设抛物线解析式为2y ax bx =+,把(2,0)A ,3)C '代入,得420933a b a b +=⎧⎪⎨+=⎪⎩ 解得33a =,23b = ∴抛物线解析式为2323y x x =-;(3)90ABF ∠=︒,60BAF ∠=︒,30AFB ∴∠=︒,又2AB =,4AF ∴=,2OF ∴=, (2,0)F ∴-,设直线BF 的解析式为y kx b =+,把B ,(2,0)F -代入,得20k b k b ⎧+=⎪⎨-+=⎪⎩,解得3k =3b =,∴直线BF 的解析式为y x =+;(4)①当M 在x 轴上方时,存在2()M x ,211:[4)]:[216:322AMF OAB S S ∆∆=⨯⨯⨯=, 得2280x x --=,解得14x =,22x =-,当14x =时,244y ,当12x =-时,2(2)(2)y =--=1M ∴,2(M -;②当M 在x 轴下方时,不存在,设点2()M x x ,211:[4)]:[216:322AMF OAB S S ∆∆=-⨯⨯⨯=, 得2280x x -+=,240b ac -<无解,综上所述,存在点的坐标为1M ,2(M -. 【点睛】此题主要考查了旋转,等边三角形的性质,菱形的判定和性质,以及待定系数法求解二次函数解析式和切线的性质定理等,能熟练应用相关性质,是解题的关键.15.AB 是O 直径,,C D 分别是上下半圆上一点,且弧BC =弧BD ,连接,AC BC ,连接CD 交AB 于E ,(1)如图(1)求证:90AEC ∠=︒;(2)如图(2)F 是弧AD 一点,点,M N 分别是弧AC 和弧FD 的中点,连接FD ,连接MN 分别交AC ,FD 于,P Q 两点,求证:MPC NQD ∠=∠(3)如图(3)在(2)问条件下,MN 交AB 于G ,交BF 于L ,过点G 作GH MN ⊥交AF于H ,连接BH ,若,6,BG HF AG ABH ==∆的面积等于8,求线段MN 的长度【答案】(1)证明见解析;(2)证明见解析;(3)2410MN =. 【解析】【分析】(1)由垂径定理即可证明; (2)利用等弧所对的圆周角相等和三角形外角性质即可得到结论;(3)由∠MPC=∠NQD 可得:∠BGL=∠BLG ,BL=BG ,作BR ⊥MN ,GT ⊥AF ,HK ⊥AB ,证明:GH 平分∠AGT ,利用相似三角形性质和角平分线性质求得△AGT 三边关系,再求出HK 与GH ,OS ⊥MN ,再利用相似三角形性质求出OS ,利用勾股定理求MN 即可.【详解】解:()1证明:∵BC BD =,AB 为直径,∴AB ⊥CD∴∠AEC=90°;()2连接,OM ON ,∵点M 是弧AC 的中点,点N 是弧DF 的中点,∴AM CM =,FN DN =,∴,OM AC ON FD ⊥⊥,∵OM=ON ,∴M N ∠=∠,∵90M MPC N NQB ∠+∠=∠+∠=︒,MPC NQD ∴∠=∠;()3如图3,过G 作GT ⊥AF 于T ,过H 作HK ⊥AB 于K ,过B 作BR ⊥MN 于R ,过O 作OS ⊥MN 于S ,连接OM ,设BG=m ,∵△ABH 的面积等于8,AG=6 ∴HK=166m +, ∵BC BD =,∴∠BAC=∠BFD ,由(2)得∠MPC=∠NQD∴∠AGM=∠FLN∴∠BGL=∠BLG∴BL=BG ,∵BR ⊥MN∴∠ABR=∠FBR∵GH ⊥MN∴GH ∥BR∴∠AGH=∠ABR∵AB 是直径,GT ⊥AF∴∠AFB=∠ATG=90°∴GT ∥BF ,又∵GH ∥BR∴∠TGH=∠FBR∴∠AGH=∠TGH ,又∵HK ⊥AG ,HT ⊥GT , ∴HT=HK=166m +, ∵FH=BG=m , ∴FT=16(8)(2)66m m m m m +--=++, ∵GT ∥BF , ∴AT AG FT BG=, ∴6(8)(2)(6)m m AT m m +-=+,616m AH m -=,48(6)(38)m KG TG m m ==+-, ∵222AT TG AG +=,代入解得:m=4; ∴AB=10,OM=5,GK=245,HK=85,OG=1 ∴GH=8105, ∵OS ⊥MN∴∠OSG=∠GKH=90°,GH ∥OS∴∠HGK=∠GOS∴△HGK ∽△GOS ,∴OS GK OG GH=, ∴310OS =, ∴222410MG OM OG =-=, ∴2410MN =; 【点睛】 本题考查了圆的性质,圆周角定理,垂径定理,相似三角形判定和性质,勾股定理等,综合性较强,尤其是第(3)问难度很大,计算量大,解题的关键是熟练掌握所学的知识,正确作出辅助线,运用数形结合的思想进行解题.16.如图,在O 中,AB 为直径,过点A 的直线l 与O 相交于点C ,D 是弦CA 延长线上一点,BAC ∠,BAD ∠的平分线与O 分别相交于点E ,F ,G 是BF 的中点,过点G 作MNAE ,与AF ,EB 的延长线分别交于点M ,N .(1)求证:MN 是O 的切线; (2)若24AE =,18AM =. ①求O 的半径;②连接MC ,求tan MCD ∠的值. 【答案】(1)见解析;(2)①13;②2741 【解析】。
北京市山谷学校小升初数学期末试卷(培优篇)(Word版 含解析)
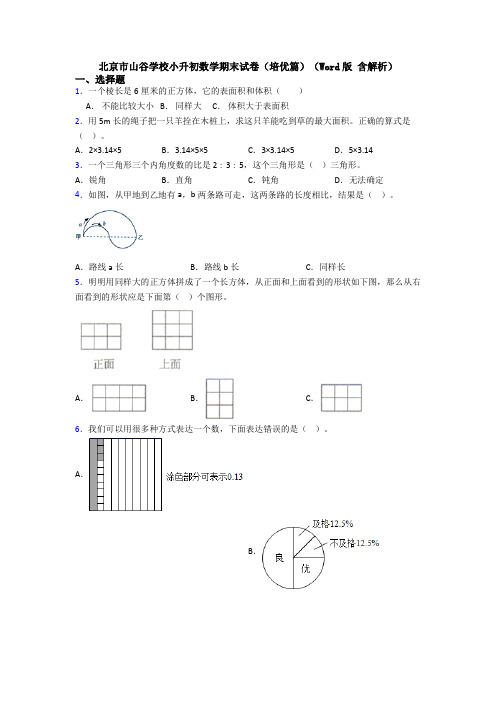
北京市山谷学校小升初数学期末试卷(培优篇)(Word版含解析)一、选择题1.一个棱长是6厘米的正方体,它的表面积和体积()A.不能比较大小 B.同样大 C.体积大于表面积2.用5m长的绳子把一只羊拴在木桩上,求这只羊能吃到草的最大面积。
正确的算式是()。
A.2×3.14×5 B.3.14×5×5 C.3×3.14×5 D.5×3.143.一个三角形三个内角度数的比是2∶3∶5,这个三角形是()三角形。
A.锐角B.直角C.钝角D.无法确定4.如图,从甲地到乙地有a,b两条路可走,这两条路的长度相比,结果是()。
A.路线a长B.路线b长C.同样长5.明明用同样大的正方体拼成了一个长方体,从正面和上面看到的形状如下图,那么从右面看到的形状应是下面第()个图形。
A.B.C.6.我们可以用很多种方式表达一个数,下面表达错误的是()。
A.B.C.D.7.笑笑用一张正方形纸如下图这样折叠4次,再沿虚线剪一刀,打开后的图形接近圆。
他这样做利用了圆的什么知识?下面说法中最贴切的是( )。
A.圆的周长永远是它的直径的兀倍B.同圆(等圆)中直径是半径的2倍C.正多边形边数越多越趋近圆D.圆是曲线图形8.出租车收费规定如下:3千米及3千米以下收费5元,超过3千米的部分(不足1千米的部分,按1千米算),每千米收费2元。
王老师上班坐出租车行驶4.6千米,应付出租车费()元。
A.10 B.9 C.79.将一张正方形纸连续对折4次后展开,其中一份占这张正方形纸的( ) .A.12B.14C.18D.116二、填空题10.34时=(______)分;3040立方厘米=(______)立方分米。
11.57的分数单位是(________),再添上(________)个这样的分数单位就是最小的质数。
12.30平方米比24平方米多(______)%,5米的(______)%是2米。
北京市山谷学校小升初数学期末试卷(培优篇)(Word版 含解析)

北京市山谷学校小升初数学期末试卷(培优篇)(Word版含解析)一、选择题1.在同一幅图上,如果点A用数对表示为(1,5),点B用数对表示为(1,1),点C 用数对表示为(3,1),那么三角形ABC一定是()三角形。
A.锐角B.直角C.钝角2.小刚小时走了千米,他每走1千米需多少小时?正确的算式是()A.÷ B.× C.÷3.一个三角形的三个内角度数的比是5∶2∶2这个三角形是()。
A.钝角三角形B.直角三角形C.锐角三角形4.用几个相同的小正方体拼成甲、乙两个图形,比较它们的表面积,结果是()。
A.表面积一样大B.甲的表面积大C.乙的表面积大D.无法比较5.如图是一个正方体纸盒的表面展开图,与数字3所在的面相对的面上的数字是()。
A.1 B.5 C.66.甲、乙、丙三个仓库各存粮食若干吨,已知甲仓库存粮是乙仓库的23,乙仓库存粮比丙仓库多25%,丙仓库存粮比甲仓库多40吨,下列说法中错误的是()。
A.丙仓库存粮是乙仓库的4 5B.甲仓库存粮是丙仓库的5 6C.甲、乙、丙三个仓库存粮的最简单的整数比是10∶15∶12D.甲仓库存粮240吨7.a是奇数,b是偶数,下面结果是奇数的式子是()。
A.a+b B.2a+b C.2(a+b)8.一种商品降价10%后再提价10%这种商品的价格()A.不变 B.低于原价 C.高于原价9.拼一个三角形用3根小棒,想一想,第8个图形需要用()根小棒。
A.24 B.17 C.20二、填空题10.地球上海洋的面积大约是三亿六千一百万平方千米,写作________平方千米,省略亿后面的尾数约是________亿平方千米。
11.136的分数单位是______,再添上______个这样的分数单位就是最小的合数。
12.已知A=2×C×7,B=2×C×5(C是不等于2,3,5的质数),A、B的最大公约数是(______),最小公倍数是(______)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、初一数学几何模型部分解答题压轴题精选(难)1.如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.(1)求证:∠EHC+∠GFE=180°.(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数. 【答案】(1)解:∵HG⊥HE,FG⊥HG∴FG∥EH,∴∠GFE+∠HEF=180°,∵AB∥CD∴∠BEH=∠CHE∴∠EHC+∠GFE=180°(2)解:设∠EHM=x,∵HG⊥HE,∴∠GHK=90°-x,∵MH平分∠CHG,∴∠EHC=90°-2x,∵AB∥CD∴∠HMB=90°-x,∴∠HMB=∠MHG=90°-x,∵AB∥CD,∴∠BMH+∠DHM=180°,即∠BMH+∠GHM+∠GHD =180°,∴90°-x+90°-x+∠GHD =180°,解得,∠GHD =2x,∴∠GHD=2∠EHM;(3)解:延长FG,GK,交CD于R,交HE于S,如图,∵AB∥CD,∠BFG=50°∴∠HRG=50°∵FG⊥HG,∴∠GHR=40°,∵HG⊥HE,∴∠EHG=90°,∴∠CHE=180°-90°-40°=50°,∵AB∥CD,∴∠FEH=∠CHE=50°,∵EP是∠HEF的平分线,∴∠SEP= ∠FEH=25°,∵GH平分∠HGF,∴∠HGS= ∠HGF=45°,∴∠HSG=45°,∵∠SEP+∠SPE=∠HSP=45°,∴∠EPS=20°,即∠NPK=20°.【解析】【分析】(1)根据HG⊥HE,FG⊥HG可证明FG∥EH,从而得∠GFE+∠HEF=180°,再根据AB∥CD可得∠BEH=∠CHE,进而可得结论;(2)设∠EHM=x,根据MH是∠CHG的平分线可得∠MHG=90°-x,∠EHC=90°-2x,根据平行线的性质得∠HMB=90°-x,从而得∠HMB=∠MHG,再由平行线的性质得∠BMH+∠DHM=180°,从而可得结论;(3)分别延长FG,GK,交CD于R,交HE于S,由AB∥CD得∠HRG=50°,由FG⊥HG得∠GHR=40°,由MH平分∠CHG得∠CHE=50°,由AB∥CD得∠MEH=∠CHE=50°,可得∠SEP=25°,最后由三角形的外角可得结论.2.探究题学习完平行线的性质与判定之后,我们发现借助构造平行线的方法可以帮我们解决许多问题。
(1)小明遇到了下面的问题:如图1,l1∥l2,点P在l1、l2内部,探究∠A,∠APB,∠B 的关系.小明过点P作l1的平行线,可证∠APB,∠A,∠B之间的数量关系是:∠APB=________.(2)如图2,若AC∥BD,点P在AB、CD外部,∠A,∠B,∠APB的数量关系是否发生变化?请你补全下面的证明过程.过点P作PE∥AC.∴∠A=________∵AC∥BD∴________∥________∴∠B=________∵∠BPA=∠BPE-∠EPA∴________.(3)随着以后的学习你还会发现平行线的许多用途.试构造平行线解决以下问题:已知:如图3,三角形ABC,求证:∠A+∠B+∠C=180°.【答案】(1)∠APB=∠A+∠B(2)∠1;PE;BD;∠EPB;∠APB=∠B -∠1(3)证明:过点A作MN∥BC∴∠B= ∠1∠C= ∠2∵∠BAC+∠1+∠2=180°∴∠BAC+∠B+∠C=180°【解析】【解答】解:(1)如图:由平行线的性质可得:∠1=∠A, ∠2=∠B,∴∠1+∠2=∠A+∠B即APB=∠A+∠B⑵解:过点P作PE∥AC.∴∠A=∠1∵AC∥BD∴ PE ∥ BD∴∠B=∠EPB∵∠APB=∠BPE-∠EPA∴∠APB=∠B -∠1【分析】根据图形做出平行辅助线,探究角度关系。
此类做辅助线的方法变式多,是考试热点问题。
3.已知:如图1,点M是线段AB上一定点,AB=12cm,C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)(1)若AM=4cm,当点C、D运动了2s,此时AC=________,DM=________;(直接填空)(2)当点C、D运动了2s,求AC+MD的值.(3)若点C、D运动时,总有MD=2AC,则AM=________(填空)(4)在(3)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值.【答案】(1)2;4(2)解:当点C、D运动了2 s时,CM=2 cm,BD=4 cm∵AB=12 cm,CM=2 cm,BD=4 cm∴AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD=12﹣2﹣4=6 cm(3)4(4)解:①当点N在线段AB上时,如图1,∵AN﹣BN=MN,又∵AN﹣AM=MN∴BN=AM=4∴MN=AB﹣AM﹣BN=12﹣4﹣4=4∴ = = ;②当点N在线段AB的延长线上时,如图2,∵AN﹣BN=MN,又∵AN﹣BN=AB∴MN=AB=12∴ = =1;综上所述 = 或1【解析】【解答】解:(1.)根据题意知,CM=2cm,BD=4cm,∵AB=12cm,AM=4cm,∴BM=8cm,∴AC=AM﹣CM=2cm,DM=BM﹣BD=4cm,故答案为:2,4;(3.)根据C、D的运动速度知:BD=2MC,∵MD=2AC,∴BD+MD=2(MC+AC),即MB=2AM,∵AM+BM=AB,∴AM+2AM=AB,∴AM= AB=4,故答案为:4;【分析】(1)根据运动速度和时间分别求得CM、BD的长,根据线段的和差计算可得;(2)由题意得CM=2 cm、BD=4 cm,根据AC+MD=AM﹣CM+BM﹣BD=AB﹣CM﹣BD可得答案;(3)根据C、D的运动速度知BD=2MC,再由已知条件MD=2AC求得MB=2AM,所以AM= AB;(4)分点N在线段AB上时和点N在线段AB的延长线上时分别求解可得.4.如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.(1)问运动多少时BC=8(单位长度)?(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是________;(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式 =3,若存在,求线段PD的长;若不存在,请说明理由.【答案】(1)解:设运动t秒时,BC=8单位长度,①当点B在点C的左边时,由题意得:6t+8+2t=24解得:t=2(秒);②当点B在点C的右边时,由题意得:6t﹣8+2t=24解得:t=4(秒)(2)解:4或16(3)解:存在关系式 =3.设运动时间为t秒,1)当t=3时,点B和点C重合,点P在线段AB上,0<PC≤2,且BD=CD=4,AP+3PC=AB+2PC=2+2PC,当PC=1时,BD=AP+3PC,即 =3;2)当3<t<时,点C在点A和点B之间,0<PC<2,①点P在线段AC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+2PC=AB﹣BC+2PC=2﹣BC+2PC,当PC=1时,有BD=AP+3PC,即 =3;点P在线段BC上时,BD=CD﹣BC=4﹣BC,AP+3PC=AC+4PC=AB﹣BC+4PC=2﹣BC+4PC,当PC= 时,有BD=AP+3PC,即 =3;3°当t= 时,点A与点C重合,0<PC≤2,BD=CD﹣AB=2,AP+3PC=4PC,当PC= 时,有BD=AP+3PC,即 =3;4°当<t 时,0<PC<4,BD=CD﹣BC=4﹣BC,AP+3PC=AB﹣BC+4PC=2﹣BC+4PC,PC= 时,有BD=AP+3PC,即 =3.∵P在C点左侧或右侧,∴PD的长有3种可能,即5或3.5【解析】【解答】解:(2)当运动2秒时,点B在数轴上表示的数是4;当运动4秒时,点B在数轴上表示的数是16.【分析】(1)设运动t秒时,BC=8(单位长度),然后分点B在点C的左边和右边两种情况,根据题意列出方程求解即可;(2)由(1)中求出的运动时间即可求出点B在数轴上表示的数;(3)随着点B的运动,分别讨论当点B和点C重合、点C在点A和B之间及点A与点C重合时的情况.5.如图1,直线MN与直线AB,CD分别交于点E,F,∠1与∠2互补(1)试判断直线AB与直线CD的位置关系,并说明理由(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH(3)如图3,在(2)的条件下,连结PH,在GH上取一点K,使得∠PKG=2∠HPK,过点P 作PQ平分∠EPK交EF于点Q,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.(温馨提示:三角形的三个内角和为180°.)【答案】(1)解:如图,∵∠1和∠2互补,∠2和∠3互补,∴∠1=∠3∴AB∥CD(2)解:如图,由(1)得AB∥CD,∴∠BEF+∠EFD=180°又∵∠BEF与∠EFD的角平分线交于点P,∴∠FEP+∠EFP= (∠BEF+∠EFD)=90°,∴∠EPF=90°,即EG⊥PF∵GH⊥EG,∴PF∥GH.(3)解:∠HPQ的大小不发生变化,理由如下:∵EG⊥HG,∴∠KGP=90°∴∠EPK=180°-∠4=180°-(180-∠3-∠KGP)=90°+∠3∵∠3=2∠6,∴∠EPK=90°+2∠6∵PQ平分∠EPK,∴∠QPK= ∠EPK=45°+∠6∴∠HPQ=∠QPK-∠6=45°∴∠HPQ的大小不发生变化,一直是45°【解析】【分析】(1)利用邻补角的定义可证得∠2与∠3互补,再根据同角的补角相等,可证得∠1=∠3,然后利用同位角相等,两直线平行,可证得结论。
