七年级数学专题规律探究题
七年级数学下学期末复习题(规律探究)与答案解析
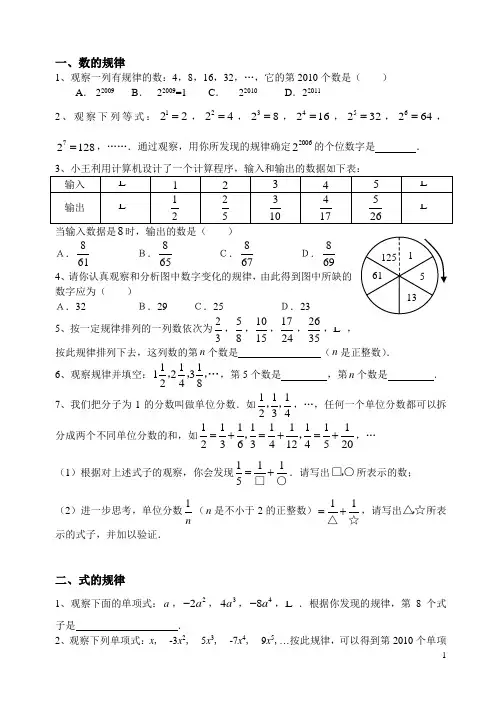
一、数的规律1、观察一列有规律的数：4，8，16，32，…，它的第2010个数是（ ）A ． 22009B ． 22009=1C ． 22010D ．220112、观察下列等式：122=，224=，328=，4216=，5232=，6264=，72128=，……．通过观察，用你所发现的规律确定20062的个位数字是 ．当输入数据是时，输出的数是（ ） Ａ．861Ｂ．865Ｃ．867Ｄ．8694、请你认真观察和分析图中数字变化的规律，由此得到图中所缺的数字应为（ ） Ａ．32 Ｂ．29 Ｃ．25 Ｄ．235、按一定规律排列的一列数依次为23，58，1015，1724，2635，，按此规律排列下去，这列数的第n 个数是（n 是正整数）．6、观察规律并填空：111123248，，，…，第5个数是 ，第n 个数是 ． 7、我们把分子为1的分数叫做单位分数．如111234，，，…，任何一个单位分数都可以拆分成两个不同单位分数的和，如11111111123634124520=+=+=+，，，…（1）根据对上述式子的观察，你会发现1115=+□○．请写出□，○所表示的数； （2）进一步思考，单位分数1n（n 是不小于2的正整数）11=+△☆，请写出△，☆所表示的式子，并加以验证．二、式的规律1、观察下面的单项式：a ，22a -，34a ，48a -，．根据你发现的规律，第8个式子是 ．2、观察下列单项式：x , -3x 2, 5x 3, -7x 4, 9x 5,…按此规律，可以得到第2010个单项式是______，第n 个单项式怎样表示________.3、观察下列一串单项式的特点：xy ，y x 22- ，y x 34 ，y x 48- ，y x 516 ，… 按此规律第9个单项式是______，第n 个单项式是______，它的系数是_____，次数是_ _.三、等式的规律1、观察下列等式：第1行 341=-第2行 594=-第3行 7169=- 第4行 92516=- … …按照上述规律，第n 行的等式为 ．2、观察下列各式：21321⨯=- 22431⨯=-23541⨯=- 24651⨯=-…………请你根据发现的规律，写出第n 个等式： ．3、已知：2222233+=⨯，2333388+=⨯，244441515+=⨯，…，若299a a b b+=⨯（a b ，为正整数），则ab = ． 4、观察下列等式：22(12)4114+-⨯=+ 22(22)4224+-⨯=+ 22(32)4334+-⨯=+ …则第n 个等式可以表示为 ．5、观察算式：211=； 21342+==； 213593++==；21357164+++==； 213579255++++==；……用代数式表示这个规律（n 为正整数）：13579(21)n ++++++-= ．6、观察下列各式：22151(11)1005225=⨯+⨯+=， 22252(21)1005625=⨯+⨯+= 22353(31)10051225=⨯+⨯+=， ……依此规律，第n 个等式（n 为正整数）为 ．7、观察下面的点阵图形和与之相对应的等式，探究其中的规律：（1）请你在④和⑤后面的横线上分别写出相对应的等式：（2）通过猜想，写出与第n 个图形相对应的等式_______________________． 8、观察下列等式111122=-⨯，1112323=-⨯，1113434=-⨯， 将以上三个等式两边分别相加得：1111111113111223342233444++=-+-+-=-=⨯⨯⨯． （1）猜想并写出：1(1)n n =+ ．（2）直接写出下列各式的计算结果： ①111112233420062007++++=⨯⨯⨯⨯ ；②1111122334(1)n n ++++=⨯⨯⨯+ ．四、图形的规律1、用M ，N ，P ，Q 各代表四种简单几何图形（线段、正三角形、正方形、圆）中的一种．图-1—图-4是由M，N，P，Q 中的两种图形组合而成的（组合用“&”表示）．M&P N&P N&Q M&Q 图-1图-2 图-3 图-4 ①401413⨯+=⨯-； ②411423⨯+=⨯-；421433⨯+=⨯-；③④ ⑤ _________________； _________________；那么，下列组合图形中，表示P&Q 的是（ ）2、如图，图①，图②，图③，……是用围棋棋子摆成的一列具有一定规律的“山”字．则第n 个“山”字中的棋子个数是 ．3、用火柴棒按以下方式搭小鱼，搭1条小鱼用8根火柴棒，搭2条小鱼用14根，，则搭n 条小鱼需要 根火柴棒．（用含n 的代数式表示）4、按如下规律摆放三角形：则第（4）堆三角形的个数为 ；第（n ）堆三角形的个数为 .5、将图①所示的正六边形进行分割得到图②，再将图②中最小的某一个正六边形按同样的方式进行分割得到图③，再将图③中最小的某一个正六边形按同样的方式进行分割，…，则第n 个图形中，其有 个六边形．参考答案：一、数的规律1、C2、43、B4、B…… 图① 图② 图③ 图④3()2()1()… 图① 图② 图③A ．B ．C ．D ．5、nn n 2122++ 6、3215，n n 21+ 7、（1）6,30；（2）1+n ，)1(+n n二、式的规律1、8128a - 2、20104019x -，n n x n )12()1(1--+ 3、y x 9256，y x n n n 112)1(-+-三、等式的规律1、22)1(12n n n -+=+2、1)1()2(2-+=+n n n3、7204、44)2(22+=-+n n n5、2n 6、225100)1()510(+⨯+=+n n n 7、（1）344134-⨯=+⨯，354144-⨯=+⨯； （2）341)1(4-=+-n n8、（1）1+n n ；（2）①20072006，②1+n n四、图形的规律1、B2、25+n3、26+n4、（1）14， （2）23+n5、23-n。
(完整)七年级数学专题规律探究题
七年级数学专题-----规律探究题题型一：数字变化类问题1 •观察下列按顺序排列的等式：引二1-*，2誌-書，巧€ 一+，4冷一+ 试猜想第n个等式（n为正整数）：a n= ______________________ .2. 下表中的数字是按一定规律填写的，表中a的值应是____ .1 2 3 5 8 13 a-2 3 5 8 13 21 34 …3. ___ 观察下面的单项式：a,- 2a2, 4a3,- 8a4, ••根据你发现的规律，第8个式子是.4. 有一组等式：1222 3232,22326272,32 42 122132,4252202212……请观察它们的构成规律，用你发现的规律写出第8个等式为__________5. 把奇数列成下表，13113213L59152333111725h-itn! ■ b ■2737—39——根据表中数的排列规律，则上起第8行，左起第6列的数是5.在计数制中，通常我们使用的是“十进位制”，即“逢十进一”。
而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据。
已知二进十进位制0123456• • •请将二进制数10101010（二）写成十进制数为_______ .6 •观察下列各数，它们是按定规律排列的，则第n个数是15 3116?眈'7.观察一列单项式：1x, 3x2, 5x2, 7x, 9x2, 11x2,…，则第2013个单项式是8•有这样一组数据a i, a2, a3, •• a,满足以下规律：且I三・❻尸—-—3 勒二 ~-—j …，且—-------- （n多且n为正整数）,贝U宠。
1312 1 _ J1 _a2n1 - a n_ L的值为________ （结果用数字表示）.9. 观察下列各式的计算过程：5X 5=0X 1 X 100+25,15X 15=1X 2X 100+25,25X 25=2X 3X 100+25,35X 35=3X 4X 100+25,请猜测，第n个算式（n为正整数）应表示为_____________________________ 10. 如图，下列各图形中的三个数之间均具有相同的规律.根据此规律，图形中M与m、n的关系是A. M=mnB. M=n（m+1）C. M=mn+1D. M=m（n+1）11. 观察下列等式：31=3, 32=9, 33=27, 34=81, 35=243, 36=729, 37=2187… 解答下列问题：3+32+33+3仃+32013的末位数字是（）A. 0B. 1C. 3D. 712. ____________________________________________ 如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2013个格子中的整数是_______________________________ .13. 将连续正整数按以下规律排列，则位于第 7行第7列的数x 是85篦一如邕二苑董三列策囚列篝三到邕七扪・・・第一行 136 10 1521 n 重二行 2 5 9 14 20 27 :第三行 413 15--- ■策四行712 1$25■・■11 17 2415 23 ■ ■•2215•电脑系统中有个“扫雷”游戏，要求游戏者标出所有的雷，游戏规则：一个 方块下面最多埋一个雷，如果无雷，掀开方块下面就标有数字，提醒游戏者此数 字周围的方块（最多八个）中雷的个数（实际游戏中，0通常省略不标,此WORD 中为方便大家识别与印刷，我还是把图乙中的0都标出来吧，以示与未掀开者的 区别），如图甲中的“ 3”表示它的周围八个方块中仅有 3个埋有雷.图乙第一行 从左数起的七个方块中（方块上标有字母），能够确定一定是雷的有 ___________________________ .（请填入方块上的字母）16. 如图，在△ ABC 中，/ A=m°，/ ABC 和/ACD 的平分线交于点 A,得/ A;/ ABC 和/ACD 的平分线交于点 A ，得/ A;…/A2012BC 和/A 2012CD 的平分线交于 点 A ?013，贝 A 2013= ______ 度。
七年级数学探究规律题
七年级数学探究规律题七年级数学探究规律题，听起来像是要挑战大脑的节奏感！小伙伴们，今天我们要揭开这个神秘面纱，看看里面到底藏着什么宝藏。
我们得了解一下，所谓的“规律题”到底是个啥意思？别担心，不是在跟你说故事，这个“规律”其实就是数学里的隐藏版秘籍。
就像是找到一个游戏的隐藏关卡一样，有了规律，数学题就变得像玩游戏一样，有章可循。
你们有没有玩过找茬游戏？有的小伙伴肯定点点头。
数学规律题就像是那种找茬游戏，一开始看起来乱糟糟的，但是只要你发现了一个规律，哇哦，整个世界都清晰了。
比如说，有一个题目让你列出一串数字，然后问你下一个数字是什么？嗯，这可不是要你胡乱猜的。
得找规律啊！这规律藏得比鬼还精，就像是小偷藏在阴影里一样。
但是，别灰心丧气！数学可不是吓人的怪兽，它其实挺好玩的。
你要是搞明白了这些规律，就像是掌握了一套无敌的招式。
别人还在瞎猜的时候，你早就轻松过关了。
还记得小时候，有时候会拆开玩具看看它是怎么组成的吗？数学规律题有点像是那个过程，你要一步步拆解它，看看它的构造。
然后，你就能看见那些看不见的联系，就像是拼图一样，一块块儿地衔接起来。
别以为数学规律题就是干巴巴的数字堆砌。
它们还藏着生活的哲理。
比如说，有一道题是让你推测一个序列的下一个数，看似毫无头绪，但是它可能在暗示着某种规律，就像是生活中的那些不经意的启发一样。
找规律就像是侦探破案一样，你得收集线索，分析证据，最后得出一个结论。
那个结论，往往是那么让人拍手称快，就像是解开了谜题的最后一块拼图。
别忘了，数学规律题不是只有一条路可走。
你得从不同的角度来审视它们，就像是从山的不同侧面去攀登，总有一条路是通的。
别把自己限制在一个固定的思维模式里，灵活点，多尝试，才能找到那些看似藏得很深的规律。
数学规律题有时候也会让你感受到一种“啊哈！”的快感，就像是突然明白了一个复杂电影情节的结局，原来一切都是那么自然而然。
所以，小伙伴们，别怕难题，敢于追求规律，挑战自己的脑细胞，说不定就能在这些数字中找到属于你自己的小秘密呢！记得，数学不只是考试题，它更是一门探索未知世界的钥匙，谁拿到了钥匙，谁就能打开属于自己的新大门。
七年级数学找规律题
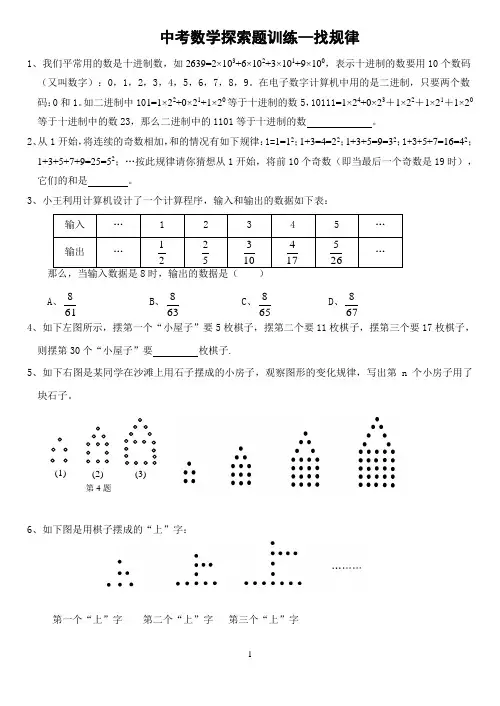
中考数学探索题训练—找规律1、我们平常用的数是十进制数，如2639=2×103+6×102+3×101+9×100，表示十进制的数要用10个数码（又叫数字）：0，1，2，3，4，5，6，7，8，9。
在电子数字计算机中用的是二进制，只要两个数码：0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5，10111=1×24+0×23＋1×22＋1×21＋1×20等于十进制中的数23，那么二进制中的1101等于十进制的数。
2、从1开始，将连续的奇数相加，和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从1开始，将前10个奇数（即当最后一个奇数是19时），它们的和是。
3、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：输入… 1 2 3 4 5 …输出…2152103174265…那么，当输入数据是8时，输出的数据是（）A、618B、638C、658D、6784、如下左图所示，摆第一个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第三个要17枚棋子，则摆第30个“小屋子”要枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第n个小房子用了块石子。
6、如下图是用棋子摆成的“上”字：第一个“上”字第二个“上”字第三个“上”字(1)(2)(3)第4题如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上”字分别需用和枚棋子；（2）第n个“上”字需用枚棋子。
7、如图一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有_______颗.8、根据下列5个图形及相应点的个数的变化规律：猜想第6个图形有个点，第n 个图形中有个点。
2023学年浙江七年级数学上学期专题训练专题02 运算思维之规律探究(解析版)
专题02运算思维之规律探究专练（解析版）学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知一列数1a ，2a ，3a ，…，具有如下规律：211n n n a a a ++=+，2n n a a =（n 是正整数）．若11a =，则37a 的值为（ ）A ．1B ．5C ．7D ．11【答案】D【分析】 根据题干公式寻找规律，从而逐步推出结果．【详解】解：由a 2n +1=a n +a n +1，a 2n =a n （n 是正整数）可得：a 37=a 18+a 19=2a 9+a 10=2（a 4+a 5）+a 5=2a 4+3a 5=2a 2+3（a 2+a 3）=5a 2+3a 3=8a 1+3a 2=11a 1=11． 故选：D ．【点睛】本题考查数字变化规律，解题关键是根据题中规律拆项．2．把一根起点为0的数轴弯折成如图所示的样子，虚线最下面第1个数字是0，往上第2个数字是6，第3个数字是21，…，则第5个数字是（ ）A ．78B ．80C ．82D ．89【答案】A【分析】 观察根据排列的规律得到第1个数字为0，第2个数字为0加6个数即为6，第3个数字为从6开始加15个数得到21，第4个数字为从21开始加24个数即45，…，由此得到后面加的数比前一个加的数多9，由此得到第5个数字为0+6+（6+9×1）+（6+9×2）+（6+9×3）．【详解】解：∵第一个数字为0，第二个数字为0+6=6，第三个数字为0+6+15=21，第四个数字为0+6+15+24=45，第五个数字为0+6+15+24+33=78，故选：A ．【点睛】此题主要考查了数字变化规律，发现数在变化过程中各边上点的数字的排列规律是解题关键．3．有一列数：123,,,,n a a a a …，若112a =-，从第2个数起，每一个数都等于“1与它前面的那个数的差的倒数”，那么2021a 的值为（ ）A ．2-B ．12-C ．23D ．3【答案】C【分析】根据每一个数都等于1与它前面那个数的差的倒数多列举几个数字，找出规律即可．【详解】解：a 1=12-，13122⎛⎫--= ⎪⎝⎭， a 2=23，21133-=， a 3=3，132-=-，a 4=12-， …，从上面的规律可以看出每三个数一循环，2021÷3=673......2，∵a 2021=a 2=23， 故选：C ．【点睛】本题主要考查数字的变化规律，总结归纳数字的变化规律是解题的关键．4．定义一种对正整数n 的“F ”运算：∵当n 为奇数时，结果为35n +；∵当n 为偶数时，结果为2k n ；（其中k 是使2k n 为奇数的正整数），并且运算可以重复进行，例如，取26n =．则：26134411F F F −−−→−−−→−−−→①②③第一次第二次第三次若49n =，则第2020次“F 运算”的结果是（ ）A ．152B ．19C ．62D ．31【答案】D【分析】计算出n =49时第1、2、3、4、5、6、7次运算的结果，找出规律再进行解答即可求解．【详解】解：本题提供的“F 运算”，需要对正整数n 分情况（奇数、偶数）循环计算，由于n =49为奇数应先进行F ∵运算，即3×49+5=152（偶数），需再进行F ∵运算，即152÷23=19（奇数），再进行F ∵运算，得到3×19+5=62（偶数），再进行F ∵运算，即62÷21=31（奇数），再进行F ∵运算，得到3×31+5=98（偶数），再进行F ∵运算，即98÷21=49（奇数），再进行F ∵运算，得到3×49+5=152（偶数），…，即第1次运算结果为152，…，第4次运算结果为31，第5次运算结果为98，…，可以发现第6次运算结果为49，第7次运算结果为152，则6次一循环，2020÷6=336…4，则第2020次“F 运算”的结果是31．故选：D ．【点睛】本题考查了有理数的混合运算，既渗透了转化思想、分类思想，又蕴涵了次数、结果规律探索问题，检测学生阅读理解、抄写、应用能力．5．观察图形并判断照此规律从左到右第四个图形是() A．B．C．D．【答案】D【详解】观察图形可知：单独涂黑的角顺时针旋转，只有D符合.故选：D.6．如图所示，下列图形都是由相同的玫瑰花按照一定的规律摆成的，按此规律摆下去，第n个图形中有120朵玫瑰花，则n的值为（）A．28B．29C．30D．31【答案】C【详解】分析：根据题目中的图形变化规律，可以求得第个图形中玫瑰花的数量，然后令玫瑰花的数量为120，即可求得相应的n的值，从而可以解答本题．详解：由图可得，第n个图形有玫瑰花：4n，令4n=120，得n=30，故选C．点睛：本题考查图形的变化类，解答本题的关键是明确题意，找出题目中图形的变化规律．7．如图，用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形，三角形、正方形的每一边用一根火柴棒．如果搭这两个图案一共用了2030根火柴棒，且正方形的个数比三角形的个数的少4个，则搭成的三角形的个数是（）A．429B．409C．408D．404【答案】C【分析】根据搭建三角形和正方形一共用了2030根火柴，且三角形的个数比正方形的个数多4个，即可得搭建三角形的个数．【详解】解：∵搭建三角形和正方形一共用了2030根火柴，且三角形的个数比正方形的个数多4个，观察图形的变化可知：搭建n个三角形需要（2n+1）根火柴棍，n个正方形需要（3n+1）根火柴棍，所以2n+1+3（n-4）+1=2030，解得n=408．故选：C．【点睛】本题考查了规律型-图形的变化类，解决本题的关键是根据图形的变化寻找规律．8．将图∵所示的正六边形进行分割得到图∵，再将图∵中最小的某一个正六边形按同样的方式进行分割得到图∵，再将图∵中最小的某一个正六边形按同样的方式进行分割，…，则第2014个图形中，共有（）个正六边形．A．4027B．6040C．6061D．10066【答案】B【分析】观察第二个图形，有1+3=4个；第三个图形，有1+3+3=7个；依此类推，发现规律即可解答．【详解】解：第二个图形中有1+3=4个；第三个图形中有1+3+3=7个；...∵第n个图形中有1+3（n-1）=3n-2个；∵第2014个图形中有1+3×（2014-1）=6040个；故选B．【点睛】本题考查了图形的变化规律：结合图形观察前几个具体数值，即可发现每一次总是多3个正六边形是关键．二、填空题9．如表是一组密码的一部分，目前已破译出“守初心”的对应口令是“担使命”，根据上述破译方法，破译出“找差距”的对应口令是_______．【答案】抓落实【分析】根据表格中汉字所在行及列的位置以及对应口令所在行和列的位置探索规律，从而求解．【详解】解：由题意“守”位于第3行第4列，其对应口令“担”位于第1行第3列“初”位于第5行第2列，其对应口令“使”位于第3行第1列“心”位于第4行第7列，其对应口令“命”位于第2行第6列∵位于第n行第m列的汉字，其对应口令位于第（n-2）行第（m-1）列，由此，“找”位于第7行第2列，其对应口令位于第5行第1列，即“抓”“差”位于第3行第2列，其对应口令位于第1行第1列，即“落”“距”位于第5行第7列，其对应口令位于第3行第6列，即“实”故答案为：抓落实．【点睛】本题考查规律探索，准确理解题意，分析汉字所在位置的规律是解题关键． 10．如图各网格中四个数之回都有相同的规律，则第9个网格中右下角的数为_________．【答案】119【分析】从图中观察出各个格子中的数据的规律，找出第九个格子的各个数字即可．【详解】解：由图中的数字可知，左上角的数字是一些连续的正整数，从1开始，左下角的数字是对应的左上角的数据加1，右上角的数字是对应的左下角的数字加2， 右下角的数字是左下角的数字与右上角的数字乘积再加左上角数字的和，故第9个正方形中的左上角的数字是9，左下角的数字是10，右上角的数字是11，右下角的数字是：10×11+9=119；故答案为：119．【点睛】本题考查数字变化的规律的相关内容，解题的关键是找出各个数字之间的规律． 11．观察下列各式：∵2204-=；∵22318-=；∵224212-=；∵225316-=；∵226420-=；……；用含自然数n 的等式表示你发现的规律：__________________．【答案】（n +2）2-n 2=4（n +1）【分析】分别列出n =0，1，2，3，4，5…的情况，再进行总结归纳即可．【详解】解：∵n =0，（0+2）2-02=4×1，∵n =1，（1+2）2-12=4×2，∵n =2，（2+2）2-22=4×3，∵n =3，（3+2）2-32=4×4，∵n =4，（4+2）2-42=4×5，…，所以n =n 时，（n +2）2-n 2=4（n +1），故答案为：（n +2）2-n 2=4（n +1）．【点睛】本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．12．设123,,a a a ，…是一列正整数，其中1a 表示第一个数，2a 表示第二个数，……，n a 表示第n 个数（n 是正整数）．若12a =，()()221411n n n a a a +=---，则（1）2a =_______（2）2021a =______．【答案】4 4042【分析】先将4a n =（a n +1-1）2-（a n -1）2，变形，结合a 1=2，a 1，a 2，a 3……是一列正整数，得出递推公式a n +1=a n +2，进而可得a n =2n ，将n =2021代入即可求得答案．【详解】解：∵a 1=2，4a n =（a n +1-1）2-（a n -1）2，a 1，a 2，a 3……是一列正整数，∵a n -1≥0，（a n +1-1）2=（a n -1）2+4a n =（a n +1）2，∵a n +1-1=a n +1，∵a n +1=a n +2，∵a 1=2，∵a 2=4，a 3=6，a 4=8，a 5=10，…∵a n =2n ，∵a 2021=2×2021=4042．故答案为：4；4042．【点睛】本题考查了数字的变化规律，由已知条件推出递推关系式，进而得出含n 字母的各项的表达式，是解题的关键．13．观察下列等式：22110=-，22321=-，22532=-，…按此规律，则第n 个等式为21n -=__________________． 【答案】()221n n --．【分析】第一个底数是从1开始连续的自然数的平方，减去从0开始连续的自然数的平方，与从1开始连续的奇数相同，由此规律得出答案即可．【详解】解：∵22110=-，22321=-，22532=-，…∵第n 个等式为：()22211n n n -=-- 故答案是：()221n n --．【点睛】本题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题的关键．14．数202020212022379⋅⋅的个位数字是____．【答案】7【分析】由3n 的个位数字是3，9，7，1四次一循环，7n 的个位数字是7，9，3，1四次一循环，9n 的个位数字是9，1，9，1四次一循环，继而可以求得32009×72010×132011的个位数字．【详解】解：∵3n （n 为从1开始的正整数）的个位数字是3，9，7，1四次一循环， 7n 的个位数字是7，9，3，1四次一循环，9n 的个位数字是9，1，9，1四次一循环，又∵2020÷4=505，2021÷4=505…1，2022÷4=505…2，∵32020的末尾数字为1，72021的末尾数字为7，92022的末尾数字为1，∵1×7×1=7，∵32020×72021×92022的个位数字是7．故答案为：7．【点睛】此题考查了尾数特征．此题难度适中，注意得到3，7，9为底数的整数幂的个位数字的规律是解此题的关键．15．阳阳和明明玩上楼梯游戏，规定一步只能上一级或二级台阶，玩着玩着两人发现：当楼梯的台阶数为一级、二级、三级…逐步增加时，楼梯的上法数依次为1，2，3，5，8，13，21，…（这就是著名的裴波那契数列），请你仔细观察这列数的规律后回答：（1）上10级台阶共有__________种上法．（2）这列数的前2020个数中共有________个偶数．【答案】89 673【分析】（1）认真观察不难发现，这列数中，任意相邻两个数的和都等于相邻的后一个数，也就是第10个数应该是第8个、9个的和；（2）观察发现，每3个数中必有一个偶数，且偶数在3个数中间，依此规律可求出问题答案．【详解】解：（1）∵1+2=3，2+3=5，3+5=8，5+8=13，8+13=21，13+21=34，21+34=55，34+55=89，∵上10级台阶共有89种上法；（2）∵2020÷3=673…1，∵偶数个数为673个．【点睛】本题考查了数字型规律，根据已知条件找寻数列中的规律是解题的关键．16．数列1,1,2,3,5,8,13,21,34,55，…的排列规律：前两个数是1，从第3个数开始，每一个数都是它前两个数的和，这个数列叫做斐波契数列，在斐波契数列前2020个数中共有_______个偶数．【答案】673【分析】由于数列1，1，2，3，5，8，13，21，34，55，…中是两个奇数然后一个偶数，接着又是两个奇数，一个偶数，由此即可确定斐波那契数列的前2020个数中共有多少个偶数．【详解】∵数列1，1，2，3，5，8，13，21，34，55，…，中是两个奇数然后一个偶数，而÷=⋅⋅⋅⋅⋅⋅；余数是1，那么这个数列的第2020个数是奇数，202036731∵斐波那契数列的前2020个数中共有673个偶数．故答案为：673.【点睛】此题主要考查了数字的变化规律，解题时首先正确理解题意，然后根据题意找出隐含的规律即可解决问题．17．如图，每一图中有若干个大小不同的菱形，第一幅图中有1个菱形，第二幅图中有3个菱形，第三幅图中有5个菱形，如果第n幅图中有2021个菱形，则n为____________．【答案】1011【分析】根据题意分析可得：第1幅图中有1个，第2幅图中有2×2-1=3个，第3幅图中有2×3-1=5个，…，可以发现，每个图形都比前一个图形多2个，继而即可得出答案．【详解】解：根据题意分析可得：第1幅图中有1个．第2幅图中有2×2-1=3个．第3幅图中有2×3-1=5个．第4幅图中有2×4-1=7个．…．可以发现，每个图形都比前一个图形多2个．故第n幅图中共有（2n-1）个．当图中有2021个菱形时，2n-1=2021，所以：n=1011，故答案为：1011．【点睛】本题考查规律型中的图形变化问题，难度适中，要求学生通过观察，分析、归纳并发现其中的规律．18．如图，边长为12320202021、、、、的正方形套在一起，形成一个庞大的回宫格，则阴影部分的面积是_______．【答案】2043231【分析】若只有1个阴影部分，则面积为20212-20202，有2个阴影部分，面积为（20212-20202）+（20192-20182），…【详解】解：阴影部分的面积为（20212-20202）+（20192-20182）+（20172-20162）+…+（32-22）+1=2021+2020+2019+2018+…+3+2+1=() 1202120212+⨯=1011×2021=2043231，故答案为：2043231．【点睛】本题考查图形的变化规律；得到阴影部分面积的组成是解决本题的难点；找到相应的计算方法是解决本题的突破点．19．如图，各网格中四个数之间都有相同的规律，则第9个网格中右下角的数为______．【答案】119【分析】观察序号与网格中上面最左边的数字的关系，第二个数字与序号的关系，左下角的数字与序号的关系，右下角数字与上面所说三个数字的关系，确定好计算即可【详解】根据题意，得网格中上面最左边的数字等于序号，第二个数字与序号+1，左下角的数字与序号+2，右下角数字等于对角线上的数字积加上序号，∵第n个网格中，右下角的数字=（n+1）（n+2）+n，当n=9时，（n+1）（n+2）+n=10×11+9=119，故答案为：119．【点睛】本题考查了数字中规律，仔细思考各数字与序号的关系是解题的关键．2,3，20．把所有的正整数按如图所示规律排列形成数表．若正整数6对应的位置记为() 12,7对应的正整数是_______．则()【答案】138【分析】2,3，可得表示方法，观察出1行1根据表格中的数据，以及正整数6对应的位置记为()列数的特点为12-0，2行2列数的特点为22-1，3行3列数的特点为32-2，…n行n列数的特点为（n2-n+1），且每一行的第一个数字逆箭头方向顺次减少1，由此进一步解决问题．【详解】2,3，解：∵正整数6对应的位置记为()即表示第2行第3列的数，12,7表示第12行第7列的数，∵()由1行1列的数字是12-0=12-（1-1）=1，2行2列的数字是22-1=22-（2-1）=3，3行3列的数字是32-2=32-（3-1）=7，…n行n列的数字是n2-（n-1）=n2-n+1，∵第12行12列的数字是122-12+1=133，∵第12行第7列的数字是138，故答案为：138．【点睛】此题考查观察分析归纳总结顾虑的能力，解答此题的关键是找出两个规律，即n 行n 列数的特点为（n 2-n +1），且每一行的第一个数字逆箭头方向顺次减少1，此题有难度． 21．数轴上，点A 的初始位置表示的数为1，现点A 做如下移动：第1次点A 向左移动3个单位长度至点1A ，第2次从点1A 向右移动6个单位长度至点2A ，第3次从点2A 向左移动9个单位长度至点3A ，…，按照这种移动方式进行下去，如果点n A 与原点的距离不小于20，那么n 的最小值是_______． 【答案】13 【分析】序号为奇数的点在点A 的左边，各点所表示的数依次减少3，序号为偶数的点在点A 的右侧，各点所表示的数依次增加3，于是可得到A 13表示的数为-17-3=-20，A 12表示的数为16+3=19，则可判断点A n 与原点的距离不小于20时，n 的最小值是13． 【详解】解：第一次点A 向左移动3个单位长度至点A 1，则A 1表示的数，1-3=-2； 第2次从点A 1向右移动6个单位长度至点A 2，则A 2表示的数为-2+6=4； 第3次从点A 2向左移动9个单位长度至点A 3，则A 3表示的数为4-9=-5； 第4次从点A 3向右移动12个单位长度至点A 4，则A 4表示的数为-5+12=7； 第5次从点A 4向左移动15个单位长度至点A 5，则A 5表示的数为7-15=-8； …则A 7表示的数为-8-3=-11，A 9表示的数为-11-3=-14，A 11表示的数为-14-3=-17，A 13表示的数为-17-3=-20，A 6表示的数为7+3=10，A 8表示的数为10+3=13，A 10表示的数为13+3=16，A 12表示的数为16+3=19，所以点A n 与原点的距离不小于20，那么n 的最小值是13． 故答案为13． 【点睛】本题考查了规律型问题，认真观察、仔细思考，找出点表示的数的变化规律是解决问题的关键．22．下列图形是由同样大小的灰、白两种不同颜色的小正方形地砖铺设而成，每一个小正方形表示一块地砖，如果按图1、2、3 的次序铺设地砖，把第n 个图形用图n 表示，那么图100中的白色小正方形地砖的块数是_______．【答案】703 【分析】根据图象中地砖个数发现规律，图n 中有()32n +块黑色地砖，图n 中一共有()105n +块地砖，就可以得到白色地砖数，令100n =即可求出结果． 【详解】解：图1中有5块黑色地砖，图2中比图1中多3块黑色地砖，有8块黑色地砖， 图3中比图2中多3块黑色地砖，有11块黑色地砖， …图n 中有()53132n n +-=+块黑色地砖， 图1中一共有5315⨯=块地砖， 图2中一共有5525⨯=块地砖， 图3中一共有5735⨯=块地砖， …图n 中一共有()521105n n +=+块地砖，∵图100中白色小正方形地砖的块数是：()10100531002703⨯+-⨯+=（块）． 故答案是：703． 【点睛】本题考查找规律，解题的关键是找出图形中的规律，并用n 将规律通过代数式表示出来． 23．2020年6日1日，湖州市政府发布了全新湖洲城市形象标识，小周同学对新形象标识很感兴趣，用电脑绘画软件绘制了如下图形，其中第（1）个图形有3个形象标识，第（2）个图形有7个形象标识，第（3）个图形有13个形象标识，按此规律绘制下去．（1）小周绘制的第（5）个图形中有_________个形象标识．（2）小周绘制的第（n）个图形中有_________个形象标识．【答案】31 （n2+n+1）【分析】观察图形可知，每个图形中形象标识的个数为序号数的平方+序号数+1，依此可求第5个和第n个图有多少个形象标识．【详解】解：由图形可知，第1个图形有12+1+1=3个形象标识，第2个图形有22+2+1=7个形象标识，第3个图形有32+3+1=13个形象标识，第4个图形有42+4+1=21个形象标识，（1）小周绘制的第（5）个图形中有52+5+1=31个形象标识．（2）小周绘制的第（n）个图形中有（n2+n+1）个形象标识．故答案为：31；（n2+n+1）．【点睛】此题考查图形的变化规律，找出图形之间的联系，找出规律是解决问题的关键．三、解答题24．探究：211112222122-=⨯-⨯=，32222-=⨯-⨯=，222212243333-=⨯-⨯=，2222122……（1）请仔细观察，写出第4个等式；（2）请你找规律，写出第n个等式；（3）计算：12320192020++++-．22222【答案】（1）25-24=2×24-1×24=24；（2）2n+1-2n=2×2n-1×2n=2n；（3）-2【分析】（1）根据给出的内容，直接可以仿写25-24=2×24-1×24=24，（2）2n +1-2n =2×2n -1×2n =2n ，（3）将原式进行变形，即提出负号后，就转化为原题中的类型，利用（1）（2）的结论，直接得出结果． 【详解】解：（1）由题意可得： 25-24=2×24-1×24=24； （2）2n +1-2n =2×2n -1×2n =2n ； （3）1232019202022222++++-=()1232019202022222++++-=1232018201922222++++-... =2-22 =-2 【点睛】此题主要考查了数字变化规律，认真观察、仔细思考，善用联想是解决这类问题的方法，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：2n +1-2n =2n 成立． 25．一列数a 1，a 2，a 3，…，a n ，其中a 1＝﹣1，a 2＝111a -，a 3＝211a -，…，a n ＝111n a --．（1）求a 2，a 3的值；（2）求a 1+a 2+a 3+…+a 2021的值． 【答案】（1）212a =，32a =；（2）1009 【分析】（1）将11a =-代入2111a a =-计算可得2a ，再将2a 代入3211a a =-，可求出3a ；（2）根据规律可得出结果． 【详解】解：（1）把11a =-代入2111a a =-得， 2111(1)2a =--=，把212a =代入3211a a =-得，312112a ==-，∵212a =，32a =； （2）将32a =代入4311a a =-得， 41112a ==-- 同理5111(1)2a ==--， 62a =，71a =-，812a =， ⋯⋯12345678920172018201932a a a a a a a a a a a a ++==++=++=⋯=++， 所以1232021111112121212222a a a a +++⋯+=-++-++-++⋯⋯-+31673122=⨯-+ 1009=．【点睛】本题考查有理数的混合运算，探索数字的变化规律，正确的计算2a ，3a ，4a ，5a ⋯⋯进而得出变化规律是解决问题的关键． 26．观察下列等式：111122=-⨯，1112323=-⨯，1113434=-⨯，将以上三个等式两边分别相加得：111122334++⨯⨯⨯11111122334=-+-+-13144=-=． （1）猜想并写出：1(1)n n =+________． （2）直接写出结果：111112233420182019++++=⨯⨯⨯⨯___________．（3）计算111124466820182020++++⨯⨯⨯⨯．【答案】（1）111n n -+；（2）20182019；（3）10094040【分析】（1）根据题目中的式子，可以写出相应的猜想； （2）先裂项，然后再计算即可；（3）根据题目中式子的特点，每项提取12，再裂项计算即可． 【详解】解：（1）由题意可得：111(1)1n n n n =-++；（2）111112233420182019++++⨯⨯⨯⨯=111111112233420182019-+-+-++- =112019- =20182019； （3）111124466820182020++++⨯⨯⨯⨯=111111111224466820182020⎛⎫-+-+-++- ⎪⎝⎭=111222020⎛⎫- ⎪⎝⎭ =1100922020=10094040【点睛】本题考查了规律型：数字的变化类：探寻数列规律：认真观察、仔细思考，善用联想是解决这类问题的方法． 27．阅读下列材料：11112(123012)23(234123)34(345234)333⨯=⨯⨯-⨯⨯⨯=⨯⨯-⨯⨯⨯=⨯⨯-⨯⨯；由以上三个等式相加，可得1122334345203⨯+⨯+⨯=⨯⨯⨯=．读完以上材料，请你计算下列各题： （1）计算：12233499100⨯+⨯+⨯++⨯（写出过程）（2）直接写出直接：122334(1)n n ⨯+⨯+⨯+⋯+⨯+=_________． （3）计算：123234345181920⨯⨯+⨯⨯+⨯⨯++⨯⨯（写出过程）【答案】（1）333300；（2）()()1123n n n ++；（3）35910 【分析】根据给定等式的变化找出变化规律()()()()()1112113n n n n n n n n +=++--+⎡⎤⎣⎦；（1）根据变化规律将算式展开后即可得出原式=1991001013⨯⨯⨯，此题得解； （2）根据变化规律将算式展开后即可得出原式=()()1123n n n ++，此题得解；（3）通过类比找出变化规律“n （n +1）（n +2）=14[n （n +1）（n +2）（n +3）-（n -1）n （n +1）（n +2）]”，依此规律将算式展开后即可得出结论． 【详解】解：观察，发现规律：112(123012)3⨯=⨯⨯-⨯⨯，123(234123)3⨯=⨯⨯-⨯⨯，134(345234)3⨯=⨯⨯-⨯⨯，…，∵()()()()()1112113n n n n n n n n +=++--+⎡⎤⎣⎦； （1）12233499100⨯+⨯+⨯++⨯=()()()111123012234123 (9910010198991003)33⨯⨯-⨯⨯+⨯⨯-⨯⨯++⨯⨯-⨯⨯ =1991001013⨯⨯⨯ =333300；（2）122334(1)n n ⨯+⨯+⨯+⋯+⨯+=()()()()()()111230122341231121.13..33n n n n n n ++--+⎡⎤⎣⎦⨯⨯-⨯⨯+⨯⨯-⨯⨯++ =()()1123n n n ++；（3）123234345181920⨯⨯+⨯⨯+⨯⨯++⨯⨯=()()()1111234012323451234 (181920211718192044)4⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯++⨯⨯⨯-⨯⨯⨯ =1181920214⨯⨯⨯⨯ =35910 【点睛】本题考查数字的变化类、有理数的混合运算，解答本题的关键是明确题意，发现题目中数字的变化特点，利用类比的数学思想解答．28．用黑白两种颜色的正方形纸片，按黑色纸片数逐渐加1的规律拼成一系列图案，请仔细观察，并回答下列问题：（1）第4个图案中有白色纸片多少张？（2）第n个图案中有白色纸片多少张？（3）第几个图案有白色纸片有2011张？（写出必要的步骤）【答案】（1）13；（2）（3n+1）张（3）第670个图案有白色纸片有2011张，见解析【分析】（1）观察图形的变化可得第4个图案中有白色纸片有3×4+1＝13张；（2）结合（1）即可得规律，第n个图案中有白色纸片（3n+1）张；（3）结合（2）发现的规律即可求得白色纸片有2011张是第几个图案．【详解】（1）观察图形的变化可知：第1个图案中有白色纸片张数为：3×1+1＝4；第2个图案中有白色纸片张数为：3×2+1＝7；第3个图案中有白色纸片张数为：3×3+1＝10；第4个图案中有白色纸片张数为：3×4+1＝13；（2）根据（1）发现规律：第n个图案中有白色纸片张数为：（3n+1）张．（3）根据（2）可知：3n+1＝2011，解得n＝670．答：第670个图案有白色纸片有2011张．【点睛】此题考查规律型-图形的变化类，解题的关键是根据图形的变化寻找规律．29．图1是用绳索织成的一片网的一部分，小明为了研究这片网的结点数（V），网眼数（F），边数（E）之间的关系，他采用由特殊到一般的方法进行探索，列表如下：V F E之间（1）表中“∵”处应填的数字为__________；根据上述探索过程，可能猜想,,满足的数量关系是__________．（2）如图2，若网眼形状为六边形，请仿照小明的探索方法，完成下面表格并猜想,,V F E 之间满足的数量关系．根据上述探索过程，可以猜想,,V F E 之间满足的数量关系是________． 【答案】（1）17，1V F E +-=；（2）表见解析，1V F E +-= 【分析】（1）根据表格中的数据可以得到表中“∵”处应填的数字并猜想出V ，F ，E 之间满足的等量关系；（2）根据（1）中的例子，可以猜想出若网眼形状为六边形，V ，F ，E 之间满足的等量关系． 【详解】解：（1）由表格可得， 表中“∵”处应填的数字为17，根据上述探索过程，可以猜想V ，F ，E 之间满足的等量关系为：V+F -E=1， 故答案为：17，V+F -E=1； （2）若网眼形状为六边形 当V=6时，F=1，E=6， 当V=10时，F=2，E=11， 当V=16时，F=4，E=19， 当V=22时，F=6，E=27，则V ，F ，E 之间满足的等量关系为V+F -E=1， 故答案为：V+F -E=1【点睛】30．先阅读下面文字，然后按要求解题．例：123100?+++⋅⋅⋅+=如果一个一个顺次相加显然太繁，我们仔细分析这100个连续自然数的规律和特点，可以发现运用加法的运算律，是可以大大简化计算，提高计算速度的．因为11002993985051101+=+=+=⋅⋅⋅=+=，所以将所给算式中各加数经过交换、结合以后，可以很快求出结果． （1）补全例题解题过程；123100(1100)(299)(398)(5051)101++++=++++++++=⨯_____=_____．（2）计算：2468100++++⋅⋅⋅+（3）计算：()(2)(3)(99)a a b a b a b a b +++++++⋅⋅⋅++． 【答案】（1）50，5050；（2）2550；（3）1004950a b + 【分析】（1）根据题干中的示例计算即可得解；（2）根据两数之和为102，再乘以数字的个数即可得；（3）将所有的a 相加、所有含b 的式子相加，含b 的代数式利用以上求和方法求解可得． 【详解】解：（1）123100+++⋯+(1100)(299)(398)(5051)++++++⋯++10150=⨯5050=，故答案为：50、5050； （2）2468100++++⋅⋅⋅+1(2100)22100=+⨯⨯10225=⨯ 2550=；（3）原式100(23499)a b b b b b =+++++⋯+99(199)1002a b ⨯+=+1004950a b =+．【点睛】本题主要考查数字的变化规律，解题的关键是熟练掌握(1)1232n n n ++++⋯+=．。
部编数学七年级下册专题11平面直角坐标系中利用点的坐标变化规律探究问题(解析版)含答案
专题11 平面直角坐标系中利用点的坐标变化规律探究问题（解析版）第一部分典例精析类型一点的运动规律探究（1）沿坐标轴运动的点的坐标规律探究1．（2022•丛台区开学）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如（1，0），（2，0），（2，1），（3，1），（3，0），（3，﹣1）…，根据这个规律探索可得，第10个点的坐标为 ，第55个点的坐标为 ．思路引领：从图中可以看出横坐标为1的有一个点，横坐标为2的有2个点，横坐标为3的有3个点，…依此类推横坐标为n的有n个点．题目要求写出第10个点和第55个点的坐标，我们可以通过加法计算算出第10个点和第50个点分别位于第几列第几行，然后对应得出坐标规律，将行列数代入规律式．解：在横坐标上，第一列有一个点，第二列有2个点…第n列有n个点，并且奇数列点数对称而偶数列点数y轴上方比下方多一个，∵1+2+3+4＝10，1+2+3+…+10＝55，∴第10个点在第4列自下而上第4行，所以奇数列的坐标为（n，n−12）（n，n−12−1）…（n，1−n2）；偶数列的坐标为（n，n2）（n，n2−1）…（n，1−n2），由加法推算可得到第55个点位于第10列自下而上第10行．代入上式得第10个点的坐标为（4，2），第55个点的坐标为（10，5），故答案为：（4，2），（10，5）．总结提升：本题是对点的变化规律的考查，观察得到横坐标相等的点的个数与横坐标相同是解题的关键，还要注意横坐标为奇数和偶数时的排列顺序不同．2．（2022•麻城市校级模拟）如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2022秒时，点P的坐标是 ．思路引领：计算P点运动过程中走一个半圆所用的时间，根据规律即可求得第2022秒P点位置．解：由题意可知，点P运动一个半圆所用的时间为：π÷π2=2（秒），∵2022＝1011×2，∴2022秒时，P在第1011个半圆的最末尾处，∴点P的坐标为（2022，0）．故答案为：（2022，0）．总结提升：本题主要考查的是坐标系中的规律探究问题，找出运动规律的同时也要考虑坐标系位置是解题的关键．3．（2021春•洛龙区期中）在平面直角坐标系中，一只蚂蚁从原点O出发，按“向上→向右→向下→向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点A1，第二次移动到点A2，…，第n次移动到点A n，则点A2021的坐标是（ ）A．（1010，0）B．（1010，1）C．（1009，0）D．（1009，1）思路引领：观察图形可知，A4，A8，…都在x轴上，求出OA4，OA8，…OA4n的长度，然后写出坐标即可；根据以上规律写出点A4n的坐标即可求出点A2020的坐标，则A2021点的坐标即可求出．解：由图可知，A4，A8，…都在x轴上，蚂蚁每次移动1个单位，∴OA4＝2，OA8＝4，…OA4n＝2n，∴点A4n的坐标为（2n，0），∴点A2020的坐标为（1010，0），∴A2021（1010，1），故选：B．总结提升：本题主要考查了点的变化规律，仔细观察图形，确定出点A 4n 都在x 轴上是解题的关键．（2）绕定点呈“回”字形运动的点的坐标变化规律4．如图是一回形图，其回形通道的宽和OB 的长均为1， 回形线与射线OA 交于A 1，A 2，A 3，…．若从O点到A 1点的回形线为第1圈（长为7），从A 1点到A 2点的回形线为第2圈，…，依此类推．则第10圈的长为 ．思路引领：如图，以点O 为原心，建立平面直角坐标系，则A 1，A 2，A 3，…的坐标分别为（－1，0），（－2，0），（－3，0），…，A 10的坐标为（－10，0），然后大致描出第10圈的形状，很轻松求出第10圈的长．解：观察图形发现：第一圈的长是2（1+2）+1=7；第二圈的长是2（3+4）+1=15；第三圈的长是2（5+6）+1=23；则第n 圈的长是2（2n-1+2n ）+1=8n-1．当n=10时，原式=80-1=79．故答案为79．题眼直击：坐标表示图形，规律探究．总结提升：依次计算第一圈长，第二圈长，……，探究这几个数的一般规律性，然后应用规律求出第10圈．5．（2022•金凤区校级二模）如图，在平面直角坐标系中，从点P 1（﹣1，0），P 2（﹣1，﹣1），P 3（1，﹣1），P 4（1，1），P 5（﹣2，1），P 6（﹣2，﹣2），…依次扩展下去，则P 2022的坐标为 ．思路引领：根据题意可得到规律，P4n（n，n），P4n+1（﹣n﹣1，n），P4n+2（﹣n﹣1，﹣n﹣1），P4n+3（n+1，﹣n﹣1），再根据规律求解即可．解：根据题意可得到规律，P1（﹣1，0），P2（﹣1，﹣1），P3（1，﹣1），P4（1，1），P5（﹣2，1），P6（﹣2，﹣2），P7（2，﹣2），P8（2，2），P12（3，3），P16（4，4），...，P4n（n，n），P4n+1（﹣n﹣1，n），P4n+2（﹣n﹣1，﹣n﹣1），P4n+3（n+1，﹣n﹣1），∵2022＝4×505+2，∴P2022（﹣506，﹣506），故答案为：（﹣506，﹣506）．总结提升：本题主要考查规律型：点的坐标，读懂题意，找出点的坐标规律是解答此题的关键．类型二图形变换的点的坐标规律探究6．（2018春•兴城市期末）如图，在平面直角坐标系中，第一次将三角形OAB变换成三角形OA1B1，第二次将三角形OA1B1换成三角形OA2B2，第三次将三角形OA2B2换成三角形OA3B3，……，若A（﹣3，1），A1（﹣3，2），A2（﹣3，4），A3（﹣3，8），点B（0，2），B1（0，4），B2（0，6），B3（0，8），按这样的规律，将三角形OAB进行2018次变换，得到三角形OA2018B2018，则A2018的坐标是 ．思路引领：探究规律后利用规律即可解决问题；解：∵A 1（﹣3，2），A 2 （﹣3，4），A 3（﹣3，8）；∴A 点横坐标为﹣3，纵坐标依次为：2，22，23，…得出：A n （﹣3，2n ），∴n ＝2018时，A 2018（﹣3，22018），故答案为（﹣3，22018）总结提升：此题主要考查了规律型：点的坐标，根据题意得出A ，B 点横纵坐标变化规律是解题关键．7．12．如图，在直角坐标系中，第一次将三角形OAB 变换成三角形OA 1B 1第二次将OA 1B 1变换成三角形OA 2B 2，第三次将三角形OA 2B 2变换成三角形OA 3B 3，已知A(1，3)，A 1(2，3)，A 2(4，3)，A 3(8，3)，B(2，0)，B 1(4，0)，B 2(8，0)，B 3(16，0)．(1)求三角形OAB 的面积；(2)写出三角形OA 4B 4的各个顶点的坐标；(3)按此图形变化规律，你能写出三角形OA n B n 的面积与三角形OAB 的面积的大小关系吗？解：(1)S 三角形OAB ＝12×2×3＝3；(2)根据图示知O 的坐标是(0，0)；已知A(1，3)，A 1(2，3)，A 2(4，3)，A 3(8，3)，对于A 1，A 2…A n 坐标找规律比较从而发现A n 的横坐标为2n ，而纵坐标都是3；同理B 1，B 2…B n 也一样找规律，规律为B n 的横坐标为2n ＋1，纵坐标为0．由上规律可知：A 4的坐标是(16，3)，B 4的坐标是(32，0)；综上所述，O(0，0)，A 4(16，3)，B 4(32，0)；(3)根据规律，后一个三角形的底边是前一个三角形底边的2倍，高相等都是4，所以OB n ＝2n ＋1，S 三角形OA n B n ＝12×2n ＋1×3＝3×2n ＝2n S 三角形OAB ，即S 三角形A n B n ＝2n S 三角形OAB 。
部编数学七年级上册专题07探究与表达规律(八大题型)专项讲练(解析版)含答案
专题07 探究与表达规律（八大题型） 专项讲练1. 解题思维过程：从简单、局部或特殊情况入手，经过提炼、归纳和猜想，探索规律，获得结论.有时候还需要通过类比联想才能找到隐含条件.一般有下列几个类型：1）一列数的规律：把握常见几类数的排列规律及每个数与排列序号n 之间的关系.2）一列等式的规律：用含有字母的代数式总结规律，注意此代数式与序号n 之间的关系.3）图形（图表）规律：观察前几个图形，确定每个图形中图形的个数或图形总数与序号n 之间的关系.4）图形变换的规律：找准循环周期内图形变换的特点，然后用图形变换总次数除以一个循环变换周期，进而观察商和余数.5）数形结合的规律：观察前n 项（一般前3项）及利用题中的已知条件，归纳猜想一般性结论.2. 常见的数列规律：1）1，3，5，7，9，… ，21n -（n 为正整数）．2） 2，4，6，8，10，…，2n （n 为正整数）．3） 2，4，8，16，32，…，2n （n 为正整数）．4）2， 6， 12， 20，…， (1)n n +（n 为正整数）．5）x -，x +，x -，x +，x -，x +，…，(1)n x -（n 为正整数）．6）特殊数列： ①三角形数：1,3,6,10,15,21，…，(1)2n n +.②斐波那契数列：1，1，2，3，5，8，13，…，从第三个数开始每一个数等于与它相邻的前两个数的和.题型1：数列的规律1．（2022·山东烟台·期末）按一定规律排列的单项式：3x ，5x -，7x ，9x -，11x ，……，第n 个单项式是（ ）A ．()211n n x --B ．()1211n n x -+-C ．()1211n n x ---D ．()211n n x +-【答案】B【分析】先观察系数与指数的规律，再根据规律定出第n 个单项式即可．【详解】解：∵3x ，5x -，7x ，9x -，11x ，……，∴系数是奇数项为-1，偶数项为1，即系数的规律是(-1)n -1,指数的规律为2n +1，∴第n 个单项式为()1211n n x -+-，故选：B．【点睛】本题考查数式的变化规律，通过观察单项式的系数和指数，找到它们的规律是解题的关键．2．（2022·江苏盐城·七年级阶段练习）已知：21＝2，22＝4，23＝8，24＝16，25＝32，…，那么22021的个位数字是（)．A．2B．4C．6D．8【答案】A【分析】观察不难发现，2n的个位数字分别为2、4、8、6，每4个数为一个循环，用2021÷4，根据余数的情况确定答案即可．【详解】解：∵21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…，∴个位数字分别为2、4、8、6依次循环，∵2021÷4=505……1，∴22021的个位数字与21个位数字相同，即22021的个位数字是2，故A正确．故选：A．【点睛】本题主要考查了尾数特征，观察数据发现每4个数为一个循环，个位数字依次循环，是解题的关键．3．（2022·山东泰安·期中）古希腊著名的毕达哥拉斯学派把1、3、6、10…，这样的数称为“三角形数”，而把1、4、9、16…，这样的数称为“正方形数”．则第5个“三角形数”与第5个“正方形数”的和是（）A．35B．40C．45D．50【答案】B【分析】分别探究“三角形数”与“正方形数”的存在规律，求出第5个“三角形数”与第5个“正方形数”，再求第5个“三角形数”与第5个“正方形数”的和．【详解】第1个“三角形数”：1，第2个“三角形数”：1+2=3，第3个“三角形数”：1+2+3=6，第4个“三角形数”：1+2+3+3=10，第5个“三角形数”：1+2+3+4+5=15，第1个“正方形数”：1，第2个“正方形数”：22=4，第3个“正方形数”：32=9，第4个“正方形数”：42=16，第5个“正方形数”：52=25，∴15+25=40．故选：B．【点睛】本题主要考查了“三角形数”与“正方形数”，解决问题的关键是探究“三角形数”与“正方形数”的规律，运用规律求数．4．（2021·广西百色·二模）观察下列一组数：﹣32，1，﹣98，1711，﹣3314，…，它们是按一定规律排列的，那么这一组数的第8个数是_____．5．（2022·内蒙古赤峰·七年级期末）边长为1的正方形OABC从如图所示的位置（点O对应数0，点A对应数－1）开始在数轴上顺时针滚动（无滑动）．当正方形的某个顶点落在数2023在数轴上对应的点处时停止运动，此时落在数2023在数轴上对应点的这个顶点是（）A．点A B．点B C．点C D．点O【答案】A【分析】滚动四次一个循环，用2023除以4，商即是循环的次数，由余数即可得到与2023重合的点．【详解】解：∵2023＝505×4＋3，∴与2023重合的点即是滚动后与3重合的点，而与1重合的是C，与2重合的是B，与3重合的是A，∴与2023重合的是A，故A正确．故选：A．【点睛】本题主要考查图形类规律探究、数轴上点表示的数，解题的关键是理解与2023重合的点即是与3重合的点．6.（2022·福建漳州七年级开学考试）观察下列各项：114，126，138，1410，…，依此规律下去，则第7项是__________；第n项是__________．【答案】1716()121nn++【分析】观察可知：整数部分是从1开始的自然数，分数部分的分子为1，分母为从2开始的自然数的两倍，据此可得．【详解】解：114=()11211+´+，126=()12221+´+，138=()13231+´+，1410=()14241+´+，…∴第7项是1716，第n项是()121nn++，故答案为：1716，()121nn++．【点睛】此题考查数字的变化规律，找出数字之间的联系，利用规律解决问题．题型2：数表的规律1．（2022·山东济南·七年级期末）将正整数按如图所示的规律排列，若用有序数对（a，b）表示第a行，从左至右第b个数，例如（4，3）表示的数是9，则（15，10）表示的数是（）A．115B．114C．113D．112【答案】A【分析】观察图形可知，每一行的第一个数字都等于前面数字的个数再加1，即可得出（15，1）表示的数，然后得出（15，10）表示的数即可．2．（2022·山东烟台·期中）我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了()n a b +（n 为非负数）的项数及各项系数的有关规律，例如：请写出8()a b +展开式中间一项的系数（ ）A ．70B ．64C ．56D ．54【答案】A【分析】根据题意可得每行第一个和最后一个数都是1，其他位置的数下面的数等于上面两个数的和，即可求出8()a b +展开式中间一项的系数．【详解】解：由题意可得下面一个数等于上面两个数的和，∴()7a b +中，各项的系数分别为：1，7，21，35，35，21，7，1，∴()8a b +中，各项的系数分别为：1，8，28，56，70，56，28，8，1，∴8()a b +展开式中间一项的系数为70，故选：A ．【点睛】此题考查了多项式的系数规律问题，解题的关键是根据题意正确分析出各项系数的有关规律．3．（2022·辽宁葫芦岛·七年级期中）将正整数按如图所示的规律排列．若用有序数对（a ，b ）表示第a 排，从左至右第b 个数．例如（4，3）表示的数是9，则（7，3）表示的数是（ ）A ．22B ．23C ．24D ．254．（2022·河北承德·七年级期末）观察下面的数：按着上述的规律排下去，那么第12行从左边数第4个数是（ ）A ．121-B ．123-C ．125-D ．127-【答案】C【分析】先根据行数确定出最后一个数的变化规律，再根据得出的规律确定出第11行的数，然后用11行的最后一个数的绝对值与4相加即可．【详解】解：因为行数是偶数时，它的最后一个数是每行数的平方，当行数是奇数时，它的最后一个数是每行数的平方的相反数，所以第11行最后一个数字是：-11×11=-121，它的绝对值是121，第12行从左边第4个数的绝对值是：121+4=125．故第12行从左边第4个数是-125．故选：C．【点睛】此题考查了数字的变化类，找出最后一个数的变化规律，确定出第11行最后一个数是解题关键．5．（2021·云南红河·七年级期末）将连续奇数1，3，5，7，9……排成如图所示的数表．用长方形框在如图所示的数表中任意框出九个数，将长方形框上下左右移动，可框住另外九个数．若这九个数中最小的数是171，则最大的数是_____．【答案】207【分析】先设九个数中最小的数为m，根据规律表示九个数m，m+2，m+4，m+16，m+18，m+20，m+32，m+34，m+36，其中最小的是m=171，求代数式的值即可．【详解】解：设九个数中最小的为m，m+2，m+4，m+16，m+18，m+20，m+32，m+34，m+36，∵这九个数中最小的数是171，∴m=171，∴这九个数中最大的数是171+36=207，故答案为：207．【点睛】本题考查数中排列规律，找出方框中九个数的规律，代数式的值，掌握数中排列规律，找出方框中九个数的规律，利用代数式的值求出最大数是解题关键．6．（2021·四川成都·七年级期中）我国南宋数学家杨辉所著的《详解九章算术》书中辑录了一个三角形数表，称之为“开方作法本源”图，即是著名的“杨辉三角形”．以下数表的构造思路源于“杨辉三角形”：该表由若干行数字组成，从第二行起，每一行中的数字均等于“其肩上”两数之和，表中最后一行仅有一个数，则这个数为___．【答案】102×299【分析】分析得出第101行有1个数，即为最后一行的数，根据每行的第一个数字得到规律，从而判断．【详解】解：由题意，第1行有101个数，第2行有100个数，…，第101行有1个数，故第1行的第一个数为：1=2×2-1，第2行的第一个数为：3=3×20，第3行的第一个数为：8=4×21，第n行的第一个数为：（n+1）×2n-2，∴第101行的第一个数为：102×299，故答案为：102×299．【点睛】本题考查了由数表探究数列规律的问题，考查学生分析解决问题的能力，属于中档题．题型3：算式的规律算式规律这一类没有固定的套路，主要依靠学生对已知算式的观察、总结、逻辑推理，发现期中的规律。
部编数学七年级上册专题04有理数运算中的规律探究(解析版)含答案
专题04 有理数运算中的规律探究1．观察下列等式：第1个等式：111111323a æö==´-ç÷´èø第2个等式：2111135235a æö==´-ç÷´èø第3个等式：3111157257a æö==´-ç÷´èø第4个等式：4111179279a æö==´-ç÷´èø……请解答下列问题：(1)按以上规律列出第5个等式：5a =________=_______(2)用含有n 的式子表示第n 个等式：（n 为正整数）n a =______=_______(3)求12341000a a a a a ++++¼+的值．【答案】(1)1911´，1112911æö´-ç÷èø(2)()()12121n n -´+，11122121n n æö´-ç÷-+èø(3)100201【解析】【分析】（1）根据所给的等式的形式求解即可；（2）根据所给的等式，进行总结可得出规律；（3）利用（2）中的规律进行求解即可．(1)解：观察等式找到规律，第5个等式为： 511119112911a æö==´-ç÷´èø故答案为：1911´，1112911æö´-ç÷èø(2)解：Q 第1个等式：111111323a æö==´-ç÷´èø第2个等式：2111135235a æö==´-ç÷´èø第3个等式：3111157257a æö==´-ç÷´èø第4个等式：4111179279a æö==´-ç÷´èø第5个等式：511119112911a æö==´-ç÷´èø……第n 个等式：()()1111212122121n a n n n n æö==´-ç÷-´+-+èø故答案为：()()12121n n -´+，11122121n n æö´-ç÷-+èø(3)解：12341000a a a a a ++++¼+=11123æö´-ç÷èø+111235æö´-ç÷èø+111257æö´-ç÷èø…+1992011112æö´-ç÷èø11111112335199201æö=-+-+×××+-ç÷èø1112201æö=-ç÷èø12002201=´100201=【点睛】本题主要考查数字的变化规律，解题的关键是由所给的等式总结出存在的规律并灵活运用．2．先阅读下列式子的变形规律：111122=-´；1112323=-´；1113434=-´；1111111113111223342233444++=-+-+-=-=´´´然后再解答下列问题：【注：第（1）小题直接写结果，不用写过程】(1)类比计算：1910=´______，120192020=´______，归纳猜想：若n 为正整数，那么猜想()11n n =+______．(2)知识运用，选用上面的知识计算111112233420192020++++´´´´LL 的结果．(3)知识拓展：试着写出111113355779+++´´´´的结果．【答案】(1)11910-；1120192020-；111n n -+(2)20192020(3)49【解析】【分析】（1）根据题意分解形式求解即可；（2）根据式子规律求解即可；（3）将113´分解成11123æö-ç÷èø的形式，其余各式比照该分解形式进行分解，然后求和计算即可．(1)解：由题意知111910910=-´1112019202020192020=-´()11111n n n n =-´++故答案为：11910-；1120192020-；111n n -+．(2)解：1111······+12233420192020+++´´´´1111111111 (223342018201920192020)=-+-+-++-+-211200=-20192020=(3)解：111113355779+++´´´´11111111111123235257279æöæöæöæö=-+-+-+-ç÷ç÷ç÷ç÷èøèøèøèø11111111123355779æö=-+-+-+-ç÷èø11129æö=´-ç÷èø49=【点睛】本题考查了数字类规律的探究．解题的关键在于概括出分解运算规律．3．（1）观察下列各式：123456733,39,327,381,3243,3729,32187,=======L1234561313,13169,132197,1328561,13371293,134826809,======L根据你发现的规律回答下列问题：①20223的个位数字是___________；9913的个位数字是___________；②9943的个位数字是___________；5543的个位数字是___________；（2）自主探究回答问题：①997的个位数字是___________，557的个位数字是___________；②9952的个位数字是___________，5552的个位数字是___________．（3）若n 是自然数，则9955n n -的个位上的数字（ ）A ．恒为0B ．有时为0，有时非0C ．与n 的末位数字相同D ．无法确定【答案】（1）①9；7 ②7；7 （2）①3；3 ②8；8 （3）A【解析】【分析】（1）根据已知式子可以得到末尾数字4个一循环，据此解得即可；（2）可以先列出7的乘方及2的乘方的式子，可以得到末尾数字4个一循环，据此解得即可；（3）根据（1）（2）中的结论可知99n 与55n 个位上的数字相同即可得出答案．【详解】解：（1）①Q 123456733,39,327,381,3243,3729,32187,=======L\3的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环20224505 (2)¸=Q \20223的个位数字是9；Q 1234561313,13169,132197,1328561,13371293,134826809,======L\13的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环99424 (3)¸=Q \9913的个位数字是7；故答案为：9；7；②由①可知尾号为3的数的乘方的个位数字依次是3，9，7，1，以此4个数为一个循环依次进行循环99424...355413 (3)¸=¸=Q ，\9943的个位数字是7，5543的个位数字是7；故答案为：7；7；（2）①123456777497343724017168077117649...======Q ，，，，，\7的乘方的个位数字依次是7，9，3，1，以此4个数为一个循环依次进行循环99424...355413 (3)¸=¸=Q ，\997的个位数字是3，557的个位数字是3故答案为：3；3②123456222428216232264...======Q ，，，，，\2的乘方的个位数字依次是2，4，8，6，以此4个数为一个循环依次进行循环\52的乘方的个位数字依次是2，4，8，6，以此4个数为一个循环依次进行循环99424...355413 (3)¸=¸=Q ，\9952的个位数字是8，5552的个位数字是8故答案为：8；8（3）由（1）（2）中的结论可知99n 与55n 个位上的数字相同\9955n n -的个位上的数字恒为0故选A ．【点睛】本题考查数字的变化规律，找出数字之间的规律是解题的关键．4．观察下列各式：3312189+=+=，而2332(12)9,12(12)+=\+=+；33312336++=，而23332(123)36,123(123)++=\++=++；33331234100+++=，而233332(1234)100,1234(1234)+++=\+++=+++；(1)猜想并填空：3333312345++++=_______2=_______；(2)根据以上规律填空：3333123n ++++=L _______2=_______；(3)求解：333331617181920++++．【答案】(1)（1+2+3+4+5），225(2)()123n ++++L ，()212n n +éùêúëû(3)29700【解析】【分析】观察题中一系列等式发现，从1开始的连续正整数的立方和等于这几个连续正整数和的平方，据些规律来求解．（1）根据上述规律填空即可求解；（2）根据上述规律填空，然后把123n ++++L 变为2n 个()1n +相乘来求解；（3）对所求的式子前面加上1到15的立方和，然后根据上述规律分别求出1到15的立方和与16到20的立方和，再求出两数相减即可求解．(1)解：由题意可知：()2333331234512345225++++=++++=．故答案为：（1+2+3+4+5），225；(2)解：()()()1121211222n n n n n n n n +éùæö+++=+++-++-+=éùç÷êúëûèøëûQ L L ()()22333311231232n n n n +éù\+++=++++=êúëûL L ．故答案为：()123n ++++L ，()212n n +éùêúëû；(3)解：333331617181920++++()()333333331232012315=+++-+++L L()()221232012315=+++-+++L L 22210120=-29700=故答案为：29700．【点睛】本题考查了探究数字规律，主要要求学生综合运用观察、想象、归纳、推理概括等思维方式，运用总结的规律解决问题的能力．找出规律是解答关键．5．爱读书的乐乐在读一本古书典籍上有这么一段记载：相传大禹治水时，“洛水”中出现了一个神龟，其背上有美妙的图案，史称“洛书”．用现在的数字翻译出来，就是三阶幻方，三阶幻方是最简单的幻方，又叫九宫格，其对角线、横行、纵向的数字之和均相等，这个和叫做幻和，正中间那个数叫中心数，且幻和恰好等于中心数的3倍．如图1，是由1、2、3，4、5、6、7、8、9所组成的一个三阶幻方，其幻和为15，中心数为5．(1)如图2所示，则幻和＝______；(2)若b＝4，c＝6，求a的值；(3)通过研究问题（1）和（2），利用你发现的规律，将5，7，-5，3，9，-1，11，-3，1这九个数字分别填入图3的九个方格中，使得横、竖、斜对角的所有三个数的和都相等．【答案】(1)-6(2)8(3)图形见解析(答案不唯一)【解析】【分析】(1)根据幻和等于九宫格中最中心数的3倍即可得答案；(2)根据b=4先求出第二行第三列的数字，根据c=6求出第一行第三列的数字，根据对角线求出第一行第一列的数字，最后根据第一行三个数字之和等于幻和即可求解；(3)根据九宫格中所有数字相加，其和为幻和的3倍先求出中心数为3，幻和为9，进一步将数据分成5与1一组，7与-1一组，-5与11一组，9与-3一组，按照此条件分组将数据填入九宫格中即可．(1)解：由题意可知：幻和等于九宫格中最中心数的3倍，∴图2中幻和=-2×3=-6．(2)解：由(1)知幻和为-6，当b＝4，c＝6时：第二行第三列的数字为：-6-b-(-2)=-6-4+2=-8，第一行第三列的数字为：-6-(-8)-c=-6+8-6=-4，根据对角线可知：第一行第一列的数字为：-6-(-2)-6=-10，∴a=-6-(-10)-(-4)=-6+10+4=8．(3)解：将图3中的九宫格分别标记为A~I，如下图所示：由于九宫格中横行、纵向的数字之和均相等，其和叫做幻和，∴九宫格中所有数字相加，其和为幻和的3倍，∴幻和=(5+7-5+3+9-1+11-3+1)÷3=9，又幻和为九宫格中最中心数的3倍，∴最中心的E代表的数为3，∵对角线、横行、纵向的数字之和是幻和的3倍，∴A+I=6，B+H=6，C+G=6，D+F=6，故5与1一组，7与-1一组，-5与11一组，9与-3一组，只需要满足此条件写出来九宫格必然满足题目要求，取A=5、B=7时，此时I=1，H=-1，G=9，C=-3，D=-5，F=11，如下图所示(答案不唯一)：【点睛】本题主要考查数字的变化规律，读懂题意，解题的关键是掌握幻方的定义及幻和与中心数的关系即可．6．探究规律，完成相关题目．将若干个数组成一个正方形数阵，若任意一行，一列及对角线上的数字之和都相等，则称具有这种性质的数字方阵为“幻方”．中国古代称“幻方”为“河图”“洛书”等．如图所示的三阶幻方，是将数字1，2，3，4，5，6，7，8，9填入到33´的方格中得到的，其每一行，每一列，每一条对角线上的三个数字之和都相等．（1）设下面的三阶幻方中间的数字是m （其中m 为正整数），请用含m 的代数式将下面的幻方填充完整；（2）若设（1）幻方中9个数的和为S ，则S 与中间的数字m 之间的数量关系为______；（3）现要用9个数：－40，－30，－20，－10，0，10，20，30，40构造一个三阶幻方，请将构造的幻方填写在下面33´的方格中．【答案】（1）答案见解析；（2）9m S =；（3）答案见解析【解析】【分析】（1）由第3列的三个代数式的和为3,m 再利用每行，每列，每一条对角线上的三个代数式之和相等逐一填好其余的空格，即可得到答案；（2）由每行，每列，每一条对角线上的三个代数式之和相等，可得()3123,S m m m =++++-从而可得答案；（3）由（2）的规律先确定最中间的数据0, 把－40，－30，－20，－10，0，10，20，30，40按从小到大的顺序排列，再把第2,4,6,8个数据放在四角的位置，再根据每行，每列，每一条对角线上的三个数之和相等，填好其余空格即可．【详解】解：（1）1m +4m -3m +2m +m 2m -3m -4m +1m -（2）由每行每列及对角线上的三个代数式的和相等可得：()31239,S m m m m =++++-=故答案为：9.S m =（3）幻方如图所示（答案不唯一）：10－4030200－20－3040－10【点睛】本题考查的是数或代数式的排列的规律的探究，有理数的加减运算，整式的加减运算，掌握以上知识是解题的关键．7．平移和翻折是初中数学两种重要的图形变化(1)平移运动①把笔尖放在数轴的原点处，先向负方向移动3个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？用算式表示以上过程及结果是 A .（＋3）＋（＋2）＝＋5；B ．（＋3）＋（﹣2）＝＋1；C ．（﹣3）﹣（＋2）＝﹣5；D ．（﹣3）＋（＋2）＝﹣1②一机器人从原点O 开始，第1次向左跳1个单位，紧接着第2次向右跳2个单位，第3次向左跳3个单位，第4次向右跳4个单位，…，依次规律跳，当它跳2017次时，落在数轴上的点表示的数是 ．(2)翻折变换①若折叠纸条，表示﹣1的点与表示3的点重合，则表示2017的点与表示 的点重合；②若数轴上A 、B 两点之间的距离为2018（A 在B 的左侧，且折痕与①折痕相同），且A 、B 两点经折叠后重合，则A 点表示 B 点表示 ．③若数轴上折叠重合的两点的数分别为a ，b ，折叠中间点表示的数为 ．（用含有a ，b 的式子表示）【答案】(1)①D ； ②﹣1009(2)①﹣2015； ②﹣1008，1010；③2a b+【解析】【分析】（1）①根据有理数的加法法则即可判断；②探究规律，利用规律即可解决问题；（2）①根据对称中心是1，即可解决问题；②由对称中心是1，AB ＝2018，可知A 点是1左边距1为1009个单位的点表示的数，B 点是1右边距1为1009个单位的点表示的数，即可求出点A 、B 所表示的数；③利用中点坐标公式即可解决问题．(1)解：①把笔尖放在数轴的原点处，先向负方向移动3个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示的数为（﹣3）+（+2），故选D ．②一机器人从数轴原点处O 开始，第1次向负方向跳一个单位，紧接着第2次向正方向跳2个单位，第3次向负方向跳3个单位，第4次向正方向跳4个单位，…，依次规律跳，当它跳2017次时，落在数轴上的点表示的数是（﹣1）+（+2）+（﹣3）+（+4）+…+（+2016）+（﹣2017）＝1×1008+（﹣2017）＝﹣1009，故答案为：﹣1009．(2)①若折叠纸条，表示﹣1的点与表示3的点重合， 132-+＝1，∴对称中心为1，∴2017﹣1＝2016，∴1﹣2016＝﹣2015，∴表示2017的点与表示﹣2015的点重合，故答案为：﹣2015；②∵对称中心为1，AB ＝2018，∴点A 所表示的数为：1﹣20182＝﹣1008，点B 所表示的数为：1+20182＝1010，故答案为：﹣1008，1010；③若数轴上折叠重合的两点的数分别为a ，b ，折叠中间点表示的数为2a b+；故答案为：2a b+．【点睛】本题考查了数轴、有理数的加减混合运算、折叠等知识，理解题意，灵活应用所学知识是解决问题的关键．8．观察下面三行数：2，4-，8，16-，32，64-，……； ①0，6-，6，18-，30，66-，……； ②1-，2，4-，8，16-，32，……； ③观察发现：每一行的数都是按一定的规律排列的．通过你发现的规律，解决下列问题．（1）第①行的第8个数是________，第n 个数是________；（2）第②行的第n 个数是________，第③行的第n 个数是________；（3）取每行数的第10个数，计算这三个数的和．【答案】（1）256-；1(1)2n n +- ；（2）1(1)22n n +--， 11(1)2()2n n+-´-或1(1)2n n --；（3）1538-【解析】【分析】（1）第①行有理数是按照1(1)2n n +-排列的；（2）第②行为第①行的数减2；第③行为第①行的数的一半的相反数，分别写出第n 个数的表达式即可；（3）根据各行的表达式求出第10个数，然后相加即可得解．【详解】解：（1）第①行的有理数分别是﹣1×2， ﹣1×22，23， ﹣1×24，…，故第8个数是861522´=-﹣，第n 个数为（﹣2）n （n 是正整数）；故答案为：256-；1(1)2n n +- ；（2）第②行的数等于第①行相应的数减2，即第n 的数为1(1)22n n +--（n 是正整数），第③行的数等于第①行相应的数的一半的相反数，即第n 个数是11(1)2()2n n +-´-或1(1)2n n --（n 是正整数）；故答案为：1(1)22n n +--， 11(1)2()2n n+-´-或1(1)2n n --；（3）∵第①行的第10个数为101011(1)22--=，第②行的第10个数为1022--，第③的第10个数为1099(1)22-=，所以，这三个数的和为：101092(22)2-+--+1024(10242)512=-+--+102410242512=---+1538=-【点睛】本题是对数字变化规律的考查，认真观察、仔细思考，善用联想是解决这类问题的方法，观察出第②③行的数与第①行的数的联系是解题的关键．9．在有些情况下，不需要计算出结果也能把绝对值符号去掉，例如：|6＋7|＝6＋7；|7－6|＝7－6；|6－7|＝－6＋7；|－6－7|＝6＋7（1）根据上面的规律，把下列各式写成去掉绝对值符号的形式：①|7＋2|＝；②|－12＋15|＝；（2）用简单的方法计算：|13－12|＋|14－13|＋|15－14|＋……＋|12021－12020|．【答案】（1）①7+2；②1125-；（2）20194042【解析】【分析】（1）①②根据正数的绝对值等于本身，负数的绝对值是其相反数可得答案；（2）根据绝对值的性质化简，再相互抵消可得答案．【详解】解：（1）①∵7+20> ，∴|7＋2|＝7+2；②∵11025-+< ，∴|－12＋15|＝1125-；（2）原式＝11111111+...+23344520202021-+-+-- ，1122021=- ，＝20194042．【点睛】本题考查有理数的混合运算，熟练地掌握运算法则和绝对值的性质是解题关键．10．给定一列数，我们把这列数中的第一个数记为1a ，第二个数记为2a ，第三个数记为3a ，以此类推，第n 个数记为n a （n 为正整数）．例如下面这列数1，3，5，7，9中，11a =，23a =，35a =，47a =，59a =．规定运算1123(:)n n sum a a a a a a =+++¼¼+，即从这列数的第一个数开始依次加到第n 个数，如在上面这列数中：1312313(:)59sum a a a a a =++=++=．（1）已知一列数-1，2，-3，4，-5，6，-7，8，-9，10．则110(:)sum a a =______．（2）已知一列有规律的数：1(1)1-´，2(1)2-´，3(1)3-´，4(1)4-´，¼¼，按照规律，这列数可以无限的写下去．①求12021(:)sum a a 的值．②是否有正整数n 满足等式1(:)50n sum a a =-成立？如果有，请直接写出n 的值．如果没有，请说明理由．【答案】（1）5；（2）①-1011；②n =99．【解析】【分析】（1）直接根据题中所给定义运算进行求解即可；（2）①由题意可知()12341,2,3,4, (1)n a a a a a n =-==-==-×，由此可得20212021a =-，然后求解即可；②由题意易得()12345....150nn -+-+-++-×=-，进而求解即可．【详解】解：（1）由题意得：110(:)123456789105sum a a =-+-+-+-+-+=，故答案为5．（2）解：由题意得：()12341,2,3,4, (1)n a a a a a n =-==-==-×，∴12021(:)sum a a =-1+2-3+4···+2020-2021=1×1010-2021=-1011．②由题意得：()12345....150nn -+-+-++-×=-，∴当n 为奇数时，则有11502n n -´-=-，解得：n =99，当n 为偶数时，则有1502n ´=-，解得：100n =-，（不符合题意，舍去），∴综上所述：n =99．【点睛】本题主要考查含乘方的有理数混合运算及数字规律问题，熟练掌握含乘方的有理数混合运算及数字规律问题是解题的关键．11．细心观察下面三个图形，按下述方法找出规律．（1）分别写出前面三个图形四角中四个数的积分别是 、 、 ；（2）分别写出前面三个图形四角中四个数的和分别是、、；（3）请你说明你发现的规律找出第四个正方形中的数，并说明理由．【答案】（1）24，60，120；（2）-10，-13，-16；（3）191，理由见解析【解析】【分析】（1）根据有理数乘法的性质计算，即可得到答案；（2）根据有理数加法的性质计算，即可得到答案；（3）根据有理数乘法和加法的性质计算，并结合前三个图形的数字规律，即可完成求解．【详解】（1）(－1)×(－2)×(－3)×(－4)＝24；(－1)×(－3)×(－5)×(－4)＝60；(－1)×(－4)×(－5)×(－6)＝120；故答案为：24，60，120；（2）(－1)＋(－2)＋(－3)＋(－4)＝－10；(－1)＋(－3)＋(－5)＋(－4)＝－13；(－1)＋(－4)＋(－5)＋(－6)＝－16；故答案为：-10，-13，-16；（3）(－1)×(－5)×(－6)×(－7)＝210；(－1)＋(－5)＋(－6)＋(－7)＝－19；∵第1个正方形中的数()241014=+-= 第2个正方形中的数()601347=+-=第3个正方形中的数()12016104=+-=∴第四个正方形中的数()21019191=+-=．【点睛】本题考查了有理数加减法、乘法，以及数字规律的知识；解题的关键是熟练掌握有理数加减法和乘法的性质，结合数字规律，从而完成求解．12．一跳蚤P 从数轴上表示﹣2的点A 1开始移动，第一次先向左移动1个单位，再向右移动2个单位到达点A 2；第二次从点A 2向左移动3个单位，再向右移动4个单位到达点A 3；第三次从点A 3向左移动5个单位，再向右移动6个单位到达点A 4，…，点P 按此规律移动，那么：（1）第一次移动后这个点P 在数轴上表示的数是 ；（2）第二次移动后这个点P 在数轴上表示的数是 ；（3）第五次移动后这个点P 在数轴上表示的数是 ；（4）这个点P 移动到点An 时，点An 在数轴上表示的数是 ．【答案】（1）﹣1；（2）0；（3）3；（4）﹣2+n ．【解析】【分析】（1）根据题意可得第一次移动后这个点P 在数轴上表示的数是﹣1；（2）第二次移动后这个点P 在数轴上表示的数是2120-+´=；（3）第五次移动后这个点P 在数轴上表示的数是2153-+´=；（4）这个点P 移动到点An 时，点An 在数轴上表示的数212n n -+´=-+．【详解】解：（1）记某次向左移动m 个单位长度，则向右移动()1m +个单位长度，从而每次移动的实际量为：123411,m m -+=-+=-++=∵一跳蚤P 从数轴上表示﹣2的点A 1开始移动，第一次先向左移动1个单位，再向右移动2个单位∴211-+=-，即第一次移动后这个点P 在数轴上表示的数是﹣1故答案为﹣1（2）∵2120,-+´=∴第二次移动后这个点P 在数轴上表示的数是0故答案为0（3）∵2153,-+´=∴第五次移动后这个点P 在数轴上表示的数是3故答案为3（4）∵212n n -+´=-+，∴这个点P 移动到点An 时，点An 在数轴上表示的数是﹣2+n 故答案为﹣2+n ，【点睛】本题考查的是点在数轴上的移动规律的探究，有理数的加法运算，掌握数轴上点的移动后对应的数的变化规律是解题的关键．13．探索规律：观察下面由※组成的图案和算式，解答问题：1+3=4=221+3+5=9=321+3+5+7=16=421+3+5+7+9=25=52（1）请写出满足上述规律的第6行等式：__________；（2）请猜想1+3+5+7+9+…+39=_____；（写出具体数值）（3）请猜想1+3+5+7+9+…+（2n ﹣1）+（2n +1）=_____；（用含n 的式子表示）（4）请用上述规律计算：51+53+55+…+87+89．（写出计算过程）【答案】（1）1+3+5+7+9+11=62；（2）400；（3）（n +1）2；（4）1400【解析】（1）类比得出第6行等式为：1+3+5+7+9+11=62；（2）由图形可知，从1开始的连续奇数的和等于奇数的个数的平方，然后根据此规律求解即可；（3）利用（1）（2）的规律推出一般规律即可；（4）用从1到89的连续奇数的和减去从1到49的连续奇数的和，进行计算即可得解．【详解】解：（1）第6行等式：1+3+5+7+9+11=62；（2）1至39共有（39+1）÷2=20个奇数，∴1+3+5+7+9+…+39=202=400；（3）1+3+5+7+9+…+（2n -1）+（2n +1）=22112n ++æöç÷èø=（n +1）2；（4）51+53+55+…+87+89=1+3+5+7+…+87+89-（1+3+5+7+…+47+49）=2289149122++æöæö-ç÷ç÷èøèø=452-252=2025-625=1400．【点睛】此题考查数字的变化规律，找出数字之间的运算规律，得出规律，解决问题．14．下列图形是由一些小正方形和实心圆按一定规律排列而成的，如图所示，124,6K K ==，……按此规律排列下去，第n 个图形中实心圆的个数表示为Kn ．（1）n K =______（用n 表示）：100K =_______（2）我们在用“*”定义一种新运算：对于任意有理数a 和正整数n ．规定*2n na K a K a n -++=，例如：223336|36|(3)*2322K K --+-+--+-+-===-．①计算：(26.6)*10-的值；②比较：3*n 与(3)*n -的大小．【答案】（1）2（n +1），202；（2）①-22；②3☆n ＞（-3）☆n 【解析】【分析】（1）由图形可知：第1个图形中有4个实心圆，第2个图形中有6个实心圆，第3个图形中有8个实心圆，…由此得出第n 个图形中有2（n +1）个实心圆，进一步代入求得答案即可；（2）①根据规定的运算顺序与计算方法，转化为有理数的混合运算计算即可；②根据规定的运算顺序与计算方法分别计算得出结果比较得出结论即可．【详解】解：（1）Q 第1个图形中有4个实心圆，第2个图形中有6个实心圆，第3个图形中有8个实心圆，¼2(1)n K n \=+；1002(1001)202K =´+=；（2）①(26.6)-*10101026.6|26.6|2K K --+-+=26.6(2102)|26.6(2102)|2--´++-+´+=22=-；②n Q 是正整数，224n K n \=+…；3\*n3|3|2n n K K -++=332n nK K -++=3=，(3)-*n3|3|2n n K K --+-+=332n nK K ---+=3=-．n>-*n．所以3*(3)【点睛】此题考查图形的变化规律，有理数的混合运算，找出图形的运算规律，理解规定的运算方法是解决问题的关键．。
专题 整式中的规律探究题(原卷版)
（苏科版）七年级上册数学《第3章 代数式》专题 整式中的规律探究题1．（2023春•耿马县期末）按一定规律排列的单项式：2a ，3a 2，4a 3，5a 4，6a 5，…，第n 个单项式是（ ）A ．（n +1）a nB ．（n +1）a 2nC ．na 2nD ．2na n2．（2022春•湖北期末）按一定规律排列的单项式：2a 2，4a 3，8a 4，16a 5，32a 6，…，第n 个单项式是（ ）A ．2n a nB ．2n ﹣1a n +1C ．2n a n +1D ．2n +1an3．（2023•大理市模拟）观察下列关于x 的单项式：x ，﹣3x 2，5x 3，﹣7x 4，9x 5，﹣11x 6，…，按此规律，第n 个单项式为（ ）A ．（2n ﹣1）x nB ．﹣（2n ﹣1）x nC ．（﹣1）n （2n ﹣1）x nD ．（﹣1）n +1（2n ﹣1）x n4．（2023•楚雄市二模）按一定规律排列的单项式：a 3，−a 25，a 39，−a 417，…，第n 个单项式是（ ）A ．(−1)n a n2n1B ．(−1)n a n 2n +11C ．(−1)n +1a n 2n 1D ．(−1)n +1a n 2n +115．（2022秋•云阳县期中）观察下列单项式：a ，﹣a 2，a 3，﹣a 4，a 5，…，按此规律第n 个单项式是 ．（n 为正整数）6．（2023•西藏）按一定规律排列的单项式：5a ，8a 2，11a 3，14a 4，…．则按此规律排列的第n 个单项式为 ．（用含有n 的代数式表示）7．按照规律填上所缺的单项式并回答问题：（1）a 、﹣2a 2、3a 3、﹣4a 4， ；（2）试写出第2008个单项式；（3）试写出第n 个单项式．8．观察下列单项式：﹣x ，3x 2，﹣5x 3，7x 4，…，﹣37x 19，39x 20，…，回答下列问题：（1）这些单项式的系数的规律是什么？（2）这些单项式的次数的规律是什么？（3）根据上面的规律，归纳出第n 个单项式是什么．（4）第2023和2024个单项式是什么？1．（2023•双柏县模拟）按一定规律排列的多项式：x ﹣y ，x 2+2y ，x 3﹣3y ，x 4+4y ，x 5﹣5y ，x 6+6y ，…，则第n 个多项式是（ ）A ．x n +（﹣1）n ny B ．（﹣1）n x n +ny C ．x n +（﹣1）n +1nyD ．（﹣1）n x n +（﹣1）n ny2．按一定规律排列的多项式：﹣x +2y ，x 2+4y ，﹣x 3+6y ，x 4+8y ，﹣x 5+10y ，x 6+12y ，…，根据上述规律，可知第n 个多项式是（ ）A ．（﹣1）n x n +ny B ．（﹣1）n x n +2ny C ．（﹣1）n +1x n +2nyD ．（﹣1）n x n +（﹣1）n ny3．一组按规律排列的多项式：a +b ，a 2﹣b 3，a 3+b 5，a 4﹣b 7，……，其中第10个式子的次数是（ ）A ．10B ．17C ．19D ．214．（2023•巧家县二模）观察下列代数式：1﹣x 2，2+x 3，3﹣x 4，4+x 5，……，根据其中的规律可得第2023个式子是（ ）A ．2022﹣x 2023B ．2022+x 2023C ．2023﹣x 2024D ．2023+x 20245．有一组多项式：a ﹣b 2，a 3+b 4，a 5﹣b 6，a 7+b 8，…，请观察它们的构成规律，用你发现的规律写出第n 个多项式为 ．6．按一定规律排列的多项式：x +2y ，﹣x 2+4y ，x 3+8y ，﹣x 4+16y ，x 5+32y ，…，根据上述规律，则第n 个多项式是 ．7．观察下列各式及其展开式（a +b ）2＝a 2+2ab +b 2（a +b ）3＝a 3+3a 2b +3ab 2+b 3（a +b ）4＝a 4+4a 3b +6a 2b 2+4ab 3+b 4（a +b ）5＝a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+b 5……请你猜想（2x ﹣1）8的展开式中含x 2项的系数是（ ）A ．224B ．180C ．112D ．488．已知一列多项式：12x 2−x ，32x 2+2x ，56x 2−3x ，76x 2+4x ，910x 2−5x ，1110x 2+6x ，1314x 2−7x ，1514x 2+8x ，⋯（1）第9个多项式是 ，第10个多项式是 ．（2）当n 是奇数时，第n 个多项式是 ，第（n +1）个多项式是 ．（3）已知2x 2+x ＝3，求前100个多项式的和．1．（2023•牡丹江模拟）按一定规律排列的一列数依次为3，6，12，24，…，按此规律排列下去，这列数的第7个数是（ ）A ．96B ．124C ．192D ．2342．（2022秋•衡南县期末）古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性，若把第一个三角数记为a 1，第二个三角数记为a 2，…，第n 个三角数记为αn ，计算a 2021﹣a 2020的值为（ ）A ．2021B ．2020C ．2019D ．20183．（2023春•镇雄县期末）一组按规律排列的式子：﹣2，52，−83，114，…．第n 个式子是（ ）（n 为正整数）A ．(−1)n +13n−1nB ．(−1)n3n−1n 1C ．(−1)n2n 1nD ．(−1)n3n−1n4．（2023春•渝北区校级期中）当x ≠﹣1时，我们把−1x 1称为x 的“和1负倒数”．如：2的“和1负倒数”为−121=−13，若x 1＝1，x 2是x 1的“和1负倒数”，x 3是x 2的“和1负倒数”…依次类推，则x 1•x 2•x 3•…x 2023的值为（ ）A ．1B ．﹣1C ．12D ．−125．（2023春•泗水县期中）将正整数按如图所示的规律排列下去，若有序数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，3）表示8，已知1+2+3+⋯+n =n(n 1)2，则表示2023的有序数对是（ ）A ．（64，7）B ．（64，64）C ．（64，58）D ．（64，57）6．（2023•新洲区模拟）有一列数，记为a 1，a 2，⋯，a n ，记其前n 项和为S n ＝a 1+a 2+⋯+a n ，定义T n =S 1S 2⋯S nn为这列数的“亚运和”，现有99个数a 1，a 2，⋯，a 99，其“亚运和”为1000，则1，a 1，a 2，⋯，a 99这100个数的“亚运和”为（ ）A ．791B ．891C ．991D ．10017．（2023•天河区校级模拟）观察按一定规律排列的一组数：2，12，27，…，其中第n个数记为a n；第n+1个数记为a n+1，第n+2个数记为a n+2，且满足1a n+1a n+2=2a n+1，则a4＝ ，a2023＝ ．8．（2023•烈山区一模）观察以下等式：第1个等式21=11+11；第2个等式23=12+16；第3个等式25=13+115；第4个等式27=14+128．……按照以上规律，解决下列问题：（1）写出第5个等式： ；（2）写出你猜想的第n个等式： （用含n的等式表示），并证明你的结论．9．（2023秋•瓯海区校级月考）观察下列等式：第1个等式：a1=11×3=12×(1−13)；第2个等式：a2=13×5=12×(13−15)；第3个等式：a3=15×7=12×(15−17)；…青解答下列问题：（1）按以上规律列出第5个等式：a5＝ ．（2）用含有n的代数式表示第n个等式：a n＝ （n为正整数）；（3）求a1+a2+…+a100的值．1．（2023•洪山区开学）如图，摆第一个图形需要4根火柴，摆第二个图形需要7根火柴，…，以此类推．那么摆第八个图形需要（ ）根火柴．A ．24B ．27C ．25D ．282．（2022秋•凤翔县期末）找出以下图形变化的规律，则第2022个图形中黑色正方形的数量是（ ）A ．3030B ．3031C ．3032D ．30333．（2023•东海县开学）如图，一张正方形桌子四周可以坐4人，如果按如图所示的方式拼桌子，六张桌子拼在一起可以坐 人．4．（2023春•凉州区期末）观察下列图形，它们是按一定规律排列的，按此规律，第100个图形中“〇”的个数为 ．5．（2022秋•无锡月考）探究规律：将棋子按下面的方式摆出正方形．（1）按图示规律，第（6）图需要 个棋子；（2）按照这种方式摆下去，摆第n（n为正整数）个正方形需要 个棋子；（3）按照这种方式摆下去，摆第2020个正方形需要多少棋子？6．下列图形按一定规律排列，观察并回答：（1）依照此规律，第四个图形共有 个★，第六个图形共有 个★；（2）第n个图形中有★ 个；（3）根据（2）中的结论，第几个图形中有2020个★？7．（2023春•肇东市期末）用棋子摆出下列一组图形：（1）填写表：图形编号123456图形中的棋子 （2）照这样的方式摆下去，那么第n个图形的棋子数是 枚；（3）如果某一图形共有102枚棋子，那么它是第 个图形．8．（2022秋•濮阳县期中）如图，自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．（1）2节链条长 cm，6节链条长 cm；（2）n节链条长多少cm？（3）如果一辆自行车的链条由60节这样的链条组成，那么这辆自行车上链条总长度是多少？9．（2022秋•永兴县期末）一串图形按如图所示的规律排列．（说明：下列所指的小正方形都是与第1个图形一样大小的正方形）（1）第5个图形中有几个小正方形？第6个图形呢？（2）求出第n个图形中小正方形的个数．（3）求出第20个图形中小正方形的个数．（4）是否存在某个图形，其小正方形的个数恰好是下列各数：①5050；②1000．给出你的判断，并说明理由．。
七年级上册找规律数学题
七年级上册找规律数学题一、数字规律题。
1. 观察下列数：1，4，9，16，25，…，按此规律，第n个数是（）- 解析：- 第1个数是1 = 1^2；- 第2个数是4=2^2；- 第3个数是9 = 3^2；- 第4个数是16=4^2；- 第5个数是25 = 5^2。
- 所以第n个数是n^2。
2. 有一组数：1, - 2,3,-4,5,-6,·s，按此规律，第n个数是（）- 解析：- 当n为奇数时，数为正数，即第n个数为n；- 当n为偶数时，数为负数，即第n个数为-n。
- 所以第n个数是( - 1)^n + 1n。
3. 观察数列：2,5,8,11,·s，则第n个数是（）- 解析：- 可以发现每一个数都比前一个数大3。
- 第1个数2 = 3×1 - 1；- 第2个数5=3×2 - 1；- 第3个数8 = 3×3-1；- 所以第n个数是3n - 1。
4. 数列1,(1)/(2),(1)/(3),(1)/(4),(1)/(5),·s，第n个数是（）- 解析：- 很明显，第n个数是(1)/(n)。
5. 找规律：0,3,8,15,24,·s，第n个数是（）- 解析：- 第1个数0 = 1^2-1；- 第2个数3=2^2-1；- 第3个数8 = 3^2-1；- 第4个数15=4^2-1；- 第5个数24 = 5^2-1；- 所以第n个数是n^2-1。
二、图形规律题。
6. 用火柴棒按下图的方式搭三角形：- 照这样的规律搭下去，搭n个这样的三角形需要多少根火柴棒？- 解析：- 搭1个三角形需要3根火柴棒；- 搭2个三角形需要3 + 2=5根火柴棒；- 搭3个三角形需要3+2×2 = 7根火柴棒；- 搭n个三角形需要3 + 2(n - 1)=2n + 1根火柴棒。
7. 观察下列图形的构成规律，根据此规律，第n个图形中有多少个圆？- 第1个图形有1个圆；- 第2个图形有1 + 2 = 3个圆；- 第3个图形有1+2 + 3=6个圆；- 第4个图形有1+2+3 + 4 = 10个圆；- 解析：- 第n个图形中圆的个数为1 + 2+3+·s+n=(n(n + 1))/(2)。
部编数学七年级上册专题05与整式有关的规律探究问题之六大题型(解析版)含答案
专题05 与整式有关的规律探究问题之六大题型单项式规律题例题：（2023下·云南玉溪·七年级统考期末）按一定规律排列的单项式：3579112,4,8,16,32,64x x x x x x ×××，第n 个单项式是（ ）A ．()211n n x -+B ．212n n x -C ．221n n x +D ．212n nx +【答案】B【分析】找出给出的一列单项式的系数和次数的规律即可解答.【详解】解：因为给出的一列单项式的系数分别是1234522,42,82,162,322=====L ，次数的规律是从1开始的连续的奇数，所以第n 个单项式是212n n x -.故选：B .【点睛】本题考查了单项式的规律探寻，根据给出的单项式找出系数和次数的规律是解题的关键.【变式训练】1．（2023下·云南昭通·八年级统考期末）一列单项式按以下规律排列：x ，23x -，25x ，7x -，29x ，211x -，13x ，L ，则第2023个单项式是（ ）A ．4045xB ．24045x -C ．24045x D ．4045x-【答案】A【分析】根据规律，系数是从1开始的连续奇数且第偶数个是负数，第奇数个是正数，x 的指数是3个循还一次，且分别是1，2，2，然后求解即可．【详解】解：根据x ，23x -，25x ，7x -，29x ，211x -，13x ，L ，所以系数是从1开始的连续奇数且第偶数个是负数，第奇数个是正数，有理数中分数的规律问题【变式训练】有理数的运算末位数字问题∴20233的末位数字为：7故选：C【点睛】此题考查了数字类变化规律，根据题意得到规律是解题的关键．【变式训练】有理数的新运算规律问题【变式训练】有理数中分数运算的规律问题【变式训练】图形类规律探究问题(1)数一数，完成下列表格．直线的条数2345【变式训练】1．（2023上·河北邢台·七年级统考期末）下面各图均由边长相同的正方形按一定规律拼接而成，请你观察、分析并解决下列问题：(1)第5个图中的正方形的个数是______；(2)求第n 个图中正方形的个数．【答案】(1)16(2)31n +【分析】（1）第1个图中正方形的个数是：3311=´+，第2个图中正方形的个数是：7321=´+，第3个图中正方形的个数是：10331=´+，则第n 个图中正方形的个数是：31n +，即可得；（2）由（1）即可得．【详解】（1）解：第1个图中正方形的个数是：3311=´+，第2个图中正方形的个数是：7321=´+，第3个图中正方形的个数是：10331=´+，…则第n 个图中正方形的个数是：31n +，即第5个图中的正方形的个数是：35116´+=，故答案为：16；（2）解：由（1）得，第n 个图中正方形的个数是31n +．(1)填写下表：三角形个数12345…故答案为：()21n +；（3）不存在三角形的个数是x 由2022根火柴棒拼成．理由如下：由（2）得出的规律可得：212022x +=，解得1010.5x =，∵火柴棒根数x 为正整数，∴1010.5x =不合题意，舍去，∴不存在三角形的个数是x 由2022根火柴棒拼成．【点睛】本题考查了图形类的变化规律，关键是通过观察图形，得出火柴棒数与三角形个数之间的规律．一、单选题A．63个B．87个C．91个【答案】D【分析】根据所给图形得到后面图形比前面图形多的“树枝”的个数用底数为而可得出答案.A．4044B．4046C．6069【答案】D二、填空题【答案】6068【分析】先根据题中的图形进行研究，分析出图形规律即可作答．【详解】解：第一个图的十字星是2个；(1)第四次裁剪后，得到的最小图形的面积占大正方形面积的______．(2)请你利用（1）中的结论，求下列各式的值：①23202211112222+++×××+=5112347解得78n =，答：需78张餐桌拼成一张大餐桌；（3）如图：由（1）同理可知，n 张桌子共坐()42n +人，42240n +=，解得59.5n =，n 是正整数，6078n =<，答：最少要用60张餐桌．【点睛】本题考查了数据规律的探究与实际应用；解题的关键是从题意观察、发现数据规律．。
七年级数学探究题
七年级数学探究题一、有理数运算探究题1. 探究规律：- 计算：1 - (1)/(2)=(1)/(2)；1-(1)/(2)-(1)/(4)=1 - ((1)/(2)+(1)/(4)) = 1-(3)/(4)=(1)/(4)；1-(1)/(2)-(1)/(4)-(1)/(8)=1-((1)/(2)+(1)/(4)+(1)/(8)) = 1 - (7)/(8)=(1)/(8)。
- 猜想：1-(1)/(2)-(1)/(4)-(1)/(8)-·s-(1)/(2^n)=___。
- 解析：- 通过前面的计算可以发现规律。
每次计算都是1减去后面分数之和，而后面分数之和的分母是最后一个分数的分母，分子比分母小1。
- 对于1-(1)/(2)-(1)/(4)-(1)/(8)-·s-(1)/(2^n)，结果应该是(1)/(2^n)。
2. 若a = (1)/(1×2)+(1)/(2×3)+(1)/(3×4)+·s+(1)/(2019×2020)，求a的值。
- 解析：- 先分析每一项的规律，(1)/(n(n + 1))=(1)/(n)-(1)/(n + 1)。
- 那么a=<=ft(1-(1)/(2))+<=ft((1)/(2)-(1)/(3))+<=ft((1)/(3)-(1)/(4))+·s+<=ft((1)/(2019)-(1)/(2020))。
- 可以发现中间项都可以消去，最后a = 1-(1)/(2020)=(2019)/(2020)。
二、整式探究题3. 探究(a + b)^2=a^2 + 2ab + b^2与(a - b)^2=a^2-2ab + b^2的关系。
- 解析：- 把(a - b)^2中的-b看作一个整体，(a - b)^2=[a+(-b)]^2。
- 根据(a + b)^2=a^2 + 2ab + b^2，可得[a+(-b)]^2=a^2+2a(-b)+(-b)^2=a^2 - 2ab + b^2。
初中数学规律探究题
1条 2条 3条 七年级数学（上）探索规律类 问题一、数字规律类：1、一组按规律排列的数：41，93，167，2513，3621，…… 请你推断第9个数是 ． 2、（2005年山东日照）已知下列等式： ① 13＝12； ② 13＋23＝32； ③ 13＋23＋33＝62； ④ 13＋23＋33＋43＝102 ；…………由此规律知，第⑤个等式是 ．3、（2005年内蒙古乌兰察布）观察下列各式；①、12+1=1×2 ；②、22+2=2×3； ③、32+3=3×4 ；………请把你猜想到的规律用自然数n 表示出来 。
4、（2005年辽宁锦州）观察下面的几个算式：①、1+2+1=4； ②、1+2+3+2+1=9；③、1+2+3+4+3+2+1=16；④、1+2+3+4+5+4+3+2+1=25，……根据你所发现的规律，请你直接写出第n 个式子 5、（2005年江苏宿迁）观察下列一组数的排列：1、2、3、4、3、2、1、2、3、4、3、2、1、…，那么第2005个数是（ ） A ．1 B ． 2 C ．3 D ．4 6、（2005年山东济南市）把数字按如图所示排列起来，从上开始，依次为第一行、第二行、第三行、……，中间用虚线围的一列，从上至下依次为1、5、13、25、……，则第10个数为________。
第1行 1第2行 －2 3第3行 －4 5 －6第4行 7 －8 9 －10（第6题图） 第5行 11 －12 13 －14 15 ……………… （第7题图） 7、（05年江苏省金湖实验区）已知一列数：1，―2，3，―4，5，―6，7，… 将这列数排成如上所示的形式：按照上述规律排下去，那么第10行从左边数第5个数等于 ． 二、图形规律类： 8、（2005年云南玉溪）一质点P 从距原点1个单位的A 点处向原点方向跳动，第一次跳动到OA 的中点1A 处，第二次从1A 点跳动到O 1A 的中点2A 处，第三次从2A 点跳动到O 2A 的中点3A 处，如此不断跳动下去，则第n 次跳动后，该质点到原点O 的距离为 。
七年级数学规律题
第3行
18
20
22
24
……
……
28
26
将正偶数按下表排成5列,并根据右表的规律，2002应排在 （ ） （A）第126行，第1列 （B）第126行，第2列 （C）第251行，第1列 （D）第251行，第2列
（5）有一列单项式：-x,2x2,-3x3, …-19x19, 20x20, …①写出第100个，第101个单项式②写出第n个，第n+1个单项式
第n层有=(n+1）（n+2）
等差规律：差乘序+某数
等差
等差
03
04
05
01
02
等差规律：差乘序+某数
4． ① ② ③ ●●● ●●●●● ●●●●●●● ● ● ● ● ● ● ● ● ●
年数n
高度h（单位：厘米）
1
115
2
130
3
145
4
…
……
115=差×序+某＝ 15×① +100改序为n
等差规律：差乘序+某数
如图，第n排有______个三角形.
第一排
第二排
第三排
…………………
第n排
2n－1
等差规律的应用：
从第一排起三角形的个数分别是1，3，5.。。。 等差，差为2，1＝差乘序+某＝2 ×① －1，改序为n
相邻之差是3
差×序+某＝ 3×① -2
第n个数是3n-2
等差规律：差乘序+某数
等差规律：差乘序+某数
树的高度与树生长的年数有关，测得某棵树的有关数据如下表：（树苗原高100厘米）年数n高度h（单位：厘米） 1)填出第4年树苗可能达到的高度； (2)请用含n的代数式表示高度h：____________
初一上数学真题专题练习---规律探究与新定义运算
规律探究与新定义运算【真题精选】1．（2020秋•161月考）按一定规律排列的一列数依次为，﹣，，﹣，，﹣，…，按此规律排列下去，这列数中第8个数是，第n个数是（n为正整数）．2．（2020秋•海淀月考）按一定规律排列的单项式：a，﹣a2，a3，﹣a4，a5，﹣a6，……第2020个单项式是（）A．2020a B．﹣2020a C．a2020D．﹣a2020 3．（2019秋•昌平区月考）观察下面的单项式：2x，4x2，8x3，16x4根据你发现的规律，写出第6个式子是，第n个式子是．4．（2020秋•房山期末）观察下列单项式：0，3x2，8x3，15x4，24x5…，按此规律写出第20个单项式是．5．（2015秋•人大附中）观察下列单项式，2x，﹣5x2，10x3，﹣17x4，…根据你发现的规律写出第8个式子是，第n个式子是．6．（2020秋•海淀校级期中）有一列式子，按照一定的规律排列成﹣3a2，9a5，﹣27a10，81a17，﹣243a26…，则第n个式子为（n为正整数）．7．（2020秋•西城校级期中）观察下列两行数：1，3，5，7，9，11，13，15，17，…1，4，7，10，13，16，19，22，25，…探究发现：第1个相同的数是1，第2个相同的数是7，…，第n个相同的数是2023，则n等于（）A．337B．338C．339D．3408．（2020秋•海淀期末）在一列数a1，a2，a3，a4，…a n中，已知a1＝2，a2＝，a3＝，a4＝，…a n＝，则a2020＝．9．（2021秋•西城期末）已知有理数a≠1，我们把称为a的差倒数，如：2的差倒数是＝﹣1，﹣2的差倒数是，如果a1＝﹣4，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…以此类推，则a1+a2+a3+a4+…+a61的值是（）A．﹣55B．55C．﹣65D．65 10．（2021•海淀月考）已知有理数a≠1，我们把称为a的差倒数，如：2的差倒数是＝﹣1，﹣1的差倒数是．如果a1＝﹣3，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数…依此类推，那么a1﹣a2+a3﹣a4…+a401﹣a402+a403﹣a404的值是（）A．B．﹣3C．D．11．（2020秋•朝阳期中）根据如图数字之间的规律，问号处应填（）A．61B．52C．43D．37 12．（2021•西城月考）如图，图1是“杨辉三角”数阵；图2是（a+b）n的展开式（按b的升幂排列）．若（1+x）45的展开式按x的升幂排列得：（1+x）45＝a0+a1x+a2x2+…+a45x45，则a2＝．13．（2021•海淀月考）我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1，3，6，10…）和“正方形数”（如1，4，9，16…），在小于200的数中，设最大的“三角形数”为m，最大的“正方形数”为n，则m+n的值为．14．（2020秋•西城期末）观察图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第2020个图形中共有（）个〇．A．6058B．6059C．6060D．6061 15．（2020秋•东城月考）观察下面一组数：﹣1，2，﹣3，4，﹣5，6，﹣7…将这组数排成如图的形式，按图中规律排下去，则第6行中从左边数第3个数是（）A．28B．﹣28C．﹣34D．34 16．（2020秋•海淀校级期中）世界上最著名的数列之一﹣﹣斐波那契数列，是从兔子繁殖问题引申出的一个数学模型．兔子在出生两个月后就具有繁殖能力，一对兔子每个月能生出一对小兔子．如果所有兔子都不死，那么一年后可以繁殖的兔子的对数会成斐波那契数列．斐波那契数列1，1，2，3，5，8，13，21，…的排列规律是：从第3个数开始，每一个数都是它前面两个数的和．在斐波那契数列的前2021个数中，共出现的偶数的个数为（）A．670B．671C．672D．673 17．（2020秋•西城期末）观察下列各算式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…根据上述算式的规律，你认为22020的末位数字应该是（）A．2B．4C．6D．818．（2020秋•海淀区校级月考）如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下一次沿顺时针方向跳两个点；若停在偶数点上，则下一次沿逆时针方向跳一个点．若青蛙从数1这点开始跳，第1次跳到数3那个点，如此，则经2020次跳后它停的点所对应的数为（）A．1B．2C．3D．519．（2020秋•西城区校级期中）如下表，从左向右依次在每个小格子中都填入一个有理数，使得其中任意四个相邻小格子中所填数之和都等于15．已知第3个数为7，第5个数为m﹣1，第16个数为2，第78个数为3﹣2m，则m的值为，第2021个数为．20．（2020秋•丰台期末）如图所示的运算程序中，若开始输入的x值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，则第2019次输出的结果为．21．（2021秋•朝阳期末）按下面的程序计算：若输入x＝100，输出结果是501，若输入x＝25，输出结果是631，若开始输入的x值为正整数，最后输出的结果为556，则开始输入的x值可能有（）A．1种B．2种C．3种D．4种22．（2020秋•海淀月考）规定一种新的运算＝ad﹣bc，那么＝．23．（2020秋•西城区校级期中）定义计算“△”，对于两个有理数a，b，有a△b＝ab﹣（a+b），例如：﹣3△2＝﹣3×2﹣（﹣3+2）＝﹣6+1＝﹣5，则3△﹣2＝，[（﹣1）△（m﹣1）]△4＝．24．（2021春•海淀区校级期末）对于任意的有理数a，b，如果满足+＝，那么我们称这一对数a，b为“相随数对”，记为（a，b）．若（m，n）是“相随数对”，则3m+2[3m+（2n﹣1）]＝．25．（2020秋•东城期末）一般情况下不成立，但有些数可以使得它成立，例如：m＝n＝0时，我们称使得成立的一对数m，n为“相伴数对”，记为（m，n）．（1）若（m，1）是“相伴数对”，则m＝；（2）（m，n）是“相伴数对”，则代数式mm﹣[n+（6﹣12n﹣15m）]的值为．规律探究与新定义运算参考答案与试题解析一．试题（共25小题）1．【分析】观察已知一列数的变化发现：分子都是1，分母是序号数的平方加1，奇数项是正数，偶数项是负数，据此可以解答．【解答】解：根据分析可知：一列数依次为：，﹣，，﹣，，﹣，…，按此规律排列下去，则这列数中的第8个数是﹣，所以第n个数是：（﹣1）n+1（n是正整数）．故答案为：﹣；（﹣1）n+1．【点评】本题考查了数字的变化规律，解题的关键是通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．2．【分析】根据题目中的单项式，可以发现单项式的变化特点，从而可以写出第n个单项式，然后即可写出第2020个单项式．【解答】解：∵一列单项式为：a，﹣a2，a3，﹣a4，a5，﹣a6，…，∴第n个单项式为（﹣1）n+1•a n，当n＝2020时，这个单项式是（﹣1）2020+1•a2020＝﹣a2020，故选：D．【点评】本题考查数字的变化类、单项式，解答本题的关键是明确题意，发现单项式的变化特点，写出相应的单项式．3．【分析】观察已知单项式，归纳总结得到一般性规律，确定出第6个式子与第n个式子即可．【解答】解：归纳总结得：第6个式子是26x6＝64x6，第n个式子是2n x n，故答案为：64x6，2n x n【点评】此题考查了单项式，根据题意归纳总结得到一般性规律是解本题的关键．4．【分析】找出单项式规律求解即可．【解答】解：由0，3x2，8x3，15x4，24x5…，可得第n项为（n2﹣1）x n，所以第20个单项式是399x20．故答案为：399x20．【点评】本题主要考查了单项式，解题的关键是正确的找出单项式规律．5．【分析】观察得到奇数位上的单项式的系数为正，偶数位上的单项式的系数为负，并且单项式的系数的绝对值为x的指数的平方加1，即第n个式子为：（﹣1）n+1（n2+1）x n，n ＝8即可得到第8个式子．【解答】解：根据所给式子可得：第n个式子为：（﹣1）n+1（n2+1）x n，则第8个式子是﹣65x8．故答案为：﹣65x8，（﹣1）n+1（n2+1）x n．【点评】本题考查了关于数字的变化规律：先要观察每个单项式的系数和字母指数的特点，得出数字变化的规律，然后写出一般规律性的式子．6．【分析】利用归纳法来求已知数列的通式．【解答】解：∵第一个式子：﹣3a2＝，第二个式子：9a5＝，第三个式子：﹣27a10＝，第四个式子：81a17＝，…．则第n个式子为：（n为正整数）．故答案是：．【点评】本题考查了单项式．此题的解题关键是找出该数列的通式．7．【分析】根据题目中的数据，可以发现数字的变化特点，从而可以求得n的值，本题得以解决．【解答】解：由题目中的数据可知，第一行是一些连续的奇数，第二行奇数个数为奇数，偶数个数为偶数，第二行的第m个数为1+3（m﹣1）＝3m﹣2，令3m﹣2＝2023，得m＝675，∵第一行和第二行第n个相同的数是2023，∴n＝（675+1）÷2＝338，故选：B．【点评】本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出n的值．8．【分析】根据已知条件进行计算分别得出前几个数，进而发现规律：每3个数一个循环，即可求解．【解答】解：∵a1＝2，∴a2＝＝﹣1；a3＝＝；a4＝＝2；…，发现规律：每3个数一个循环，所以2020÷3＝673…1，则a2020＝a1＝2．故答案为：2．【点评】本题考查了规律型：数字的变化类，解决本题的关键是观察数字的变化寻找规律，运用规律．9．【分析】根据题意可以写出前几项，然后即可发现数字的变化规律，然后即可求得所求式子的值，本题得以解决．【解答】解：由题意可得，a1＝﹣4，a2＝，a3＝，a4＝﹣4，a5＝，a6＝，…，∵﹣4+＝＝﹣，61÷3＝20…1，∴a1+a2+a3+a4+…+a61＝20×（﹣）+（﹣4）＝﹣51+（﹣4）＝﹣55，故选：A．【点评】本题考查数字的变化类、倒数，解答本题的关键是明确题意，发现数字的变化特点，求出所求式子的值．10．【分析】根据差倒数定义分别求出前几个数字，即可发现规律进而得结果．【解答】解：∵a1＝﹣3，∴a2＝＝，a3＝＝，a4＝＝﹣3，……∴这个数列以﹣3，，依次循环，∵404÷3＝134…2，∴a403的值是﹣3，a404的值是，那么a1﹣a2+a3﹣a4…+a401﹣a402+a403﹣a404＝﹣3﹣++3+﹣﹣3﹣++3+﹣﹣ (3)＝﹣3﹣＝﹣．故选：A．【点评】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．11．【分析】由图可知每个圆中的规律为左边与上边对应的数相乘得到的积再加上右边的数，所得结果为最下边的数．【解答】解：由图可知每个圆中的规律为：1×2+2＝4，2×3+3＝9，3×5+4＝19，4×7+5＝33，∴最后一个圆中5×11+6＝61，∴？号所对应的数是61，故选：A．【点评】本题考查数字的变化规律；能够通过图形找到每个圆中的四个数之间的关系是解题的关键．12．【分析】根据图形中的规律即可求出（1+x）45的展开式中第三项的系数为前44个数的和，计算得到结论．【解答】解：由图2知：（a+b）1的第三项系数为0，（a+b）2的第三项的系数为：1，（a+b）3的第三项的系数为：3＝1+2，（a+b）4的第三项的系数为：6＝1+2+3，…∴发现（1+x）3的第三项系数为：3＝1+2；（1+x）4的第三项系数为6＝1+2+3；（1+x）5的第三项系数为10＝1+2+3+4；不难发现（1+x）n的第三项系数为1+2+3+…+（n﹣2）+（n﹣1），∴（1+x）45＝a0+a1x+a2x2+…+a45x45，则a2＝1+2+3+…+44＝＝990；故答案为：990．【点评】本题考查了完全平方式，也是数字类的规律题，首先根据图形中数字找出对应的规律，再表示展开式：对应（a+b）n中，相同字母a的指数是从高到低，相同字母b的指数是从低到高．13．【分析】由图形知第n个三角形数为1+2+3+…+n＝，第n个正方形数为n2，据此可以得出最大的三角形数和正方形数，即可以求得m和n的值，从而可以计算出m+n的值．【解答】解：由图形知第n个三角形数为1+2+3+…+n＝，第n个正方形数为n2，当n＝19时，＝190＜200，当n＝20时，＝210＞200，所以最大的三角形数m＝190；当n＝14时，n2＝196＜200，当n＝15时，n2＝225＞200，所以最大的正方形数n＝196；则m+n＝190+196＝386，故答案为：386．【点评】本题考查数字的变化类，解答本题的关键是明确题意，发现三角形数和正方形数的变化特点，求出m、n的值．14．【分析】观察图形的变化可得第n个图形中共有〇的个数，进而可得第2020个图形中共有〇的个数．【解答】解：观察图形的变化可知：第1个图形中共有3×1+1＝4个〇；第2个图形中共有3×2+1＝7个〇；第3个图形中共有3×3+1＝10个〇；…所以第n个图形中共有（3n+1）个〇；所以第2020个图形中共有〇的个数为：3×2020+1＝6061．故选：D．【点评】本题考查了图形的变化类问题，解题的关键是仔细观察图形并发现图形变化的规律．15．【分析】根据数字的变化情况寻找规律即可求解．【解答】解：因为第一行﹣1第二行2，﹣3，4第三行﹣5，6，﹣7，8，﹣9第四行10，﹣11，12，﹣13，14，﹣15，16，共7个数；所以，第五行﹣17，18，﹣19，20，﹣21，22，﹣23，24，﹣25，共9个数；第六行26，﹣27，28，﹣29，…34，﹣35，36，共11个数．所以第6行中从左边数第3个数是28．【点评】本题考查了数字的变化类，解决本题的关键是寻找规律．16．【分析】从题目上可看出第3个，第6个，第9个为偶数，依此类推每3项就是一个偶数，2021÷3＝673．所以应该有673个偶数．【解答】解：从数列中可看出每3个，就有一个偶数，2021÷3＝673．所以有673个偶数．故选：D．【点评】本题是一个规律性题目，关键是看出每3个数中就有一个偶数，可求解．17．【分析】通过观察发现：2n的个位数字是2，4，8，6四个一循环，所以根据2020÷4＝505，得出22020的个位数字与24的个位数字相同，是6．【解答】解：2n的个位数字是2，4，8，6四个一循环，所以2020÷4＝505，则22020的末位数字是6．故选：C．【点评】本题考查了规律型：数字的变化类，解决本题的关键是根据数字的变化寻找规律．18．【分析】利用青蛙停在奇数点上，则下一次沿顺时针方向跳两个点，若停在偶数点上，则下一次沿逆时针方向跳一个点这一规律，找出青蛙跳跃停留的点对应的数字是以3，5，2，1循环往复，由此得到结论．【解答】解：由题意得：青蛙第1次跳到的那个点是3，∵若青蛙停在奇数点上，则下一次沿顺时针方向跳两个点，∴青蛙第2次跳到的那个点是5，∴青蛙第3次跳到的那个点是2．∵若青蛙停在偶数点上，则下一次沿逆时针方向跳一个点，∴青蛙第4次跳到的那个点是1，∴青蛙第5次跳到的那个点是3；归纳类推得：青蛙跳后它停的点所对应的数是以3，5，2，1循环往复的，∵2020＝4×505，∴经2020次跳后它停的点所对应的数与经4次跳后它停的点所对应的数相同，即为1，【点评】本题主要考查了数字的变化的规律，准确找出变化的数字的循环规律是解题的关键．19．【分析】根据题意，任意四个相邻格子中的和等于15，列出等式，找出规律，计算出m 的值；再求出第2021个数是几即可．【解答】解：∵任意四个相邻小格子中所填数之和都等于15，∴第5个数（5﹣4＝1）与第1个数相同，都为m﹣1；第16个数（16÷4＝4）与第4个数相同，都为2；第78个数（78÷4＝19…2）与第2个数相同，都为3﹣2m；∴m﹣1+3﹣2m+7+2＝15，解得m＝﹣4，则m﹣1＝﹣4﹣1＝﹣5，3﹣2m＝11，∵2021÷4＝505…1，∴第2021个数是﹣5．故答案为：﹣4；﹣5．【点评】本题主要考查有理数的加法及数字的变化规律，解决此题的关键是根据题意，列出等式，求出字母的值，找出规律．20．【分析】根据设计的程序进行计算，找到循环的规律，根据规律推导计算．【解答】解：由设计的程序，知依次输出的结果是50，25，32，16，8，4，2，1，8，4，2，1…，发现从8开始循环．则2019﹣4＝2015，2015÷4＝503…3，故第2019次输出的结果是2．故答案为：2【点评】此题主要考查了数字的变化规律，正确发现循环的规律，根据循环的规律进行推广．该题中除前4次不循环外，后边是4个一循环．21．【分析】由5x+1＝556，解得x＝111，即开始输入的x为111，最后输出的结果为556；当开始输入的x值满足5x+1＝111，最后输出的结果也为556，可解得x＝22；当开始输入的x值满足5x+1＝22，最后输出的结果也为556，但此时解得的x的值为小数，不合题意．【解答】解：∵输出的结果为556，∴5x+1＝556，解得x＝111；而111＜500，当5x+1等于111时最后输出的结果为556，即5x+1＝111，解得x＝22；当5x+1＝22时最后输出的结果为556，即5x+1＝22，解得x＝4.2（不合题意舍去），所以开始输入的x值可能为22或111．故选：B．【点评】本题考查了代数式求值：先把代数式进行变形，然后把满足条件的字母的值代入计算得到对应的代数式的值．也考查了解一元一方程．22．【分析】根据题意给出的运算法则以及整式的运算法则即可求出答案．【解答】解：原式＝4﹣2（1﹣x）＝4﹣2+2x＝2+2x故答案为：2+2x【点评】本题考查整式的运算法则，解题的关键是熟练运用整式的运算法则，本题属于基础题型．23．【分析】先根据定义得出算式，再根据整式的加减法则求出即可．【解答】解：3△﹣2＝3×（﹣2）﹣[3+（﹣2）]＝﹣7，[（﹣1）△（m﹣1）]△4＝[﹣m+1﹣m+2]△4＝（﹣2m+3）△4＝（﹣2m+3）×4﹣（﹣2m+3+4）＝﹣8m+12+2m﹣7＝﹣6m+5，故答案为：﹣7，﹣6m+5．【点评】本题考查了整式的加减，能正确根据运算法则进行化简是解此题的关键．24．【分析】根据（m，n）是“相随数对”得出9m+4n＝0，再将原式化成9m+4n﹣2，最后整体代入求值即可．【解答】解：∵（m，n）是“相随数对”，∴，∴，整理得：9m+4n＝0，∴3m+2[3m+（2n﹣1）]＝3m+2[3m+2n﹣1]＝3m+6m+4n﹣2＝9m+4n﹣2＝0﹣2＝﹣2，故答案为：﹣2．【点评】本题考查代数式求值，理解“相随数对”的意义是正确计算的关键．25．【分析】（1）利用新定义“相伴数对”列出算式，计算即可求出m的值；（2）利用新定义“相伴数对”列出关系式，原式去括号合并后代入计算即可求出值．【解答】解：（1）根据题意得：+＝，去分母得：15m+10＝6m+6，移项合并得：9m＝﹣4，解得：m＝﹣；（2）由题意得：+＝，即＝，整理得：15m+10n＝6m+6n，即9m+4n＝0，则原式＝m﹣n﹣3+6n+m＝m+5n﹣3＝（9m+4n）﹣3＝﹣3，故答案为：（1）﹣；（2）﹣3【点评】此题考查了整式的加减﹣化简求值，弄清题中的新定义是解本题的关键．。
七年级数学人教版(上册)【知识讲解】小专题(五)有理数中的规律探究
3．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现这 样一组数：1，1，2，3，5，8，13，…，根据这组数的规律第 10 个 数是 55 ．
类型 2 有理数运算中的规律 4．根据如图所示的数字之间的规律，问号处的数字为( A ) A．61 B．52 C．43 D．37
5．观察下列等式：1＝12，1＋3＝22，1＋3＋5＝32，1＋3＋5＋ 7＝42，……
第一章 有理数
小专题(五) 有理数中的规律探究
类型 1 一列数中的规律
1．(2021·黄冈期中)观察下列各数的排列规律：0，－3，8，－
15，…，照这样排列，第 8 个数应是( CLeabharlann )A．55B．－56
C．－63
D．65
2．找规律，并按规律填写第 5 个数：－32，54，－78，196，－3112 ．
则 1＋3＋5＋7＋…＋2 021＝ 1 0112 ．
6．计算：21－1＝1，22－1＝3，23－1＝7，24－1＝15，25－1＝ 31，……归纳各计算结果中的个位数字规律，猜测 22 022－1 的个位 数字是 3 ．
7．(2021·自贡)如图，某学校“桃李餐厅”把 Wi-Fi 密码做成了 数学题．小红在餐厅就餐时，思索了一会儿，输入密码后顺利地连 接到了“桃李餐厅”的无线网络．那么她输入的密码是 244872 ．
1157 5 7 (2)计算：6＋8＋7＋9＋42＋72.
1515 1717 解：原式＝(6＋7＋6×7)＋(8＋9＋8×9)
＝1＋1 ＝2.
类型 3 数轴上的规律
9．(2021·黄冈期末)如图，把周长为 4 个单位长度的圆放到数轴(单位
长度为 1)上，点 A，B，C，D 将圆四等分，将点 A 与数轴上表示 1 的点
七年级数学探究规律题
规律探究1．图1是一组有规律的图案，第1个 图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n (n 是正整数)个图案中由 个基础图形组成．2 .观察下列各式数：0，3，8，15，24，……。
试按此规律写出的第100个数是＿＿＿。
”3．如图，是用火柴棍摆成的边长分别是1，2，3 根火柴棍时的正方形．当边长为n 根火柴棍时，设摆出的正方形所用的火柴棍的根数为s ，则s ＝ ． （用n 的代数式表示s ）4．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是 ．5．某校生物教师李老师在生物实验室做试验时，将水稻种子分组进行发芽试验；第1组取3粒，第2组取5粒，第3组取7粒……即每组所取种子数目比该组前一组增加2粒，按此规律，那么请你推测第n 组应该有种子数（ ）粒。
A 、12+n B 、12-n C 、n 2 D 、2+n6．如图5，每一幅图中有若干个大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第4幅图中有 个，第n 幅图中共有 个． 7．观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形有 （ ）个 ．找规律专题练习1、你喜欢吃拉面吗？拉面馆的师傅，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面条拉成了许多细的面条，如下面草图所示。
这样捏合到第 次后可拉出64根细面条。
第一次捏合 第二次捏合 第三次捏合(3) …… 图1 (1) (2) … … 第1幅 第2幅 第3幅 第n 幅 图5第1个第2个第3个…… n =1 n =2 n =32、如下图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去； （1）填表：（2（3）如果剪了100次，共剪出多少个小正方形？（4）观察图形，你还能得出什么规律？3、小明写作业时不慎将墨水滴在数轴上，根据图中的数值，判定墨迹盖住部分的整数的和是 ．（2）当x 非常大时，2100x 的值接近于什么数？5、现有黑色三角形“▲”和“△”共200个，按照一定规律排列如下：▲ ▲△△▲△▲▲△△▲△▲▲……则黑色三角形有 个，白色三角形有 个。
七年级数学上册人教版整式的加减专题复习——规律探究(解析版)
整式的加减专题复习——规律探究（解析版）第一部分典例剖析+针对训练类型一数式规律典例1（2021秋•南岗区校级期中）有一列数，按一定规律排列而成：﹣1，3，﹣9，27，﹣81，243，…，其中某三个相邻数的和是1701，则这三个数中最小的数是．思路引领：设三个数中最前面的数为x，则另外两个数分别为﹣3x，9x，根据三个数之和为1701，即可得出关于x的一元一次方程，解之即可得出x的值，再将其代入﹣3x和9x 中，取其中最小值即可得出结论．解：设三个数中最前面的数为x，则另外两个数分别为﹣3x，9x，依题意，得：x﹣3x+9x＝1701，解得：x＝243，∴﹣3x＝﹣729，9x＝2187．∵﹣729＜243＜2187，故答案为：﹣729．总结升华：本题考查了一元一次方程的应用以及规律型：数字的变化类，找准等量关系，正确列出一元一次方程是解题的关键．典例2（2022秋•涟水县校级月考）观察下面三行数，并按规律填空：①﹣2，4，﹣8，16，﹣32，64，，，…；②0，6，﹣6，18，﹣30，66，，…；③﹣3，3，﹣9，15，﹣33，63，，…．（1）按第①行数的规律，分别写出第7和第8个数；（2）请你分别写出第②③行的第7个数；（3）取每行数的第9个数，计算这三个数的和．思路引领：（1）根据已知数据都是前一个数乘2的到得，再利用第奇数个系数为负数即可得出答案；（2）根据3行数据关系分别分析得出即可；（3）根据（2）得出的规律分别求出每行第9个数，再把它们相加即可．解：（1）∵①﹣2，4，﹣8，16，﹣32，64，∴第7个数是﹣128，第八个数是256；（2）第②行数是第①行数加上2，第③行数正好比第①行数少1得到的，即第二行的第7个数是﹣128+2＝﹣126，第三行的第7个数是﹣128﹣1＝﹣129；（3）根据以上所求得出：第一行第9个数为﹣512，第二行第9个数为﹣512+2＝﹣510，第三行第9个数为﹣512﹣1＝﹣513，则这三个数的和是：﹣512﹣510﹣513＝﹣1535．总结升华：此题主要考查了数字变化规律，根据已知数据得出得数字第②行数是第①行数加上2，第③行数正好比第①行数少1得到的是解题关键．针对训练11．（2021•武汉）按照一定规律排列的n个数：﹣2、4、﹣8、16、﹣32、64、…，若最后三个数的和为768，则n为（）A．9B．10C．11D．12思路引领：观察得出第n个数为（﹣2）n，根据最后三个数的和为768，列出方程，求解即可．解：由题意，得第n个数为（﹣2）n，那么（﹣2）n﹣2+（﹣2）n﹣1+（﹣2）n＝768，当n为偶数：整理得出：3×2n﹣2＝768，解得：n＝10；当n为奇数：整理得出：﹣3×2n﹣2＝768，则求不出整数．故选：B．总结升华：此题考查规律型：数字的变化类，找出数字的变化规律，得出第n个数为（﹣2）n是解决问题的关键．2．（2021秋•新洲区期中）有一串数：﹣2018，﹣2014，﹣2010，﹣2006，﹣2002…按一定的规律排列，那么这串数中前个数的和最小．思路引领：根据题目中数据的特点，可以写出第n个数，然后令第n个数等于0，即可得到相应的n的值，从而可以解答本题．解：∵有一串数：﹣2018，﹣2014，﹣2010，﹣2006，﹣2002…∴这串数的第n个数为﹣2018+4（n﹣1）＝4n﹣2022，当4n﹣2022＝0时，解得，n＝505…2，∴那么这串数中前505个数的和最小，故答案为：505．总结升华：本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出第多少个数的值为0．类型二数阵、数表规律典例3（2020秋•江汉区月考）将全体正偶数排成一个三角形数阵：按照以上规律排列，第25行第20个数是．思路引领：观察数字的变化，第n行有n个偶数，求出第n行的第一个数，结论可得．解：观察数字的变化可知：第n行有n个偶数．∵第1行的第一个数是：2＝1×0+2；第2行第一个数是：4＝2×1+2；第3行第一个数是：8＝3×2+2；第4行第一个数是：14＝4×3+2；•∴第n行第一个数是：n（n﹣1）+2．∴第25行第一个数是：25×24+2＝602．∴第25行第20个数是：602+2×19＝640．故答案为：640．总结升华：本题主要考查了数字的变化的规律，有理数的混合运算．准确找出数字的变化规律是解题的关键．典例4（2019秋•江汉区期中）有这样一对数，如下表，第n+3个数比第n个数大2（其中n是正整数）第1个第2个第3个第4个第5个……a b c（1）第5个数表示为；第7个数表示为；（2）若第10个数是5，第11个数是8，第12个数为9，则a＝，b＝，c＝；（3）第2019个数可表示为．思路引领：（1）根据第n+3个数比第n个数大2，即可求解；（2）根据第n+3个数比第n个数大2，分别求出第10、11、12个数即可求出结果；（3）根据数字的变化规律，解：（1）∵第n+3个数比第n个数大2，∴第5个数比第2个数大2，∴第5个数为b+2．∵第4个数比第1个数大2，∴第4个数为a+2，∴第7个数比第4个数大2，∴第7个数为a+4．故答案为b+2、a+4．（2）∵第10个数为a+6，第11个数为b+6，第12个数为c+6，∴a+6＝5，b+6＝8，c+6＝9解得a＝﹣1，b＝2，c＝3．故答案为﹣1、2、3．（3）第一组数是a、b、c第二组数是a+2、b+2、c+2第三组数是a+4、b+4、c+4第四组数是a+6、b+6、c+6…第n组数的第三个数是c+（2n﹣2）2019÷3＝673，第2019个数是第673组的第三个数，∴第673组的第三个数是c+2×673﹣2＝c+1344．故答案为c+1344．总结升华：本题考查了数字的变化类，解决本题的关键是寻找数字的变化规律．针对训练21．（2021秋•播州区期中）如表被称为“杨辉三角”或“贾宪三角”．其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和．表中两平行线之间的一列数：1，3，6，10，15，…，我们把第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为a n，则a6＝，a2020＝．思路引领：根据题目中的数据，可以写出前几项，从而可以数字的变化特点，然后即可得到a6和a2020的值．解：由题意可得，a1＝1，a2＝1+2＝3，a3＝1+2+3＝6，a4＝1+2+3+4＝10，a5＝1+2+3+4+5＝15，…，∴a n＝1+2+3+…+n=n(n+1)2，∴当n＝6时，a6=6×72=21，当n＝2020时，a2020=2020×20212=2041210，故答案为：21，2041210．总结升华：本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出所求项的值．2．（2018秋•江夏区期中）已知一列数：1、﹣2、3、﹣4、5、﹣6、……，将这列数排成下列形式：按照上述规律排列下去，第10行数的第1个数是（）A．﹣46B．﹣36C．37D．45思路引领：观察排列规律得到第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，则可计算出前9行的数的个数45，而数字的序号为偶数时，数字为负数，于是可判断第10行数的第1个数为﹣46．故选A．解：第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，所以前9行的数的个数为1+2+3+…+9＝45，而数字的序号为奇数时，数字为正数，数字的序号为偶数时，数字为负数，所以第10行数的第1个数为﹣46．故选：A．总结升华：本题考查了规律型：数字的变化类：认真观察、仔细思考，利用数字与序号数的关系解决这类问题．3．（2017秋•海淀区校级期中）如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．（1）可求得x＝，第2017个格子中的数为．（2）判断：前m个格子中所填整数之和是否可能为2018？若能，求出m的值，若不能，请说明理由．（3）若取前3格子中的任意两个数记作a、b，且a≥b，那么所有的|a﹣b|的和可以通过计算|9﹣★|+|9﹣☆|+|★﹣☆|得到，其结果为；若a、b为前19格子中的任意两个数记作a、b，且a≥b，则所有的|a﹣b|的和为．思路引领：（1）根据三个相邻格子的整数的和相等列式求出x的值，再根据第9个数是2可得☆＝2，然后找出格子中的数每3个为一个循环组依次循环，在用2014除以3，根据余数的情况确定与第几个数相同即可得解；（2）可先计算出这三个数的和，再照规律计算．（3）由于是三个数重复出现，因此可用前三个数的重复多次计算出结果．解：（1）∵任意三个相邻格子中所填整数之和都相等，∴9+★+☆＝★+☆+x，解得：x＝9，★+☆+x＝☆+x﹣6，∴★＝﹣6，所以，数据从左到右依次为9、﹣6、☆、9、﹣6、☆、…，第9个数与第三个数相同，即☆＝2，所以，每3个数“9、﹣6、2”为一个循环组依次循环，∵2017÷3＝672…1，∴第2017个格子中的整数与第1个格子中的数相同，为9．故答案为：9，9；（2）9﹣6+2＝5，2018＝2015+3＝2015+9﹣6，2015÷5＝403，403×3＝1209，所以是第1209+1+1＝1211个数，即m＝1211，故前1211个数的和为2018；（3）∵取前3格子中的任意两个数，记作a、b，且a≥b，∴所有的|a﹣b|的和为：|9﹣（﹣6）|+|9﹣2|+|﹣6﹣2|＝30．∵由于是三个数重复出现，那么前19个格子中，这三个数，9出现了7次，﹣6和2各出现了6次．∴代入式子可得：|9﹣（﹣6）|×7×6+|9﹣2|×7×6+|2﹣（﹣6）|×6×6＝1212．故答案为：30，1212．总结升华：本题主要考查数字的变化规律，解答的关键是找出数字间的关系，得出规律．类型三图形的增长规律典例4（2021•汉川市模拟）古希腊著名的毕达哥拉斯学派把1、3、6、10、…，这样的数称为“三角形数”，而把1、4、9、16、…，这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．则第10个图形中右下方的“三角形数”中的所有点数是．思路引领：观察图象中点的个数的规律有第一个图形是4＝1+3，第二个图形是9＝3+6，第三个图形是16＝6+10，…则按照此规律得到第10个图形的规律即可．解：∵第1个图形是4＝1+（1+2），第2个图形是9＝（1+2）+（1+2+3），第3个图形是16＝（1+2+3）+（1+2+3+4），…∴第10个图形是112＝（1+2+3+4+5+6+7+8+9+10）+（1+2+3+4+5+6+7+8+9+10+11）＝55+66．故答案为：66．总结升华：此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．典例5（2020秋•江夏区期中）按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的数量是（）A．360B．363C．365D．369思路引领：观察图形可知，黑色与白色的地砖的个数的和是连续奇数的平方，而黑色地砖比白色地砖多1个，求出第n个图案中的黑色与白色地砖的和，然后求出黑色地砖的块数，再把n＝14代入进行计算即可．解：第1个图案只有（2×1﹣1）2＝12＝1块黑色地砖，第2个图案有黑色与白色地砖共（2×2﹣1）2＝32＝9，其中黑色的有12（9+1）＝5块，第3个图案有黑色与白色地砖共（2×3﹣1）2＝52＝25，其中黑色的有12（25+1）＝13块，…第n 个图案有黑色与白色地砖共（2n ﹣1）2，其中黑色的有12[（2n ﹣1）2+1]，当n ＝14时，黑色地砖的块数有12×[（2×14﹣1）2+1]=12×730＝365．故选：C ．总结升华：本题考查图形的变化规律，观察图形找出黑色与白色地砖的总块数与图案序号之间的关系是解题的关键． 针对训练31．（2021秋•中山市期中）观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第10个图形共有 个〇．思路引领：观察图形的变化先得前几个图形中圆圈的个数，可以发现规律：第n 个图形共有（3n +1）个〇，进而可得结果． 解：观察图形的变化可知： 第1个图形共有1×3+1＝4个〇； 第2个图形共有2×3+1＝7个〇； 第3个图形共有3×3+1＝10个〇； …所以第n 个图形共有（3n +1）个〇； 所以第10个图形共有10×3+1＝31个〇； 故答案为：31．总结升华：本题考查了规律型：图形的变化类，解决本题的关键是根据图形的变化寻找规律．2．（2018秋•硚口区期中）对于大于或等于2的整数的平方进行如下“分裂”，如下分别将22、32、42分裂成从1开始的连续奇数的和，依此规律，则20182的分裂数中最大的奇数是 ．思路引领：由题意可知：每个数中所分解的最大的奇数是前边底数的2倍减去1．由此得出答案即可．解：自然数n2的分裂数中最大的奇数是2n﹣1．20182分裂的数中最大的奇数是2×2018﹣1＝4035，故答案为：4035．总结升华：此题考查数字的变化规律，注意根据具体的数值进行分析分解的最大的奇数和底数的规律，从而推广到一般．3．（2022•仙居县校级开学）如图，都是由棱长为1的正方体叠成的立体图形，例如第（1）个图形由1个正方体叠成，第（2）个图形由4个正方体叠成，第（3）个图形由10个正方体叠成，依次规律，第（10）个图形由（）个正方体叠成．A．120B．165C．220D．286思路引领：根据图形的变换规律，可知第n个图形中的正方体的个数为1+3+6+⋯+ n(n+1)2，据此可得第（6）个图形中正方体的个数．解：由图可得：第（1）个图形中正方体的个数为1；第（2）个图形中正方体的个数为4＝1+3；第（3）个图形中正方体的个数为10＝1+3+6；第（4）个图形中正方体的个数为20＝1+3+6+10；故第n个图形中的正方体的个数为1+3+6+⋯+n(n+1)2，∴第10个图形中正方体的个数为1+3+6+10+15+21+28+36+45+55＝220．故选：C．总结升华：本题主要考查了图形变化类问题，解决问题的关键是依据图形得到变换规律．解题时注意：第n个图形中的正方体的个数为1+3+6+⋯+n(n+1)2．类型四乘方规律典例6（2022•内蒙古）观察下列等式：70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，…，根据其中的规律可得70+71+72+…+72022的结果的个位数字是（ ） A ．0B ．1C ．7D ．8思路引领：由已知可得7n 的尾数1，7，9，3循环，则70+71+…+72022的结果的个位数字与70+71+72的个位数字相同，即可求解．解：∵70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，… ∴7n 的尾数1，7，9，3循环， ∴70+71+72+73的个位数字是0， ∵2023÷4＝505…3，∴70+71+…+72022的结果的个位数字与70+71+72的个位数字相同， ∴70+71+…+72022的结果的个位数字是7， 故选：C ．总结升华：本题考查数的尾数特征，能够通过所给数的特点，确定尾数的循环规律是解题的关键．典例7（2022秋•东港区校级月考）求1+2+22+23+……+22007的值，可令S ＝1+2+22+23+……+22007，则2S ＝2+22+23+24+……+22008，因此2S ﹣S ＝22009﹣1，即S ＝22009﹣1，仿照以上推理，计算出1+3+32+33+……+32022值为32023−12．思路引领：令S ＝1+3+32+33+……+32022，则3S ＝3+32+33+……+32023，作差求出S 即可． 解：令S ＝1+3+32+33+……+32022， 则3S ＝3+32+33+……+32023， ∴3S ﹣S ＝32023﹣1， 则S =32023−12，即1+3+32+33+……+32022=32023−12．故答案为：32023−12．总结升华：本题考查数字的变化规律，通过观察所给的求和方法，灵活应用此方法求和是解题的关键． 针对训练41．（2021秋•罗湖区期中）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；……，已知按一定规律排列的一组数：2501，2502，2503，……，2999，21000．若2500＝a ，用含a 的式子表示这组数之和是（ ） A ．2a 2﹣2aB ．2a 10﹣2a 5﹣2C ．2a 2﹣aD ．2a 20﹣a思路引领：把所求的数列的各数提取2500，可得：2500×（2+22+23+…+2499+2500），利用所给的等式的规律求解即可．解：∵2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…， ∴2+22+23+…+2n ＝2n +1﹣2， ∴2501+2502+2503+…+2999+21000 ＝2500×（2+22+23+…+2499+2500） ＝2500×（2500+1﹣2） ＝2500×（2×2500﹣2）， ∵2500＝a ， ∴原式＝a （2a ﹣2） ＝2a 2﹣2a ． 故选：A ．总结升华：本题主要考查了规律型：数字的变化类，有理数的混合运算，解答的关键是由所给的等式总结出规律．2．（2019秋•汾阳市期末）任意大于1的正整数m 的三次幂均可“分裂”成m 个连续奇数的和，如：23＝3+5，33＝7+9+11，43＝13+15+17+19，…按此规律，若m 3分裂后，其中有一个奇数是203，则m 的值是（ ） A ．13B ．14C ．15D ．16思路引领：观察可知，分裂成的奇数的个数与底数相同，然后求出到m 3的所有奇数的个数的表达式，再求出奇数203的是从3开始的第101个数，然后确定出101所在的范围即可得解．解：∵底数是2的分裂成2个奇数，底数为3的分裂成3个奇数，底数为4的分裂成4个奇数，∴m 3分裂成m 个奇数，所以，到m 3的奇数的个数为：2+3+4+…+m =(m+2)(m−1)2，∵2n +1＝203，n ＝101，∴奇数203是从3开始的第101个奇数， ∵(13+2)(13−1)2=90，(14+2)(14−1)2=104，∴第101个奇数是底数为14的数的立方分裂的奇数的其中一个， 即m ＝14． 故选：B ．总结升华：本题是对数字变化规律的考查，观察出分裂的奇数的个数与底数相同是解题的关键，还要熟练掌握求和公式．3．在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图所示：则第4个方框中x+y的值是（）A．11B．12C．13D．14思路引领：找出求解过程图中的规律，利用此规律求得m，n，x，y的值，将相应字母的值代入即可得出结论．解：求解过程图中的表格中的规律为：第一行前两个格为十位数字的平方，后两个格为个位数字的平方，平方后不是两位数，十位数字用0代替，第二行从第二个格开始表示的是两位数中个位数字与十位数字的乘积的2倍，第三行为从右开始将一二行数字相加的和，足10进1，∵62＝36，∴m＝3，n＝6，∵6×7×2＝84，∴x＝8，y＝4，∴x+y＝12．故选：B．总结升华：本题主要考查了有理数的乘方，求代数式的值，找出求解过程图中的规律是解题的关键．类型五幻方规律典例8（2021秋•江阴市期中）小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中a+b的值为（）A．﹣6或﹣3B．﹣8或1C．﹣1或﹣4D．1或﹣1思路引领：由于八个数的和是4，所以需满足两个圈的和是2，横、竖的和也是2．列等式可得结论．解：设小圈上的数为c，大圈上的数为d，﹣1+2﹣3+4﹣5+6﹣7+8＝4，∵横、竖以及内外两圈上的4个数字之和都相等，∴两个圈的和是2，横、竖的和也是2，则﹣7+6+b+8＝2，得b＝﹣5，6+4+b+c＝2，得c＝﹣3，a+c+4+d＝2，a+d＝1，∵当a＝﹣1时，d＝2，则a+b＝﹣1﹣5＝﹣6，当a＝2时，d＝﹣1，则a+b＝2﹣5＝﹣3，故选：A．总结升华：本题考查了有理数的加法．解决本题的关键是知道横竖两个圈的和都是2．典例9（2020•冷水江市一模）我国的《洛书》中记载着世界上最古老的一个幻方：将1～9这九个数字填入3×3的方格内，使三行、三列、两对角线上的三个数之和都相等．如图的幻方中，m＝．思路引领：根据“每行、每列、每条对角线上的三个数之和相等”解答即可．解：1+2+3+…+9＝45，根据“每行、每列、每条对角线上的三个数之和相等”，可知三行、三列、两对角线上的三个数之和都等于15，∴第一列第三个数为：15﹣2﹣5＝8，第三列第二个数为：15﹣3﹣5＝7，第三个数为：15﹣2﹣7＝6，如图所示：∴m＝15﹣8﹣6＝1．故答案为：1．总结升华：本题考查数的特点和有理数的加法，抓住每行、每列、每条对角线上的三个数之和相等，数的对称性是解题的关键．针对训练51．（2021秋•南安市期中）现有七个数﹣1，﹣2，﹣2，﹣4，﹣4，﹣8，﹣8将它们填入图1（3个圆两两相交分成7个部分）中，使得每个圆内部的4个数之积相等，设这个积为m，如图2给出了一种填法，此时m＝64，在所有的填法中，m的最大值为256．思路引领：观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣4，其中﹣4m＝256解：观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣4，其中﹣4放在中心位置，如图∴m＝（﹣8）×（﹣8）×（﹣1）×（﹣4）＝256总结升华：本题考查有理数的乘法，关键是找到两个（﹣8）的位置．2．将9个数填入幻方的九个方格中，使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等，如表一：按此规律将满足条件的另外6个数填入表二，则表二中这9个数的和为（用含a的整式表示）．表一492357816表二a+5a+1a﹣1思路引领：根据同一横行、同一竖列、同一斜对角线上的三个数的和相等作出图形，根据题意列出关于a与x的方程，可得x＝a+2，进一步求出这9个数的和即可．解：如图所示：4+x+a﹣1+a+3＝a﹣3+a+1+a+3，解得x＝a﹣5，a+3+x+a+3＝2a+6+a﹣5＝3a+1，3（3a+1）＝9a+3．故答案为：9a+3．总结升华：此题考查了列代数式，整式的加减，熟练掌握运算法则是解本题的关键．类型六其他规律典例10（2019秋•武昌区校级期中）某初中七（5）班学生军训排列成7×7＝49人的方阵，做了一个游戏，起初全体学生站立，教官每次任意点4个不同学号的学生，被点到的学生，站立的蹲下，蹲下的站立，且学生都正确完成指令，同一名学生可以多次被点，则15次点名后蹲下的学生人数可能是（）A．3B．27C．49D．以上都不可能思路引领：假设站立记为“+1”，则蹲下为“﹣1”．原来49个“+1”，乘积为“+1”，每次改变其中的4个数，即每次运算乘以4个“﹣1”，即乘以了“+1”，乘积为“+1”，即可得出结论．解：假设站立记为“+1”，则蹲下为“﹣1”．原来49个“+1”，乘积为“+1”，每次改变其中的4个数， 即每次运算乘以4个“﹣1”，即乘以了“+1”， 15次点名后，乘积仍然是“+1”， 所以，最后出现“﹣1”的个数为偶数， 即蹲下的学生人数为偶数， 选项A ，B ，C 都不符合题意， 故选：D ．总结升华：此题主要考查了奇数与偶数，有理数乘法中积的符号的判断，解决本题的关键是利用有理数的乘法进行解决． 针对训练61．（2019秋•硚口区期中）把几个不同的数用大括号括起来，相邻两个数之间用逗号隔开，如：{1，2}；{1，4，7}；…我们称之为集合，其中的每一个数称为该集合的元素．规定：当整数x 是集合的一个元素时，100﹣x 也必是这个集合的元素，这样的集合又称为黄金集合，例如{﹣1，101}就是一个黄金集合．若一个黄金集合所有元素之和为整数m ，且1180＜m ＜1260，则该黄金集的元素的个数是（ ） A ．23B ．24C ．24或25D ．26思路引领：由黄金集合的定义，可知一个整数是x ，则必有另一个整数是100﹣x ，则这两个整数的和为x +100﹣x ＝100，只需判断1180＜m ＜1260内100的个数即可求解． 解：在黄金集合中一个整数是x ，则必有另一个整数是100﹣x ， ∴两个整数的和为x +100﹣x ＝100， 由题意可知，1180＜m ＜1260时， 100×12＝1200，100×13＝1300， ∴这个黄金集合的个数是24或25个； 故选：C ．总结升华：本题考查有理数，新定义；理解题意，通过两个对应元素和的特点，结合m 的取值范围，进而确定元素个数是解题关键．第二部分 专题提优训练1．观察下面一列数：1，12，2，13，1，3，14，23，32，4，15，12，1，2，5，16，…（已写出了第1至第16个数）．（1）第7，第8，第9，第10个数的积是 ，前16个数的积是 ； （2）按此规律，第30个数是 ；（3）在上面这列数中，从左起第m 个数记为F （m ），当F （m ）=92020时，求m 的值． 思路引领：（1）根据规律直接写出数计算即可；（2）根据题意将数字从左边开始分别以1个数，2个数，3个数，…，为一组，每组数据的积为1，且分子递增1，分母递减1，然后根据规律得出第30个数即可； （3）根据F （m ）=92020判断出F （m ）是第几组第几个数即可得出m 的值． 解：（1）根据题意知，第7，第8，第9，第10个数的积是14×23×32×4＝1，前16个数的积是1×（12×2）×（13×1×3）×（14×23×32×4）×（15×24×1×42×5）×16=16，故答案为：1，16；（2）由（1）知，将数字从左边开始分别以1个数，2个数，3个数，…，为一组，每组数据的积为1，且分子递增1，分母递减1， ∵1+2+3+4+5+6+7＝28，∴第30个数在第8组的第2个数，即1+18−1=27，故答案为：27；（3）∵F （m ）=92020，2020+9＝2029，∴F （m ）是第2028组第9个数，前面有2027组数， ∴m ＝（1+2+3+4+…+2027）+9=1+20272×2027+9=2055387． 总结升华：本题主要考查数字的变化规律，根据数字的变化分组分析规律是解题的关键．2．（2021秋•丹江口市期中）观察一列数：1，﹣2，3，﹣4，5，﹣6，7，…，将这列数排成下列形式：（1）在表中，第12行第6个数是 ；（2）在表中，“2021”是其中的第 行，第 个数；（3）将表中第i 行的最后一个数记为a i ，如第1行的最后一个数记为a 1，即a 1＝1，第2行的最后一个数记为a 2，即a 2＝3，如此下去，a 3＝﹣6，a 4＝﹣10，…，第n 行的最后一个数记为a n ，则用含n 的式子表示|a n |为 ； （4）在（3）的条件下，计算1a 1+1a 2−1a 3−1a 4+1a 5+1a 6−1a 7−1a 8+1a 9+1a 10．思路引领：（1）先求出前11行一共有66，即可求解；（2）求出前n 行共有n(n+1)2个数，再求前63行共有2016个数，即可求2021的位置；（3）由题意可得，1+2+3+......+n =n(n+1)2，即可求解； （4）原式=2(1−12+12−13+13−14+......+19−110+110−111)，再运算即可． 解：（1）由题可知，第一行1个数，第二行2个数，…，第n 行n 个数， ∴前11行一共有1+2+3+…+11＝66， ∴第12行第一个数是67， ∴第12行第6个数是﹣72， 故答案为：﹣72；（2）由题意可得，前n 行共有n(n+1)2个数，∴当n ＝63时，前63行共有2016个数， ∴2021时第64行的第5个数， 故答案为：64，5；（3）由题意可得，1+2+3+......+n =n(n+1)2， ∴|a n |=n(n+1)2， 故答案为：n(n+1)2； （4）1a 1+1a 2−1a 3−1a 4+1a 5+1a 6−1a 7−1a 8+1a 9+1a 10=11+13+16+110+......+145=2(11×2+12×3+13×4+......+19×10+110×11) =2(1−12+12−13+13−14+......+19−110+110−111)=2(1−111) =2011．总结升华：本题考查数字的变化规律，根据题意探索数字的排列规律是解的关键． 3．（2022•东莞市校级一模）找出以下图形变化的规律，则第2022个图形中黑色正方形的数量是 3033 ．思路引领：仔细观察图形并从中找到规律，然后利用找到的规律即可得到答案． 解：∵当n 为偶数时第n 个图形中黑色正方形的数量为n +12n 个；当n 为奇数时第n 个图形中黑色正方形的数量为n +12（n +1）个，∴当n ＝2022时，黑色正方形的个数为2022+1011＝3033个． 故答案为：3033．总结升华：本题考查了图形的变化类问题，解题的关键是仔细的观察图形并正确的找到规律．4．（2020秋•西城区校级期中）古希腊毕达格拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数，比如：他们研究过图1中的1，3，6，10，…．由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…，这样的数为正方形数．（1）请你写出一个既是三角形数又是正方形数的自然数 ．（2）类似地，我们将k 边形数中第n 个数记为N （n ，k ）（k ≥3）．以下列出了部分k 边形数中第n 个数的表达式： 三角形数：N （n ，3）=12n 2+12n 正方形数：N （n ，4）＝n 2 五边形数：N （n ，5）=32n 2−12n 六边形数：N （n ，6）＝2n 2﹣n …根据以上信息，得出N （n ，k ）＝ ．（用含有n 和k 的代数式表示）思路引领：（1）由题意得第8个图的三角形数是36，所以既是三角形数又是正方形数，且大于1的最小正整数为36；（2）由已知等式进行变形进而可推出结果．解：（1）由题意第8个图的三角形数为12×8（8+1）＝36，∴既是三角形数又是正方形数，且大于1的最小正整数为36， 故答案为36．（2）∵N （n ，3）=n 2+n 2=(3−2)n 2+(4−3)n2，N （n ，4）＝n 2=2n 2+0×n 2=(4−2)n 2+(4−4)n2， N （n ，5）=32n 2−12n =(5−2)n 2+(4−5)n2，N （n ，6）＝2n 2﹣n =4n 2−2n 2=(6−2)n 2+(4−6)n2， 由此推断出N （n ，k ）=(k−2)n 2+(4−k)n2（k ≥3）．故答案为：(k−2)n 2+(4−k)n2（k ≥3）．总结升华：本题考查三角形数、正方形数的规律、完全平方数与归纳推理等知识，观察已知式子的规律并改写形式是解决问题的关键．5．（2020秋•江夏区校级月考）观察下列等式：12＝1，22＝4，32＝9，42＝16，52＝25，…，若12+22+32+42+52+…+n 2的个位数字是1（0＜n ≤2020，且n 为整数），下列选项中，n 的最大值是（ ） A ．2001B ．2006C ．2011D ．2019思路引领：通过计算发现每10个数，末位数字循环一次，再结合选项进行判断即可求解． 解：∵12＝1，22＝4，32＝9，42＝16，52＝25，62＝36，72＝49，82＝64，92＝81，102＝100，112＝121，122＝144，132＝169，…， ∴每10个数，末位数字循环一次， ∴1+4+9+6+5+6+9+4+1+0＝45， ∵2001÷10＝200……1， ∴200×45+1＝9001； ∵2006÷10＝200……6， ∴200×45+1+4+9+6+5+6＝9031； ∵2011÷10＝201……1， ∴201×45+1＝9046； ∵2019÷10＝201……9， ∴202×45＝9090； ∵2006＞2001， ∴n 的最大值为2006， 故选：B ．总结升华：本题考查数字的变化规律，通过探索每个数的尾数的循环规律，并运用规律求解是解题的关键．6．（2021•碧江区 模拟）观察等式：2+22＝23﹣2：2+22+23＝24﹣2；2+22+23+24＝25﹣2，…已知按一定规律排列的一组数：250、251、252、…、299、2100，若250＝a，则用含a的式子表示这组数的和是．思路引领：由等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2，得出规律：2+22+23+…+2n＝2n+1﹣2，那么250+251+252+…+299+2100＝（2+22+23+…+2100）﹣（2+22+23+…+249），将规律代入计算即可．解：∵2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…∴2+22+23+…+2n＝2n+1﹣2，∴250+251+252+…+299+2100＝（2+22+23+...+2100）﹣（2+22+23+ (249)＝（2101﹣2）﹣（250﹣2）＝2101﹣250，∵250＝a，∴2101＝（250）2•2＝2a2，∴原式＝2a2﹣a．故答案为：2a2﹣a．总结升华：本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于得出规律：2+22+23+…+2n＝2n+1﹣2．7．（2019秋•武汉期中）如图，在边长为1厘米的正方形网格有12个格点，用这些格点做三角形顶点，一共可以连成面积为2平方厘米的三角形个数为（）A．24B．32C．28D．12思路引领：根据面积等于底乘以高依次分情况分析既可以得到三角形个数．解：①如图以AB为底时，与对边CF的四个顶点都可以构成面积等于2平方厘米的三角形，类似这样的三角形共有16个，②如图以AC为底与线段BE上的三个点可以构成面积等于2平方厘米的三角形，类似这样的三角形共有12个，其中有四个直角三角形是重复的，故三角形总个数：16+12﹣4＝24个，。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
七年级数学专题-----规律探究题
————————————————————————————————作者：————————————————————————————————日期：
七年级数学专题-----规律探究题
题型一：数字变化类问题
1．观察下列按顺序排列的等式：，，，，…，试猜想第n个等式（n为正整数）：a n=__________．
2.下表中的数字是按一定规律填写的，表中a的值应是．
1 2 3 5 8 13 a …
2 3 5 8 13 21 34 …
3.观察下面的单项式：a，﹣2a2，4a3，﹣8a4，…根据你发现的规律，第8个式子是．
4.有一组等式：
2222222222222222
1233,2367,341213,452021
++=++=++=++=……请观察它们的构成规律，用你发现的规律写出第8个等式为_________
5.把奇数列成下表，
根据表中数的排列规律，则上起第8行，左起第6列的数是．
5.在计数制中，通常我们使用的是“十进位制”，即“逢十进一”。
而计数制方
法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据。
已知二进位制与十进位制的比较如下表：
十进位
制
0 1 2 3 4 5 6 …
二进
制0 1 1
1
1
100 101 110 …
请将二进制数10101010
（二）
写成十进制数为 .
6．观察下列各数，它们是按一定规律排列的，则第n个数是．，，，，，…
7.观察一列单项式：1x，3x2，5x2，7x，9x2，11x2，…，则第2013个单项式是．8．有这样一组数据a1，a2，a3，…a n，满足以下规律：
，（n≥2且n为正整数），则a2013的值为______（结果用数字表示）．
9.观察下列各式的计算过程：
5×5=0×1×100+25，
15×15=1×2×100+25，
25×25=2×3×100+25，
35×35=3×4×100+25，
…………
请猜测，第n个算式(n为正整数)应表示为____________________________．10.如图，下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是
A．M=mn B．M=n(m+1) C．M=mn+1 D．M=m(n+1)
11.观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187…
解答下列问题：3+32+33+34…+32013的末位数字是（）
A．0 B．1 C．3 D．7
12.如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所
填整数之和都相等，则第2013个格子中的整数是.
－4 a b c 6 b －
2
…
13.将连续正整数按以下规律排列，则位于第7行第7列的数x是85．
题型二：图形变化类问题
14.如图，是用火柴棒拼成的图形，则第n个图形需__________根火柴棒.
15.电脑系统中有个“扫雷”游戏，要求游戏者标出所有的雷，游戏规则：一个方块下面最多埋一个雷，如果无雷，掀开方块下面就标有数字，提醒游戏者此数字周围的方块（最多八个）中雷的个数（实际游戏中，0通常省略不标,此WORD 中为方便大家识别与印刷，我还是把图乙中的0都标出来吧，以示与未掀开者的区别），如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙第一行从左数起的七个方块中（方块上标有字母），能够确定一定是雷的有.（请填入方块上的字母）
16.如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠
A 1BC和∠A
1
CD的平分线交于点A
2
，得∠A
2
；…∠A
2012
BC和∠A
2012
CD的平分线交于
点A
2013，则∠A
2013
= 度。
3
()图甲A B C D G
E F
234
13
2242
2
2
2 11
11
1
1
113
3
()
图乙
00
17.为庆祝“六•一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律，摆第（n）图，需用火柴棒的根数为．
18.从所给出的四个选项中，选出适当的一个填入问号所在位置，使之呈现相同的特征
19.如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第6个五边形数是．
20.如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（）根火柴．
A．156 B．157 C．158 D．159
21.当白色小正方形个数n等于1,2，3…时，由白色小正方形和和黑色小正方形
组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个
A B
D C A C B
D A B C D A C B D …
数总和等于_____________.（用n 表示，n 是正整数）
22.如图，在菱形ABCD 中，边长为10，∠A =60°.顺次连结菱形
ABCD 各边中点，可得四边形A 1B 1C 1D 1；顺次连结四边形 A 1B 1C 1D 1各边中点，可得四边形A 2B 2C 2D 2；顺次连结四边 形A 2B 2C 2D 2各边中点，可得四边形A 3B 3C 3D 3；按此规律继 续下去…….则四边形A 2B 2C 2D 2的周长是 ▲ ；四边 形A 2013B 2013C 2013D 2013的周长是 ▲ . 23.如图所示，以O 为端点画六条射线后OA ，OB ，OC ，OD ，OE ，O 后F ，再从射线OA 上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…后，那么所描的第2013个点在射线 上．
24.观察下列图形中点的个数，若按其规律再画下去，可以得到第n 个图形中所有的个数为 （用含n 的代数式表示）．。