三角形全等sss练习题
11.2 三角形全等的判定(SSS)(含答案)

11.2 三角形全等的判定(SSS)题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
◆课堂测控测试点边边边1.如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF,∠A=•43°,求∠D的度数,下面是小红同学的求解过程,请你说明每一步的理由.解:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.在△ABC与△DEF中,,,AB DEAC DFBC EF=⎧⎪=⎨⎪=⎩所以△ABC≌△DEF().所以∠D=∠A=43°().2.已知:如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE.◆课后测控3.如图,AC=BD,AB=DC,求证:∠B=∠C.4.已知:如图,点A,C,B,D都在一条直线上,AC=BD,AM=CN,BM=DN.求证:AM∥CN.5.三月三放风筝,下图是小明制作的风筝,他根据DE=DF,EH=FH,不用度量,就知道∠DEH=∠DFH.请你用所学知识给予证明.◆拓展测控6.有一块三角形的厚铁板(如图),根据实际生产需要,工人师傅要把∠MAN平分开,现在他手边只有一把尺子(没有刻度)和一根细绳,•你能帮助工人师傅想个办法吗?并说明你这样做的理由.答案:1.SSS 全等三角形对应角相等2.∵C是AB的中点,∴AC=BC.在△ACD与△CBE中,,,,AC CBAD CECD BE=⎧⎪=⎨⎪=⎩∴△ACD≌△CBE(SSS).[总结反思]三条边对应相等的两个三角形全等,•运用此结论可证明两个三角形全等.3.证明:在△ABD与△DCA中,,,,AB DCDB ACAD DA=⎧⎪=⎨⎪=⎩∴△ABD≌△DCA(SSS),∴∠B=∠C.[解题规律]证明线段相等或角相等时,常证明它们所在的两个三角形全等,本题中证明两个三角形全等已具备两个条件,运用公共边这个隐含条件是解题关键.4.∵AC=BD,∴AC+CB=BD+CB,即AB=CD.在△AMB和△CND中,,,,AM CNBM DNAB CD=⎧⎪=⎨⎪=⎩∴△AMB≌△CND(SSS).∴∠A=∠NCD,∴AM∥CN.[解题技巧]题目中条件AC=BD不能直接用来证明,可运用等式的性质变为AB=CD.5.证明:连结DH.在△DEH和△DFH中,,,.DE DFEH FHDH DH=⎧⎪=⎨⎪=⎩∴△DEH≌△DFH(SSS),∴∠DEH=∠DFH.[解题规律]连结EH即将原图形分成一对三角形,利用公共边运用SSS可得两个三角形全等.6.用绳子的一定长度在AM,AN边上截取AB=AC,再选取适当长度的绳子,将其对折,得绳子的中点D,把绳子的两端点固定在B,C两点,拽住绳子中点D,向外拉直BD和CD,•再在铁板上点出D的位置,作射线AD,则AD平分∠MAN.理由如下:如图,∵在△ABD和△ACD中,,,,AB ACBD CDAD AD=⎧⎪=⎨⎪=⎩∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD,即AD平分∠MAN.[解题技巧]这是一道实际应用问题,通过构造两个三角形全等将∠MAN平分,•解题关键是得到绳子的中点并拉直绳子,从而可知DB=DC.可以编辑的试卷(可以删除)This document is collected from the Internet, which is convenient for readers to use. If there is any infringement, please contact the author and delete it immediately.。
全等三角形判定SSS练习题
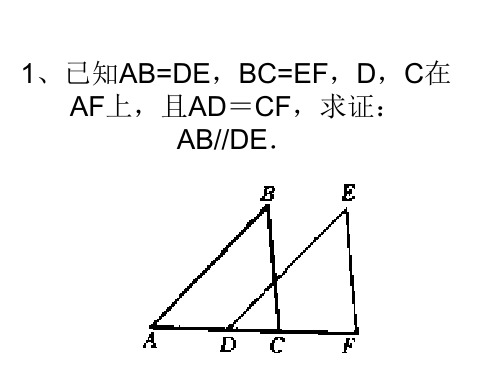
5、已知:如图,AB=DC,AD=BC, 求证:∠A=∠C
A
D
B
C
全等三角形判定SSS练习题
6、已知:如图 , AB=AC , AD=AE , BD=CE.求证:∠BAC=∠DAE.
A
E
D
B
C
全等三角形判定SSS练习题
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
4、 如图,已知AB=CD,AC=BD, 求证:∠A=∠D.
AD
O
B
C
全等三角形判定SSS练习题
5、如图,已知AB=AD,AC=AE, BC=DE,求证:∠1=∠2
A
12ELeabharlann CBD全等三角形判定SSS练习题
1、已知AD=BE,BC=EF, AC=DF,求证EF//BC
D
A
E
F
B
C
全等三角形判定SSS练习题
1、已知AB=DE,BC=EF,D,C在 AF上,且AD=CF,求证: AB//DE.
全等三角形判定SSS练习题
2、已知AB=DE,BC=EF,AF=CD, 求证EF//BC:
E
F1
A
2
C
D
B
全等三角形判定SSS练习题
3、如图,已知AB=AC,AD为 △ABC的中线,求证:AD⊥BC
A
BD C
全等三角形判定SSS练习题
2、如图,△ABC中,D是BC边的中 点,AB=AC,求证:∠B=∠C
A
B
D
C
全等三角形判定SSS练习题
3、已知:如图,B、E、C、F在一 条直线上,且BE=CF,AB=DE, AC=DF。 求证:△ABC≌△DEF
全等三角形的判定(SSSSAS、ASA、AAS)练习题

)
A. 2 对 B . 3 对 C .4 对
D
.5 对
16.如图, AB AC , BD CD , 1 2 ,欲得到 BE CE ,?可先利用 _______, 证明 ABC ≌ DCB ,得到 ______=______,再根据 ___________,?证明 ________? ≌ ________,即可得到 BE CE . 17.如图,已知 AD // BC , AD BC . 求证: ADC ≌ CBA
)
A. 1 对 B . 2 对 C . 3 对
D
.4 对
12.如图, CD AB 于 D , BE AC 于 E , AO 平分 BAC ,则图中全等三角形有(
)
A. 1 对 B . 2 对 C . 3 对
D
.4 对
13.已知 AB A B , A A , B B ,则 ABC ≌ A B C 的根据是(
)
A. 3 对
B
.4 对
C
.5对
D
.6 对
10.如图, ABC 和 DEF 中,下列能判定 ABC ≌ DEF 的是(
)
A. AC DF , BC EF , A D B . B E , C F , AC DF
C. A D , B E , C F D . B E , C F , AC DE
11.如图, AD BC , AC BD ,则图中全等三角形有(
6.如图,线段 AB 、 CD 互相平分交于点 O ,则下列结论错误的是(
)
A. AD BC B . C D C . AD // BC D . OC OB
7. 已知两边及其中一边的对角,作三角形,下列说法中正确的是(
)
A.能作唯一的一个三角形
12全等三角形判定一SSS,SAS提高巩固练习
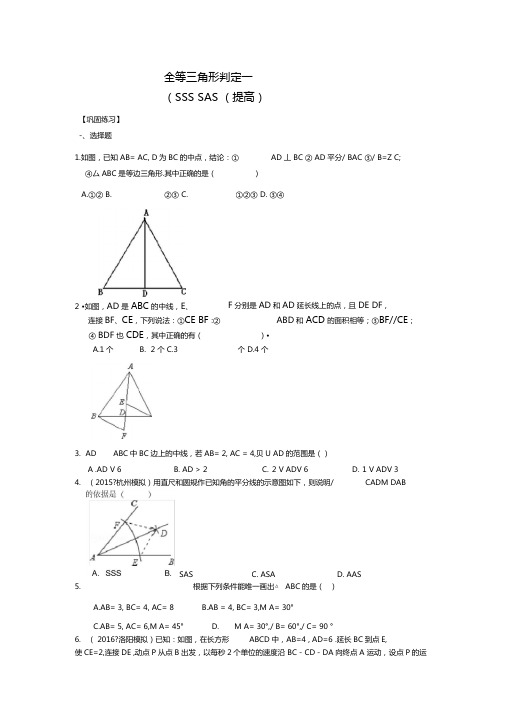
全等三角形判定一(SSS SAS (提高)【巩固练习】-、选择题1.如图,已知 AB= AC, D为BC的中点,结论:①④厶ABC是等边三角形.其中正确的是()F分别是AD和AD延长线上的点,且DE DF ,连接BF、CE,下列说法:①CE BF :②ABD和ACD的面积相等;③BF//CE;④ BDF也CDE,其中正确的有()•3.AD ABC中BC边上的中线,若AB= 2, AC = 4,贝U AD的范围是()4.(2015?杭州模拟)用直尺和圆规作已知角的平分线的示意图如下,则说明/ CADM DAB5.根据下列条件能唯一画出△ABC的是()A.AB= 3, BC= 4, AC= 8B.AB = 4, BC= 3,M A= 30°C.AB= 5, AC= 6,M A= 45°D. M A= 30°,/ B= 60°,/ C= 90 °6.( 2016?洛阳模拟)已知:如图,在长方形ABCD中,AB=4 , AD=6 .延长BC到点E,使CE=2,连接DE ,动点P从点B出发,以每秒2个单位的速度沿 BC - CD - DA向终点A 运动,设点P的运A.①② B. ②③ C. ①②③ D. ③④AD丄 BC ② AD平分/ BAC ③/ B=Z C;2 •如图,AD是ABC的中线,E、B.2 个C.3 个D.4 个A .AD V 6 B. AD > 2 C.2 V ADV 6 D.1 V ADV 3C. ASAD. AASA.1个SAS动时间为t秒,当t的值为()秒时,△ ABP和厶DCE全等.如图,△ ABC 是三边均不等的三角形, 使所作的三角形与△ ABC 全等,这样的三角形最多可以画△ABC 和△FED 中,AD=FC ,AB=FE ,当添加条件(只需填写一个即可)12. 把两根钢条AA', BB'的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)A . 1B . 1 或 3C . 1 或 7 D.二、填空题如图,AB= CD AC= DB,Z ABD= 25° 7. ,/ AOB= 82° ,则/ DCB=DE= BC,以D E 为两个顶点画位置不同的三角形,个•C Dr(2016?微山县二模)如图,四边形 9. 使厶 ABC ◎△ CDA .ABCD 中,/ 1 = / 2,请你补充一个条件8.B» ED,若/ ABC= 54°,则/ E=10. (2014春?鹤岗校级期末)如图:在如图,若测得 AB= 5厘米,则槽宽为 厘米.三、解答题13. (2014秋?天津期末)如图在 △ ABE 中,已知 AB=AE , AD=AC , /仁/ 2 .求证:△ ABC 也△ AED .14. 如图, B= C, BD = CE, CD = BF.1求证:EDF = 90 - - A 215. 已知:如图,BE CF 是厶ABC 的高,且 BP= AC, CQ= AB, 求证:API AQ.【答案与解析】 一.选择题1.【答案】C【解析】由SSS 证全等可得①②③是正确的2.【答案】D;3.【答案】D;【解析】用倍长中线法;4.【答案】A;【解析】解:从角平分线的作法得出,△ AFD与厶AED的三边全部相等,则厶 AFD^A AED故选A.5.【答案】C;【解析】A不能构成三角形,B没有SSA定理,D没有AAA定理.6.【答案】C;【解析】解:因为 AB=CD,若/ ABP= / DCE=90 ° BP=CE=2,根据SAS证得△ ABP◎△ DCE,由题意得:BP=2t=2,所以 t=1 ,因为 AB=CD,若/ BAP= / DCE=90 ° AP=CE=2,根据 SAS 证得△ BAP◎△ DCE,由题意得:AP=16 - 2t=2,解得t=7 .所以,当t的值为1或7秒时.△ ABP和厶DCE全等. 故选C.二.填空题7.【答案】66°;82【解析】可由 SSS证明厶AB3A DCB / OBC=Z OCB^ —41,所以/ DCB=/ ABG= 25°+ 41 °= 66 °8.【答案】4;【解析】在DE的两侧可以各画2个.9.【答案】AD=BC ;【解析】由题意知,已知条件是△ABC与厶CDA对应角/ 1 = / 2、公共边AC=CA,所以根据全等三角形的判定定理SAS来证△ ABC ◎△ CDA时,需要添加的条件是 AD=BC.10. 【答BC=ED 或/ A= / F.11. 【答27;【解可证△ ADB^A CDB^A CDE.12. 【答5;_ -解答题13. 【解证明:•••/仁/ 2,••• / 1 + / DAC= / 2+ / DAC ,••• / BAC= / EAD ,在厶ABC和厶AED中,\ ZBAC=ZEAD ,I AC=AB•••△ ABC ◎△ AED ( SAS).14.【解析】证明:在厶 ABC中,/ B=Z C,1•••/ B = 90/ A2在厶 DBF和△ ECD中BD CEB CBF CD•••△ DBF^A ECD( SAS•••/ BFD=Z CDE1 •••/ EDM 180°—/ BD1/ CDE= 180° -(Z BDF^Z BFD) =Z B = 90 —/ A .215.【解析】证明:T BEX AC CF丄AB(已知)•Z ACF+Z BAC= 90°,/ ABE^Z BAC= 90°,(三角形内角和定理)/ ACF=Z ABE(等式性质)在厶ACQ^n^ PBA中CQ ABACF ABPAC BP• △ ACQ^ PBA( SAS•Z Q=Z BAP (全等三角形对应角相等)•/ CFX AB (已知)•Z Q+Z QAF= 90°,(垂直定义)•Z BAP+Z QAF= 90°,(等量代换)•AP丄AQ.(垂直定义)。
三角形全等的判定(含例题)

1.判定两个三角形全等的基本事实:边边边(SSS)(1)基本事实:三边分别相等的两个三角形全等,简写成“__________”或“SSS”.(2)这个基本事实告诉我们:当三角形的三边确定后,其形状、大小也随之确定.这也是三角形具有稳定性的原因.2.判定两个三角形全等的基本事实:边角边(SAS)(1)基本事实:两边和它们的夹角分别相等的两个三角形全等,简写成“边角边”或“__________”.(2)此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【注意】(1)此方法是证明两个三角形全等最常用的方法之一,应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要误认为有两边一角就能判定两个三角形全等.(2)在书写时也要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.3.判定两个三角形全等的基本事实:角边角(ASA)(1)基本事实:两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“__________”.(2)用“ASA”来判定两个三角形全等,一定要证明这两个三角形有两个角以及这两个角的夹边分别相等,证明时要加强对夹边的认识.4.判定两个三角形全等的基本事实:角角边(AAS)(1)基本事实:两角和其中一个角的对边分别相等的两个三角形全等,简写成“角角边”或“__________”.(2)这一结论很容易由“ASA”推得,将这一结论与“ASA”结合起来,即可得出:两个三角形如果具备两角和一条边对应相等,就可判定其全等.5.直角三角形全等的判定方法:斜边、直角边(HL)(1)基本事实:斜边和一条直角边分别相等的两个直角三角形全等,简写成“斜边、直角边”或“________”.(2)“HL ”定理是直角三角形所独有的,对于一般三角形不成立. 【归纳】判定两个三角形全等常用的思路方法如下: HL SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎪⎩一直角边一斜边—已知两边找夹角—找另一边—边为角的对边—找任一角—找夹角的另一边—已知一边一角边为角的邻边找夹边的另一角—找边的对角—找夹边—已知两角找任一角的对边—K 知识参考答案:1.(1)边边边2.(1)SAS 3.(1)ASA4.(1)AAS5.(1)HLK —重点 三角形全等的判定K —难点 三角形全等的判定和性质的综合运用 K —易错三角形全等的判定一、用边边边(SSS )证明三角形全等明确要证明全等的两个三角形,在书写两个三角形全等时,“≌”左边三角形的三边与“≌”右边三角形的三边的前后顺序要保持一致.【例1】如图,ABC △中,AB AC =,EB EC =,则由“SSS ”可判定A .ABD △≌ACD △B .ABE △≌ACE △△D.以上答案都不对C.BDE△≌CDE【答案】B二、用边角边(SAS)证明三角形全等此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.【例2】如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC【答案】C【解析】∵AB=AC(已知),∠A=∠A(公共角),∴只需要AE=AD,∴△ABE≌△ACD,故选C.三、用角边角、角角边(ASA、AAS)证明三角形全等1.不能说“有两角和一边分别相等的两个三角形全等”,这是因为:假设这条边是两角的夹边,则根据角边角可知正确;假设一个三角形的一边是两角的夹边,而与另一个三角形相等的边是其中一等角的对边,则两个三角形不一定全等.2.有三个角对应相等的两个三角形不一定全等.【例3】如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长,就得出AB的长,判定△EDC≌△ABC的理由是A.SSS B.SASC.SAA D.ASA【答案】D【解析】∵BF⊥AB,DE⊥BD,∴∠ABC=∠BDE.又∵CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA).故选D.【例4】如图,已知点B、C、F、E在同一直线上,∠A=∠D,BF=EC,AB∥DE,若∠1=80°,求∠BFD 的度数.四、用斜边、直角边(HL)证明直角三角形全等1.当证明两个直角三角形全等时,若不适合应用“HL”,也可考虑用“SAS”“ASA”或“AAS”来证明.2.在用一般方法证明时,因为两个直角三角形中已具备一对直角相等的条件,故只需找另外两个条件即可,在实际证明中可根据条件灵活选用不同的方法.【例5】如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌△Rt△DCF,则还需要添加一个条件是A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC【答案】D五、全等三角形的判定和性质的综合寻找解决问题的思路方法可以从求证的结论出发,结合已知条件,逐步寻求解决问题所需要的条件.同时要注意对图形本身隐含条件的挖掘,如对顶角、公共角、公共边等.【例6】如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为A.50°B.30°C.80°D.100°【答案】B【解析】∵OA=OC,OD=OB,∠AOD=∠COB,∴△AOD≌△COB(SAS),∴∠D=∠B=30°.故选B.【例7】如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.【解析】∵∠CAB=∠DBA,∠CBD=∠DAC,∴∠DAB=∠CBA.在△ADB与△BCA中,CAB DBA AB ABDAB CBA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADB≌△BCA(ASA),∴BC=AD.。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
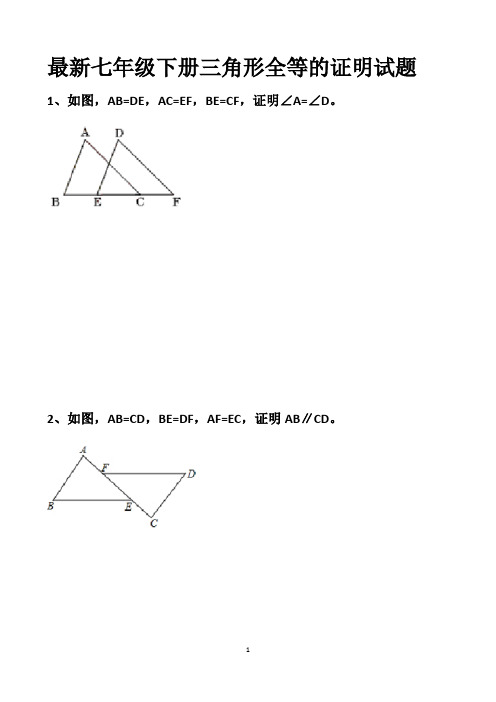
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
全等三角形判定一(SSS,SAS)(基础)巩固练习
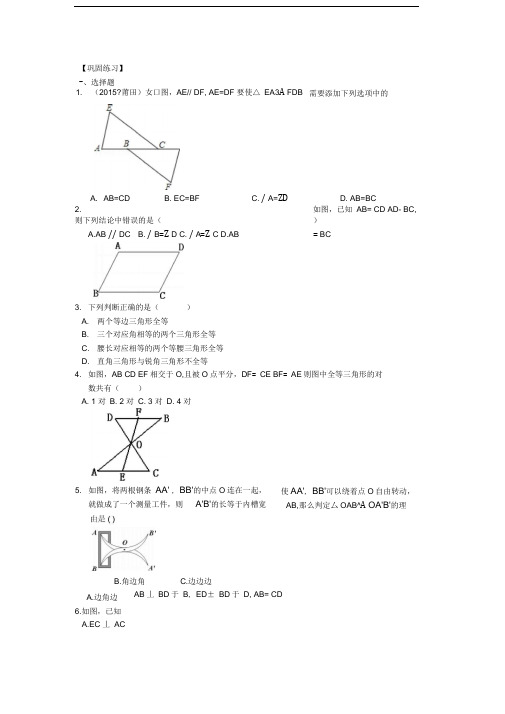
【巩固练习】-、选择题2.如图,已知AB= CD AD- BC,则下列结论中错误的是()A.AB // DCB. / B=Z DC. / A=Z CD.AB = BC3. 下列判断正确的是()A. 两个等边三角形全等B. 三个对应角相等的两个三角形全等C. 腰长对应相等的两个等腰三角形全等D. 直角三角形与锐角三角形不全等4. 如图,AB CD EF相交于O,且被O点平分,DF= CE BF= AE则图中全等三角形的对数共有()A. 1 对B. 2 对C. 3 对D. 4 对B.角边角C.边边边AB丄BD于B, ED± BD于D, AB= CD1. (2015?莆田)女口图,AE// DF, AE=DF 要使△ EA3A FDB 需要添加下列选项中的B. EC=BFC. / A=ZDD. AB=BC5. 如图,将两根钢条AA' , BB'的中点O连在一起,就做成了一个测量工件,则A'B'的长等于内槽宽使AA', BB'可以绕着点O自由转动,AB,那么判定厶OAB^A OA'B'的理A.边角边6.如图,已知A.EC 丄ACA. AB=CDB.EC = ACC.ED + AB = DBD.角角边BC= ED,以下结论不正确的是(D.DC = CB12.、填空题如图,AB= CD AC= DB,Z ABD= 25°,/ AOB= 82°,则/ DCB=点D在AB上,点E在AC上, CD与BE相交于点0,且AD= AE, AB= AC,若/ B = 贝y C= .,△ AD®7.AC BD互相平分,则图中全等三角形共有(2015?虎林市校级二模)如图,已知BD=AC,那么添加一个条件后,能得11.8.9.,/ 3= 26°,则/ CBBAC= ABC^如图,20°,12.三、解答题13. (2014春?章丘市校级期中)如图A B两点分别位于一座小山脚的两端,小明想要测量A、B两点间的距离,请你帮他设计一个测量方案,测出AB的距离.并说明其中的道理.14•已知:如图,AB // CD , AB = CD .求证:AD // BC .分析:要证AD// BC只要证/ ________ =Z __________ ,又需证______ 也_______ .证明:••• AB // CD ( ),二 / ________ =/ _________ ( ),在厶 ______ 和厶_____ 中,_____ 二____ ( ),< _____ = _____ (),、---- = -------- ()‘•••△_______ A___________ ( ).二 / ________ =/ ______ ( ).•- _____ // ______ ( ).15.如图,已知AB= DC AC= DB, BE= CE求证:AE= DE.【答案与解析】一. 选择题1. 【答案】A;【解析】解:••• AE// FD,•••/ A=Z D,•/ AB=CD•AC=BD在厶AEC和厶DFB中,f AE=DF-ZA=ZD,AC=DBk•△EAC^A FDB( SAS ,故选:A.2. 【答案】D;【解析】连接AC或BD证全等.3. 【答案】D;4. 【答案】C;【解析】△ DOF^A COE △ BOF^A AOE △ DOB^A COA.5. 【答案】A;【解析】将两根钢条AA' , BB'的中点O连在一起,说明OA= OA', OB= OB',再由对顶角相等可证•6. 【答案】D;【解析】△ ABC^^ EDC Z ECD^Z ACB=Z CA聊/ ACB= 90°,所以ECL AC, ED + AB = BC+ CD= DB.二. 填空题7. 【答案】66°;82 °【解析】可由SSS证明厶ABC^A DCB Z OBC=Z OCB= 41 , 所以Z DCB=2Z ABC= 25°+ 41 °= 66°8. 【答案】4;【解析】△ AOD^A COB △ AOB^A COD △ ABD^A CDB △ ABC^A CDA.9. 【答案】BC=AD ;【解析】解:添加BC=AD ,r AC=BD•••在△ ABC 和厶BAD 中」BC=AD ,i AB 二AB•△ ABC ◎△ BAD ( SSS),故答案为:BC=AD .10. 【答案】56°;【解析】Z CBE= 26°+ 30°= 56° .11. 【答案】20°;【解析】△ ABE^A ACD( SAS12. 【答案】△ DCB △ DAB【解析】注意对应顶点写在相应的位置上.三. 解答题13. 【解析】解:如图所示:在AB下方找一点O,连接BO并延长使BO=B O,连接AQ并延长使AO=A O,在厶AOB和厶A OB中:f AO=OA?“ ZAOB=ZA V0B y,QB 二OB'•••△AOB2A A OB ( SAS, ••• AB=A B ,量出A B'的长即可.14. 【解析】3, 4;ABD CDB已知;1, 2;两直线平行,内错角相等;ABD CDBAB, CD已知;/ 1 = 7 2,已证;BD= DB公共边;ABD CDB SAS3 , 4,全等三角形对应角相等;AD, BC内错角相等,两直线平行15. 【解析】证明:在厶ABC^n^ DCB中AB = DCAC = DBBC =CB• △ABC^A DCB(SSS•••7 ABC=7 DCB 在厶ABE和△ DCE中AB = DCABC = DCBBE =CE•••△ ABE^A DCE( SAS ••• AE= DE.。
全等三角形的判定精选练习题分SSSSASAASASAHL分专题

全等三角形的判定(SSS)1、如图1,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是()A。
120°B.125°C。
127° D。
104°2、如图2,线段AD与BC交于点O,且AC=BD,AD=BC,•则下面的结论中不正确的是( )A.△ABC≌△BAD B。
∠CAB=∠DBA C.OB=OC D。
∠C=∠D3、在△ABC和△A1B1C1中,已知AB=A1B1,BC=B1C1,则补充条件____________,可得到△ABC≌△A1B1C1.4、如图3,AB=CD,BF=DE,E、F是AC上两点,且AE=CF.欲证∠B=∠D,可先运用等式的性质证明AF=________,再用“SSS”证明______≌_______得到结论。
5、如图,已知AB=CD,AC=BD,求证:∠A=∠D.6、如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:⑴∠D=∠B;⑵AE∥CF.7、已知如图,A、E、F、C四点共线,BF=DE,AB=CD.⑴请你添加一个条件,使△DEC≌△BFA;⑵在⑴的基础上,求证:DE∥BF.全等三角形的判定(SAS)1、如图1,AB∥CD,AB=CD,BE=DF,则图中有多少对全等三角形( )A.3 B。
4 C.5 D。
6CBA 2、如图2,AB=AC ,AD=A E,欲证△A BD ≌△A CE ,可补充条件( ) A 。
∠1=∠2B .∠B=∠C C.∠D=∠ED 。
∠BAE=∠C AD 3、如图3,AD=B C,要得到△AB D和△CD B全等,可以添加的条件是( )A .AB∥CD B。
AD ∥B CC .∠A=∠C D.∠ABC =∠CDA4、如图4,AB 与CD 交于点O ,O A=OC ,OD =OB ,∠A OD =________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,A D平分∠BAC ,请补充完整过程说明△A BD≌△ACD 的理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形全等sss练习题
2.如图,已知AC=FE、BC=DE,点A、D、B、F在一条直线上,AD=FB.要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
E
A
BC
达标训练:
3.如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 ___________.
A
A
O
B
B
D
第 1 题
C
C
第题
4.如图,已知OA = OB,AC = BC,∠1=30°,则∠
ACB的度数是________.
5.如图,AB = AD,DC = BC,∠B与∠D相等吗?为什么?
6.已知如图,小明根据条件“AB = DC,AC = DB,AC、BD交于点O”,探索图形中的三角形全等关系时,他发现△ABC≌△DCB,请写出探索过程,并说明理由.
课后作业
7.如图,△ABC中,AB?AC,EB?EC,则由“SSS”可以判定
A.△ABD≌△ACD B.△ABE≌△ACE C.△BDE≌△CDE D.以上答案都不对
A
CD
B
A
D
B
C
△ABC中,AB?AC,AE?CF,BE?AF,8.如图,则?E??________,?CAF??__________.
9.如图,AB=DE,AC=DF,BF=EC,△ABC和△DEF全等吗?请说明理由.
三角形全等的判定SSS练习题
1.如图,AC=DF,BC=EF,AD=BE,∠BAC=72°,∠F=32°,则∠
2.如图,已知AB=AC,BD=DC,那么下列结论中不正确的是
A.△ABD≌△ACD B.∠ADB=90°
C.∠BAD是∠B的一半D.AD平分∠BAC
3.如图,是一个风筝模型的框架,由DE=DF,EH=FH,就说明∠DEH=∠DFH。
试用你所学的知识说明理由。
4.如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,请说明∠A=∠
C.
中考
1.如图,AD=BC,AB=DC. 求证:∠A+∠D=180°
2.已知:如图,在四边形ABCD中,AB=CB,AD=CD.
求证:∠C=∠A.
参考答案:
随堂检测:
1、②①③.解析:本题是利用SSS画全等三角形的尺规作图步骤,“作直线BP,在BP上截取BC=a”也可表达为“画线段BC=a”
2、由全等可得 AD垂直平分BC
3、公共边相等是两个三角形全等的一个条件.
由于AC=AD,BC=BD,AB=AB,所以,△ABC≌△ABD,所以,∠CAB=∠DAB,即AB平分∠CAD. 拓展提高:
1、76.解析:先证明全等,再利用全等三角形的对应角相等和三角形内角和定理答案: 0
2、C.解析:利用SSS证明两个三角形全等
3、由于已知DE=DF,EH=FH,连结DH,这是两三
角形的公共边,于是,
?DE?DF?在△DEH和△DFH中, ?EH?FH
?DH?DH?
所以△DEH≌△DFH,所以∠DEH=∠DFH。
4、根据条件OA=OC,EA=EC,OA、EA和OC、EC恰好分别是△EAC和△EBC的两条边,故可以构造两个三角形,利用全等三角形解决
解:连结OE
在△EAC和△EBC中
?OA=OC??EA=EC
?OE=OE?
∴△EAC≌△EBC
∴∠A=∠C
体验中考:
1、由条件可构造两个全等三角形
证明:连结AC
∵AD=BC,AB=DC,AC=CA
∴△ABC≌△CDA
∴∠BAC=∠ACD
∴AB∥CD
∴∠A+∠D=180°
2、证明:连接BD.
在△ABD和△CBD中,
∵AB=CB,AD=CD,BD=BD,
∴△ABD≌△CBD.
∴∠C=∠A.
全等三角形的判定练习题
?ABE≌?DCF,1.如图,点A和点D、点E和点F分别是对应点,则AB= ,?A?,若AE?BC,则DF与BC的关系是. B
D
第1题图
第2题图
第
4题图
?ABC≌?AED,AB2.如图,若?B?40?,?E
?D?,?DAC?.
?30?,?C?45?,则?BAC?,
3.已知?ABC≌?DEF,若?ABC的周长为23,AB=8,BC=6,则AC= ,EF= .
4.如图,若AB=AC,BE=CD,AE=AD,则?ABE?ACD,所以
?AEB?,?BAE?,?BAD?
5.如图,?ABC≌?ADC,点B与点D是对应点,?BAC?26?,且?B?20?,
S?ABC?1,求?CAD,?D,?ACD的度数及?ACD的面积.
6.如图,?ABC≌?DEF,?A?50?,BC?9cm,CE?5cm,求?DEF 的度数及CF的长.
7.如图,已知:AB=AD,AC=AE,BC=DE,求证:?BAE??CAD 8.如图,在?ABC中?C?90?,D、E分别为AC、AB上的点,且BE=BC,DE=DC,求证:DE?AB;BD平分?ABC
D
9.如图,已知AB=EF,BC=DE,AD=CF,求证:
①?ABC≌?FED;②AB//EF
F
10.如图,已知AB=AD,AC=AE,BC=DE,求证:?BAD??CAE E。
