2013-2014高数B1重修试题A卷
2013-2014高数IIB试卷A
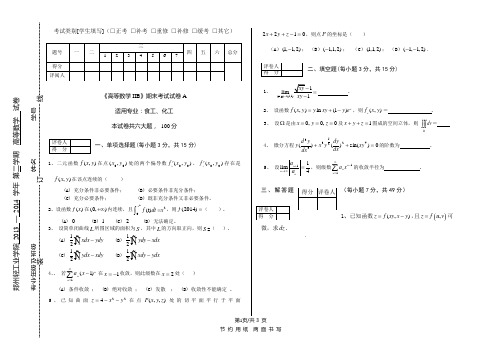
第1页/共3 页 考试类别[学生填写]（□正考 □补考 □重修 □补修 □缓考 □其它）《高等数学IIB 》期末考试试卷A适用专业：食工、化工 本试卷共六大题， 100分一、单项选择题(每小题3分，共15分)1、二元函数),(y x f 在点),(00y x 处的两个偏导数),(00y xf x '，),(00y x f y '存在是),(y x f 在该点连续的（ ）(A) 充分条件非必要条件； (B) 必要条件非充分条件；(C) 充分必要条件； (D) 既非充分条件又非必要条件。
2、设函数()f x 在(0,)+∞内连续，且22(t)x f dt x =⎰，则(2014)f =（ ）.(A) 0 (B) 1 (C) 2 (D) 无法确定。
3、 设简单闭曲线L 所围区域的面积为S ，其中L 的方向取正向，则S =（ ）. (A)12L xdx ydy -⎰Ñ (B) 12L ydy xdx -⎰Ñ (C) 12L ydx xdy -⎰Ñ (D) 12L xdy ydx -⎰Ñ4、、 若∑∞=-1)1(n n nx a在1-=x 收敛，则此级数在2=x 处（ ）(A) 条件收敛 ； (B) 绝对收敛 ； (C) 发散 ； (D) 收敛性不能确定 。
5、已知曲面224yx z --=在点(,,)P x y z 处的切平面平行于平面0122=-++z y x ，则点P 的坐标是（ ）（A ）(1,1,2)-； （B ）(1,1,2)-； （C ）(1,1,2)； （D ）(1,1,2)--．二、填空题(每小题3分，共15分)1、 (x,y)(1,1)lim→= .2、 设函数(,)ln (1)xf x y y xy y e =+-，则(,)x f x y ＝ .3、 设Ω是由0,0,0x y z ===及1x y z ++=围成的空间立体，则dv Ω⎰⎰⎰＝4、 微分方程0)sin()()(4225333=++xy dx dy y x dxy d y 的阶数为 .5、 设11lim 4n n na a +→∞=，则级数11n n n a x ∞-=∑的收敛半径为 .三、解答题（每小题7分，共49分）1、 已知函数(,)z f xy x y =-，且(),z f u v =可微，求dz .．线 订 装郑州轻工业学 2013 — 2014 学年 第二学期 高等数学 试卷专业年级及班级 姓名 学号第2页/共3 页2、交换积分次序10xydx dy y⎰⎰，并求其值.3、计算曲线积分⎰，其中L 为ln y x =上点(1,0)与点(,1)e 间的弧段.4、计算2 2Ly dx xydy +⎰,其中L ：2y x =从()0,0O 到()1,1A .5． 判定级数2123n n n n ∞=∑的敛散性..6．计算二重积分()22Dx y dxdy +⎰⎰，其中D ：221x y +≤.7．求微分方程56x y y y e '''-+=通解第3页/共3 页四、解答题（本题9分）求幂级数2121n n x n +∞=+∑的收敛域及和函数五、应用题（本题满分9分）计算由曲面22x y z +=与2z =所围成立体的体积.六、证明题（本题满分3分）设函数()f x 在[0,1]上连续， 证明1112001()()[()]2xdx f x f y dy f x dx =⎰⎰⎰.线订装第4页/共3 页。
同济大学2013-2014学年高等数学(B)上期末考试试卷
本资料仅供参考复习练手之用，无论是重修只求及格，还是为了拿优保研，复习课本上的基础知识点和例题、课后习题才是重中之重，作为一个重修过高数的学长，望大家不要舍本求末，记住这样一句话，只有当你付出了，你才可能有收获。
同济大学2013-2014学年第一学期高等数学B(上)期终试卷一. 选择与填空题(3'824'⨯=) 1. 极限262lim()1nn n e n -→∞-=+2. 利用定积分的几何意义，积分4-=⎰92π3. 微分方程"'120y y y +-=的通解为4312x xy C e C e -=+4. 已知敌方的导弹阵地位于坐标原点处，发射的导弹飞行轨迹为光滑曲线()y f x =，我方 拦截导弹的阵地位于x 轴正向2000公里处，发射的拦截导弹飞行速度是敌方导弹速度的 两倍，如果由计算机控制，在敌方导弹发射时我方的拦截导弹同时发射，并且我方导弹的 运行轨迹是直线，如果两导弹的相撞点为00(,)x y ，则该点满足的方程为2x =⎰5. 0{}x 是有界数列, 则该数列单调是数列极限存在的什么条件 【A 】 ()A 充分条件; ()B 必要条件; ()C 充分必要条件; ()D 无关条件.6. ()f x 是连续函数, 曲线段()()xaf t dt a x b ≤≤⎰的弧长s 的计算公式为 【C 】()a A s =⎰; ()a B s =⎰;())aC s d x =⎰; ()aD s =⎰无关条件.7. 函数()f x 具有三阶连续导数，如果"()0,[,]f x x a b >∈，则下列四项积分中，积分值 确定为正数的积分为 【A 】 ()['()'()]baA I f b f x d x =-⎰; ()'()baB I f x dx =⎰;()[()()]baC I f x f a d x=-⎰; ()'"()baD I f x dx =⎰. 8. 利用换元ln(1)x t =+, 积分2()x f e dx ⎰等于 【D 】20(1)()1f t A dt t ++⎰; 210()(1)e B f t dt -+⎰; 20(1)()1e f t C dt t ++⎰; 210(1)()1e f t D dt t -++⎰. 二. 计算下列各题(6'636'⨯=)1. 试计算由23ln 3x x y y +++=所确定的曲线在(1,1)点的切线方程.[22213'3470(31)4x y x y y x +=-=-⇒+-=+] 2. 求由参数方程t tx e y e t -⎧=⎨=+⎩所确定函数()y y x =的导数22;dy d ydx dx . [22322();22t t t t dy d y e e e e dx dx=-+=+] 3. 求不定积分[322(1)3x x c +-+] 4. 曲线段3:()L y x a x a =-≤≤的弧长为s , n D 是xoy 平面上与L 距离不超过n 的点集,即222{(,)(')('),(',')}n D x y x x y y n x y L =-+-≤∈,n D 的面积为n A ,求极限2limnn A n →∞.[222()lim n n n A n A n s nπππ→∞≤≤+⇒=] 三. (8')计算反常积分31arctan x dx x +∞⎰. [121arctan 11[arctan ]22x x x x +∞=-++=]四. (8')()f x 具有二阶导数, 如果极限201()(2)lim1x f x xf x x→++=-, 求(0),'(0),"(0)f f f . [(01,'(0)1,"(0)6f f f =-==-] 五. (8')可导函数()f x 满足方程40()2()1xf x tf t dt x -=--++⎰, 求函数()f x .[232(0)1,'()2()4()2(1)3x f f x xf x x f x x e -==-+⇒=-+] 六. (10')求函数231xx y xe ++=的单调区间与极值, 并求出该函数在区间[2,2]-上的最值.[23111'(21)(1)(,1],[1,],[,);22x x y x x e ++=++⇒-∞-↑--↓-+∞↑极小1()2y -=极大1(1)y e -=-; 11min max 2(2),(2)2y y e e-=-=]七. (10')计算由曲线21x y e =-, 直线41y e =-以及y 轴所围图形的面积; 并求出由该图 形绕y 轴旋转所得旋转体的体积. [224244240031[(1(1)];2()(51)222x x A e e dx e V x e e dx πππ=---=+=-=-⎰⎰]八. (8')计算极限12ln(1)0(12)limtxx x t dt t +→-⎰.[11222ln(1)(12)(12)1(ln(1)),ln(1)2txx t dt x x x x x L t eξξξξ+--=-++<<⇒⇒=⎰]。
2013-2014高等数学A(1)_A卷答案
π
六 (7 分) 求由曲线 y = arcsin x (0 ≤ x ≤ 1) ， y = 绕 y 轴旋转的旋转体体积. 解： Vy = π
∫
π 2
0
sin ydy = π ∫
2
π 2
0
2 1 − cos 2 y 1 ⎡1 ⎤2 π . dy = π ⎢ y − sin 2 y ⎥ = 2 4 ⎣2 ⎦0 4
−1 0
−1
−1
0
t 0 dt = [t − 2 ln(2 + t ) ]−1 = 1 − 2 ln 2 . 2+t
三、计算下列各题. (每小题 6 分，满分 24 分) 1.
∫ x( x
1
2
+ 1)
dx . (拆项) 解： ∫
1 1 x dx = ∫ ( − 2 )dx = ln | x | − ln( x 2 + 1) + C . x( x + 1) x x +1 2
x − 1 ln x = 0 ； f (1) = 0 ；
因 f (1 ) = f (1 ) = f (1) ，故 f ( x) 在 x = 1 处连续. (2) f −′(1) = lim −
x →1
−
+
−1 − ln x f ( x) − f (1) 1 − x ln x x = lim = = = 0； lim lim 1 x →1− x →1− x −1 x −1 1 − x x →1− − 2 1 −x
∫
四 (7 分) 试分析函数 f ( x ) = | x − 1| ln x ， ( x > 0) 在 x = 1 处的连续性和可导性(说明理由). 解：(1) f (1 ) = lim f ( x) = 1 − x ln x = 0 ； f (1 ) = lim f ( x) = − +
2013年全国高中数学联赛A卷一试真题+答案
8.
已知数列 an 共有 9 项，其中 a1
a9
1 ，且对每个 i 1,2,,8，均有 ai1
ai
2,1,
1 2
，则这样的
数列个数为__________.
二、解答题
9. 给定正整数列 xn 满足 Sn 2Sn1, n 2,3, ，这里 Sn x1 x2 xn .证明：存在常数 C 0 ，
6
3
V 1 3 2 6 ， S 3 3 1 1
34
12
4
2
2
2
3 6
2
3 2
3 ，故 r
2
；
6
1
5、
4
b 1 一次函数区间端点取最值，故
，由于 a b 2 1 a 2 b2 2ab 1 ，
a b 1
6、 232 323
且 a 2 b2 2ab ，故 4ab 1 ab 1 ，取“=”时， a b 1 ；
y1 y2 4
2；
3、11
cos A cosB C cos B cos C sin B sin C cos A sin A ，所以 sin A 11cos A ，
10 10 tan A sin A 11；
cos A
2
4、
V 1 Sr ，其中 r 为内切球半径， S 为表面积，根据数据可算出，
5. 设 a, b 为实数，函数 f x ax b 满足：对任意 x 0,1，有 f x 1.则 ab 的最大值为________.
6. 从1,2,,20 中任取 5 个不同的数，其中至少有两个是相邻数的概率为__________.
7. 若实数 x, y 满足 x 4 y 2 x y ，则 x 的取值范围是__________.
2013-2014学年度下学期高三第一次月考-数学(理)(精)
（A）6（B）1（C） （D，现在要用分层抽样的方法从两个班抽出16人参加视力测试，则一班和二班分别被抽取的人数是（）
（A）8，8（B）9，7（C）10，6（D）12，4
3．一个简单几何体的正视图、侧视图如图所示，则其俯视图可能为：
3.做答第Ⅱ卷时，请按题号顺序在各题目规定的答题区域内做答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效.
4.保持答题卡面清洁，不得折叠、不要弄破、弄皱，不准用涂改液、修正带、刮纸刀.
第Ⅰ卷（选择题共60分）
一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．
（A）充分不必要条件（B）必要不充分条件
（C）充分必要条件（D）既不充分也不必要条件
7．双曲线 的渐近线与圆 相切，则双曲线的离心率为（）
（A） （B） （C） （D）
8．已知函数① ，② ，则下列结论正确的是（）
（A）两个函数的图象均关于点 成中心对称
（B）两个函数的图象均关于直线 成轴对称
（C）两个函数在区间 上都是单调递增函数
2013-2014学年度下学期高三二轮复习
数学（理）综合验收试题（1）【新课标】
考试说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟
1.答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.
2.做答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，写在本试卷上无效.
已知函数
（1）当 时，求函数 的定义域；
（2）当函数 的值域为 时，求实数 的取值范围．
中国农业大学2013-2014学年秋季学期高数A试题(A卷)答案
201３～2014学年秋季学期（2０14、01）高等数学Ａ课程考试试题(Ａ卷) 答案一、填空题(本题共有５道小题,每小题3分，满分15分),请将答案填在横线上。
1、、2、曲线在点处得切线方程就是、3、数列中最大得项为、4、设，，则=、5、若函数得一个原函数为，则＝、二、单项选择题（本题共有5道小题，每小题3分，满分15分）,请将合适选项填在括号内.１.设函数在区间上连续,则就是函数得【 B 】、（A）跳跃间断点（B)可去间断点(C）无穷间断点（D）振荡间断点、2、下列变量中，就是无穷小量得为【B】、(A）（Ｂ）(C）（D)、3、函数得单调增加且图形为凹得区间就是【 C 】、（A)(B）（C)（Ｄ)、4、设,若反常积分收敛,则应满足【Ａ】、(A）（B) (C) （Ｄ）、5、在空间直角坐标系中表示【 D 】、（A）旋转抛物面（Ｂ）球面(C）抛物柱面(D）顶点在坐标原点、开口向上得圆锥面、三、计算下列各题(本题共有４道小题，每小题5分，满分20分)、１．求极限、解（解法一)（解法二）2。
求曲线在ｔ=0相应得点处得切线方程及法线方程、解所以，切线斜率切线方程为法线方程为3、设，求、解令，则，为常数。
即,亦即解得或。
所以或.４、求极限、解原式四、(本题满分10分)已知方程有且只有一个正根，求实数得取值范围、解设函数可得，为得极大值，为得极小值。
又，f（0)＝0,与,从而得图像如下：不难瞧出，当k〉４时f(x)=ｋ有唯一正根 ,故实数k得取值范围就是(4，+）、五、（本题满分10分）求以点、、为顶点得三角形得面积、解三角形得面积等于以、为邻边得平行四边形面积得一半，而，,，所以、六、证明下列各题（本题共有２道小题,每小题6分,满分１2分）、1。
证明成立证当x>0时，,因而当x>0时,ｆ（x)>f（０）,即所以２．设，试证明：证明:令，则所以＝七、（本题满分1２分）设有抛物线:,试确定常数得值,使得⑴与直线相切；⑵与轴所围图形绕轴旋转所得旋转体得体积最大、解设切点为,，切线斜率,代入切线方程,得、又旋转体体积,，解得或者，，,故时,体积最大，求得,所以，、八、(本题满分6分）求证：点与抛物线间得最短线段所在直线就是抛物线得法线。
高等数学A(一)2013-2014(B)
第 1 页 共 6 页上 海 海 事 大 学 试 卷2013 — 2014 学年第一学期期末考试《 高等数学A （一）》（B 卷） （本次考试不能使用计算器）班级 学号 姓名 总分一、单项选择题（在每个小题四个备选答案中选出一个正确答案，填在题末的括号中） (本大题分5小题, 每小题2分, 共10分)1、当x →0时，()2cos 1x -是sin 2x 的 （ ）。
(A)高阶无穷小; (B)同阶无穷小;但不等价; (C)等价无穷小; (D)低阶无穷小xx D x x x x C x x x x e B x x e A y x x e y 222222csc sec cot csc tan sec cot csc tan sec 11csc sec 11csc sec arctan 2++++++++-='-+=． ．． ．）（，则、设 也无水平渐近线无铅直渐近线又有水平渐近线，有铅直渐近线无水平渐近线）有铅直渐近线无铅直渐近线，有水平渐近线）渐近线的正确结论是（、关于曲线,)(,)(,(,)(1cos 32D C B A xxy +=⎰⎰⎰-=⎥⎦⎤⎢⎣⎡-202022sin 2)( 0)(sin )(sin )(sin 224ππππππxdxD C xdxB xdx A x x y 、 、 、 、 ）轴围成图形的面积为（与上的曲线，、在--------------------------------------------------------------------------------------装订线------------------------------------------------------------------------------------第 2 页 共 6 页5、曲面22y x z +-=是（ ）（A ）zox 平面上曲线z x =绕z 轴旋转而成的旋转曲面;（B ）zoy 平面上曲线y z -=绕z 轴旋转而成的旋转曲面; （C ）zox 平面上曲线z x =绕x 轴旋转而成的旋转曲面; （D ）zoy 平面上曲线y z -=绕y 轴旋转而成的旋转曲面.二、填空题（将正确答案填在横线上） (本大题分4小题, 每小题4分, 共16分)1、处的法线方程为曲线在设曲线方程为1,sin sin 122=⎪⎩⎪⎨⎧+=++=x tt y tt x 2、='⋅⋅+⎰x x f x f x x xx f d )()( , sin 1sin )(则的一个原函数为已知3、设a b c ,,均为非零向量，且a b c b c a c a b =⨯=⨯=⨯,,b ++=4、⎰-=223_______________cos ππxdx三 计算题（必须有解题过程，否则不给分） （本大题分10小题，每题6分，共 60分）1、之值。
高等数学下重修练习题
高等数学(下)重修练习题1．设a 是从点A (2, 1, 2)到点B (1, 2, 1)的向量, 则与a 同方向的单位向量为a ︒=_______. 2．设向量a ={2, 1, 2}, b ={1, 2, 1}, 则|a +b |=________. 3．设向量a ={2, 1, 2}, b ={1, 2, 1}, 则|a -b |=________. 4．设向量a ={2, 1, 2}, b ={1, 2, 1}, 则a ⨯b =________.5．设向量a ={2, 1, 2}, b ={1, 2, 1}, 则与a 和b 都垂直的向量c =_______ 6．设向量a ={2, 1, 2}, b ={1, 2, 1}, 则cos(a ,^ b )=________.7．设向量a ={2, 1, 2}, 则与a 的方向相同而模为2的向量b =________.8．1. 以向量a =(1, 1, 2)与b =(2, -1, 1)为邻边的平行四边形的面积为________.9．以曲线⎩⎨⎧==+x z zy x 222为准线, 母线平行于z 轴的柱面方程是________.10．2. 以曲线220x y zx y z ⎧+=⎨+-=⎩为准线, 母线平行于z 轴的柱面方程是________.11．2. 曲线⎩⎨⎧==-+00222y z z x 绕z 轴旋转所得的旋转曲面的方程为________.12．2. 曲线2220y z z x ⎧+-=⎨=⎩绕z 轴旋转所得的旋转曲面的方程为________.13．2. 旋转抛物面x 2+y 2=z 与平面x +z =1的交线在xoy 面上的投影方程为________.14．2.锥面z =x =z 2的交线在xoy 面上的投影方程为_________.15．2. 过点M (1, 2, -1)且与直线2341x t y t z t =-+⎧⎪=-⎨⎪=-⎩垂直的平面方程是________.16．2. 过点M (1, 2, -1)且与直线421131y x z +-+==-垂直的平面方程是________. 17．2. 过点M (1, 2, 1)且与平面2x +3y -z +2=0垂直的直线方程是_________. 18．2. 过点M (1, -1, 2)且与平面x -2y +1=0垂直的直线方程是________.19．函数f (x , y )在点P 0处的偏导数存在是函数f (x , y )在P 0处连续的( ). (A)充分条件; (B)必要条件; (C)充要条件; (D)既非充分又非必要条件. 20．函数f (x , y )在点P 0处连续是函数f (x , y )在P 0处的偏导数存在的( ). (A)充分条件; (B)必要条件; (C)充要条件; (D)既非充分又非必要条件. 21．函数f (x , y )在点P 0处连续是函数f (x , y )在P 0处可微分的( ).(A)充分条件; (B)必要条件; (C)充要条件; (D)既非充分又非必要条件. 22．若f (x , y )在点P 0的某个邻域内( ), 则f (x , y )在P 0处可微.(A)连续; (B)有界; (C)存在两个偏导数; (D)存在连续的一阶偏导数.23．3. 设z =f (x 2+y 2, x 2-y 2, 2xy ), 且f (u , v , w )可微分, 则xz∂∂=________.24．3. 设w =f (u , v ), u =xy , v =x 2+y 2, 且f (u , v )可微分, 则w x∂=∂________.25．3. 设z =ln(1+x 2+y 2), 则d z |(1, 1)= ________.26．设f (x , y , z )=x 2+y 2+z 2, 则梯度grad f (1, -1, 2)= ________. 27．设f (x , y , z )= x 3y 2z , 则梯度grad f (1, 1, 1)= ________.28．函数f (x , y , z )=x 2+y 2+z 2在点(1, -1, 2)处沿方向________的方向导数最大.29．函数f (x , y , z )= x 3y 2z 在点(1, 1, 1)处沿方向_____{3,2,1}_______的方向导数最大. 30．函数f (x , y , z )=x 2+y 2+z 2在点(1, -1, 2)处方向导数的最大值为________. 31．函数f (x , y , z )= x 3y 2z 在点(1, 1, 1)处方向导数的最大值为________. 32．交换二次积分的积分次序, 则100d (,)d yy f x y x ⎰⎰=________. 33．交换二次积分的积分次序, 则11d (,)d xx f x y y ⎰⎰=________.34．交换二次积分的积分次序,则10d (,)d y y x y x ⎰=________.35．交换二次积分的积分次序, 则210d (,)d xxx f x y y ⎰⎰=________.36．设D 为上半圆域x 2+y 2≤4(y ≥0), 则二重积分d Dσ⎰⎰=________.37．设D 是由两个坐标轴与直线x +y =1所围成的区域, 则二重积分d Dσ⎰⎰=______.38．设D 是由直线x =1、y =x 及x 轴所围成的区域, 则二重积分d Dσ⎰⎰=________.39．设D 是由椭圆221916y x +=所围成的区域, 则二重积分d Dσ⎰⎰=________.40．设L为上半圆y则曲线积分d Ls ⎰=________.41．设L 为圆x 2+y 2=1,则曲线积分Ls ⎰=________.42．设L为上半圆y 则曲线积分22ln(1)d L x y s ++⎰=________.43．设L 为圆x 2+y 2=1, 则曲线积分22ln(1)d Lx y s ++⎰=________.44．设L 是以O (0, 0), A (1, 1), B (0, 1)为顶点的三角形区域的正向边界, 则22d d Lxy x x y +⎰=________. 45．设L 是以O (0, 0), A (1, 1), B (0, 1)为顶点的三角形区域的正向边界, 则 (e cos )d e sin d x x Ly x x y y --⎰=________.46．设L 是以O (0, 0), A (1, 1), B (0, 1)为顶点的三角形区域的正向边界, 则 22d (2)d Lxy x x x y ++⎰=________.47．设L是由上半圆y x 轴所围成的区域的正向边界, 则22d (2)d Lxy x x x y ++⎰=________.48．若p 满足________,则级数n ∞=. 49．若p 满足________,则级数n ∞=.50．若q 满足________, 则级数0()2n n q a ∞=∑收敛.51．若p 满足________, 则级数01()2n n n p ∞=+∑收敛. 52．若p 满足________, 则级数2011()pn n n ∞=+∑收敛. 53．设1n n u ∞=∑是任意项级数, 则lim 0n n u →∞=是级数1n n u ∞=∑收敛的( )条件.(A)充分; (B)必要; (C)充分必要; (D)无关.54．设1n n u ∞=∑是任意项级数, 则级数1n n u ∞=∑收敛是级数1n n ku ∞=∑(k ≠0)收敛的( )条件.(A)充分; (B)必要; (C)充分必要; (D)无关. 55．下列级数中收敛是( A ).(A)11(1)1nn n ∞=-+∑; (B)11n n ∞=∑; (C)111()2n n n ∞=+∑;(D)n ∞=.56．下列级数中绝对收敛的是( C ).(A)1(1)nn ∞=-∑ (B)11(1)n n n ∞=-∑; (C)11(1)2n n n ∞=-∑; (D)11(1)(1)n n n n ∞=-+∑.57．下列级数中绝对收敛的是( D ).(A)1(1)nn ∞=-∑ (B)11(1)n n n ∞=-∑; (C)11(1)(1)nn n n ∞=-+∑; (D)211(1)n n n ∞=-∑.58．设幂级数0nn n a x ∞=∑的收敛半径为R , 则当x =R 时, 幂级数0n n n a x ∞=∑ ( ).(A)条件收敛; (B)发散; (C)绝对收敛; (D)可能收敛, 也可能发散. 59．设幂级数0nn n a x ∞=∑的收敛半径为R , 则当x =-R 时, 幂级数0n n n a x ∞=∑ ( ).(A)条件收敛; (B)发散; (C)绝对收敛; (D)可能收敛, 也可能发散. 60．如果幂级数0n n n a x ∞=∑在x =2处收敛, 则收敛半径为R 满足( ).(A)R =2; (B)R >2; (C)R ≥2; (D)R <2.61．如果幂级数0n n n a x ∞=∑在x =-2处收敛, 则收敛半径为R 满足( C ).(A)R =2; (B)R >2; (C)R ≥2; (D)R <2.62．将函数21()1f x x =+展开为x 的幂级数, 则f (x )=_______.63．将函数21()1f x x =-展开为x 的幂级数, 则f (x )=________.64．将函数1()4f x x =-在区间________可展开为x 的幂级数.65．将函数1()12f x x=+在区间________可展开为x 的幂级数.66．求通过直线113y x z==和点(2, -1, 1)的平面方程.67．求过三点A (1, 0, -1)、B (0, -2, 2)及C (1, -1, 0)的平面的方程.68．求通过点(1, 2, -1)且与直线23503240x y z x y z -+-=⎧⎨+--=⎩垂直的平面方程.69．求通过点(1, 2, -1)且与直线23503240x y z x y z -+-=⎧⎨+--=⎩平行的直线方程.70．求通过点(1, 2, -1)且与平面2x -3y +z -5=0和3x +y -2z -4=0都平行的直线方程.71．设z =x sin(x +y )+e xy, 求z y ∂∂, 22z y∂∂, 2z y x ∂∂∂.72．设z =ln(1+xy )+e 2x +y, 求z x ∂∂, 22z x∂∂, 2z x y ∂∂∂.73．设z =(2x +3y )2+x y, 求z x ∂∂, 22z x∂∂, 2z x y ∂∂∂.74．设z =x y, 求z x ∂∂, 22z x∂∂, 2z x y ∂∂∂.75．设z =x y, 求z y ∂∂, 22z y ∂∂, 2z y x∂∂∂.76．设z =x sin(2x +3y ), 求z x ∂∂, 22zx∂∂, 2z x y ∂∂∂.77．设z =f (x , y )由方程x e x -y e y =z e z 确定的函数, 求z x ∂∂, zy ∂∂.78．设z =f (x , y )由方程x +y -z =x e x -y -z 确定的函数, 求z x∂∂, zy ∂∂.79．已知z =u 2ln v , 而x u y =, v =3x -2y , 求z x ∂∂, zy∂∂.80．设z =u ⋅sin v , 而u =e x +y , v =x 2y , 求z x ∂∂, zy ∂∂.81．设z =e u sin v , 而u =x -y , v =x 2y , 求z x ∂∂, zy∂∂.82．求曲面z =ln(1+x 2+y 2)上点(1, 0, ln2)处的切平面方程. 83．求曲面z =1+2x 2+y 2上点(1, 1, 4)处的切平面方程. 84．求曲面e z -z +xy =3上点(2, 1, 0)处的切平面方程.85．求空间曲线2231y x z x =⎧⎨=+⎩在点M 0(0, 0, 1)处的切线方程.86．求空间曲线x =a cos t , y =a sin t , z =bt 在对应于t =0处的切线方程.87．计算二重积分22()d Dx y x σ+-⎰⎰, 其中D 是由直线y =2, y =x 及y =2x 轴所围成的闭区域.88．计算二重积分2d Dxy σ⎰⎰, 其中D 是由直线y =x , y =0, x =1所围成的区域.89．计算二重积分sin d Dx y σ⎰⎰, 其中D 是由直线y =x , y =0, x =π所围成的区域.90．计算二重积分(e )d y Dxy σ+⎰⎰, 其中D 是由直线y =x , y =1, x =-1所围成的区域.91．计算二重积分3(Dx σ+⎰⎰, 其中D 是由曲线y =x 2, 直线y =1, x =0所围成的区域.92．计算二重积分22e d xy Dσ+⎰⎰, 其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域.93．计算二重积分221d 1Dx yσ++⎰⎰, 其中D 是由圆周x 2+y 2=4及坐标轴所围成的在第一象限内的闭区域.94．计算三重积分d z v Ω⎰⎰⎰, 其中Ω是由曲面z z =0所围成的闭区域.95．计算三重积分d z v Ω⎰⎰⎰, 其中Ω是由曲面z =1-x 2-y 2及平面z =0所围成的闭区域.96．计算三重积分d z v Ω⎰⎰⎰, 其中Ω是由柱面x 2+y 2=1及平面z =0, z =1所围成的闭区域.97．计算曲线积分2(1)d lx s +⎰, 其中l 为圆周x 2+y 2=1.98．计算曲线积分s ⎰，其中l 为抛物线y =x 2(-1≤x ≤1).99．计算曲线积分22()d (2)d CI x y x x y =+++⎰, 其中C 是以O (0, 0), A (1, 0), B (0, 1)为顶点的三角形的正向边界.100．计算曲线积分222()d ()d LI x y x x y y =+++⎰, 其中L 是从O (0, 0)到A (1, 1)的抛物线y =x 2,及从A (1, 1)到O (0, 0)的直线.101．计算曲线积分43224(4)d (65)d LI x xy x x y y y =++-⎰, 其中L 是从(-2, 0)到(2, 0)的半圆x 2+y 2=4(y ≥0).102．计算曲线积分22d d LI xy x x y y =+⎰, 其中L 是曲线y =ln x 上从A (1, 0)到B (e , 1)的一段.∑104．计算曲面积分22()d x y S ∑+⎰⎰, 其中∑为平面x +y +z =1含于柱面x 2+y 2=1内的部分.105．计算曲面积分2d d z x y ∑⎰⎰, 其中∑为上半球面z 含于柱面x 2+y 2=1内的部分的上侧.106．计算曲面积分22d d d d d d y z x y x y z x y z x ∑++⎰⎰, 其中∑是由圆柱面x 2+y 2=R 2和平面x =0,y =0, z =0及z =h (h >0)所围的在第一卦限中的一块立体的表面外侧.107．计算曲面积分22(2)d d d d d d x z y x x y z x xz x y ∑-+-⎰⎰，其中∑是正方体0≤x ≤a , 0≤y ≤a ,0≤z ≤a 的表面的外侧.108．判别级数021!n n n ∞=+∑的敛散性. 109．判别级数213n n n ∞=∑的敛散性.110．判别级数1e()n n π∞=∑的敛散性.111．判别级数∑∞=1!100n nn 的敛散性112．判别级数111(1)2n n n n ∞--=-∑是否收敛？若收敛, 是绝对收敛还是条件收敛？113．求幂级数1(1)nn n ∞-=-∑. 114．求幂级数234234x x x x -+-+⋅⋅⋅的收敛半径和收敛区间.115．求幂级数1nn n x n∞=∑的收敛半径和收敛区间.116．将1()2f x x =+展成x 的幂级数, 并写出展开式成立的区间.117．将f (x )=x 3e -x 展成x 的幂级数, 并写出展开式成立的区间.118．将1()2f x x=+展开为(x -1)的幂级数, 并写出展开式成立的区间.119．将1()4f x x=-展开为(x -2)的幂级数, 并写出展开式成立的区间.120．求函数f (x , y )=2x +2y -x 2-y 2的极值. 121．求函数f (x , y )=3x +2y -x 3-y 2的极值.122．求函数f (x , y )=x 2+5y 2-6x +10y +6的极值. 123．求函数f (x , y )=y 3-x 2+6x -12y +5的极值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学生数 122印数 130 考核方式 闭卷 考核时间 120 分钟
答案写在试卷上，否则无效！
一.填空题：（每空2分，共12分）
1. 数列n u 收敛的必要条件是。
2. 1=x 是函数 的 间断点。
3.3
512lim 22++-∞→x x x x =。
4. 设⎩
⎨⎧-=-=t y t t x cos 1sin ，dx dy =。
5. 设dy x y ,2arcsin ==。
6. 函数7186223---=x x x y 的单调递增区间为。
二．求下列函数的极限（每小题5分，共15分）。
（1） （2）
（3）
三. 求下列函数的导数（每小题5分，共10分）。
（1）2tan x y =，求'y (2))0(sin >=x x y x ,求'y
四．计算下列不定积分（每小题5分，共20分）。
（1）xdx x ⎰28sec tan （2）
x e x x 1lim 30-→x x x 11lim 0-+→x
x x x 21lim ⎪⎭⎫ ⎝⎛+∞→dx
x x ⎰--2112
（3）dx e x ⎰ （4）⎰xdx arcsin
五．计算下列定积分（每小题5分，共15分）。
（1）xdx x cos sin 203⎰π
（2）dx x
x ⎰
--122
（3）dx xe x ⎰-10
六．求函数242x x y +-=的极值（8分）。
七．求曲线53523++-=x x x y 的拐点和凹凸区间（10分）。
1
y
=与直线2
y所围成的图形的面积（10分）。
x
=x
,=
八．求由曲线
x。