华东师大版数学七年级下册第九章多边形单元测试4

合集下载

华东师大版七年级数学下册第九章《多边形》单元达标检测卷(含答案)

ＭＡＣＥＢＤ华东师大版七年级数学下册第九章《多边形》单元达标检测卷时间:120分钟总分:120分一你的数学风采，在于你的合理选择（每题3分，共30分）1. 如图ABC △中，BC 边上的高是（）Ａ．AD Ｂ．BE Ｃ．CF Ｄ．以上都不对2．三角形中，最大角α的取值范围是（）A ．0°＜α＜90°B ．60°＜α＜180°C ．60°≤α＜90°D ．60°≤α＜180°3．在ABC △中，如果2:1:1::=∠∠∠C B A ，那么它是（）Ａ．钝角三角形Ｂ．锐角三角形Ｃ．直角三角形Ｄ．等边三角形4．如图1，下列关系一定成立的是（）Ａ．AEB DBC >∠∠ Ｂ．ADB BED >∠∠Ｃ．AE AB BC +> Ｄ．C ABE <∠∠5．已知等腰三角形的两边长是4和10，则它的周长是（）Ａ．18 Ｂ．24 Ｃ．18或24 Ｄ．146．以长为3cm ，5cm ，7cm ，10cm 的四条线段中的三条线段为边，可以构成三角形的个数是（）Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个 7. 如图，AB CD ∥，38A ∠=o ，80C ∠=o ，那么M ∠等于（）Ａ．52o Ｂ．42o Ｃ．10o Ｄ．40o8. 如果一个多边形的内角和是外角和的1.5倍，那么这个多边形的边数是（）Ａ．5 Ｂ．6 Ｃ．7 Ｄ．89. 有下列图形：①直角三角形；②梯形；③任意四边形；④五边形；⑤正七边形；⑥正九边形，其中能够铺满地面的图形有（）Ａ．2个Ｂ．3个Ｃ．4个Ｄ．6个10.用一块等边三角形的硬纸片（如图1）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图2），在△ABC 的每个顶点处各需剪掉一个四边形，其中四边形AMDN 中，MDN ∠的度数为（）Ａ．100o Ｂ．110oＣ．120o Ｄ．130o二用你敏锐的思维，写出简洁的结果（每题3分，共30分）BD M N C 图1 图21 2 Ａ第15题图A B 11. 一个等腰三角形中角平分线、高线和中线的总数最多的是条．12. 如图，11352125∠=∠=o o ，，则A ∠= ． 13. 若13a a ++，，5是三角形的三边，则a 的取值范围是． 14. n 边形与m 边形内角和度数的差为︒720，则n 与m 的差为___________.15.如图，一花坛的形状是正六边形(设其为六边形ABCDEF )，管理员从BC 边上的一点H 出发，沿HC →CE →EF →FG →GA →AB →BH 的方向走了一圈回到H 处，则管理员从出发到回到原处在途中身体转过了_________度.16．如图，是用形状、大小完全相同的等腰梯形密铺成的图案，则这个图案中的等腰梯形的底角（指钝角）是度．17. 如图，一扇窗户打开后，用窗钩AB 可以将其固定，这样做的数学根据是_______.18.小明同学在计算多边形的内角和时，将一个多边形的内角和误求为1125°，他检查时，发现计算时少算了一个内角，则这个多边形是________边形.19.能与正三角形组合在一起进行密铺的正多边形有______________(至少写出3个).20．如图2，用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是__________2cm 三圆满的解答，是你萌动的智慧(每题10分,共60分)21．某农场有一块三角形土地，准备分成面积相等的4块，分别承包给4位农户，请你设计两种不同的分配方案（在已给的图形中直接画图，保留画图痕迹，不写画法）第16题图第17题AB C A B C22．小明和小亮分别利用图11中（1），（2）的不同方法求出了五边形的内角和都是540o．请你考虑在图（3）中再用另外一种方法求五边形的内角和，并写出求解的过程．23.如图，某长方形广场的四角都有一块半径相同的四分之一圆形的草地，若圆形的半径为r 米，长方形长为a 米，宽为b 米．（１）请用代数式表示空地的面积．（２）若长方形长为300米，宽为200米，圆形的半径为10米，求广场空地的面积（计算结果保留）图11 （3）（1）（2）24.如图，在△ABC 中，∠B=60°，∠BAC=50°，AD 平分∠BAC ，D 点在BC 上，求∠1、∠2的度数。

2020-2021学年七年级数学华东师大版下册习题课件第九章单元复习(四) 多边形

2
2
1∠ACD－1∠ABC ＝1(∠ACD－∠ABC)＝1∠A，即∠BEC ＝1∠BAC
2
2
2
2
2
(4)在(3)的条件下，若CE∥AB，求∠ACB的度数．
因为CE∥AB，所以∠A＝∠ACE＝50°，因为CE平分 ∠ACD，所以∠ACD＝100°，所以∠ACB＝180°－ 100＝80°
第9章多边形
二、不能准确作出三角形的高【例2】数学课上，同学们在练习画△ABC中AC边上的高时，有一部分同学画出如图所示四种图形，请你判断一下，正确的是( C )
分析：因没有理解三角形高的定义，认为AC边上的高要经过A点，并且要与AC 垂直，结果出现错误．
【对应训练】
2．如图，AC⊥BC，CD⊥AB，DE⊥BC，下列说法错误的是( C )
8．若三角形的两边长分别为7 cm和10 cm，则第三边的取值范围是多少？如果第三边的取值是正整数，那么所取的边长有没有可能围成一个等腰三角形，此时的三角形腰长应为多少？
因为此三角形的两边长分别为7 cm和10 cm，所以第三边长的取值范围是：10 －7＝3＜第三边＜10＋7＝17.因为第三边为整数，所以第三边可以为：4，5 ，6，7，8，9，10，11，12，13，14，15，16，所以第三边长为7 cm或10 cm 时，为等腰三角形，腰长为7 cm或10 cm
2
x＝4，
(2)若 x＋1y＝9，解得 y＝10.
2
因为 4＋10＞10，能构成三角形，所以此种情况成立．答：这个等腰三角形的底边长为 4 cm，
腰长为 10 cm
17．小刚准备用一段长50米的篱笆围成一个三角形形状的场地，用于饲养鸡，
已知第一条边长为m米，由于条件限制第二条边长只能比第一条边长的3倍少2

【完整版】华师大版七年级下册数学第9章多边形含答案

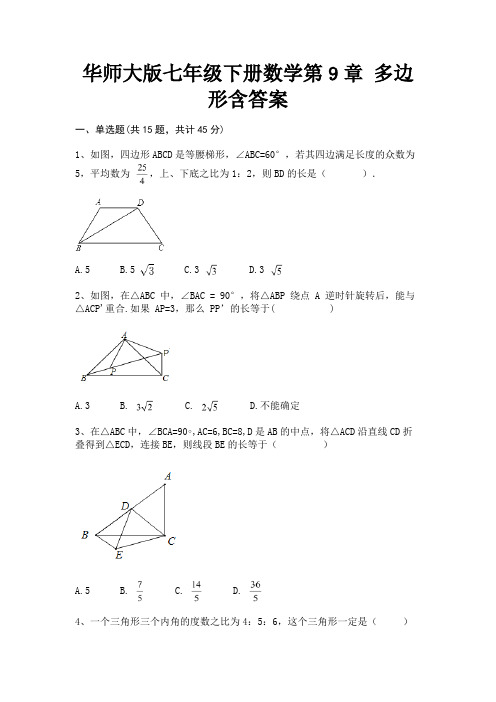
华师大版七年级下册数学第9章多边形含答案一、单选题(共15题，共计45分)1、如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为，上、下底之比为1：2，则BD的长是（）．A.5B.5C.3D.32、如图，在△ABC 中，∠BAC = 90°，将△ABP 绕点 A 逆时针旋转后，能与△ACP'重合.如果 AP=3，那么PP’的长等于( )A.3B.C.D.不能确定3、在△ABC中，∠BCA=90∘,AC=6,BC=8,D是AB的中点，将△ACD沿直线CD折叠得到△ECD，连接BE，则线段BE的长等于（）A.5B.C.D.4、一个三角形三个内角的度数之比为4：5：6，这个三角形一定是（）A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形5、如果一个正多边形的中心角等于，那么这个多边形的内角和为（）A. B. C. D.6、在△ABC中，∠A=70°，∠B=55°，则△ABC是（）A.钝角三角形B.等腰三角形C.等边三角形D.等腰直角三角形7、如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB 为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（）A.∠1＝∠2＋∠AB.∠1＝2∠A＋∠2C.∠1＝2∠2＋2∠A D.2∠1＝∠2＋∠A8、如图，OP＝1，过点P作PP1⊥OP，且PP1＝1，得OP1＝；再过点P1作P 1P2⊥OP1且P1P2＝1，得OP2＝；又过点P2作P2P3⊥OP2且P2P3＝1，得OP3＝2……依此法继续作下去，得OP2018的值为（）A. B. C. D.9、如图，内接于，，过点A作平行于，交的延长线于点D，则的度数（）A. B. C. D.10、如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为，上、下底之比为1：2，则BD的长是（）．A.5B.5C.3D.311、如图，四边形ABCD是等腰梯形，∠ABC=60°，若其四边满足长度的众数为5，平均数为，上、下底之比为1：2，则BD的长是（）．A.5B.5C.3D.312、三角形两边的长分别是 8 和 6，第三边的长是方程 x2﹣12x+20＝0 的一个实数根，则三角形的外接圆半径是( )A.4B.5C.6D.813、如图，四边形中，，，，点，分别为线段，上的动点（含端点，但点不与点重合），点，分别为，的中点，则长度的最大值为A.8B.6C.4D.514、如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB 为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（）A.∠1＝∠2＋∠AB.∠1＝2∠A＋∠2C.∠1＝2∠2＋2∠A D.2∠1＝∠2＋∠A15、如图所示，在△ABC中，AB=AC，DE垂直平分腰AB，若AC=CD，AB∥CD，则∠A的度数为（）A.36°B.72°C.120°D.44°二、填空题(共10题，共计30分)16、如图，等边△ABC中，BC＝6，D、E分别在BC、AB上，且DE∥AC，MN是△BDE的中位线．将线段DE从BD＝2处开始向AC平移，当点D与点C重合时停止运动，则在运动过程中线段MN所扫过的区域面积为________．17、如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是________．18、如图，在平行四边形ABCD中，BE⊥AC，AC＝24，BE＝5，AD＝8，则两平行线AD与BC间的距离是________．19、如果三角形的两边长为2和6，第三边为偶数，那么三角形的周长为________．20、如图，等边△ABC中，BC＝6，D、E分别在BC、AB上，且DE∥AC，MN是△BDE的中位线．将线段DE从BD＝2处开始向AC平移，当点D与点C重合时停止运动，则在运动过程中线段MN所扫过的区域面积为________．21、如图，等边△ABC中，BC＝6，D、E分别在BC、AB上，且DE∥AC，MN是△BDE的中位线．将线段DE从BD＝2处开始向AC平移，当点D与点C重合时停止运动，则在运动过程中线段MN所扫过的区域面积为________．22、若一个多边形的内角和等于外角和，那么这个多边形的边数是________．23、一个n边形的内角和是900 ，那么n=________.24、在平面直角坐标系中，A（4，0），直线l：y=6与y轴交于点B，点P是直线l上点B右侧的动点，以AP为边在AP右侧作等腰Rt△APQ，∠APQ=90°，当点P的横坐标满足0≤x≤8，则点Q的运动路径长为________．25、如图.边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是________.三、解答题(共5题，共计25分)26、如图所示，已知∠A=48°，∠D=25°，FD⊥BC于E，求∠B的度数．27、如图，在△ABC中，AD⊥BC于D，AB=3，BD=2，DC=1，求AC的值．28、正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一实线上；②连结三个格点，使之构成直角三角形，小华在下边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在下面的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．29、一个等腰三角形的一个外角为150°，求这个等腰三角形的其中一个底角的度数．30、如图，在等边△ABC中，点P在△ABC内，点Q在△ABC外，B，P，Q三点在一条直线上，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试证明你的结论．参考答案一、单选题(共15题，共计45分)1、B2、B3、C4、C5、B6、B7、B8、D9、C10、B11、B12、B13、D14、B15、C二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、。

华东师大版七年级数学下册《第九章多边形》单元检测试题(含答案)

七年级数学下册第九章多边形单元检测试题姓名：__________班级：__________一、单项选择题〔共10题；共30分〕.△ABC中，∠B是∠A的2倍，∠C比∠A大20°，那么∠A等于()A.40°B.60C.80°D°.90°2.如图，在△ABC中，BC边上的高是〔〕A.CEB.ADC.CFD.AB3.假如一个正多边形的一个外角为30°，那么这个正多边形的边数是〔〕A.6B.11C.12D.184.〕如图，矩形 ABCD，一条直线将该矩形 ABCD切割成两个多边形，那么所得任一多边形内角和度数不行能是〔〕A.720°B.540°C.360°D.180°5.一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为〔〕A.5B.5或6C.5或7D.5或6或76.以下列图方格纸中的三角形是〔〕A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形7.如图，在△ABC中，E是BC上的一点，EC2BE D是AC的中点，设△ABC△ADF△BEF＝，点，，的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC＝12，那么S△ADF－S△BEF＝()A.1B.2C.3D.4,BD是AC边上的高，8.如图，在△ABC中，AB=AC,∠A=36那么∠DBC的度数是〔〕°°°°9.AD是△ABC的中线，BE是△ABD的中线，假定△ABC的面积为20，那么△ABE的面积为〔〕A.5B.10C.15D.1810.如图，那么∠A+∠B+∠C+∠D+∠E=〔〕度A.90B.180C.200D.360二、填空题〔共8题；共24分〕11.如图,在△ABC中,AB=AC,AD⊥BC于点D,假定AB=6,CD=4,那么△ABC的周长是________12.如图，墙上钉了根木条，小明想查验这根木条能否水平，他拿来一个以下列图的测平仪，再这个测平仪中，AB=AC,BC边的中点D处有一个重锤，小明建BC边与木条重合，察看此重锤能否经过A点，如经过A点，那么是水平的，此中的道理是________.113.三角形片ABC中，∠A=55°，∠B=75°，将片的一角折叠，使点C落在△ABC内〔如〕，∠1+∠2的度数________度．14.在△ABC中，AB=13cm，AC=20cm，BC上的高12cm，△ABC的面________cm2．15.在△ABC中，AB=AC=17，BC=16，AD⊥BC于点D，AD=________.16.假定一个四形的四个内角度数的比3∶4∶5∶6，个四形的四个内角的度数分________．17.假定+=0，以的等腰三角形的周.18.如，∠MON=30°，点A1,A2,A3,⋯在射ON上，点B1,B2,B3,⋯在射OM上，△A1B1A2,△A2B2A3,△A3B3A4,⋯均等三角形，假定OA1=2，△A5B5A6的________．三、计算题〔共4题；共24分〕19.如，假定∠B=28°，∠C=22°，∠A=60°，求∠BDC．20.如，AB⊥BC，DC⊥BC，假定∠DBC=45°，∠A=70°，求∠D，∠AED，∠BFE的度数．21.如，△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，∠AFD=152°，求∠A的度数．22.如所示，在△ABC中，D是BC上一点，∠1=∠2，∠3=∠4，∠BAC=78°，求∠DAC的度数．2（（（（（（（（（（（（（（四、解答题〔共4题；共34分〕（23.以下列图，AD，AE是三角形A BC的高和角均分线，∠B=36°，∠C=76°，求∠DAE的度数．（（（（（（（（（（（（24.如图，在△ABC中，BD是∠ABC的均分线，CD是外角∠ACE的均分线．求证：∠D=∠A．（（（（（（（（（（（（（〔1〕等腰三角形的一边长等于8cm，一边长等于9cm，求它的周长；〔2〕等腰三角形的一边长等于6cm，周（长等于28cm，求其余两边的长.（（（（（（（（（（（（26.如图，AD为△ABC的中线，BE为△ABD的中线．（1〕∠ABE=15°，∠BAD=40°，求∠BED的度数；（2〕作图：在△BED中作出BD边上的高EF；BE边上的高DG；3〔3〕假定△ABC的面积为40，BD=5，那么△BDE中BD边上的高EF为多少？假定BE=6，求△BED中BE边上的高DG为多少？答案分析局部一、单项选择题1.【答案】A2.【答案】B3.【答案】C4.【答案】A5.【答案】D6.【答案】A7.【答案】B 8.【答案】A 9.【答案】A 10.【答案】B二、填空题2021.等腰三角形底边上的中线与底边上的高相互重合13.100 14.126或66 15.15 16.60o，80o，100o，18.32．三、计算题19.解：以下列图：连接BC．∵∠A=60°，∴∠ABC+ACB=120°．∵∠B=28°，∠C=22°，∴∠DBC+∠DCB=70°．∴∠BDC=180°﹣70°=110°．20.解：∵DC⊥BC，∠DBC=45°，∴∠D=90°﹣∠DBC=90°﹣45°=45°；AB⊥BC，DC⊥BC，∴AB∥CD，∴∠AED=∠A=70°；在△DEF中，∠BFE=∠D+∠AED=45°+70°=115°．21.解：∵DF⊥BC，∴∠FDC=90°，∵∠AFD=152°，∴∠C=∠AFD﹣∠FDC=152°﹣90°=62°，4∵∠B=∠C，∴∠A=180°﹣∠B﹣∠C=180°﹣62°﹣62°=56°22.解：∠3=∠1+∠2，∠1=∠2，∴∠3=2∠1，∵∠3=∠4，∴∠4=2∠1，∴180°﹣4∠1+∠1=78°，解得，∠1=34°，∴∠DAC=78°﹣∠1=44°．四、解答题23.解：∵∠B=36°，∠C=76°∴∠BAC=68°∵AE均分∠BAC∴∠EAC=68°÷2=34°∵AD是高线∴∠DAC=90°-76°=14°∴∠DAE=∠EAC－∠DAC=34°－14°=20°24证明：依据三角形外角性质有∠3+∠4=∠1+∠2+∠A．由于BD、CD是∠ABC和∠ACE的均分线，因此∠1=∠2，∠3=∠4．进而2∠4=2∠1+∠A，即∠4=∠1+∠A①在△BCD中，∠4是一个外角，因此∠4=∠1+∠D，②由①、②即得∠D=∠A．25.〔1〕解：8cm是腰长时，三角形的三边分别为8cm、8cm、9cm，能构成三角形，周长=8+8+9=25cm，8cm是底边时，三角形的三边分别为8cm、9cm、9cm，能构成三角形，周长=8+9+9=26cm，综上所述，周长为25cm或26cm〔2〕解：6cm是腰长时，其余两边分别为6cm，16cm，6+6=12＜16，∴不可以构成三角形，6cm是底边时，腰长为〔28-6〕=11cm，三边分别为6cm、11cm、11cm，能构成三角形，因此，其余两边的长为11cm、11cm26.〔1〕解:∵∠BED是△ABE的外角，∴∠BED=∠ABE+∠BAD=15°+40°=55°2〕解:绘图以下：3〕解:∵AD为△ABC的中线，BE为△ABD的中线，∴△ABD的面积=△ABC的面积=20，△BDE的面积=△ABD的面积=10，BD·EF=10，×5EF=10，解得EF=4，BE·DG=10，×6DG=10，5华东师大版七年级数学下册《第九章多边形》单元检测试题(含答案) EF=6。

华师版七年级数学下册第九章多边形复习试题及答案全套.doc

最新华师版七年级数学下册第九章多边形复习试题及答案全套名师点金：本章主要内容是三角形及相关概念，三角形的分类，三角形的内角和与外角，多边形的内角和与外角和，常考的题型有选择题、填空题、解答题，更多的是渗透到其他内容之中，是各类考试命题的重要内容；本章的考点可概括为：四个概念，两个关系，四种思想.概念1:与三角形有关概念1.如图，(1)图中共有儿个三角形？请分别表示出来.(2)以ZAEC为内角的三角形有哪些？(3)以ZADC为内角的三角形有哪些？(4)以BD为边的三角形有哪些？概念2：三角形中主要线段2・如图，在厶ABC 中，ZBAC = 80°, AD丄BC 于点D, AE 平分ZDAC, ZB = 60°, 求ZDAE 的度数.(第2题)概念3：三角形的内角和与外角3. 如图，在AABC 中，ZA = 60°, ZB = 80°,则外角ZACD 的度数是（）4. 如图，已知 BD 是ZABC 的平分线，DE 〃BC 交 AB 于 E, ZA=45°, ZBDC = 60。

, 求ZDBC 和ZC 的度数.概念4：多边形的内角和与外角和5. 若一个多边形的内角和小于其外角和，则这个多边形的边数是（）A. 3 B ・ 4 C. 5 D. 66. 已知：如图，五边形ABCDE 中，AE 〃CD, ZA=121°, ZB=1O7°,求ZC 的度数.澳口考玄2两个关系关系1:三角形的三边关系7. 已知ZiABC 的三边长分别为a, b, c,且|b+c-2a| + （b+c-5）2 = 0,求b 的取值范关系2：多边形的内角和与边数之间的关系8. 有一个多边形，除去一个内角外，其余内角之和是2 570°,求这个内角的度数.［熱口考点3四种思想A. 110°B. 120°C. 130°（第6题）思想1:方程思想9.如图，在AABC中，ZA=|ZC=|ZABC, BD是角平分线，求ZA及ZBDC的度数.（第9题）思想2：分类讨论思想10.用一条长为36 c加的细绳围成一个等腰三角形，能围成一个有一边长为8亡加的等腰三角形吗？为什么？11.在AABC中，AB = AC, AC边上的中线BD把AABC的周长分为24和18两部分, 求AABC的三边长.思想3：转化思想12.如图，试说明：ZA+ZB+ZC+ZD+ZE=180°.思想4：从特殊到一般的思想13. 已知在AABC 屮，ZA=100°.⑴若ZABC, ZACB 的平分线相交于点0,如图①所示，试求ZB0C 的度数；（2）若ZABC, ZACB 的三等分线（即将一个角平均分成三份的射线）分别相交于点0,0】，如图②所示，试求ZB0C 的度数；（3）以此类推，若ZABC, ZACB 的n 等分线自下而上依次相交于点0, Oi ，02,…，如图③所示，试探究ZBOC 的大小与n 的关系，并判断当ZBOC=170°吋，是几等分线相交所成的角. 答案专训1. 解：（1）图中有 8 个三角形，分别是厶ABC, AABD, AAEO, AAEC, AADC, AAOC, AODC, AEBC.(2) 以ZAEC 为内角的三角形有△ AEO, AAEC.(3) 以ZADC 为内角的三角形有AADC, AODC.(4) 以BD 为边的三角形只有AABD.点拨：用字母表示一个三角形时，不要漏写符号“△” •2・解：因为AD 丄BC,所以ZBDA = 90°.因为ZB = 60°,所以ZBAD =180°-90°一60。

华师大版数学七年级下册第9章多边形单元测试卷(含解析)

初中数学华师大版七年级下学期第9章测试卷一、单选题1.若一个三角形的两边长分别为4和8，则第三边长可以是( )A. 4B. 12C. 13D. 102.如图所示，在△ABC中，D为AB上一点，E为BC上一点，且AC = CD = BD = BE，∠A = 50°，则∠CDE的度数为（）A. 50°B. 51°C. 51.5°D. 52.5°3.如图，是等边三角形，是等腰直角三角形，，连接BD，则的度数为（）A. B. C. D.4.如果在中，，则等于（）A. B. C. D.5.下列长度的三根小木棒能构成三角形的是（）A. 1cm，2 cm，3 cmB. 2 cm，4 cm，6 cmC. 3 cm，4 cm，8 cmD. 6 cm，8 cm，10 cm6.已知一个等腰三角形两内角的度数之比为，则这个等腰三角形顶角的度数为（）A. B. C. 或 D.7.用下列边长相同的正多边形组合，能够铺满地面不留缝隙的是（）A. 正八边形和正三角形B. 正五边形和正八边形C. 正六边形和正三角形D. 正六边形和正五边形8.如图所示的图形中，能够用一个图形镶嵌整个平面的有（）个A. 1B. 2C. 3D. 4二、填空题9.已知△ABC的两条边长分别为2和5，则第三边c的取值范围是________.10.如果小明沿着坡度为的山坡向上走了130米，那么他的高度上升了________米．11.一个多边形的每个外角都等于72°，则这个多边形的边数为________.12.在数学活动课中我们学习过平面镶嵌.若给出下面一些边长均为1的正三角形、正大边形卡片。

要求必须同时使用这两种卡片，不重叠、无继隙，围绕某一个顶点拼在一起，成一个平面图案，则共拼出________种不同的图案：其中所拼的图案中最大的周长为________.三、综合题13.如图，在中，，，是边上的高，是边延长线上一点.求：（1）的度数；（2）的度数.14.在一个各内角都相等的多边形中，每一个内角都比相邻的外角的3倍还大20°．（1）求这个多边形的边数．（2）求这个多边形的内角和及对角线的条数．答案解析部分一、单选题1.【答案】D解：由题意可得：4=8-4<第三边长<4+8=12，观察选项可得：10可以为第三边长.故答案为：D.2.【答案】D解：∵AC=CD，∠A=50°，∴∠CDA=∠A=50°.∵CD=BD，∴∠B=∠DCB=∠CDA=×50°=25°.∵BD=BE，∴∠BDE=∠BED==77.5°.∵∠CDB=180°-∠CDA=180°-50°=130°，∴∠CDE=∠CDB-∠BDE=130°-77.5°=52.5°.故答案为：D.3.【答案】B解：是等边三角形，是等腰直角三角形，，，，，，，.故答案为：B.4.【答案】C解：，，三角形的内角和为. 故答案为：C.5.【答案】D解：A、∵1+2=3，∴这三根小木棒不能构成三角形，故A不符合题意；B、∵2+4=6，∴这三根小木棒不能构成三角形，故B不符合题意；C、∵3+4=7＜8，∴这三根小木棒不能构成三角形，故C不符合题意；D、∵6+8=14＞10，∴这三根小木棒能构成三角形，故D符合题意；故答案为：D.6.【答案】C解：设两内角的度数为x、4x；当等腰三角形的顶角为x时，x+4x+4x=180°，x=20°；当等腰三角形的顶角为4x时，4x+x+x=180°，x=30°，4x=120°；因此等腰三角形的顶角度数为20°或120°．故答案为：C．7.【答案】C解：A、正八边形的每个内角为：180°-360°÷8=135°，正三角形的每个内角60°，135m+60n=360°，n=6- m，显然m取任何正整数时，n不能得正整数，故不能铺满；B、正五边形每个内角是180°-360°÷5=108°，正八边形的每个内角为：180°-360°÷8=135°，108m+135n=360°，m取任何正整数时，n不能得正整数，故不能铺满；C、正六边形的每个内角是120°，正三角形的每个内角是60°，∵ 2×120°+2×60°=360°，或120°+4×60°=360°，能铺满；D、正六边形的每个内角是120°，正五边形每个内角是180°-360°÷5=108°，120m+108n=360°，m取任何正整数时，n不能得正整数，故不能铺满.故答案为：C.8.【答案】C解：等腰三角形的内角和是180°，能被360°整除，放在同一顶点处能够用一种图形镶嵌整个平面；四边形的内角和是360°，能被360°整除，放在同一顶点处能够用一种图形镶嵌整个平面；正六边形的每个内角是120°，能被360°整除，能够用一种图形镶嵌整个平面；正五边形的每个内角是108°，不能被360°整除，放在同一顶点处不能够用一种图形镶嵌整个平面；圆不能够用一种图形镶嵌整个平面；综上所述，能够用一种图形镶嵌整个平面的有3个．故答案为：C．二、填空题9.【答案】3＜c＜7解：由题意，得5﹣2＜c＜5+2，即3＜c＜7.故答案为：3＜c＜7.10.【答案】解：设高度上升了h，则水平前进了2.4h，由勾股定理得：，解得h=50．故答案为50．11.【答案】五解：由一个多边形的每个外角都等于72°，可得：多边形的边数为：，故答案为：五.12.【答案】3；10解：正六边形每个内角为120°，正三角形每个内角为60°。

2019-七年级数学下学期第九章多边形单元测试题华东师大版

2019-2020 年七年级数学下学期第九章多边形单元测试题华东师大版一、填空题（ 20 分）1、三角形三个内角的比为1： 3： 5，则最大的内角是 __100 度2、如图 1所示，写出1、2、 3000的度数为 1 _____ , 2 _____ , 3____ .3、如图2，在 ABC 中，ABC C, BD均分ABC ，若是A360，那么ADB_____ .04、按图 3所示的条件，则BAE ____ 0 , CBD_____ 0 .5、两根木棒的长分别为 3cm 和 5cm ，要选择第三根木棒，将它钉成一个三角形，若第三根木棒的长为偶数，则第三根木棒的长是_____ cm.6、若等腰三角形的两边长分别是3cm 和 7cm；则这个三角形的周长是_____ cm.7、工人师傅在做完门框后．为防小变形常常像图 4 中所示的那样上两条斜拉的木条（即图 4 中的 AB， CD两根木条），这样做依照的数学道理是 _____.8、如图 5，依照题中条件，则 1 _____ 0 , 2 ____ 0.9、图 6 是三个完好相同的正多边形拼成的无缝隙、不重叠的图形的一部分，这种多边形是正 _____边形10 、若一个多边形的每一个内角都等于1350，则这个多边形是____边形，它的内角和等于 ____.二、选择题（30 分）1 、如图 7， AC BC， CD正确的选项是（）A 、 AC是ABC的高C 、 DE是ABE的高AB， DE BC，分别交B、 DE是D、 AD是BC， AB， BC于BCD的高ACD的高C， D， E：以下说法中不2、如图 8， BE， CF是ABC的角均分线， A 65 0那么BOC等于（）A、0B、0C、0 D 、11503、三角形三条高的交点必然在（）A、三角形的内部B、三角形的外面C、三角形的内部或外面．D、三角形的内部、外面或极点4、适合条件 A B 1C 的ABC是（）2A 、锐角三角形B、直角三角形C、钝角三角形D、不能够确定5、 D 、 E 是△ ABC的边 AB、 AC上一点，把△ ABC沿 DE 折叠，当点 A 落在四边形 BCED内部时，如图（ 10）。

华师大七级数学下第九章《多边形》单元试题含答案

七年级数学下册第九章《多边形》单元测试题一．选择题（每小题3分，共30分）1．一个三角形的内角中，至少有（）A、一个锐角B、两个锐角C 、一个钝角D、一个直角2．三角形中，最大角α的取值范围是（）A、0°＜α＜90°B、60°＜α＜180°C、60°≤α＜90°D、60°≤α＜180°3．下列长度的各组线段中，能作为一个三角形三边的是（）A、1、2、3B、2、4、4、C、2、2、4D、a, 11 (a是自然数)4．已知4条线段的长度分别为2、3、4、5，若三条线段可以组成一个三角形，则这四条线段可以组成( ）个三角形A、1 B、2 C、3 D、45．已知a>b>c>0，则以a、b、c为三边组成三角形的条件是（）A、>aB、>bC、>cD、以上都不对6．下列正多边形的组合中，能够铺满地面不留缝隙的是（）A、正八边形和正三角形；B、正五边形和正八边形；C、正六边形和正三角形；D、正六边形和正五边形7．如果三角形的一个外角小于与它相邻的内角，那么这个三角形一定是（）A、锐角三角形B、直角三角形C、钝角三角形D、任意三角形8．下面的说法正确的是（）A．三角形的角平分线、中线和高都在三角形内B．直角三角形的高只有一条C．三角形的高至少有一条在三角形内D．钝角三角形的三条高都在三角形外那么9．如果一个多边形的边数增加1倍，它的内角和是2160 o，那么原来多边形的边数是（）A、5B、6C、7D、810．用一种正多边形能进行平面图形铺设的条件是（）A、内角都是整数度数B、边数是3的整数倍C、内角整除360oD、内角整除180o二．填空题（每空2分，共34分）11．n边形有一个外角是600，其它各外角都是750,则。

12. 从n边形一个顶点出发共可作5条对角线，则这个n边形的内角和=13．n边形的内角和与外角和相等，则14．三角形中，∠B和∠C的平分线交于O，若∠400，则∠15．用同一种正多边形能铺满地面的有；能够铺满地面的任意多边形有，。

华东师大版七年级数学下册第九章多边形单元测试题含答案

华东师大版七年级数学下册第九章多边形单元测试一、选择题(本大题共8小题，每小题3分，共24分；在每小题给出的四个选项中，只有一项符合题意)1．下列各组线段中，能组成三角形的是()A．a＝3 cm，b＝8 cm，c＝5 cmB．a＝5 cm，b＝5 cm，c＝10 cmC．a＝12 cm，b＝5 cm，c＝6 cmD．a＝15 cm，b＝10 cm，c＝7 cm2．下列说法正确的是()A．所有的等腰三角形都是锐角三角形B．等边三角形属于等腰三角形C．不存在既是钝角三角形又是等腰三角形的三角形D．一个三角形里有两个锐角，则一定是锐角三角形图13．如图1，若∠1＝100°，∠C＝70°，则∠A的度数是()A．10°B．20°C．30°D．80°4．在△ABC中，AD是BC边上的中线，下列五种说法：①AD把∠BAC分成相等的两部分；②AD 将线段BC分成相等的两部分；③AD把△ABC分成形状相同的两个三角形；④AD把△ABC分成周长相等的两个三角形；⑤AD把△ABC分成面积相等的两个三角形．其中正确的说法有() A．2个B．3个C．4个D．5个5．在△ABC中，若∠B是∠A的2倍，∠C比∠A大20°，则∠A等于()A．40°B．60°C．80°D．90°6．如图2中三角形的个数是()图2A．6 B．7 C．8 D．97．已知三角形两边的长分别是6和12，则此三角形第三边的长可能是()A．5 B．6 C．12 D．198．若一个正多边形的一个外角是45°，则这个正多边形的边数是()A．10 B．9 C．8 D．6二、填空题(本大题共10题，每小题4分，共40分)9．一个多边形的内角和是它的外角和的4倍，则这个多边形的边数为________．10．已知△ABC的三边长为a，b，c，化简|a＋b－c|－|b－a－c|－|2b|的结果是________．11．如图3，自行车的三角形支架利用的是三角形的________．图3 图412．如图4，直线AB，CD被BC所截，若AB∥CD，∠1＝45°，∠2＝35°，则∠3＝________°.13．如图5，在△ABC中，AD是BC边上的中线，若AB＝6 cm，AC＝4 cm，则△ABD和△ACD 的周长之差为________．图5 图614．如图6，在△ABC中，P是△ABC三个内角平分线的交点，则∠PBC＋∠PCA＋∠P AB＝________度．图715．如图7，直角三角形ABC的两条直角边AC，BC分别经过正九边形的两个顶点，则图中∠1＋∠2的度数是________．16．若等腰三角形的周长为16，其一边长为6，则另外两边长为________．17．用边长相等的正三角形和正六边形地砖拼地板，在每个顶点周围有a块正三角形和b块正六边形的地砖(ab≠0)，则a－b的值为________．18．如图8，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线相交于点A1，得∠A1；∠A1BC 和∠A1CD的平分线相交于点A2，得∠A2；…；∠A2018BC和∠A2018CD的平分线交于点A2019，则∠A2019＝________度．图8三、解答题(本大题共3小题，共36分)19．(10分)用两种方法证明“三角形的外角和等于360°”．已知：如图9，∠BAE，∠CBF，∠ACD是△ABC的三个外角．求证：∠BAE＋∠CBF＋∠ACD＝360°.证法1：∵________________________________________________________________，∴∠BAE＋∠1＋∠CBF＋∠2＋∠ACD＋∠3＝180°×3＝540°，∴∠BAE＋∠CBF＋∠ACD＝540°－(∠1＋∠2＋∠3)．∵______________，∴∠BAE＋∠CBF＋∠ACD＝540°－180°＝360°.请把证法1补充完整，并用不同的方法完成证法2.图920．(12分)如图10，在△ABC中，BD是角平分线，CE是高，且∠ACB＝60°，∠ADB＝97°，求∠A和∠ACE的度数．图1021．(14分)如图11，在△ABC中，点E在AC上，∠AEB＝∠ABC.(1)图①中，作∠BAC的平分线AD，分别交CB，BE于D，F两点，求证：∠EFD＝∠ADC；(2)图②中，作△ABC的外角∠BAG的平分线AD，分别交CB，BE的延长线于D，F两点，试探究(1)中的结论是否仍成立？为什么？图11教师详解详析1．[解析] D根据三角形三边的关系：任意两边之和大于第三边．2．[解析] B等腰三角形的顶角可以是钝角，因此等腰三角形可以是钝角三角形；等边三角形属于等腰三角形，内角为30°，30°，120°的三角形既是钝角三角形又是等腰三角形；有三个内角是锐角的三角形才是锐角三角形．3．[解析] C根据三角形外角的性质知∠1＝∠A＋∠C，∴100°＝∠A＋70°，∴∠A＝30°.4．[解析] A D只是BC的中点，不平分角，故①错误；②正确；AD把△ABC分成的两个三角形的形状不一定相同，故③错误；AD把△ABC分成的两个三角形的周长不一定相等，面积相等，故④错误，⑤正确．5．[解析] A由题意得∠B＝2∠A，∠C＝∠A＋20°，所以∠A＋∠B＋∠C＝∠A＋2∠A＋∠A ＋20°＝180°，解得∠A＝40°.6．[解析] C确定两个顶点，找第三个顶点，比如：确定A，B，可找F，D，确定A，E，可找C，D，确定B，E，可找D，确定A，F，可找D，确定A，C，可找D，确定F，C，可找D.7．[答案] C8．[答案] C9．[答案] 10[解析] 设这个多边形的边数为n，根据题意，得(n－2)×180°＝360°×4，解得n＝10.10．[答案] －2c[解析] 根据三角形的三边关系得a＋b>c，a＋c>b，∴|a＋b－c|－|b－a－c|－|2b|＝|a＋b－c|－|b－(a ＋c)|－|2b|＝a＋b－c－(a＋c－b)－2b＝a＋b－c－a－c＋b－2b＝－2c.11．[答案] 稳定性12．[答案] 8013．[答案] 2 cm[解析] 根据三角形中线的定义可得BD＝CD，△ABD和△ACD的周长的差就是AB和AC的差，计算即可．14．[答案] 90[解析] 因为P是△ABC三个内角平分线的交点，所以∠PBC＋∠PCA＋∠PAB的和是三角形内角和的一半．15．[答案] 190°[解析] 如图，正九边形的一个内角为（9－2）×180°9＝140°，∠3＋∠4＝90°，两个正九边形的内角减去∠3＋∠4即得∠1＋∠2＝280°－90°＝190°.16．[答案] 6，4或5，5[解析] 当腰长是6时，则另外两边长是4，6，4＋6>6，满足三边关系定理；当底边长是6时，另外两边长是5，5，5＋5>6，满足三边关系定理，故该等腰三角形的另外两边长为6，4或5，5.17．[答案] 0或318．[答案]m22019 [解析] 利用角平分线性质、三角形外角性质，易证∠A 1＝12∠A ，进而可求∠A 1，由于∠A 1＝12∠A ，∠A 2＝12∠A 1＝122∠A ，…，以此类推，可知∠A 2019＝122019∠A.19．解：∠BAE ＋∠1＝∠CBF ＋∠2＝∠ACD ＋∠3＝180° ∠1＋∠2＋∠3＝180° 证法2：如图，过点A 作射线AP ，使AP ∥BD.∵AP ∥BD ，∴∠CBF ＝∠PAB ，∠ACD ＝∠EAP. ∵∠BAE ＋∠PAB ＋∠EAP ＝360°， ∴∠BAE ＋∠CBF ＋∠ACD ＝360°. 20．解：∵∠ADB ＝∠DBC ＋∠ACB ，∴∠DBC ＝∠ADB －∠ACB ＝97°－60°＝37°. ∵BD 是角平分线，∴∠ABC ＝74°， ∴∠A ＝180°－∠ABC －∠ACB ＝46°. ∵CE 是高，∴∠AEC ＝90°， ∴∠ACE ＝90°－∠A ＝44°.21．解：(1)证明：∵AD 平分∠BAC ， ∴∠BAD ＝∠DAC.∵∠EFD ＝∠DAC ＋∠AEB ，∠ADC ＝∠ABC ＋∠BAD ，∠AEB ＝∠ABC ， ∴∠EFD ＝∠ADC.(2)(1)中的结论仍成立．理由：∵AD 平分∠BAG ， ∴∠BAD ＝∠GAD. ∵∠FAE ＝∠GAD ， ∴∠FAE ＝∠BAD.∵∠EFD ＝∠AEB －∠FAE ，∠ADC ＝∠ABC －∠BAD ，∠AEB ＝∠ABC ， ∴∠EFD ＝∠ADC.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A．3 次以上 B．3 次 C．2 次 D．1 次 3．如图（2），在大房间一面墙壁上，边长 15cm 的正六边形 A（如图（1））横排 20 片和以其一部分所形成的梯形 B，三角形 C、D 上，菱形 F 等六种瓷砖毫无空隙地排列在一起．已知墙壁高 3.3m，请你仔细观察各层瓷砖的排列特点，计算其中菱形 F 瓷砖需使用（）
A．220 片 B．200 片 C．180 片 D．190 片 4．已知四边形 ABCD 的对角线 AC 与 BD 相交于点 O，若 S△AOB=4，S△COD=9，则四边形 ABCD 的面积 S 四边形 ABCD 的最小值为（） A．21 B．25 C．26 D．36 5．为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里），则能把电力输送到这四个村庄的输电线路的最短总长度应该是（）
一次测量 AM（AD）即可得 AD，AM 长，即可算出 DM 长，由 = ，即可求出△ABC 的面积是△DBC 的面积的几倍．
多边形单元测试
考试范围：xxx；考试时间：100 分钟；命题人：xxx
学校：___________姓名：___________班级：___________考号：___________
题号
一
二
三
总分
得分
评卷人得分
一．选择题（共 10 小题） 1．边长都是整数的不等边三角形的最大边为 8，则满足条件的三角形的个数为（） A．7 B．8 C．9 D．10 2．如图，要判断△ABC 的面积是△DBC 的面积的几倍，只有一把仅有刻度的直尺，需要度量的次数最少是（）
度．
评卷人得分
三．解答题（共 6 小题）
15．已知，如图，在△ABC 中，∠B＜∠C，AD，AE 分别是△ABC 的高和角平分
线，
（1）若∠B=30°，∠C=50°．则∠DAE 的度数是
．（直接写出答案）
（2）写出∠DAE、∠B、∠C 的数量关系：
，并证明你的结论．
16．如图，已知 D 为△ABC 边 BC 延长线上一点，DF⊥AB 于 F 交 AC 于 E，∠A=30°， ∠D=40°，求∠ACD 的度数．
A．20° B．30° C．40° D．50°
评卷人得分
二．填空题（共 4 小题）
11．正六边形的每个内角等于
°．
12．如图，在△ABC 中，AD，BE 是两条中线，则 S△EDC：S△ABC=
．
13．已知一个多边形的内角和与外角和的差是 1260°，则这个多边形边数
是
．
14．如图，已知正五边形 ABCDE，AF∥CD，交 DB 的延长线于点 F，则∠DFA=
参考答案与试题解析
一．选择题（共 10 小题） 1．边长都是整数的不等边三角形的最大边为 8，则满足条件的三角形的个数为（） A．7 B．8 C．9 D．10 【分析】其余两边都小于 8，不相等，之和应大于 8，按规律找到适合的三边即可．【解答】解：设另两边是 x，y．则 x＜8，y＜8，x≠y 且 x+y＞8，并且 x，y 都是整数．不妨设 x＜y，满足以上几个条件的 x，y 的值有：2，7；3，6；3，7；4，5；4， 6；4，7；5，6；5，7；6，7 共有 9 种情况，因而满足条件的三角形的个数为 9 个．故选 C．
．
（3）若点 P 运动到边 AB 的延长线上，如图 3，则∠α、∠1、∠2 之间有何关系？
猜想并说明理由
19．如图，在△ABC 中，AD⊥BC，垂足为 D，AE 平分∠BAC，且∠ABC＞∠C．求证：∠DAE= （∠ABC﹣∠C）．
20．三角形不等式是指一个三角形的两边长度之和大于第三边的长度．在图中， E 位于线段 AC 上，D 位于线段 BE 上．（1）说明为什么 AB+AE＞DB+DE；（2）说明为什么 AB+AC＞DB+DC；（3）AB+BC+CA 与 2（DA+DB+DC），哪一个更大？证明你的答案；（4）AB+BC+CA 与 DA+DB+DC，哪一个更大？证明你的答案．
明理由．
18．△ABC 中，∠C=80°，点 D、E 分别是△ABC 边 AC、BC 上的点，点 P 是一动
点，令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．．
（1）若点 P 在边 AB 上，且∠α=50°，如图 1，则∠1+∠2=
；
（2）若点 P 在边 AB 上运动，如图 2 所示，则∠α、∠1、∠2 之间的关系为
A．19.5 B．20.5 C．21.5 D．25.5 6．用三块正多边形的木块铺地，拼在一起相交于一点的各边完全吻合，设它们的边数为 m、n、p，则（）
A．
B．
C．
D．
7．已知三角形的一个外角等于和它相邻的内角的 2 倍，且等于和它不相邻的一个内角的 4 倍，那么这个三角形是（） A．锐角三角形 B．直角三角形 C．钝角三角形 D．以上三种都有可能 8．如图，AE⊥BC 于 E，BF⊥AC 于 F，CD⊥AB 于 D，则△ABC 中 AC 边上的高是
17．（1）如图①，∠DCE=∠ECB=α，∠DAE=∠EAB=β，∠D=30°，∠B=40°
①用 α 或 β 表示∠CNA，∠MPA，∠CNA=
，∠MPA=
②求∠E 的大小．
（2）如图②，∠B，则∠E 与∠B，
∠D 之间是否存在某种等量关系？若存在，写出结论，说明理由；若不存在，说
2．如图，要判断△ABC 的面积是△DBC 的面积的几倍，只有一把仅有刻度的直尺，需要度量的次数最少是（）
A．3 次以上 B．3 次 C．2 次 D．1 次【分析】根据同底三角形的面积比等于高之比，即可得到答案．【解答】解：连接 AD 并延长交 BC 于 M，作 DF∥BC 交 AP 于点 F．
哪条垂线段（）
A．BF B．CD C．AE D．AF 9．如图，∠BAC=80°，BO、CO 分别平分∠ABC 和∠ACB，则∠BOC=（）
A．100°B．130°C．140°D．150° 10．如图，三角形 ABC 中，D 是 AB 上一点，E 是 AC 上一点，∠ADE=70°，∠B=70°， ∠AED=30°，则∠C 的度数是（）

华东师大版数学七年级下册第九章多边形单元测试4

最新华师大版七年级数学下册第9章多边形单元测试题及答案

华东师大版七年级数学下册 第九章《多边形》单元达标检测卷(含答案)

2020-2021学年七年级数学华东师大版下册习题课件 第九章 单元复习(四) 多边形

【完整版】华师大版七年级下册数学第9章 多边形含答案