第1章 非平衡态热力学2
合集下载
热力学第二定律
二. 熵（entropy）S
dQ T 0 R
1 R2 R1
2
存在一个与过程 无关的状态量
( 2)
p
d Q (1) d Q T T 0 (1) ( 2)
R1 R2
0
( 2)
V
d Q ( 2) d Q ( 2) d Q 令 S2 S1 S T T T (1) (1) (1) R1 R2 R —任意可逆过程 熵增(量)
10
二 . 不可逆过程是相互沟通的 热二律的 开氏表述
功全部转换成热而不产生其 它影响的过程是不可逆的
（否则热全部转换为功而不产生其它影响成立， 这就违背了热二律的开氏说法。） 热二律的 克氏说法 有限温差热传导不可逆
开氏、克氏 表述的等价
功、热转换 的不可逆性
热传导的 不可逆性
11
实际上，一切不可逆过程都是相互沟通的。 例如： 功变热而不产生其他影 响之不可逆（开氏表述） 可导出 证明： T
25
SCu
Q吸 mc(T1 T2 ) 水恒温吸热：S水 0 T2 T2 T1 T1 S总 S水 SCu mc( 1 ln ) 0（自己证） T2 T2
dT T2 mc mc ln 0 T T1 T1
T2
[例2] 已知： 1mol理气经绝热自由膨胀体积加倍
气体
气体自由膨 胀之不可逆
T
Q T
绝热壁
A=Q 等 价
Q
气体
A=Q
设气体能 气体 T 自动收缩 导致
循环，无变化
不成立 不成立 任何一种不可逆过程的表述，都可作为热力学第 二定律的表述！ 12
§4.4 卡诺定理（Carnot theorem）
工程热力学思考题答案,第一章
第一章基本概念与定义1。
闭口系与外界无物质交换，系统内质量保持恒定，那么系统内质量保持恒定的热力系一定是闭口系统吗? 答：不一定.稳定流动开口系统内质量也可以保持恒定.2.有人认为，开口系统中系统与外界有物质交换，而物质又与能量不可分割，所以开口系统不可能是绝热系。
对不对,为什么？答：这种说法是不对的。
工质在越过边界时,其热力学能也越过了边界。
但热力学能不是热量，只要系统和外界没有热量地交换就是绝热系。
3.平衡状态与稳定状态有何区别和联系,平衡状态与均匀状态有何区别和联系?答:只有在没有外界影响的条件下，工质的状态不随时间变化，这种状态称之为平衡状态。
稳定状态只要其工质的状态不随时间变化，就称之为稳定状态，不考虑是否在外界的影响下，这是他们的本质区别.平衡状态并非稳定状态之必要条件.物系内部各处的性质均匀一致的状态为均匀状态。
平衡状态不一定为均匀状态，均匀并非系统处于平衡状态之必要条件。
4。
倘使容器中气体的压力没有改变，试问安装在该容器上的压力表的读数会改变吗？绝对压力计算公式b e p p p =+()e p p >，b e p p p =-()e p p <中，当地大气压是否必定是环境大气压?答:压力表的读数可能会改变,根据压力仪表所处的环境压力的改变而改变.当地大气压不一定是环境大气压。
环境大气压是指压力仪表所处的环境的压力。
5.温度计测温的基本原理是什么?答：选作温度计的感应元件的物体应具备某种物理性质随物体的冷热程度不同有显著的变化。
有两个系统分别和第三个系统处于热平衡,则两个系统彼此必然处于热平衡。
6.经验温标的缺点是什么?为什么？答：任何一种经验温标不能作为度量温度的标准.由于经验温标依赖于测温物质的性质,当选用不同测温物质的温度计、采用不同的物理量作为温度的标志来测量温度时，除选定为基准点的温度，其他温度的测定值可能有微小的差异。
7。
促使系统状态变化的原因是什么?举例说明答：系统内部各部分之间的传热和位移或系统与外界之间的热量的交换与功的交换都是促使系统状态变。
热力学第二定律
若Tamb不变，则
∆S amb = −
Qsy Tamb
§3.4 熵变的计算
1.单纯PVT变化过程系统熵变的计算 由式 对定温过程
Q δ r dS = 出发 T δ r Qr Q ∆S = ∫ = T T
δQp＝ dH ＝nCp,mdT
（3-12）
(1) 液体或固体的 p,V,T 变化 ①定压变温
所以
得
− W Q1 + Q2 T1 − T2 = = Q1 Q1 T1
T1 {p} A(pA,VA,T1) • Q1 D• (pD,VD,T2) Q
B(pB,VB,T1) •
2
− W Q1 + Q2 T1 − T2 η= = = Q1 Q1 T1
(1-63）
T2
• C (pC,VC,T2) {V}
结论：理想气体卡诺热机的效 率η只与两个 热源的温度(T1，T2）有 关， 温差愈大，η愈大。
结论：自然界中发生的一切实际过程(指宏观过程，下同)都有 一定方向和限度。不可能自发按原过程逆向进行，即自然界中一切 自然界中一切 实际发生的过程都是不可逆的。 实际发生的过程都是不可逆的
2. 热力学第二定律的经典表述 克劳休斯说法：热不能自动从低温物体传递给高温物体，而 克劳休斯 不产生其他变化。 开尔文说法：不可能从单一热源吸热使之完全变为功，而不 开尔文 产生其他变化。 应明确：致冷机 ：低温物体 热Q传递 高温物体，但环境消 耗了能量(电能)； 理想气体可逆定温膨胀,系统从单一热源吸的热全转变为对环 境作的功，但系统的状态发生了变化(膨胀了)。 亦可以用“第二类永动机不能制成”来表述热力学第二定律。 热力学第二定律的实质是：自然界中一切实际进行的过程都是 热力学第二定律的实质是 不可逆的。
热统第一章1
二、气体的物态方程
1、理想气体的物态方程
FBC ( pB ,VB ; pC ,VC ) 0
则A与B必达到热平衡: FAB ( p A , VA ; pB , VB ) 0 喀喇氏温度定理（1909年）：处于热平衡状态 下的热力学系统，存在一个状态函数，对互为热平衡的 系统，该函数值相等。
A和C达到平衡
FAC ( pA ,VA ; pC ,VC ) 0
（2）系统处于平衡态时宏观性质不随时间变化，但组成
系统的大量粒子还在不停地运动着，只是这些运动的平
均效果不变而已。因此热力学平衡态又称热动平衡；
（3）处于平衡态的系统，其宏观性质会发生一些起伏变
化，叫涨落。一般宏观物质系统的涨落很小，在热力学
的范围内将其忽略不予考虑；
（4）弛豫时间的概念。
二、状态参量 1、状态参量：在力学中质点的运动状态用位移、
热力学· 统计物理
教材：汪志诚《热力学· 统计物理》 参考书：F.Mandl,Statistical Physics F.Reif, Fundamentals of Statistical and Thermal Physics K.Huang,Statistical Mechanics 吴大猷《热力学、气体运动论及统计力学》 林宗涵《热力学与统计物理学》
§1.1 热力学系统的平衡状态及其描述
一、平衡态 1.热力学系统：把研究的若干个物体看成一个整 体，即为系统。
外界：系统之外的所有物质称为外界
系统
孤立系统：系统与外界既无物质交换， 又无能量交换。 闭系：系统与外界有能量交换， 系统 但无物质交换。 开系：系统与外界既有物质交换， 又有能量交换。
（2）统计物理： 从物质的微观结构出发，考虑微观粒子的热运 动，讨论微观量与宏观量的关系，通过求统 计平均来研究宏观物体热性质与热现象有关 的一切规律。 优点：它可以把热力学的几个基本定律归结 于一个基本的统计原理，阐明了热力学定律 的统计意义； 缺点：可求特殊性质，但可靠性依赖于微观 结构的假设，计算较复杂。
热学 第一章 导论
我国殷商时期
五行学说：金、木、水、 火、土是构成世界万物的五种基本元素， 称为五行。中国古代提出的元气说，就认 为热（火） 是物质元气聚散变化的表现。
3
从钻木取火到商周的青铜器
伽利略温度计 16世纪 (明)
4
清 初
瓦特早期蒸汽机
5
6
1807年
嘉庆12年
7
1823年
道光3年
8
1892年
33
三、热力学温标 1. 热力学温标是建立在第二定律基 础上，不 依赖于任何物质的特性 的温标。 2. 热力学温度国际单位为“开尔 文”，简称开.记为K 3. 可证明在理想气体温标有效范围 内，热力学温标与理想气体温标 完全一致。 不依赖于测温物质和测温属性的温标
34
开尔文
四、摄氏温标、华氏温标与兰氏温标
V＝V0 1 p t
m，p一定
m,V 一定
22
p p0 1 V t
二、理想气体物态方程
p1V1 p2V2 常量 T1 T2
令1mol气体的常量为R
pVm RT R＝8.31 Jmol 1K 1
若气体的物质的量为
普适气体 常量
与热力学温度 的关系
T=T
通用 情况 国际 通用
热力学温度 K
摄氏温标 华氏温标
C F
t
tF - 459.67 0
32.00 32.02
t T 273 .15 100.00 0 C K t 9 T 459 .67 英美 212.00 0 F 5 K 等国
兰氏温标 R TR
491.67 491.69 67初步知识 • 液体、固体、相变等物性学
热力学 第一章
（3）状态参量：描述热力学系统平 衡状态的宏观性质的物理量。
描述系统状态的宏观参量一般可以 直接测量。
广延量和强度量
3、均匀系与非均匀系
（1）均匀系：一个系统各部分的性质完全
一致，称为一个均匀系。（也称为一个相 —单相系） （2）非均匀系：复相系
§1.2 热平衡定律和温度
一、热平衡定律（热力学第零定律） 实验
2 3 3 6 1
如果保持温度不变，将1mol的水从1 1000 pn ，求：外界所做的功。
pn
加压到
§1.5 热力学第一定律
一、热量：系统与外界仅由于温度差，通过边界 所传递的能量。（通过分子间的碰撞来实现）
Q 过程量 热量是能量传递的另一种方式 Q 0 系统从外界吸收热量
Q 0 系统向外界放出热量
3 6 2 3
1
§1.6 热容量和焓
一、热容量
1、引入：桶的装水量（水容量）
M 水容： C h
Q 电容： C U
2、热容量：一个系统在某一过程中温度升 高1K所吸收的热量。
Q C lim T T dQ C dT
单位：焦耳/开尔文 J / K
3、系统的质量对热容量的影响：
an2 ( p 2 )(V nb) nRT V
1mol : a ( p 2 )( v b) RT v
3、简单固体和液体：
V (T , p) V0 (T0 ,0)1 (T T0 ) KT p
例1、一个简单可压缩系统，已知
nR 1 a ; KT pV p V
作业：1、1mol理想气体，在27℃的恒温下 发生膨胀，其压强由 20Pn 准静态地降到 1Pn ，求：气体所做的功和所吸取的热量。 2、在27℃，压强在0至 1000pn 之间，测得 水的体积为V (18.066 0.71510 p 0.04610 p )cm mol 如果保持温度不变，将1mol的水从1 pn 加压至 1000pn ，求：外界所做的功。
热力学第二定律
五、热力学第二定律的统计意义
A
B
不可逆过程的初态和终态存在怎样的差别?
以气体自由膨胀为例，假设A中装有a、b、c、d
4个分子（用四种颜色标记）。开始时，4个分子都 在A部，抽出隔板后分子将向B部扩散并在整个容器 内无规则运动。
分布
详细分布
（宏观态） （微观态）
A4B0（宏观态） 微观态数 1
A3B1（宏观态） 微观态数4
六、熵的计算
为了正确计算熵变，必须注意以下几点：
1. 对于可逆过程熵变可用下式进行计算
S2
S1
12
dQ T
2. 如果过程是不可逆的不能直接应用上式。
由于熵是一个态函数，熵变和过程无关，可以
设计一个始末状态相同的可逆过程来代替，然后再
应用上式进行熵变的计算。
例6-11 今有1kg 0 ºC的冰熔化成0 ºC 的水，求其熵 变（设冰的熔解热为3.35105 J/kg)。
温馨 提示
1. 热一律给出了内能与其他形式的能量相互转化时， 总数量的守恒关系。热二律则指明了内能和其他 形式的能量相互转化时，自发进行的方向。
2. 热二律是从大量宏观事实中概括出来的，对有限 范围内的宏观过程适用，对少量粒子的微观体系 不适用。
3. 热力学第二定律的实质：一切与热现象有关的实 际宏观过程都是不可逆的。
微观态为6，几率最大为6/16。
若系统分子数为N，则总微观态数为2N，N个分
子自动退回A室的几率为1/2N。 1mol气体的分子自由膨胀后，所有分子退回到A
室的几率为 1 / 26.0231023 意味着此事件观察不到。
分子处于均匀分布的宏观态，相应的微观态出现 的几率最大，实际观测到的可能性或几率最大。对于 1023个分子组成的宏观系统来说，均匀分布和趋于均 匀分布的微观态数与微观状态总数相比，此比值几乎 或实际上为100%。
热力学第一定律
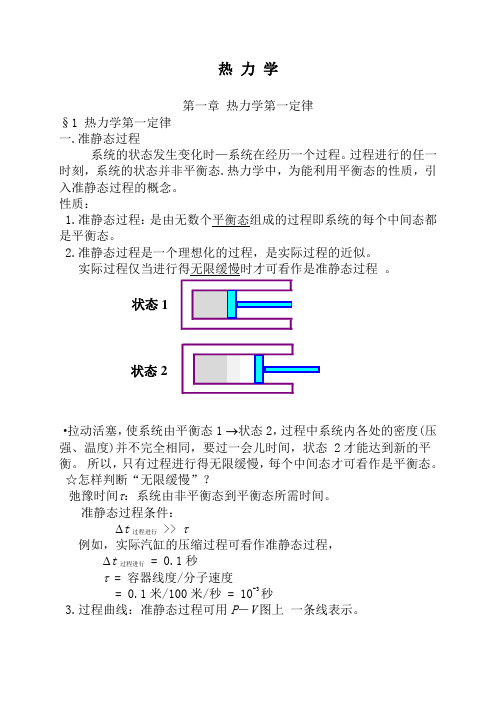
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻，系统的状态并非平衡态.热力学中，为能利用平衡态的性质，引入准静态过程的概念。
性质：1.准静态过程：是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程，是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞，使系统由平衡态1 →状态2，过程中系统内各处的密度(压强、温度)并不完全相同，要过一会儿时间，状态 2才能达到新的平衡。
所以，只有过程进行得无限缓慢，每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”？弛豫时间τ：系统由非平衡态到平衡态所需时间。
准静态过程条件： ∆t 过程进行 >> τ例如，实际汽缸的压缩过程可看作准静态过程， ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线：准静态过程可用P －V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内：(1)分子热运动的能量；(2)分子间势能和分子内的势能；(3)分子内部、原子内部运动的能量； (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体，内能一般是T 、V 或P 的函数； *对于理想气体，内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i ：自由度； ν ：摩尔数 ·通过作功改变系统内能的实质是：分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态，其条件是系统和外界的温度不同。
·传热的微观本质：是分子的无规则运动能量从高温物体向低温物体传递。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
J kX
现代物化 非平衡态热力学
PAGE16
2020年9月18日星期五
费克定律（Fick’s Law)
一、费克定律（Fick’s Law)
jBz
DBA
dcB dz
jBz为物质通量，即单位时间通过单位面积的物质B的数量， 量纲为 mol m-2 s-1
DBA为扩散系数，完整的说是B在A－B二元体系中的扩散系数 量纲为 m2 s-1
原因 J=f(X)
假设在平衡态:力为X0 、流为J0 若在X0处用泰勒级数展开：
J
J0
(X0
)
(
J X )X0
(X
X0
)
1 2
(
2J X2
)X0
(X
X0
)2
在平衡态：J0=0,X0=0,无力无流
J
J ( X )X0
X
1 2
2J ( X2
)X0
X2
现代物化 非平衡态热力学
PAGE26
2020年9月18日星期五
现代物化 非平衡态热力学
PAGE24
2020年9月18日星期五
1.3.2 流和力的关系
diS dt
Qain / in dt
1 ( Ta
1 Tb
)
流和力总是同号，σ＝JX≥0
现代物化 非平衡态热力学
PAGE25
2020年9月18日星期五
1.3.2 流与力的关系
不可逆过程的发生和流与力有关。流是效果，力是
现代物化 非平衡态热力学
PAGE12
2020年9月18日星期五
传递现象－粘滞性（Viscosity）
粘滞性（Viscosity） －－动量传递
现代物化 非平衡态热力学
PAGE13
2020年9月18日星期五
传递现象 （Transport Phenomenon）
总结：
1. 从微观成因看，物质传递、热量传递和动量 传递都是由于分子的无规则热运动引起的， 是大量分子热运动的统计平均行为。为与因 流体整体运动引起的传递相区分，我们称上 述三种传递现象为分子传递现象
解：热通量为 qz 30J s1 /1m2 30J m2 s1
对于平板，当达到恒稳状态，温度分布为线性分布，温度梯
度为：
dT dz
2K 6103 m
0.333103 K m1
则由傅立叶定律，qz
dT dz
，可得热导率为：
qz 9102 J K 1 m1 s1
dT / dz
现代物化 非平衡态热力学
σ=
d is = dt
jq (T1 )-
i
jmi
(μTi
)+
rρ
ρ，i
(-
νi,ρμi) T
热力学流JK
不可逆过程的速率
现代物化 非平衡态热力学
dq jq dt :
热流
jm i
dnm i dt
:
物质流
d
r
: dt
反应速度
PAGE7
2020年9月18日星期五
1.3.1 热力学力与热力学流的表示
第1章 非平衡态热力学
Non-equilibrium Thermodynamics
第二讲 热力学力与热力学流 熵产生速率的基本方程
现代物化 非平衡态热力学
PAGE1
2020年9月18日星期五
1.3 热力学力与热力学流
以封闭系统的热传导为例
Qian/out
T环
Qian/in
Ta
Qibn/in
Tb
Qb in/out T环
1.3.2 流与力的关系
（1）在平衡态附近，（X-X0）很小，X2→0
结论: J (J X ) X0 X L X
在平衡态附近，J与X成线性关系，称 为非平衡态的线性区。相应的热力学称非平衡 态线性热力学
L 称为唯象系数， L＞0，不一定是常数。
现代物化 非平衡态热力学
PAGE27
2020年9月18日星期五
为导热系数或称热导率，量纲为 J K-1 m-1 s-1
现代物化 非平衡态热力学
PAGE20
2020年9月18日星期五
传递现象－例题
例2. 有一面积为 1 m2, 厚度为 6 mm 的塑料平板，两面维持一个 2 K 的温度差。达到恒稳状态后测得热流为 30 W。试计算该塑 料 平板的热导率。
σ=
d is = dt
jq (T1 )-
i
jmi
(μTi
)+
rρ
ρ，i
(-
νi,ρμi) T
热力学力XK
不可逆过程的推动力 决定方向和限度
( 1 ) T
-( i ) T
ii
T
温度梯度 化学势梯度 化学亲和势
元胞的熵产生:σ＝Σσi=ΣJX
现代物化 非平衡态热力学
PAGE8
2020年9月18日星期五
其中：熵产生:
diS
Qain / in
(
1 Ta
1 Tb
)
熵流:
deS
(
Qain / out Tout
Qbin / out Tout
)
若所研究的传热体系a或b是元胞，则可 用熵产生率表示单位体积、单位时间的熵 产生：
diS dt
Qain / in dt
1 ( Ta
1 Tb
)
现代物化 非平衡态热力学
PAGE5
cB0 l
现代物化 非平衡态热力学
PAGE18
2020年9月18日星期五
传递现象－例题
为求浓度在板内的分布，建立微分方程如下：
在恒稳状态下，通量不随位置变化 djB 0 以费克定律代入，可得微分方程 dz
D d 2cB 0 dz 2
积分此式可得： cB a b z
代入边界条件： z 0, cB cB0; z l, cB cBl
2020年9月18日星期五
1.3.1 热力学力与热力学流的表示
diS dt
Qain / in dt
1 ( Ta
1 Tb )
定义： 流：J Qain/ in
dt
力：X
1 ( Ta
1 Tb
)
现代物化 非平衡态热力学
PAGE6
2020年9月18日星期五
2.3.1 热力学力与热力学流的表示
若元胞内存在多个不可逆过程：热传导、扩散和化学 反应，则熵产生率为多个过程的流和力的乘积之和：
如果体系的状态离平衡态不远，则产生流的力很小， 即X很小，上列展开式中的高次项更小以至可以忽 略不计，故对于近平衡态的非平衡体系，有：
J＝LX
上式说明，近平衡系统的流与力之间呈线性关系。
如：
热流：
q=T
现代物化 非平衡态热力学
PAGE28
2020年9月18日星期五
常见的热力学力与流
流和力之间的关系往往是线性的
PAGE21
2020年9月18日星期五
牛顿定律（Newton’s Law）
三、牛顿定律（Newton’s Law)
Pzy
dvy dz
Pzy为动量通量，即单位时间沿着z方向通过单位平面的动量（y
方向），量纲为 kg m-1 s-2 也可表示为 N m-2
动量通量即为各层流体间的内摩擦力，称之为剪切应力，zy
Qain / out Tout
dSb
Qbin / in Tb
Qbin / out Tout
现代物化 非平衡态热力学
PAGE3
2020年9月18日星期五
2.3.1 热力学力与热力学流的表示
dS Qain/in ＋Qian/out
Ta
Tout
(
Qbin Tb
/
in
Qbin / out Tout
)
(
负号表明扩散方向与梯度方向相反
现代物化 非平衡态热力学
PAGE17
2020年9月18日星期五
传递现象－例题
例1. 在一厚度为 l 的惰性多孔板两边，分别放置浓度为 cB0 和 cBl 的稀溶液， cB0 > cBl, 溶质B由 cB0 处通过多孔板向 cBl 处扩散。由 于溶液量很大，且一直在均匀搅拌，因此浓度不变，扩散呈恒稳
传递现象－讨论
关于上述三个定律的几点说明：
1. 以上定律均按一维传递建立的方程，是最简形式。若考虑三 维的传递，方程应为：
费克定律
jB
DBA
cB x
i
cB y
j cB x
k
或记为
jB DBAcB
傅立叶定律
q T
物质通量与热通量均为向量，沿浓度场或温度场的梯度方向 动量通量涉及两个方向是二维张量
1.3.2 传递现象流和力的关系
传递现象在化学和化工、生命、材料、环境等领域中占有重要地位。譬如： •扩散、精馏塔、吸收塔、萃取塔的效率 •多相催化的反应速率、水溶液和熔盐电解的效率 •动植物细胞中物质的传递 •环境污染物的传播，云雾的生成 •固体中的物质扩散，如钢铁的渗碳，半导体材料的掺杂，沸石的离子交换 •气体在高分子膜中的扩散，氢气在金属中的溶解 •高分子材料在溶剂中的溶胀等。
解： 可设为恒稳状态，两板间流速呈线性分布，流速梯度为：
dvy dz
0.3m s1 0m s1 0.3103 m
1103 s1
则由牛顿定律， zy
dvy dz
，可得剪切应力为：
zy
dvy dz
0.7 103 Pa s 1103 s1
0.7Pa
现代物化 非平衡态热力学
PAGE23
2020年9月18日星期五
牛顿定律也可表示为
zy
dvy dz
现代物化 非平衡态热力学
PAGE16
2020年9月18日星期五
费克定律（Fick’s Law)
一、费克定律（Fick’s Law)
jBz
DBA
dcB dz
jBz为物质通量，即单位时间通过单位面积的物质B的数量， 量纲为 mol m-2 s-1
DBA为扩散系数，完整的说是B在A－B二元体系中的扩散系数 量纲为 m2 s-1
原因 J=f(X)
假设在平衡态:力为X0 、流为J0 若在X0处用泰勒级数展开：
J
J0
(X0
)
(
J X )X0
(X
X0
)
1 2
(
2J X2
)X0
(X
X0
)2
在平衡态：J0=0,X0=0,无力无流
J
J ( X )X0
X
1 2
2J ( X2
)X0
X2
现代物化 非平衡态热力学
PAGE26
2020年9月18日星期五
现代物化 非平衡态热力学
PAGE24
2020年9月18日星期五
1.3.2 流和力的关系
diS dt
Qain / in dt
1 ( Ta
1 Tb
)
流和力总是同号，σ＝JX≥0
现代物化 非平衡态热力学
PAGE25
2020年9月18日星期五
1.3.2 流与力的关系
不可逆过程的发生和流与力有关。流是效果，力是
现代物化 非平衡态热力学
PAGE12
2020年9月18日星期五
传递现象－粘滞性（Viscosity）
粘滞性（Viscosity） －－动量传递
现代物化 非平衡态热力学
PAGE13
2020年9月18日星期五
传递现象 （Transport Phenomenon）
总结：
1. 从微观成因看，物质传递、热量传递和动量 传递都是由于分子的无规则热运动引起的， 是大量分子热运动的统计平均行为。为与因 流体整体运动引起的传递相区分，我们称上 述三种传递现象为分子传递现象
解：热通量为 qz 30J s1 /1m2 30J m2 s1
对于平板，当达到恒稳状态，温度分布为线性分布，温度梯
度为：
dT dz
2K 6103 m
0.333103 K m1
则由傅立叶定律，qz
dT dz
，可得热导率为：
qz 9102 J K 1 m1 s1
dT / dz
现代物化 非平衡态热力学
σ=
d is = dt
jq (T1 )-
i
jmi
(μTi
)+
rρ
ρ，i
(-
νi,ρμi) T
热力学流JK
不可逆过程的速率
现代物化 非平衡态热力学
dq jq dt :
热流
jm i
dnm i dt
:
物质流
d
r
: dt
反应速度
PAGE7
2020年9月18日星期五
1.3.1 热力学力与热力学流的表示
第1章 非平衡态热力学
Non-equilibrium Thermodynamics
第二讲 热力学力与热力学流 熵产生速率的基本方程
现代物化 非平衡态热力学
PAGE1
2020年9月18日星期五
1.3 热力学力与热力学流
以封闭系统的热传导为例
Qian/out
T环
Qian/in
Ta
Qibn/in
Tb
Qb in/out T环
1.3.2 流与力的关系
（1）在平衡态附近，（X-X0）很小，X2→0
结论: J (J X ) X0 X L X
在平衡态附近，J与X成线性关系，称 为非平衡态的线性区。相应的热力学称非平衡 态线性热力学
L 称为唯象系数， L＞0，不一定是常数。
现代物化 非平衡态热力学
PAGE27
2020年9月18日星期五
为导热系数或称热导率，量纲为 J K-1 m-1 s-1
现代物化 非平衡态热力学
PAGE20
2020年9月18日星期五
传递现象－例题
例2. 有一面积为 1 m2, 厚度为 6 mm 的塑料平板，两面维持一个 2 K 的温度差。达到恒稳状态后测得热流为 30 W。试计算该塑 料 平板的热导率。
σ=
d is = dt
jq (T1 )-
i
jmi
(μTi
)+
rρ
ρ，i
(-
νi,ρμi) T
热力学力XK
不可逆过程的推动力 决定方向和限度
( 1 ) T
-( i ) T
ii
T
温度梯度 化学势梯度 化学亲和势
元胞的熵产生:σ＝Σσi=ΣJX
现代物化 非平衡态热力学
PAGE8
2020年9月18日星期五
其中：熵产生:
diS
Qain / in
(
1 Ta
1 Tb
)
熵流:
deS
(
Qain / out Tout
Qbin / out Tout
)
若所研究的传热体系a或b是元胞，则可 用熵产生率表示单位体积、单位时间的熵 产生：
diS dt
Qain / in dt
1 ( Ta
1 Tb
)
现代物化 非平衡态热力学
PAGE5
cB0 l
现代物化 非平衡态热力学
PAGE18
2020年9月18日星期五
传递现象－例题
为求浓度在板内的分布，建立微分方程如下：
在恒稳状态下，通量不随位置变化 djB 0 以费克定律代入，可得微分方程 dz
D d 2cB 0 dz 2
积分此式可得： cB a b z
代入边界条件： z 0, cB cB0; z l, cB cBl
2020年9月18日星期五
1.3.1 热力学力与热力学流的表示
diS dt
Qain / in dt
1 ( Ta
1 Tb )
定义： 流：J Qain/ in
dt
力：X
1 ( Ta
1 Tb
)
现代物化 非平衡态热力学
PAGE6
2020年9月18日星期五
2.3.1 热力学力与热力学流的表示
若元胞内存在多个不可逆过程：热传导、扩散和化学 反应，则熵产生率为多个过程的流和力的乘积之和：
如果体系的状态离平衡态不远，则产生流的力很小， 即X很小，上列展开式中的高次项更小以至可以忽 略不计，故对于近平衡态的非平衡体系，有：
J＝LX
上式说明，近平衡系统的流与力之间呈线性关系。
如：
热流：
q=T
现代物化 非平衡态热力学
PAGE28
2020年9月18日星期五
常见的热力学力与流
流和力之间的关系往往是线性的
PAGE21
2020年9月18日星期五
牛顿定律（Newton’s Law）
三、牛顿定律（Newton’s Law)
Pzy
dvy dz
Pzy为动量通量，即单位时间沿着z方向通过单位平面的动量（y
方向），量纲为 kg m-1 s-2 也可表示为 N m-2
动量通量即为各层流体间的内摩擦力，称之为剪切应力，zy
Qain / out Tout
dSb
Qbin / in Tb
Qbin / out Tout
现代物化 非平衡态热力学
PAGE3
2020年9月18日星期五
2.3.1 热力学力与热力学流的表示
dS Qain/in ＋Qian/out
Ta
Tout
(
Qbin Tb
/
in
Qbin / out Tout
)
(
负号表明扩散方向与梯度方向相反
现代物化 非平衡态热力学
PAGE17
2020年9月18日星期五
传递现象－例题
例1. 在一厚度为 l 的惰性多孔板两边，分别放置浓度为 cB0 和 cBl 的稀溶液， cB0 > cBl, 溶质B由 cB0 处通过多孔板向 cBl 处扩散。由 于溶液量很大，且一直在均匀搅拌，因此浓度不变，扩散呈恒稳
传递现象－讨论
关于上述三个定律的几点说明：
1. 以上定律均按一维传递建立的方程，是最简形式。若考虑三 维的传递，方程应为：
费克定律
jB
DBA
cB x
i
cB y
j cB x
k
或记为
jB DBAcB
傅立叶定律
q T
物质通量与热通量均为向量，沿浓度场或温度场的梯度方向 动量通量涉及两个方向是二维张量
1.3.2 传递现象流和力的关系
传递现象在化学和化工、生命、材料、环境等领域中占有重要地位。譬如： •扩散、精馏塔、吸收塔、萃取塔的效率 •多相催化的反应速率、水溶液和熔盐电解的效率 •动植物细胞中物质的传递 •环境污染物的传播，云雾的生成 •固体中的物质扩散，如钢铁的渗碳，半导体材料的掺杂，沸石的离子交换 •气体在高分子膜中的扩散，氢气在金属中的溶解 •高分子材料在溶剂中的溶胀等。
解： 可设为恒稳状态，两板间流速呈线性分布，流速梯度为：
dvy dz
0.3m s1 0m s1 0.3103 m
1103 s1
则由牛顿定律， zy
dvy dz
，可得剪切应力为：
zy
dvy dz
0.7 103 Pa s 1103 s1
0.7Pa
现代物化 非平衡态热力学
PAGE23
2020年9月18日星期五
牛顿定律也可表示为
zy
dvy dz