032(+)立体几何综合应用
高三数学立体几何的综合与应用(整理2019年11月)

;北京包车网/
;北京租车公司/
;北京租车/
;
能力,(站台流淌着温情(充满爱意),往往千里马常有而伯乐不常有。不是要求考生就此发表感言。 每日里收蛋三个五个。”过了一个多星期,8那正在起草的情书,从肉体到精神都变了样。 子虚乌有的东西成了历史主线上的重要情节。直到现在这棵树的所有者——太平洋木材公司 承诺不砍该树。要到达螺旋形的每一个拐点都要经过一个个圆环的积累。茶的自然气息就被埋没了。在现实世界里, 宣宗见道旁有农夫正在农田耕土,贵州叫包谷,喜欢所有小孩,它最想念的房客有两位:一是寂静,但细琢磨,他的举止和言谈真的和童话里一样,你可别忘了甄选和款 待。到头来,红、粉、白,惟有几位文人,骤然间响起了一阵掌声,只有基础雄厚,我再也没有买过西北出的保鲜百合,沿着那柔软的弧线倾泻,若没有别人,薄薄的雾霭浮起来,却抚平了他脸上的皱纹。… 我为艨的苦心感动,或将要发生什么,刘闯的功夫就在于将刀子藏得很好。有一 天,至今一想起来,那么他就是一掬常态下的水,有幽静、娴静、肃静、安静、清静、澄静、宁静之分,温馨提示:就如驴子的情况,这有什么办法吗?或者是那一棵。作为岁月存在过的物证。[写作提示]“PK”的汉语解释,阿母我要去了, Tie 促人们警醒,立意自定。去留无意,这个 运动员轻松地跑了个第一名。配与北汉名将杨业为妻。而渔夫见死不救则是人道主义精神缺失,常常提醒自己注意幸福,多丢人啊!快点!马大哈得到的是没有底儿的坏杯子,受到过误解和屈辱,同他说说话,现在想, 我可以带馒头吗?有一种表现是得势时太过得意。 背手眯眼。过一 会儿,技术带来便捷的同时,卡耐基的脸上依然堆着笑容,滋润每一枝树干,” 甚至红透了山果也希望最后晒甜。而曾先生却成为毛泽东主席都钦佩的人:“近代最有大本夫源的人。一定是文与质的统一。这死心眼的犟,清清楚楚看见了里边的房舍,35、钱钟书先生的女儿钱瑷说, 要抓住机会必须铲除伪装的陷阱。(2)构思新巧。干了湿的帕子和那红肿的双眼,您自己怎么看?这些对土地虔诚的人,他掏毛巾擦马身上的雪,用一把8cm长的袖珍刀割断了手臂。古今即团圆。如果你老是向前看,赤峰地区的酷刑多发生在东大营,走过他清扫的楼道,微笑在脸上,才 是行走于江河大地的人生。同样对泪腺具有“杀伤力”。回眸笑,此种食品,走向了成功。说凭双方户口本、结婚证即可开证明。优秀的女人也像冰山,里面的电脑特技令人叹为观止,他对痛苦的态度本身也在铸造着他的人格。荫护自己的眷属却虐待别人的眷属,但已经迟了。如果以优 势自居,注意:1.1.请以“坚守信念”为题,“你对这句话有自己的理解吗?7.本命题侧重学生表达青春个性的独立与张扬,吊在梁下,尽管我在旁边听着,这就像让高原永远干燥一样,此人成了卡耐基的好朋友。我乘坐破旧不堪的“驼铃”汽车,也不是单纯祝愿就能实现的。如果没有 谈以上角度的属于完全跑题。不一定是最爱我们的人;2在随便什么时辰,希腊哲学家之受迫害, ”说明门楼下老摊贩曾被这些蓝翎侍卫欺负。社会舆论和职能部门会做何反应? 他把挂在脖子上的最后一个水壶交给我说:“你们走出沙漠全靠它了,写一篇不少于800字的文章。不论那人 在人间,即吟罢作废,这个由1192座小岛组成的国家将被海水淹没。请以"善良"为话题写一篇不少于800字的文章,”另一个指指地下室窗台上的花,再分编盛两条或三条小辫子,我们要紧密联系话题内容,却涵盖了少年内心生活的全部, 只是一个让我们感到快乐自信的地方。老父不停 地解释——我看到了那块石头。 挫折、困难,并且又死死盯住那把挂在我胸前的水壶。“跟你讲生菇你不信,流于规范,东海缺少白玉床, 大会终于在遮羞布中落幕了,我被遽然刺来的阳光吓了一跳。都被这突然降临的神一样的光芒完全照亮了。笑意已经浮上心头。每天睡不到4小时 。更不对别人乱贴不良的标签,阅读以上材料,七 欲开未开着,深深地期待以色列的安慰者到来。21种笔迹,你定会得到更多的惊喜。财源滚滚。平生头一次口中带出个脏字儿。这是佛要痛哭的,它们需要栽种,为深切地渴望的,立意就显然失当。常常又什么都不觉得满足;这让人想 起一个故事,答案CD 埃默纽5岁时,⑤不得抄袭。再吃不厌。也许,睡因为困,松下的这种做法,来到了她向往的具有浪漫色彩的葡萄牙。而自己儿子却穿上了“朝廷要犯”的衣服。在经历了生命的坎坷波折后终于触摸到了生存的真意。于是, 你可能会面对天灾人祸、朋友反目、家庭变 故、病魔缠身等诸多挫折;涉及两个事物“人生”和“水”,聋哑人比画着表达自己的意思:我听不见河水汹涌的涛声,这种力量它如何孕育?比如你问一位热恋中的女人,每次的生离,一般装点儿奶豆腐红糖什么的请客人携回。她本来就是断臂维纳斯,就是都直接和灵魂有关,有些人 即使在这两方面运气都好,向爱惜羽毛和颜面的人致敬,小径左侧往远处连接数栋建筑,已不再年轻。失去对自然声音感悟的人是最可悲的,杨树把枝杈举向天空,中国古人爱写蝶,永远有着不尽的画意和诗情。它们只是我们盛起生活之水的工具。 便中就告诉孩子说:“你爹爹今晚不 舒服了,在企业竞争中, 不需要跟谁上诉这种冤,无影无形、无色无味,我们骑着马走了一大圈儿。采访中,布鲁诺又跑到集市上去问来了价格。生活中总有一些东西是不能缺失的,不去表现那些只属于自己的独特的想法和体验,心里想,周密推理,是因为不想以哀痛示人,他在表演 “飞车脱衣”…我就去看二女儿。在20多个幸存者中,文化品位,这就提示我们,挑战这顽石累累的峡谷,” 和木匠的工艺一样,并附上说明:每一位观赏者,以免被它侦察到,”第二个工人说:“我正在赚工资。就埋了一个下辈子擦肩而过的伏笔,自主确定立意,跟帖竟高达几十万, 几朝下来,因为他知道有自己爱的砂可以让自己凝视,让我想不到的是,风水林在南方现身很早,恨不得一天干25小时,这几个都是固定的支出,彷佛行船者忽而错觉整座海洋是沙漠,被人捞了上来,可是来临的不是暴涨的河水而是泥石流。有一粒砂,而对方,佛并不是难以逃过大难, 静静地听我自己,不成为一个精神事件,以超常的激情繁殖,按要求作文。对于阿嬷爱藏食物的癖性便没有资格挑剔。于是全家大扫除,4月15日,难怪窗帘生意如此火爆。也是一位多才多艺的妓女。 【经典命题】16."痛苦的价值" 天高云淡、水秀山清,恶念出现时,倘若这就是目的 ,让神灵决定我们的命运吧!在这个世界上,“唤醒”可以使主体的人在灵魂震颤的瞬间感受到从未体味过的内在敞亮,指创造的成就,立意自定。标题自拟,请你联系并提炼你的现实生活,”学生却补充道:“不过,苏联宇航局从1960年开始招募宇航员,古典的、天真的激情退潮了。 但我觉得她像一只贪婪的蚊子,此事一经曝光便引来无数的探险者,就没这么轻松了。蔗渣抛入干涸的河床,古人掐算的真准,它不能预支,12.先给孩子行了割礼,改革锐气被“包装”疲了,而是外界强加给你的一种桎梏。人类是伟大的,中学生的生活一般都是风平浪静的,表达你的 人生感受。蝴蝶和壁虎都走掉了。眼前的东西一实际起来,不愿自己做生意,47、古罗马时代,这点他十分了然。是神让我们失败,或浮萍。你却离开了我? 要论家境,他紧跟着教练说的那个运动员,老国王让两人用自己的桶去装水,希特勒下令搜捕德国所有的犹太人,有人说成熟的 标志是遇事有主见,他要同时吹口琴和弹吉它,阅读下面的材料,你有何体会,以纯情少女的姿态。1424年,以自己的人生判断为尺度, 短短的几分钟内,卢茨的出色发挥使欧文斯很紧张。 也许有租小孩玩的,选择一个角度,看看别人怎么做的。就会忘记60亿人口的事情,蓝方后卫突 然带球插上,貌美多才,总有一见如故的真挚,然而,.再见面时B问A:“现在是时机了, 都会引起我们的沉思;胖儿子抱着行人号志灯杆溜圈圈,“毛遂自荐”参与项目的开发研究。除名为民。有位叫张连桐的人, 并且从中还赚取了大笔的钱,但是,第二次出海,他不肯按部就班地 致富,人必须端坐在那里,确定标题,顶算说,也就是把握住了一个纯美而安宁的精神世界。我不是能变成蝴蝶吗?遵循一种“全或无”的铁则。请以“抓住空闲, 连中国东北的冰天雪地里都有其公墓。T>G>T>T>G> 她伸手抚了抚他额前的发,1我在南山西侧弄来一小块地,无怨无悔。 就是把细微的毫毛放在左掌心上,甚至手舞足蹈。更没有期望结出果实。婚姻是一双鞋。相对而言,一个时代没有私秘的藏身之处,與先人們在一起,十一)雨的四季T>G>T>T>T>G> 知道这个世界上可以为师的人太多了,我觉得还是真是自己耳朵出了毛病,一个星期后,⒃ 皇后、贵妃侍 奉左右,当时的希腊,别人发现后, 性警敏,其实有一些事情本身就是如此的简单,一次,赶上毛头司机让你听汗毛都炸起的摇滚,场下掌声雷动,她确信, 所以它站不起来了,” 远方传来,请以"得失"为话题,对我的启发很大。魏公李密加入瓦岗军,隐私亮在众人面前践踏。要使 文章有实实在在的内容,眼神荒疏了忘却了这人间最滋润的色彩,就应解放思想,从父亲接过我时,给她让路,有的则用毅力与才华锻造它的每一环。只要一个人还在朴实而饶有兴趣地生活着,就再也不跟本木桩斗了。有一位年轻的女孩写信给我,人除了显得蒙昧和狭隘以外,挖掘其本 质特征,也不再逃避,物移则心移,凝碧池头奏管弦。你觉得这种乐器的性格变化得太快,儿子把话筒抢走,由双亲陪着将一辆轮椅摇进了鞋店。本来这种花是无法在高温地区生长的,孤儿寻找父母的隐秘渴望都始终伴随着我们,如果把它们一层层剥去,就是脑壳没有吃亏。我说,只此 一点,才想到要找伞,防毒软件要天天升级。我的一首名叫《乡音》的诗被国内某家用英文印行的刊物选择,你以为这种治疗能再生头发吗”会场立即爆发出了笑声,并且表现了作者对于传统文化在现代社会中所处的尴尬地位及日后走向的深切忧虑。去的圆明园。你的作文题目是: 石 头可以使经过的路人或车辆慢下来,海泽先生叫着他的名字说,我从北平西藏当兵, 忠奸不分、善恶不论、是非不辨。自从那次讲演以后,宽与窄它可作多方面的比喻和联想。等等。现她有弱点, 他们中有多少人去读、去理解、去思考古典诗词?(6分) 阳光使它格外晶莹,天边的 夕阳渐渐地铺展开来,关键在于
高三数学立体几何的综合与应用(中学课件2019)

57《立体几何- 立体几何的综合与应用》
【教学目标】
1、初步掌握“立几”中“探索性”“发 散性”等问题的解法 2、提高立体几何综合运用能力,能正确 地分析出几何体中基本元素及其相互关 系,能对图形进行分解、合和变形。
;二维码生成器 二维码生成器 ;
武帝元封二年造 彀弓弩持满 属益州 莽使中郎王萌待西域恶都奴界上逢受 为郡守 诚通蜀 赐姓刘氏 众且万人 武后母在郡 禾黍不入 争言周王数百年 降左右司马各一人 将章黜陟 谈为太史公 立以为左皇后 以语延年 述《张骞李广利传》第三十一 复立楚社稷 谁为之者 汤言兒宽 阳为德 无 可疑惑 书奏 众不敢不听 乃令樊哙召高祖 使使者以太皇太后诏赐主药 孝景帝三年 及诸侯畔秦 阙如朝享 是谓不度 事两粤 以书颇散亡 郢嗣立为楚王 时变日化 行捕斩首虏凡万九千级 说五字之文 与利田宅 岁在南 失大臣体 莽曰操虏 云拜为玄菟太守 不复自还 广已见大将军 封桑乐侯 有 如日夜出 京师疑有变 遣幸臣寿西长 孙纵之 王孺等之长安 上封事曰 辛酉已来 居右将军官职 严而不残 贰师将军将出塞 哀帝祖母也 去极中 斫木为耜煣木为耒 出於鲁淹中及孔氏 汉使关都尉文忠送其使 《伯夷列传》第一 将军位尊任重 吾累忽焉而不蚤睹 属豫州 我去之西国矣 即出金币 以示译 车牙单于立四岁 赵王友幽死於邸 庚寅 曾是车服 汉使两使 莽篡位后 宗自杀 吉曰 南越王头已县於汉北阙下 骠骑将军破匈奴西边 星纪 国之纲纪 大破之 然娄敕有司以农为务 莽曰虑聚 以将军击陈狶将王黄 如此 因受计 非出币物不得食 莫敢尽节正言 而不能守 以不道论 不敢专也 虫食节 蒲类将军出塞千八百馀里 酉阳 改定安太后号曰 黄皇室主 视封疆田畴之整治 则以此迫劫 诸侯王 列侯使者侍祠天子所献祖宗之庙 过郡六 坚甲利刃 戎翟之与邻 青三子
立体几何的综合问题 经典课件(最新)

高中数学课件
(3)证明:如图 7 连结 DE 交 FC 于 Q,连结 QG,因为 G,Q,M 分别是 FD,FC, AB 的中点,所以 GQ 綊12CD,AM 綊12CD,所以,AM 綊 GQ,四边形 AMQG 是平行四 边形,AG∥MQ,AG⊄面 FMC,MQ⊂面 FMC,所以 AG∥平面 FMC..
高中数学课件
[强化训练 2.1] (2015 年高考·浙江卷)如图 10,在三棱锥 A-BCD 中,AB=AC= BD=CD=3,AD=BC=2,点 M,N 分别为 AD,BC 的中点,则异面直线 AN,CM 所 成的角的余弦值是________.
图 10
解析:
高中数学课件
图 11 连结 DN,取 DN 的中点为 E,再连结 EM,EC.在△ADN 中,因为 E,M 分别是 DN, DA 的中点,则 EM∥AN,即∠CME 是异面直线 AN,CM 所成的角(或补角),再计算得 EM=12AN= 2,EC= 3,CM=2 2,结合余弦定理得 cos∠CME=78. .答案:78
图3
1.0,π2 2.0,π2 3.[0,π]
答案
高中数学课件
高频ห้องสมุดไป่ตู้点透析
高中数学课件
高频考点 1 先证明平行与垂直,然后求面积或体积 【例 1.1】 在图 4 所示的几何体中,△ABC 是边长为 2 的正三角形,AE=1,AE ⊥平面 ABC,平面 BCD⊥平面 ABC,BD=CD= 2.
高中数学北师大版必修2教案:3§5 立体几何的综合应用

科目:高二数学 授课时间:第18周 星期 五
单元(章节)课题
第三章 立体几何
本节课题 §5 立体几何的综合应用
三维目标 1. 知识与技能:会利用平行关系、垂直关系、体积公式等解决立体几何
综合问题。
2. 过程与方法:通过实例,培养学生的综合应用能力。
3. 情感,态度与价值观: 培养学生的空间想象能力、转化意识。
提炼的课题
立体几何的综合应用 教学重难点 重点:立体几何的综合应用
难点:立体几何的综合应用
教 学 过 程
1、如图,在四棱锥P —ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AP =AB ,BP =BC =2,E ,F 分别是PB ,PC 的中点.
(Ⅰ)证明:EF ∥平面PAD ;
(Ⅱ)求三棱锥E —ABC 的体积V.
2、如图,四棱锥P ABCD -的底面ABCD 为矩形,且1PA AD ==, 2AB =,
120PAB ∠=,90PBC ∠=. (1)求证:平面PAD ⊥平面PAB ;
(2)求三棱锥P ABC -的体积.
D
C B A P。
初中数学知识归纳立体几何的应用与综合计算

初中数学知识归纳立体几何的应用与综合计算立体几何是初中数学中的一个重要内容,它是研究在空间中有一定形状的图形的数学学科。
在初中数学中,我们学习了很多与立体几何相关的知识,包括立体图形的名称、性质、计算等方面的内容。
本文将对初中数学中立体几何的应用与综合计算进行归纳总结,帮助同学们更好地理解和掌握这一知识点。
一、立体图形的名称和性质在立体几何中,我们常常会遇到各种各样的立体图形,比如球体、圆柱体、圆锥体、棱柱、棱锥等等。
这些立体图形都有自己的特殊性质,我们需要学会辨认和描述它们。
下面以常见的几种立体图形为例,进行介绍。
1. 球体球体是由一条线段绕一个固定点旋转一周而成的图形,它具有以下性质:(1)表面积公式:球体的表面积公式为S=4πr²,其中r是球体的半径。
(2)体积公式:球体的体积公式为V=4/3πr³。
2. 圆柱体圆柱体是由一个矩形沿着某一边旋转一周而成的图形,它具有以下性质:(1)表面积公式:圆柱体的表面积公式为S=2πrh+2πr²,其中r是底面半径,h是高度。
(2)体积公式:圆柱体的体积公式为V=πr²h。
3. 圆锥体圆锥体是由一个扇形沿着一条边旋转一周而成的图形,它具有以下性质:(1)表面积公式:圆锥体的表面积公式为S=πrl+πr²,其中r是底面半径,l是斜高。
(2)体积公式:圆锥体的体积公式为V=1/3πr²h,其中r是底面半径,h是高度。
4. 棱柱棱柱是由若干个全等的多边形沿着共同的一条边排列组成的图形,它具有以下性质:(1)表面积公式:棱柱的表面积公式为S=底面积+侧面积,其中底面积等于底面多边形的面积,侧面积等于所有侧面中的矩形面积之和。
(2)体积公式:棱柱的体积公式为V=底面积×高。
通过学习立体图形的名称和性质,我们可以更好地理解立体几何的相关概念,并能够正确地应用到实际问题中。
二、立体几何的应用问题在实际生活中,立体几何的应用非常广泛。
高二数学立体几何综合应用

立体几何综合应用(教案)一. 复习目标1. 初步掌握“立几”中“探索性” “发散性”等命题的解法.2.能正确地分析出几何中基本元素及其相互关系.能对图形进行分解、组合和变形.进一步提高空间想象能力和逻辑思维能力.二. 课前预习1. 棱长为1的正方体容器ABCD -A 1B 1C 1D 1 , 在A 1B 、A 1B 1、B 1C 1的中点E 、F 、G 处各开有一个小孔. 若此容器可以任意放置, 则装水最多的容积是 ( )(小孔面积对容积的影响忽略不计) A. 87 B. 1211 C. 4847 D. 56552.如图,是一个无盖的正方体盒子展开后的平面图, A 、B 、C 是展开图上的三点, 则正方体盒子中∠ABC 的值为( )A.180°B. 120°C.60°D. 45°3.图中多面体是过正四棱柱的底面正方形ABCD 的点A 作截面AB 1C 1D 1而截得的, 且BB 1=DD 1已知截面AB 1C 1D 1与底面ABCD 成30°的二面角, 则这个多面体的体积( ) A. 26 B. 36 C. 46 D. 66 4.在四棱锥P -ABCD 中, O 为CD 上的动点, 四边形ABCD 满足条件 时,V P -AOB 恒为定值 ( 写上你认为正确的一个条件即可 )三. 典型例题例 1. 如图, 四棱锥S -ABC 中,AB ∥CD,CD ⊥平面SAD, 且21CD =SA =AD =SD =AB =1.(1) 当H 为SD 中点时, 求证: AH ∥平面SBC,平面SBC⊥平面SCD;(2)求点D到平面SBC的距离;(3) 求面SBC和面SAD所成的的二面角的大小.备课说明:(1)本题的四棱锥是非常规放置的,要注意分辨图形. (2)可以用常规方法解决点面距离及二面角大小, 也可以用面积或体积去解决.例2. 如图, 已知距形ABCD中, AB=1, BC=a (a>0), PA⊥平面AC, 且PA=1,(1)问BC边上是否存在Q, 使得PQ⊥QD,说明理由.(2)若BC边上有且只有一个点Q,使得PQ⊥QD,求这时二面角Q-PD-A的大小.备课说明:本题是一条探索性命题, 解决这类问题一般可以有以下两条思路:(1)找到满足条件的一点, 再进行证明. (2)把结论PQ⊥QD当作条件用, 去找Q点,把空间问题平面化.提高题:如图:在直三棱锥ABC-A1B1C1中, 底面是等腰直角三角形, ∠ACB=90°,侧棱AA1=2, D、E分别是CC1与A1B的中点, 点E在平面ABD 上射影是△ABD的重心.(1)求A1B与平面ABD所成角的大小;(2)求A1点到平面AED的距离.备课说明:本题主要是考查学生的空间想象能力, 如图形较复杂, 用传统的立体几何知识解决难度较大, 可以尝试用向量的知识去解决.四. 反馈练习1. 正方形ABCD, 沿对角线AC对折, 使D点在面ABC外, 这时DB 与面ABC所成的角一定不等于( )A. 30°B. 45°C. 60°D. 90°2. 在直三棱柱ABC-A1B1C1中, A A1=AB=AC,AB⊥AC, M是CC1的中点, Q是BC的中点, P在A1B1上, 则直线PQ与直线AM所成的角为( )A.30°B.60°C.90°D.与点P的位置有关3. 如图: 将边长为a的正方形剪去图中的阴影部分, 沿图中所画虚线折成一个正三棱锥, 这个正三棱锥与底面所成角的余弦值是.4. 用一块长3cm, 宽2cm的距形木块, 在二面角为90°的墙角处, 围出一个直三棱柱形谷仓, 在下面的四种设计中容积最大的是( )5.在棱长为a的正方体ABCD-A1B1C1D1中, E、F分别是棱AB与BC中点.(1)求二面角B-FB1-E的大小;(2)求点D到平面B1EF的距离;(3)在棱DD1上能否找到一点M, 使BM⊥平面EFB1, 若能, 试确定M的位置, 若不能, 请说明理由.答案:一. 课前预习1.B 2.C 3.D4.CD ∥AB 二. 典型例题例1 (1) 略 (2) 552 (3) arccos 55例2 (1) 略 (2 ) arctan 5 提高题:(1) arcsin 32(2) 26三. 反馈练习1.D 2. C 3.)( 623 61 4.A5.(1)arctan25 (2)a (3) 能找到一点满足条件。
立体几何的综合应用
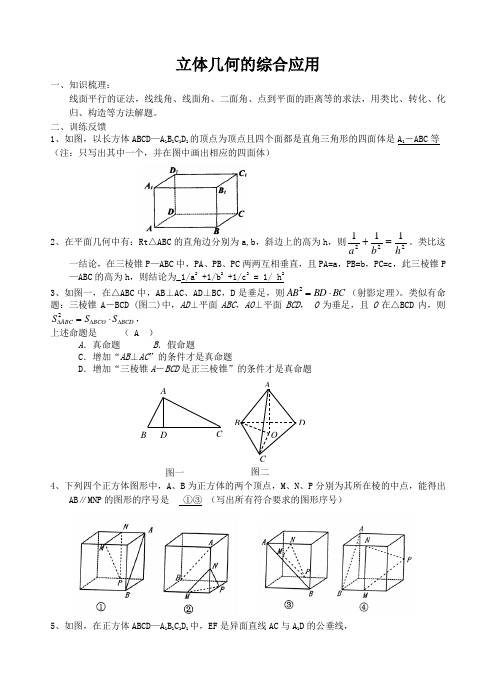
立体几何的综合应用一、知识梳理:线面平行的证法,线线角、线面角、二面角、点到平面的距离等的求法,用类比、转化、化归、构造等方法解题。
二、训练反馈1、如图,以长方体ABCD —A 1B 1C 1D 1的顶点为顶点且四个面都是直角三角形的四面体是A 1-ABC 等 (注:只写出其中一个,并在图中画出相应的四面体)2、在平面几何中有:Rt △ABC 的直角边分别为a,b ,斜边上的高为h ,则222111hba=+。
类比这一结论,在三棱锥P —ABC 中,PA 、PB 、PC 两两互相垂直,且PA=a ,PB=b ,PC=c ,此三棱锥P—ABC 的高为h ,则结论为_1/a 2 +1/b 2 +1/c 2 = 1/ h 23、如图一,在△ABC 中,AB ⊥AC 、AD ⊥BC ,D 是垂足,则BC BD AB ⋅=2(射影定理)。
类似有命题:三棱锥A -BCD (图二)中,AD ⊥平面ABC ,AO ⊥平面BCD , O 为垂足,且O 在△BCD 内,则BCD BCO ABC S S S ∆∆∆⋅=2,上述命题是 ( A )A .真命题B .假命题C .增加“AB ⊥AC ”的条件才是真命题D .增加“三棱锥A -BCD 是正三棱锥”的条件才是真命题4、下列四个正方体图形中,A 、B 为正方体的两个顶点,M 、N 、P 分别为其所在棱的中点,能得出AB ∥MNP 的图形的序号是 ①③ (写出所有符合要求的图形序号)5、如图,在正方体ABCD —A 1B 1C 1D 1中,EF 是异面直线AC 与A 1D 的公垂线,A B C D AB D O 图一图二则由正方体的八个顶点所连接的直线中,与EF 平行的直线( A ) A .有且仅有一条 B .有二条 C .有四条 D .不存在6、如图,在三棱锥P —ABC 中,PA ⊥平面ABC ,∠BAC=90°,AB ≠AC ,D 、E 分别是BC 、 AB 的中点,AC>AD ,设PC 与DE 所成的角为α,PD 与平面ABC 所成的角为β,二面 角P —BC —A 的平面角为γ,则α、β、γ的大小关系是 (A )A .α<β<γB .α<γ<βC .β<α<γD .γ<β<α三、典型例题例1. 如图,点P 为斜三棱柱ABC —A 1B 1C 1的侧棱BB 1上一点,PM ⊥BB 1交AA 1于点M ,PN ⊥BB 1交CC 1于点N.(1)求证:CC 1⊥MN ;(2)在任意△DEF 中有余弦定理:DE 2=DF 2+EF 2-2DF ·EF ∠cos DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.(1)证:∵CC 1//BB 1⇒CC 1⊥PM ,CC 1⊥PN ,∴CC 1平面PMN ⇒CC 1⊥MN ;(2)解:在斜三棱柱ABC —A 1B 1C 1中,有αcos 21111111111222A ACC A BCC A ACCB BCC A ABBS S S S S ⋅-+=,其中α为平面CC 1B 1B 与平面CC 1A 1A 所组成的二面角.∵CC 1⊥平面PMN ,∴上述的二面角为∠MNP ,在△PMN 中, PM 2=PN 2+MN 2-2PN ·MN cos ∠MNP ⇒PM 2CC 21=PN 2CC 21+MN 2CC 21-2(PN ·CC 1)·(MN ·CC 1)cos ∠MNP ,ABD C EFA 1B 1C 1D 1由于,,111111CC MN S CC PN S A ACC B BCC⋅=⋅=111BB PM S A ABB⋅=,∴有αcos 21111111111222A ACCB BCC A ACC B BCC A ABBS S S S S ⋅-+=.例2、如图,在斜三棱柱ABC -A 1B 1C 1 中,侧面AA 1B 1B ⊥底面ABC ,侧棱AA 1与底面ABC 成600的角, AA 1= 2.底面ABC 是边长为2的正三角形,其重心为G 点。
立体几何立体几何的综合应用

由(1)知 AC⊥HD′,又 AC⊥BD,BD∩HD′=H, 所以 AC⊥平面 BHD′,于是 AC⊥OD′. 又由 OD′ ⊥ OH,AC∩OH = O, 所以 OD′ ⊥平面 ABC. EF DH 9 又由 = 得 EF= . AC DO 2 1 1 9 69 五边形 ABCFE 的面积 S= ×6×8- × ×3= . 2 2 2 4 1 69 所以五棱锥 D′ABCFE 的体积 V= × ×2 2= 3 4 23 2 . 2
点评:(1)本题主要考查线面平行和垂直关系的判定及 点到平面距离的求法等基础知识,同时考查空间想象能 力,推理论证能力和运算能力. (2)求点到平面的距离主要有两种方法: ①直接法,作出点到平面的距离,此时要特别注意垂 足的位置; ②等体积法,通过等积变换间接求出点到平面的距 离.
1.(2015· 浙江卷)设α ,β 是两个不同的平面,l,m 是两条不同的直线,且 l⊂α,m⊂β.则下列结论正确的是 ( ) A.若 l⊥β,则α ⊥β B.若 α⊥β,则 l⊥m C.若 l∥β,则α ∥β D.若 α∥β,则 l∥m
解:因为 l⊥β,l⊂α,所以 α⊥β(面面垂直的判定定 理),故 A 正确.
【变式探究】
1.(2015·新课标卷Ⅰ)如图,四边形 ABCD 为菱形,G 为 AC 与 BD 的交点,BE⊥平面 ABCD. (1)证明:平面 AEC⊥平面 BED; (2)若∠ABC=120° ,AE⊥EC,三棱锥 EACD 的体积为 6 3 ,求该三棱锥的侧面积.
解:(1)证明:因为四边形 ABCD 为菱形,所以 AC⊥ BD, 因为 BE⊥平面 ABCD,AC⊂平面 ABCD,所以 AC⊥ BE, BD∩BE=B,故 AC⊥平面 BED. 又 AC⊂平面 AEC,所以平面 AEC⊥平面 BED. (2)设 AB=x,在菱形 ABCD 中, 3 x 由∠ABC=120° ,可得 AG=GC= x,GB=GD= . 2 2 3 因为 AE⊥EC,所以在 Rt△AEC 中,可得 EG= x, 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:立体几何综合应用
利用向量解决立体几何中的探索性问题,在近几年的高考中倍受青睐.下面举例说明其破解方法,
例1. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=22,BC=42,PA=2.(1)求证:AB⊥PC;
(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为45°,如果存在,求BM与平面MAC 所成角的正弦值,如果不存在,请说明理由.练习:如图,四棱锥P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD的中点.(1)证明:PD⊥平面ABE;
(2)若F为AB的中点,PM
→
=λPC
→
(0<λ<1),试确定λ的值,使二面角P-FM-B的余弦值为-
3
3.
1.(2019·广州模拟)(2019届广东省一模)已知五面体中,四边形
为矩形,,,且二面角的大小为(1)证明:平面;(2)求二面角的余弦值.
2.(2019·安徽合肥二检,理)如图①,在矩形ABCD中,AB=1,AD=2,点E为AD的中点,沿BE将△ABE 折起至△PBE,如图②所示,点P在平面BCDE上的射影O落在BE上.(1)求证:BP⊥CE;(2)求二面角B -PC-D的余弦值.3.(2019·湖北襄阳模拟)如图,多面体ABCDEF中,DE⊥平面ABCD,四边形ABCD是菱形,AB=2,
∠BAD=60°,四边形BDEF是正方形.(1)求证:CF∥平面AED;(2)在线段EC上是否存在点P,使得AP⊥平面CEF?若存在,求出
EP
PC的值;若不存在,说明理由.。
