5.1函数概念和图像
新版高中数学北师大版必修1课件3.5.1-3.5.2对数函数的概念、对数函数y=log2x的图像和性质

当堂检测
一
二
三
二、反函数
对数函数y=logax(a>0,a≠1)和指数函数y= ax (a>0,a≠1)互为反函
数.
【做一做 2】
若函数 f(x)=
1 3
������
的反函数是 y=g(x),则
g(3)=( )
A.217
B.27
C.-1
D.1
解析:由已知得 g(x)=log1x,于是 g(3)=log13=-1.
-2-
5.1 对数函数的概念 5.2 对数函数y=log2x的图像和性质
首页
课前篇 自主预习
课堂篇 探究学习
当堂检测
一
二
三
一、对数函数的概念
一般地,函数 y=logax (a>0,a≠1)叫作对数函数,其中x是自变量,函 数的定义域是(0,+∞).a叫作对数函数的底数.特别地,我们称以10为
底的对数函数y=lg x为常用对数函数;称以无理数e为底的对数函数
⑥y=12log3x 中,系数是12,而不是 1,故不是对数函数.
答案:(1)2 (2)①
-9-
5.1 对数函数的概念 5.2 对数函数y=log2x的图像和性质
探究一
探究二
探究三
首页 易错辨析
课前篇 自主预习
课课堂堂篇篇 探探究究学学习习
当堂检测
1.对数函数是一个形式定义:
2.求对数函数的解析式时,主要采用待定系数法求出底数a的值, 即得其解析式.
y=ln x为自然对数函数.
【做一做1】 若函数f(x)=(a2-a+1)log(a+1)x是对数函数,则实数
a=
.
解析:由a2-a+1=1,解得a=0,1.
《函数的概念和图象》示范公开课教案【高中数学苏教版】

第5章函数概念与性质5.1 函数的概念和图象第2课时函数的概念和图象1. 了解构成函数的要素;2. 理解函数图象是点的集合,能熟练作出一些初等函数的图象;3.能求简单函数的定义域和值域.教学重点:熟练作出一些初等函数的图象.教学难点:求简单函数的定义域.课件.PPT一、新课导入问题1:1. 函数定义中的“三性”是指哪些?2.函数的三要素是指什么?师生活动:学生先回忆总结,老师补充.预设的答案:1.函数定义中强调“三性”:任意性、存在性、唯一性,即对于非空数集A 中的任意一个(任意性)元素x,在非空数集B中都有(存在性)唯一(唯一性)的元素y与之对应.这三性只要有一个不满足,便不能构成函数.2.定义域、值域与对应关系.【想一想】初中如何求一个函数中自变量的取值范围的?高中又如何求出函数的定义域?设计意图:承上启下,引入新课.引语:要解决这个问题,就需要进一步学习函数的概念和图象.(板书:5.1.1函数的概念和图象)【探究新知】问题2:画出函数f (x )=-x 2+2x +3的图象,并根据图象回答下列问题. (1)比较f (0),f (1),f (3)的大小; (2)若x 1<x 2<1,比较f (x 1)与f (x 2)的大小. 师生活动:学生分析解题思路,给出答案.预设的答案:抛物线f (x )=-x 2+2x +3的顶点为(1,4)和x 轴交点为(-1,0),(3,0),和y 轴交点为(0,3)得函数图象如图.(1)根据图象,容易发现f (0)=3,f (1)=4,f (3)=0,所以f (3)<f (0)<f (1). (2)根据图象,容易发现当x 1<x 2<1时,有f (x 1)<f (x 2). 问题3:如何求函数23()112x f x x x =+-的定义域. 师生活动:学生分析解题思路,给出答案.预设的答案:由23()112x f x x x =++-可得:12010x x ->⎧⎨+≠⎩, 解得:12x <,且1x ≠- , ∴函数23()112x f x x x =+-的定义域为:()1,11,2⎛⎫-∞-- ⎪⎝⎭,故答案为:()1,11,2⎛⎫-∞-- ⎪⎝⎭.追问:(1)已知()y f x =的定义域为[0,1],求函数2(1)y f x =+的定义域;(2)已知(21)y f x =-的定义域为[0,1],求()y f x =的定义域;预设的答案:(1)∵2(1)y f x =+中的21x +的范围与()y f x =中的x 的取值范围相同.∴2011x +≤≤,∴0x =,即2(1)y f x =+的定义域为{0}.(2)由题意知(21)y f x =-中的[0,1]x ∈,∴1211x --≤≤. 又(21)y f x =-中21x -的取值范围与()y f x =中的x 的取值范围相同, ∴()y f x =的定义域为[1,1]-. 问题4:求下列函数的值域: (1)y =x +1,x ∈{1,2,3,4,5}; (2)y =x 2-2x +3,x ∈[0,3)师生活动:学生分析解题思路,给出答案.预设的答案:(1)(观察法)因为x∈{1,2,3,4,5},分别代入求值,可得函数的值域为{2,3,4,5,6}.(2)(配方法)y=x2-2x+3=(x-1)2+2,由x∈[0,3),再结合函数的图象,可得函数的值域为[2,6).设计意图:培养学生分析和归纳的能力.【巩固练习】例1. 作出下列函数的图象.(1)y=1-x(x∈Z且|x|≤2);(2)y=2x2-4x-3(0≤x<3).师生活动:学生分析解题思路,给出答案.预设的答案:(1)∵x∈Z且|x|≤2,∴x∈{-2,-1,0,1,2}.∴图象为一直线上的孤立点(如图(1)).(2)∵y=2(x-1)2-5,∴当x=0时,y=-3;当x=3时,y=3;当x=1时,y=-5.所画函数图象如图.∵x∈[0,3),故图象是一段抛物线(如图(2)).反思与感悟:作函数y=f(x)的图象分两种类型:(1)若y=f(x)是已学过的基本初等函数,则通过描出y=f(x)的图象上的一些关键点画出y=f(x)的图象;(2)若y=f(x)不是已学过的基本初等函数,则需要通过列表,描点、连线,这些基本步骤作出y=f(x)的图象.设计意图:明确函数的图象的画法.例2. 求下列函数的定义域:(1)y=2(1)11xxx+-+;(2)y5x-.师生活动:学生分析解题思路,给出答案.预设的答案:(1)要使函数有意义,自变量x的取值必须满足10,10,xx+≠⎧⎨-⎩≥解得x≤1且x≠-1,即函数的定义域为{x|x≤1,且x≠-1}.(2)要使函数有意义,自变量x的取值必须满足50,||30.xx-⎧⎨-≠⎩≥解得x≤5且x≠±3,即函数的定义域为{x|x≤5,且x≠±3}.设计意图:明确函数的定义域的求法.例3. 求下列函数的值域:(1)y=x+1,x∈{1,2,3,4,5};(2)y=x2-2x+3,x∈[0,3);(3)y=213xx+-.师生活动:学生分析解题思路,给出答案.预设的答案:(1)(观察法)因为x∈{1,2,3,4,5},分别代入求值,可得函数的值域为{2,3,4,5,6}.(2)(配方法)y=x2-2x+3=(x-1)2+2,由x∈[0,3),再结合函数的图象[如图(1)],可得函数的值域为[2,6).(3)(分离常数法)y=213xx+-=2(3)73xx-+-=2+73x-,显然73x-≠0,所以y≠2.故函数的值域为(-∞,2)∪(2,+∞).设计意图:明确函数的值域的求法.【课堂小结】1.板书设计:5.1.1函数的概念和图象1. 函数的图象的画法例12. 求函数的定义域例23. 求函数的值域例32.总结概括:问题:1.求函数的定义域应关注哪些问题?2. 求函数值域的方法是什么?3.如何求复合函数定义域?师生活动:学生尝试总结,老师适当补充. 预设的答案:1.求函数的定义域应关注四点:(1)要明确使各函数表达式有意义的条件是什么,函数有意义的准则一般有:①分式的分母不为0;②偶次根式的被开方数非负;③y =x 0要求x ≠0.(2)不对解析式化简变形,以免定义域变化.(3)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时,定义域是使得各式子都有意义的公共部分的集合.(4)定义域是一个集合,要用集合或区间表示,若用区间表示数集,不能用“或”连接,而应该用并集符号“∪”连接.2. 求函数值域,应根据各个式子的不同结构特点,选择不同的方法: (1)观察法:对于一些比较简单的函数,其值域可通过观察得到;(2)配方法:此方法是求“二次函数类”值域的基本方法,即把函数通过配方转化为能直接看出其值域的方法;(3)分离常数法:此方法主要是针对有理分式,即将有理分式转化为“反比例函数类”的形式,便于求值域.3.(1)已知()f x 的定义域为[,]a b ,求(())f g x 的定义域:解不等式()a g x b ≤≤即可得解;(2)已知(())f g x 的定义域为[,]a b ,求()f x 的定义域:求出()y g x =在[,]a b 上的值域即可得解;(3)已知(())f g x 的定义域为[,]a b ,求(())f h x 的定义域:先用类型二求出()f x 的定义域,再用类型一求出(())f h x 的定义域.设计意图:通过梳理本节课的内容,能让学生更加明确函数的概念与图象的有关知识. 布置作业: 【目标检测】1. 函数()1x f x 的定义域为( )A .()1,00,2⎛⎫-+∞ ⎪⎝⎭ B .1,02⎛⎫- ⎪⎝⎭C .()1,00,2⎡⎫-+∞⎪⎢⎣⎭D .1,2⎡⎫-+∞⎪⎢⎣⎭设计意图:巩固函数的定义域的求法。
北师大版数学必修一第三章 5 5.1 5.2 对数函数y=log2x的图像和性质

返回导航
上页
下页
二、反函数 指数函数 y=ax(a>0,a≠1)是对数函数 y=logax(a>0,a≠1)的 反函数 ;指数函数 y=ax(a>0,a≠1)与对数函数 y=logax(a>0,a≠1,x>0) 互为反函数 . 三、画 y=log2x(x>0)的图像的方法 (1) 描点法 ; (2) 变换法 .
x+1>0 解析:(1)要使函数有意义,需 1-x>0 x>-1 ,即 x<1
.
∴-1<x<1,∴函数的定义域为(-1,1). 5-x>0 (2)要使函数有意义,需x-2>0 x-2≠1 ∴定义域为(2,3)∪(3,5). x<5 ,∴x>2 . x≠3
∴函数的定义域为{x|0<x<2 且 x≠1}.
北师大版数学 ·必修1
探究二 [典例 2] 写出下列函数的反函数. 求函数的反函数
返回导航
上页
下页
1x (1)y=log 1 x;(2)y=ln x;(3)y=( ) ;(4)y=2x-1. e 6 1 1x [解析] (1)对数函数 y=log 1 x 的底数是 ,它的反函数是指数函数 y=( ) . 6 6 6
(2)对数函数 y=ln x 的底数是 e,它的反函数是指数函数 y=ex. 1x 1 (3)指数函数 y=( ) 的底数是 , 它的反函数是对数函数 y=log 1 x(x>0), 即 y=-ln x(x>0). e e e (4)由 y=2x-1 得 2x=y+1, ∴x=log2(y+1),
北师大版数学 ·必修1
北师大版数学 ·必修1
返回导航
5.1函数的概念和图象(第1课时函数的概念)课件高一上学期数学(1)

【课标要求】1.会用集合语言和对应关系刻画函数.2.理解函数的概念,了解构成函数的要素.3.会求简单函数的定义域与值域.
要点深化·核心知识提炼
知识点1. 函数的概念
概念
给定两个非空实数集合 和 ,如果按照某种对应关系 ,对于集合 中的每一个实数 ,在集合 中都有唯一的实数 和它对应,那么就称 为从集合 到集合 的一个函数
跟踪训练1(1) 下列图形中不是函数图象的是( )
A
A. B. C. D.
(2)下列各组函数表示同一个函数的是( )
BCD
D
C
4
5
6
7
7
6
4
5
3
4
5
6
4
6
5
4
C
A.3 B.4 C.5 D.7
BCD
1
2
3
4
5
2
3
4
2
3
BCD
A.2 B.3 C.4 D.5
(1)函数的表示:与用哪个字母表示无关;
(2)解析式的化简:在化简解析式时,必须是等价变形.
题型分析·能力素养提升
【题型一】函数的概念
例1(1) 下列各组函数是同一个函数的是( )
C
规律方法 1.判断一个对应关系是否为函数的方法
2.判断两个函数是否为同一个函数的注意点 (1)先求定义域,定义域不同则不是同一个函数; (2)若定义域相同,再看对应关系是否相同.
0
2
B
4.(多选题)下列四个对应关系,构成函数的是( )
AD
A. B. C. D.
4
(1)求函数的定义域;
B层 能力提升练
高中数学 第3章 §5 5.1+2 对数函数的概念 对数函数y=log2x的图像和性质优质课件 北师

例2:求下列函数的定义域 :
(1)y loga x2 ; (2)y loga (4 x).
答案 :(1){x|x≠0};
对数(duì shù)的真 数大于0!
(2){x|x < 4}.
第十一页,共27页。
【变式练习
(liànxí)】 求下列(xiàliè)函数的定义域:
(1) y loga (9 x);
于x取1,10,100,0.1时ຫໍສະໝຸດ 函数值.第九页,共27页。
解:(1)当x=1时,y log2 x log2 1 0 当x=2时, y log2 x log2 2 1 当x=4时, y log2 x log2 4 2 (2)当x=1时,y=lgx=lg1=0 当x=10时,y=lgx=lg10=1 当x=100时,y=lgx=lg100=2 当x=0.1时,y=lgx=lg0.1=-1
y (0, )
有唯一确定的 x 值与之对应,若把 y 当作自变量,则 x 就
是 y 的函数(hánshù).把函数(hánshù)
(hánshù).
x loga y
叫作对数函数
第五页,共27页。
习对惯于上(d,uì自yúx变)函量l数o用gxa 表y 示,y表示函数(hánshù),所以
这
个函数我(们hán把sh函ù)数就y 写lo成ga x(a 0且a 1) 叫作对数函
我们知道,指数函数y a x (a 0, a 1), 对于x的每一个确定的值,
y 都有唯一确定的值和它对应;并且x1 x2时,y1 y2 .
指数函数(háynshùa)x (a 0且a 1) 反映了数集 R 与数集
y y 0之间是一种一一对应关系。 .
在这个关系式中, 对于任意的
2020-2021学年北师大版高一数学必修1课件:第三章5对数函数

3.函数y=logax,y=logbx,y=logcx,y=logdx的图像如图所示,则a,b,c,d的大小顺序是( A ) A.c<d<1<a<b B.1<d<c<a<b C.c<d<1<b<a D.d<c<1<a<b
解析
5.2+5.3 刷基础
题型1 对数函数的图像
4.函数
f
x=
x x
loga
x0
a
1
的图像大致为(
B
)
解析
5.2+5.3 刷基础
题型1 对数函数的图像
5.已知实数a,b满足等式log2a=log3b,给出下列五个关系式: ①a>b>1;②b>a>1;③a<b<1;④b<a<1;⑤a=b.其中可能成立的关系式是_②__④__⑤___.
解析
5.2+5.3 刷基础
15.
(C )
解析
5.1 对数函数的概念 刷易错
易错点2 忽视指数函数与对数函数的反函数关系而致错
16.已知函数 f x=log1 x2 的定义域为(1,7],则它的反函数f-1(x)的定义域为[_-__2_,__-__1.)
3
解析
5.2+5.3 刷基础
题型1 对数函数的图像
1.[江苏七校联盟2019高一期中]函数y=log2(x+1)的图像大致是( C )
5.1 对数函数的概念 刷易错
易错点1 忽视指数、对数运算而致错
13.与函数y=10lg(x-1)相等的函数是( A )
解析
5.1 对数函数的概念 刷易错
易错点1 忽视指数、对数运算而致错
14.
1
=___2_____.
苏教版高中同步学案数学必修第一册精品课件 第5章 函数概念与性质 5.1 函数的概念和图象

变式训练2
函数 f(x)=√1 +
A.[-1,+∞)
B.(-∞,0)∪(0,+∞)
C.[-1,0)∪(0,+∞)
D.R
2
− 的定义域是(
)
答案 C
解析 要使函数 f(x)=√1 +
2
− 有意义,
1 + ≥ 0,
应关系不同,故不是同一个函数;
对于 C,f(t)=
1+
与
1-
g(x)=
1+
的定义域均为[-1,1),函数对应关系相同,故是同
1-
一个函数;
对于 D,f(x)=1 的定义域为
故选 C.
1
R,g(x)=x·的定义域为{x|x≠0},故不是同一个函数.
探究点二 求函数的定义域
【例2】 求下列函数的定义域:
提示确定.
知识点3 函数的图象
将自变量的一个值x0作为 横坐标 ,相应的函数值f(x0)作为纵坐标,就得到
坐标平面上的一个点 (x0,f(x0))
.当自变量取遍函数定义域A中的每一个
值时,就得到一系列这样的点.所有这些点组成的集合(点集)为
{(x,f(x))|x∈A},
即{(x,y)|y=f(x),x∈A},
1- ≥ 0,
即函数定义域为{x|x≤1,且 x≠-1}.
规律方法
求函数定义域的常用方法
(1)若f(x)是分式,则应考虑使分母不为零.
(2)若f(x)是偶次根式,则被开方数大于或等于零.
(3)若f(x)是指数幂,则函数的定义域是使幂运算有意义的实数集合.
第三章§5.5.1、5.5.2对数函数y=log2x的图像和性质
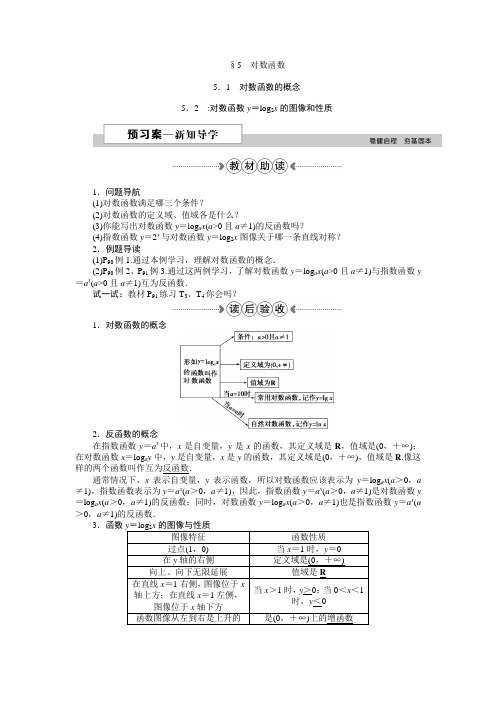
§5对数函数5.1对数函数的概念5.2:对数函数y=log2x的图像和性质1.问题导航(1)对数函数满足哪三个条件?(2)对数函数的定义域、值域各是什么?(3)你能写出对数函数y=log a x(a>0且a≠1)的反函数吗?(4)指数函数y=2x与对数函数y=log2x图像关于哪一条直线对称?2.例题导读(1)P90例1.通过本例学习,理解对数函数的概念.(2)P90例2、P91例3.通过这两例学习,了解对数函数y=log a x(a>0且a≠1)与指数函数y =a x(a>0且a≠1)互为反函数.试一试:教材P91练习T3、T4你会吗?1.对数函数的概念2.反函数的概念在指数函数y=a x中,x是自变量,y是x的函数,其定义域是R,值域是(0,+∞);在对数函数x=log a y中,y是自变量,x是y的函数,其定义域是(0,+∞),值域是R.像这样的两个函数叫作互为反函数.通常情况下,x表示自变量,y表示函数,所以对数函数应该表示为y=log a x(a>0,a ≠1),指数函数表示为y=a x(a>0,a≠1),因此,指数函数y=a x(a>0,a≠1)是对数函数y =log a x(a>0,a≠1)的反函数;同时,对数函数y=log a x(a>0,a≠1)也是指数函数y=a x(a >0,a≠1)的反函数.3.函数1.判断正误(正确的打“√”,错误的打“×”)(1)若a >0且a ≠1,x =log a y 和y =log a x 都是对数函数.( )(2)已知a >0且a ≠1,则y =a x 的图像与x =log a y 的图像相同;与y =log a x 的图像关于直线y =x 对称.( )(3)函数y =log 2x 与y =log 12x 的图像关于x 轴对称.( )答案:(1)√ (2)√ (3)√2.设P =2log 23,Q =log 23,R =log 25,则( ) A .R <Q <P B .P <R <Q C .Q <R <P D .R <P <Q 解析:选C.因为P =3,Q =log 23<log 24=2, R =log 25<log 28=3,又因为R >log 24=2, 所以Q <R <P ,故选C.3.函数f (x )=log 2x 的定义域为________. 解析:由log 2x ≥0,即log 2x ≥log 21, 因为y =log 2x 在(0,+∞)上是递增的,所以x ≥1,故f (x )=log 2x 的定义域为{x |x ≥1}. 答案:{x |x ≥1}4.对数函数f (x )的图像经过点⎝⎛⎭⎫19,2,则f (3)=________. 解析:设f (x )=log a x (a >0,且a ≠1),因为对数函数f (x )的图像经过点⎝⎛⎭⎫19,2,所以f ⎝⎛⎭⎫19=log a19=2.所以a 2=19. 所以a =⎝⎛⎭⎫1912=⎣⎡⎦⎤⎝⎛⎭⎫13212=13.所以f (x )=log 13x .所以f (3)=log 133=log 13⎝⎛⎭⎫13-1=-1.答案:-1对数函数必需满足三个条件(1)log a x 前面的系数必须是1;(2)底数为大于0且不等于1的常数; (3)对数的真数仅有自变量x .对数函数的概念下列函数是对数函数的序号是________.①y =log x 2;②y =-log 3x ;③y =log 0.4x ;④y =log (2a -1)x ⎝⎛⎭⎫a >12,且a ≠1,x 是自变量;⑤y =log 2(x +1).[解析] ①式中的自变量在对数的底数的位置,不是对数函数;②式中y =-log 3x =log 13x 是对数函数;③式中y =log 0.4x =log 0.42x 是对数函数;④式中对数的底数2a -1是一个大于0且不等于1的常数,符合对数函数的定义;⑤式中函数在对数的真数处不只是自变量x ,而是关于x 的表达式x +1,故不是对数函数.由此可知只有②③④是对数函数.[答案] ②③④方法归纳(1)判定对数函数的标准要满足三个条件;(2)有些函数要在变形后进行判断,观察问题的实质.1.下列函数是对数函数的有________. ①y =3log 21x ; ②y =log 2x ;③y =log a x x (a >0且a ≠1); ④y =log x x (x >0且x ≠1).解析:①y =log 21x 3=log 321x 是对数函数; ②y =log 2x =log 4x 是对数函数;③由于真数为x x ,且无论怎样变形均不符合对数函数的三个条件,所以不是对数函数; ④由于底数和真数都是变量,不是对数函数. 答案:①②反函数写出下列函数的反函数: (1)y =ln x ;(2)y =log 12x ; (3)y =πx ;(4)y =⎝⎛⎭⎫13x.[解] (1)对数函数y =ln x ,它的底数是无理数e ,它的反函数是y =e x .(2)对数函数y =log 12x ,它的底数是12,它的反函数是y =⎝⎛⎭⎫12x .(3)指数函数y =πx,它的底数是π,它的反函数为y =log πx .(4)指数函数y =⎝⎛⎭⎫13x ,它的底数是13,它的反函数是y =log 13x .方法归纳(1)求一个函数的反函数的步骤:①由y =a x (或y =log a x )解得x =log a y (或x =a y ).②将x =log a y (或x =a y )中的x 与y 互换位置,得y =log a x (或y =a x ). ③由y =a x (或y =log a x )的值域,写出y =log a x (或y =a x )的定义域. (2)互为反函数的两个函数的图像关于直线y =x 对称.2.(1)已知函数y =g (x )的图像与函数y =log 3x 的图像关于直线y =x 对称,则g (2)的值为( )A .9 B. 3 C. 2 D .log 32(2)若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,其图像经过点(a ,a ),则f (x )=( )A .log 2xB .log 12xC .2-xD .x 2解析:(1)选A.y =g (x )与y =log 3x 互为反函数, 故g (x )=3x , 故g (2)=32=9.(2)选B.由题意知(a ,a )在y =a x上,可得a a=a =a 12,即a =12.因为y =(12)x 的反函数为y =log 12x ,所以f (x )=log 12x .函数y =log 2x 的图像与性质根据函数f (x )=log 2x 的图像和性质解决以下问题. (1)若f (a )>f (2),求a 的取值范围;(2)求y =log 2(2x -1)在x ∈[2,14]上的最值. [解] 函数y =log 2x 的图像如图所示.(1)因为y =log 2x 是增函数,若f (a )>f (2),即log 2a >log 22,则a >2. 所以a 的取值范围为(2,+∞).(2)因为2≤x ≤14,所以3≤2x -1≤27, 所以log 23≤log 2(2x -1)≤log 227=3log 23.所以函数y =log 2(2x -1)在x ∈[2,14]上的最小值为log 23,最大值为3log 23.借助本例f (x )=log 2x 的图像,试判断方程⎝⎛⎭⎫12x -log 2x =0解的个数.解:在同一坐标系中画出函数y =⎝⎛⎭⎫12x 与y =log 2x 的图像,如图所示.由图知它们的图像有一个交点,即方程⎝⎛⎭⎫12x =log 2x 仅有一个解,也就是方程⎝⎛⎭⎫12x -log 2x=0有一个解.方法归纳与对数函数有关的图像的画法(1)列表描点法:列表,描点,连线. (2)平移变换法:左加右减,上加下减.(3)对称变换法:y =f (x )与y =f (-x )关于y 轴对称;y =f (x )与y =-f (x )关于x 轴对称;y =f (x )与y =-f (-x )关于原点对称.3.(1)函数f (x )=|log 12x |在下列哪个区间上是增加的( )A.⎝⎛⎦⎤0,12 B .(0,1] C .(0,+∞)D .[1,+∞)(2)设函数f (x )=⎩⎪⎨⎪⎧21-x,x ≤1,1-log 2x ,x >1,则满足f (x )≤2的x 的取值范围是( )A .[-1,2]B .[0,2]C .[1,+∞)D .[0,+∞)解析:(1)选D.f (x )=⎩⎨⎧-log 12x ,x ≥1,log 12x ,0<x <1.其图像如图.所以f (x )在[1,+∞)上是增加的.(2)选D.因为f (x )≤2,所以有⎩⎪⎨⎪⎧x ≤1,21-x ≤2或⎩⎪⎨⎪⎧x >1,1-log 2x ≤2,解得x ≥0,故选D.已知f (x )=|log 2x |,若1c>a >b >1,则( )A .f (a )>f (b )>f (c )B .f (c )>f (b )>f (a )C .f (c )>f (a )>f (b )D .f (b )>f (a )>f (c )[解析] 先作出函数y =log 2x 的图像,再将图像在x 轴下方的部分沿x 轴翻折到上方,这样,我们便得到了y =|log 2x |的图像,如图.由图可知,f (x )=|log 2x |在(0,1)上是减少的,在(1,+∞)上是增加的,于是f ⎝⎛⎭⎫1c >f (a )>f (b ),又f ⎝⎛⎭⎫1c =|log 21c|=|-log 2c |=|log 2c |=f (c ).所以f (c )>f (a )>f (b ).[答案] C[感悟提高] (1)作绝对值函数|f (x )|的图像是正确求解的关键,作图时充分利用f (x )与|f (x )|之间的关系.(2)利用函数单调性来比较大小,必须使自变量在同一单调区间上.(3)利用对数的运算性质来寻找f (1c )与f (c )的关系.1.下列各项中表示同一个函数的是( ) A .y =2log 2x 与y =log 2x 2 B .y =10lg x 与y =lg 10x C .y =x 与y =x log x x D .y =x 与y =ln e x解析:选D.对于A 中两个函数的定义域不同,因此不是同一个函数.同样B 、C 中两个函数的定义域也都不同,故不是同一个函数.2.已知f (x )是函数y =log 2x 的反函数,则y =f (1-x )的图像是( )解析:选C.f (x )与y =log 2x 互为反函数,因此f (x )=2x ,故y =f (1-x )=21-x =(12)x -1,该函数图像是由y =(12)x 的图像向右平移1个单位得到的,故选C.3.已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >1,3x ,x ≤1,则f (1)+f (2)=( )A .1B .4C .9D .12解析:选B.由题意知,f (1)=31=3;f (2)=log 22=1, 所以f (1)+f (2)=3+1=4.4.函数f (x )=1log 2x -1的定义域为________.解析:由题意得:⎩⎪⎨⎪⎧x >0,log 2x -1>0,可得:x ∈(2,+∞).答案:(2,+∞)[A.基础达标]1.与函数y =2log2(x -2)表示同一个函数的是( )A .y =x -2B .y =x 2-4x +2C .y =|x -2|D .y =(x -2x -2)2解析:选D.y =2log2(x -2)=x -2(x >2),对于A :x ∈R ,排除A ;对于B :y =x -2(x ≠-2),排除B ;对于C :y =|x -2|=⎩⎪⎨⎪⎧x -2,x ≥2,2-x ,x <2,排除C ;故选D.2.在同一坐标系中,函数y =3-x 与函数y =log 3x 的图像可能是( )解析:选C.y =3-x =(13)x 是减函数,y =log 3x 是增函数.3.函数f (x )=⎩⎪⎨⎪⎧4x -4,x ≤1,x 2-4x +3,x >1的图像与函数g (x )=log 2x 图像交点个数是( )A .1B .2C .3D .4解析:选C.在同一个坐标系中画出f (x )和g (x )的图像,如图,由图像可知f (x )与g (x )的交点个数为3.4.设函数f (x )=⎩⎪⎨⎪⎧2x,x ≤0log 2x ,x >0,则f (f (-1))=( )A .2B .1C .-2D .-1解析:选D.因为-1<0,所以f (-1)=2-1=12;因为12>0,所以f (12)=log 212=log 22-1=-1.故f (f (-1))=-1.5.已知函数f (x )=log 2x ,其中|f (x )|≥1,则实数x 的取值范围是( )A.⎝⎛⎭⎫-∞,12B.⎝⎛⎦⎤0,12∪[2,+∞) C .[2,+∞) D.⎝⎛⎭⎫-∞,12∪[2,+∞) 解析:选B.因为|f (x )|≥1,所以log 2x ≥1或log 2x ≤-1.由于log 2x 在(0,+∞)上是增函数,故x ≥2或x ≤12.所以,x 的取值范围是⎝⎛⎦⎤0,12∪[2,+∞). 6.若函数y =f (x )是函数y =5x 的反函数,则f (f (5))=________. 解析:因为y =f (x )与y =5x 互为反函数,所以f (x )=log 5x . 所以f (f (5))=f (log 55)=f (1)=log 51=0. 答案:07.设f (x )是奇函数,当x >0时,f (x )=log 2x ,则当x <0时,f (x )=________.解析:当x <0时,-x >0,f (-x )=log 2(-x ).又因为f (x )为奇函数,所以f (-x )=-f (x )=log 2(-x ),故当x <0时,f (x )=-log 2(-x ).答案:-log 2(-x )8.设函数f (x )=⎩⎪⎨⎪⎧4x ,x ≤1,log 0.5x ,x >1.若f (f (a ))=-1,则a =________.解析:由x ≤1时4x∈(0,4],x >1时,log 0.5x <0可知f (a )>1,且a ≤1.故f (f (a ))=f (4a )=log 0.54a =-2a =-1,可得a =12.答案:129.已知全集U =R ,集合A ={x |-1≤x ≤3},B ={x |log 2(x -a )<1,a ∈R }. (1)若a =2,求A ∩(∁U B );(2)若A ∪B =A ,求实数a 的取值范围.解:B ={x |log 2(x -a )<1,a ∈R }={x |a <x <a +2}.(1)当a =2时,B ={x |2<x <4},∁U B ={x |x ≤2或x ≥4},A ∩(∁U B )={x |-1≤x ≤2}.(2)由A ∪B =A ,得B ⊆A ,所以⎩⎪⎨⎪⎧a ≥-1,a +2≤3,得-1≤a ≤1.10.已知函数f (x )=log 21-mxx -1的图像关于原点对称,求m 的值.解:因为f (x )=log 21-mxx -1的图像关于原点对称,所以f (x )为奇函数,所以f (-x )=-f (x ),所以log 21+mx -x -1=-log 21-mx x -1=log 2x -11-mx ,所以1+mx -x -1=x -11-mx,所以1-m 2x 2=-x 2+1,所以m 2=1,所以m =1或m =-1.当m =1时不满足题意,舍去,故m =-1.[B.能力提升] 1.已知函数y =f (log 12x )的定义域为[14,12],则函数y =f (2x )的定义域为( )A .[-1,0]B .[0,2]C .[-1,2]D .[0,1]解析:选D.当x ∈[14,12]时,log 12x ∈[1,2],故1≤2x ≤2,可得x ∈[0,1].2.定义在R 上的函数f (x )=⎩⎪⎨⎪⎧log 2(4-x ),x ≤0,f (x -1)-f (x -2),x >0,则f (3)的值为( )A .-1B .-2C .1D .2解析:选B.由题意知,因为3>0,所以f (3)=f (2)-f (1)=f (1)-f (0)-f (1)=-f (0). 又f (0)=log 2(4-0)=2.故f (3)=-f (0)=-2.3.已知函数f (x )=|log 2x |,正实数m ,n 满足f (m )=f (n ),若f (x )在区间[m 2,n ]上的最大值为2,则m ,n 的值分别为________.解析:由f (x )=|log 2x |=⎩⎪⎨⎪⎧log 2x ,x ≥1,-log 2x ,0<x <1的图像(图略)及f (m )=f (n ),可知0<m <1<n ,所以0<m 2<m <1.可知f (x )在[m 2,n ]上的最大值为f (m 2)=|log 2m 2|=-log 2m 2=2.解得m =12,对f (n )=f (m )=f (12)=|log 212|=1(n >1),所以log 2n =1,所以n =2.答案:12,24.已知函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)是减少的,若实数a 满足f (log 2a )+f (log 12a )≥2f (1),则a 的取值范围是________.解析:因为f (log 2a )+f (log 12a )=f (log 2a )+f (-log 2a )=2f (log 2a )≥2f (1),所以f (log 2a )≥f (1).由f (x )是定义在R 上的偶函数,且在区间[0,+∞)上是减少的,所以|log 2a |≤1,即-1≤log 2a ≤1,所以12≤a ≤2.答案:⎣⎡⎦⎤12,25.已知f (x )=log 2x +1x -1.(1)求f (x )的定义域和值域; (2)判断f (x )的奇偶性并证明.解:(1)由题可得:x +1x -1>0,解得:x <-1或x >1;所以定义域为(-∞,-1)∪(1,+∞).设u =x +1x -1=1+2x -1,当x ∈(-∞,-1)∪(1,+∞)时,u ∈(0,1)∪(1,+∞),所以y =log 2u ∈(-∞,0)∪(0,+∞), 所以f (x )值域为(-∞,0)∪(0,+∞). (2)f (x )的定义域关于原点对称,f (x )+f (-x )=log 2x +1x -1+log 2-x +1-x -1=log 2x +1x -1+log 2x -1x +1=log 2⎝ ⎛⎭⎪⎫x +1x -1·x -1x +1=log 21=0.所以f (-x )=-f (x ),所以f (x )为奇函数.6.(选做题)设f (x )=2(log 2x )2+2a log 21x +b ,已知x =12时,f (x )有最小值-8.(1)求a 与b 的值; (2)求f (x )>0的解集A .解:(1)因为x >0,log 2x ∈R ,令u =log 2x ,则 f (x )=2(log 2x )2-2a log 2x +b=2⎝⎛⎭⎫log 2x -a 22-a 22+b=2⎝⎛⎭⎫u -a 22-a22+b . 由题意得u =-1时,f (x )最小=-8,所以⎩⎨⎧a2=-1,-a 22+b =-8,所以⎩⎪⎨⎪⎧a =-2,b =-6.(2)由(1)得,f (x )=2(log 2x )2+4log 2x -6,f (x )>0,即2u 2+4u -6>0,即u 2+2u -3>0, 所以u <-3或u >1,所以log 2x <-3或log 2x >1,故0<x <18或x >2,即f (x )>0的解集为A =⎝⎛⎭⎫0,18∪(2,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k
b 3 4k b
1
,解得
k
b
2 5
13
5
⸫DE’解析式为 y 2 x 13 55
y y
x
2 5
x
13 5
解得
x
y
13 7
13 7
⸫Q(-
13,- 13), 77
此时距离之和为 DE’的长度= 52 22 29
考点一 平面直角坐标系(5年1考)
导案【基础过关 】
点 P2015 的坐标是 (0,0) .
故选: A .
考点二 自变量取值范围(5年0考)
6. 在 函 数 y 3 x2
___x_≥_-_1_且___x_≠_2__. _______.
x 1 中 , 自 变量 x 的 取 值 范围 是
2. 函数 y= x 中的自变量 x 的取值范围是( A ) x 1
B’
、C’
;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平
CCC
555
4
B’ BB’’
44
3
33
2
212
A
AA
11 -6 -5 -4 -3 -2 -1 O 1
'
A
2 AA'3'
B
BB
4 5 6x
面内任一点 P(A,B)关于第一、三象限的角平分线 l 的
对称点 P 的坐标为
(不必证明);
(3)已知两点 D(1,-3)、E(-1,-4),试在直线 l 上确定一点 Q,
四边形 ABCD 的周长是: AB BC AD CD 2 3 5 3 2 10 2 3 ,
由图象可得,
故答案为:10 2 3 .
AN 5 4 1 , ND CM 7 5 2 , DM 2 ,
考点三 函数表示方法(5年3考)
导案【能力提升 】
9.如图,矩形 ABCD 中, AB 3 , AD 4 ,直线l 从点 D 出发,沿射线 DA 方向以每秒 1 个 单位的速度平移运动,至直线经过 B 点时停止运动.若直线l / / AC ,与 DA (或 AB) 交于点 M ,与 DC (或 CB) 交于点 N .设直线l 运动时间为t (秒) , DMN 的面积为 y ,则 y 关 于 t 的函数图象是 ( C )
此规律继续 以 A、B、C 为对称中心重复前面的操作,依次得到 P4,P5,P6,…,则点 P2015 的坐标是( )
A.(0,0)
B.(0,2)
C.(2,﹣4)
D.(﹣4,2)
解:设 P1(x, y) ,Q 点 A(1,1) 、 B(1, 1) 、C(0,1) ,
同理可得, P1(2, 4) , P2 (4, 2) , P3(4,0) , P4 (2, 2) ,
P5 (0,0) , P6 (0, 2) , P7 (2, 4) ,,
点 P(0, 2) 关于 A 的对称点为 P1 , P1 关于 B 的对称点 P2 ,
பைடு நூலகம்
每 6 个数循环一次.
x 1 , y 2 1 ,解得 x 2 , y 4 ,
2
2
Q 2015 3355 , 6
P1(2, 4) .
考点一 平面直角坐标系(5年1考)
导案【能力提升 】
777 yy
10.如图,在平面直角坐标系中,直线 l 是第一、三象限的角平分线.
666
l ll
(1)由图易知 A(0,2)关于直线 l 的对称点 A 的坐标为(2,0),
请在图中分别标明 B(5,3) 、C(-2,5) 关于直线 l 的对称
点 B 、 C 的位置,并写出他们的坐标:
5.1函数的概念和图像
山东山大基础教育集团初三数学备课组
考点一 平面直角坐标系(5年1考)
导案【基础过关 】
2.点 P(2m-1,3)在第二象限,则 m 的取值范围是_________
【课堂检测 】
4.将点 (1,2) 向左平移 1 个单位,再向下平移 2 个单位后得到对应点的坐标是
.
5.点 P(-2,3)关于 x 轴的对称点的坐标是________.关于 y 轴对称的点的坐标是________.
A. x≥0
B. x≠﹣1
C. x>0
D. x≥0 且 x≠﹣1
导案【能力提升 】
【课堂检测 】
考点三 函数表示方法(5年3考)
4.如图 1,在四边形 ABCD 中,AD∥BC,∠B=30°,直线 l⊥AB.当直线 l 沿射线 BC 方向,从点 B 开始向右平移时, 直线 l 与四边形 ABCD 的边分别相交于点 E,F.设直线 l 向 右平移的距离为 x,线段 EF 的长为 y,且 y 与 x 的函数关 系如图 2 所示,则四边形 ABCD 的周长是________.
使点 Q 到 D、E 两点的距离之和最小,并求出 Q 点坐
标.
--66
--55E’--44
--33
Q--22 --11----1121 OO 11 22
---232
'
D
33
44 55
C’
66 xx
'
E
---343
'
EE '
---454 ---565
'
DD '
第1(0第题图-2-662题图)
((第第2222题题图图))
7y
6
5
B’
C
4
3
2A
1
E’ Q -6 -5 -4 -3 -2 -1 O 1 -1 -2
'
A
23
-3
'
D
'
E
-4
-5
-6
l B 4 5 6x
(第22题图)
解:作 E 关于 l 的对称点 E’(-4,-1),连接 DE’,交直线 l 于点 Q,点 Q 即为所求。
设
DE’解析式为
y=kx+b,将(1,-3)(-4,-1)代入得
P1(-3,-2) P2(3,-2) P3(-3,2)
P4(-3,-2).......
考点一 平面直角坐标系(5年1考)
课检【聚焦济南 】
(2015•济南•3 分)在平面直角坐标系中有三个点 A(1,﹣1)、B(﹣1,﹣1)、C(0,1),
点 P(0,2)关于 A 的对称点为 P1,P1 关于 B 的对称点 P2,P2 关于 C 的对称点为 P3,按
3.在平面直角坐标系中,一颗棋子从点 P(-3,2)处开始跳动,第一次跳到点 P 关于 x 轴的 对称点 P1 处,接着跳到点 P1 关于 y 轴的对称点 P2 处,第三次再跳到点 P2 关于原点的对 称点处 P3,…,如此循环下去.当跳动第 2020 次时,棋子落点处 P2020 的坐标是 (3,-2) .
导案【基础过关 】
解:Q B 30 ,直线 l AB , BE 2EF , 由图可得, AB 4cos30 4 3 2 3 ,
2 BC 5 ,
Q B 30 , EF AB , M 60 , 又Q DM MC 2 , DMC 是等边三角形, DC DM 2 ,
AD 7 4 3 ,
