COX回归模型的样本含量的计算方法及软件实现_徐英
COX回归

§13.3 Cox Regression过程上面给大家介绍的是两种生存分析方法,但它们只能研究一至两个因素对生存时间的影响,当对生存时间的影响因素有多个时,它们就无能为力了,下面我给大家介绍Cox Regression 过程,这是一种专门用于生存时间的多变量分析的统计方法。
Cox Regression过程主要用于:1、用以描述多个变量对生存时间的影响。
此时可控制一个或几个因素,考察其他因素对生存时间的影响,及各因素之间的交互作用。
例13.3 40名肺癌患者的生存资料(详见胡克震主编的《医学随访统计方法》1993,77页)注:原数据库是用亚变量定义肺癌分类:0,0,0为其它癌;1,0,0为鳞癌;0,1,0为小细胞癌;0,0,1为腺癌。
表中的最后一个变量是我加上去的癌症类别,1为鳞癌;2为小细胞癌;3为腺癌;4为其它癌。
实践表明结果与用亚变量计算一样。
13.3.1 界面说明图9 Cox回归主对话框【Time】框、【Status】框前文已经介绍过了,这里我就不再废话唠叨的了。
Block 1 of 1右边的Next钮被激活。
这个按钮用于确定不同自变量进入回归方程的方法,详见Method 框的内容。
用同一种方法进入回归方程的自变量在同一个Covariates框内。
【Covariates】框选入自/协变量,即选入你认为可能对生存时间有影响的变量。
【Method】框选择自变量进入Cox回归方程的方法,SPSS提供下面几种方法:∙Enter: Covariates框内的全部变量均进入回归模型。
∙Forward: Conditional: 基于条件参数估计的向前法。
∙Forward: LR: 基于偏最大似然估计的向前法。
∙Forward: Wald: 基于Wald统计量的向前法。
∙Backward: Conditional: 基于条件参数估计的后退法。
∙Backward: LR: 基于偏最大似然估计的后退法。
cox模型校准曲线(测试集)的6种实现方法

Cox模型校准曲线是生存分析中非常重要的概念之一。
它可以帮助我们评估Cox比例风险模型对于实际观测数据的拟合情况,并且在一定程度上反映了模型的预测准确性。
在实际工作中,对Cox模型校准曲线的实现方法有着不同的需求,因此有多种实现方法可以供我们选择。
在本文中,我们将探讨Cox模型校准曲线在测试集中的6种实现方法,并对这些方法进行全面评估和比较。
1. 目标理解在开始讨论6种实现方法之前,让我们首先回顾一下Cox模型校准曲线的概念。
Cox比例风险模型是用于分析生存数据的一种常见统计模型,它可以帮助我们评估某些危险因素对于生存时间的影响。
而Cox模型的校准曲线则是用来评估模型对于未来事件的预测能力,通常用来检验模型是否存在预测偏差或准确性问题。
准确地实现Cox模型校准曲线对于我们正确评估模型的性能至关重要。
2. 实现方法一:基于R语言的survival包第一种实现方法是使用R语言中的survival包来绘制Cox模型校准曲线。
这种方法在生存分析领域非常常见,survival包提供了丰富的函数和工具来进行生存分析相关的统计计算和图形展示。
通过调用survival 包中的函数,我们可以很容易地在测试集上实现并绘制Cox模型的校准曲线。
3. 实现方法二:基于Python的lifelines包另一种常见的实现方法是使用Python中的lifelines包来实现Cox模型校准曲线。
lifelines包是针对生存分析任务的Python包,它提供了类似于survival包的功能,并且可以方便地绘制Cox模型的校准曲线。
相比于R语言,使用Python进行生存分析的优势在于其丰富的数据处理和机器学习库,例如numpy、pandas和scikit-learn,可以更加方便地进行数据预处理和模型评估。
4. 实现方法三:基于SPSS的生存分析模块除了使用编程语言进行实现外,我们还可以使用统计软件SPSS中的生存分析模块来实现Cox模型校准曲线。
COX回归模型的样本含量的计算方法及软件实现

性 。因此 ,00年 , i 20 Hs h和 L v r在 C nrl dCii l 一 e a oi o tol 1 c e na
算公式 。但是 , 简单的忽略这部分数据 , 往往会造 成信 息的损
失。如果考虑删失数据 , 则样本量 的计算 又变得非 常复杂 , 因 此, 直到今天 , 这个问题依然是 国内外统计学 者研 究的热 点之
型所需样本量的计算公式及其目前可以实现该计算方法的软件, 并通过实例说明了该公式的应用 , 以期提高今 后研究工作的效 率。
关键词 : 生存分析 ; C OX回归模型 ; 样本量 ; 统计软件
C X回归模型在生存分析 中应用 非常广泛 , 而 , 0 然 关于应
治疗组 人数所 占的 比例。l △是指风险 比的对 数。该 公式主 o g 要是用来计算随机 化分组研 究的设计 所需 的样本量 , 用于 适
1 ・ 8
通讯作者 : 骆福添
中图分类号 : 151 R 9.
文献标识码 : A
・ 医学教 学模型探讨 ・
C X回归模型 的样本含量 的计算方法及软件实现 O
徐 英 骆福添
( 广东药学院卫生统计学教研室 广州 50 1) 13 0
摘 要: 目 前生存分析中 C X回归模型到底需要多少样本量往往靠经验法来估计 。旨在介绍并推广生存分析 中 C X回归 模 O O
一
as l 上将 Sh e f d的计算公式进行了扩展 [ , eone l 3 现介绍如下 : ]
生存分析:cox回归建模
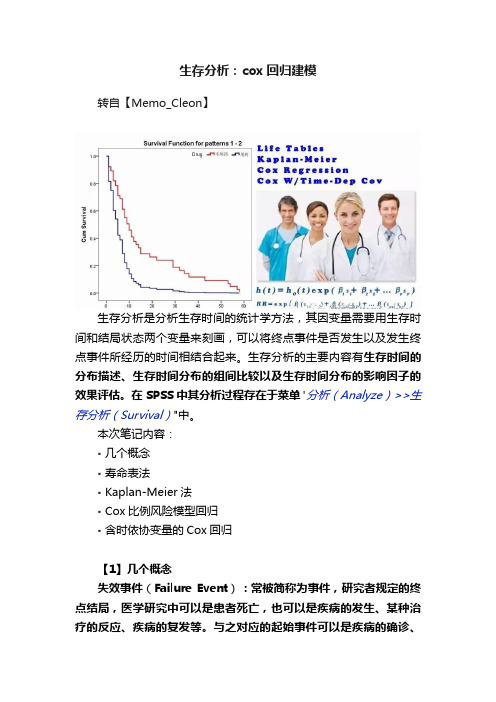
生存分析:cox回归建模转自【Memo_Cleon】生存分析是分析生存时间的统计学方法,其因变量需要用生存时间和结局状态两个变量来刻画,可以将终点事件是否发生以及发生终点事件所经历的时间相结合起来。
生存分析的主要内容有生存时间的分布描述、生存时间分布的组间比较以及生存时间分布的影响因子的效果评估。
在SPSS中其分析过程存在于菜单"分析(Analyze)>>生存分析(Survival)"中。
本次笔记内容:▪几个概念▪寿命表法▪Kaplan-Meier法▪Cox比例风险模型回归▪含时依协变量的Cox回归【1】几个概念失效事件(Failure Event):常被简称为事件,研究者规定的终点结局,医学研究中可以是患者死亡,也可以是疾病的发生、某种治疗的反应、疾病的复发等。
与之对应的起始事件可以是疾病的确诊、某种治疗的开始等。
生存时间(Survival Time):常用t表示,从规定的起始事件开始到失效事件出现所持续的时间。
对于失访者,是失访前最后一次随访的时间。
删失/截尾(Censoring):由于某些原因在随访中并没有观测到失效事件而不知道确切的生存时间,此部分数据即删失数据。
常见原因有失访、患者退出试验、事件发生是由于非研究性疾病(如研究病人发生脑卒中后的生存时间,结果病人因为车祸死亡)、研究结束时研究对象仍未发生失效事件。
删失数据的生存时间为起始事件到截尾点所经历的时间。
生存函数(Survival Function)与风险函数(Hazard Function):生存函数也称为积累生存函数/概率(Cumulative Survival Function)或生存率,符号S(t),表示观察对象生存时间越过时间点t的概率,t=0时生存函数取值为1,随时间延长生存函数逐渐减小。
以生存时间为横轴、生存函数为纵轴连成的曲线即为生存曲线。
风险函数表示生存时间达到t后瞬时发生失效事件的概率,用h(t)表示,h(t)=f(t)/S(t)。
cox 标准化回归系数 -回复

cox 标准化回归系数-回复什么是cox标准化回归系数?Cox标准化回归系数是一种用于解释生存数据的统计方法。
生存数据通常用于研究预测生存时间的因素,例如生存病人的存活时间或某个事件发生的时间。
Cox回归模型是常用于分析生存数据的一种方法,它可以考虑多个预测变量对生存时间的影响。
标准化回归系数是回归模型中的系数,它反映了每个预测变量对生存时间的影响程度,通常用于衡量变量的重要性。
标准化回归系数可以使不同变量之间的比较更加直观,并且可以考虑到变量的度量单位差异。
Cox回归模型的表达式如下所示:h(t) = h0(t) * exp(b1x1 + b2x2 + ... + bpxp)其中,h(t)表示在给定时间t的风险函数,h0(t)是基准风险函数,x1, x2, ..., xp是预测变量,b1, b2, ..., bp是标准化回归系数。
模型的核心思想是,基准风险函数在所有预测变量的影响下乘以一个指数项来得到实际的风险函数。
接下来,我们将一步一步介绍如何计算Cox标准化回归系数:步骤1:收集生存数据和预测变量首先,需要收集生存数据和预测变量。
例如,我们可能有关于病人的年龄、性别、病情严重程度等预测变量,以及关于病人存活时间或某个事件发生时间的生存数据。
步骤2:拟合Cox回归模型接下来,需要使用已收集的数据拟合Cox回归模型。
拟合模型的目的是估计每个预测变量的回归系数。
回归系数表示了预测变量对生存时间的影响程度。
步骤3:计算标准化回归系数一旦拟合了Cox回归模型并得到了回归系数的估计值,就可以计算标准化回归系数。
标准化回归系数可以通过标准化估计的回归系数得到,标准化的方式可以是除以该变量的标准差或范围。
步骤4:解释标准化回归系数最后,我们可以根据标准化回归系数的值来解释预测变量对生存时间的影响程度。
较大的标准化回归系数表示该预测变量对生存时间有更大的影响,而较小的标准化回归系数表示该预测变量对生存时间的影响较小。
cox回归的临床决策模型python

cox回归的临床决策模型python(原创实用版)目录1.介绍 Cox 回归模型及其在临床决策中的应用2.Python 在 Cox 回归模型实现中的优势3.如何使用 Python 实现 Cox 回归临床决策模型4.实际案例分析和应用正文Cox 回归模型是一种广泛应用于生存分析的统计模型,它可以用于研究多个自变量与因变量(通常为生存时间或时间事件)之间的关系。
在临床决策中,Cox 回归模型可以帮助医生预测患者的疾病进展或生存时间,从而制定更准确的治疗方案。
Python 作为一门强大的编程语言,拥有丰富的库和工具,可以方便地实现 Cox 回归模型,使得临床决策更加科学和有效。
首先,Python 提供了很多用于数据分析和可视化的库,如 Pandas、NumPy 和 Matplotlib,这些库可以方便地处理和分析临床数据。
其次,Python 还有许多用于统计建模和机器学习的库,如 Scikit-learn 和Stan,这些库可以帮助我们快速地实现 Cox 回归模型。
要使用 Python 实现 Cox 回归临床决策模型,通常需要以下几个步骤:1.准备数据:收集患者的临床数据,包括患者的基本信息、病史、实验室检查结果等。
这些数据可以为我们提供 Cox 回归模型所需的自变量信息。
2.数据预处理:使用 Pandas 等库对数据进行清洗和整理,处理缺失值、异常值等问题,以保证模型的准确性。
3.构建模型:使用 Scikit-learn 等库实现 Cox 回归模型,根据模型结果确定自变量对因变量的影响程度。
4.模型评估:使用交叉验证等方法评估模型的性能,确定模型的泛化能力。
5.临床决策:根据模型结果,为临床医生提供决策建议,帮助他们制定更准确的治疗方案。
实际案例分析和应用:以某医院的肺癌患者为例,我们可以收集患者的基本信息、病史、实验室检查结果等数据,使用 Python 实现 Cox 回归模型,研究不同因素对患者生存时间的影响。
cox回归参数估计法 -回复

cox回归参数估计法-回复题目:基于回归分析的cox回归参数估计法摘要:Cox回归是一种常用的生存分析方法,用于评估与事件发生时间相关的因素。
本文将对Cox回归的参数估计方法进行详细介绍。
首先,将探讨Cox 回归模型和其假设,并解释为什么它是一个半参数模型。
然后,我们将介绍Cox回归的似然函数和参数估计的基本原理。
接下来,将介绍两种常用的参数估计方法:最大似然估计和偏离最大似然估计。
最后,将讨论Cox 回归的一些局限性和改进方法。
一、引言Cox回归模型是一种用于生存分析的半参数模型,其特点在于不对基准风险函数进行直接建模,而是通过比例风险假设来评估危险因素对事件发生时间的影响。
二、Cox回归模型Cox回归模型可以形式化为以下函数:h(t X) = h0(t) * exp(β1*X1 + β2*X2 + ... + βn*Xn)其中,h(t X)是给定协变量X情况下在时刻t发生事件的危险率;h0(t)是基准危险率函数;β1, β2, ..., βn是回归系数;X1, X2, ..., Xn是协变量。
三、Cox回归的假设为了利用Cox回归进行参数估计,我们需要满足以下两个假设:1. 比例风险假设:在任意时刻,不同个体之间的风险比例保持稳定,即不随时间变化。
2. 独立性假设:事件发生时间之间是相互独立的。
满足这两个假设的情况下,我们可以通过估计β系数来评估危险因素对事件发生时间的影响。
四、似然函数和参数估计Cox回归的似然函数可以通过广义极大似然方法进行估计。
似然函数的形式如下:L(β) = ∏(exp(β1*X1i + β2*X2i + ... + βn*Xni)) / ∑(exp(β1*X1i + β2*X2i + ... + βn*Xni))其中,∏表示对所有的i进行累乘,∑表示对所有的i进行求和。
通过极大化似然函数,可以得到最大似然估计(MLE)的参数估计结果。
五、参数估计方法1. 最大似然估计法(MLE):最大似然估计是一种常用的参数估计方法,在Cox回归中也被广泛使用。
医学科研基本方法:cox回归模型

logistic回归
Cox回归
数据类型 Y数值变量
Y分类变量
Y二分类变量+时间
模型结构 变量筛选
X数值变量、分类变量、等级变量
m
Y 0 1x1 i xi mxm
xi i
ln
P 1 P
0
1x1
i0
前进法;后退法;逐步法
i xi
m
m xm i xi i0
h(t / X ) h0 (t) exp( 1X1 2 X 2 p X p )
A.病例-对照研究设计 B.交叉设计
C.队列研究设计
D.配对设计
2.某医师研究某种急性白血病的患者的生存率时, 收集了20例患者的生存时间,并打算分析两个因 素(一个为定性,另一个为定量)对生存时间的 影响。第一个骨髓AG检验结果(阴阳性)、第2 个是白细胞计数(WBC)。问可用什么回归分析 方法分析此资料?
x ij
)
m
lR j
exp( i i 1
x il
)
1
m
exp(
i1
i
x
ij
)
生存函数的估计
e i xi
S(t | X ) S 0 (t)
e i ( xi xi )
S(t | X ) S(t | X )
RR的估计
m
h(t | X * ) g( X * ) i (xi*xi )
RR
e i1
h(t/X)—t 时 刻 风 险 函 数 、 风 险 率 或 瞬 时 死 亡 率(hazard function)。
h0(t)— 基 准 风 险 函 数 , 即 所 有 变 量 都 取 0 时 t 时刻风险函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:2007-10-20 通讯作者:骆福添 *中山大学公共卫生学院卫生统计与流行病学系
The Optimum Analysis with Queuing Theory Model in Hospital Management
Han Xinhuan ,e t al
(Department o f mathematics and computer ,Nanjing Med ical University ,Nanjing 210029)A bstract This ar ticle analy sed queuing theo ry model and defined suitable medical resoume fo r outpatient services in o rder to receive be st benefit .It o ffered reference that the hospital g overnors improve medical serv -ice with queuing theo ry .
Key words queuing theo ry ;random mo del ;hospital manag ement
文章编号:1004-4337(2008)01-0018-02 中图分类号:R195.1 文献标识码:A
·医学数学模型探讨·
COX 回归模型的样本含量的计算方法及软件实现
徐 英 骆福添*
(广东药学院卫生统计学教研室 广州510310)
摘 要: 目前生存分析中COX 回归模型到底需要多少样本量往往靠经验法来估计。
旨在介绍并推广生存分析中COX 回归模型所需样本量的计算公式及其目前可以实现该计算方法的软件,并通过实例说明了该公式的应用,以期提高今后研究工作的效率。
关键词: 生存分析; COX 回归模型; 样本量; 统计软件
CO X 回归模型在生存分析中应用非常广泛,然而,关于应用该模型到底需要多少样本含量的问题一直未得到很好地解决。
主要原因就是生存分析中往往涉及到数据删失的问题,如果不考虑删失数据,则可以利用率的比较所需样本量的计算公式。
但是,简单的忽略这部分数据,往往会造成信息的损失。
如果考虑删失数据,则样本量的计算又变得非常复杂,因此,直到今天,这个问题依然是国内外统计学者研究的热点之一。
本研究仅介绍其中一种较为成熟的计算方法及其相应的实现软件,并通过实例说明该公式应该逐渐被研究者们广泛应用,从而达到提高研究效率的目的。
1 公式介绍
以往,对于CO X 回归模型所需的样本量往往凭经验去估计,即至少需要相当于协变量个数10~15倍的阳性结局事件。
1983年,Schoenfeld 在Bio me trics 杂志上撰文,提出了一个计算比例风险模型样本含量的公式[1,2]:
D =(Z 1-α+Z β)2[P (1-P )lo g Δ)2
]
-1
这里,D 是指发生阳性结局的总人数,P 是指分配到第一
治疗组人数所占的比例。
lo g Δ是指风险比的对数。
该公式主要是用来计算随机化分组研究的设计所需的样本量,适用于二分类自变量。
同时,当考虑其他协变量对生存时间的影响时,则要求主要感兴趣的研究变量与其他变量间相互独立。
然而,在实际的工作当中,变量之间有时并不能满足独立性。
因此,2000年,H sieh 和L avo ri 在Contro lled Clinical T ri -als 上将Schoenfeld 的计算公式进行了扩展[3],现介绍如下:
N =(Z 1-α/2+Z 1-β)2
P (1-R 2)σ2B
2
等号左边,N 表示所需要的样本含量。
等号右边Z 1-α/2,Z β表示给定检验水准和检验功效时的z 界值;P 表示整个研究期间阳性结局事件的发生率;B 表示对
数风险比,即lo g Δ;σ2
表示感兴趣的研究因素X 1的方差,这
里假定X 1服从正态分布,对于非正态分布的X 1,如二项分布,可通过p (1-p )进行估计,这里,p 表示X 1取“0”或“1”的比例。
与Scho enfeld 的计算公式不同的是,该公式引入了“方差膨胀因子”(V IF ),即1/(1-R 2)。
R 2表示X 1对其他协变量作回归分析时的确定系数,取值范围0~1,当取值为“0”时,
·
18·Journal o f M athematical M edicine
Vo l .21 No .1 2008
一般表示只考虑一个自变量X1的情形。
亦即当变量间不满足独立性时,需要通过VIF来增加参数估计值的方差。
上述各指标可通过查阅相关文献或进行预试验确定。
2 软件实现
目前,有许多统计软件可以用来计算生存分析所需的样本量,但是大部分软件都是针对log-rank检验的,或是要求生存时间服从指数分布,比如S-plus、PS、N Q ue ry A dv iso r、S T A-T A、PA SS等。
然而,逐渐地也有不少软件开始引入针对CO X回归分析所需样本量的计算程序,比如ST A T A和PA SS。
现介绍如下:
2.1 ST A T A软件的应用
程序如下:stpow er COX[coef][,o ptions]
[coef]:用来设定感兴趣的研究因素X1的对数风险比,即logΔ;
[,options]:选择项,常用的有:
*alpha(numlist):检验水准,默认0.05;
*po wer(numlist):检验效能,默认0.8;
*onesided:单侧检验,默认双侧检验;
*sd(#):感兴趣的研究因素X1的标准差,默认0.5;
*r2(#):确定系数,默认0;
*failpr ob(#):阳性结局事件发生率,默认100%。
2.2 P ASS软件的应用
PA SS是N CSS软件中执行检验功效分析和计算样本量大小的一个功能模块。
操作步骤如下:
①打开N CSS软件,进入类似SPSS的操作界面;
②点击PA SS下拉菜单,选择“survival and reliability”子菜单,选择“CO X reg re ssio n”,进入相关参数设置对话框;
③设置相关参数,点击工具栏“play”,完成操作。
3 实例应用
K rall,U thoff and Har ley(1975)研究了65例多发性骨髓瘤患者预后的影响因素,一共9个变量(具体数据参见sas phreg过程中的数据集M yelo ma)。
如研究者主要感兴趣的变量为X1(lo gBU N),预估计其对数风险比lo gΔ=1,研究结束时死亡率P=48/65=73.8%,按照单侧0.05的检验水准和预期80%的检验效能,估计所需的样本量的计算过程如下:
①估计X1的标准差,得σ=0.3126;
②对X1和其他协变量作多重线性回归分析,得R2=0.1839;
③利用ST A T A或PA SS软件,将上述参数带入计算,得样本含量N=107。
按照Hsieh和Lav ori所提供的公式,若要达到80%的检验效能,估计所需的样本量为107例。
故对于该项研究而言,若只研究65例患者,则需慎重对待所得结论。
4 讨论
本研究中提到的公式,有效地解决了在生存分析中广泛应用的COX回归模型的样本含量的计算问题,为医学科研工作者在今后的研究中提高研究效率、节省人力物力财力提供了一定的科学依据。
该公式适用于任何分布的生存时间,只要满足CO X比例风险假定即可。
另外,该公式不仅适用正态分布的自变量,也适用非正态分布的自变量,比如二分类的自变量,此时,可以计算出近似所需的样本量。
该公式不仅仅局限于对单个影响因素的研究,还可以综合考虑其他协变量的影响。
这一点在公式中主要体现在R2的取值上。
对于单个自变量的研究,R2取“0”即可;对于多个自变量的研究,则需要通过回归分析估计R2。
由于ST A T A软件被广大研究者所熟悉,而PA SS界面又非常友好,操作简单,只需要输入相应的参数既可以得到所需的结果。
此外,该公式相对较简单,亦可以直接计算。
因此,期待能在今后的生存分析中得到广泛的应用,以提高研究的工作效率。
另外,当已知样本含量时,也可以利用该公式和上述两个软件估计检验功效,以判断当阴性结果出现时,是否由于样本含量不足导致。
参 考 文 献
1 S choenfeld,David A.Sample-Size Formu la fo r the Proportional-Hazards Regres s ion M odel.Biometrics,1983,39:499~503.
2 赵耐青.生存分析的最小样本含量计算.上海医科大学学报,1994, 21(5):333~337.
3 H sieh,F.Y.and Lavori,P.W.Sample-Siz e Calcu lation s fo r th e COX Proportional Hazards Regression M odel w ith Nonbinary Co-variates.Controlled Clinical Trials,2000,21:552~560.
·
19
·
数理医药学杂志2008年第21卷第1期。
