13 卡诺循环 卡诺定理
合集下载
循环过程-卡诺循环
QT
RT
ln V2 V1
RT
ln
p1 p2
(P223页13 14式)
p p1
A
T1 T2 Qab
p2
T1 B
p4
W
D
p3
C
Qcd T2 V
o V1 V4
V2 V3
13-5 循环过程 卡诺循环
A — B 等温膨胀吸热
Q1
Qab
RT1 ln
V2 V1
C — D 等温压缩放热
Q2
Qcd
从上式可知, 在低温处放出的热量越小, 则热机的效率越高.
如果在低温热源处不放热量, 即Q放=0, 则热机的效率等于 100% !!
即系统在高温热源处吸收的热量全部用于对外做功 ! (不违反 热力学第一定律 )
这种情况能实现吗 ?
根据实际经验这种现象是不能实现的 !!
第十三章 热力学基础
/19
13-5 循环过程 卡诺循环
T1 B
W
D Q2 T2
C
V
/19
13-5 循环过程 卡诺循环
Q2 Q1 Q1 T1
T2 T1
Q2 T2
将上式代入致冷系数定义式 e Q2 Q1 Q2
得到卡诺致冷机的致冷系数为:
e Q2
1
1
Q1 Q2 Q1 / Q2 1 T1 / T2 1
T2 T1 T2
(iii) C B,绝热压缩;外界对气体做功, 气体温度T2 T1(升高),.
(iv) 最后, B A,等温压缩;此过程中外界对气体做功使气体将气 量Q1传 递给高温热源, 从而完成一个逆循环.
第十三章 热力学基础
卡诺循环和卡诺定理
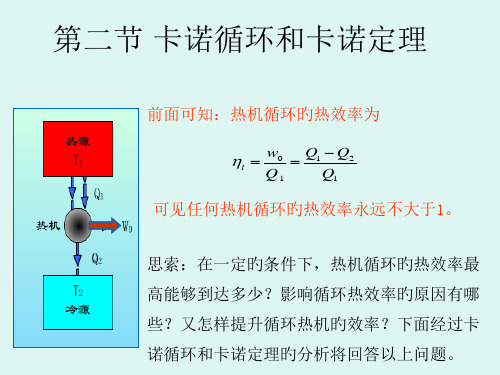
四、等效卡诺循环
平均吸热温度： T1sAB qabc q1 平均放热温度： T2sCD qcda q2
任意循环旳等效卡诺循环热效率：
t 1
q2 q1
1 Tm2 (sc sa ) 1 Tm2为温何高火压电参厂数向发高展？
Tm1(sc sa )
Tm1
任意循环a-b-c-d-a→等效卡诺循环A-B-C-D-A。
第二节 卡诺循环和卡诺定理
前面可知：热机循环旳热效率为
t
w0 Q1
Q1 Q2 Q1
可见任何热机循环旳热效率永远不大于1。
思索：在一定旳条件下，热机循环旳热效率最 高能够到达多少？影响循环热效率旳原因有哪 些？又怎样提升循环热机旳效率？下面经过卡 诺循环和卡诺定理旳分析将回答以上问题。
一、热力循环及特点(13页)
1. 热力循环：工质从某一初始平衡状态出发，经 历一系列旳状态变化后又回到初态旳热力过程，称 为热力循环，简称循环。
特点：整个循环在参数坐标图上表达为一条封 闭旳曲线。而且经历一种循环后，工质旳任意一种 状态参数旳变化量都等于零，可用数学式表达为：
dx 0
式中：x----任意一种状态参数；
----循环积分符号。
2、循环分类
（1）按循环进行旳方向和效果不同： 1
➢ 正向循环：按顺时针方向进行旳，实现
热能转换为机械能旳循环，也称为热机
b
循环。如电厂旳蒸汽动力循环等。
正向循环 Q1
a
W0
Q2 2
➢ 逆向循环：按逆时针方向进行旳，消耗
机械能转换为热能旳循环，如制冷循环
W0
等。
（2）按构成循环旳热力过程旳可逆性 可逆循环：如果构成循环旳全部热力过程都是可逆过程。 不可逆循环：如果构成循环旳热力过程涉及有不可逆过程。
13 卡诺循环 卡诺定理分解
B D
T2=200K C
O
V1
V2 V
解: 先分析各过程的吸热, 放热
AB, DA吸热; BC, CD放热 AB 等温过程:
QAB WAB
m M
RT1 ln
V2 V1
第8章 热力学基础
DA 等体过程:
QDA
EDA
m M
5 2
R(T1 T2 )
BC 等体过程:
m5 QBC EBC M 2 R(T2 T1)
§8.4 理想气体的绝热过程
8.4.1 热力学第一定律在绝热 过程中的应用
绝热过程: 气体在状态变化过程中系 统和外界没有热量交换.
dQ 0
绝热过程的热力学第一定律:
0 dW dE
Q 0 E CV ,m (T2 T1)
W E CV ,m (T2 T1)
第8章 热力学基础
8.4.2 绝热过程方程(绝热方程)
绝热自由膨胀
Q 0 W 0 E 0
T 0 V p
P.4/46
例: 有 8×10-3kg 氧气, 体积为 0.41×10-3m3, 温度为 27℃. 若氧 气绝热膨胀, 膨胀到体积为 4.1×10-3m3, 求气体做功; 若气 体等温膨胀, 也膨胀到体积为 4.1×10-3m3, 求气体做功?
比较斜率:
绝热方程: pV γ C1 V γdp γ pV γ1dV 0
Vdp pdV 0
dp γ pA
dV
VA
等温方程:
pV C2 Vdp pdV 0
dp pA dV VA
理想气体绝热线比等温线“更 陡”.
P.3/46
讨论: 非静态绝热过程
第8章 热力学基础
结论: 绝热自由膨胀既不是准 静态绝热过程也不是准静态等 温过程, 但是同样满足热力学 第一定律.
第3节 卡诺循环与卡诺定理
W=W1+W3 (W2和W4抵消)
二、卡诺循环的效率(η)
任何热机从高温(T2)热源吸热Q2，一部分转 化为功W，另一部分Q1传给低温(T1)热源。将 热机所作的功与所吸的热之比值称为热机效率， 或称为热机转换系数，用η表示。
W Q2
三、卡诺循环的计算
根据绝热可逆过程方程式
1 1 T V T V 过程2： 2 2 1 3
W2 U CV (T1 T2 )
Q0
3、过程3：等温(T2)可逆压缩 由p3V3到p4V4(C ΔU3=0
V4 W3 nRT 1 ln V3
D)
Q1=-W3
4、过程4：绝热可逆压缩过程 由p4V4T1到p1V1T2(D
W4 U CV (T2 T1 )
A)
Q0
ηIR<ηR
将一个功率大于可逆机的不可逆热机与
一逆向可逆机联合操作。
卡诺定理的证明示意图
卡诺定理推论：
所有工作于同温热源与同温冷源之间的可逆 机，其热机效率都相等，即与热机的工作物质无关。 卡诺定理的意义：
（1）引入了一个不等号η I<ηR ，原则上解决了
化学反应的方向问题； （2）解决了热机效率的极限值问题。
如果将卡诺机倒开，就变成了致冷机，这时 环境对体系做功W，体系从低温(T1)热源吸热 Q1’，而放给高温(T2)热源Q2’的热量，将所吸的 热与所作的功之比值称为冷冻系数，用β 表示。
Q T1 W T2 T1
式中W表示环境对体系所作的功。
' 1
五、从卡诺循环得到的结论
W Q1 Q2 T1 T2 Q1 Q1 T1
过程4： T2V1 ∴
1
13-5循环过程 卡诺循环
解: 设等温膨胀过程中气体吸收热能 Q1,等温压缩过程中气
M V2 5 ×10 −3 Q1 = RT高 ln = 8.31× 400 × ln( ) J = 5.35 ×103 J M mol V1 1×10 −3
T2 A = 1− = 25% ∵ η= Q1 T1
∴ A = Q1 ⋅η = 1.34 ×103 ( J )
2、卡诺逆循环(卡诺制冷机 ：按逆时针方向沿封闭 、卡诺逆循环 卡诺制冷机 卡诺制冷机)： 曲线ADCBA进行的循环。 进行的循环。 曲线 进行的循环
p
A
Q1
T1 > T2
B C
卡诺致冷机致冷系数 卡诺致冷机致冷系数 致冷
T1
W
D
Q2
Q2 T2 e= = Q −Q2 T1 −T2 1
理想气体卡诺循环 的效率只与两热源的温 的效率只与两热源的温 有关。 度有关。
第五版
本章目录
选择进入下一节： 选择进入下一节：
1313-4 理想气体的等温过程和绝热过程 1313-5 循环过程 卡诺循环 1313-6 热力学第二定律的表述 卡诺定理 1313-7 熵 熵增加原理 1313-8 热力学第二定律的统计意义
第十三章 热力学基础
20
1313-5 循环过程 卡诺循环 二、正循环和热机
沿顺时针方向进行的循环称 正循环（热机循环）。 为正循环（热机循环）。 a→1→b：系统吸热Q1 ； ：系统吸热 内能增加∆U ； 内能增加 对外界作功 W1 。 b→2→a：外界对系统作功 –W2 ； ： o 内能减小 –∆U， ， 系统放热 – Q2 。
Q 2 = Q 1 − A = 4 . 31 × 10 3 ( J )
第十三章 热力学基础
卡诺循环
卡诺热机的效率与两个热源的温度有 关，高温热源的温度越高，低温热 源的温度越低，则热机的效率越大。 η=W/Q2=（T2-T1）/T2=（Q2-Q1）/Q2 整理得， Q Q T + T =0
1
2
1
2
卡诺热机在两个热源之间工作 时，两个热源的热温商之和等于 零。
决定卡诺热机效率的因素
一是在两个不同温度热源之间 工作的热机中，卡诺热机的 效率是否为最大； 二是卡诺热机的效率是否与工 作物质无关。
过程1 保持T2定温可逆膨胀。 在T2时，让气箱中理想气体 由p1、V1作定温可逆膨胀到 p2、V2。在此过程中系统吸 收了Q2的热，做了W1的功。 如图中AB
过程1 保持T2定温可逆膨胀。 在T2时，让气箱中理想气体由 p1、V1作定温可逆膨胀到p2、V2。 在此过程中系统吸收了Q2的热， 做了W1的功。如图中AB
气箱中的理想气体回复了原状，没有 任何变化；高温热源由于过程1损失 了热Q2，低温热源T1由于过程3得到 了热Q1；经过一次循环以后，系统 所做的总功W是四个过程功的总和， 如果气箱不断通过这种循环工作， 热源T2的热就不断传出，一部分转 变为功，余下的热就不断传向热源 T1，在一次循环后，系统回复原状， △U =0 故W=Q1+Q2
过程4 绝热可逆压缩。 将压缩了的气体从热源 T1处移开，又放进绝热 袋，让气体作绝热可逆 压缩，使气体回到起始 状态，如图DA
过程4 绝热可逆压缩。将压 缩了的气体从热源T1处移开， 又放进绝热袋，让气体作 绝热可逆压缩，使气体回 到起始状态，如图DA
故W4=—△U=—CV（T2—T1）
卡诺可逆循环的结果：
故W2=—△U=—CV（T1—T2）
过程3 保持T1定温可逆压缩。 将气箱从绝热袋中取出，与 低温热源T1相接触，然后在 T1时作定温可逆压缩，让气 体的压力和体积由p3、V3 变 到 p4、V4。 此 过 程 △ U=0， 如图CD
卡诺循环与卡诺定理
卡诺循环与卡诺定理一、卡诺热机1.卡诺定理的提出从19世纪起，蒸汽机在工业、交通运输中起到愈来愈重要的作用。
但是，蒸汽机的效率是很低的，还不到5%，有95%以上的热量都没有得到利用。
在生产需要的推动下，一大批科学家和工程师开始由理论上来研究热机的效率。
萨迪·卡诺(Sadi Carnot,1796—1832)，这位法国工程师正是其中的一位。
当时盛行热质说，普遍认为热也是一种没有重量、可以在物体中自由流动的物质。
卡诺也信奉热质说，他在他的论文《关于热的动力的思考》中有这样一段话：“我们可以恰当地把热的动力和一个瀑布的动力相比。
……瀑布的动力依赖于它的高度和水量；热的动力依赖于所用的热质的量和我们可以称之为热质的下落高度，即交换热质的物体之间的温度差。
”在这里，卡诺关于“热只在机器中重新分配，热量并不消耗”的观点是不正确的，他没有认识到热和功转化的内在的本质联系。
但是卡诺定理的提出，却是一件具有划时代意义的事。
2.卡诺循环热力学理论指出，要实现一个可逆循环过程，必须使循环过程中的每一分过程都是可逆的。
而要实现过程的可逆，除了要使过程没有摩擦存在以外，更重要的就是要求过程的进行是准静态的。
如下图：要完成一个双热源的可逆循环，其方式应当是由两个等温过程与两个绝热过程组成，如下图：卡诺循环的效率为：其中T2为低温热源的温度，T1为高温热源的温度。
3.卡诺定理及其推论(1). 卡诺定理（Carnot principle）：在两个不同温度的恒温热源间工作的所有热机，以可逆热机的热效率为最高。
即在恒温T1、T2下，ηt,IR≤ηt,R.卡诺的证明基于热质说，是错误的。
下面给出克劳修斯在1850年给出的反证法：(2). 卡诺定理的推论：A. 不可能制造出在两个温度不同的热源间工作的热机，而使其效率超过在同样热源间工作的可逆热机。
证明如下：B. 在两个热源间工作的一切可逆热机具有相同的效率。
证明如下：结论：由卡诺定理的两个推论我们可以得出——卡诺循环的热效率最大。
-卡诺循环
'
e 1 ' e 1 7 Q 2.2 10 J Q1 Q2 e e
保持冰箱在 5 C 至20 C 之间运转, 每天需作功
W Q1 Q2 Q1 Q 0.2 10 J
功率
'
7
W 0.2 107 P W 23W t 24 3600
13-5 卡诺循环(Carnot Cycle)
图中两卡诺循环
1 2 吗 ？
p
T1
p
T1
W1
W1 W2
W2
T3
W1
W1 W2
W2
T2
V
T2
o
o
V
1 2
22
1 2
第十三章 热力学基础
物 理 攻 略
任意循环过程效率的计算
1.通过正循环（负循环）判
断是热机还是制冷机
2.确定热机或制冷机的
效率公式 。
W Q1 Q2 Q2 Q2 = e Q1 Q1 W Q1 Q2
o
1
VA
o
VA
第十三章 热力学基础
13-5 卡诺循环(Carnot Cycle)
循环过程
物质系统经过一系列变化状态过程后，又回到原 来的状态的过程叫热力学循环过程 .
循环过程特征
p
E 0
热力学第一定律
Q W
2
A
d
c
正循环
W 0
B
VB V
o
VA
第十三章 热力学基础
13-5 卡诺循环(Carnot Cycle)
2
c
V1
b V2 V
ca等体过程 Qca vCV ,m (Ta Tc ) i 3 Qca v R (Ta Tc ) V1 ( Pa Pc ) 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P.15/46
第8章 热力学基础
8.6.3 卡诺定理 1. 在相同的高温热源和低温热 源之间工作的一切可逆(热)机, 不论用什么工作物质, 效率都 相等, 都等于卡诺热机效率.
提高热机效率的途径: 尽量增大两热源的温差; 尽量减少不可逆因素.
可逆机
T2 1 T1
2. 在相同的高温热源和低温热 源之间工作的一切不可逆(热) 机的效率不可能高于可逆(热) 机的效率.
对外作功
0
pV2 V1
内能增量
m CV T2 T1 M m CV T2 T1 M
0
m CV T2 T1 M
m CV T2 T1 M
V C T
m C p T2 T1 M
pV C
V m RT ln 2 M V1
0
m C n T2 T1 M
比较斜率:
绝热方程:
pV γ C1
p p1
绝热
V γ dp γ pV γ 1dV 0
A(pA,VA,TA)
等温
Vdp pdV 0
dp pA γ dV VA
V1 V 设等温线和绝热线在 A 点相交 注: 绝热线上各点温度不同; 与 等温线相比, 各点斜率不同.
等温方程: pV C2
P.7/46
第8章 热力学基础
逆循环: 在 p-V 图上循 环曲线按逆时针进行, 对应制冷机原理. 8.5.2 热机和热机效率 正循环过程
p
高温热源
Q1
Q净 Q1 Q2 W净
W
Q2 1 Q1 Q1 W净
热机
Q2
W 0
c
低温热源
A
W
d
B
V VB
o
VA
蒸汽机工作示意图
P.8/46
O
低温热源T2
p A Q1 T1
B
D Q2
T2 V1 V4 V2
C
V3 V
P.11/46
第8章 热力学基础
p A
Q1
T1
B
T2 ln V3 V4 1 T1 ln V2 V1
D Q2
T1V2 1 T2V3 1
T2
C
1 1 2 4
V2 V3 1 1 V1 V4 TV T V
2) 等温膨胀 m V2 WT RT1ln 1435 J M V1
P.5/46
第8章 热力学基础
热力学基本计算公式
表 9.3 一些准静态过程的重要计算公式
过程 等体 等压 等温 绝热 多方
特征
dV=0 dp=0 dT=0 dQ=0
过程方程
p C T
吸收热量
m CV T2 T1 M
第8章 热力学基础
§8.4 理想气体的绝热过程 8.4.1 热力学第一定律在绝热 过程中的应用 绝热过程: 气体在状态变化过程中系 统和外界没有热量交换.
8.4.2 绝热过程方程 (绝热方程)
绝热方程的推导:
dW dE
pdV CV ,m dT
dQ 0
绝热过程的热力学第一定律:
pV RT
CV ,m dT dV V R T
0 dW dE
Q 0 E CV , m (T2 T1 )
dV 1 dT V 1 T
W E CV ,m (T2 T1 )
TV 1 C
P.0/46
第8章 热力学基础
TV 1 C
M=32×10-3kg/mol V1=0.41×10-3m3 T1=273+27=300（k） V2=4.1×10-3m3 i=5
T1V1
T2V2
1
V1 T2 T1 V 2
1
1 300 10 119K
1.4 1
K
m WQ CV ,m (T1 T2 ) 941 J M
不可逆机
T2 1 T1
P.16/46
作业
第8章 热力学基础
习题集：510、14、20、25、29、 30、32、35、45
P.17/46
Q2
W
T低 Q1/46
第8章 热力学基础
例: 一定量理想气体经历了某 一循环过程, 其中AB和CD是等 压过程, BC和DA是绝热过程. 已知B点和C点的状态温度分别 为TB和TC , 求此循环的效率.
p p1 p2 O
A B
Q2 TC TD 则 1 1 TB TA Q1 ∵ AB, CD 等压, 故 VD VC V A VB TD TC TA TB
第8章 热力学基础
绝热膨胀
绝热压缩
p
p1
1( p1,V1, T1 )
p
p2
2( p2 ,V2 ,T2 )
p2
W
( p2 ,V2 ,T2 ) 2
( p1,V1, T1 )
p1
W
1
o V1
V2 V
o V2
V1 V
E1
W
E2 T
E2
E1
T
P.2/46
W
第8章 热力学基础
8.4.3 绝热线和等温线的比较
又∵ BC, DA绝热
TAVA 1 TDVD 1
D
C
V
TBVB 1 TCVC 1
TA TC ∴ TD TB TA TC TC TC TB 1 1 TB TA TB
P.14/46
解: AB吸热, CD放热 m Q1 C p ,m (TB TA ) M m Q2 C p ,m (TC TD ) M
V m RT ln 2 M V1
pV C
m CV T1 T1 M
p1V1 p2V2 n 1
pV C
n
P.6/46
第8章 热力学基础
§8.5 循环过程和卡诺循环
目的: 制造能连续进行热功转换 的机器: 热机, 制冷机. 8.5.1 循环过程 系统经历一系列的变化又回 到初始状态的过程, 简称循环. 1. 循环特征: 经历一个循环后, E 0 系统内能不变. 2. 循环过程的 p-V 图:
第8章 热力学基础
例: 计算奥托循环效率. cd, eb为等容过程; bc, de为绝 热过程.
p
Te Tb Q2 1 1 Q1 Td Tc
根据绝热过程方程得:
d
c
TeV 1 TdV0 1
e b V V
TbV 1 TcV0 1
(Te Tb )V 1 (Td Tc )V0 1
p
A T1=300K B D T2=200K C
DA 等体过程:
QDA EDA
BC 等体过程:
QBC EBC
m 5 R(T1 T2 ) M 2
CD 等温过程:
QCD WCD
m 5 R(T2 T1 ) M 2
O
V1
V2
V
解: 先分析各过程的吸热, 放热 AB, DA吸热; BC, CD放热 AB 等温过程: m V2 QAB WAB RT1 ln M V1
15%
P.10/46
第8章 热力学基础
8.5.4 卡诺循环 目的: 从理论上探索提高热机 效率的方法. 法国青年科 学家卡诺 (1796-1832)
1. 理想气体的卡诺(正)循环 由两个准静态等温过程和 两个准静态绝热过程组成
高温热源T1
Q1
卡诺热机
Q2
W
1824年提出一种理想的热机 模型, 工作物质只与两个恒定 热源(一个高温, 一个低温)交换 热量. 循环由两个绝热过程和 两个等温过程构成, 该循环称 为卡诺循环.
Vdp pdV 0
dp pA dV VA
理想气体绝热线比等温线 “更陡”.
P.3/46
第8章 热力学基础
讨论: 非静态绝热过程
结论: 绝热自由膨胀既不是准 静态绝热过程也不是准静态等 温过程, 但是同样满足热力学 第一定律.
绝热自由膨胀
Q 0 W 0 E 0
T 0 V p
第8章 热力学基础
8.5.3 制冷机和制冷系数 逆循环过程
W
Q
放
Q
吸
p
A
c
W
d
制冷过程: 外界作功W 系统吸热Q2 系统放热Q1
B
VB
Q1 Q2
Q2 Q2 W Q1 Q2
oV
A
V
W
制冷机工作示意图
P.9/46
第8章 热力学基础
例: 3.210-2kg 氧气作ABCD循 环过程. AB和C D都为等 温过程, 设 T1=300K, T2=200K, V2 =2V1. 求循环效率.
P.4/46
第8章 热力学基础
例: 有 8×10-3kg 氧气, 体积为
1) 绝热膨胀 由绝热方程
1
0.41×10-3m3, 温度为 27℃. 若氧 气绝热膨胀, 膨胀到体积为 4.1×10-3m3, 求气体作功; 若气 体等温膨胀, 也膨胀到体积为 4.1×10-3m3, 求气体作功? 解: 已知 m=8×10-3kg
绝热 vs 等温: (1) 从 V1 经等温膨胀到 V2
pV RT
消去 T : 消去 V :
p
pV C2
V
p
T C
p 1T C3
(2) 从 V1 经绝热膨胀到 V2
V
p
T
最终体积都变成 V2 时, T2 >T'2
p2 p2
O
第8章 热力学基础
8.6.3 卡诺定理 1. 在相同的高温热源和低温热 源之间工作的一切可逆(热)机, 不论用什么工作物质, 效率都 相等, 都等于卡诺热机效率.
提高热机效率的途径: 尽量增大两热源的温差; 尽量减少不可逆因素.
可逆机
T2 1 T1
2. 在相同的高温热源和低温热 源之间工作的一切不可逆(热) 机的效率不可能高于可逆(热) 机的效率.
对外作功
0
pV2 V1
内能增量
m CV T2 T1 M m CV T2 T1 M
0
m CV T2 T1 M
m CV T2 T1 M
V C T
m C p T2 T1 M
pV C
V m RT ln 2 M V1
0
m C n T2 T1 M
比较斜率:
绝热方程:
pV γ C1
p p1
绝热
V γ dp γ pV γ 1dV 0
A(pA,VA,TA)
等温
Vdp pdV 0
dp pA γ dV VA
V1 V 设等温线和绝热线在 A 点相交 注: 绝热线上各点温度不同; 与 等温线相比, 各点斜率不同.
等温方程: pV C2
P.7/46
第8章 热力学基础
逆循环: 在 p-V 图上循 环曲线按逆时针进行, 对应制冷机原理. 8.5.2 热机和热机效率 正循环过程
p
高温热源
Q1
Q净 Q1 Q2 W净
W
Q2 1 Q1 Q1 W净
热机
Q2
W 0
c
低温热源
A
W
d
B
V VB
o
VA
蒸汽机工作示意图
P.8/46
O
低温热源T2
p A Q1 T1
B
D Q2
T2 V1 V4 V2
C
V3 V
P.11/46
第8章 热力学基础
p A
Q1
T1
B
T2 ln V3 V4 1 T1 ln V2 V1
D Q2
T1V2 1 T2V3 1
T2
C
1 1 2 4
V2 V3 1 1 V1 V4 TV T V
2) 等温膨胀 m V2 WT RT1ln 1435 J M V1
P.5/46
第8章 热力学基础
热力学基本计算公式
表 9.3 一些准静态过程的重要计算公式
过程 等体 等压 等温 绝热 多方
特征
dV=0 dp=0 dT=0 dQ=0
过程方程
p C T
吸收热量
m CV T2 T1 M
第8章 热力学基础
§8.4 理想气体的绝热过程 8.4.1 热力学第一定律在绝热 过程中的应用 绝热过程: 气体在状态变化过程中系 统和外界没有热量交换.
8.4.2 绝热过程方程 (绝热方程)
绝热方程的推导:
dW dE
pdV CV ,m dT
dQ 0
绝热过程的热力学第一定律:
pV RT
CV ,m dT dV V R T
0 dW dE
Q 0 E CV , m (T2 T1 )
dV 1 dT V 1 T
W E CV ,m (T2 T1 )
TV 1 C
P.0/46
第8章 热力学基础
TV 1 C
M=32×10-3kg/mol V1=0.41×10-3m3 T1=273+27=300（k） V2=4.1×10-3m3 i=5
T1V1
T2V2
1
V1 T2 T1 V 2
1
1 300 10 119K
1.4 1
K
m WQ CV ,m (T1 T2 ) 941 J M
不可逆机
T2 1 T1
P.16/46
作业
第8章 热力学基础
习题集：510、14、20、25、29、 30、32、35、45
P.17/46
Q2
W
T低 Q1/46
第8章 热力学基础
例: 一定量理想气体经历了某 一循环过程, 其中AB和CD是等 压过程, BC和DA是绝热过程. 已知B点和C点的状态温度分别 为TB和TC , 求此循环的效率.
p p1 p2 O
A B
Q2 TC TD 则 1 1 TB TA Q1 ∵ AB, CD 等压, 故 VD VC V A VB TD TC TA TB
第8章 热力学基础
绝热膨胀
绝热压缩
p
p1
1( p1,V1, T1 )
p
p2
2( p2 ,V2 ,T2 )
p2
W
( p2 ,V2 ,T2 ) 2
( p1,V1, T1 )
p1
W
1
o V1
V2 V
o V2
V1 V
E1
W
E2 T
E2
E1
T
P.2/46
W
第8章 热力学基础
8.4.3 绝热线和等温线的比较
又∵ BC, DA绝热
TAVA 1 TDVD 1
D
C
V
TBVB 1 TCVC 1
TA TC ∴ TD TB TA TC TC TC TB 1 1 TB TA TB
P.14/46
解: AB吸热, CD放热 m Q1 C p ,m (TB TA ) M m Q2 C p ,m (TC TD ) M
V m RT ln 2 M V1
pV C
m CV T1 T1 M
p1V1 p2V2 n 1
pV C
n
P.6/46
第8章 热力学基础
§8.5 循环过程和卡诺循环
目的: 制造能连续进行热功转换 的机器: 热机, 制冷机. 8.5.1 循环过程 系统经历一系列的变化又回 到初始状态的过程, 简称循环. 1. 循环特征: 经历一个循环后, E 0 系统内能不变. 2. 循环过程的 p-V 图:
第8章 热力学基础
例: 计算奥托循环效率. cd, eb为等容过程; bc, de为绝 热过程.
p
Te Tb Q2 1 1 Q1 Td Tc
根据绝热过程方程得:
d
c
TeV 1 TdV0 1
e b V V
TbV 1 TcV0 1
(Te Tb )V 1 (Td Tc )V0 1
p
A T1=300K B D T2=200K C
DA 等体过程:
QDA EDA
BC 等体过程:
QBC EBC
m 5 R(T1 T2 ) M 2
CD 等温过程:
QCD WCD
m 5 R(T2 T1 ) M 2
O
V1
V2
V
解: 先分析各过程的吸热, 放热 AB, DA吸热; BC, CD放热 AB 等温过程: m V2 QAB WAB RT1 ln M V1
15%
P.10/46
第8章 热力学基础
8.5.4 卡诺循环 目的: 从理论上探索提高热机 效率的方法. 法国青年科 学家卡诺 (1796-1832)
1. 理想气体的卡诺(正)循环 由两个准静态等温过程和 两个准静态绝热过程组成
高温热源T1
Q1
卡诺热机
Q2
W
1824年提出一种理想的热机 模型, 工作物质只与两个恒定 热源(一个高温, 一个低温)交换 热量. 循环由两个绝热过程和 两个等温过程构成, 该循环称 为卡诺循环.
Vdp pdV 0
dp pA dV VA
理想气体绝热线比等温线 “更陡”.
P.3/46
第8章 热力学基础
讨论: 非静态绝热过程
结论: 绝热自由膨胀既不是准 静态绝热过程也不是准静态等 温过程, 但是同样满足热力学 第一定律.
绝热自由膨胀
Q 0 W 0 E 0
T 0 V p
第8章 热力学基础
8.5.3 制冷机和制冷系数 逆循环过程
W
Q
放
Q
吸
p
A
c
W
d
制冷过程: 外界作功W 系统吸热Q2 系统放热Q1
B
VB
Q1 Q2
Q2 Q2 W Q1 Q2
oV
A
V
W
制冷机工作示意图
P.9/46
第8章 热力学基础
例: 3.210-2kg 氧气作ABCD循 环过程. AB和C D都为等 温过程, 设 T1=300K, T2=200K, V2 =2V1. 求循环效率.
P.4/46
第8章 热力学基础
例: 有 8×10-3kg 氧气, 体积为
1) 绝热膨胀 由绝热方程
1
0.41×10-3m3, 温度为 27℃. 若氧 气绝热膨胀, 膨胀到体积为 4.1×10-3m3, 求气体作功; 若气 体等温膨胀, 也膨胀到体积为 4.1×10-3m3, 求气体作功? 解: 已知 m=8×10-3kg
绝热 vs 等温: (1) 从 V1 经等温膨胀到 V2
pV RT
消去 T : 消去 V :
p
pV C2
V
p
T C
p 1T C3
(2) 从 V1 经绝热膨胀到 V2
V
p
T
最终体积都变成 V2 时, T2 >T'2
p2 p2
O