学而思作业6
学而思天天练1-60每日两题(题目)

1、2+4+6+8+10+12+14+16+182、5+7+9+11+13+15+17+19+21+23天天练第2天(4月23日)1、34+78+66+159+222、847-136-64天天练第3天(4月24日)1、500-76-41-59-242、64+451-27+36-73+549天天练第4天(4月25日)1、821-19-81-203-972、969-23-39天天练第5天(4月26日)1、191+89-83-17+112、218-35-44-36-2-3天天练第6天(4月27日)1、288-(88+56)2、263-(163+38)天天练第7天(4月28日)1、236-165+652、782-324+1241、99999+9999+999+99+92、2001+2002+2003+2004天天练第9天(4月30日)1、299+59+2+72、96+97+98+99+10天天练第10天(5月1日)1、 89+92+91+87+86+932、19+18-17+16-15+14-13+12-11天天练第11天(5月5日)1、 2+12+102+1002+100022、24+204+2004+20004+200004天天练第12天(5月6日)1、62-3-3-3-3-3-32、45+9+9+9+9+9天天练第13天(5月7日)1、1只河马的体重等于2只大象的体重,1只大象的体重等于10匹马的体重,1匹马的体重是320千克,这只河马的体重是多少千克?2、1个菠萝的重量等于2个梨的重量,1个梨的重量等于4个香蕉的重量,4个香蕉的重量等于5个土豆的重量,那么,1个菠萝等于几个土豆的重量?天天练第14天(5月8日)1、下图一共有()条线段?2天天练第15天(5月9日)1、用l6个边长为2分米的小正方形拼成一个大正方形.大正方形的周长是()分米222、求下图所示图形的周长.周长是()分米.平移前天天练第16天答案及详解(5月10日)1.已知1个☆ = 3个△,1个△ = 5个□ .那么1个☆ =()个□2、某池中的睡莲所遮盖的面积,每天扩大一倍,10天恰好遮住整个水池 .问:若只遮住水池的一半需要多少天?天天练第17天答案及详解(5月11日)1、数一数,图中一共有()个正方形?天天练第18天(5月12日)1、拼图游戏图形中一个有20个小正方形,分成大小相等的4块,每块应该含有5个小正方形 .怎样分?2、一个长方形,切掉一个角,剩下的图形还有()个角?(注:此题答案不唯一)天天练第19天(5月13日)1、一本书,共80页,小兵已经看了24页,再看多少页就能看到这本书的一半?2、妈妈买来14米布,做裙子用去3米,做裤子用的米数和做裙子用的同样多.还剩多少米布?天天练第20天(5月14日)1、20-19+18-17+16-15+…+4-3+2-12、39-38+37-36+35-34+…+5-4+3-2+1)天天练第21天(5月15日)1、在合适的地方填入“+”,使等式成立(位置相邻的两个数字可以组成一个数)1 2 3 4 5 6 = 661 2 3 4 5 6 7 = 1272、在下面每两个数之间填上“+”或“-”,使等式成立。
学而思五年级春季下学期超长123班讲义学案试题(8-13讲)
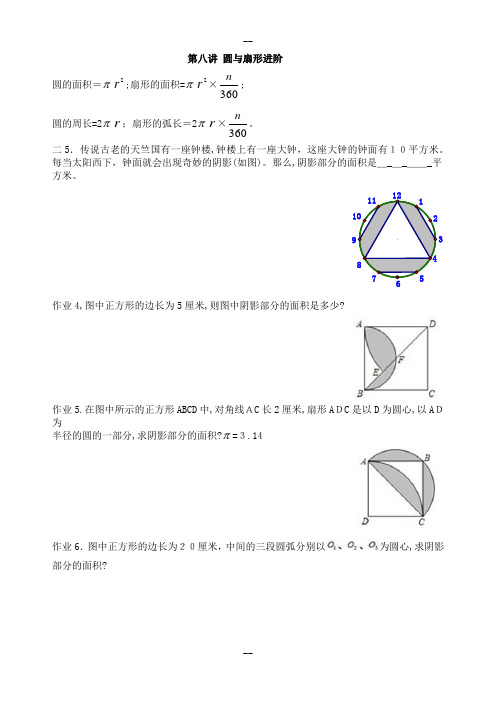
第八讲 圆与扇形进阶圆的面积=π2r ;扇形的面积=π2r ×360n ;圆的周长=2πr ;扇形的弧长=2πr ×360n 。
二5.传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米。
每当太阳西下,钟面就会出现奇妙的阴影(如图)。
那么,阴影部分的面积是_______平方米。
作业4,图中正方形的边长为5厘米,则图中阴影部分的面积是多少?作业5.在图中所示的正方形ABCD 中,对角线AC 长2厘米,扇形A DC 是以D 为圆心,以A D为半径的圆的一部分,求阴影部分的面积?π=3.14作业6.图中正方形的边长为20厘米,中间的三段圆弧分别以为圆心,求阴影部分的面积?第九讲 比较与估算 一.大小比较 1.通分 2.化成小数 3.倒数法 4.参考值法 5.交叉相乘 6、糖水原理 1.a b <c a d b ++<c d 7.糖水原理 2.a b <ma mb ++ 二.估算1、整体放缩 2、部分放缩 3、中项放缩 4、分组放缩一1.把32、53、75、1915按照从小到大的顺序排列。
一2.将250131、4021、0.52o3o、0.523o、0.52o从小到大排列,第三个数是_______。
一3.比较大小:2713和5728;1111111和111111111。
交叉相乘若ab >cd (a 、b、c 、d 为正整数),则bc>ad 。
一5.下式中五个分数都是最简真分数,要使不等式成立,这些分母的和最小是多少? ﻩ(__)1>(__)2>(__)3>(__)4>(__)5一.7设321311301++=a ,521511501491481++++=b ,则在a 与b中,较大的数是______。
参考值法 二6.将178、2413、3518、5931按从小到大的顺序排列。
糖水原理-结论1 若0<ab <cd <1,则a b <c a d b ++<cd导问4.如果一个班的女生人数占全班人数的31和83之间,这个班至少有多少人?补充.54<?25<65糖水原理-结论2 若0<ab <1,m>0,则ab <ma mb ++原理解读:(1)横向看:分子分母同时“+”一个常数,分数值变大;(2)纵向看:每个分数的“分母-分子”差是相同的,也就是说这个糖水原理的应用条件是:如果“分母-分子”差不同,可以通过扩倍变成差相同,之后就可以应用糖水原理 二2(2).比较75、2320、3329、161149的大小。
学而思六年级数学教材(含部分答案)

学而思六年级数学测试1·计算篇1. 计算=⨯+++++++128)288122411681120180148124181( 答案:25692. =++⨯++++-+++⨯+++)1119171()131111917151()1311119171()111917151( 答案:1653. 计算:2004×2003-2003×2002+2002×2001-2001×2000+…+2×1=答案:200820084.有一列数:1111,,,251017……第2008个数是________ . 答案:140320655.看规律13 = 12,13 + 23 = 32,13 + 23 + 33 = 62 ……,试求36+ 73 + … + 143 答案:1+2+3+…+9=4536+ 73 + … + 143=245第1讲 小升初专项训练·计算 ✧ 四五年级经典难题回顾✧例1、求下列算式计算结果的各位数字之和:20062005666666725⨯⨯答案2006200611105550 例2、求数1111110111219++++的整数部分是几?答案:1✧ 小升初重点题型精讲例1、=÷+÷+÷595491474371353251.答案:123例2、=+⨯⨯÷+--+)19956.15.019954.01993(22.550276951922.510939519答案:54例3、=++÷++)25118100412200811()25138100432200831( . 答案:20112009巩固、计算:=+⨯+⨯+⨯+⨯416024340143214016940146 . 答案:2例4、计算:22221235013355799101++++=⨯⨯⨯⨯ . 答案:1275101拓展计算:57191232348910+++=⨯⨯⨯⨯⨯⨯ . 答案:2315例5 、1⨯2+2⨯3+3⨯4+4⨯5+5⨯6+6⨯7+7⨯8+8⨯9+9⨯10= .答案:330巩固:2⨯3+3⨯4+4⨯5++100⨯101= . 答案:343398拓展、计算:1⨯2⨯3+2⨯3⨯4+3⨯4⨯5++9⨯10⨯11= .答案:2970例6、[2007 –(8.5⨯8.5-1.5⨯1.5)÷10]÷160-0.3= .答案:12.2巩固、计算:53×57 – 47×43 = .答案:1000例7、计算:11×19 + 12×18 + 13×17 + 14×16 = .答案:870拓展、计算:1×99 + 2×98 + 3×97 ++ 49×51 = . 答案:82075例8、计算:1×99 + 2×97 + 3×95 ++ 50×1 = . 答案:42925家庭作业 1. =÷+÷+÷797291585381373172 . 答案:1532. =-⨯⨯+÷)5246.5(402323153236 . 答案:11543. =++÷++)2231966913200711()2237966973200771( . 答案:100710044. 计算:222222222231517119931199513151711993119951++++++++++=----- . 答案:99799719965. 计算:11×29 + 12×28 + … + 19×21 = .答案:3315名校真题1. 如图,AD = DB , AE = EF = FC ,已知阴影部分面积为5平方厘米,△ABC 的面积是_________平方厘米.答案:302. 如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为_________.答案:63. 如图,长方形ABCD的面积是36,E是AD的三等分点,AE = 2ED,则阴影部分的面积是 .答案:2.74. 如图,边长为1的正方形ABCD中,BE = 2EC,CF = FD,求三角形AEG的面积.答案:275. 如图,3个边长为3的正方形,甲的中心在乙的一个顶点上,乙的中心在丙的一个顶点上,甲与丙不重叠,求甲、乙、丙叫共覆盖的面积是。
学而思奥数第六级第六讲逻辑思维综合(邹、陈、罗)

学而思奥数第六级第六讲 逻辑推理综合逻辑推理作为数学思维中重要的一部分,经常出现在各种数学竞赛中,除此以外,逻辑推理还经常作为专项的内容出现在各类选拔考试,甚至是面向成年人的考试当中。
对于学生学习数学来说,逻辑推理既有趣又可以开发智力,学生自主学习研究性比较高。
本讲我们主要从各个角度总结逻辑推理的解题方法。
一、 列表推理法逻辑推理问题的显著特点是层次多,条件纵横交错.如何从较繁杂的信息中选准突破口,层层剖析,一步步向结论靠近,是解决问题的关键.因此在推理过程中,我们也常常采用列表的方式,把错综复杂的约束条件用符号和图形表示出来,这样可以借助几何直观,把令人眼花缭乱的条件变得一目了然,答案也就容易找到了.二、 假设推理用假设法解逻辑推理问题,就是根据题目的几种可能情况,逐一假设.如果推出矛盾,那么假设不成立;如果推不出矛盾,而是符合题意,那么假设成立.解题突破口:找题目所给的矛盾点进行假设三、 计算中的逻辑推理能够利用数论等知识通过计算解决逻辑推理题.一、 列表推理法【例 1】 刘刚、马辉、李强三个男孩各有一个妹妹,六个人进行乒乓球混合双打比赛.事先规定:兄妹二人不许搭伴.第一盘:刘刚和小丽对李强和小英;第二盘:李强和小红对刘刚和马辉的妹妹.问:三个男孩的妹妹分别是谁?【巩固】 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:⑴张贝从未上过天;⑵跳伞运动员已得过两块金牌;⑶李丽还未得过第一名,她与田径运动员同年出生.请根据上述情况判断王文、张贝、李丽各是什么运动员?例题精讲知识结构【例2】张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:⑴张明不在北京工作,席辉不在上海工作;⑵在北京工作的不是教师;⑶在上海工作的是工人;⑷席辉不是农民.问:这三人各住哪里?各是什么职业?【巩固】甲、乙、丙三人,他们的籍贯分别是辽宁、广西、山东,他们的职业分别是教师、工人、演员.已知:⑴甲不是辽宁人,乙不是广西人;⑵辽宁人不是演员,广西人是教师;⑶乙不是工人.求这三人各自的籍贯和职业.【例3】甲、乙、丙、丁四个人的职业分别是教师、医生、律师、警察.已知:⑴教师不知道甲的职业;⑵医生曾给乙治过病;⑶律师是丙的法律顾问(经常见面);⑷丁不是律师;⑸乙和丙从未见过面.那么甲、乙、丙、丁的职业依次是:.【巩固】甲、乙、丙三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长.一次数学测验,这三个人的成绩是:⑴丙比大队长的成绩好.⑵甲和中队长的成绩不相同.⑶中队长比乙的成绩差.请你根据这三个人的成绩,判断一下,谁是大队长呢?【例4】甲、乙、丙、丁每人只会中、英、法、日四种语言中的两种,其中有一种语言只有一人会说.他们在一起交谈可有趣啦:⑴乙不会说英语,当甲与丙交谈时,却请他当翻译;⑵甲会日语,丁不会日语,但他们却能相互交谈;⑶乙、丙、丁找不到三人都会的语言;⑷没有人同时会日、法两种语言.请问:甲、乙、丙、丁各会哪两种语言?【巩固】宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:⑴数学博士夸跳高冠军跳的高⑵跳高冠军和大作家常与宝宝一起看电影⑶短跑健将请小画家画贺年卡⑷数学博士和小画家关系很好⑸贝贝向大作家借过书⑹聪聪下象棋常赢贝贝和小画家问:宝宝、贝贝、聪聪各有哪两个外号吗?【例5】六年级四个班进行数学竞赛,小明猜想比赛的结果是:3班第一名,2班第二名,1班第三名,4班第四名.小华猜想比赛的结果是:2班第一名,4班第二名,3班第三名,1班第四名.结果只有小华猜到的4班为第二名是正确的.那么这次竞赛的名次是班第一名,班第二名,班第三名,班第四名。
学而思2024测试题及答案

学而思2024测试题及答案一、选择题(每题2分,共20分)1. 根据题目分析,下列哪个选项是正确的?A. 地球是平的B. 光速是可变的C. 植物通过光合作用制造氧气D. 水在标准大气压下100°C沸腾正确答案:D2. 以下哪个历史事件标志着第二次世界大战的结束?A. 珍珠港事件B. 诺曼底登陆C. 广岛原子弹爆炸D. 日本无条件投降正确答案:D3. 在化学中,下列哪个元素的原子序数是26?A. 铁(Fe)B. 铜(Cu)C. 锌(Zn)D. 银(Ag)正确答案:C4. 以下哪个公式是计算圆面积的公式?A. A = πr²B. A = 2πrC. A = πdD. A = πd²/4正确答案:A5. 根据题目分析,下列哪个是生态系统中生产者?A. 狮子B. 草C. 蚯蚓D. 蘑菇正确答案:B二、填空题(每题2分,共10分)6. 牛顿第二定律的表达式是________。
答案:F = ma7. 世界上最深的海沟是________。
答案:马里亚纳海沟8. 光合作用过程中,植物将________转化为葡萄糖和氧气。
答案:二氧化碳9. 根据题目分析,中国历史上的四大发明是________、________、________和________。
答案:造纸术、印刷术、火药、指南针10. 根据题目分析,下列哪个是元素周期表中的金属元素?答案:Fe(铁)三、简答题(每题5分,共10分)11. 简述牛顿第三定律的内容。
答案:牛顿第三定律,又称作用与反作用定律,指出:对于两个相互作用的物体,它们之间的作用力和反作用力大小相等、方向相反。
12. 描述一下生态系统中消费者的作用。
答案:消费者在生态系统中扮演着重要的角色,它们通过捕食生产者或其他消费者,促进能量的流动和物质的循环,维持生态系统的平衡。
四、计算题(每题5分,共10分)13. 一个物体的质量是2千克,受到的重力是19.6牛顿,求物体受到的加速度。
中班学而思作业数字

中班学而思作业数字摘要:一、引言1.学而思的背景介绍2.中班阶段的重要性3.学而思中班作业的概述二、学而思中班作业的特点1.结合课程进度2.培养自主学习能力3.激发创新思维三、学而思中班作业的优势1.提高学生的学术成绩2.培养良好的学习习惯3.增强学生的自信心四、学而思中班作业的具体内容1.语文作业2.数学作业3.英语作业五、学而思中班作业的反馈与建议1.家长满意度高2.学生积极参与3.持续改进与优化六、结论1.学而思中班作业的重要性和优势2.学生通过完成作业获得的成长和进步3.展望学而思中班作业的未来发展正文:学而思,作为我国知名的课外教育培训机构,一直以来都致力于为学生提供优质的课外辅导。
在中班阶段,学生的学习任务逐渐加重,学而思的中班作业则起到了很好的辅助作用。
本文将围绕学而思中班作业的概述、特点、优势以及具体内容等方面进行详细阐述。
一、引言学而思成立于2003年,以“激发兴趣、培养习惯、塑造品格”为教育理念,以“成就客户、务实、创新、合作”为企业文化,旨在为广大学子提供全方位的教育服务。
中班阶段是学生从幼儿园向小学过渡的关键时期,学而思针对这一阶段的学生特点,设计了一系列富有针对性的课程和作业。
二、学而思中班作业的特点学而思中班作业紧密结合课程进度,旨在帮助学生巩固课堂所学知识。
同时,通过设置富有挑战性和趣味性的题目,培养学生的自主学习能力,激发他们的创新思维。
三、学而思中班作业的优势学而思中班作业在提高学生学术成绩方面取得了显著成果,同时也培养了学生良好的学习习惯。
此外,学而思中班作业通过多元化的评价方式,增强了学生的自信心,让他们在学习过程中不断挑战自我,实现自我突破。
四、学而思中班作业的具体内容学而思中班作业涵盖了语文、数学和英语三门学科。
其中,语文作业注重培养学生的阅读能力和写作能力,数学作业则侧重于锻炼学生的逻辑思维能力,英语作业旨在提高学生的听说读写水平。
五、学而思中班作业的反馈与建议学而思中班作业得到了广大家长的认可和好评,学生也积极参与其中。
学而思2011年暑假新四年级超常123班难题汇总
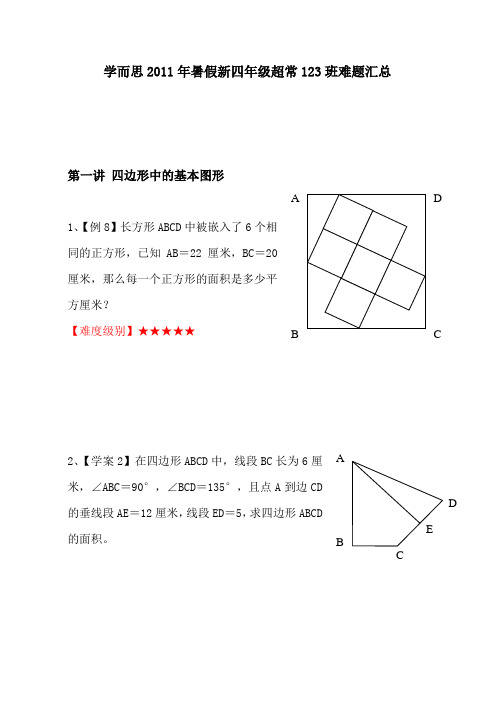
学而思2011年暑假新四年级超常123班难题汇总第一讲四边形中的基本图形1、【例8】长方形ABCD中被嵌入了6个相同的正方形,已知AB=22厘米,BC=20厘米,那么每一个正方形的面积是多少平方厘米?【难度级别】★★★★★2、【学案2】在四边形ABCD中,线段BC长为6厘米,∠ABC=90°,∠BCD=135°,且点A到边CD 的垂线段AE=12厘米,线段ED=5,求四边形ABCD 的面积。
D C3、【学案3】等腰梯形ABCD 中,交于O 点的两条对角线互相垂直,三角形ECB 是直角三角形,OC 比AO长20厘米。
已知三角形ADE 的面积是250平方厘米,则梯形ABCD 的面积是多少平方厘米?4、【学案4】一块边长为180厘米的正方形铁片,四角各被截去一个边长为40厘米的小正方形铁片,现在要从剩下的铁片中剪出一块完整的正方形铁片来,剪出的正方形面积最大为多少平方厘米?5、【作业5】请仅用刻度尺画一个面积是5平方厘米的正方形,保留必要的作图痕迹。
O B C D EA第二讲乘法原理6、【例7】1到1999的自然数中,有多少个与5678相加时,至少发生一次进位?7、【例8】有______个四位数满足下列条件:它的各位数字都是奇数,它的各位数字互不相同,它的每个数字都能整除它本身。
8、【学案1】计算机上编程序打印出前10000个正整数:1,2,3,……,10000时,不幸打印机有毛病,每次打印数字3时,它都打印出x,问其中被错误打印的共有多少个数?9、【学案4】有9张同样大小的圆形纸片,其中标有数码“1”的有1张,标有数码“2”的有2张,标有数码“3”的有3张,标有数码“4”的有3张,把这9张圆形纸片如图所示放置在一起,但标有相同数码的纸片不许挨在一起。
(1)如果M处放标有数码“3”的纸片,一共有多少种不同的放置方法?(2)如果M处放标有数码“2”的纸片,一共有多少种不同的放置方法?10、【越玩越聪明】在例6的后面。
学而思二年级寒假作业答案

一棵,小路总长:100+30=130(米),130÷5=26(段),26+1=27(棵)。 5.100÷10=10(段),一端种,彩旗数=段数。10 面。 6.41-1=40(段),800÷40=20(米) 7.24+24-1+24-1+24-2=92(棵) 脑筋转一转:夜明珠在哪里? 答案:1 号屋的女子说的是真话,夜明珠在 3 号屋子内。假设夜明珠在 1 号屋内,那么 2 号屋和 3 号屋 的女子说的都是真话,因此不在 1 号屋内;假设夜明珠在 2 号屋内,那么 1 号屋和 3 号屋的女子说的 都是真话,因此不在 2 号屋内;假设夜明珠在 3 号屋内,那么只有 1 号屋的女子说的是真话,因此, 夜明珠在 3 号屋里内。
2.如果都看成小汽车,那么一共是 14×4=56(个)轮子,还差 72-56=16(个)轮子,小汽车比大 卡车少 2 个轮子,所以就 16÷2=8(辆)大卡车.还剩下 14-8=6(辆)就是小汽车。
3.⑴ 先画 10 个头,如果全是鹤,应该画几条腿?2×10=20(条) ⑵ 比已知条数少了几条腿?36-20=16(条) ⑶ 一只龟比一只鹤多几条腿?4-2=2(条) ⑷ 可以把几只鹤换成龟?16÷2=8(只) ⑸ 有几只鹤?10-8=2(只)答:有 2 只鹤,8 只龟。
7.182+74=256(本),256÷4=64(本),64+132=196(本) 脑筋转一转:猜猜它是几? 答案:把每个立方体如图标为 a,b,c,d,e,f 根据规则 1,a 上写有 3 的面相对的面上写的数为 7-3=4; 根据规则 2,a 上写有 4 的面相接于 b 的面上应写的数为 8-4=4; 根据规则 1,b 上写有 4 的面相对的面上写的数为 7-4=3; 根据规则 2,b 上写有 3 的面相接的 c 的面上应写的数为 8-3=5; 此时 c 上写有 1 的面的对面上写的数是 7-1=6,写有 5 的面的对面上写的数是 7-5=2,c 的右侧面上 写的数是 3 或 4. (1)如果 c 的右侧面上写的数字是 3: 根据规则 2,和 c 的 3 的面相接的 d 的面上的数为 8-3=5; 根据规则 1,和 d 的 5 的面相对的面上的数为 7-5=2; 根据规则 2,和 d 的 2 的面相接的 e 的面上的数为 8-2=6; 根据规则 1,和 e 的 6 的面相对的面上的数为 7-6=1; 根据规则 2,和 e 的 1 的面相接的 f 的面上的数为 8-6=7; (2)如果 c 的右侧面上写的数字是 4: 根据规则 2,和 c 的 4 的面相接的 d 的面上的数为 8-4=4; 根据规则 1,和 d 的 4 的面相对的面上的数为 7-4=3; 根据规则 2,和 d 的 3 的面相接的 e 的面上的数为 8-3=5; 根据规则 1,和 e 的 5 的面相对的面上的数为 7-5=2; 根据规则 2,和 e 的 2 的面相接的 f 的面上的数为 8-2=6; 根据规则 1,和 f 的 6 的面相对的面上的数为 7-6=1;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上一段12级楼梯,规定每一步只能上一级或两级楼梯,要登上第11级楼梯,不同的走法共有种。
【练练9】
上一段15级楼梯,规定每一步只能上一级或两级或三级楼梯,要登上第10级楼梯,不同的走法共有种。
【练练10】
现在有足够的1cm×2cm的长方形纸条.用这种纸条去覆盖2cm×3cm的长方形纸,使它们既不重叠,也不超出和留间隙,有3种不同的方法(如左下图).那么,将这1cm×2cm的长方形纸条覆盖由24个边长为1cm的正方形组成的图形(如右下图),共有()种不同的方法.
在一种排列顺序里,我们把所有“怨言”的总数叫“怨言数”。(注:一个人可以有两次以上的“怨言”。)
例如:下面的排列,其“怨言数”就是4。
(前) “怨言”
1年级生0次
4年级生0次
3年级生1次
2年级生2次
6年级生0次
5年级生1次
“怨言数”…4次
问:“怨言数”为7的排列顺序有几种?
【练练30】
整数1,2,3,……,14排成一排,满足:每个数或者大于它前面的所有数,或者小于它前面的所有数。那么总共有个满足条件的排列方式。
【练练26】
(2006年“迎春杯”中年级组决赛)
有6个木箱,编号为1,2,3,……,6,每个箱子有一把钥匙,6把钥匙各不相同,每个箱子放进一把钥匙锁好.先撬开1,2号箱子,可以取出钥匙去开箱子上的锁,如果最终能把6把锁都打开,则说这是一种放钥匙的“好”的方法,那么“好”的方法共有种.
【练练27】
给你一架天平和两个砝码,这两个砝码分别重 克和 克,如果再添三个砝码,则这
一般地,对于 的方格网,相对的两个顶点之间的最短路线有 种.
本题中,从 到 的最短路线共有 种;从 到 的最短路线共有 种,从 到 的最短路线共有 种,根据乘法原理,从 到 且必须经过 的最短路线有 种,所以,从 到 且不经过 的最短路线有 种。
【练练2答案】
小王在一年中去少年宫学习56次,如图所示,小王家在 点,他去少年宫都是走最近的路,且每次去时所走的路线正好互不相同,那么少年宫在________点处.
现在要覆盖如下图
可分为两类:
第一类:拐弯部分分为两类:
第一步;覆盖前面2×6的长条的方法有:13种;
第二步;覆盖后面2×2方格的方法有:2种;
此时有2×13=26种。
第二类:拐弯部分也可能是竖放,此时:
左边2×4的长方形纸条有:5种方法。
所以共有:26+5=31种方法。
【练练8答案】
上一段12级楼梯,规定每一步只能上一级或两级楼梯,要登上第11级楼梯,不同的走法共有种。
【练练3答案】
如图,某城市的街道由5条东西向马路和6条南北向马路组成,现在要从西南角的 处沿最短的路线走到东北角 处,由于修路,十字路口 不能通过,那么共有种不同走法.
【分析】使用标数法可以得到共有66种不同走法.或者,由于从 到 的最短路线有 种,从 到 的最短路线有 种,所以从 到 且经过 的最短路线有 种;由于从 到 的最短路线有 种,所以从 到 且不经过 的最短路线有 种。
【练练20】
平面上的5个圆和1条直线最多能把平面分成多少部分?
【练练21】
平面上的5个圆和3条直线最多能把平面分成多少部分?
【练练22】
用10个 的小长方形去覆盖 的方格网,一共有 种不同的覆盖方法.
【练练23】
用10个 的小长方形去覆盖 的方格网,一共有多少种不同的覆盖方法。
【练练24】
证明 ,n为自然数
数学加油站(六年级):252271825
(2)秀情老师从中选优秀作业,赠送我独有的精美礼品
(3)两周一次进行——【情学好问】直播答疑
情学好问(五年级):62834135
情学好问(六年级):283789167
【练练1】
如图,某城市的街道由5条东西向马路和7条南北向马路组成,现在要从西南角的 处沿最短的路线走到东北角 出,由于修路,十字路口 不能通过,那么共有种不同走法.
杨秀情——六年级暑假——配套练习
【作业要求】
(1)建议打印下来,归类整理好,一个学期下来,装订成册
(2)先看秀情老师网校的课程视频,再做这些作业哈
(3)可根据自己的情况,有选择性的做题哦
(4)书写规范,步骤清晰
【温馨提示】
(1)做完后可以拍照,上传到秀情老师的群:数学加油站
数学加油站(五年级):236427726
【练练7】
(第15届日本算术奥林匹克预赛试题)
有足够的1cm×2cm的长方形纸条。用这种纸条去覆盖2cm×3cm的长方形纸,使它们既不重叠,也不超出和留间隙,有3种不同的方法(如左下图)。那么,将这1cm×2cm的长方形纸条覆盖由16个边长为1cm的正方形组成的图形(如右下图),共有多少种不同的方法?
③现已知某个平面图有999个顶点,且围成了999个区域,试根据以上关系确定这个图有多少条边.
【练练32】
个人进行篮球训练,互相传球接球,要求每个人接球后马上传给别人,开始由甲发球,并作为第一次传球,第五次传球后,球又回到甲手中,问有多少种传球方法?
【练练1答案】
如图,某城市的街道由5条东西向马路和7条南北向马路组成,现在要从西南角的 处沿最短的路线走到东北角 出,由于修路,十字路口 不能通过,那么共有种不同走法.
【练练5答案】
(2007年第五届走美初赛六年级第15题)
如图,27个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有条。
【分析】最短路线有384条。
【练练6答案】
游乐园的门票1元1张,每人限购1张。现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱,问有多少种排队方式,使得售票员总能找的开零钱。
【分析】标数法,假设1元的为横线,2元的为竖线。
则共有 (种)排队的方法使得其成立。
【练练7答案】
(第15届日本算术奥林匹克预赛试题)
有足够的1cm×2cm的长方形纸条。用这种纸条去覆盖2cm×3cm的长方形纸,使它们既不重叠,也不超出和留间隙,有3种不同的方法(如左下图)。那么,将这1cm×2cm的长方形纸条覆盖由16个边长为1cm的正方形组成的图形(如右下图),共有多少种不同的方法?
【分析】找规律:
发现,用1×2的长方形纸条去覆盖2×1的有1种方法;
去覆盖2×2的有2种方法;
去覆盖2×3的有3种方法;
去覆盖2×4的有2+3=5种方法;
去覆盖2×5的有3+5=8种方法;
去覆盖2×6的有5+8=13种方法。
以后类似的,覆盖2×n的方法总数是覆盖2×(n-1)的方法总数与覆盖2×(n-2)的方法总数之和。
【练练31】
(第六届“华杯赛”复赛)
①.下面的(a)、(b)、(c)、(d)为四个平面图.数一数,每个平面图各有多少个顶点?多少条边?它们分别围成了多少个区域?请将结果填入下表(按填好的样子做).
顶点数
边数
区域数
(a)
4
6
3
(b)
(c)
(d)
②观察上表,推断一个平面图的顶点数、边数、区域数之间有什么关系?
五个砝码可以称的重量种类最多是________种。(天平的左右两盘均可放砝码)
【练练2ห้องสมุดไป่ตู้】
有30个石子,一个人分若干次取,每次可以取1个,2个或3个,但是每次取完之后不能留下质数个,有多少方法取完?石子之间不作区分,即只考虑石子个数。
【练练29】
有从一年级到六年级的儿童各一人,排成一列领取糖果。如果一个高年级的儿童站在低年级的儿童前面,那么高级年儿童后面所有比他年级低的儿童都会各有一次“怨言”。
【分析】本题是最短路线问题.要找出共有多少种不同走法,关键是保证不重也不漏,一般采用标数法.如上图所示,共有120种.
另解:本题也可采用排除法.由于不能经过 ,可以先计算出从 到 的最短路线有多少条,再去掉其中那些经过 的路线数,即得到所求的结果.
对于从 到 的每一条最短路线,需要向右6次,向上4次,共有10次向右或向上;而对于每一条最短路线,如果确定了其中的某6次是向右的,那么剩下的4次只能是向上的,从而该路线也就确定了.这就说明从 到 的最短路线的条数等于从10次向右或向上里面选择6次向右的种数,为 .
【练练4】
(2007年第五届走美五年级初赛第15题)
如图,8个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有条。
【练练5】
(2007年第五届走美初赛六年级第15题)
如图,27个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有条。
【练练6】
游乐园的门票1元1张,每人限购1张。现在有10个小朋友排队购票,其中5个小朋友只有1元的钞票,另外5个小朋友只有2元的钞票,售票员没有准备零钱,问有多少种排队方式,使得售票员总能找的开零钱。
学学和思思一起洗 个互不相同的碗,思思洗好的碗一个一个往上摞,学学再从最上面一个一个地拿走放入碗柜摞成一摞,思思一边洗,学学一边拿,那么学学摞好的碗一共有种不同的摞法。
【练练17】
平面上4个圆最多能把平面分成多少部分?
【练练18】
10个三角形最多将平面分成几个部分?
【练练19】
一个长方形把平面分成两部分,那么三个长方形最多把平面分成部分.
【练练25】
传说在印度的佛教圣地贝拿勒斯圣庙里安放着个一个黄铜板,板上插着三根宝石针,在第一根宝石针上,从下到上穿着由大到小的64片中心有孔的金片.每天都有一个值班僧侣按下面规则移动金片:把金片从第一根宝石针移到其余的某根宝石针上.要求一次只能移动一片,而且小片永远要放在大片的上面.当时传说当64片金片都按上面的规则从第一根宝石针移到另一根宝石针上时,世界将在一声霹雳中毁灭.所以有人戏称这个问题叫“世界末日”问题(也称为“Hanoi塔”问题),当然,移金片和世界毁灭并无联系,这只是一个传说而已,但说明这是一个需要移动很多很多次才能办到的事情.解这个问题的方法在算法分析中也常用到.究竟按上述规则移动完成64片金片需要移动多少次呢?
