运筹学上机实验报告
运筹学上机实践报告LINGO软件

Southwest university of science and technology实验报告LINGO软件在线性规划中的运用学院名称环境与资源学院专业名称采矿工程学生姓名学号____________________________________ 指导教师陈星明教授二◦一五年十一月实验LINGO软件在线性规划中的运用实验目的掌握LINGO软件求解线性规划问题的基本步骤,了解LINGO软件解决线性规划问题的基本原理,熟悉常用的线性规划计算代码,理解线性规划问题的迭代关系。
实验仪器、设备或软件电脑,LINGO软件实验内容1. LINGO软件求解线性规划问题的基本原理;2•编写并调试LINGO软件求解线性规划问题的计算代码;实验步骤1•使用LINGO计算并求解线性规划问题;2 •写出实验报告,并浅谈学习心得体会(线性规划的基本求解思路与方法及求解过程中出现的问题及解决方法)。
实验过程有一艘货轮,分为前、中、后三个舱位,它们的容积与允许载重量如下表所示。
现有三种商品待运,已知有关数据列于下表中。
又为了航运安全,要求前、中、后舱在实际载重量上大体保持各舱最大允许载重量的比例关系。
具体要求前、后舱分别与中舱之间的载重量比例偏差不超过15%,前、后舱之间不超过10%。
问货轮首先分析问题,建立数学模型:确定决策变量假设i=1,2,3分别代表商品A、B C, 8用j=1,2,3分别代表前、中、后舱,设决策变量X ij为装于j舱位的第i种商品的数量(件)。
确定目标函数商品A的件数为:x11- x12x13商品B的件数为:x21x22x23商品A的件数为:X31 - X32 - X33为使运费最高,目标函数为:确定约束条件前、中、后舱位载重限制为:前、中、后舱位体积限制为:A、B、C三种商品数量的限制条件:各舱最大允许载重量的比例关系构成的约束条件:且决策变量要求非负,即X j > 0,i=1,2;j=1,2,3。
管理运筹学上机实验

实验报告2:P153习题1某公司在三个地方有三个分厂,生产同一种产品,其产量分别为300箱、600箱、500箱。
需要供应四个地方的销售,这四地的产品需求分别为400箱、250箱、350箱、200箱。
三个分厂到四个产地的单位运价如表所示。
应如何安排运输方案,使得总运费为最小。
在此问题中,三个分厂的总产量为1400单位,而总需求量为1200单位。
因此此问题为供求不相等的运输问题,且供大于求。
为此,除已有的四个销地外,可假设一销地,且三个分厂运往此销地的单位运费均为0。
即将假设的销地看为存储的仓库。
求解过程最优解如下********************************************起至销点发点 1 2 3 4-------- ---- ----- ----- -----1 0 250 0 502 400 0 0 03 0 0 350 150此运输问题的成本或收益为: 19800此问题的另外的解如下:起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 0 250 50 02 400 0 0 03 0 0 300 200此运输问题的成本或收益为: 19800(2)如果2 分厂产量提高到600,则为产销不平衡问题最优解如下******************************************** 起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 0 250 0 02 400 0 0 2003 0 0 350 0此运输问题的成本或收益为: 19050注释:总供应量多出总需求量200第1 个产地剩余50第3 个产地剩余150(3)销地甲的需求提高后,也变为产销不平衡问题最优解如下******************************************** 起至销点发点 1 2 3 4-------- ----- ----- ----- -----1 50 250 0 02 400 0 0 03 0 0 350 150此运输问题的成本或收益为: 19600总需求量多出总供应量150第1 个销地未被满足,缺少100第4 个销地未被满足,缺少50P255 习题1这是一个最短路问题,要求我们求出从v1 到v7 配送的最短距离。
运筹学上机实验报告

学生实验报告实验课程名称《运筹学》开课实验室计算机中心第二机房学院专业学生姓名学号开课时间 2015 至 2016 学年第二学期实验一中小型线性规划模型的求解与Lingo软件的初步使用一、实验目的了解Lingo软件的基本功能和简单线性规划模型的求解的输入和输出结果。
二、实验内容1.在Lingo中求解下面的线性规划数学模型:max z=2x1+3x2x 1+2x2≤84x1≤164x2≤12x 1, x2≥02.在Lingo中求解教材P55习题(1)的线性规划数学模型;3.建立教材P42例8的数学模型并用Lingo求解;4.建立教材P57习题的数学模型并用Lingo求解。
三、实验要求1.给出所求解问题的数学模型;2.给出Lingo中的输入;3.能理解Solution Report中输出的四个部分的结果;4.能给出最优解和最优值;5.能理解哪些约束是取等式和哪些约束取不等式。
四、实验步骤五、结论1.该线性规划模型的目标函数值为14,该线性规划经过一次迭代求得最优解,有2个总决策变量,包括目标函数一共有4个约束,最优解的变量X1=4,X2=2 。
2. 该线性规划模型的目标函数值为2,该线性规划经过2次迭代求得最优解,有4个总决策变量,包括目标函数一共有4个约束,最优解的变量X1=0、x2=8、x3=0、x4=-6。
3.该线性规划模型的目标函数值为-2,该线性规划经过0次迭代求得最优解,有3个总决策变量,包括目标函数一共有4个约束,最优解的变量x1=4、x2=1、x3=9。
4.该线性规划模型的目标函数值为150,该线性规划经过4次迭代求得最优解,有6个总决策变量,包括目标函数一共有7个约束,最优解的变量x1=60、x2=10、x3=50、x4=0、x5=30、x6=0。
实验二中小型运输问题数学模型的Lingo软件求解一、实验目的熟悉运输问题的数学模型,掌握简单运输问题数学模型的Lingo软件求解的方法,掌握解报告的内容。
运筹学上机实验报告

运筹学实验报告一、实验项目名称:运筹学综合实验二、实验目的:1、熟悉WinQSB的用户界面2、学习建立数学模型的方法3、掌握用WinQSB求解运筹学的方法及步骤4、解读计算机运行结果,结合所学知识给出文字定性结论三、实验环境:WinQSB软件,计算机四、实验内容及步骤:①该项工程从施工开始到全部结束的最短周期;②如果引道混凝土施工工期拖延10天,对整个工程进度有何影响;③若装天花板的施工时间从12天缩短到8天,对整个工程进度有何影响;④为保证工期不拖延,装门这项作业最晚从哪一天开始开工;⑤如果要求该项工程必须在75天内完工,是否应采取措施及应从哪些方面采取措施。
2、分析题目并决定运用软件3、根据分析运用WinQSB软件进行求解1)、点击开始—程序—WinQSB—PERT-CTM,启动程序2)、点击file----New Problem----建立新问题,如图(1)(2)所示,填写问题名称,项目数量,问题类型,输入模式及时间分布类型,点击OK(1)(2)i3)、求解第①问:由题输入数据,结果如下图(3)所示(3)4)数据输入完毕后,求解问题的答案,点击Solve and Analyze-----Solve Critical Path,软件运行结果如图(4)所示(4)由图可知问题①的答案及从施工开始到全部结束的最短路线为80天。
为进一步得出其关键路线,可分别点击图标,得出下图(5)(6)(5)(6)6)、同样步骤求解第②问,即引道混凝土施工工期拖延10天的情况下,输入数据得到如下图图(7)所示结果(7)(8)(9)(10)由上图(7)(8)(9)(10)可知当引道混凝土工期拖延10天时,其最短周期还是80天,关键路线不变,即无影响。
7)、同样步骤求解第③问,即装天花板时间由12天缩短为8天情况下,输入数据得到如下图所示结果(11)(12)(13)(14)由图(11)(12)(13)(14)可知,当装天花板的施工时间从12天缩短为8天时,其最短周期由原来的80天缩短为76天,提前4天。
运筹学上机实验报告

西安邮电大学运筹学上机实验报告院系:_______经济与管理学院____班级:________电子商务1201_____姓名:_________邓博__________学号:________02122023________实验一.线性规划与对偶理论线性规划启动程序:开始/程序/WinQSB/Liear and Integer Programming/File/New Problem输入变量数3、约束数3、目标最大化(默认)、表格输入形式(默认)、非负连续变量(默认)。
单击O K 弹出数据编辑窗口,并输入数据执行菜单命令:Solve and Analyze有3求解方式:选择第1项Solve the Problem,得运行结果选择第2 项Solve and Display Steps,由最终单纯表可直接见到最优解和最优值x1=4,x2=1,x3=9目标函数值为z=-2.对偶理论Max z=x1+2x2+4x3+2x43x1+9x3+5x4≤156x1+4x2+x3+7x4≤304x2+3x3+4x4≤205x1+x2+8x3+3x4≤40xj≥0,j=1,2,3,4(1)建立新问题,如下图:(2).求对偶问题,如图:分析结果实验二.目标规划与整数规划目标规划执行“程序/WinQSB/Goal Programming/File/New Problem”单击“OK”生成表格,生成类似于数据编辑窗口,但包括偏差变量均为x 的下标变量。
执行菜单命令“File/Variable Names”,修改偏差变量名单击“OK”,返回数据窗口并按数学模型输入数据执行菜单命令:“Solve and Analyze/Sove the Problem”得运行结果由运行结果可见,该解为无界解。
整数规划启动程序:开始/程序/WinQSB/Liear and Integer Programming/File/New Problem输入变量数6、约束数7、目标最小化、表格输入形式(默认),单击OK弹出数据编辑窗口更改变量名称:Edit/Variable Names执行菜单命令:Solve and Analyze/Solve the Problem,得运行结果由运行结果可见:(1)最优生产方案是使用第3种生产方式生产3500kg,总成本13500元(其中变量成本10500元,固定成本3000元)。
运筹学上机实验建模报告
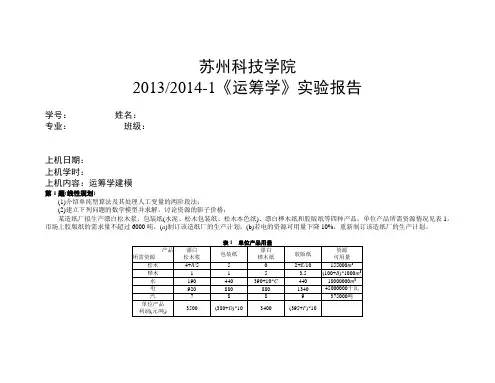
苏州科技学院2013/2014-1《运筹学》实验报告学号:姓名:专业:班级:上机日期:上机学时:上机内容:运筹学建模第1题(线性规划)(1)介绍单纯型算法及其处理人工变量的两阶段法;(2)建立下列问题的数学模型并求解,讨论资源的影子价格;某造纸厂拟生产漂白松木浆、包装纸(水泥、松木包装纸、松木本色纸)、漂白桦木纸和胶版纸等四种产品,单位产品所需资源情况见表1,市场上胶版纸的需求量不超过6000吨。
(a)制订该造纸厂的生产计划;(b)若电的资源可用量下降10%,重新制订该造纸厂的生产计划。
(3)结合本题,谈谈你对线性规划的认识。
Hint: 若参数为5,5,5,5,5,5,则最优目标函数值为(a)167236800;(b)167236800。
(1)单纯形法是求解线性规划问题的通用方法。
单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。
因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
两阶段单纯形法也是一种人工变量法,它的算法可分为两个阶段:第一阶段,引入人工变量,构造一个具有标准基的新线性规划,求解这个新线性规划,其结果有两种可能:或者将原问题的约束方程组化成具有标准基的形式,或者提供信息,表明原问题没有可行解。
第二阶段,利用第一阶段所得的标准基,对原问题求解。
(2)a)令A=B=C=D=E=F=10,设漂白松木浆,包装纸,漂白桦木纸,胶版纸的产量依次为x1,x2,x3,x4则,利润最大为max=3500*x1+3900*x2+3400*x3+4050*x4;6*x1+5*x2+3*x4<=155000;x1+x2+5*x3+3.5*x4<=110000;190*x1+440*x2+490*x3+440*x4<=18000000;920*x1+880*x2+880*x3+1340*x4<=45000000;7*x1+8*x2+8*x3+9*x4<=375000;x4<=6000;由lingo分析得出,x1=8582.915,x2=17100.5,x3=12663.32,x4=6000时,此时取得最大利润为0.164*10^9元。
运筹学上机实验
运筹学课内实验报告这个学期我们进行了为期三周的运筹学上机实验。
这次的实验内容主要是线性规划,对偶理论以及运输问题。
在实验中我们依靠WinQSB软件来实现各个问题的解答。
WinQSB是一种教学软件,对于非大型的问题一般都能计算,较小的问题还能演示中间的计算过程,特别适合多媒体课堂教学。
该软件可应用于管理科学、决策科学、运筹学及生产运作管理等领域的求解问题,首先我们要做得第一步就是熟悉软件的界面,内容以及操作方式。
我们主要进行的操作就是建立新问题,输入模型,求解模型,以及对结果的简单分析。
在第一部分线性规划问题中,我们要解决的问题分别是夹菜第一章第六节的例10、例11、例13以及课后作业题1.9和1.11。
下面我将展示我的求解过程和求解结果。
例10的求解过程合理利用线材问题。
现在要做100套钢架,每套用长为2.9m,2.1m和1.5m 的元钢各一根。
已知原料长7.4m,问应如何下料,使用的原材料最省。
在解题过程中,我们NEW PROBLEM命令中输入所需的变量,输入完成后出现下图。
在菜单中选择运行结果。
得出的结果如下图。
从图中我们可以看出,X1为方案1,按方案1应下料30根,X2为方案2,按方案2 应下料10根,X3为方案3,按方案3应下料50根。
即需90根原材料可以制造100套钢架。
例11.某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。
已知产品规格要求,产品单价,每天能供应的原材料数量以及原材料单价,分别见表,该厂如何安排生产,使利润收入为最大。
用WINQSB求解问题如下。
在NEW PROBLEM中输入所需变量。
点击确定,出现下表。
点击运行,求出结果如下。
由上图可以看出,每天只生产产品A为200KG,分别需要用原料C为100KG,P为50KG,H为50KG.1.9,某昼夜服务的公交线路每天各时间区段内所需司机和乘务人员数如下,设司机和乘务人员分别在各时间区段一开始时上班,并连续工作八小时,问该公交线路至少配备多少名司机和乘务人员。
运筹学上机实验报告
运筹学上机实验报告运筹学上机实验报告一、引言运筹学是一门研究如何在有限资源下做出最优决策的学科。
通过数学建模和优化算法,可以解决许多实际问题,如生产调度、物流配送、资源分配等。
本次实验旨在通过上机实践,加深对运筹学理论的理解,并掌握运筹学在实际问题中的应用。
二、实验目的本次实验的主要目的是通过运筹学软件的使用,解决一个实际问题。
具体目标包括:1. 掌握运筹学软件的基本操作方法;2. 学会进行数学建模,将实际问题转化为数学模型;3. 运用优化算法求解数学模型,得到最优解;4. 分析并评价所得解的合理性和可行性。
三、实验过程1. 问题描述本次实验的问题是一个生产调度问题。
某工厂有3台机器和6个任务需要完成,每个任务所需时间不同。
任务之间存在一定的先后顺序,即某些任务必须在其他任务完成后才能开始。
目标是找到一个最优的调度方案,使得所有任务完成所需的总时间最短。
2. 数学建模首先,将该问题转化为数学模型。
假设任务1到任务6的完成顺序为x1到x6,其中xi表示任务i在调度中的位置。
定义变量ti表示任务i的完成时间。
则该问题可以用如下的数学模型表示:目标函数:minimize t6约束条件:t1 = 0t2 ≥ t1 + x2t3 ≥ t2 + x3t4 ≥ t1 + x4t5 ≥ max(t2 + x5, t3 + x5)t6 ≥ max(t4 + x6, t5 + x6)3. 软件操作在运筹学软件中,根据上述数学模型进行建模。
首先,定义变量和约束条件,并设置目标函数为t6的最小化。
然后,使用优化算法求解该模型,得到最优解。
4. 结果分析根据软件求解结果,得到最优调度方案为x1=1, x2=2, x3=3, x4=4, x5=5, x6=6。
对应的任务完成时间为t1=0, t2=1, t3=3, t4=5, t5=7, t6=9。
因此,所有任务完成所需的总时间最短为9个单位时间。
五、实验总结本次实验通过运筹学软件的使用,解决了一个生产调度问题。
管理运筹学上机实习报告
管理运筹学上机实习报告实习目的:通过实习掌握线性规划的运输问题的计算机求解; 掌握“运输问题检验数”的应用和经济意义计算软件求解某建材公司所属的三个水泥厂321,,A A A ,生产水泥销往四个销售点4321,,,B B B B 。
已知水泥的日产量(百吨),各销售点的日销量(百吨)以及各工厂运往各销售点的单位运价(百元/百吨)如下表7-23所示表7-235423469429157412378 3214321销量产量产地销地A A A B B B B在QM 中的求解步骤 1、选择运输规划模块2、新建一个项目3、设置标题、产地个数、销地个数4输入单位运价、产量和销量5、选择初始调运方案的方法(西北角法、最小元素法、V ogel’s)6、点击“SoLve”进行求解7、计算的迭代过程目的:通过实习掌握纯整数线性规划和混合整数线性规划的计算机求解;掌握0-1规划的的计算机求解及实际建模应用要求:写书实习报告计算机求解以8.1的例8.2题说明QM 求解纯整数规划的过程。
⎪⎪⎩⎪⎪⎨⎧≥≤+≤++=整数,0,13522445.1020max 2121212121x x x x x x x x st x x z1、 在QM 软件包选择整数规划模块点击“Module ”按钮,在下拉式菜单中,选择“integer programming ”回车。
2、 新建一个项目(选择“New ”,并按回车键)3、设置标题、约束条件数、变量数和选择最大最小4输入目标函数系数、约束条件5点击“Slove”按钮进行求解。
6、在“Window”窗口中查看迭代过程、图形(两个变量)等信息。
目的:通过实习掌握指派问题的计算机求解;掌握指派问题的流程和应用要求:写书实习报告某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:问:座的学生总数。
目的:通过实习掌握多目标线性规划问题计算机求解步骤;学会分析多目标线性规划问题的求解结果要求:写书实习报告目标规划的计算机求解一家生产某种产品的公司在生产周期内的正常生产时间为100小时。
运筹学上机实践报告
运筹学实验报告姓名:学号:班级:采矿1103 教师:(一)实验目的(1)学会安装并利用Lingo软件(2)利用Lingo求解一样线性,运输,一样整数和分派问题(二)实验设备(1)运算机(2)Lingo软件(三)实验步骤(1)打开已经安装Lingo软件的运算机,进入Lingo(2)成立数学模型和Lingo语言(3)输入完Lingo语言后运行得出求解结果LINGO是用来求解线性和非线性规化问题的简易工具。
LINGO内置了一种成立最优化模型的语言,能够简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
当在windows 下开始运行LINGO系统时,会取得类似下面的一个窗口:外层是主框架窗口,包括了所有菜单命令和工具条,其它所有的窗口将被包括在主窗口之下。
在主窗口内的题目为LINGO Model–LINGO1的窗口是LINGO的默许模型窗口,成立的模型都都要在该窗口内编码实现。
下面是以一样线性,运输,一样整数和分派问题为例进行实验的具体操作步骤:A:一样线性计划问题数学模型(讲义31页例11)求解线性计划:Minz=-3x1+x2+x3x1 - 2x2 + x3<=11-4x1 + x2 + 2x3>=3-2x1 + x3=1x1,x2,x3>=0打开lingo输入min=-3*x1+x2+x3;x1-2*x2+x3<=11;-4*x1+x2+2*x3>=3;-2*x1+x3=1;End如下图:然后按工具条的按钮运行显现如下的界面,也即是运行的结果和所求的解:结果分析:由longo运行的结果界面能够取得最优解为xb=(x1,x2,x3)T=(4,1,9)T,最优目标函数z=-2.到此运用lingo解决了一样线性计划问题B:运输问题数学模型(讲义80页例1)例1 某公司有三个生产同类产品的加工厂(产地),生产的产品由四个销售点(销地)出售,各加工厂的生产量,各销售点的销售量(假设单位均为吨)和各个加工厂到各销售点的单位运价(元/吨)是如下表,问产品如何调运才能使总运费最小?B1 B2 B3 B4 产量产销A1 4 12 4 11 8A2 2 10 3 9 5A3 8 5 11 6 11销量7 7 6 7 24运用lingo软件,编制程序的程序解决3发点4收点的运输问题:Model:Sets:Xiao/1..4/:s;Chan/1..3/:h;Link(chan,xiao):x,y;EndesetsData:Y=4 12 4 112 103 98 5 11 6H=8 5 11;S=4 7 6 7;EnddataMin=@sum(link:x*y);@for(xiao(j):@sum(chan(i):x(i,j))=s(j);@for(chan(i):@sum(xiao(j):x(i,j))=h(i);现在lingo的框内如下所示:然后按工具条的按钮运行显现如下的界面,也即是运行的结果和所求的解:结果:由longo运行的结果界面能够取得该运输问题的最优运输方案为运6吨至B3;运2吨至B4,由A2运4吨至B1,运1吨至B4,由A3运吨7至B2,运4吨至B4,现在对应的的目标函数值为Z=6X4+2X11+4X2+1X9+7X5+4X6+122(元)到此lingo软件已经解决了运输问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 线性规划问题(利用excel 表格求解)
12121
21212max 1502102310034120..55150,0
z x x x x x x s t x x x x =++≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩
解:1 将光标放在目标函数值存放单元格(C7),点击“工具”,出现下图:
2 点击“规划求解”出现下图
3.在可变单元格中选择决策变量单元格B2,C2,出现下图。
4. 点击“添加”,出现下图。
5.输入约束条件
6. 输入约束条件,点击“确定”,出现下图。
7. 点击“选项”,出现下图。
8. 点击确定,回到规划求解对话框,出现下图。
9.点击“求解”,出现下图‘
10.点击“确定”,回到Excell 工作表,出现下图。
在工作表中,给出了最优解情况:120,30,max 6300x x z === 。
二、 求解整数线性规划(excel 表格处理) 某公司从两个产地A1,A2将物品运往三个销地B1,B2,
B3,各产地的产量、各销地的销量和各产地运往各销地的每件物品的运费如下表所示:
应如何调运,是的总运费最小? 1、建立模型
分析:这个问题是一个线性规划问题。
故应该确定决策变量、目标函数及约束条件。
设X ij 表示从产地A i 调运到B j 的运输量(i=1,2;j=1,2,3),根据问题的要求
由分析可得如下模型:
minW =6X 11+4X
12+6X 13+6X 21+5X 22+5X 23 (所需费用最低)
X 11+ X 12+ X 13=200; X 21+ X 22+ X 23=300;
约束条件 X 11+ X 21=150;
X 12+ X 22=150; X 13+ X 23=200; X ij >=0(i=1,2;j=1,2,3).
建立规划求解工作表,如下图所示:
1、在可变单元格(B4:G4)中输入初始值(1,1,1,1,1, 1)
2、在上图有关单元格输入如下公式
单元格地址公式
B5 =B3+C3+D3
B6 =E3+F3+G3
B7 =B3+E3
B8 =C3+F3
B9 =D3+G3
B10 =B2*B3+C2*C3+D2*D3+E2*E3+F2*F3+G2*G3
3、求最佳组合解:
●单击[office开始]→[excel选项] →[加载项] →[转到]
→[线性规划加载项] →[确定] →[数据] →[规划求解]出现如下对话窗:
●在“设置目标单元格”窗口,输入B10。
●选定“最小值”选项。
●在可变单元格中输入B4:G4。
●选取“添加”,出现“添加约束”窗口,在“添加约束”
窗口输入:
单元格引用位置运算符号约束值
B5 = C5
单击“添加”,再输入以下约束条件:
B6 = C6
单击“添加”,再输入以下约束条件:
B7 = D7
单击“添加”,再输入以下约束条件:
B8 = D8
单击“添加”,再输入以下约束条件:
B9 = D9
单击“添加”,再输入以下约束条件:
B10 = D10 单击“添加”,再输入以下约束条件:
B3:G3 >= 0,单击“确定”
●在“规划求解参数”窗口,选择“求解。
”
●选择“确定”,(计算结果如下表所示)
●在“规划求解结果”对话框中选定保存“规划求解结果”,
单击“确定”。
于是我们就得到如下运算结果报告
表1 Microsoft Excel 9.0 运算结果报告
目标函数的初值:当变量X=(1,1,1,1,1, 1)时目标函数的值。
目标函数的终值:经过运算后的目标函数的最优值。
此表说明函数的最优值为2500。
表2 可变单元格式
从此表看出我们的最优解(终值)为(50 , 150 , 0 , 100 , 0 , 200)。
三、分派问题(OR求解)
有五个工人,要分派他们分别完成5项工作,每人做各项
工作所消耗的时间如表所示,问应分派哪个人去完成哪项任务,可使总的消耗时间为最小。
如下图,在OR中输入数据
点击运行,得到如下运行结果
四、运输问题(excel求解)
某食品公司下设三个加工厂和各厂产量分别为A1——7t ,A2——4t,A3——9t,将这些产品运往4个销售地区及每天的销售量分别为B1——3t,B2——6t,B3——5t,B4——6t,问如何调运,使在满足各销售地区销售量的情况下,总运费最小?
用Excel求解运输问题
运输问题的形式:
在Excel中的形式:
步骤:
1、 F1:F3填产量表,A5:D5填售量表,A7:D9填运价表。
2、E1填=SUM(A1:D1),并复制到E3;A4填=SUM(A1:A3),并复制到D4;A6填=SUMPRODUCT(A1:D3,A7:D9)。
3、启动规划求解:
设置目标单元格:$A$6
等于:最小值
可变单元格:$A$1:$D$3
约束:A4=A5, B4=B5, C4=C5, D4=D5, E1<=F1, E2<=F2, E3<=F3
在选项中选中:采用线性模型,假定非负
4、求解
得到答案:
A1给B3调运5t,B4调运2
A2给B1调运3t,B4调运1t
A3给B2调运6t,B4调运3t
A4给B1调运3t,B2调运6t,B3调运5t,B4调运6t 总运费最少为85
五、总结及感悟:
本次实验中,出现了各种麻烦,在同学之间互相探讨,借用网上资源查阅资料的方式下将之一一解决了。
对excel 表格的使用更进一步。
同时,认识了一个解决运筹学问题的新工具OR。
