(常考题)北师大版初中数学九年级数学下册第三单元《圆》测试(答案解析)

合集下载

(常考题)北师大版初中数学九年级数学下册第三单元《圆》检测(有答案解析)(1)

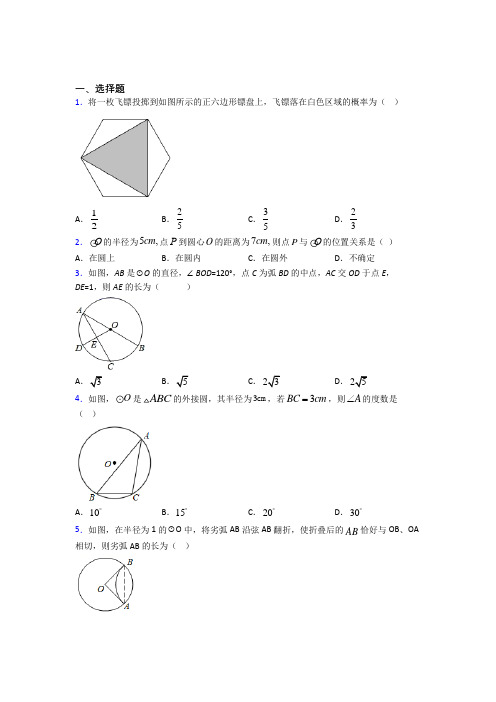
一、选择题1．将一枚飞镖投掷到如图所示的正六边形镖盘上，飞镖落在白色区域的概率为（）A ．12B ．25C ．35D ．23 2．О的半径为5,cm 点Р到圆心O 的距离为7,cm 则点P 与О的位置关系是（） A ．在圆上 B ．在圆内 C ．在圆外 D ．不确定 3．如图，AB 是⊙O 的直径，∠BOD =120°，点C 为弧BD 的中点，AC 交OD 于点E ，DE =1，则AE 的长为（）A ．3B ．5C ．23D ．25 4．如图，O 是ABC 的外接圆，其半径为3cm ，若3BC cm =，则A ∠的度数是（）A ．10︒B ．15︒C ．20︒D ．30︒5．如图，在半径为1的⊙O 中，将劣弧AB 沿弦AB 翻折，使折叠后的AB 恰好与OB 、OA 相切，则劣弧AB 的长为（）A ．12πB ．13π C ．14π D ．16π 6．下列关于正多边形的叙述，正确的是（）A ．正七边形既是轴对称图形又是中心对称图形B ．存在一个正多边形，它的外角和为720︒C ．任何正多边形都有一个外接圆D ．不存在每个外角都是对应每个内角两倍的正多边形7．如图，AB 是O 的直径，CD 是O 的弦，30,3ACD AD ∠=︒=，下列说法错误的是（）A ．30B ∠=︒B ．60BAD ∠=︒C ．23BD = D ．23AB = 8．已知：O 的半径为2，3OA =，则正确的图形可能为（）A ．B ．C ．D ．9．如图．PA ，PB 是⊙O 的两条切线，切点分别为A ，B ，连接OA ，OB ，OP ，AB ．若 OA =1，∠APB =60°，则△PAB 的周长为（）A ．3B ．4C ．3D ．3 10．如图，已知⊙O 的直径8CD =，AB 是⊙O 的弦，AB CD ⊥，垂足为M ，2OM =，则AB 的长为（）A ．2B ．23C ．4D ．43 11．如图，O 的直径为10，弦AB 的长为6，P 为弦AB 上的动点，则线段OP 长的取值范围是（）A ．35OP ≤≤B ．45OP <<C ．45OP ≤≤D ．35OP <<12．如图，在Rt △ABC 中，∠C =90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”.当AC =4，BC =3时，则阴影部分的面积为（）A ．6B ．6πC ．52π D ．12二、填空题13．如图，四边形ABCD 是O 的内接四边形，且AC BD ⊥， OF CD ⊥，垂足分别为E F 、，若52OF =，则AB =_____．14．如图，圆O 是△ABC 的外接圆，BC=2，∠BAC=30°，则圆O 的直径为___________．15．如图，在ABC 中，90ACB ∠=︒，60A ∠=︒，2AC =，ABC 绕顶点C 逆时针旋转60︒得到A B C ''，点A 的对应点A '恰好落在AB 上，连接A B ''，则图中阴影部分的面积为__________．16．如图，在平面直角坐标系中，过点()11,0A 作x 轴的垂线交直线y x =于点B ，以О为圆心，1OB 为半径作弧，交x 轴于点2A ；过点2A 作x 轴的垂线交直线y x =于点2B ，以O 为圆心，2OB 为半径作弧，交x 轴于点3A ；过点3A 作x 轴的垂线交直线y x =于点3B ，以О为圆心，3OB 为半径作弧，交x 轴于点4A ，……，按此做法进行下去，设由11A B ，12A A ，弧21A B 围成的图形面积记为1S ，由22A B ，23A A ，弧32A B 围成的图形面积记为2S ，由33A B ，34A A ，弧43A B 围成的图形面积记为3S ，……，那么2020S 为_______：17．如图，半径为2的O 中有弦AB ，以AB 为折痕对折，劣弧恰好经过圆心O ，则弦AB 的长度为__________．18．如图，在平面直角坐标系中，D 是直线6y x =-+上的一个动点，O 的半径为2，过点D 作O 的切线，切点为A ，则AD 长度的最小值为____________．19．如图，已知O 的半径为2，ABC 内接于O ，135ACB ∠=︒，则弓形ACB （阴影部分）的面积为_____________．20．如图，将半径为3cm 的圆形纸片沿AB 折叠后，圆弧恰好能经过圆心,O 用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为____________________cm ．(结果用含根号的式子表示)三、解答题21．已知关于x 的一元二次方程x 2+2mx ﹣n 2+5＝0．（1）当m ＝1时，该一元二次方程的一个根是1，求n 的值；（2）若该一元二次方程有两个相等的实数根．①求m 、n 满足的关系式；②在x 轴上取点H ，使得OH ＝|m |，过点H 作x 轴的垂线l ，在垂线l 上取点P ，使得PH ＝|n |，则点P 到点（3，4）的距离最小值是．22．如图，在Rt △ABC 中∠B ＝30°，∠ACB ＝90°，AB ＝6．延长CA 到O ，使AO ＝AC ，以O 为圆心，OA 长为半径作⊙O 交BA 延长线于点D ，连结OD ，CD ．（1）求扇形OAD 的面积．（2）判断CD 与⊙O 的位置关系，并说明理由．23．已知，如图，在ABC 中，90C ∠=︒，D 为BC 边中点．（1）尺规作图：以AC 为直径作O ，交AB 于点E （保留作图痕迹，不需写作法）；（2）连接DE ，求证：DE 为O 的切线．24．如图，在由边长为1个单位长度的小正方形组成的网格中，给出了以格点（网格线的交点）为顶点的ABC ∆，且90B ∠=︒．（1）将ABC ∆绕点O 顺时针旋转90°后得到EFG ∆（其中,,A B C 三点旋转后的对应点分别是,,E F G ），画出EFG ∆．（2）设EFG ∆的内切圆的半径为r ，EFG ∆的外接圆的半径为R ，则r R=__________．25．如图，点E 是ABC 的内心，AE 的延长线和ABC 的外接圆O 相交于点D ，过D 作直线//DG BC ．（1）求证：DG 是O 的切线；（2）求证：DE CD =；（3）若25DE =，8BC =，求O 的半径．26．如图，已知AB 是O 的直径，BC AB ⊥，连接OC ，弦//AD OC ，直线CD 交BA 的延长线于点E .（1）求证：CD 是O 的切线；（2）若2DE BC =，O 的半径为2，求线段EA 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】算出白色区域的面积与整个图形的面积之比即为所求概率．【详解】解：如图，过点A 作AG BF ⊥于点G∵ 六边形ABCDEF 为正六边形，∴BAF=120∠︒，=60FAG ∠︒设正六边形的边长为a ，则32322a a AG FG a ==⨯=，BF=2 ∴ 空白部分的面积为：213333322ABFa a S S a ==⨯⨯⨯=△空白正六边形的面积为：22333642S a a =⨯=六 ∴飞镖落在白色区域的概率为：2233a 14=233S P S a ==空白六故选：A【点睛】本题考查概率的求解，确定白色区域面积占整个图形面积的占比是解题的关键． 2．C解析：C【分析】根据点与圆的位置关系的判定方法进行判断；【详解】∵O 的半径为5cm ，点P 到圆心O 的距离为7cm ，∴OP ＞O 的半径，∴点P 在O 外；故答案选C ．【点睛】本题主要考查了点与圆的位置关系，准确判断是解题的关键．3．A解析：A【分析】连接AD，可证∠ODA=∠OAD=∠AOD=60°，根据弧中点，得出∠DAC=30°，△ADE是直角三角形，用勾股定理求AE即可．【详解】解：连接AD，∵∠BOD=120°，AB是⊙O的直径，∴∠AOD=60°，∵OA=OD，∴∠OAD=∠ODA =60°，∵点C为弧BD的中点，∴∠CAD=∠BAC=30°，∴∠AED=90°，∵DE=1，∴AD=2DE=2，AE=2222AD DE-=-=，213故选：A．【点睛】本题考查了圆周角的性质、勾股定理，解题关键是通过连接弦构造直角三角形，并通过弧相等导出30°角．4．D解析：D【分析】连接OB、OC，则判断△OBC是等边三角形，则∠BOC=60°，再根据圆周角定理，即可得到答案．【详解】解：连接OB、OC，如图：∵3OB OC BC cm ===，∴△OBC 是等边三角形，∴∠BOC=60°，∴∠BAC=30°，故选：D ．【点睛】本题考查了圆周角定理，等边三角形的判定和性质，解题的关键是熟练掌握圆周角定理进行解题．5．A解析：A【分析】如图画出折叠后AB 所在的⊙O ＇，连O ＇B ，O ＇A ，根据题意可得O ＇B ⊥OB 、O ＇A ⊥OA ，且OB=OA=O ＇B=O ＇A,得到四边形O ＇BOA 是正方形，即∠O=90°，最后根据弧长公式计算即可．【详解】解：如图：画出折叠后AB 所在的⊙O ＇，连O ＇B ，O ＇A∵AB 恰好与OA 、OB 相切∴O ＇B ⊥OB 、O ＇A ⊥OA∵OB=OA=O ＇B=O ＇A,∴四边形O ＇BOA 是正方形∴∠O=90°∴劣弧AB 的长为9011801802n r πππ︒⨯⨯==︒．故选择：A ．【点睛】本题考查了折叠的性质、正方形的判定与性质、弧长公式等知识点，其中掌握弧长公式和折叠的性质是解答本题的关键．6．C解析：C【分析】根据中心对称图形、轴对称图形的定义、多边形外角和定理、正多边形的性质对各选项逐一判断即可得答案．【详解】A.正七边形是轴对称图形，不是中心对称图形，故该选项错误，B.任意多边形的外角和都等于360°，故该选项错误，C.任何正多边形都有一个外接圆，故该选项正确，D.∵正三角形的每个外角为120°，对应的每个内角为60°，∴存在每个外角都是对应每个内角两倍的正多边形，故该选项错误，故选：C．【点睛】本题考查正多边形的性质、中心对称图形、轴对称图形的定义及多边形外角和定理，熟练掌握相关性质及定理是解题关键．7．C解析：C【分析】根据圆周角定理得到∠ADB=90°，∠B=∠ACD=30°，再利用互余可计算出∠BAD的度数，然后利用含30度的直角三角形三边的关系求出BD、AB的长即可．【详解】解：∵AB是⊙O的直径，∴∠ADB=90°，∵∠B=∠ACD=30°，∴∠BAD=90°-∠B=90°-30°=60°，故选项A、B不符合题意，在Rt△ADB中，，故选项C符合题意，选项D不符合题意，故选：C．【点睛】本题考查了圆周角定理以及含30°角的直角三角形的性质等知识；熟练掌握圆周角定理是解题的关键．8．C解析：C【分析】根据圆的半径和OA的大小确定点A与圆的位置关系，从而作出判断即可．【详解】∵根据图的意义，得OA=2，与OA=3矛盾，∴A选项错误；∵根据图的意义，得OA＜2，与OA=3矛盾，∴B选项错误；∵根据图的意义，得OA＞2，且离圆较近，与OA=3相符，∴C选项正确；∵根据图的意义，得OA＞2，且离圆较远，与OA=3不符合，∴D选项错误；故选C．【点睛】本题考查了点与圆的位置关系，熟练掌握圆心到点的距离与圆的半径的大小比较是解题的关键．9．C解析：C【分析】根据切线的性质和切线长定理证明△PAB是等边三角形，PA⊥AO，根据直角三角形性质求出PA，问题得解．【详解】解：∵PA，PB是⊙O的两条切线，∠APB=60°，∴PA=PB，∠APO=1∠APB=30°，PA⊥AO，2∴△PAB是等边三角形，∵PA⊥AO，∠APO==30°，∴OP=2OA=2，∴PA=∴△PAB的周长为故选：C【点睛】本题考查了切线长定理，切线的性质，等边三角形的判定，含30°角直角三角形性质，勾股定理等知识，考查知识点较多，熟知相关定理并能熟练运用是解题关键．10．D解析：D【分析】连接OB，根据勾股定理计算BM=AB=2BM计算即可．【详解】∵直径8CD =，AB CD ⊥，2OM =∴BM=22OB OM -=2242-=23，根据垂径定理，得AB=2BM=43，故选D ．【点睛】本题考查了垂径定理，勾股定理，熟练掌握连接半径构造直角三角形，灵活运用垂径定理和勾股定理求解是解题的关键．11．C解析：C【分析】由垂线段最短可知当OP ⊥AB 时最短，当OP 是半径时最长．根据垂径定理求最短长度．【详解】解：如图，连接OA ，作OP ⊥AB 于P ，∵⊙O 的直径为10，∴半径为5，∴OP 的最大值为5，∵OP ⊥AB 于P ，∴AP=BP ，∵AB=6，∴AP=3，在Rt △AOP 中，OP=222594OA AP -=-=；此时OP 最短，所以OP 长的取值范围是4≤OP≤5．故选：C ．本题考查了垂径定理、勾股定理，解题的关键是确定OP 的最小值，所以求OP 的范围问题又被转化为求弦的弦心距问题，而解决与弦有关的问题时，往往需构造以半径、弦心距和弦长的一半为三边的直角三角形，若设圆的半径为r ，弦长为a ，这条弦的弦心距为d ，则有等式r 2=d 2+（2a ）2成立，知道这三个量中的任意两个，就可以求出另外一个． 12．A解析：A【分析】先根据勾股定理求出AB ，然后根据S 阴影=S 半圆AC ＋S 半圆BC ＋S △ABC －S 半圆AB 计算即可．【详解】根据勾股定理可得5=∴S 阴影=S 半圆AC ＋S 半圆BC ＋S △ABC －S 半圆AB =22211112222222AC BC AB AC BC πππ⎛⎫⎛⎫⎛⎫++•- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=()222141115343222222πππ⎛⎫⎛⎫⨯⨯+⨯⨯+⨯⨯-⨯⨯ ⎪ ⎪⎝⎭⎝⎭=6故选A ．【点睛】此题考查的是求不规则图形的面积，掌握用勾股定理解直角三角形、半圆的面积公式和三角形的面积公式是解决此题的关键．二、填空题13．【分析】连接DO 并延长与⊙O 相交于点G 连接BGCG 由AC ⊥BDDG 是直径可得∠DBG=90°=∠DCG 可证AC ∥BG 可得可得AB=CG 由OF ⊥CD 可证OF ∥CG 可证△DOF ∽△DGC 由性质由OF=可解析：【分析】连接DO 并延长，与⊙O 相交于点G ，连接BG ，CG ，由AC ⊥BD ， DG 是直径，可得∠DBG=90°=∠DCG 可证AC ∥BG ，可得AB CG =，可得AB=CG ，由OF ⊥CD ，可证OF ∥CG ，可证△DOF ∽△DGC ，由性质DO OF 1==DG CG 2，由OF=52，可求CG 5=2OF=2=52⨯即可．【详解】解：如图，连接DO 并延长，与⊙O 相交于点G ，连接BG ，CG ，∵AC ⊥BD ，DG 是直径，∴∠DBG=90°=∠DCG，∴BG⊥DB,∴AC∥BG，∴AB CG=，∴AB=CG，∵OF⊥CD，∴OF∥CG，∴∠DOG=∠DGC∴△DOF∽△DGC，，∴DO OF1==，DG CG2∵OF=5，2∴CG5=2OF=2=5⨯，2所以AB=CG=5．故答案为：5．【点睛】本题考查平行弦的性质，圆的性质，直径所对圆周角的性质，相似三角形的判定与性质，掌握平行弦的性质，圆的性质，直径所对圆周角的性质，相似三角形的判定与性质是解题关键．14．4【分析】延长BO交⊙O于E连接CE根据圆周角定理得到∠E=∠A=30°∠ECB=90°根据直角三角形的性质即可得到结论【详解】解：延长BO交⊙O于E连接CE则∠E=∠A=30°∠ECB=90°∴B解析：4【分析】延长BO交⊙O于E，连接CE，根据圆周角定理得到∠E=∠A=30°，∠ECB=90°，根据直角三角形的性质即可得到结论．【详解】解：延长BO 交⊙O 于E ，连接CE ，则∠E=∠A=30°，∠ECB=90°，∴BE=2BC=2×2=4．故答案为：4．【点睛】本题考查了圆周角定理，直角三角形的性质，正确的作出辅助线是解题的关键． 15．【分析】先分别求解然后根据进行求解即可【详解】由题意知在中∴∴由题意旋转角为即：且∴为等边三角形设交于点∵∴∴四边形为梯形又∵∴则在中∴∴∴故答案为：【点睛】本题考查旋转的性质以及扇形面积计算相关问解析：23π【分析】先分别求解ABC S ，BCB S '扇形，AA B C S ''梯形，然后根据ABC BCB AA B C S S S S '''=+-△阴影扇形梯形进行求解即可．【详解】由题意知，在Rt ABC 中，30ABC ∠=︒，∴24AB AC ==，23BC = ∴112232322ABC S AC BC ==⨯⨯=△，由题意，旋转角为60︒，即：60ACA BCB ''∠=∠=︒，且AC A C '=，23BC B C '==，∴ACA '为等边三角形，2A C '=，30A CD '∠=︒，设A B ''交BC 于点D ，∵60A CA D '∠=∠=︒，∴60ACA CA D ''∠=∠=︒，∴//AC A B ''，四边形AA B C ''为梯形，又∵90ACB ∠=︒，∴90CDA '∠=︒，则在Rt CDA '△中，112A D A C ''==，3CD = ∴()()112433322AABC S AC A B CD ''''=+=⨯+=梯形∴()260232360BCB S ππ'⨯==扇形，∴2323323ABC BCB AA B C S S S S ππ'''=+-=+-=-△阴影扇形梯形，故答案为：23π-．【点睛】本题考查旋转的性质以及扇形面积计算相关问题，灵活对不规则图形进行转换，运用规则图形的面积进行求解是解题关键．16．【分析】根据点A 的取法罗列出部分点A 的横坐标由此可发现规律即的横坐标为：再结合已知即可得到答案【详解】观察发现规律：的横坐标为：的横坐标为：的横坐标为：的横坐标为：的横坐标为：故答案为：【点睛】本题解析：2017201822π-【分析】根据点A 的取法，罗列出部分点A 的横坐标，由此可发现规律，即n A 的横坐标为：)12n -，再结合已知即可得到答案．【详解】观察，发现规律：1A 的横坐标为：1，2A 23A 的横坐标为：22，⋯，∴n A 的横坐标为：12n - n B ∴的横坐标为：12n -404020192019201720182020452122223602S ππ⨯⨯∴=-⨯⨯=⋅-故答案为：2017201822π⋅-．【点睛】本题考查了一次函数图像上点的坐标特征以及规律型中的点的变换，解题关键是找出n A 的横坐标为：12n -这一规律．17．【分析】如果过O作OC⊥AB于D交折叠前的于C根据折叠后劣弧恰好经过圆心O根据垂径定理及勾股定理即可求出AD的长进而求出AB的长【详解】解：如图过O作OC⊥AB于D交折叠前的于C∵的半径为又∵折叠后解析：23【分析】如果过O作OC⊥AB于D，交折叠前的AB于C，根据折叠后劣弧恰好经过圆心O，根据垂径定理及勾股定理即可求出AD的长，进而求出AB的长．【详解】解：如图，过O作OC⊥AB于D，交折叠前的AB于C，∵O的半径为2，又∵折叠后劣弧恰好经过圆心O，∴OA=OC=2，∴OD＝CD＝1，在Rt△OAD中，∵OA＝2，OD＝1，∴2222-=-OA OD213AB＝2AD＝3故答案为：3【点睛】本题考查了垂径定理和勾股定理的综合运用，利用好条件：劣弧折叠后恰好经过圆心O是解题的关键．18．4【分析】当OD与直线y=-x+6垂直时连接AOAD此时OD最小AD也最小根据等腰直角三角形的性质得到OD根据勾股定理即可得到结论【详解】解：如图∵DA为切线∴OA⊥DAOA=∴当OD最小时AD的值解析：4【分析】当OD与直线y=-x+6垂直时，连接AO，AD，此时OD最小，AD也最小，根据等腰直角三角形的性质得到OD，根据勾股定理即可得到结论．【详解】解：如图∵DA 为切线,∴OA ⊥DA ，2∴当OD 最小时，AD 的值最小.∴当OD 与直线y=−x+6垂直时，AD 的值最小，如图，设y=−x+6交x ，y 轴于B ，C ，B(6，0)，C(0，6)，∴OB=OC=6.∵∠BOC= 90°，∴△OBC 为等腰直角三角形，∴22OB OC +2 ，∴OD=122 即OD 的最小值为2在Rt △OAD 中，AD 最小值22OD OA -()()22322164-==故答案为：4【点睛】本题主要考查切线的性质，掌握过切点的半径与切线垂直是解题的关键，用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题. 19．【分析】根据圆内接四边形对角互补和同弧所对的圆心角是圆周角的二倍可以求得∠AOB 的度数然后根据弓形ACB 的面积=S 扇形OAB-S △OAB 得出结果即可【详解】解：设点D 为优弧AB 上一点连接ADBDOA解析：2π-【分析】根据圆内接四边形对角互补和同弧所对的圆心角是圆周角的二倍，可以求得∠AOB 的度数，然后根据弓形ACB 的面积=S 扇形OAB -S △OAB 得出结果即可．【详解】解：设点D 为优弧AB 上一点，连接AD 、BD 、OA 、OB ，如图所示，∵⊙O 的半径为2，△ABC 内接于⊙O ，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴弓形ACB 的面积=S 扇形OAB -S △OAB =29021223602π⨯⨯-⨯⨯=2π-，故答案为：2π-．【点睛】本题主要考查求弓形的面积，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．20．【分析】作OC ⊥AB 根据折叠的性质得OD 等于半径的一半即OA ＝2OD 再根据含30°的直角三角形三边的关系得∠OAD ＝30°同理∠OBD ＝30°所以∠AOB ＝120°则利用弧长公式算出弧AB 的长利用圆解析：2【分析】作OC ⊥AB ，根据折叠的性质得OD 等于半径的一半，即OA ＝2OD ，再根据含30°的直角三角形三边的关系得∠OAD ＝30°，同理∠OBD ＝30°，所以∠AOB ＝120°，则利用弧长公式算出弧AB 的长，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，得到圆锥的底面圆的半径，从而结合勾股定理求高即可．【详解】如图，过O 点作OC ⊥AB ，垂足为D ，交⊙O 于点C ，由折叠的性质可知，1122OD OC OA ==，由此可得，在Rt AOD △中，30OAD ∠=︒，同理可得30OBD ∠=︒，在AOB 中，由三角形内角和定理，得180120AOB OAD OBD ∠=︒-∠-∠=︒． ∴弧AB 的长为()12032180cm ππ⨯=．设围成的圆锥的底面半径为r cm ，则22ππ=r ，∴1r cm =．∴圆锥的高为()22-=．3122cm故答案为：22．【点睛】本题考查了折叠的性质，弧长公式的计算，直角三角形的性质等，掌握弧长公式的计算以及圆锥相关基本结论是解题的关键．三、解答题21．（1）2；（2）①m2+n2＝5；②55【分析】（1）把m=1，x=1代入方程得1+2-n2+5=0，然后解关于n的方程即可；（2）①利用判别式的意义得到△=4m2-4（-n2+5）=0，从而得到m与n的关系；②利用勾股定理得到22m n+5P在以O5上，然后根据点与圆的位置关系判断点P到点（3，4）的距离最小值．【详解】解：（1）把m＝1，x＝1代入方程得1+2﹣n2+5＝0，解得n＝2，即n的值为2；（2）①根据题意得△＝4m2﹣4（﹣n2+5）＝0，整理得m2+n2＝5；②∵OH＝|m|，PH＝|n|，∴OP22+5m n即点P在以O5∴原点与点（3，4）的连线与⊙O的交点P使点P到点（3，4）的距离最小，∵原点到点（3，422+5，34∴点P到点（3，4）的距离最小值是55故答案为55【点睛】本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．也考查了点与圆的位置关系．22．（1）求扇形OAD的面积为32π；（2）CD与⊙O相切，理由见解析．【分析】（1）求出∠OAD＝60°，得出等边三角形OAD，求出半径和圆心角，利用扇形的面积公式求得即可；（2）求出∠ADC＝∠ACD＝12∠OAD＝30°，进而求出∠ODC＝90°，即可证得CD是⊙O的切线．【详解】（1）证明：∵AB＝4，∠ACB＝90°，∠B＝30°，∴AC＝12AB＝2，∠BAC＝60°，∴∠OAD＝∠BAC＝60°，∵OD＝OA，∴△OAD是等边三角形，∴∠AOD＝60°，∵AO＝AC=2，∴S扇形AOD＝23623 602ππ⨯⨯=；（2）CD所在直线与⊙O相切，证明：∵△OAD是等边三角形，∴AD＝OA，∵AO＝AC，∴AD=AC，∴∠ADC＝∠ACD，∵∠OAD＝60°，∴∠ADC＝30°，∴∠ODC＝60°+30°＝90°，∴OD⊥DC，∴CD是⊙O的切线．【点睛】本题考查了扇形的面积，切线的判定，含30度角的直角三角形的性质，勾股定理，等边三角形的性质和判定的应用，主要考查学生综合运用性质进行推理和计算的能力，综合性比较强，有一定的难度．23．（1）作图见解析；（2）见解析．【分析】（1）先作AC的中垂线，找到AC的中点O，然后以AC为直径作圆，与AB的交点即为所求；（2）由题意可知DE为Rt BEC△斜边BC上的中线，从而得到CD=DE，即=∠∠ECD DEC ，由OC=OE 得到OEC OCE ∠=∠，再由90ACB ∠=︒即可得到OE ⊥DE ，即可得证．【详解】（1）作图如图所示．（2）证明：如上图，连结OE ，CE ， AC 为直径，90AEC ∴∠=︒， D 为BC 边中点，DE ∴为Rt BEC △斜边BC 上的中线，12DE DC DB BC ∴===， ECD DEC ∴∠=∠，OC OE =，OEC OCE ∴∠=∠，90OED OEC CED OCE DCE ACB ∴∠=∠+∠=∠+∠=∠=︒OD DE ∴⊥，DE ∴为O 的切线．【点睛】本题考查了尺规作图以及切线的判定，正确找到垂直条件是判断切线的关键． 24．（1）见解析；（2）25【分析】（1）根据旋转的性质，作出点A 、B 、C 的对应点，依次连接即可（2）结合图形，EG 为外接圆的直径，用勾股定理求出EG ，则可求R ，根据三角形内切圆的性质，和切线长定理可求得r ，进而可求得答案【详解】解（1）EFG ∆如图所示，（2）EFG ∆的内切圆的半径为r ，2EF FG EG r +-∴= 4,3EF FG ==,2222435EG EF FG =++= 43512r +-∴== EFG ∆的外接圆的半径为R1522R EG ∴== 25r R ∴= 【点睛】本题考查了旋转图形的画法，勾股定理，三角形内心性质，切线长定理，解题关键是熟练掌握基本知识，是中考常考题．25．（1）见解析；（2）见解析；（3）5【分析】（1）连接OD 交BC 于H ，如图，利用三角形内心的性质得到∠BAD=∠CAD ，则BD CD =，利用垂径定理得到OD ⊥BC ，BH=CH ，从而得到OD ⊥DG ，然后根据切线的判定定理得到结论；（2）利用三角形内心的性质，等腰三角形的判定和性质，同圆或等圆中等角对等弦，即可得到结论；（3）根据垂径定理可知OD 垂直平分BC ，在Rt BHD △利用勾股定理求出DH 长，设半径为r ，在Rt BHO 中利用勾股定理即可求解【详解】（1）证明：连接OD 交BC 于H ，如图，∵点E 是ABC 的内心，∴AD 平分BAC ∠，即BAD CAD ∠=∠，∴BD CD =，∴OD BC ，BH CH = ∵//DG BC ，∴OD DG ⊥，∴DG 是O 的切线；（2）连接BD ，如图，∵点E 是ABC 的内心，∴ABE CBE ∠=∠，∵DBC BAD ∠=∠，∴DEB BAD ABE DBC CBE DBE ∠=∠+∠=∠+∠=∠，BDE ∴为等腰三角形BD DE ∴=BAD CAD BD DC∠=∠∴= ∴DE DC =．（3）BD DC =，∴OD 垂直平分BC 90BHD BHO ∴∠=∠=︒8142BC BH BC =∴== 25DE BD ==∴在Rt BHD △中2220162DH BD BH -=-=设半径为r ，则,2OB r OH r ==-∴在Rt BHO 中,222OB OH BH =+()22242r r ∴=+-解得=5r ∴⊙O 的半径为：5．【点睛】本题考查了三角形的外接圆与内心，切线的判定定理，等腰三角形的判定和性质，垂径定理，勾股定理等知识，解题关键是熟练掌握三角形内心的性质：三角形的内心与三角形顶点的连线平分这个内角．26．（1）见解析；（2）22AE =．【分析】（1）连接OD ，通过证明△COD ≌△COB 得到90CDO CBO ∠=∠=︒即可得到结论；（2）根据全等三角形的性质，在结合平行线分线段成比例的性质，即可求解【详解】（1）如图，连接OD .∵//AD OC ，∴DAO COB ∠=∠，ADO COD ∠=∠.又∵OA OD =，∴DAO ADO ∠=∠，∴COD COB ∠=∠.∵OD OB =，OC OC =，∴在COD △和COB △中OD OB COD COB OC OC =⎧⎪∠=∠⎨⎪=⎩∴()SAS COD COB ≌△△， ∴90CDO CBO ∠=∠=︒.又∵点D 在O 的切线. ∴CD 是O 的切线.（2）∵COD COB ≌△△，∴CD CB =.∵2DE BC =， ∴2ED CD =.∵//AD OC ，∴DE AE CE OE=.∵O 的半径为2，∴2AE AE =+， ∴AE =【点睛】本题考查了圆切线的判定，以及平行线分线段成比例的性质，熟练掌握圆切线的判定定理是解题关键．。

2022学年北师大版九年级数学下册第3章《圆》综合测试题附答案解析

2022-2023学年九年级数学下册第3章《圆》综合测试题（满分120分）一、选择题(每题3分，共30分)1．下列命题为真命题的是()A ．两点确定一个圆B ．度数相等的弧相等C ．垂直于弦的直径平分弦D ．相等的圆周角所对的弧相等，所对的弦也相等2．已知⊙O 的半径为5，点P 到圆心O 的距离为6，那么点P 与⊙O 的位置关系是()A ．点P 在⊙O 外B ．点P 在⊙O 内C ．点P 在⊙O 上D ．无法确定3．如图，⊙O 是△ABC 的外接圆，∠BOC ＝120°，则∠BAC 的度数是()A ．70°B ．60°C ．50°D ．30°4．如图，AB ，AC 为⊙O 的切线，B 和C 是切点，延长OB 到D ，使BD ＝OB ，连接AD .如果∠DAC ＝78°，那么∠ADO 等于()A ．70°B ．64°C ．62°D ．51°5．如图，AB ︵＝BC ︵＝CD ︵，OB ，OC 分别交AC ，BD 于点E ，F ，则下列结论不一定正确的是()A ．AC ＝BD B ．OE ⊥AC ，OF ⊥BD C ．△OEF 为等腰三角形D ．△OEF 为等边三角形6．如图，在直角坐标系中，一个圆经过坐标原点O ，交坐标轴于点E ，F ，OE ＝8，OF ＝6，则圆的直径长为()A ．12B ．10C ．14D ．157．如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC ∥QR ，则∠AOQ 等于()A ．60°B ．65°C ．72°D ．75°8．秋千拉绳长3m ，静止时踩板离地面0.5m ，某小朋友荡秋千时，秋千在最高处踩板离地面2m(左右对称)，如图所示，则该秋千所荡过的圆弧AB ︵的长为()A ．πmB ．2πm C.43πm D.32πm9．如图，PA ，PB 切⊙O 于A ，B 两点，CD 切⊙O 于点E ，交PA ，PB 于点C 和点D .若△PCD 的周长为⊙O 半径的3倍，则t a n ∠APB 等于()A.125 B.3513 C.2313 D.51210．如图，在平面直角坐标系中，⊙P 的圆心坐标是(3，a )(a ＞3)，半径为3，函数y ＝x 的图象被⊙P 截得的弦AB 的长为42，则a 的值是()A ．4B ．3＋2C ．32D ．3＋3二、填空题(每题3分，共24分)11．如图，AB 为⊙O 的直径，CD ⊥AB ，若AB ＝10，CD ＝8，则圆心O 到弦CD 的距离为________．12．如图，EB ，EC 是⊙O 的两条切线，B ，C 是切点，A ，D 是⊙O 上两点，如果∠E ＝46°，∠DCF ＝32°，那么∠A ＝________．13．如图，DB 切⊙O 于点A ，∠AOM ＝66°，则∠DAM ＝________．14．如图，AB ，CD 是⊙O 的弦，AB ⊥CD ，BE 是⊙O 的直径，若AC ＝3，则DE ＝________．15．如图，水平放置的圆柱形油槽的截面直径是52c m ，装入油后，油深CD 为16c m ，那么油面宽度AB＝________.16．如图，在扇形OAB 中，∠AOB ＝90°，点C 为OA 的中点，CE ⊥OA 交AB ︵于点E ，以点O 为圆心，OC为半径作CD ︵交OB 于点D .若OA ＝2，则阴影部分的面积为________．17．如图，在△ABC 中，∠C ＝90°，AC ＝3，AB ＝5，D 为BC 边的中点，以AD 上一点O 为圆心的⊙O 和AB ，BC 均相切，则⊙O 的半径为________．18．如图，在⊙O 中，C ，D 分别是OA ，OB 的中点，MC ⊥AB ，ND ⊥AB ，M ，N 在⊙O 上．下列结论：①MC ＝ND ；②AM ︵＝MN ︵＝NB ︵；③四边形MCDN 是正方形；④MN ＝12AB .其中正确的结论有_____(填序号)．三、解答题(19题8分，20，21每题10分，22，23每题12分，24题14分，共66分)19．如图，AB 是⊙O 的直径，PA 切⊙O 于A ，OP 交⊙O 于C ，连接BC ，若∠P ＝30°，求∠B 的度数．20．如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长BD 到点C ，使DC ＝BD ，连接AC ，过点D 作DE ⊥AC ，垂足为E .(1)求证：AB ＝AC .(2)若⊙O 的半径为4，∠BAC ＝60°，求DE 的长．21．如图，点P 在y 轴上，⊙P 交x 轴于A ，B 两点，连接BP 并延长交⊙P 于点C ，过点C 的直线y ＝2x＋b 交x 轴于点D ，且⊙P 的半径为5，AB ＝4.(1)求点B ，P ，C 的坐标．(2)求证：CD 是⊙P 的切线．22．如图，CB和CD切⊙O于B，D两点，A为圆周上一点，且∠1:∠2:∠3＝1:2:3，BC＝3，求∠AOD所对扇形的面积S.23．如图，一拱形公路桥，圆弧形桥拱的水面跨度AB＝80m，桥拱到水面的最大高度为20m.(1)求桥拱所在圆的半径．(2)现有一艘宽60m，顶部截面为长方形且高出水面9m的轮船要经过这座拱桥，这艘轮船能顺利通过吗？请说明理由．24．如图，已知在△ABP中，C是BP边上一点，∠PAC＝∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E.(1)求证：PA是⊙O的切线．(2)过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG·AB＝12，求AC的长．(3)在满足(2)的条件下，若AF∶FD＝1∶2，GF＝1，求⊙O的半径及sin∠ACE的值．参考答案一、1.C 2.A3.B4.B5.D6.B 7．D 8.B 9.A 10.B二、11.3【点拨】如图，连接OC ，设AB ⊥CD 于E .∵AB 为⊙O 的直径，AB ＝10，∴OC ＝5.∵CD ⊥AB ，CD ＝8，∴CE ＝4，∴OE ＝OC 2－CE 2＝52－42＝3.12．99°【点拨】易知EB ＝EC .又∠E ＝46°，所以∠ECB ＝67°.从而∠BCD ＝180°－67°－32°＝81°.在⊙O 中，∠BCD 与∠A 互补，所以∠A ＝180°－81°＝99°.13．147°【点拨】因为DB 是⊙O 的切线，所以OA ⊥DB .由∠AOM ＝66°，得∠OAM ＝12×(180°－66°)＝57°.所以∠DAM ＝90°＋57°＝147°.14．3【点拨】∵BE 是⊙O 的直径，∴∠BDE ＝90°.∴∠BDC ＋∠CDE ＝90°.又∵AB ⊥CD ，∴∠ACD ＋∠CAB ＝90°.∵∠CAB ＝∠BDC ，∴∠ACD ＝∠CDE .∴AD ︵＝CE ︵.∴AD ︵－AE ︵＝CE ︵－AE ︵.∴DE ︵＝AC ︵.∴DE ＝AC ＝3.15．48cm16.32＋π12【点拨】连接OE .∵点C 是OA 的中点，∴OC ＝12OA ＝1.∵OE ＝OA ＝2，∴OC ＝12OE .∵CE ⊥OA ，∴∠OEC ＝30°.∴∠COE ＝60°.在Rt △OCE 中，CE ＝OE 2－OC 2＝3，∴S △OCE ＝12OC ·CE ＝32.∵∠AOB ＝90°，∴∠BOE ＝∠AOB －∠COE ＝30°.∴S 扇形BOE ＝30π×22360＝π3.又S 扇形COD ＝90π×12360＝π4.因此S 阴影＝S 扇形BOE ＋S △OCE －S 扇形COD ＝π3＋32－π4＝32＋π12.17.6718．①②④【点拨】连接OM ，ON ，易证Rt △OMC ≌Rt △OND ，可得MC ＝ND ，故①正确．在Rt △MOC中，CO ＝12MO ，可得∠CMO ＝30°，所以∠MOC ＝60°.易得∠MOC ＝∠NOD ＝∠MON ＝60°，所以AM ︵＝MN ︵＝NB ︵，故②正确．易得CD ＝12AB ＝OA ＝OM ，∵MC ＜OM ，∴MC ＜CD .∴四边形MCDN 不是正方形，故③错误．易得MN ＝CD ＝12AB ，故④正确．三、19.解：∵PA 切⊙O 于A ，AB 是⊙O 的直径，∠P ＝30°，∴∠AOP ＝60°.∴∠B ＝12∠AOP ＝30°.20．(1)证明：如图，连接AD .∵AB 是⊙O 的直径，∴∠ADB ＝90°.∵DC ＝BD ，∴AB ＝AC .(2)解：由(1)知AB ＝AC ，∵∠BAC ＝60°，∠ADB ＝90°，∴△ABC 是等边三角形，∠BAD ＝30°.在Rt △BAD 中，∠BAD ＝30°，AB ＝8，∴BD ＝4，即DC ＝4.又∵DE ⊥AC ，∴DE ＝DC ·sin C ＝4·sin 60°＝4×32＝2 3.21．(1)解：如图，连接CA .∵OP ⊥AB ，∴OB ＝OA ＝2.∵OP 2＋OB 2＝BP 2，∴OP 2＝5－4＝1，即OP ＝1.∵BC 是⊙P 的直径，∴∠CAB ＝90°.∵CP ＝BP ，OB ＝OA ，∴AC ＝2OP ＝2.∴B (2，0)，P (0，1)，C (－2，2)．(2)证明：∵直线y ＝2x ＋b 过C 点，∴b ＝6.∴y ＝2x ＋6.∵当y ＝0时，x ＝－3，∴D (－3，0)．∴AD ＝1.∵OB ＝AC ＝2，AD ＝OP ＝1，∠CAD ＝∠POB ＝90°，∴△DAC ≌△POB .∴∠DCA ＝∠ABC .∵∠ACB ＋∠ABC ＝90°，∴∠DCA ＋∠ACB ＝90°，即CD ⊥BC .∴CD 是⊙P 的切线．22．解：∵CD 为⊙O 的切线，∴∠ODC ＝90°，即OD ⊥CD .∵∠1:∠2:∠3＝1:2:3，∴∠1＝15°，∠2＝30°，∠3＝45°.连接OB .∵CB 为⊙O 的切线，∴OB ⊥BC ，BC ＝CD .∴∠CBD ＝∠3＝45°，∴∠OBD ＝45°.又∠1＋∠2＝45°，∴∠BOD ＝90°，即OD ⊥OB .∴OD ∥BC ，CD ∥OB .∴四边形OBCD 为正方形．∵BC ＝3，∴OB ＝OD ＝3.∵∠1＝15°，∴∠AOB ＝30°，∴∠AOD ＝120°.∴S ＝120360×π×32＝3π.23．解：(1)如图，设点E 是桥拱所在圆的圆心．过点E 作EF ⊥AB 于点F ，延长EF 交AB ︵于点C ，连接AE ，则CF ＝20m ．由垂径定理知，F 是AB 的中点，∴AF ＝FB ＝12AB ＝40m.设半径是r m ，由勾股定理，得AE 2＝AF 2＋EF 2＝AF 2＋(CE －CF )2，即r 2＝402＋(r －20)2.解得r ＝50.∴桥拱所在圆的半径为50m.(2)这艘轮船能顺利通过．理由：当宽60m 的轮船刚好可通过拱桥时，如图，MN 为轮船顶部的位置．连接EM ，设EC 与MN 的交点为D ，则DE ⊥MN ，∴DM ＝30m ，∴DE ＝EM 2－DM 2＝502－302＝40(m )．∵EF ＝EC －CF ＝50－20＝30(m)，∴DF ＝DE －EF ＝40－30＝10(m)．∵10m>9m ，∴这艘轮船能顺利通过．24．(1)证明：如图，连接CD .∵AD 是⊙O 的直径，∴∠ACD ＝90°.∴∠CAD ＋∠ADC ＝90°.又∵∠PAC ＝∠PBA ，∠ADC ＝∠PBA ，∴∠PAC ＝∠ADC .∴∠CAD ＋∠PAC ＝90°.∴PA ⊥DA .而AD 是⊙O 的直径，∴PA 是⊙O 的切线．(2)解：由(1)知，PA ⊥AD ，又∵CF ⊥AD ，∴CF ∥PA .∴∠GCA ＝∠PAC .又∵∠PAC ＝∠PBA ，∴∠GCA ＝∠PBA .而∠CAG ＝∠BAC ，∴△CAG ∽△BAC .∴AGAC ＝ACAB ，即AC 2＝AG ·AB .∵AG ·AB ＝12，∴AC 2＝12.∴AC ＝2 3.(3)解：设AF ＝x ，∵AF ∶FD ＝1∶2，∴FD ＝2x .∴AD ＝AF ＋FD ＝3x .易知△ACF ∽△ADC ，∴ACAD ＝AFAC ，即AC 2＝AF ·AD .∴3x 2＝12，解得x ＝2或x ＝－2(舍去)．∴AF ＝2，AD ＝6.∴⊙O 的半径为3.在Rt △AFG 中，AF ＝2，GF ＝1，根据勾股定理得AG ＝AF 2＋GF 2＝22＋12＝5，由(2)知AG ·AB ＝12，∴AB ＝12AG ＝1255.连接BD ，如图所示．∵AD 是⊙O 的直径，∴∠ABD ＝90°.在Rt △ABD 中，∵sin ∠ADB ＝ABAD ，AD ＝6，AB ＝1255，∴sin ∠ADB ＝255.∵∠ACE ＝∠ADB ，∴sin ∠ACE ＝255.。

(基础题)北师大版九年级下册数学第三章圆含答案

北师大版九年级下册数学第三章圆含答案一、单选题(共15题，共计45分)1、如图，⊙O是△ABC的外接圆，BC=2，∠BAC=45°，则劣弧BC的长为（）A. B. C.π D.2、如图，OA，OC是⊙O的半径，点B在⊙O上，若AB∥OC，∠BCO=21°，则∠AOC的度数是（）A.42°B.21°C.84°D.60°3、如图，AB是⊙O的直径，C是⊙O上的一点，OD⊥BC于点D，AC=6，则OD的长为（）A.2B.3C.3.5D.44、如图，在两个同心圆O中，大圆的弦AB交小圆于C、D两点，则AD与BC的数量关系是（）A.AD＞BCB.AD=BCC.AD＜BCD.无法确定5、如图，AB是⊙O的直径，C、D是⊙O上的点，且OC∥BD，∠A=30°，则∠CBD=（）A.10°B.15°C.30°D.45°6、如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E，设∠AED=α，∠AOD=β，则( )A.3α+β=180°B.2α+β=180°C.3α-β=90°D.2α-β=90°7、以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）A. B. C. D.8、如图，正内接于半径是1的圆，则阴影部分的面积是（）A. B. C. D.9、如图，为的直径，为弦，，垂足为E，若，则的度数为（）．A.135°B.120°C.150°D.110°10、在平面直角坐标系xOy中，以点(－3，4)为圆心，4为半径的圆( )A.与x轴相交，与y轴相切B.与x轴相离，与y轴相交C.与x轴相切，与y轴相交D.与x轴相切，与y轴相离11、如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG，点B的对应点E落在边CD上，且DE=EF，若AD= ，则的长为( )A. B. C. D.π12、若⊙O的半径是5 cm，点A在⊙O内，则OA的长可能是（）A.2 cmB.5 cmC.6 cmD.10 cm13、已知⊙O的半径为5，点P到圆心O的距离为6，那么点P与⊙O的位置关系是（）A.点P在⊙O上B.点P在⊙O内C.点P在⊙O外D.无法确定14、如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么（）秒钟后⊙P与直线CD相切．A.4B.8C.4或6D.4或815、如图⊙O中，半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC，若AB=8，CD=2，则EC的长度为（）A.2B.8C.2D.2二、填空题(共10题，共计30分)16、如图所示，AB是⊙O的直径，CD是⊙O的弦，连接AC，AD，若∠CAB＝36°，则∠ADC的度数为________．17、如图，在平面直角坐标系中，已知点，为平面内的动点，且满足，为直线上的动点，则线段长的最小值为________.18、如图，在的正方形网格中，两条网格线的交点叫做格点，每个小正方形的边长均为1．以点为圆心，5为半径画圆，共经过图中________个格点（包括图中网格边界上的点）．19、圆周角是24度，那么它所对的弧是________度.20、如图，AB是半圆的直径，点C在半圆周上，连接AC，∠BAC=30°，点P在线段OB上运动．则∠ACP的度数可以是________．21、如图，点是上⊙O两点，，点是⊙O上的动点（与不重合），连结，过点分别作于，于，则________.22、如图，DB为半圆的直径，A为BD延长线上一点，AC切半圆于点E，BC⊥AC 于点C，交半圆于点F．已知BD=2，设AD=x，CF=y，则y关于x的函数解析式是________．23、如图，在一张直径为20cm的半圆形纸片上，剪去一个最大的等腰直角三角形，剩余部分恰好组成一片树叶图案，则这片树叶的面积是________cm2.24、如图，平行四边形ABCD中，AB=AC=4，AB⊥AC，O是对角线的交点，若⊙O 过A、C两点，则图中阴影部分的面积之和为________.25、如图，已知直线AB与⊙O相交于A．B两点，∠OAB=30°，半径OA=2，那么弦AB=________．三、解答题(共5题，共计25分)26、如图，AB、CD是⊙O的直径，弦CE∥AB，的度数为70°．求∠EOC的度数．27、如图，⊙O的半径为2，弦AB=2 ，点C在弦AB上，AC= AB，求OC 的长．28、如图，在梯形ABCD中，AD∥BC，∠C=90°，AD+BC=AB，以AB为直径作⊙O，求证：CD是⊙O的切线．29、如图，在⊙O中，AB为直径，点B为的中点，直径AB交弦CD于E，CD=2， AE=5．（1）求⊙O半径r的值；（2）点F在直径AB上，连接CF，当∠FCD=∠DOB时，求AF的长．30、已知：如图， AB为⊙O的直径，CE⊥AB于E，BF∥OC，连接BC，CF．求证：∠OCF=∠ECB．参考答案一、单选题(共15题，共计45分)1、D2、A3、B4、B5、C6、D7、A8、A9、B10、C11、B12、A13、C14、D15、D二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)。

(常考题)北师大版初中数学九年级数学下册第三单元《圆》检测卷(答案解析)(2)

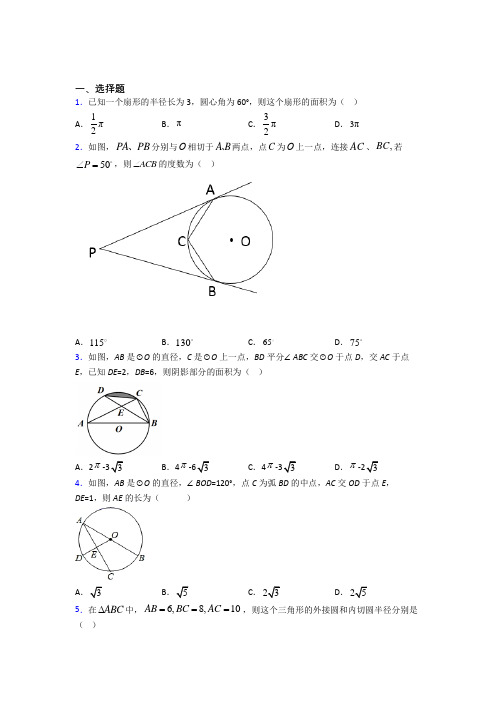
一、选择题1．已知一个扇形的半径长为3，圆心角为60°，则这个扇形的面积为（）A ．12πB ．πC ．3π2D ．3π2．如图，PA PB 、分别与О相切于A B 、两点，点C 为О上一点，连接AC 、,BC 若50P ∠=，则ACB ∠的度数为（）A ．115B ．130C ．65D ．753．如图，AB 是⊙O 的直径，C 是⊙O 上一点，BD 平分∠ABC 交⊙O 于点D ，交AC 于点E ，已知DE =2，DB =6，则阴影部分的面积为（）A ．2π-33B ．4π-63C ．4π-33D ．π-23 4．如图，AB 是⊙O 的直径，∠BOD =120°，点C 为弧BD 的中点，AC 交OD 于点E ，DE =1，则AE 的长为（）A 3B 5C ．23D ．255．在ABC ∆中，6,8,10AB BC AC ===，则这个三角形的外接圆和内切圆半径分别是（）A ．5,1B ．4,3C ．5,2D ．5,46．如图．PA ，PB 是⊙O 的两条切线，切点分别为A ，B ，连接OA ，OB ，OP ，AB ．若 OA =1，∠APB =60°，则△PAB 的周长为（）A ．23B ．4C ．33D ．23+2 7．如图，P 是正方形ABCD 内的一点，将△ABP 绕点B 顺时针方向旋转到与△CBP '重合，若PB ＝3，则点P 经过的路径长度为（）A ．23B ．32C ．32πD ．34π 8．如图，ABC 中，10,8,4AB AC BC ===，以点A 为圆心，AB 为半径作圆，交BC 的延长线于点D ，则CD 长为（）A ．10B ．9C ．45D ．89．如图，在平面直角坐标系中，以原点O 为圆心，6为半径的O 与直线(0)y x b b =-+>交于A ，B 两点，连接,OA OB ，以,OA OB 为邻边作平行四边形OACB ，若点C 恰好在O 上，则b 的值为（）A ．33B ．23C ．32D ．22 10．如图，O 是ABC 的外接圆，BC 的中垂线与AC 相交于D 点，若60A ∠=︒，70B ∠=︒，则AD 的度数为（）A ．80︒B ．70︒C ．20︒D ．3011．如图，AB 是圆O 的直径，C 、D 、E 都是圆上的点，其中C 、D 在AB 下方，E 在AB 上方，则∠C +∠D 等于（）A ．60°B ．75°C ．80°D ．90°12．如图，在扇形BOC 中，∠BOC ＝60°，点D 为弧BC 的中点，点E 为半径OB 上一动点，若OB ＝2，则阴影部分周长的最小值为（）A ．2＋6πB ．323＋3πC ．322＋6πD ．22＋3π 二、填空题13．如图，放置在直线l 上的扇形OAB ．由图①滚动（无滑动）到图②，再由图②滚动到图③．若半径2OA =，45AOB ∠=︒，则点 O 所经过的最短路径的长是 ______ ．14．如图，等边△ABC 内接于☉O ，BD 为⊙O 内接正十二边形的一边，CD=52，则图中阴影部分的面积等于_________．15．如图，从一块直径为2m 的圆形铁皮上画出一个圆心角为90的扇形．若随机在圆及其内部投针，则针孔扎在扇形（阴影部分）的概率为____．16．如图，C ∠是O 的圆周角，45C ∠=︒，则AOB ∠的度数为____．17．如图，ABC 内接于O ，30CAB ∠=︒，45CBA ∠=︒，CD AB ⊥于点D ，若O 的半径为4，则CD 的长为______．18．正六边形的半径为1,则正六边形的面积为________．19．在数学课上，老师提出如下问题：如图，AB 是⊙O 的直径，点C 在⊙O 外，AC ，BC 分别与⊙O 交于点D ，E ，请你作出ABC 中BC 边上的高．小文说：连结AE ，则线段AE 就是BC 边上的高．老师说：“小文的作法正确”请回答：小文的作图依据是__________．20．如图，在矩形ABCD 中，4AB =，6BC =，点E 是AD 上的动点（不与端点重合），在矩形ABCD 内找点F ，使得EF AD ⊥，且满足2·AF AE AD =，则线段BF 的最小值是__________．三、解答题21．已知O 的直径4AB =，C 为O 上一点，2AC =．（1）如图①，点P 是BC 上一点，求APC ∠的大小：（2）如图②，过点C 作O 的切线MC ，过点B 作BD MC 于点D ，BD 与O 交于点E ，求DCE ∠的大小及CD 的长．22．在下列网格图中，每个小正方形的边长均为1个单位．Rt ABC 中，∠C ＝90°，AC ＝3，BC ＝4（1）试在图中作出ABC 绕A 顺时针方向旋转90°后的图形11AB C △；（2）求1BB 的长．23．已知EF 为O 的一条弦，OB EF ⊥交O 于点B ，A 是弦EF 上一点（不与E ，F 重合），连接BA 并延长交O 于点C ，过点C 作O 的切线交EF 的延长线于点D ．（1）如图1，若EF 在圆心O 的上方，且与OB 相交于点H ，求证：ACD △是等腰三角形；（2）如图2，若EF 是O 的直径，25AB =，O 的半径为4，求线段DC 的长；（3）如图3，若EF 在圆心O 的下方，且与BO 的延长线相交于点H ，试判断线段DA ，DE ，DF 之间的数量关系，并说明理由．24．如图，AB 是O 的一条弦，⊥OD AB ，垂足为C ，OD 交O 于点D ，点E 在O 上．（1）若40AOD ∠=︒，求DEB ∠的度数；（2）若3OC =，5OA =，求弦AB 的长．25．如图，已知BC 是O 的直径，AC 切O 于点C ，AB 交O 于点D ，E 为AC 的中点，连接CD ，DE ．（1）求证：DE 是O 的切线；（2）若8BD =，6CD =，求AC 的长．26．如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上，点B 的坐标为（1，0）（1）画出△ABC 关于x 轴对称的△A 1B 1C 1；（2）画出将△ABC 绕原点O 按逆时针旋转90°所得的△A 2B 2C 2，求出A 运动经过的路径的长度．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据计算公式直接套用求解即可．【详解】根据题意，得260333602S ππ⨯⨯==，故选C ．【点睛】本题考查了扇形的面积计算问题，熟记扇形面积计算公式，准确判断计算条件是解题的关键．2．A解析：A【分析】由切线的性质得出∠OAP=∠OBP=90°，利用四边形内角和可求∠AOB=130°，再利用圆周角定理可求∠ADB=65°，再根据圆的内接四边形对角互补可求∠ACB ．【详解】解：如图所示，连接OA 、OB ，在优弧AB 上取点D ，连接AD 、BD ，∵ AP 、BP 是切线，∠P=50°，∴ ∠OAP=∠OBP=90°，∴∠AOB=360°-90°-90°-50°=130°，∴∠ADB=65°，又∵圆的内接四边形对角互补，∴∠ACB=180°-∠ADB=180°-65°=115°．故选：A ．本题考查了切线的性质、圆周角定理、圆内接四边形的性质、解题的关键是连接OA 、OB ，求出∠AOB ．3．A解析：A【分析】证明△DAE ~△DBA ，求得DA 23=，由AB 是⊙O 的直径，利用勾股定理求得⊙O 的直径，求得∠ABD=30︒，∠COD=60︒，再利用OCD OCD S S S=-阴影扇形即可求解．【详解】连接OC 、OD 、AD ，∵BD 平分∠ABC ，∴AD CD =，∴∠DAC=∠DBA ，∴△DAE ~△DBA ，∴DA DE DB DA =，即26DA DA=， ∴212DA =，∴DA 23=， ∵AB 是⊙O 的直径，∴∠ADB=90︒，∴222AD BD AB +=，∴AB=43∴⊙O 的半径为3∵DA=OA=OD 23=， ∴△DOA 是等边三角形，∴∠COD=∠AOD=60︒，∴OCD OCD S S S =-阴影扇形(2602312323603602π⨯=-⨯︒233π=-【点睛】本题考查了相似三角形的判定与性质、等边三角形的判定与性质、勾股定理、扇形与等边三角形的面积等知识点，熟练掌握相关性质及定理是解题的关键．4．A解析：A【分析】连接AD，可证∠ODA=∠OAD=∠AOD=60°，根据弧中点，得出∠DAC=30°，△ADE是直角三角形，用勾股定理求AE即可．【详解】解：连接AD，∵∠BOD=120°，AB是⊙O的直径，∴∠AOD=60°，∵OA=OD，∴∠OAD=∠ODA =60°，∵点C为弧BD的中点，∴∠CAD=∠BAC=30°，∴∠AED=90°，∵DE=1，∴AD=2DE=2，AE=2222-=-=，213AD DE故选：A．【点睛】本题考查了圆周角的性质、勾股定理，解题关键是通过连接弦构造直角三角形，并通过弧相等导出30°角．5．C解析：C【分析】首先根据勾股定理逆定理判断△ABC是直角三角形，得其斜边是10，即可求得外接圆半径和内切圆半径．【详解】∵AC=6，BC=8，AC=10，2226810+=，∴222AC BC AC+=，∴△ABC是直角三角形，且斜边是AC=10，∴其外接圆的半径为5，三角形的内切圆半径=681022+-=，故选：C．【点睛】本题考查了三角形的外接圆和内切圆，勾股定理的逆定理；解题的关键是灵活运用勾股定理的逆定理判断△ABC是以AC为斜边的直角三角形．第II卷（非选择题）请点击修改第II卷的文字说明6．C解析：C【分析】根据切线的性质和切线长定理证明△PAB是等边三角形，PA⊥AO，根据直角三角形性质求出PA，问题得解．【详解】解：∵PA，PB是⊙O的两条切线，∠APB=60°，∴PA=PB，∠APO=12∠APB=30°，PA⊥AO，∴△PAB是等边三角形，∵PA⊥AO，∠APO==30°，∴OP=2OA=2，∴PA=∴△PAB的周长为故选：C【点睛】本题考查了切线长定理，切线的性质，等边三角形的判定，含30°角直角三角形性质，勾股定理等知识，考查知识点较多，熟知相关定理并能熟练运用是解题关键．7．C解析：C【分析】根据旋转的性质，可得BP′的长，∠PBP′的度数，得到P点运动轨迹为四分之一圆，圆的半径为3，根据弧长公式即可求解．【详解】由旋转的性质，得BP′=BP=3，∠PBP′=∠ABC=90°，P点运动轨迹为四分之一圆，圆的半径为3，∴弧PP ' =90331801802n r πππ⨯⨯== 故选C ．【点睛】此题考查旋转的性质、正方形的性质、弧长公式，重点是熟记弧长公式．8．B解析：B【分析】如图，过点A 作AE ⊥BD 于点E ，连接AD ，可得AD=AB=10，根据垂径定理可得DE=BE ，得CE=BE-BC=DE-4，再根据勾股定理即可求得DE 的长，进而可得CD 的长．【详解】解：如图，过点A 作AE ⊥BD 于点E ，连接AD ，∴AD=AB=10，根据垂径定理，得DE=BE ，∴CE=BE-BC=DE-4，根据勾股定理，得AD 2-DE 2=AC 2-CE 2，102-DE 2=82-（DE-4）2，解得DE=132， ∴CD=DE+CE=2DE-4=9，故选：B ．【点睛】本题考查了垂径定理，解决本题的关键是掌握垂径定理．9．C解析：C【分析】如图，连接OC 交AB 于T ．想办法求出点T 的坐标，利用待定系数法即可解决问题．【详解】解：如图，连接OC 交AB 于T ，设直线AB 交x 轴于M ，交y 轴于N ．∵直线AB的解析式为y=-x+b，∴N（0，b），M（b，0），∴OM=ON，∴∠OMN=45°，∵四边形OACB是平行四边形，OA=OB，∴四边形OACB是菱形，∴OC⊥AB，∴∠COM=45°，∵OC=6，∴C（3232∵OT=TC，∴T（322，322），把T点坐标代入y=-x+b，可得b=32故选：C．【点睛】本题考查圆周角定理，平行四边形的性质，菱形的判定，一次函数的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．10．C解析：C【分析】首先连接OB，OC，AO，设DO交BC于点E，由∠B＝70°，∠A＝60°，又由△ABC的边BC 的垂直平分线与△ABC的外接圆相交于点D，根据圆周角定理，即可求得∠AOB与∠BOE 的度数，继而求得答案．【详解】解：如图，连接OB，OC，AO，设DO交BC于点E，∵OD 是△ABC 的边BC 的垂直平分线，∴∠BOE ＝12∠BOC ， ∵∠BAC ＝12∠BOC ， ∴∠BOE ＝∠BAC ，∵∠A ＝60°，∠B ＝70°，∴50∠=°ACB ，∴∠BOE ＝∠BAC ＝60°，∴∠BOD ＝180°−∠BOE ＝180°−60°＝120°，∵∠AOB ＝2∠ACB ＝100°，∴AB 的度数为：100°，∴AD 的度数为：120°−100°＝20°．故选：C ．【点睛】此题考查了圆周角定理以及线段垂直平分线的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．11．D解析：D【分析】连接OE ，根据圆周角定理即可求出答案．【详解】解：连接OE ，根据圆周角定理可知：∠C ＝12∠AOE ，∠D ＝12∠BOE ，则∠C +∠D ＝12（∠AOE +∠BOE ）＝90°，故选：D ．【点睛】本题考查了圆周角的性质，解题关键是连接半径，构造圆心角，依据圆周角与圆心角的关系进行计算．12．D解析：D【分析】作点C 关于OB 对称点点A ，连接AD 与OB 的交点即为E ，此时CE+ED 最小，进而得到阴影部分的周长最小，再由勾股定理求出AD 的长，由弧长公式求出弧CD 的长．【详解】解：阴影部分的周长=CE+ED+弧CD 的长，由于C 和D 均为定点，E 为动点，故只要CE+ED 最小即可，作C 点关于OB 的对称点A ，连接DA ，此时即为阴影部分周长的最小值，如下图所示：∵A 、C 两点关于OB 对称，∴CE=AE ，∴CE+DE=AE+DE=AD ，又D 为弧BC 的中点，∠COB=60°，∴∠DOA=∠DOB+∠BOA=30°+60°=90°，在Rt △ODA 中，2222=+=DA OD OA ，弧CD 的长为302=1803ππ⨯⨯， ∴阴影部分周长的最小值为2+3π，故选：D ．【点睛】本题考查了轴对称图形求线段的最小值，弧长公式，勾股定理等，本题的关键是找出阴影部分周长最小值时点E 的位置进而求解．二、填空题13．【分析】利用弧长公式计算即可【详解】解：如图点的运动路径的长的长的长故答案是：【点睛】本题考查轨迹弧长公式等知识解题的关键是理解题意灵活运用所学知识解决问题解析：52π．【分析】利用弧长公式计算即可．【详解】解：如图，点O 的运动路径的长1OO =的长1223O O O O ++的长902452902180180180πππ⋅⋅⋅⋅⋅⋅=++ 52π=，故答案是：52π．【点睛】本题考查轨迹，弧长公式等知识，解题的关键是理解题意，灵活运用所学知识解决问题． 14．【分析】首先连接OBOCOD 由等边△ABC 内接于⊙OBD 为内接正十二边形的一边可求得∠BOC ∠BOD 的度数则证得△COD 是等腰直角三角形并利用勾股定理求得圆的半径最后利用S 阴影=S 扇形OCD-S △O解析：252542π- 【分析】首先连接OB ，OC ，OD ，由等边△ABC 内接于⊙O ，BD 为内接正十二边形的一边，可求得∠BOC ，∠BOD 的度数，则证得△COD 是等腰直角三角形，并利用勾股定理求得圆的半径，最后利用S 阴影=S 扇形OCD -S △OCD 进行计算后即可得出答案．【详解】解：连接OB ，OC ，OD ，∵等边△ABC 内接于⊙O ，BD 为内接正十二边形的一边，∴∠BOC ＝13×360°＝120°，∠BOD ＝112×360°＝30°， ∴∠COD ＝∠BOC−∠BOD ＝90°，∵OC ＝OD ，∴∠OCD ＝45°，∴OC 2+ OD 2＝CD 2．即2OC 2=50，∴OC=5， ∴S 阴影=S 扇形OCD -S △OCD=90251252555360242ππ-⨯⨯=-．故答案为：252542π-．【点睛】此题考查了正多边形与圆、扇形面积的计算等知识，掌握辅助线的作法以及数形结合思想的应用是解题的关键． 15．【分析】连接AC 根据圆周角定理得出AC 为圆的直径解直角三角形求出AB 求出扇形面积和面积两者的面积比即是针孔扎在扇形（阴影部分）的概率【详解】解：连接AC ∵从一块直径为2m 的圆形铁皮上剪出一个圆心角为解析：12【分析】连接AC ，根据圆周角定理得出AC 为圆的直径，解直角三角形求出AB ，求出扇形面积和O 面积，两者的面积比，即是针孔扎在扇形（阴影部分）的概率．【详解】解：连接AC ，∵从一块直径为2m 的圆形铁皮上剪出一个圆心角为90︒的扇形，即∠ABC=90︒， ∴AC 为直径，即AC=2m ，AB=BC （扇形的半径相等），∵AB 2+BC 2=22，∴m ，∴S 阴影部分=2903602ππ︒⨯=︒（m 2），则：P 针孔扎在扇形（阴影部分）=212==2OS S OA =阴影部分ππ故答案为：12．【点睛】本题考查了几何概率：求概率时，已知和未知与几何有关的就是几何概率．计算方法是长度比，面积比，体积比等．16．【分析】根据圆周角定理计算即可；【详解】∵∴；故答案是【点睛】本题主要考查了圆周角定理准确分析计算是解题的关键解析：90︒【分析】根据圆周角定理计算即可；【详解】∵45C ∠=︒，∴290AOB C ∠=∠=︒；故答案是90︒．【点睛】本题主要考查了圆周角定理，准确分析计算是解题的关键．17．【分析】连接COOB 则∠O ＝2∠CAB ＝60°得到△BOC 是等边三角形求得BC ＝4根据等腰直角三角形的性质即可得到结论【详解】解：如图连接COOB ∵则∠O ＝2∠CAB ＝60°∵OC ＝OB ∴△BOC 是解析：【分析】连接CO ，OB ，则∠O ＝2∠CAB ＝60°，得到△BOC 是等边三角形，求得BC ＝4，根据等腰直角三角形的性质即可得到结论．【详解】解：如图，连接CO ，OB ，∵30CAB ∠=︒则∠O ＝2∠CAB ＝60°，∵OC ＝OB ，∴△BOC 是等边三角形，∵⊙O 的半径为4，∴BC ＝4，∵CD ⊥AB ，∠CBA ＝45°，∴CD 2BC 2×4=2，故答案为：2【点睛】本题考查了三角形的外接圆与外心，圆周角定理，等腰直角三角形的性质，正确的作出辅助线是解题的关键．18．【分析】正六边形的面积有6个全等的边长为1的等边三角形面积组成计算一个等边三角形的面积乘以6即可【详解】如图所示等边三角形ABC 的边长为1∵OC 是AB 上的高∴AC=CB=∠AOC=∠AOB=30°∴ 332【分析】正六边形的面积有6个全等的边长为1的等边三角形面积组成，计算一个等边三角形的面积，乘以6即可.【详解】如图所示，等边三角形ABC 的边长为1，∵OC 是AB 上的高，∴AC=CB=12，∠AOC=12∠AOB=30°， ∴222211()2OA AC -=- =3 ∴12AOB S AB OC =⋅=13122⨯⨯=3，∴正六边形的面积为：333642⨯=.故答案为33.【点睛】本题考查了正多边形的面积，熟练把多边形的面积转化为三角形面积的倍数计算是解题的关键.19．半圆（或直径）所对的圆周角是直角【分析】根据直径所对的圆周角是直角即可得出结论【详解】解：∵半圆（或直径）所对的圆周角是直角∴连结AE 则线段AE就是BC边上的高故答案为：半圆（或直径）所对的圆周角是解析：半圆（或直径）所对的圆周角是直角【分析】根据直径所对的圆周角是直角即可得出结论．【详解】解：∵半圆（或直径）所对的圆周角是直角，∴连结AE，则线段AE就是BC边上的高．故答案为：半圆（或直径）所对的圆周角是直角．【点睛】本题考查了作图-基本作图，掌握圆周角定理是解答此题的关键．20．2【分析】连结FD由可证△FAE∽△DAF可得∠DFA=90°可知点F在以AD中点为圆心3为半径的半圆上运动由BFO三点共线时利用两点之间线段最短知BF 最短在Rt△ABO中由勾股定理得BO=可求BF解析：2【分析】连结FD，由2·AF AE AD=可证△FAE∽△DAF，可得∠DFA=90°，可知点F在以AD中点为圆心，3为半径的半圆上运动，由B、F、O三点共线时，利用两点之间线段最短知BF最短,在Rt △ABO 中，由勾股定理得BO=22AB +AO =5，可求BF=5-3=2．【详解】连结FD ，∵2·AF AE AD =，∴AF AD AE AF=， ∵∠FAE=∠DAF ，∴△FAE ∽△DAF ，∴∠FEA=∠DFA ，∵EF AD ⊥，即∠FEA=90°，∴∠DFA=90°，∴点F 在以AD 中点为圆心，3为半径的半圆上运动，当B 、F 、O 三点共线时，BF 最短,在Rt △ABO 中，由勾股定理得，BO=22AB +AO =5，BF=5-3=2，BF 的最小值为2，故答案为：2．【点睛】本题考查三角形相似判定与性质，圆周角性质，勾股定理，两点之间线段最短，掌握三角形相似的判定方法和性质的应用，会根据直角确定点F 在圆周上运动，利用两点之间线段最短解决问题是关键．三、解答题21．（1）30°；（2）30DCE ∠=︒；3CD =【分析】（1）连接OC ，由AB 是圆O 的直径，AB=2AC ，得到AOC △为等边三角形，根据等边三角形的性质得到60AOC ∠=︒，即可得到结论（2）连接OE ，OC ，根据切线的性质得到MC OC ⊥，得到EOB △是等边三角形，根据等边三角形的性质得到60EOB ∠=︒，求得18060COE EOB AOC ∠=︒-∠-∠=︒，推出OCE △是等边三角形，于是得到2CE OC ==，60EOC ∠=︒，根据勾股定理即可得到结论【详解】.解：（1）如图，连接OC ．O 的直径4AB =，2OA OC ．2AC =，OA OC AC ∴==．AOC ∴是等边三角形．60AOC ∴∠=︒．3102PC C A AO ∴∠=∠=︒．（2）如图，连接OC ，OE ．MC 是O 的切线，MC OC ∴⊥．BD MC ⊥，90MCO CDB ∴∠=∠=︒．//BD OC ∴．60B AOC ∴∠=∠=︒．OB OE =，EOB ∴是等边三角形．60EOB ∴∠=︒．18060COE EOB AOC ∴∠=︒-∠-∠=︒．OC OE =，OCE ∴是等边三角形．2CE OC ∴==，60ECO ∠=︒．9030DCE ECO ∴∠=︒-∠=︒在Rt CDE △中，2CE =， 112DE CE ∴==，2222213CD CE DE =-=-=．【点睛】本题考查了切线的性质，等边三角形的性质和判定，圆周角定理，平行线的判定和性质，正确作出辅助线是解题关键，22．（1）见解析；（2）52π．【分析】（1）根据△ABC 绕A 顺时针方向旋转90°，即可得到△AB 1C 1；（2）根据弧长计算公式，即可得出点B 运动路径的长．【详解】解：（1）如图所示，△AB 1C 1即为所求；（2）Rt ABC 中，∠C ＝90°，AC ＝3，BC ＝4∴2222AB AC BC 345=++=又∠BAB 1=90°，∴点B 的运动路径的长为：90551802ππ⨯=．【点睛】本题考查了利用旋转变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键． 23．（1）见解析；（2）线段DC 的长为3；（3）线段DA ，DE ，DF 之间的数量关系为2DA DE DF =⋅，理由见解析．【分析】（1）连接OC ，由题意易得OC DC ⊥，∠B=∠OCB ，则有9090DCA ACO B ∠=︒-∠=︒-∠，进而可得DAC DCA ∠=∠，然后问题可求证；（2）连接OC ，则OC DC ⊥，由勾股定理可得2AO =，由（1）可得DA DC =，设DC x =，则2OD x =+，然后再由勾股定理可求DC 的长；（3）连接CF ，CE ，连接CO 并延长交O 于点G ，连接GF ，由题意可得9090DCA OCB HBA ∠=︒-∠=︒-∠，则有DA DC =，进而可得CED DCF ∠=∠，然后有CDF EDC ∽△△，则根据相似三角形的性质及线段的等量关系可求解．【详解】（1）证明：如图，连接OC ，则OC DC ⊥，∵OB=OC ，∴∠B=∠OCB ，∴9090DCA ACO B ∠=︒-∠=︒-∠，又∵90DAC BAH B ∠=∠=︒-∠，∴DAC DCA ∠=∠，∴DA DC =，∴ACD △是等腰三角形；（2）如图，连接OC ，则OC DC ⊥，∵在Rt ABO △中，25AB =，O 的半径为4，∴2AO =，由（1）可得DA DC =，设DC x =，则2OD x =+，∴在Rt OCD △中，()22242x x +=+， ∴3x =，即线段DC 的长为3；（3）线段DA ，DE ，DF 之间的数量关系为2DA DE DF =⋅，理由：如图，连接CF ，CE ，连接CO 并延长交O 于点G ，连接GF ， ∵DC 为O 的切线，∴9090DCA OCB HBA ∠=︒-∠=︒-∠，又∵90BAH HBA ∠=︒-∠，CAD BAH ∠=∠，∴∠=∠DCA CAD ，∴DA DC =，∵CG 是O 的直径，∴90CFG ∠=︒，∴90CED CGF GCF ∠=∠=︒-∠，又∵90DCF GCF ∠=︒-∠，∴CED DCF ∠=∠，又∵D D ∠=∠，∴CDF EDC ∽△△， ∴DC DF DE DC=， ∴2DC DE DF =⋅，∴2DA DE DF =⋅．【点睛】本题主要考查相似三角形的性质及切线的性质定理，熟练掌握相似三角形的性质及切线的性质定理是解题的关键．24．（1）20°；（2）8【分析】（1）欲求DEB ∠，又已知一圆心角，可利用圆周角与圆心角的关系求解；（2）利用垂径定理可以得到142A C B C B A ===，从而得到结论．【详解】解：（1）OD AB ⊥，∴AD BD =，11402022DEB AOD ∴∠=∠=⨯︒=︒．（2）3OC =，5OA =，且⊥OD AB ，4AC ∴=，OD AB ⊥， ∴12AD BD AB ==， 142AC BC AB ∴===， 8AB ∴=．【点睛】此题考查了圆周角与圆心角定理以及垂径定理，熟练掌握垂径定理得出4AC CB ==是解题关键．25．（1）证明见解析；（2）152 【分析】（1）连接OD ，根据切线的性质和直角三角形斜边的中线以及等腰三角形的性质得出，EDC ECD ∠=∠，ODC OCD ∠=∠，然后利用等量代换即可得出DE OD ⊥，从而证明结论；（2）首先根据勾股定理求出BC 的长度，然后证明BCD BAC ∽△△，最后利用CD BD AC BC=求解即可．【详解】（1）证明：连接OD ，如图，∵BC 是O 的直径，∴90BDC ∠=︒，∴90ADC ∠=︒，∵E 为AC 的中点，∴12DE EC AC ==， ∴EDC ECD ∠=∠，∵OD OC = ， ∴ODC OCD ∠=∠，∵AC 切O 于点C ，∴AC OC ⊥，∴90EDC ODC ECD OCD ∠+∠=∠+∠=︒，∴DE OD ⊥，∴DE 是O 的切线；（2）解：在Rt BCD 中，∵8BD =，6CD =， ∴2210BC BD CD =+=∵90BDC BCA ∠=∠=︒，B B ∠=∠，∴BCD BAC ∽△△，∴CD BD AC BC=，即6810AC =， ∴152AC =．【点睛】本题主要考查圆的综合问题，掌握切线的判定及性质，相似三角形的判定及性质是解题的关键．26．（1）见解析；（2）见解析；2π【分析】（1）根据轴对称的性质画图即可；（2）根据旋转的性质画图即可；利用公式求弧长即可．【详解】（1）如图所示：（2）OA 222222+=,A 90222ππ⨯=；【点睛】本题考查了利用旋转变换与轴对称变换作图以及求弧长，熟练掌握网格结构，准确找出对应点的位置，熟练运用弧长公式是解题的关键．。

北师大版九年级数学下册第三章-圆单元测试题(含答案)

九年级数学圆单元测试题一、选择题1．若⊙O 所在平面内一点 P 到⊙O 上的点的最大距离为 a ，最小距离为 b （a>b ），则此圆的半径为（）A ．2a b + B ．2a b- C ．2a b +或2a b - D ． a + b 或a - b 2．如图 24—A —1，⊙O 的直径为 10，圆心 O 到弦 AB 的距离 OM 的长为 3，则弦 AB 的长是（） A ．4 B ．6 C ．7 D ．8 3．已知点 O 为△ABC 的外心，若∠A=80°，则∠BOC 的度数为（） A ．40° B ．80° C ．160° D ．120° 4．如图 24—A —2，△ABC 内接于⊙O ，若∠A=40°，则∠OBC 的度数为（） A ．20° B ．40° C ．50° D ．70°图 24—A —2图 24—A —3 图 24—A —4 图 24—A —55．如图 24—A —3，小明同学设计了一个测量圆直径的工具，标有刻度的尺子 OA 、OB 在 O 点钉在一起，并使它们保持垂直，在测直径时，把 O 点靠在圆周上，读得刻度 OE=8 个单位，OF=6 个单位，则圆的直径为（） A ．12 个单位 B ．10 个单位 C ．1 个单位 D ．15 个单位 6．如图 24—A —4，AB 为⊙O 的直径，点 C 在⊙O 上，若∠B=60°，则∠A 等于（） A ．80° B ．50° C ．40° D ．30° 7．如图 24—A —5，P 为⊙O 外一点，PA 、PB 分别切⊙O 于 A 、B ，CD 切⊙O 于点 E ，分别交 PA 、PB 于点 C 、D ，若 PA=5，则△PCD 的周长为（） A ．5 B ．7 C ．8 D ．10 8．若粮仓顶部是圆锥形，且这个圆锥的底面直径为 4m ，母线长为 3m ，为防雨需在粮仓顶部铺上油毡，则这块油毡的面积是（）A ．6m 2B ． 6πm 2C ．12m 2D ．12πm 29．如图 24—A —6，两个同心圆，大圆的弦 AB 与小圆相切于点 P ，大圆的弦 CD 经过点 P ，且 CD=13，PC=4，则两圆组成的圆环的面积是（） A ．16π B ．36π C ．52π D ．81π10．已知在△ABC 中，AB=AC=13，BC=10，那么△ABC 的内切圆的半径为（） A ．103 B ．125C ．2D ．311．如图 24—A —7，两个半径都是 4cm 的圆外切于点 C ，一只蚂蚁由点 A 开始依 A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的 8 段长度相等的路径绕行，蚂蚁在这 8 段路径上不断爬行，直到行走 2006π cm 后才停下来，则蚂蚁停的那一个点为（）A ．D 点B ．E 点C ．F 点D ．G 点二、填空题12．如图 24—A —8，在⊙O 中，弦 AB 等于⊙O 的半径，OC ⊥AB 交⊙O 于点 C ，则∠ AOC= 。

2022年必考点解析北师大版九年级数学下册第三章圆专项练习试卷(含答案详解)

北师大版九年级数学下册第三章圆专项练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，Rt△ABC中，∠A＝90°，∠B＝30°，AC＝1，将Rt△ABC延直线l由图1的位置按顺时针方向向右作无滑动滚动，当A第一次滚动到图2位置时，顶点A所经过的路径的长为（）B C D．（πA2、如图，O是正方形ABCD的外接圆，若O的半径为4，则正方形ABCD的边长为（）A．4 B．8 C．D．3、如图，⊙O中，半径OC⊥AB于D，且CD＝2，弦AB＝8，则⊙O的半径的长等于（）A ．3B ．4C ．5D ．64、到三角形三个顶点距离相等的点是此三角形（）A ．三条角平分线的交点B ．三条中线的交点C ．三条高的交点D ．三边中垂线的交点5、已知半径为5的圆，直线l 上一点到圆心的距离是5，则直线和圆的位置关系为（）A ．相切B ．相离C ．相切或相交D ．相切或相离6、如图，已知O 中，50AOB ∠=︒，则圆周角ACB ∠的度数是（）A ．50°B ．25°C ．100°D ．30°7、如图，直径AB ＝6的半圆，绕B 点顺时针旋转30°，此时点A 到了点A '，则图中阴影部分的面积是（）A ．3πB ．34πC ．πD ．3π8、下列说法正确的是（）A ．等弧所对的圆周角相等B ．平分弦的直径垂直于弦C ．相等的圆心角所对的弧相等D ．过弦的中点的直线必过圆心9、如图，菱形ABCD 中，60C ∠=°，2AB =．以A 为圆心，AB 长为半径画BD ，点P 为菱形内一点，连PA ，PB ，PD ．若PA PB =，且120APB ∠=︒，则图中阴影部分的面积为（）A ．23y π= B ．23y π= C ．23y π= D ．23y π=10、若正六边形的边长为6，则其外接圆半径与内切圆半径的大小分别为（）A ．6，B ．6，C ． 6D ．6，3第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，已知圆锥的母线AB 长为40 cm ，底面半径OB 长为10 cm ，若将绳子一端固定在点B ，绕圆锥侧面一周，另一端与点B 重合，则这根绳子的最短长度是______________．2、如图，AB 是半圆O 的直径，AB ＝4，点C ，D 在半圆上，OC ⊥AB ，2BD CD =，点P 是OC 上的一个动点，则BP ＋DP 的最小值为______．3、已知正六边形的周长是24，则这个正六边形的半径为_____ ．4、在半径为3的圆中，60°的圆心角所对的劣弧长等于_____．5、如图，五边形ABCDE是⊙O的内接正五边形，则ODC的度数是____．三、解答题（5小题，每小题10分，共计50分）1、如图，射线AB和射线CB相交于点B，∠ABC＝α（0°＜α＜180°），且AB＝CB．点D是射线CB 上的动点（点D不与点C和点B重合），作射线AD，并在射线AD上取一点E，使∠AEC＝α，连接CE，BE．（1）如图①，当点D在线段CB上，α＝90°时，请直接写出∠AEB的度数；（2）如图②，当点D在线段CB上，α＝120°时，请写出线段AE，BE，CE之间的数量关系，并说明理由；（3）当α＝120°，tan∠DAB＝13时，请直接写出CEBE的值．2、如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作O的切线交CE的延长线于点D．（1）求证：DB=DE；（2）若AB=12，BD=5，求AC长．3、如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且：CF是⊙O的切线．（1）求证：∠DCF＝∠CAD．（2）探究线段CF，FD，FA的数量关系并说明理由；（3）若cos B35=，AD＝2，求FD的长．4、在平面直角坐标系xOy中，⊙O的半径为1．对于线段AB，给出如下定义：若线段AB沿着某条直线l对称可以得到⊙O的弦A′B′，则称线段AB 是⊙O的以直线l为对称轴的“反射线段”，直线l称为“反射轴”．（1）如图，线段CD，EF，GH中是⊙O的以直线l为对称轴的“反射线段”有；（2）已知A点坐标为（0，2），B点坐标为（1，1），①若线段AB是⊙O的以直线l为对称轴的“反射线段”，求反射轴l与y轴的交点M的坐标．②若将“反射线段”AB沿直线y＝x的方向向上平移一段距离S，其反射轴l与y轴的交点的纵坐标y M的取值范围为12≤y M136≤，求S．（3）已知点M，N是在以原点为圆心，半径为2的圆上的两个动点，且满足MN＝1，若MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，求反射轴l未经过的区域的面积．（4）已知点M，N是在以（2，0MN=MN是⊙O的以直线l为对称轴的“反射线段”，当M点在圆上运动一周时，请直接写出反射轴l与y轴交点的纵坐标的取值范围．5、在平面直角坐标系xOy 中，已知抛物线212y x bx =+．（1）求抛物线顶点Q 的坐标；（用含b 的代数式表示）（2）抛物线与x 轴只有一个公共点，经过点（0，2）的直线与抛物线交于点A ，B ，与x 轴交于点K ．①判断△AOB 的形状，并说明理由；②已知E （2，0），F （4，0），设△AOB 的外心为M ，当点K 在线段EF 上时，求点M 的纵坐标m 的取值范围．-参考答案-一、单选题1、C【分析】根据题意，画出示意图，确定出点A 的运动路径，再根据弧长公式即可求解．【详解】解：根据题意可得，Rt △ABC 的运动示意图，如下：Rt △ABC 中，∠A ＝90°，∠B ＝30°，AC ＝1，∴60ACB ∠=︒，2BC =，AB =由图形可得，点A 的运动路线为，先以C 为中心，顺时针旋转120︒，到达点1A ，经过的路径长为120121803ππ⨯=，再以1B 为中心，顺时针旋转150︒，到达点2A ，顶点A 所经过的路径的长为23π=故选：C【点睛】此题考查了旋转的性质，圆弧弧长的求解，解题的关键是根据题意确定点A 的运动路线．2、D【分析】连接OB ，OC ，过点O 作OE ⊥BC 于点E ，由等腰直角三角形的性质可知OE =BE ，由垂径定理可知BC =2BE ，故可得出结论．【详解】解：连接OB ，OC ，过点O 作OE ⊥BC 于点E ，∴OB =OC ，∠BOC =90°，∴∠OBE =45°，45BOE ∠=︒∴OE =BE ，∵OE 2+BE 2=OB 2，∴BE =∴BC =2BE =ABCD 的边长是故选：D【点睛】本题考查的是圆周角定理、垂径定理及勾股定理，根据题意作出辅助线，构造出等腰直角三角形是解答此题的关键．3、C【分析】根据垂径定理得出AD =BD =118422AB ，设⊙O 的半径的长为x ，根据勾股定理222OB OD BD =+，即()22224x x =-+，解方程即可．【详解】解：∵半径OC ⊥AB 于D ，弦AB ＝8， ∴AD =BD =118422AB ，设⊙O 的半径的长为x ，∴OD =OC -CD =x -2，在Rt△ODB 中，根据勾股定理222OB OD BD =+，即()22224x x =-+，解得x =5，∴⊙O的半径的长为5．故选择C．【点睛】本题考查垂径定理，勾股定理，解拓展一元一次方程，掌握垂径定理，勾股定理，解拓展一元一次方程是解题关键．4、D【分析】由题意根据线段的垂直平分线上的性质，则有三角形三边中垂线的交点到三角形的三个顶点距离相等．【详解】解：∵垂直平分线上任意一点，到线段两端点的距离相等，∴到三角形三个顶点的距离相等的点是三角形三边中垂线的交点．故选：D．【点睛】本题考查了线段的垂直平分线的性质，解题的关键是注意掌握线段的垂直平分线上的点到线段的两个端点的距离相等．5、C【分析】根据若直线上一点到圆心的距离等于圆的半径，则圆心到直线的距离等于或小于圆的半径，此时直线和圆相交或相切．【详解】解：∵半径为5的圆，直线l上一点到圆心的距离是5，∴圆心到直线的距离等于或小于5，∴直线和圆的位置关系为相交或相切，故选：C ．【点睛】本题考查了直线和圆的位置关系，判断的依据是半径和直线到圆心的距离的大小关系：设⊙O 的半径为r ，圆心O 到直线l 的距离为d ，①直线l 和⊙O 相交⇔d ＜r ；②直线l 和⊙O 相切⇔d ＝r ；③直线l 和⊙O 相离⇔d ＞r ．6、B 【分析】根据圆周角定理，即可求解．【详解】解：∵1,502ACB AOB AOB ∠=∠∠=︒ ，∴25ACB ∠=︒ ．故选：B 【点睛】本题主要考查了圆周角定理，熟练掌握同圆（或等圆）中，同弧（或等弧）所对的圆周角等于圆心角的一半是解题的关键． 7、D 【分析】阴影面积为旋转后'A B 为直径的半圆面积加旋转后扇形面积减去旋转前AB 为直径的半圆面积，则阴影面积为旋转后的扇形面积，由扇形面积公式计算即可．【详解】∵直径AB ＝6的半圆，绕B 点顺时针旋转30° ∴A'B ABA'AB S S S S =+-阴影为直径的半圆扇形为直径的半圆又∵'AB A B =∴A'B AB S S =为直径的半圆为直径的半圆∴ABA'S S =阴影扇形 ∵AB =6，∠ABA ’=30° ∴223063360360ABA'n r S S π︒⋅π⋅====π︒︒阴影扇形故答案为：D ．【点睛】本题考查了扇形面积公式的应用，扇形面积公式为2360n r π︒，由旋转的性质得出阴影面积为扇形面积是解题的关键． 8、A 【分析】根据圆周角定理，垂径定理的推论，圆心角、弧、弦的关系，对称轴的定义逐项排查即可．【详解】解：A . 同弧或等弧所对的圆周角相等，所以A 选项正确；B .平分弦（非直径）的直径垂直于弦，并且平分弦所对的弧，所以B 选项错误；C 、在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦相等，所以C 选项错误；D .圆是轴对称图形，任何一条直径所在的直线都是它的对称轴，所以D 选项错误.故选A. 【点睛】本题主要考查了圆心角、弧、弦的关系,轴对称图形，垂径定理，圆周角定理等知识点．灵活运用相关知识成为解答本题的关键． 9、C【分析】过点P 作PM AB ⊥交于点M ，由菱形ABCD 得60DAB C ∠=∠=︒，2AB AD ==，由PA PB =，120APB ∠=︒得112AM AB ==，1602APM APB ∠=∠=︒，故可得30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，根据SAS 证明ABP ADP ≅，求出PM =ABPADPABD S S SS=--阴扇形．【详解】如图，过点P 作PM AB ⊥交于点M ， ∵四边形ABCD 是菱形，∴60DAB C ∠=∠=︒，2AB AD ==， ∵PA PB =，120APB ∠=︒， ∴112AM AB ==，1602APM APB ∠=∠=︒， ∴30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，在ABP △与ADP △中，AB ADPAB PAD AP AP =⎧⎪∠=∠⎨⎪=⎩， ∴()ABP ADP SAS ≅， ∴ABP ADP S S =△△，在Rt AMP △中，30PAM ∠=︒， ∴2AP PM =，222AP PM AM =+，即2241PM PM =+，解得：PM =∴260211222360223ABP ADPABD S S S Sππ⋅=--=-⨯⨯=阴扇形故选：C ．【点睛】此题主要考查了菱形的性质以及求不规则图形的面积等知识，掌握扇形的面积公式是解答此题的关键． 10、B 【分析】如图1，⊙O 是正六边形的外接圆，连接OA ，OB ，求出∠AOB =60°，即可证明△OAB 是等边三角形，得到OA =AB =6；如图2，⊙O 1是正六边形的内切圆，连接O 1A ，O 1B ，过点O 1作O 1M ⊥AB 于M ，先求出∠AO 1B ＝60°，然后根据等边三角形的性质和勾股定理求解即可．【详解】解：（1）如图1，⊙O 是正六边形的外接圆，连接OA ，OB ， ∵六边形ABCDEF 是正六边形， ∴∠AOB =360°÷6=60°， ∵OA =OB ，∴△OAB 是等边三角形， ∴OA =AB =6；（2）如图2，⊙O1是正六边形的内切圆，连接O1A，O1B，过点O1作O1M⊥AB于M，∵六边形ABCDEF是正六边形，∴∠AO1B＝60°，∵O1A= O1B，∴△O1AB是等边三角形，∴O1A= AB=6，∵O1M⊥AB，∴∠O1MA＝90°，AM＝BM，∵AB＝6，∴AM＝BM，∴O 1M 故选B ．【点睛】本题主要考查了正多边形与圆，等边三角形的性质与判定，勾股定理，熟知正多边形与圆的知识是解题的关键．二、填空题1、【分析】根据底面圆的周长等于扇形的弧长求解扇形的圆心角90,BAB '∠=︒ 再利用勾股定理求解即可. 【详解】解：圆锥的侧面展开图如图所示：设圆锥侧面展开图的圆心角为n °，圆锥底面圆周长为210=20，40=20,180n BB 则n =90，∵40,AB AB224040402,BB即这根绳子的最短长度是，故答案为：【点睛】本题考查的是圆锥的侧面展开图，弧长的计算，掌握“圆锥的底面圆的周长等于展开图的弧长求解圆心角”是解本题的关键.2、【分析】如图，连接AD，PA，PD，OD．首先证明PA=PB，再根据PD+PB=PD+PA≥AD，求出AD即可解决问题．【详解】解：如图，连接AD，PA，PD，OD．∵OC⊥AB，OA=OB，∴PA=PB，∠COB=90°，∵2BD CD，∴∠DOB=23×90°=60°，∵OD=OB，∴△OBD是等边三角形，∴∠ABD=60°∵AB是直径，∴∠ADB=90°，∴AD=AB•sin∠ABD∵PB+PD=PA+PD≥AD，∴PD+PB∴PD+PB的最小值为故答案为：【点睛】本题考查圆周角定理，垂径定理，圆心角，弧，弦之间的关系等知识，解题的关键是学会用转化的思想思考问题．3、4【分析】由于正六边形可以由其半径分为六个全等的正三角形，而三角形的边长就是正六边形的半径，由此即可求解．【详解】解：∵正六边形可以由其半径分为六个全等的正三角形，而三角形的边长就是正六边形的半径，又∵正六边形的周长为24，∴正六边形边长为24÷6=4，∴正六边形的半径等于4．故答案为4．【点睛】此题主要考查正多边形和圆，解题的关键是熟练掌握基本知识，属于中考基础题．4、π【分析】弧长公式为l ＝n 180rπ，把半径和圆心角代入公式计算就可以求出弧长．【详解】解：半径为3的圆中，60°的圆心角所对的劣弧长＝603180π⨯＝π，故答案为：π．【点睛】本题主要考查了弧长计算，关键是掌握弧长计算公式． 5、54︒ 【分析】根据圆内接正五边形的定义求出∠COD ，利用三角形内角和求出答案．【详解】解：∵五边形ABCDE 是⊙O 的内接正五边形， ∴∠COD=360725︒=︒， ∵OC=OD ，∴ODC ∠=(180)5412COD ︒-∠=︒，故答案为：54︒．【点睛】此题考查了圆内接正五边形的性质，三角形内角和定理，同圆的半径相等的性质，熟记圆内接正五边形的性质是解题的关键．三、解答题1、（1）45°；（2）AE +CE ，理由见解析；（3【分析】（1）连接AC，证A、B、E、C四点共圆，由圆周角定理得出∠AEB＝∠ACB，证出△ABC是等腰直角三角形，则∠ACB＝45°，进而得出结论；（2）在AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，证△ABF≌△CBE（SAS），得出∠ABF＝∠CBE，BF＝BE，由等腰三角形的性质得出FH＝EH，由三角函数定义得出FH＝EH，进而得出结论；（3）分两种情况，由（2）得FH＝EH，由三角函数定义得出AH＝3BH＝32BE，分别表示出CE，进而得出答案．【详解】解：（1）连接AC，如图①所示：∵α＝90°，∠ABC＝α，∠AEC＝α，∴∠ABC＝∠AEC＝90°，∴A、B、E、C四点共圆，∴∠AEB＝∠ACB，∵∠ABC＝90°，AB＝CB，∴△ABC是等腰直角三角形，∴∠ACB＝45°，∴∠AEB＝45°；（2）AE+CE，理由如下：在AD 上截取AF ＝CE ，连接BF ，过点B 作BH ⊥EF 于H ，如图②所示：∵∠ABC ＝∠AEC ，∠ADB ＝∠CDE ，∴180°﹣∠ABC ﹣∠ADB ＝180°﹣∠AEC ﹣∠CDE ，∴∠A ＝∠C ，在△ABF 和△CBE 中，AF CE A C AB CB =⎧⎪∠=∠⎨⎪=⎩， ∴△ABF ≌△CBE （SAS ），∴∠ABF ＝∠CBE ，BF ＝BE ，∴∠ABF +∠FBD ＝∠CBE +∠FBD ，∴∠ABD ＝∠FBE ，∵∠ABC ＝120°，∴∠FBE ＝120°，∵BF ＝BE ，∴∠BFE ＝∠BEF ＝11(180)(180120)3022FBE ︒︒︒︒⨯-∠=⨯-=， ∵BH ⊥EF ，∴∠BHE ＝90°，FH ＝EH ，在Rt△BHE中，1,2BH BE FH EH ====，∴22EF EH ===， ∵AE ＝EF +AF ，AF ＝CE ，∴.AE CE=+；（3）分两种情况：①当点D在线段CB上时，在AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，如图②所示，由（2）得：FH＝EH，∵tan∠DAB＝13 BHAH=，∴332AH BH BE==，∴32CE AF AH FH BE==-==，∴CEBE=；②当点D在线段CB的延长线上时，在射线AD上截取AF＝CE，连接BF，过点B作BH⊥EF于H，如图③所示，同①得：3,32FH EH AH BH BE ====，∴32CE AF AH FH BE==+==，∴CE BE综上所述，当α＝120°，1tan3DAB∠=时，CEBE【点睛】本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、四点共圆、圆周角定理、三角函数定义等知识；本题综合性强，构造全等三角形是解题的关键．2、（1）见解析；（2）15 2【分析】（1）由切线性质及等量代换推出∠4=∠5，再利用等角对等边可得出结论；（2）由已知条件得出sin∠DEF和sin∠AOE的值，利用对应角的三角函数值相等推出结论. 【详解】（1）如图，∵DC⊥OA，∴∠1+∠3=90°，∵BD为切线，∴OB⊥BD，∴∠2+∠5=90°，∵OA=OB，∴∠1=∠2，∵∠3=∠4，∴∠4=∠5，在△DEB中，∠4=∠5，∴DE=DB.(2)如图，作DF⊥AB于F，连接OE，∵DB=DE，∴EF=12BE=3，在Rt△DEF中，EF=3，DE=BD=5，∴DF4=∴sin∠DEF=DFDE=45，∵∠AOE90A A AEC+∠=︒=∠+∠,AEC DEF∠=∠，∴∠AOE=∠DEF，∴在Rt△AOE 中，sin∠AOE =45AE AO = ， ∵AE =6，∴AO =152. 【点睛】本题考查了圆的性质，切线定理，三角形相似，三角函数等知识，结合图形正确地选择相应的知识点与方法进行解题是关键.3、（1）见解析；（2）2·FC FD FA =，见解析；（3）187【分析】（1）连接OC ，根据直径所对的圆周角为直角及切线的性质和各角之间的等量关系即可证明；（2）根据相似三角形的判定定理可得ΔΔΔΔ~ΔΔΔΔ，依据相似三角形的性质：对应边成比例即可得出；（3）根据同弧所对的圆周角相等可得：B ADC ∠=∠，3cos cos 5ADC B ∠=∠=，在Rt ACD ∆中，利用锐角三角函数可得65CD =，由勾股定理确定85AC =，由此得出34CD AC =，即为（2）中的相似比，设3FD x =，则4FC x =，32AF x =+，将其代入（2）中结论求解即可．【详解】解：（1）连接OC ，如图所示：∵AD 为O 直径，∴90ACD ∠=︒，90CAD ADC ∠+∠=︒，∵CF 为O 的切线，∴90OCF ∠=︒，即90OCD DCF ∠+∠=︒，∵OC OD =，∴OCD ADC ∠=∠，∴DCF CAD ∠=∠；（2）在ΔΔΔΔ与AFC ∆中，∵DCF CAD ∠=∠，F F ∠=∠，∴ΔΔΔΔ~ΔΔΔΔ， ∴FCFDAF FC =，∴2·FC AF FD =；（3）∵B ADC ∠=∠， ∴3cos cos 5ADC B ∠=∠=，在Rt ACD ∆中，2AD =，3cos 5CDADC AD ∠==， ∴6·cos 5CD AD ADC =∠=，∴85AC ==， ∴34CDAC =，由（2）结论可得：ΔΔΔΔ~ΔΔΔΔ，∴34FC FD CD AF FC AC ===，设3FD x =，则4FC x =，32AF x =+，将其代入结论（2）可得：()()24332x x x =+，解得：67x =或0x =（舍去）， ∴1837FD x ==．【点睛】题目主要考查圆周角定理、相似三角形的判定和性质、锐角三角函数解三角形、勾股定理等，理解题意，综合运用这些知识点是解题关键．4、（1）2；（2）①1(0,)2M ；②02S ≤≤；（3）1916π⎛ ⎝⎭;（4）1y >或1y <- 【分析】（1）O 的半径为1，则O 的最长的弦长为2，根据两点的距离可得2,EF CD EF ===而即可求得答案；（2）①根据定义作出图形，根据轴对称的方法求得对称轴，反射线段经过对应圆心的中点，即可求得M 的坐标；②由①可得当0S =时，y M 1=2，设当S 取得最大值时，过点1O 作1O P y ⊥轴，根据题意，122,,O A B 分别为沿直线y ＝x 的方向向上平移一段距离S 后,,O A B '的对应点，则1O P PO '=S =，根据余弦求得11cos cos QO PO MOQ O OP OM OO ∠=∠==进而代入数值列出方程，解方程即可求得S 的最大值，进而求得S 的范围；（3）根据圆的旋转对称性，找到MN 所在的2O 的圆心，如图，以MN 为边在O 内作等边三角形2O MN ，连接2OO ，取2OO 的中点R ,过R 作2OO 的垂线l ，则l 即为反射轴,反射轴l 未经过的区域是以O 为圆心OR 为半径的圆，反射轴l 是该圆的切线，求得半径为1算即可；（4）根据（2）的方法找到MN 所在的圆心3O ,当M 点在圆上运动一周时，如图，取3OO 的中点1A ，OT 的中点S ，即3OO 的中点1A 在以S l 与y 轴交点的纵坐标y 的取值范围【详解】（1）O 的半径为1，则O 的最长的弦长为2根据两点的距离可得2,EF CD EF ===2,2,2EF CD EF ∴<<>故符合题意的“反射线段”有2条；故答案为：2（2）①如图，过点B 作BO y '⊥轴于点O '，连接11A BA 点坐标为（0，2），B 点坐标为（1，1），∴AB ==45BAO '∠=︒，(0,1)O 'O 的半径为1，1190AOB ∠=︒11A B ∴1145B A O =︒线段AB 是⊙O 的以直线l 为对称轴的“反射线段”，()00O ，，(0,1)O ' 1(0,)2M ∴ ②由①可得当0S =时，y M 1=2如图，设当S 取得最大值时，过点1O 作1O P y ⊥轴，根据题意，122,,O A B 分别为沿直线y ＝x 的方向向上平移一段距离S 后,,O A B '的对应点，则1O P PO '=S =， (0,1)O '1(,1)O S S ∴+()222211221OO S S S S ∴=++=++ 过1OO 中点Q ，作直线l 1OO ⊥交y 轴于点M ,则l 即为反射轴1(,)22S S Q +∴ 12≤y M 136≤，136OM ∴= 11cos cos QO PO MOQ O OP OM OO ∠=∠== 即11112136OO S OO += 即()21113126OO S =+⨯ ∴()2113126S S S ++=+ 解得1252,6S S ==-（舍）02S ∴≤≤（3）1MN =∴1M N ''= O 的半径为1，则M N O ''是等边三角形，根据圆的旋转对称性，找到MN 所在的2O 的圆心，如图，以MN 为边在O 内作等边三角形2O MN ，连接2OO ，取2OO 的中点R ,过R 作2OO 的垂线l ，则l 即为反射轴, ∴反射轴l 未经过的区域是以O 为圆心OR 为半径的圆，反射轴l 是该圆的切线222OO ∴==2112OR OO ∴==∴当M 点在圆上运动一周时，求反射轴l 未经过的区域的面积为2191=16ππ⎛⎛ ⎝⎭⎝⎭．（4）如图，根据（2）的方法找到MN 所在的圆心3O ,设(2,0)T则TM =2MN =3O MN 是等腰直角三角形3O L ML ∴,TL ∴==3TO ∴=当M 点在圆上运动一周时，如图，取3OO 的中点1A ，OT 的中点S ，1SA ∴是3OO T 的中位线1312SA O T ∴==,13SA TO ∥即3OO 的中点1A 在以S∴若MN 是⊙O 的以直线l 为对称轴的“反射线段”，则l 为S 的切线设S 与y 轴交于点,C D 112OS OT ==，1SC SA =1OC ∴=同理可得1OD =∴反射轴l 与y 轴交点的纵坐标y 的取值范围为1y >或1y <-【点睛】本题考查了中心对称与轴对称，圆的相关知识，切线的性质，三角形中位线定理，余弦的定义，掌握轴对称与中心对称并根据题意作出图形是解题的关键．5、（1）（-b ，-12b 2）；（2）①直角三角形，见解析；②94≤Δ≤3 【分析】（1）y =12x 2+bx =12（x +b ）2-12b 2，即可求解；（2）①求出抛物线的表达式为y=12x2，联立y=12x2和y=kx+2并整理得：x2-2kx-4=0，证明△ADO∽△OEB，即可求解；②△AOB的外心为M，则点M是AB的中点，MP是梯形BADG的中位线，则m=k2+2，进而求解．【详解】解：（1）∵y=12x2+bx=12（x+b）2-12b2，∴抛物线的顶点Q坐标为（-b，-12b2）；（2）①∵抛物线与x轴只有一个公共点，∴△=b2-4×12×0=0，解得b=0，∴抛物线的表达式为y=12x2，如下图，分别过点A、B作x轴的垂线，垂足分别为D、G，设经过点（0，2）的直线的表达式为y=kx+2，联立y=12x2和y=kx+2并整理得：x2-2kx-4=0，则x1+x2=2k，x1x2=-4，∴y1=12x12，y2=12x22，则y1y2=14x12x22=4=-x1x2，∵AD=y1，DO=-x1，BE=y2，OE=x2，∴AD OD OE BE，∴∠ADO=∠BEO=90°，∴△ADO∽△OEB，∴∠AOD=∠OBE，∵∠OBG+∠BOG=90°，∴∠BOG+∠AOD=90°，即AO⊥BO，∴△AOB为直角三角形；②过点A作x轴的平行线交EB的延长线于点H，过点M作MN与y轴平行，交AH于N，∵△AOB的外心为M，MN∥y轴∥BH，∴点M是AB的中点，MP是梯形ABGD的中位线，∴MP=12（AD+BG）=12（y2+y1），则m=MP=12（y1+y2）=12（kx1+2+kx2+2）=12[k（x1+x2）+4]=k2+2，令y=kx+2=0，解得x=-2k，即点K的坐标为（-2k，0），由题意得：2≤-2k≤4，解得-1≤k≤12且k≠0，∴94≤k2+2≤3，即点M的纵坐标m的取值范围94≤m≤3．【点睛】本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．。

2022-2023学年北师大版九年级数学下册第三章圆《3-1—3-5》综合测试题(附答案)

2022-2023学年北师大版九年级数学下册第三章圆《3.1—3.5》综合测试题（附答案）一．选择题（共8小题，满分40分）1．如图，AB是⊙O的直径，点D，C在⊙O上，∠DOC＝90°，AD＝，BC＝1，则⊙O 的半径为（）A．B．C．D．2．如图，AB为⊙O的直径，C为半圆的中点，E为上一点，CE＝，AB＝，则EB的长为（）A．B．2C．D．3．如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AD＝DC，分别延长BA、CD，交点为E，作BF⊥EC，并与EC的延长线交于点F．若AE＝AO，BC＝6，则CF的长为（）A．B．C．D．4．如图，AB是半⊙O的直径，点C是半圆弧的中点，点D是弧BC的中点，下列结论中：①∠CBD＝∠DAB；②CG＝CH；③AH＝2BD；④BD2+GD2＝AG2；⑤AG＝DG．其中正确的结论有（）A．2个B．3个C．4个D．5个5．如图，在半径为5的⊙O内有两条互相垂直的弦AB和CD，AB＝8，CD＝8，垂足为E．则tan∠OEA的值是（）A．1B．C．D．6．如图，⊙O的直径AB与弦CD相交于点P，且∠APC＝45°，若PC2+PD2＝8，则⊙O 的半径为（）A．B．2C．2D．47．如图，点C是半圆O的中点，AB是直径，CF⊥弦AD于点E，交AB于点F，若CE＝1，EF＝，则BF的长为（）A．B．1C．D．8．如图，半径为R的⊙O的弦AC＝BD，且AC⊥BD于E，连接AB、AD，若AD＝，则半径R的长为（）A．1B．C．D．二．填空题（共8小题，满分40分）9．如图，AB为⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD＝OA，CD的延长线交⊙O于点E，若∠C＝23°，则∠EOB的度数为．10．如图，在四边形ABCD中，∠BAD＝∠CDA＝90°，AB＝1，CD＝2，过A，B，D三点的⊙O分别交BC，CD于点E，M，下列结论：①DM＝CM；②；③⊙O的直径为2；④AE＝AD．其中正确的结论有（填序号）．11．如图，在⊙O中，弦BC，DE交于点P，延长BD，EC交于点A，BC＝10，BP＝2CP，若＝，则DP的长为．12．如图，AB，CD是⊙O的两条弦，它们相交于点P，连接AD、BD，已知AD＝BD＝4，PC＝6，那么CD的长是．13．如图，已知A、B、C是⊙O上的三个点，且AB＝15cm，AC＝3cm，∠BOC＝60度．如果D是线段BC上的点，且点D到直线AC的距离为2cm，那么BD＝cm．14．如图，在△ABC中，tan∠BAC•tan∠ABC＝1，⊙O经过A、B两点，分别交AC、BC 于D、E两点，若DE＝10，AB＝24，则⊙O的半径为．15．如图，已知在Rt△ABC中，∠ACB＝90°，cos B＝，BC＝3，P是射线AB上的一个动点，以P为圆心，P A为半径的⊙P与射线AC的另一个交点为D，直线PD交直线BC 于点E．设线段BE的中点为Q，射线PQ与⊙P相交于点F，点P在运动过程中，当PE ∥CF时，则AP的长为．16．如图，在平行四边形ABCD中，以对角线AC为直径的圆O分别交BC，CD于点E，F．若AB＝13，BC＝14，CE＝9，则线段EF的长为．三．解答题（共4小题，满分40分）17．如图，⊙O的直径MN⊥弦AB于C，点P是AB上的一点，且PB＝PM，延长MP交⊙O 于D，连接AD．（1）求证：AD∥BM；（2）若MB＝6，⊙O的直径为10，求sin∠ADP的值．18．如图，在△ABC中，AB＝AC，∠BAC＝90°，以AB为直径的⊙O交BC于点F，连接OC，过点B作BD∥OC交⊙O于点D．连接AD交OC于点E（1）求证：BD＝AE．（2）若OE＝1，求DF的值．19．已知A，B，C，D是⊙O上的四个点．（1）如图1，若∠ADC＝∠BCD＝90°，AD＝CD，求证：AC⊥BD；（2）如图2，若AC⊥BD，垂足为E，AB＝2，DC＝4，求⊙O的半径．20．如图，半径为2的⊙O内有互相垂直的两条弦AB、CD相交于P点．（1）求证：P A•PB＝PC•PD；（2）设BC的中点为F，连接FP并延长交AD于E，求证：EF⊥AD；（3）若AB＝8，CD＝6，求OP的长．参考答案一．选择题（共8小题，满分40分）1．解：如图延长DO交⊙O于E，作EF⊥CB交CB的延长线于F，连接BE、EC．∵∠AOD＝∠BOE，∴＝，∴AD＝BE＝，∵∠DOC＝∠COE＝90°，OC＝OB＝OE，∴∠OCB＝∠OBC，∠OBE＝∠OEB，∴∠CBE＝（360°﹣90°）＝135°，∴∠EBF＝45°，∴△EBF是等腰直角三角形，∴EF＝BF＝1，在Rt△ECF中，EC＝＝＝，∵△OCE是等腰直角三角形，∴OC＝＝．故选：C．2．解：连接AC、BC，延长BE，过C作CH⊥BE的延长线于H，∵AB为⊙O的直径，C为半圆的中点，∴∠ACB＝90°，AC＝BC，∴∠CAB＝45°，∴∠2＝135°，∴∠1＝45°，∵CH⊥BE，∴∠CHE＝90°，∴∠HCE＝45°，∴CH＝HE，∵CE＝，∴CH＝HE＝1，∵AB＝，∴BC＝，∴BH＝＝3，∴EB＝3﹣1＝2，故选：B．3．解：如图，连接AC，BD，OD，∵AB是⊙O的直径，∴∠BCA＝∠BDA＝90°．∵BF⊥EC，∴∠BFC＝90°，∵四边形ABCD是⊙O的内接四边形，∴∠BCF＝∠BAD，∴Rt△BCF∽Rt△BAD，∴＝，即＝，∵OD是⊙O的半径，AD＝CD，∴OD垂直平分AC，∴OD∥BC，∴＝，∴△EOD∽△EBC，∴＝＝，＝，而AE＝AO，即OE＝2OB，BE＝3OB，BC＝6∴＝＝＝，＝2，∴OD＝4，CE＝DE，又∵∠EDA＝∠EBC，∠E公共角，∴△AED∽△CEB，∴DE•EC＝AE•BE，∴DE•DE＝4×12，∴DE＝4，∴CD＝2，则AD＝2，∴＝，∴CF＝．故选：A．4．解：连接BG，延长BD交AC的延长线于T．∵AB是直径，∴∠ACB＝90°，∵＝，∴AC＝CB，OC⊥AB，∴∠ACO＝∠BCO＝45°，∠CAB＝∠CBA＝45°，∵＝，∴∠CBD＝∠DAB＝∠CAD，故①正确，∵∠CGH＝∠ACG+∠CAG＝45°+∠CAG，∠CHG＝∠CBO+∠DAB＝45°+∠DAB，∴∠CGH＝∠CHG，∴CG＝CH，故②正确，∵∠ACH＝∠BCT＝90°，AC＝CB，∠CAH＝∠CBT，∴△ACH≌△BCT（ASA），∴AH＝BT，∵AB是直径，∴∠ADB＝∠ADT＝90°，∴∠DAB+∠ABD＝90°，∠CAD+∠T＝90°，∴∠T＝∠ABD，∴AT＝AB，∵AD⊥BT，∴BD＝DT，∴AH＝2BD，∵OC⊥AB，OA＝OB，∴GA＝GB，∵∠GDB＝90°，∴BD2+DG2＝BG2＝AG2，故④正确，∵GA＝GB，∴∠GAB＝∠GBA，∵∠CAB＝45°，∠CAD＝∠DAB＝∠CBD，∴∠GAO＝∠GAB＝∠CBD＝22.5°，∵∠CBA＝45°，∴∠CBG＝22.5°，∴∠DBG＝45°，∴△DBG是等腰直角三角形，∴BG＝AG＝DG，故⑤正确，故选：D．5．解：作OM⊥AB于M，ON⊥CD于N，连接OB，OD，由垂径定理得：BM＝AM＝AB＝4，DN＝CN＝CD＝4，由勾股定理得：OM＝＝＝3，同理：ON＝3，∵弦AB、CD互相垂直，OM⊥AB，ON⊥CD，∴∠MEN＝∠OME＝∠ONE＝90°，∴四边形MONE是矩形，∴ME＝ON＝3，∴tan∠OEA＝＝1，故选：A．6．解：作CM⊥AB于M，DN⊥AB于N，连接OC，OD，∴∠NDP＝∠MCP＝∠APC＝45°又∵OC＝OD，∴∠ODP＝∠OCP，∵∠COM＝45°+∠OCD，∠ODN＝45°+∠ODC，∴∠NDO＝∠COM，在Rt△ODN与Rt△COM中，，∴Rt△ODN≌Rt△COM，∴ON＝CM＝PM，OM＝ND＝PN又∵OC2＝CM2+OM2，OD2＝DN2+ON2∴OC2＝CM2+PN2，OD2＝DN2+PM2∴OC2+OD2＝CM2+PN2+DN2+PM2＝PC2+PD2＝8∴OC2＝4，∴OC＝2，故选：B．7．解：如图，连接AC，BC，OC，过点B作BH⊥CF交CF的延长线于H，设OC交AD 于J．∵＝，∴AC＝BC，OC⊥AB，∵AB是直径，∴ACB＝90°，∴∠ACJ＝∠CBF＝45°，∵CF⊥AD，∴∠ACF+∠CAJ＝90°，∠ACF+∠BCF＝90°，∴∠CAJ＝∠BCF，∴△CAJ≌△BCF（ASA），∴CJ＝BF，AJ＝CF＝1+＝，∵OC＝OB，∴OJ＝OF，设BF＝CJ＝x．OJ＝OF＝y，∵∠AEC＝∠H＝90°，∠CAE＝∠BCH，CA＝CB，∴△ACE≌△CBH（AAS），∴EC＝BH＝1，∵∠ECJ＝∠FCO，∠CEJ＝∠COF＝90°，∴△CEJ∽△COF，∴＝＝，∴＝＝，∴EJ＝，∵BF＝CJ，∠H＝∠CEJ，∠CJE＝∠BFH，∴△BHF≌△CEJ（AAS），∴FH＝EJ＝，∵AE∥BH，∴＝，∴＝，整理得，10x2+7xy﹣6y2＝0，解得x＝y或x＝﹣y（舍弃），∴y＝2x，∴＝，解得x＝或﹣（舍弃）．∴BF＝，故选：A．8．解：∵弦AC＝BD，∴，∴，∴∠ABD＝∠BAC，∴AE＝BE；如图，连接OA，OD，∵AC⊥BD，AE＝BE，∴∠ABE＝∠BAE＝45°，∴∠AOD＝2∠ABE＝90°，∵OA＝OD，∴AD＝R，∵AD＝，∴R＝1，故选：A．二．填空题（共8小题，满分40分）9．解：∵CD＝OA，OA＝OD，∴CD＝OD，∵∠C＝23°，∴∠DOC＝∠C＝23°，∴∠EDO＝∠C+∠DOC＝46°，∵OD＝OE，∴∠E＝∠EDO＝46°，∴∠DOE＝180°﹣∠E﹣∠EDO＝88°，∵∠DOC＝23°，∴∠EOB＝180°﹣∠DOC﹣∠DOE＝180°﹣23°﹣88°＝69°，故答案为：69°．10．解：如下图，连接AM，连接MB，∵∠BAD＝∠CDA＝90°，∴AM过圆心O，而A、D、M、B四点共圆，∴四边形ADMB为矩形，而AB＝1，CD＝2，∴CM＝2﹣1＝1＝AB＝DM，即：①DM＝CM，正确；又AB∥CD，∴四边形ABMC为平行四边形，∴∠AEB＝∠MAE，＝，故②正确；∵四边形ADMB为矩形，∴AB＝DM，∴＝，∴∠DAM＝∠AMB，过点O作OG⊥AD于G，OH⊥AE于H，∴OG＝OH，∴AD＝AE，∴④正确；由题设条件求不出直径的大小，故③⊙O的直径为2，错误；故答案为①②④．11．解：如图，作CH∥DE交AB于H．设DP＝2a．∵PD∥CH，∴＝＝＝，∴CH＝3a，∵BD：AD＝2：3，∴BD：AD＝BD：BH，∴AD＝BH，∴BD＝AH，∴AH：AD＝2：3，∴CH∥DE，∴＝＝，∴DE＝a，∴PE＝a﹣2a＝a，∵BC＝10，BP：PC＝2：1，∴PB＝，PC＝，∵PB•PC＝PD•PE，∴5a2＝，∴a＝（负根已经舍弃），∴PD＝2a＝．故答案为．12．解：连接AC，由圆周角定理知，∠C＝∠B，∵AD＝BD∴∠B＝∠DAB，∴∠DAP＝∠C∴△DAP∽△DCA，∴AD：CD＝DP：AD，得AD2＝DP•CD＝CD•（CD﹣PC），把AD＝4，PC＝6代入得，CD＝8．13．解：作DE⊥AC于E，BF⊥AC于F∵∠BOC＝60°，∴∠A＝30°在Rt△ABF中，AB＝15cm∴BF＝cm，AF＝cm∴CF＝AF﹣AC＝cm在Rt△BCF中，BC＝＝3cm ∵DE∥BF∴＝设BD＝x，则＝解得x＝，即BD＝cm．14．解：如图，延长AO交⊙O于H，连接AE，BH．∵tan∠BAC•tan∠ABC＝1，∴∠BAC+∠ABC＝90°，∴∠C＝90°，∴∠CAE+∠AEC＝90°，∵∠AEC+∠AEB＝180°，∠AEB+∠H＝180°，∴∠AEC＝∠H，∵∠H+∠BAH＝90°，∴∠CAE＝∠BAH，∴＝，∴DE＝BH＝10，∵AH是直径，∴∠ABH＝90°，∴AH＝＝＝26，∴OA＝OH＝AH＝13，故答案为13．15．解：如图，连接CF，过点P作PG⊥AC于G，设P A＝x．在Rt∠ACB中，∵ACB＝90°，BC＝3，cos B＝＝，∴AB＝5，AC＝＝＝4，∵PG⊥AD，∴AG＝DG＝P A•cos∠BAC＝x，∴AD＝x，CD＝4﹣x，∵∠ABC+∠A＝90°，∠PEC+∠CDE＝90°，∵∠A＝∠PDA，∴∠ABC＝∠PEC，∵∠ABC＝∠EBP，∴∠PEC＝∠EBP，∴PB＝PE，∵点Q为线段BE的中点，∴PQ⊥BC，∴PQ∥AC∴当PE∥CF时，四边形PDCF是平行四边形，∴PF＝CD，当点P在边AB的上时，x＝4﹣x，x＝，当点P在边AB的延长线上时，x＝x﹣4，x＝，综上所述，当PE∥CF时，AP的长为或．16．解：如图，连接AE，AF．∵BC＝14，CE＝9，∴BE＝BC﹣EC＝14﹣9＝5，∵AC是直径，∴∠AEC＝∠AEB＝90°，∴AE＝＝＝12，∴AC＝＝＝15，∵四边形ABCD是平行四边形，∴AD∥BC，AB＝CD＝13，∴∠DAC＝∠ACB，∵∠AFE＝∠ACB，∴∠AFE＝∠DAC，∵∠AEF＝∠ACD，∴△AFE∽△DAC，∴＝，∴＝，∴EF＝，故答案为．三．解答题（共4小题，满分40分）17．（1）证明：∵PB＝PM，∴∠PMB＝∠PBM，∵∠PBM＝∠D，∴∠PMB＝∠D，∴AD∥BM．（2）解：连接OB，设OC＝x，BC＝y，∵MN⊥AB，∴∠BCO＝∠BCM＝90°，则有，解得x＝，∴MC＝5﹣＝，由（1）可知，∠ADP＝∠ABM，∴sin∠ADP＝sin∠ABM＝＝＝．解法二：设MC＝x，在直角三角形MCB和OCB中，利用勾股定理可以得到x的值，从而求出角D的正弦值．18．（1）证明：∵AB是直径，∴∠ADB＝90°，∵BD∥OC，∴∠AEO＝∠ADB＝90°，∵∠OAC＝90°，∴∠OAE+∠AOC＝90°，∠AOC+∠ACO＝90°，∴∠BAD＝∠ACE，∵AB＝AC，∠ADB＝∠AEC＝90°，∴△ADB≌△CEA（AAS），∴AE＝BD．（2）∵OE∥BD，AO＝OB，∴AE＝ED，∴BD＝2OE＝2，∴AE＝BD＝DE＝2，∴AB＝＝2，∵△ADB≌△CEA，∴EC＝AD＝4，设AD交BC于K．∵EC∥BD，∴＝＝2，∴DK＝，∴BK＝＝，∵∠ABK＝∠FDK，∠AKB＝∠FKD，∴△AKB∽△FKD，∴＝，∴＝，∴DF＝．19．解：（1）∵∠ADC＝∠BCD＝90°，∴AC、BD是⊙O的直径，∴∠DAB＝∠ABC＝90°，∴四边形ABCD是矩形，∵AD＝CD，∴四边形ABCD是正方形，∴AC⊥BD；（2）连接DO，延长交圆O于F，连接CF、BF．∵DF是直径，∴∠DCF＝∠DBF＝90°，∴FB⊥DB，又∵AC⊥BD，∴BF∥AC，∠BDC+∠ACD＝90°，∵∠FCA+∠ACD＝90°∴∠BDC＝∠FCA＝∠BAC∴四边形ACFB是等腰梯形，∴CF＝AB．根据勾股定理，得CF2+DC2＝AB2+DC2＝DF2＝20，∴DF＝，∴OD＝，即⊙O的半径为．20．（1）证明：∵∠A、∠C所对的圆弧相同，∴∠A＝∠C，∴Rt△APD∽Rt△CPB，∴，∴P A•PB＝PC•PD；（2）证明：∵F为BC的中点，△BPC为直角三角形，∴FP＝FC，∴∠C＝∠CPF．又∠C＝∠A，∠DPE＝∠CPF，∴∠A＝∠DPE．∵∠A+∠D＝90°，∴∠DPE+∠D＝90°，∴EF⊥AD；（3）解：作OM⊥AB于M，ON⊥CD于N，连接PO，∴OM2＝（2）2﹣42＝4，ON2＝（2）2﹣32＝11，易证四边形MONP是矩形，∴OP＝．。

2023年北师大版九年级数学下册第三章《圆》复习检测试卷附答案解析

2023年九年级数学下册第三章《圆》复习检测试卷一、单选题1．如图，AB 是⊙O 的直径，点C ，D 在⊙O 上，且点C ，D 在AB 的异侧，连接AD ，BD ，OD ，OC ，若∠ABD ＝15°，且AD ∥OC ，则∠BOC 的度数为（）A ．120°B ．105°C ．100°D ．110°2．如图，⊙O 的直径BC=12cm ，AC 是⊙O 的切线，切点为C ，AC=BC ，AB 与⊙O 交于点D ，则 CD的长是（）A ．πcmB ．3πcmC ．4πcmD ．5πcm 3．已知⊙O 的半径为3，点P 到圆心O 的距离为4，则点P （）A ．在⊙O 内B ．在⊙O 上C ．在⊙O 外D ．无法确定4．三角板ABC 中，∠ACB=90°，∠B=30°，AC=2，三角板绕直角顶点C 逆时针旋转，当点A 的对应点A′落在AB 边的起始位置上时即停止转动，则B 点转过的路径长为（）A ．32πB πC ．2πD ．3π5．如图，ABC 中，8AB AC ==，BC =BC 边上一点O 为圆心作O ，分别与AB ，AC 相切于点D ，E ，则AD 的长为（）A ．4.5B ．5C ．5.5D ．66．如图，四边形ABCD 的顶点B ，C ，D 都在A 上，//AD BC ，140BAD ∠=︒，3AC =，则 BC的弧长为（）A ．53πB ．52πC ．32πD ．56π7．如图，在扇形纸片OAB 中，10,36,OA AOB OB =∠=︒在桌面内的直线l 上.现将此扇形在直线l 上按顺时针方向旋转（旋转过程中无滑动），当OA 落在l 上时，停止旋转.则点O 所经过的路线长为（）A ．13πB ．12πC ．11πD ．10π8．如图，⊙O 是Rt △ABC 的外接圆，∠ACB ＝90°，过点C 作⊙O 的切线，交AB 的延长线于点D.设∠A ＝α，∠D ＝β，则（）A ．α﹣βB ．α+β＝90°C ．2α+β＝90°D ．α+2β＝90°9．两直角边分别为15和20的直角三角形的外接圆半径为（）A ．12.5B ．25C ．20D ．1010．如图，在平面直角坐标系中，已知⊙A 经过点E ，B ，O ，C 且点O 为坐标原点，点C 在y 轴上，点E 在x 轴上，A （﹣3，2），则cos ∠OBC 的值为（）A ．23B ．13C ．13D ．211．如图，四边形ABCD 是⊙O 的内接四边形，⊙O 的半径为4，∠B=135°，则 AC 的长（）A．4πB．2πC．πD．2 3π12．如图，在平面直角坐标系中，动点A、B分别在x轴上和函数y=x的图象上，AB＝4，CB⊥AB，BC ＝2，则OC的最大值为（）A．22＋2B．22＋4C．25D．25＋2二、填空题13．如图，AB为⊙O的直径，C，D为⊙O上两点，若∠BCD=40°，则∠ABD的大小为.14．如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，能完全覆盖这个平面图形的圆面的最小半径是mm．15．如图，MN是⊙O的直径，若∠A=10°，∠PMQ=40°，以PM为边作圆的内接正多边形，则这个正多边形是边形．16．如图，已知点C是弧AB上的一点，圆周角∠ACB为125°，则圆心角∠AOB=度.17．如图，在△ABC中，∠C=90°，AC=BC，斜边AB=2，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF，弧EF经过点C，则图中阴影部分的面积为．三、解答题18．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，求线段OE的长．19．如图，等腰三角形ABC中，BA=BC，以AB为直径作圆，交BC于点E，圆心为O．在EB上截取ED=EC，连接AD并延长，交⊙O于点F，连接OE、EF．（1）试判断△ACD的形状，并说明理由；（2）求证：∠ADE=∠OEF．20．已知：如图，∠PAC=30°，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O交射线AP于E、F两点，求圆心O到AP的距离及EF的长．21．如图，⊙O的直径AB垂直弦CD于点E，AB＝8，∠A＝22.5°，求CD的长．22．已知：如图，∠PAC=30o，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O，交射线AP于E、F两点，求圆心O到AP的距离及EF的长．23．如图，直线y=333x 与x轴、y轴分别相交于A，B两点，圆心P的坐标为(1，0)，圆P与y轴相切于点O.若将圆P沿x轴向左移动，当圆P与该直线相交时，求横坐标为整数的点P的个数.答案解析部分1．B2．B3．C4．C5．A6．A7．B8．9．A 10．B11．B12．A 13．50°14．5015．616．11017．4π﹣1218．解：连接OC ，∵弦CD ⊥AB ，∴CE=12CD=8，在Rt △OCE 中，OE==6．19．【答案】解：（1）△ACD 是等腰三角形．理由：连接AE ，∵AB 是⊙O 的直径，∴∠AED=90°，∴AE ⊥CD ，∵CE=ED ，∴AC=AD ，∴△ACD 是等腰三角形；（2）证明：∵∠ADE=∠DEF+∠F ，∠OEF=∠OED+∠DEF ，而∠OED=∠B ，∠B=∠F ，∴∠ADE=∠OEF ．20．【答案】解：过点O 作OG ⊥AP 于点G连接OF ∵DB=10cm ，∴OD=5cm ∴AO=AD+OD=3+5=8cm∵∠PAC=30°∴OG=12AO=cm∵OG ⊥EF ，∴EG=GF∵GF=cm ∴EF=6cm ．21．【答案】解：∵AB=8，∴OC=OA=4，∵∠A=22.5°，∴∠COE=2∠A=45°，∴CE=OE∵直径AB 垂直弦CD 于E ，∴222CE OE OC +=，即2216CE =∴CE =，∴CD ＝．22．【答案】解：过点O 作OG ⊥AP 于点G ，连接OF ，解直角三角形OAG 可得OG ，AG 的值，然后再利用垂径定理求EF 的值．23．【答案】解：∵直线y=3x +与x 轴、y 轴分别相交于A ，B 两点，∴A 点的坐标为(-3，0)，B 点的坐标为(0，)，∴AB=2.如图，将圆P 沿x 轴向左移动，当圆P 与该直线相切于C 1时，连结P 1C 1，则P 1C 1=1，易知△AP 1C 1∽△ABO ，=，∴AP 1=2，∴P 1的坐标为(-1，0)，同理可得P 2的坐标为(-5，0).-5与-1之间的整数(不含-5和-1)有：-4，-3，-2，故满足题意的点P 的个数是3\。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、选择题1．如图，EM 经过圆心O ，EM ⊥CD 于M ，若CD=4，EM=6，则弧CED 所在圆的半径为（）A ．3B ．4C ．83D ．1032．下列命题说法正确的有（）①三点确定一个圆；②长度相等的弧是等弧；③等边三角形都相似；④直角三角形都相似；⑤平分弦的直径垂直于弦．⑥一条弧所对的圆周角等于它所对的圆心角的一半．A ．1个B ．2个C ．3个D ．4个 3．如图，AB 是⊙O 的直径，∠BOD =120°，点C 为弧BD 的中点，AC 交OD 于点E ，DE =1，则AE 的长为（）A ．3B ．5C ．23D ．25 4．如图，AB 是O 的直径，8AB =，点C 、D 、E 在O 上，45CAB ∠=︒，CD DE EB ==，P 是直径AB 上的一动点，则PCE 周长的最小值为（）A ．243+B ．43+C ．83+D ．12 5．如图，O 是ABC 的外接圆，其半径为3cm ，若3BC cm =，则A ∠的度数是（）A ．10︒B ．15︒C ．20︒D ．30︒6．如图，在平面直角坐标系xOy 中，半径为2的⊙O 与x 轴的正半轴交于点A ，点B 是O 上一动点，点C 为弦AB 的中点，直线334y x =-与x 轴、y 轴分别交于点D E 、，则CDE △面积的最小值为（）A ．2B ．2.5C ．3D ．347．已知⊙O 的半径是一元二次方程2690x x -+=的解，且点O 到直线AB 的距离为2，则⊙O 与直线AB 的位置关系为( )A ．相交B ．相切C ．相离D ．无法确定 8．已知O 的半径为8cm ，如果一点P 和圆心O 的距离为8cm ，那么点P 与O 的位置关系是（）A ．点P 在O 内B ．点P 在O 上C ．点P 在O 外D ．不能确定 9．如图，AB 为半圆O 的直径，C 是半圆上一点，且60COA ∠=º，设扇形AOC 、COB △、弓形BmC 的面积为1S 、2S 、3S ，则他们之间的关系是（）A ．123S S S <<B ．213S S S <<C ．132S S S <<D ．321S S S <<10．图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成，如果中间一块阴影的面积等于上下两块面积之和，则这两圆的公共弦长是（）A ．52B ．62C ．21252π-D ．21162π- 11．如图，四边形ABCD 中，对角线AC ，BD 交于点E ．若BAC BDC ∠=∠，则下列结论中正确的是（）①AE BE DE CE = ②ABE △与DCE 的周长比为BE CE③ADE ABC =∠∠ ④ABE DCE ADE BCE SS S S ⋅=⋅ A ．③④B ．①②③C ．①②④D ．①②③④ 12．如图，点,,A B C 为O 上三点，40OAB ∠=︒，则ACB ∠的度数等于（）A ．100︒B ．80︒C ．50︒D ．40︒二、填空题13．圆锥的底面半径是13_____． 14．如图，AB 、CD 是O 的两条弦，连接AD 、BC ．若60BAD ∠=︒，则BCD ∠的度数为______度．15．如图，ABC 内接于O ，∠BAC=70°，D 是BC 的中点，且∠AOD=156°，AE ，CF 分别是BC ，AB 边上的高，则∠BCF 的度数是____________．16．如图，在矩形ABCD 中，线段DF 平分ADC ∠交BC 边于点F ，点E 为BC 边上一动点，连接AE ，若在点E 移动的过程中，点B 关于AE 所在直线的对称点有且只有一次落在线段DF 上，则:BC AB =_____________．17．已知扇形的圆心角为120°，半径为3cm ，则这个扇形的面积为_____cm 2． 18．如图，PA ，PB 是圆O 的切线，切点为A 、B ，∠P ＝50°，点C 是圆O 上异于A ，B 的点，则∠ACB 等于_____．19．一个边长为4的正多边形的内角和是其外角和的2倍，则这个正多边形的半径_______．20．如图，在平面直角坐标系中，过点()11,0A 作x 轴的垂线交直线y x =于点B ，以О为圆心，1OB 为半径作弧，交x 轴于点2A ；过点2A 作x 轴的垂线交直线y x =于点2B ，以O 为圆心，2OB 为半径作弧，交x 轴于点3A ；过点3A 作x 轴的垂线交直线y x =于点3B ，以О为圆心，3OB 为半径作弧，交x 轴于点4A ，……，按此做法进行下去，设由11A B ，12A A ，弧21A B 围成的图形面积记为1S ，由22A B ，23A A ，弧32A B 围成的图形面积记为2S ，由33A B ，34A A ，弧43A B 围成的图形面积记为3S ，……，那么2020S 为_______：三、解答题21．如图，已知AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 的延长线交于点P ，连接AC ，若CA ＝CP ，∠A ＝30°．（1）求证：CP 是⊙O 的切线；（2）若OA ＝1，求弦AC 的长．22．如图，AB 为⊙O 的直径，D 为AB 延长线上的点，AC 为弦，且∠A ＝∠D ＝30°．（1）求证：DC 是⊙O 的切线；（2）若⊙O 的半径为1cm ，求图中阴影部分的面积．23．如图，AB 是O 的弦，半径OE AB ⊥，交AB 于点,G P 为AB 延长线上一点，PC 与O 相切于点,C CE 与AB 交于点F ．（1）求证：PC PF =；（2）连接,OB BC ，若3//,32,tan 4OB PC BC P ==，求FB 的长．24．如图，AB 为O 的直径，点C 在O 上，AD 与过点C 的切线互相垂直，垂足为D ，连接BC 并延长，交AD 饿延长线于点E ．（1）求证：AE AB =；（2）若20AB =，16BC =，求CD 的长．25．已知EF 为O 的一条弦，OB EF ⊥交O 于点B ，A 是弦EF 上一点（不与E ，F 重合），连接BA 并延长交O 于点C ，过点C 作O 的切线交EF 的延长线于点D ．（1）如图1，若EF 在圆心O 的上方，且与OB 相交于点H ，求证：ACD △是等腰三角形；（2）如图2，若EF 是O 的直径，25AB =O 的半径为4，求线段DC 的长；（3）如图3，若EF 在圆心O 的下方，且与BO 的延长线相交于点H ，试判断线段DA ，DE ，DF 之间的数量关系，并说明理由．26．如图，AB 是O 的一条弦，⊥OD AB ，垂足为C ，OD 交O 于点D ，点E 在O 上．（1）若40AOD ∠=︒，求DEB ∠的度数；（2）若3OC =，5OA =，求弦AB 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】连接OC ，设弧CED 所在圆的半径为R ，则OC ＝R ，OM ＝6−R ，根据垂径定理求出CM ，根据勾股定理得出方程，求出即可．【详解】解：连接OC ，设弧CED 所在圆的半径为R ，则OC ＝R ，OM ＝6−R ，∵EM 经过圆心O ，EM ⊥CD 于M ，CD ＝4，∴CM ＝DM ＝2，在Rt △OMC 中，由勾股定理得：OC 2＝OM 2＋CM 2，R 2＝（6−R ）2＋22，R ＝103，故选：D ．【点睛】本题考查了勾股定理，垂径定理的应用，用了方程思想，题目比较典型，难度适中． 2．B解析：B【分析】根据确定圆的条件对①进行判断；根据等弧的定义对②进行判断；根据相似三角形的判定对③④进行判断；根据垂径定理对⑤进行判断；根据圆周角定理对⑥进行判断．【详解】解：①不在同一直线上的三点确定一个圆，故①错误；②在同圆或等圆中，长度相等的弧是等弧，故②错误；③等边三角形的三个角都是60°，根据“两个三角形的两个角分别对应相等，则这两个三角形相似”可判定等边三角形都相似，故③正确；④直角三角形只有一个直角可以确定对应相等，其他条件不确定，故④错误；⑤平分弦（非直径）的直径垂直于弦，故⑤错误；⑥圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半，故⑥正确．故选B．【点睛】本题考查了确定圆的条件，等弧的定义，相似三角形的判定，垂径定理，圆周角定理等知识．熟练掌握基本知识是解题的关键．3．A解析：A【分析】连接AD，可证∠ODA=∠OAD=∠AOD=60°，根据弧中点，得出∠DAC=30°，△ADE是直角三角形，用勾股定理求AE即可．【详解】解：连接AD，∵∠BOD=120°，AB是⊙O的直径，∴∠AOD=60°，∵OA=OD，∴∠OAD=∠ODA =60°，∵点C为弧BD的中点，∴∠CAD=∠BAC=30°，∴∠AED=90°，∵DE=1，∴AD=2DE=2，AE==故选：A．【点睛】本题考查了圆周角的性质、勾股定理，解题关键是通过连接弦构造直角三角形，并通过弧相等导出30°角．4．B解析：B【分析】根据圆周角定理可知∠COB=90°，结合圆的对称性可知PCE 周长的最小值为CE C E '+，根据圆周角定理可得90CEC '∠=︒，再根据弧与圆心角的关系可知30CC E '∠=︒，解直角三角形即可．【详解】解：如下图所示，连接CO 并延长至C '，连接CE ，OE ，EC '，∵45CAB ∠=︒，∴∠COB=90°，∴C 点与C '点关于AB 所在直线对称，故当P 为EC '与AB 的交点时，PCE 周长的最小，此时CP PE C E '+=，∵CD DE EB ==， ∴1303BOE BOC ∠=∠=︒ ，60COE BOC BOE ∠=∠-∠=︒， ∴30CC E '∠=︒，∵CC '为直径，∴90CEC '∠=︒，8CC AB '==，∴2214,()432CE CC C E CC CE '''===-=， ∴PCE 周长为CE EP CP ++，最小值为443CE C E '+=+，故选：B ．【点睛】本题考查圆周角定理，弧、圆心角的关系，勾股定理，圆的对称性，含30°角的直角三角形．能结合圆的对称性正确作出辅助线是解题关键．5．D解析：D【分析】连接OB 、OC ，则判断△OBC 是等边三角形，则∠BOC=60°，再根据圆周角定理，即可得到答案．【详解】解：连接OB 、OC ，如图：∵3OB OC BC cm ===，∴△OBC 是等边三角形，∴∠BOC=60°，∴∠BAC=30°，故选：D ．【点睛】本题考查了圆周角定理，等边三角形的判定和性质，解题的关键是熟练掌握圆周角定理进行解题．6．A解析：A【分析】连接OB ,取OA 的中点M ，连接CM ，过点M 作MN DE ⊥于N ，先证明点C 的运动轨迹是以点(1,0)M 为圆心，1为半径的M ，设M 交MN 于点C '，解得直线DE 与坐标轴的交点，即可解得OD OE 、的长，再由勾股定理解得DE 的长，接着证明DNM DOE 解得MN 的长，最后当点C 与点C '重合时，此时CDE △面积的最小值，据此解题．【详解】解：如图，连接OB ,取OA 的中点M ，连接CM ，过点M 作MN DE ⊥于N ，,AC CB AM OM ==112MC OB ∴== C ∴的运动轨迹是以点(1,0)M 为圆心、半径为1的圆，设M 交MN 于点C '，直线DE 的解析式为334y x =-，令0x =，得3y =- (0,3)E ∴-令0y =，得4x =(4,0)D ∴3,4,OE OD ∴==3DM =22345DE ∴+=,MDN ODE MND DOE ∠=∠∠=∠DNM DOE ∴MN DM OE DE ∴= 335MN ∴= 95MN ∴= 94155C N '∴=-= 当点C 与点C '重合时，此时CDE △面积的最小值11452225DE C N '=⋅=⨯⨯= 故选：A ．【点睛】本题考查圆的综合题，涉及一次函数与坐标轴的交点、勾股定理、相似三角形的判定与性质等知识，是重要考点，难度一般，掌握相关知识是解题关键．7．A解析：A【分析】解方程确定圆的半径为3，圆心距d=2,比较半径与圆心距的大小，根据法则判断即可.【详解】∵2690x x-+=，∴123x x==，∴圆的半径为3，∵点O到直线AB的距离为2，即d=2，∴d＜R，∴直线与圆相交，故选A.【点睛】本题考查了用半径、圆心距判定直线和圆的位置关系，熟练解方程，熟记d，R法则是解题的关键.8．B解析：B【分析】根据点与圆的位置关系进行判断即可；【详解】∵圆的半径为8cm，P到圆心O的距离为8cm，即OP=8，∴点P在圆上故选：B．【点睛】本题考查了点与圆的位置关系，点与圆的位置关系有3种：设OO的半径为r，点P到圆心的距离OP=d，则有：点P在圆外→d>r；点P在圆上→d=r；点P在圆内→d<r；9．B解析：B【分析】设出半径，作出△COB底边BC上的高，利用扇形的面积公式和三角形的面积公式表示出三个图形面积，比较即可求解．【详解】解：作OD⊥BC交BC与点D，∵∠COA＝60°，∴∠COB ＝120°，则∠COD ＝60°．∴S 扇形AOC ＝22603606ππ=R R ； S 扇形BOC ＝221203603ππ=R R ．在三角形OCD 中，∠OCD ＝30°，∴OD ＝2R ，CD ＝3R ，BC ＝3R ， ∴S △OBC ＝23R ，S 弓形＝2233R R π-＝2(433)π-R ， 2(433)π-R ＞26πR ＞23R ， ∴S 2＜S 1＜S 3．故选：B ．【点睛】此题考查扇形面积公式及弓形面积公式，解题的关键是算出三个图形的面积，首先利用扇形公式计算出第一个扇形的面积，再利用弓形等于扇形﹣三角形的关系求出弓形的面积，进行比较得出它们的面积关系．10．D解析：D【分析】由题意得到四边形ABCD 为矩形，BC=2，再根据中间一块阴影的面积等于上下两块面积之和，得到BC•AB -（S 半圆AD +S 半圆BC -S ）=S ，即2AB-π•12+S=S ，可求出AB=2π，则OP=12AB=4π，在Rt △OEP 中，利用勾股定理可计算出EP ，即可得到两圆的公共弦长EF ．【详解】解：∵AB ，CD 为两等圆的公切线，∴四边形ABCD 为矩形，BC=2，设中间一块阴影的面积为S ，∵中间一块阴影的面积等于上下两块面积之和，∴BC•AB -（S 半圆AD +S 半圆BC -S ）=S ，即2AB-π•12+S=S ，∴AB=2π．如图，EF 为公共弦，PO ⊥EF ，OP=12AB=4π， ∴EP=22OE OF -=222161()4ππ--=， ∴EF=2EP=21162π-．故选：D ．【点睛】本题考查了垂径定理、勾股定理，公切线，连心线的性质，熟练掌握相关知识是解题的关键．11．C解析：C【分析】根据相似三角形可得①②正确，由四点共圆可知③不符合题意，面积比转化成边长比可得④正确．【详解】解：∵BAC BDC ∠=∠，AEB DEC ∠=∠∴ABE DCE ∴AE BE DE CE= ∴①正确；相似三角形周长比等于相似比，②正确∵BAC BDC ∠=∠，且△BDC 和△BAC 共有底BC∴得到A ，B ，C ，D 四点共圆；若ADE ABC =∠∠，则=ADE ABC ACB =∠∠∠，则AB=AC ，但题目中并没有告诉这个条件，所以③不一定正确；∵△ABE 和△ADE 共有高， ∴ABEADE SBE S DE =， ∵△CBE 和△CDE 共有高， ∴BCE DCE BE S DE S = ∴ABEBCEADE DCE S BE S S DE S ==即，ABE DCE ADE BCE S S S S ⋅=⋅，故 ④正确；∴①②④正确，选C.【点睛】此题主要考查了相似三角形的判断及其性质，解决本题的关键是合理作辅助圆，熟练掌握相似三角的性质定理．12．C解析：C【分析】根据等边对等角得到40OBA OAB ∠=∠=︒，利用三角形内角和可得100AOB ∠=︒，根据圆周角定理即可求解．【详解】解：∵OA OB =，∴40OBA OAB ∠=∠=︒，∴100AOB ∠=︒， ∴1502ACB AOB ∠=∠=︒，故选：C ．【点睛】本题考查圆周角定理，掌握圆周角定理是解题的关键．二、填空题13．180°【分析】先根据勾股定理求出圆锥的母线为2进而求得展开图的弧长然后根据弧长公式即可求解【详解】解：设圆锥的母线为a 根据勾股定理得：a ＝＝2设圆锥的侧面展开图的圆心角度数为n°根据题意得2π•1解析：180°【分析】先根据勾股定理求出圆锥的母线为2，进而求得展开图的弧长，然后根据弧长公式即可求解．【详解】解：设圆锥的母线为a ，根据勾股定理得：a 2，设圆锥的侧面展开图的圆心角度数为n °，根据题意得2π•1＝2180n π⋅⋅，解得n ＝180，即圆锥的侧面展开图的圆心角度数为180°．故答案为：180°．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长.14．【分析】利用同圆中同弧上的圆周角相等求解即可【详解】∵∴故答案为：60°【点睛】本题考查了圆的基本性质熟练掌握性质并灵活运用是解题的关键解析：【分析】利用同圆中，同弧上的圆周角相等求解即可．【详解】∵BAD ∠=BCD ∠，60BAD ∠=︒∴60BCD ∠=︒，故答案为：60°．【点睛】本题考查了圆的基本性质，熟练掌握性质并灵活运用是解题的关键．15．23°【分析】连接OBOC 根据垂径定理求出再根据角的性质计算出根据计算出从而能够求出最后根据⊥求出的大小【详解】连接OBOC ∵D 是BC 的中点∴∵∴∴∵⊥∴故答案为：【点睛】本题考查圆的垂径定理圆周角解析：23°【分析】连接OB 、OC ，根据垂径定理求出BOD ∠，再根据角的性质计算出AOB ∠，根据OA OB =计算出ABO ∠，从而能够求出ABC ∠，最后根据CF ⊥AB ，求出BCF ∠的大小．【详解】连接OB 、OC∵OB OC =，D 是BC 的中点 ∴1702BOD BOC BAC ===︒∠∠∠ 1567086AOB AOD BOD =-=︒-︒=︒∠∠∠∵OA OB =∴18086472ABO ︒-︒==︒∠ 907020OBC =︒-︒=︒∠∴472067ABC ABO OBC =+=︒+︒=︒∠∠∠∵CF ⊥AB∴90906723BCF ABC =︒-=︒-︒=︒∠∠故答案为：23︒【点睛】本题考查圆的垂径定理，圆周角和圆心角关系，以及直角三角形的性质，属于基础题． 16．：1【分析】先找到点B 关于AE 所在直线的对称点H 由直角三角形的性质可求解【详解】解：如图以点A 为圆心AB 为半径的圆与DF 相切于点H 则点H 为点B 关于AE 所在直线的对称点∴AB=AHAH ⊥DF ∵DF 平分解析：2：1【分析】先找到点B 关于AE 所在直线的对称点H ，由直角三角形的性质可求解．【详解】解：如图，以点A 为圆心，AB 为半径的圆与DF 相切于点H ，则点H 为点B 关于AE 所在直线的对称点，∴AB=AH ，AH ⊥DF ，∵DF平分∠ADC，∴∠ADF=∠CDF=45°，∴∠ADF=∠DAH=45°，∴AH=DH，∴AB，∴BC：：1，1．【点睛】本题考查了矩形的性质，轴对称的性质，直角三角形的性质，灵活运用这些性质解决问题是解题的关键．17．3π【分析】根据扇形的面积公式即可求解【详解】解：扇形的面积＝＝3πcm2故答案是：3π【点睛】本题考查了扇形的面积公式正确理解公式是解题的关键解析：3π【分析】根据扇形的面积公式即可求解．【详解】解：扇形的面积＝21203360π⨯＝3πcm2．故答案是：3π．【点睛】本题考查了扇形的面积公式，正确理解公式是解题的关键．18．65°或115°【分析】连接OAOB进而求出∠AOB=130°再分两种情况：当C在劣弧AB上当C在劣弧AB上理由圆周角定理和圆内接四边形的性质即可得出结论【详解】解：如图连接OAOB∵PAPB分别切解析：65°或115°．【分析】连接OA，OB，进而求出∠AOB=130°，再分两种情况：当C在劣弧AB上，当C在劣弧AB 上，理由圆周角定理和圆内接四边形的性质，即可得出结论．【详解】解：如图，连接OA、OB，∵PA、PB分别切⊙O于点A、B，则∠OAP＝∠OBP＝90°；在四边形APBO中，∠P＝50°，∴∠AOB＝360°﹣∠OAP﹣∠P﹣∠OBP＝360°﹣50°﹣90°﹣90°＝130°①当点C在优弧AB上时，∠ACB＝12∠AOB（同弧所对的圆周角是所对的圆心角的一半），∴∠ACB＝65°；当点C在劣弧AB上时，记作C'，由①知，∠ACB＝65°，∵四边形ACBC'是⊙O的内接四边形，∴∠AC'B＝180°﹣∠ACB＝180°﹣65°＝115°，故答案为：65°或115°．【点睛】本题考查了切线的性质，圆周角定理，圆内接四边形的性质，求出∠AOB是解本题的关键．19．【分析】先求出正多边形边数为6再根据正六边形性质即可求解【详解】解：设正多边形的边数为n由题意得解得n=6∴正多边形为正六边形∵边长为4的正六边形可以分成六个边长为4的正三角形∴该正多边形的半径等于解析：4【分析】先求出正多边形边数为6，再根据正六边形性质即可求解．【详解】解：设正多边形的边数为n，由题意得()21803602n-︒=︒⨯，解得 n=6∴正多边形为正六边形，∵边长为4的正六边形可以分成六个边长为4的正三角形，∴该正多边形的半径等于4．故答案为：4【点睛】本题考查了正多边形的相关概念，和正六边形的性质，熟知相关概念是解题关键．20．【分析】根据点A的取法罗列出部分点A的横坐标由此可发现规律即的横坐标为：再结合已知即可得到答案【详解】观察发现规律：的横坐标为：的横坐标为：的横坐标为：的横坐标为：的横坐标为：故答案为：【点睛】本题解析：20172018π-22【分析】根据点A的取法，罗列出部分点A的横坐标，由此可发现规律，即n A的横坐标为：)12n-，再结合已知即可得到答案．【详解】观察，发现规律：1A 的横坐标为：1，2A 的横坐标为：2，3A 的横坐标为：()22，⋯，∴n A 的横坐标为：()12n -n B ∴的横坐标为：()12n -()()()404020192019201720182020452122223602S ππ⨯⨯∴=-⨯⨯=⋅-故答案为：2017201822π⋅-．【点睛】本题考查了一次函数图像上点的坐标特征以及规律型中的点的变换，解题关键是找出n A 的横坐标为：()12n -这一规律．三、解答题21．（1）见解析；（2）AC ＝3．【分析】（1）连接OC ，由等腰三角形的性质得出∠A=∠ACO=30°，∠P=30°，求出∠ACP 的度数，则可求出答案；（2）连接BC ，由勾股定理可求出答案．【详解】解：（1）证明：连接OC ，如图1，∵OA ＝OC ，∠A ＝30°，∴∠A ＝∠ACO ＝30°，∵CA ＝CP ，∴∠A ＝∠P ＝30°，∴∠ACP ＝180°﹣∠A ﹣∠P ＝180°﹣30°﹣30°＝120°，∴∠OCP ＝∠ACP ﹣∠ACO ＝120°﹣30°＝90°，∴OC ⊥CP ，∴CP 是⊙O 的切线；（2）解：如图2，连接BC，∵OA＝OB＝1，∴AB＝2，∵AB是⊙O的直径，∴∠ACB＝90°，∵∠A＝30°，∴BC＝12AB＝1，∴AC＝22AB BC-＝3．【点睛】本题考查了切线的判定，等腰三角形的性质，勾股定理，圆周角定理，直角三角形的性质，熟练掌握切线的判定是解题的关键．22．（1）见解析；（2）36π-【分析】（1）连接OC．由圆周角定理得：∠COD＝2∠A ＝60°．根据三角形内角和可求∠OCD＝90°即可；（2）阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积即可．【详解】解：（1）证明：连接OC，∵∠A ＝∠D＝30°，由圆周角定理得：∠COD＝2∠A ＝60°．∴∠DCO＝180°﹣∠COD-∠D=180°-60°﹣30°＝ 90°，∴OC⊥CD．∵OC为半径，∴DC 是⊙O 切线．（2）在Rt △OCD 中，∠D ＝30°，OC ＝1cm ，∴OD ＝2cm ，由勾股定理得：DC ＝3cm ． ∴图中阴影部分的面积21601313236026OCD OB SS S 扇形C ．【点睛】此题综合考查了圆周角性质、切线的判定方法、扇形的面积计算方法，解题的关键是用割补法求引用面积阴影部分的面积OCD OB SS S 扇形C ．23．（1）见解析；（2）2FB =【分析】（1）由切线的性质可得∠OCP=90°，由等腰三角形的性质可得∠E=∠OCE ，可得∠CFP=∠FCP ，可得PC=PF ；（2）过点B 作BH ⊥PC ，垂足为H ，由题意可证四边形OCHB 是正方形，由勾股定理可得BH=CH=3，可求PH ，BP 的长，即可求BF 的长．【详解】解：（1）连接OC ．OE AB ⊥，90EGF ∴∠=︒． PC 与C 相切于点C ，90OCP ∠=︒，90E EFG OCF PCF ∴∠+∠=∠+∠=︒．OE OC =，E OCF ∴∠=∠，EFG PCF ∴∠=∠．EFG PFC ∠=∠，PCF PFC ∴∠=∠，PC PF ∴=．（2）过点B 作BH PC ⊥于点H ．//,90OB PC OCP ∠=︒，90BOC ∴∠=︒．OB OC =，∴四边形OCHB 是正方形，∴BH=CH ，∵BH2+CH 2=BC 2，BC=∴BH=CH=3，在Rt BHP 中，4tan BH PH P==， ∴PF=PC=3+4=7，5BP =，752FB ∴=-=．【点睛】本题考查了切线的性质，勾股定理，等腰三角形的性质，正方形的判定与性质，平行线的性质，以及锐角三角函数等知识，需要学生灵活运用所学知识．24．（1）见解析；（2）485CD =【分析】（1）连接AC 、OC ，由题意易得OC CD ⊥，进而可得//OC AE ，然后有2AE OC =，最后根据圆的基本性质可求解；（2）由题意及（1）可得12CE CB ==，20AE AB ==，进而可得12AC =，然后根据等积法可求解．【详解】（1）证明：连接AC 、OC ，∵CD 是O 的切线，∴OC CD ⊥，∵CD AE ⊥，∴//OC AE ，∵O 是AB 中点，∴OC 是ABE △的中位线，∴2AE OC =，∵22AB OA OC ==，∴AE AB =；（2）解：∵AB 是O 的直径，∴90ACB ∠=︒， ∵20AB =，16BC =，AB=AE∴16CE CB ==，20AE AB ==，∴在Rt △ACB 中，由勾股定理可得12AC =， ∵1122ACE S AE CD AC CE =⋅=⋅， ∴20CD 1612⨯=⨯， ∴485CD =．【点睛】本题主要考查切线的性质定理，熟练掌握切线的性质是解题的关键．25．（1）见解析；（2）线段DC 的长为3；（3）线段DA ，DE ，DF 之间的数量关系为2DA DE DF =⋅，理由见解析．【分析】（1）连接OC ，由题意易得OC DC ⊥，∠B=∠OCB ，则有9090DCA ACO B ∠=︒-∠=︒-∠，进而可得DAC DCA ∠=∠，然后问题可求证；（2）连接OC ，则OC DC ⊥，由勾股定理可得2AO =，由（1）可得DA DC =，设DC x =，则2OD x =+，然后再由勾股定理可求DC 的长；（3）连接CF ，CE ，连接CO 并延长交O 于点G ，连接GF ，由题意可得9090DCA OCB HBA ∠=︒-∠=︒-∠，则有DA DC =，进而可得CED DCF ∠=∠，然后有CDF EDC ∽△△，则根据相似三角形的性质及线段的等量关系可求解．【详解】（1）证明：如图，连接OC ，则OC DC ⊥，∵OB=OC ，∴∠B=∠OCB ，∴9090DCA ACO B ∠=︒-∠=︒-∠，又∵90DAC BAH B ∠=∠=︒-∠，∴DAC DCA ∠=∠，∴DA DC =，∴ACD △是等腰三角形；（2）如图，连接OC ，则OC DC ⊥，∵在Rt ABO △中，25AB =，O 的半径为4，∴2AO =，由（1）可得DA DC =，设DC x =，则2OD x =+，∴在Rt OCD △中，()22242x x +=+， ∴3x =，即线段DC 的长为3；（3）线段DA ，DE ，DF 之间的数量关系为2DA DE DF =⋅，理由：如图，连接CF ，CE ，连接CO 并延长交O 于点G ，连接GF ， ∵DC 为O 的切线，∴9090DCA OCB HBA ∠=︒-∠=︒-∠，又∵90BAH HBA ∠=︒-∠，CAD BAH ∠=∠，∴∠=∠DCA CAD ，∴DA DC =，∵CG 是O 的直径，∴90CFG ∠=︒，∴90CED CGF GCF ∠=∠=︒-∠，又∵90DCF GCF ∠=︒-∠，∴CED DCF ∠=∠，又∵D D ∠=∠，∴CDF EDC ∽△△， ∴DC DF DE DC=， ∴2DC DE DF =⋅，∴2DA DE DF =⋅．【点睛】本题主要考查相似三角形的性质及切线的性质定理，熟练掌握相似三角形的性质及切线的性质定理是解题的关键．26．（1）20°；（2）8【分析】（1）欲求DEB ∠，又已知一圆心角，可利用圆周角与圆心角的关系求解；（2）利用垂径定理可以得到142A C B C B A ===，从而得到结论．【详解】解：（1）OD AB ⊥，∴AD BD =，11402022DEB AOD ∴∠=∠=⨯︒=︒．（2）3OC =，5OA =，且⊥OD AB ，4AC ∴=，OD AB ⊥，∴12AD BD AB ==， 142AC BC AB ∴===， 8AB ∴=．【点睛】此题考查了圆周角与圆心角定理以及垂径定理，熟练掌握垂径定理得出4AC CB ==是解题关键．。