变量与函数经典例题
初中数学专题训练--变量函数--变量与函数经典例题
例1、下面的表分别给出了变量x 与y 之间的对应关系,判断y 是x 的函数吗?如果不是,解:(1)y 是x 的函数; (2)y 是x 的函数;(3)y 不是x 的函数,因为对于变量x=1,变量y 有1与-1两个值与它对应; (4)y 是x 的函数说明:对于x 的每一个值,y 都有唯一的值与它对应.第四个是常数函数它符合函数的定义. 例 2、判断下列关系是不是函数关系? (1)长方形的宽一定时,其长与面积; (2)等腰三角形的底边长与面积; (3)某人的年龄与身高; (4)关系式| y |=x 中的y 与x.分析:判断一个关系是不是函数关系,第一要看是不是一个变化过程;第二要看在这个变化过程中,是不是有两个变量;第三要看自变量每取一个确定值,函数是不是都有唯一确定的值与它对应. 解:(1)长方形的宽一定时,其长所取的每一个确定的值,面积都有唯一确定的值与它对应,所以长与面积是函数关系.(2)因为三角形的面积受底和高两个因素的影响,当等腰三角形的底取一个定值时,它的面积又受高的影响,不能有唯一确定的值和底相对应,所以底边长与面积不是函数关系.(3)人的任意一个确定的年龄,都有唯一确定的身高与之相对应,所以某人的年龄与身高是函数关系.(4)x 每取一个正值,y 都有两个值与它对应,所以| y | = x 不是函数关系.说明:年龄与身高的变化不按某种规律,但某人每一个确定的年龄,必有唯一确定的身高和它相对应,因此函数关系是一定的,所以不要以为存在一定比例关系或一定规律,能用解析式表示的才是函数关系.例 3、汽车由北京驶往相距850千米的沈阳,它的平均速度为80千米/小时,求汽车距沈阳的路程S (千米)与行驶时间t (小时)的函数关系式,写出自变量的取值范围.分析:北京距沈阳850千米,汽车距沈阳的路程等于全程减去已行驶的路程,已行驶的路程等于速度乘以时间. 解:85080S t =-0S t ≥⎧⎨≥⎩ 得850800tt -⎧⎨≥⎩850.8t ∴≤≤于是汽车距沈阳的路程S 与时间t 的函数关系式为85080S t =-,自变量t 的取值范围是850.8t ≤≤例 4、求下列函数中自变量x 的取值范围:(1)235y x =- (2)21y x =+ (3)22y x =- (4)2123x y x x -=--(5)y = (6)y =(7)y =(8)y =分析:求自变量的取值范围,应考虑自变量的取值使函数解析式有意义.(1)、(2)小题函数解析式是整式,故自变量可取任意实数;(3)、(4)小题解析式是分式,自变量可取使分母不为0的任意实数;(5)、(7)、(8)小题的解析式是二次根式,自变量取值应使被开方数非负;(6)小题既有分母又有二次根式,自变量取值应使分母不为0,又要使二次根式的被开方数非负. 解:(1)函数235y x =-的自变量x 的取值范围是躯体实数 (2)函数21y x =+的自变量x 的取值范围是躯体实数 (3)20,2,x x -=∴=∴当2x =时,分母20x -=,∴函数22y x =-的自变量的取值范围是2x ≠; (4)由2230x x --=解得123,1,x x ==-∴ 当3x =或1x =-时,分母2230x x --=,∴ 函数2123x y x x -=--的自变量x 的取值范围是3x ≠且1x ≠-(5)由230x -≥解得32x ≤,∴函数y =x 的取值范围是 32x ≤; (6)由30x +≥得3x ≥-,由20x +=得2x =-,当2x ≠-时,分母20x +≠,∴函数2y x =+的自变量x 的取值范围是3x ≥-且2x ≠-; (7)22224213(1)30,x x x x x ++=+++=++≥即对于任意实数x ,224x x ++都是非负的,∴函数y =x 的取值范围是全体实数;(8)由630,360x x -≥⎧⎨-≥⎩得112,122x x x ⎧≥⎪⎪∴=⎨⎪≤⎪⎩因此,函数y =x 的取值范围是12x =.典型例题五例 已知函数的图象经过A(1,4)、B(2,2)两点,请你写出满足上述条件的两个不同的函数解析式,并简要说明解答过程.(2002年山东省青岛市中考题)分析 :由于题中所经过A(1,4)、B(2,2)两点的函数解析式的类型未告知,因此所确定函数解析式的形式可能是直线型,也可能是双曲线、抛物线型,还可能是其他形状的,故可采用下列几种途径来确定满足题设条件的解析式:(1)若经过A 、B 两点的函数的图象是直线,设其解析式为b kx y +=,则有⎩⎨⎧+=+=.22,4b k b k 解之,得⎩⎨⎧=-=.6,2b k 此时,函数解析式为.62+-=x y(2)由于A 、B 两点的横、纵坐标的积相等,都等于4,所以,经过A 、B 两点的函数的图象还可以是双曲线,其解析式为:xy 4=. (3)如果经过A 、B 两点的函数的图象是抛物线,设其解析式为 c bx ax y ++=2(0≠a ),则有 ⎩⎨⎧++=++=.242,4c b a c b a解之,得⎩⎨⎧+=--=.6,23a c a b因此,只要a 、b 、c 同时满足关系式23--=a b 和62+=a c ,即可保证二次函数c bx ax y ++=2(0≠a )的图象经过A(1,4)、B(2,2)两点;显然,这样的二次函数有无数个.如取a =1,则有b =-5,c =8,相应图象所对应的二次函数的解析式为:852+-=x x y .(4)其他略.典型例题六例 (北京市海淀区,1999)如图,在矩形ABCD 中,P BC AB ,7,4==是BC 边上与B 点不重合的动点,过点P 直线交CD 的延长线于R ,交AD 于Q (Q 与D 不重合),且045=∠RPC 。
数学:《变量与函数(一)》同步典型例题分析专题(华东师大版八年级下)

初中数学同步典型例题分析专题:变量与函数(一)题1.判断下列变量之间的关系是否是函数关系:(1)下列关于变量x ,y 的关系:①023=-y x ,②152=-y x ,③x y 3=,④x y ±=中的y 与x ;(2)正方体中的棱长与表面积(3)下面的表分别给出了变量x 与y 之间的对应关系,判断y 是x 的函数吗? x 12 3 4 3 2 y1 12 2 23 (4)下面图象分别给出了变量x 与y 之间的对应关系,判断 y 是x 的函数吗?题2.求下列函数中自变量x 的取值范围:⑴x x y +=22; ⑵3+=x y ;⑶31-+=x x y ; ⑷11+-=x x y ; ⑸2-=x x y ; ⑹x x y -+-=33.⑺123--=x x y ;⑻1253-+-=x x y .题3.一个正方形的边长为5cm ,•它的边长减少xcm•后得到的新正方形的周长为ycm ,写了y 与x 的关系式,并指出自变量的取值范围.题 4.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km /h ,水流速度为5 km /h .轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t (h ),航行的路程为s (km ),则s 与t 的函数图象大致是( )题 5.矩形的面积为S ,则长a 和宽b 之间的关系为S = ,当长一定时, 是常量, 是变量.题6.函数11y x =+的自变量x 的取值范围是( ).A .1x >-B .1x <-C .1x ≠-D .1x ≠题7.已知水池中有800立方米的水,每小时抽50立方米.(1)写出剩余水的体积Q 立方米与时间t (时)之间的函数关系式.(2)写出自变量t 的取值范围.题8.小华的爷爷每天坚持体育锻炼,某天他慢步到离家较远的绿岛公园,打了一会儿太极拳后跑步回家.下面能反映当天小华的爷爷离家的距离y 与时间x 的函数关系的大致图象是( )以上课后练习答案及详解如下:题1.答案: (1)①③中y 是x 的函数 (2)是 (3)不是 (4)A 、C 、D 中y 是x 的函数,B 中y 不是x 的函数解析:判断两个变量之间是否函数关系,主要要抓住定义本身,即对于x 的每一个值,y 都有唯一的值与它对应.(1)①③中当x 取一个值时y 都有唯一的值与它对应同,故y 是x 的函数,而②④中当x 取一个值时y 不是唯一的值与它对应同,故不是函数关系;(2)正方形的表面积等于棱长平方的6倍,当棱长发生变化时,其表面积随之而变化,故它们是函数关系;(3)y 不是x 的函数,因为对于变量2=x ,变量y 有1与3两个值与之对应;(4)A 、C 、D 中当x 取一个值时,变量y 有唯一的值与之对应,但B 中当x 在其正半轴上任意取一个值时,变量y 却有两个值与之对应,故不是函数关系.题2.答案: (1)全体实数;(2)3-≥x ;(3)3≠x 且3-≠x ;(4)1- x ;(5)20≠≥x x 且;(6)3=x ;(7)51≠≥x x 且;(8)5321≤≤x . 解析:函数解析式以及函数自变量的实际意义确定自变量的取值范围是中考数学试卷中的一个考查热点,其中根据函数解析式确定自变量的取值范围可分为以下类型:⑴整式型:当函数解析是整式时,自变量的取值范围是全实数.⑵分式型:当函数解析式是分式时,自变量的取值范围是使分母不为零的一切实数.注意不能随意约分,同时要区分“且”和“或”的含义.⑶偶次根式型:当函数解析式是偶次根式时,自变量的取值范围是使被开方式为非负数.⑷零次幂或负整数次幂型:当零次幂或负整数次幂的底数中含有自变量时,该底数不为零.特别要注意综合考虑各种情况,如(5)需要满足的条件是⎩⎨⎧≠-≥020x x ;(6)需要满足的条件是⎩⎨⎧≥-≥-0303x x ;(7)需要满足的条件是⎩⎨⎧≠--≥-01201x x ;(8)需要满足的条件是⎩⎨⎧≥-≥-012053x x .题3.答案:解:y 与x 的函数关系式为y=20-4x ,自变量的取值范围是0≤x<5.解析:周长y=4(5-x );自变量的范围应能使正方形的边长是正数,即满足不等式组500x x ->⎧⎨≥⎩. 题4.答案: C解析:本题考查学生对函数图象的理解,轮般先从甲地顺水航行到乙地,再从乙地逆流航行回到甲地,所以先用的速度要快,从图象观察A 、B 是错误的;由于在乙地停留一段时间,所以D 图象也是错误的,故此题选C .题5.答案:ab ,a ,S ,b解析:先根据矩形的面积公式确定函数关系,再根据不变的量是常量,变化着的量是变量来确定答案.题6.答案:C解析:由分母不为零,得x+1≠0,即x≠-1. 故选C.题7.答案:解:(1)t Q 50800-=(2)160≤≤t解析:水池中剩余的水=原有的水-抽出的水,又因为每小时抽50立方米。
初中数学《一次函数变量与函数》典型例题及答案解析

解:由题意,得 ,
解得x≤3且x≠2,
故选:C.
【点睛】
本题考查了函数自变量的取值范围,利用被开方数是非负数,分母不能为零得出不等式组是解题关键.
10.下列各曲线中,不能表示y是x的函数的是( )
A. B. C. D.
【答案】D
【Hale Waihona Puke 析】【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.
【答案】C
【解析】
【分析】
根据函数定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,解答即可.
【详解】
A项中,长方形的宽一定,是常量,而面积=长×宽,长与面积是两个变量,若长改变,则面积也变,是函数关系;
B项中,正方形的周长与面积是两个变量,给出一个周长的值C,边长即为 ,相应地面积为 ,是函数关系;
【答案】A
【解析】
【分析】
由三角形外角性质可得结论.
【详解】
∵三角形一个外角等于与它不相邻的两个内角和,
∴y=x+60.
故选:A.
【点睛】
考查了三角形外角的性质,解题关键是运用三角形一个外角等于与它不相邻的两个内角和得出关系式.
5.小明和他爸爸做了一个实验,小明由一幢245米高的楼顶随手放下一只苹果,由他爸爸测量有关数据,得到苹果下落的路程和下落的时间之间有下面的关系:
【详解】
解;观察表格,得
时间在变,人口在变,故C正确;
故选;C.
【点睛】
本题考查的知识点是常量与变量,解题关键是利用常量与变量的定义.
12.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
函数与变量知识点与练习(复习用)

第一讲 变量及函数知识点1: 常量及变量常量(或常数):数值保持不变的量变量: 可以取不同数值且变化的量注: 常量和变量是相对而言的, 它由问题的条件确定。
如s =vt 中, 若s 肯定时, 则 s 是常量, v, t 是变量若v 肯定时, 则 v 是常量, s, t 是变量若t 肯定时, 则 t 是常量, s, v 是变量(1) 例1 分别指出下列关系式中的变量及常量:(2) 一个物体从高处自由落下, 该物体下落的距离及它下落的时间的关系式为(其中);一个多边形的内角和A 及边数(, 且为整数)存在关系;长方体的体积及长, 宽, 高之间的关系式为。
知识点2: 函数的概念 及函数思想(难点)一般地, 设在一个变化的过程中有两个变量x, y,假如对于x 在它允许取值范围内的每一个值, y 都有唯一确定的值及它对应, 那么就说x 是自变量, y 是x 的函数.对函数概念的理解, 主要抓住以下三点:1 有两个变量;一个变量的数值随着另一个变量的数值的变化而变化; 对于自变量每一个确定的值, 函数有且只有一个值及之对应。
例如:y=±x, 当x=1时, y 有两个对应值, 所以y=±x 不是函数关系。
对于不同的自变量x 的取值, y 的值可以相同, 例如, 函数:y=|x|, 当x=±1时, y 的对应值都是1。
注: (1)函数体现的是一个变化的过程: 一个变量的变化对另一个变量的影响。
(2)在变化的过程中有且只有两个变量: 自变量(一般在等号的右边)和 因变量(一般在等号的左边)。
(3)函数的实质是两个变量之间的对应关系: 自变量x 每取一个值, 因变量有唯一确定的值及它对应。
(4)含有一个变量的代数式可以看作这个变量的函数。
例1 推断下列变量之间是不是存在函数关系并说明理由(1)长方形的宽肯定时, 其长及面积; (2)等腰三角形的底边长及面积 (3)某人的身高及年龄 (4)弹簧的总长度y (cm )及所挂物体质量x (kg )例2 下列变量x, y 的关系中, y 是x 的函数的()x 是y 的函数的()3x -y =5 ②y =|x | ③2210x y -=例3 下列各曲线中, 不能表示y 是x 函数的为( )A .B .C .D .知识点3: 函数的自变量的取值范围 (重点, 常考点)(1)若函数关系式是整式, 则自变量的取值范围是: 全体实数。
【含8套中考卷】2019年中考数学一轮复习《变量与函数》专题练习卷含答案

1. 2. 3. 4. 5. 6.7.变量与函数专题在平面直角坐标系中,点(-3,2)所在的象限是A.第一象限C.第三象限【答案】B函数y=VEE2中自变量X的取值范围是x-3A.x>2B.xN2【答案】CB.第二象限D.第四象限C.xN2且xU3若一次函数y=(k-2)x+1的函数值y随x的增大而增大,则A.k<2B.k>2C.k>0D.k<0D.x"3【答案】B一次函数y=x+2的图象与y轴的交点坐标为A.(0,2)【答案】AB.(0,-2)C.(2,0)D.(-2,0)将直线y=2x-3向右平移2个单位长度,A.y=2x-4B.y=2x+4再向上平移3个单位长度后,所得的直线的表达式为C.y=2x+2D.y=2x-2【答案】A如图,在矩形A0BC中,A(-2,1A.--2【答案】A1B.-20),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为C.-2D.2如图,直线y二kx+b(k"0)经过点A(-2,4),则不等式kx+b>4的解集为A.x>-2 D.x<4【答案】A8.如图,直线1是一次函数y=kx+b 的图象,若点A (3, m)在直线1上,则m 的值是【答案】C9.反比例函数y=§的图象经过点(3, -2),下列各点在图象上的是xA. (-3, -2)B. (3, 2)C. ( - 2, - 3)D. ( -2, 3)【答案】D10.如图,已知直线y=k 1X (虹尹0)与反比例函数y=4 (k 2^0)的图象交于M, N 两点.若点M 的坐标x是(1, 2),则点N 的坐标是A. ( - 1> - 2)C. (1, -2)B. ( -1, 2)D. ( -2, - 1)【答案】A11.如图,点C 在反比例函数y=* (x>0)的图象上,过点C 的直线与x 轴,y 轴分别交于点A, B,且AB=BC,X△A0B 的面积为1,则k 的值为A. 1B. 2C. 3D. 4【答案】D12.某通讯公司就上宽带网推出A, B,C 三种月收费方式.这三种收费方式每月所需的费用y (元)与上网时间x (h)的函数关系如图所示,则下列判断错误的是65503012025 50 55ox(h)A. 每月上网时间不足25h 时,选择A 方式最省钱B. 每月上网费用为60元时,B 方式可上网的时间比A 方式多C. 每月上网时间为35h 时,选择B 方式最省钱D. 每月上网时间超过70h 时,选择C 方式最省钱【答案】D13.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长,根据如图,在下列选项中指出白昼时长低于11小时的 节气白昼时长伺咽A.惊蛰B.小满C.立秋D.大寒【答案】D14.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s (单位:m )与时间r (单位:min )之间函数关系的大致图象是B.—°/(min)D.【答案】B15.在平面直角坐标系中,一个智能机器人接到如下指令:从原点0出发,按向右,向上,向右,向下的方向依次不断移动,每次移动Im.其行走路线如图所示,第1次移动到Au 第2次移动到A 2,…,第n 次移动到A ”.则左OA 2A 20i9的面积是16.17.A, 504m 2【答案】A22二次函数y=ax 2+bx+c (a^O)的部分图象如图所示,则下列结论错误的是A. 4a+b=0C. a : c= - 1 : 5【答案】DD.当-1W x W5 时,y>0如图,若二次函数y=ax 2+bx+c (a 尹0)图象的对称轴为x=l,与y 轴交于点C,与x 轴交于点A 、点B ( - 1, 0),则①二次函数的最大值为a+b+c ;②a - b+c<0;(3)b 2 - 4ac<0;④当y>0时,其中正确的个数是【答案】B18. P (3, -4)到x 轴的距离是【答案】419.抛物线y=2(x+2)纤4的顶点坐标为.【答案】(-2,4)20.如图,抛物线y=ax,与直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1),则方程ax^bx+c的解是.【答案】xi=-2,x2=l21.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB=m时,矩形土地ABCD的面积最大.【答案】1503, 22.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t-一尸.在2飞机着陆滑行中,最后4s滑行的距离是m.【答案】2423.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.【答案】(4扼-4)24.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.(1)求k、b的值;(2)若点D在y轴负半轴上,且满足S acod=|saboc,求点D的坐标.【解析】(1)当X=1时,y=3x=3,.•.点C 的坐标为(1, 3) .将 A ( - 2, 6)、C (1, 3)代入 y=kx+b,得:—2k + 〜=6k + b = 3,解徐’k = -l b = 4(2)由(1)得直线AB 的解析式为y=-x+4.当 y=0 时,有-x+4=0,解得:x=4,.•.点B 的坐标为(4, 0).设点D 的坐标为(0, m ) (m<0),1 nn 1 1 1S acod = — S aboc ,即m = — X — X 4X 3,3 2 3 2解得:m= - 4,.•.点D 的坐标为(0, -4).25.抛物线y=-|x +bx+c 经过点A (3 0, 0)和点B (0, 3),且这个抛物线的对称轴为直线1,顶点121 9 l【解析】(1) •抛物线y = +版+。
变量与函数的例子

变量与函数的例子
1. 想象一下,你去超市买东西,买的东西数量不就是一个变量嘛,而总价就是数量这个变量的函数呀!比如你买苹果,一个苹果 2 块钱,你买了 5 个,那总价不就是 10 块嘛,这就是变量与函数的简单例子呀!
2. 嘿,你看天气的变化,每天的气温是不是一个变量呀,而根据气温我们穿不同的衣服,这穿什么衣服不就是气温这个变量的函数嘛!难道不是很有趣?
3. 咱再说说打游戏哈,你每一局游戏的得分就是个变量,而你的游戏水平就像是决定得分这个变量的函数呢!你说是不是?
4. 哎呀呀,你想想看,你每天运动的时间不就是个变量嘛,然后你的身体健康状况就和这个运动时间的变量有着密切关系呢,这不就像函数一样嘛,难道不是吗?
5. 嘿,比如说你学习的时间,这是个变量吧,然后你的学习成果就可以看作是由学习时间决定的函数呀,很形象吧?
6. 你想想去旅游的时候,去的地方不同就是变量呀,而你的心情和收获就像是这个变量的函数,肯定会不一样呀,对吧?
7. 哇哦,像做饭的时候,食材的用量就是变量,做出来的饭菜味道就是用量这个变量的函数呀!是不是很神奇呢!
我觉得变量与函数就在我们生活的方方面面呀,到处都能看到它们的影子呢!。
变量与函数练习题

变量与函数练习题一、变量练习题1. 小明买了一本书,书的价格是200元,他付了300元,求小明找回的零钱是多少?解答:书的价格是200元,小明付了300元,找回的零钱 = 付的钱 - 书的价格所以,找回的零钱 = 300 - 200 = 100元。
2. 请计算长方形的面积和周长,长为5,宽为3。
解答:长方形的面积 = 长 ×宽长方形的周长 = 2 × (长 + 宽)所以,长方形的面积 = 5 × 3 = 15,长方形的周长 = 2 × (5 + 3) = 16。
二、函数练习题1. 编写一个函数,接受两个参数,计算并返回两个参数的和。
解答:```pythondef calculate_sum(a, b):return a + b# 测试print(calculate_sum(3, 5)) # 输出:8print(calculate_sum(10, -2)) # 输出:8```2. 编写一个函数,接受一个字符串作为参数,返回字符串的长度。
解答:```pythondef calculate_length(string):return len(string)# 测试print(calculate_length("Hello")) # 输出:5print(calculate_length("Python")) # 输出:6```三、综合练习题1. 编写一个程序,接受用户输入的两个数字,计算并输出两个数字的和、差、积、商和余数。
解答:```pythonnum1 = float(input("请输入第一个数字:"))num2 = float(input("请输入第二个数字:"))sum_result = num1 + num2difference = num1 - num2product = num1 * num2quotient = num1 / num2remainder = num1 % num2print("和:", sum_result)print("差:", difference)print("积:", product)print("商:", quotient)print("余数:", remainder)```以上是关于变量和函数的练习题,请根据题目要求编写代码,并对结果进行验证。
八年级数学下册 17.1 变量与函数 话说变量与函数题型素材 (新版)华东师大版

话说变量与函数题型题型一:函数概念及自变量的取值范围在某一变化过程中有两个变量x,y,对于x 的每一个值,y 都有唯一的值与之对应,此时我么称y 是x 的函数,其中x 是自变量.使函数有意义的自变量的取值的全体,我们叫做函数自变量的取值范围,自变量的取值范围必须满足:①自变量的代数式有意义;②还要满足实际问题的实际意义.例1:函数12y x -=-x 的取值范围是( ) A .1x -≥ B .2x >C .1x >-且2x ≠D .1x -≥且2x ≠分析:函数自变量的取值范围满足被开方数为非负和分式中分母不为零.所以⎩⎨⎧≠-≥+0201x x 所以1x -≥且2x ≠.故选D .题型二:求实际问题的函数解析式关于确立函数解析式的问题,需要分析实际问题中的等量关系,找出含有自变量和函数的等式,其具体方法和列方程解应用题类似.例2:用规格为50cm ×50cm 的地板砖密铺客厅恰好需要60块.如果改用规格为acm ×acm 的地板砖y 块也恰好能密铺该客厅,那么y 与a 之间的关系为( ) A.2150000a y = B.ay 150000= C.2150000a y = D.a y 150000= 分析:因为用规格为50cm ×50cm 的地板砖密铺客厅恰好需要60块,所以客厅的面积为50×50×60=1500002cm ,若改用acm ×acm 的地板砖y 块也恰好能密铺该客厅,则2150000ay =,所以y 与a 之间的关系为A 选项. 例3:某学校要印刷一批宣传材料,甲印务公司提出售制版费900元,另外每份材料收印刷费0.5元;乙印务公司提出不受制版费,每份材料收印刷费0.8元.(1)分别写出两家印务公司的收费y(元)与印刷材料的份数x(份)之间的函数关系式.(2)若学校预计要印刷5000份以内的宣传材料,请问学校应选择哪一家印务公司更合算?分析:直接根据题意,写出y 与x 之间的函数关系式.解: (1)甲:x y 5.09001+= 乙:x y 8.02=(2)当x=5000时, ;340050005.09005.09001=⨯+=+=x y 400050008.08.02=⨯==x y所以21y y 所以选择甲印务公司更合算.迁移点拨:根据实际应用问题列函数解析式和方程的等量关系类似.题型三:函数图象(读图能力)画函数图象,一般按下列步骤进行:列表,描点,连线.列表时要注意自变量的取值范围,既要使自变量的取值具有代表性,又不至于使自变量所对应的函数值太大或太小,以利于描点和全面反映图象情况,当图象有端点时,要注意端点是否有等号,有等号时画实心点,无等号时画空心圈.例3: 如图⑴是某公共汽车线路收支差额y(票价总收人减去运营成本)与乘客量 x 的函数图象.目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,以此举实现扭亏. 公交公司认为:运营成本难以下降,公司己尽力,提高票价才能扭亏.根据这两种意见,可以把图⑴分别改画成图⑵和图⑶ ,⑴ 说明图⑴中点 A 和点 B 的实际意义:⑵你认为图⑵和图⑶两个图象中,反映乘客意见的是 ,反映公交公司意见的是 .⑶如果公交公司采用适当提高票价又减少成本的办法实现扭亏为赢,请你在图⑷中画出符合这种办法的 y 与 x 的大致函数关系图象.分析:注意点A 的意义,点B 的意义及将射线AB 旋转的角度.解:⑴点A 表示这条路线的运营成本为1万元; 点B 表示乘客数达1.5万人时,这条线路收支达到平衡.⑵图⑶,图⑵⑶将图⑴中的射线AB 绕点A 逆时针适当旋转且向上平移(图略).迁移点拨:我们要密切关注函数图象问题中不同图象代表的不同的意义,如函数增加的图象,函数平行于x 轴的图象,函数递减的图象.小试牛刀:1.函数21--=x x y 的自变量x 的取值范围是_______. 2. 某种灯的使用寿命为1000小时,它的可使用天数y 与平均 每天使用的小时数x 之间的关系式为 .3.一辆汽车由内江匀速驶往成都,下列图像中能大致反映汽车距离成都的路程s(千米)和行驶时间t(小时)的关系的是( )4.一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;(2)如果该司机匀速返回时,用了4.8小时,求返回时的速度.参考答案:1.;且21≠≥x x2. xy 1000= 3. C 4. (1)t v 480= (2) v =100(千米/小时).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
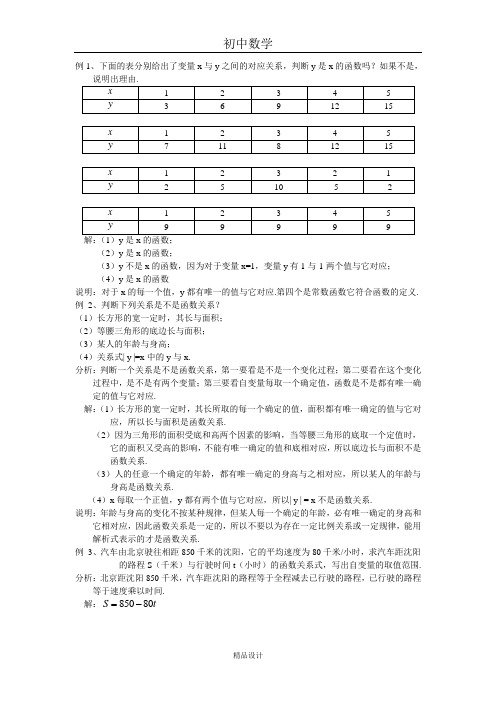
例1、下面的表分别给出了变量x 与y 之间的对应关系,判断y 是x 的函数吗?如果不是,解:(1)y 是x 的函数; (2)y 是x 的函数;(3)y 不是x 的函数,因为对于变量x=1,变量y 有1与-1两个值与它对应; (4)y 是x 的函数说明:对于x 的每一个值,y 都有唯一的值与它对应.第四个是常数函数它符合函数的定义. 例 2、判断下列关系是不是函数关系? (1)长方形的宽一定时,其长与面积; (2)等腰三角形的底边长与面积; (3)某人的年龄与身高; (4)关系式| y |=x 中的y 与x.分析:判断一个关系是不是函数关系,第一要看是不是一个变化过程;第二要看在这个变化过程中,是不是有两个变量;第三要看自变量每取一个确定值,函数是不是都有唯一确定的值与它对应. 解:(1)长方形的宽一定时,其长所取的每一个确定的值,面积都有唯一确定的值与它对应,所以长与面积是函数关系.(2)因为三角形的面积受底和高两个因素的影响,当等腰三角形的底取一个定值时,它的面积又受高的影响,不能有唯一确定的值和底相对应,所以底边长与面积不是函数关系.(3)人的任意一个确定的年龄,都有唯一确定的身高与之相对应,所以某人的年龄与身高是函数关系.(4)x 每取一个正值,y 都有两个值与它对应,所以| y | = x 不是函数关系.说明:年龄与身高的变化不按某种规律,但某人每一个确定的年龄,必有唯一确定的身高和它相对应,因此函数关系是一定的,所以不要以为存在一定比例关系或一定规律,能用解析式表示的才是函数关系.例 3、汽车由北京驶往相距850千米的沈阳,它的平均速度为80千米/小时,求汽车距沈阳的路程S (千米)与行驶时间t (小时)的函数关系式,写出自变量的取值范围.分析:北京距沈阳850千米,汽车距沈阳的路程等于全程减去已行驶的路程,已行驶的路程等于速度乘以时间. 解:85080S t =-0S t ≥⎧⎨≥⎩ 得850800tt -⎧⎨≥⎩850.8t ∴≤≤于是汽车距沈阳的路程S 与时间t 的函数关系式为85080S t =-,自变量t 的取值范围是850.8t ≤≤例 4、求下列函数中自变量x 的取值范围:(1)235y x =- (2)21y x =+ (3)22y x =- (4)2123x y x x -=--(5)y =(6)2y x =+(7)y =(8)y =+分析:求自变量的取值范围,应考虑自变量的取值使函数解析式有意义.(1)、(2)小题函数解析式是整式,故自变量可取任意实数;(3)、(4)小题解析式是分式,自变量可取使分母不为0的任意实数;(5)、(7)、(8)小题的解析式是二次根式,自变量取值应使被开方数非负;(6)小题既有分母又有二次根式,自变量取值应使分母不为0,又要使二次根式的被开方数非负. 解:(1)函数235y x =-的自变量x 的取值范围是躯体实数 (2)函数21y x =+的自变量x 的取值范围是躯体实数 (3)20,2,x x -=∴=∴当2x =时,分母20x -=,∴函数22y x =-的自变量的取值范围是2x ≠; (4)由2230x x --=解得123,1,x x ==-∴ 当3x =或1x =-时,分母2230x x --=,∴ 函数2123x y x x -=--的自变量x 的取值范围是3x ≠且1x ≠-(5)由230x -≥解得32x ≤,∴函数y =x 的取值范围是 32x ≤; (6)由30x +≥得3x ≥-,由20x +=得2x =-,当2x ≠-时,分母20x +≠,∴函数2y x =+的自变量x 的取值范围是3x ≥-且2x ≠-; (7)22224213(1)30,x x x x x ++=+++=++≥即对于任意实数x ,224x x ++都是非负的,∴函数y =x 的取值范围是全体实数;(8)由630,360x x -≥⎧⎨-≥⎩得112,122x x x ⎧≥⎪⎪∴=⎨⎪≤⎪⎩因此,函数y =+x 的取值范围是12x =.典型例题五例 已知函数的图象经过A(1,4)、B(2,2)两点,请你写出满足上述条件的两个不同的函数解析式,并简要说明解答过程.(2002年山东省青岛市中考题)分析 :由于题中所经过A(1,4)、B(2,2)两点的函数解析式的类型未告知,因此所确定函数解析式的形式可能是直线型,也可能是双曲线、抛物线型,还可能是其他形状的,故可采用下列几种途径来确定满足题设条件的解析式:(1)若经过A 、B 两点的函数的图象是直线,设其解析式为b kx y +=,则有⎩⎨⎧+=+=.22,4b k b k 解之,得⎩⎨⎧=-=.6,2b k 此时,函数解析式为.62+-=x y(2)由于A 、B 两点的横、纵坐标的积相等,都等于4,所以,经过A 、B 两点的函数的图象还可以是双曲线,其解析式为:xy 4=. (3)如果经过A 、B 两点的函数的图象是抛物线,设其解析式为c bx ax y ++=2(0≠a ),则有⎩⎨⎧++=++=.242,4c b a c b a解之,得⎩⎨⎧+=--=.6,23a c a b因此,只要a 、b 、c 同时满足关系式23--=a b 和62+=a c ,即可保证二次函数c bx ax y ++=2(0≠a )的图象经过A(1,4)、B(2,2)两点;显然,这样的二次函数有无数个.如取a =1,则有b =-5,c =8,相应图象所对应的二次函数的解析式为:852+-=x x y .(4)其他略.典型例题六例 (北京市海淀区,1999)如图,在矩形ABCD 中,P BC AB ,7,4==是BC 边上与B 点不重合的动点,过点P 直线交CD 的延长线于R ,交AD 于Q (Q 与D 不重合),且045=∠RPC 。
设x BP =,梯形ABPQ 的面积为y ,求y 与x 之间的函数关系,并求自变量x 的取值范围。
解 在矩形ABCD 中,7==BC AD ,090,4=∠==C DC AB 。
∵ 045=∠RPC ,∴ .450RPC R ∠==∠ ∴ .RC PC = ∵ ,x BP =∴ .7x PC -= ∵ AD ∥BC ,∴RCRDPC QD =。
∴ .347x x DC RC RD QD -=--=-== ∴ .4)3(7x x QD AD AQ +=--=-= ∵ ,)(21AB BP AQ S ABCD ⋅+=梯形∴ .84+=x y 当Q 与D 重合时,.3,4===BP DC PC ∵P 与B 不重合,Q 与D 不重合, ∴ 自变量x 的取值范围是.30<<x典型例题七例 下列函数中与y=3x 表示同一函数的是( )(1)333y x = (2)23x y x=(3)2y = (4)y = (5)y =分析:只有对应关系相同,自变量的取值范围相同,函数值的取值范围也相同的函数才是同一函数.解:(1)y ==与y=3x 的对应关系不同,所以它们不是同一函数.(2)23x y x=中x 不能取0,而y=3x 中x 可取任意实数,因此,自变量的取值范围不同,它们不是同一函数.(3)2y =中x 的取值范围是非负数,所以它与y=3x 表示不同的函数.(4)|3|y x ==中函数值范围是非负数.所以y =与y=3x 不是同一函数.(5)3y x ==因为y =y=3x 的对应关系相同,函数值的取值范围也相同,所以它们是同一函数.典型例题八例 求下列函数中自变量x 的取值范围:(1)235y x =- (2)21y x =+ (3)22y x =- (4)2123x y x x -=--(5)y =(6)2y x =+(7)y =(8)y =+分析:求自变量的取值范围,应考虑自变量的取值使函数解析式有意义。
(1)、(2)小题函数解析式是整式,故自变量可取任意实数;(3)、(4)小题解析式是分式,自变量可取使分母不为0的任意实数;(5)、(7)、(8)小题的解析式是二次根式,自变量取值应使被开方数非负;(6)小题既有分母又有二次根式,自变量取值应使分母不为0,又要使二次根式的被开方数非负。
解:(1)函数235y x =-的自变量x 的取值范围是躯体实数 (2)函数21y x =+的自变量x 的取值范围是躯体实数 (3)20,2,x x -=∴=∴当2x =时,分母20x -=,∴函数22y x =-的自变量的取值范围是2x ≠;(4)由2230x x --=解得123,1,x x ==-∴ 当3x =或1x =-时,分母2230x x --=,∴ 函数2123x y x x -=--的自变量x 的取值范围是3x ≠且1x ≠- (5)由230x -≥解得32x ≤,∴函数y =x 的取值范围是 32x ≤;(6)由30x +≥得3x ≥-,由20x +=得2x =-,当2x ≠-时,分母20x +≠,∴函数2y x =+的自变量x 的取值范围是3x ≥-且2x ≠-; (7)22224213(1)30,x x x x x ++=+++=++≥即对于任意实数x ,224x x ++都是非负的,∴函数y =x 的取值范围是全体实数;(8)由630,360x x -≥⎧⎨-≥⎩得112,122x x x ⎧≥⎪⎪∴=⎨⎪≤⎪⎩因此,函数y =+x 的取值范围是12x =典型例题九例 下列函数中与x y 5=表示同一函数的是一个函数?(1)x y =与x x y 2)(=;(2)x y 2=与332x y =; (3)x y 3=与2)3(x y =; (4)x y 1=与2xx y =. 解:(1)它们不是同一函数。
(x 的取值范围不同) (2)它们不是同一函数。
(函灵敏的对应关系不同)(3)它们不是同一函数 (函数值的取值范围不同) (4)它们是同一函数(对应关系相同,自变量,函数值的取值范围均相同)典型例题十例 求下列函数自变量的取值范围: (1)321-=x y ;(2)xy -=21; (3)3-=x y ;(4)325-=x y ;(5)31--=x x y ;(6)4212++=x x y . 解:(1)自变量x 的取值范围是一切实数(函数表达式为整式,x 取一切实数) (2)02≠-x ,2≠∴x(函数表达式为分式,取分母不为0的一切实数) (3)03≥-x 3≤∴x(函数表达式为二次根式取被开方数不小于0的实数) (4)x 取一切实数(函数表达式为三次根式,x 为任意实数) (5)⎩⎨⎧≠-≥-0301x x (这里不能用“或”应用“且”)解得⎩⎨⎧≠≥31x x∴自变量的取值范围是1≥x ,且3≠x 的一切实数(6)03)1(4222≠++=++x x x(配方是关键)∴x 为任意实数时,y 均有意义即自变量x 的取值范围为一切实数.典型例题十一例 已知函数x a a y 4162+-=,当2=x 时,1-=y ,(1)确定此函数(2)求当21=x 时,y 的值解:(1)当2=x ,1-=y (要理解函数值的定义)时,有241612⨯+-=-a a 即0962=+-a a(实际是解方程) 解出:3=a把3=a ,代入xa a y 4162+-=得(求出的a 值代回函数中)xy 2-=∴自变量的取值范围是0≠x 的全体实数(这一步要注明) (2)x y 2-= 当21=x 时,4212=-=y(实际是求代数式的值)∴当21=x 时,函数值y 是4-.典型例题十二例 一盛满10吨水的水箱,每小时流出5.0吨水。
