数学基本名词
数学常用名词定义
数学思想与方法，经常用到的数学名词有以下三十五个，现给出解释，供参考。
1、数学思想：是对数学知识的本质认识，是对数学规律的理性认识，是从某些数学内容和对数学的认识过程中提炼上升的数学观点，它在认识活动中被反复运用，带有普遍的指导意义，是建立数学和用数学解决问题的指导思想，例如：化归思想；分类思想；模型思想；极限思想；最优化思想）等。
2、数学方法：是指从数学角度提出问题、解决问题（包括数学内部问题和实际问题）的过程中所采用的各种方式、手段、途径等，其中包括变换数学形式。
数学思想和数学方法是紧密联系的，一般来说，强调指导思想时，称数学思想，强调操作过程时称数学方法。
3、化归目标简单性原则：是指化归应朝着目标简单的方向进行，即复杂的待解决问题应向简单的较易解决的问题化归。
和谐统一性原则：是指化归应朝着是待解决问题在表现形式上和谐，在量、形、关系方面趋于统一的方向进行，是问题的条件与结论表现得更匀称和恰当。
具体化原则：是指化归的方向一般应由抽象到具体，即分析问题和解决问题时，应着力将问题向具体的问题转化，以使其中的数量关系更易把握。
标准形式化原则：将待解决的问题在形式上向该类问题的标准形式化归。
低层次化原则：解决数学问题时，应尽量将高维空间的问题化归成低维空间的问题，高次数的问题化归成低次数的问题，多元问题化归成少原问题。
4、解析法：将平面几何问题转化解析几何问题的化归方法，具体步骤：（1）建立坐标系，（2）设定点的座标与曲线方程，化几何元素为解析式，（3）进行运算与推理，即在上述两步的基础上利用解析几何的知识进行具体的解答，（4）返回几何结论，断言论题的解。
5、复数法：将坐标平面变成复平面，几何问题化归为复数问题的化归方法。
6、一般化策略：将待解、代征问题看成特殊问题，通过对它的一般形式问题的解决而得到原问题的划归策略就是一般化策略。
7、特殊化策略：对于待解待证问题，先解决它的特殊情况，然后把解决特殊情况的方法或结果应用到一般情况，使原问题获解的策略。
常用的数学名词术语100个
常用的数学名词术语100个1.数（Number）：数学中用于计数、测量和表达数量的概念。
2.整数（Integer）：不带小数部分的数，可以是正数、负数或零。
3.分数（Fraction）：表示一个整体被平均分割成若干部分的数，由分子和分母组成。
4.小数（Decimal）：用十进制表示的数，包含整数部分和小数部分。
5.等号（Equal sign）：表示两个表达式或数相等的符号。
6.不等号（Inequality）：表示两个表达式或数不相等或大小关系的符号。
7.加法（Addition）：将两个或多个数值相加的操作。
8.减法（Subtraction）：从一个数中减去另一个数的操作。
9.乘法（Multiplication）：将两个或多个数值相乘的操作。
10.除法（Division）：将一个数分割成若干相等部分的操作，或将一个数除以另一个数。
11.平方（Square）：一个数乘以自身的结果。
12.平方根（Square root）：一个数的平方根是使其平方等于该数的非负数。
13.指数（Exponent）：表示一个数要连乘多少次自身。
14.对数（Logarithm）：表示一个数是以另一个数为底的幂的指数。
15.多项式（Polynomial）：包含有限个变量和系数的表达式，由常数项、一次项、二次项等组成。
16.方程（Equation）：描述两个表达式相等的数学语句，包含未知数。
17.不定方程（Diophantine equation）：包含整数未知数的方程。
18.几何（Geometry）：研究空间、形状、大小和相对位置的数学学科。
19.直线（Line）：由无限多个点组成的无限延伸的路径。
20.曲线（Curve）：在平面或空间上的连续路径。
21.圆（Circle）：平面上所有到一个固定点的距离相等的点的集合。
22.三角形（Triangle）：由三条线段组成的多边形。
23.角（Angle）：由两条射线共享一个端点而形成的空间区域。
谜材 数学名词 数学用语
边、差、长、乘、除、底、点、度、分、高、勾、股、行、和、弧环、集、加、减、积、角、解、宽、棱、列、面、秒、幂、模、球式、势、商、体、项、象、线、弦、腰、圆十位、个位、几何、子集、大圆、小圆、元素、下标、下凸、下凹百位、千位、万位、分子、分母、中点、约分、加数、减数、数位通分、除数、商数、奇数、偶数、质数、合数、乘数、算式、进率因式、因数、单价、数量、约数、正数、负数、整数、分数、倒数乘方、开方、底数、指数、平方、立方、数轴、原点、同号、异号余数、除式、商式、余式、整式、系数、次数、速度、距离、时间方程、等式、左边、右边、变号、相等、解集、分式、实数、根式对数、真数、底数、首数、尾数、坐标、横轴、纵轴、函数、常显变量、截距、正弦、余弦、正切、余切、正割、余割、坡度、坡比频数、频率、集合、数集、点集、空集、原象、交集、并集、差集映射、对角、数列、等式、基数、正角、负角、零角、弧度、密位函数、端点、全集、补集、值域、周期、相位、初相、首项、通项公比、公差、复数、虚数、实数、实部、虚部、实轴、虚轴、向量辐角、排列、组合、通项、概率、直线、公理、定义、概念、射线线段、顶点、始边、终边、圆角、平角、锐角、纯角、直角、余角补角、垂线、垂足、斜线、斜足、命题、定理、条件、题设、结论证明、内角、外角、推论、斜边、曲线、弧线、周长、对边、距离矩形、菱形、邻边、梯形、面积、比例、合比、等比、分比、垂心重心、内心、外心、旁心、射影、圆心、半径、直径、定点、定长圆弧、优弧、劣弧、等圆、等弧、弓形、相离、相切、切点、切线相交、割线、外离、外切、内切、内径、外径、中心、弧长、扇形轨迹、误差、视图、交点、椭圆、焦点、焦距、长袖、短轴、准线法线、移轴、转轴、斜率、夹角、曲线、参数、摆线、基圆、极轴极角、平面、棱柱、底面、侧面、侧棱、楔体、球缺、棱锥、斜高棱台、圆柱、圆锥、圆台、母线、球面、球体、体积、环体、环面球冠、极限、导数、微分、微商、驻点、拐点、积分、切面、面角极值被减数、被乘数、被除数、假分数、代分数、质因数、小数点多位数、百分数、单名数、复名数、统计表、统计图、比例尺循环节、近似数、准确数、圆周率、百分位、十分位、千分位万分位、自然数、正整数、负整数、相反数、绝对值、正分数负分数、有理数、正方向、负方向、正因数、负因数、正约数运算律、交换律、结合律、分配律、最大数、最小数、逆运算奇次幂、偶次幂、平方表、立方表、平方数、立方数、被除式代数式、平方和、平方差、立方和、立方差、单项式、多项式二项式、三项式、常数项、一次项、二次项、同类项、填空题选择题、判断题、证明题、未知数、大于号、小于号、等于号恒等号、不等号、公分母、不等式、方程组、代入法、加减法公因式、有理式、繁分式、换元法、平方根、立方式、根指数小数点、无理数、公式法、判别式、零指数、对数式、幂指数对数表、横坐标、纵坐标、自变量、因变量、函数值、解析法解析式、列表法、图象法、指点法、截距式、正弦表、余弦表正切表、余切表、平均数、有限集、描述法、列举法、图示法真子集、欧拉图、非空集、逆映射、自反性、对称性、传递性可数集、可数势、维恩图、反函数、幂函数、角度制、弧度制密位制、定义城、函数值、开区间、闭区间、增函数、减函数单调性、奇函数、偶函数、奇偶性、五点法、公因子、对逆性比较法、综合法、分析法、最大值、最小值、递推式、归纳法复平面、纯虚数、零向量、长方体、正方体、正方形、相交线延长线、中垂线、对预角、同位角、内错角、无限极、长方形平行线、真命题、假命题、三角形、内角和、辅助线、直角边全等形、对应边、对应角、原命题、逆命解、原定理、逆定理对称点、对称轴、多边形、对角线、四边形、五边形、三角形否命题、中位线、相似形、比例尺、内分点、外分点、平面图同心圆、内切圆、外接圆、弦心距、圆心角、圆周角、弓形角内对角、连心线、公切线、公共弦、中心角、圆周长、圆面积反证法、主视图、俯视图、二视图、三视图、虚实线、左视图离心率、双曲线、渐近线、抛物线、倾斜角、点斜式、斜截式两点式、一般式、参变数、渐开线、旋轮线、极坐标、公垂线斜线段、半平面、二面角、斜棱柱、直棱柱、正梭柱、直观图正棱锥、上底面、下底面、多面体、旋转体、旋转面、旋转轴拟柱体、圆柱面、圆锥面、多面角、变化率、左极限、右极限隐函数、显函数、导函数、左导教、右导数、极大值、极小值极大点、极小点、极值点、原函数、积分号、被积式、定积分无穷小、无穷大、连分数、近似数、弦切角混合运算、乘法口诀、循环小数、无限小数、有限小数、简易方程四舍五人、单位长度、加法法则、减法法则、乘法法则、除法法则数量关系、升幂排列、降幂排列、分解因式、完全平方、完全立方同解方程、连续整数、连续奇数、连续偶数、同题原理、最简方程最简分式、字母系数、公式变形、公式方程、整式方程、二次方根三次方根、被开方数、平方根表、立方根表、二次根式、几次方根求根公式、韦达定理、高次方程、分式方程、有理方程、无理方程分数指数、同次根式、异次根式、最简根式、同类根式、常用对数换底公式、反对数表、坐标平面、坐标原点、比例系数、一次函数二次函数、三角函数、正弦定理、余弦定理、样本方差、集合相交等价集合、可数集合、对应法则、指数函数、对数函数、自然对数指数方程、对数方程、单值对应、单调区间、单调函数、诱导公式周期函数、周期交换、振幅变换、相位变换、正弦曲线、余弦曲线正切曲线、余切曲线、倍角公式、半角公式、积化和差、和差化积三角方程、线性方程、主对角线、副对角钱、零多项式、余数定理因式定理、通项公式、有穷数列、无穷数列、等比数列、总和符号特殊数列、不定方程、系数矩阵、增广炬阵、初等变换、虚数单位共轭复数、共轭虚数、辐角主值、三角形式、代数形式、加法原理乘法原理、几何图形、平面图形、等量代换、度量单位、角平分线互为余角、互为补角、同旁内角、平行公理、性质定理、判定定理斜三角形、对应顶点、尺规作图、基本作图、互逆命题、互逆定理凸多边形、平行线段、逆否命题、对称中心、等腰梯形、等分线段比例线段、勾股定理、黑金分割、比例外项、比例内项、比例中项比例定理、相似系数、位似图形、位似中心、内公切线、外公切线正多边形、扇形面积、互否命题、互逆命题、等价命题、尺寸注法标准方程、平移公式、旋转公式、有向线段、定比分点、有向直线经验公式、有心曲线、无心曲线、参数方程、普通方程、极坐标系等速螺线、异面直线、直二面角、凸多面体、祖恒原理、体积单位球面距离、凸多面角、直三角面、正多面体、欧拉定理、连续函数复合函数、中间变量、瞬间速度、瞬时功率、二阶导数、近似计算辅助函数、不定积分、被积函数、积分变量、积分常数、凑微分法相对误差、绝对误差、带余除法、微分方程、初等变换、立体几何平面几何、解析几何、初等函数、等差数列四舍五入法、纯循环小数、一次二项式、二次三项式、最大公约数最小公倍数、代入消元法、加减消元法、平方差公式、立方差公式立方和公式、提公因式法、分组分解法、十字相乘法、最简公分母算数平方根、完全平方数、几次算数根、因式分解法、双二次方程负整数指数、科学记数法、有序实数对、两点间距离、解析表达式正比例函数、反比例函数、三角函数表、样本标准差、样本分布表总体平均数、样本平均数、集合不相交、基本恒等式、最小正周期两角和公式、两角差公式、反三角函数、反正弦函数、反余弦函数反正切函数、反余切函数、第一象限角、第二象限角、第三象限角第四象限角、线性方程组、二阶行列式、三阶行列式、四阶行列式对角钱法则、系数行列式、代数余子式、降阶展开法、绝对不等式条件不等式、矛盾不等式、克莱姆法则、算术平均数、几何平均数一元多项武、乘法单调性、加法单调性、最小正周期、零次多项式待定系数法、辗转相除法、二项式定法、二项展开式、二项式系数数学归纳法、同解不等式、垂直平分线、互为邻补角、等腰三角形等边三角形、锐角三角形、钝角三角形、直角三角形、全等三角形边角边公理、角边角公理、边边边定理、轴对称图形、第四比例项外角平分线、相似多边形、内接四边形、相似三角形、内接三角形内接多边形、内接五边形、外切三角形、外切多边形、共轭双曲线斜二测画法、三垂线定理、平行六面体、直接积分法、换元积分法第二积分法、分部积分法、混循环小数、第一积分法、同类二次根一元一次方程、一元二次方程、完全平方公式、最简二次根式直接开平方法、半开半闭区间、万能置换公式、绝对值不等式实系数多项式、复系数多项式、整系数多项式、不等边三角形中心对称图形、基本初等函数、基本积分公式、分部积分公式二元一次方程、三元一次方程一元一次不等式、一元二次不等式、二元一次方程组三元一次方程组、二元二次方程组、平面直角坐标系等腰直角三角形、二元一次不等式、二元线性方程组三元线性方程组、四元线性方程组、多项式恒等定律一元一次不等式组、三元一次不定方程、三元齐次线性方程组。
数学名词大全
数学名词大全一、集合论1. 集合：由确定的、彼此不同的对象组成的整体。
2. 空集：不包含任何元素的集合。
3. 子集：如果一个集合A中的所有元素都是集合B的元素，那么集合A是集合B的子集。
4. 真子集：如果一个集合A是集合B的子集，并且集合A不等于集合B，那么集合A是集合B的真子集。
5. 幂集：一个集合的所有子集构成的集合。
6. 并集：由两个或多个集合中的所有元素组成的集合。
7. 交集：包含两个或多个集合中共有元素组成的集合。
8. 补集：在全集U中，不包含集合A的元素组成的集合。
9. 对称差：两个集合A和B的对称差是由属于A而不属于B的元素和属于B而不属于A的元素组成的集合。
10. 集合的基数：一个集合中元素的个数。
二、关系与函数1. 关系：集合A和集合B的元素之间的一种对应关系。
2. 函数：一种特殊的二元关系，对于集合A中的每一个元素，都有集合B中唯一确定的元素与之对应。
3. 单射函数：如果函数f的值域中每一个元素都对应原象集合A 中唯一的元素，那么函数f是单射的。
4. 满射函数：如果函数f的值域等于其定义域B，那么函数f是满射的。
5. 双射函数：既是单射又是满射的函数。
6. 恒等函数：将每一个元素映射到自身的函数。
7. 反函数：如果函数f是双射的，那么存在一个函数g，使得g(f(x))=x，f(g(x))=x，那么函数g是函数f的反函数。
8. 复合函数：由两个函数f和g组成的函数，定义为(f∘g)(x)=f(g(x))。
三、代数1. 域：一种代数系统，包含加法、减法、乘法和除法运算，且满足交换律、结合律、分配律和消去律。
2. 环：一种代数系统，包含加法和乘法运算，且满足交换律、结合律和分配律。
3. 布尔代数：一种特殊的环，包含两个元素0和1，以及加法、乘法、补运算。
4. 群：一种代数系统，包含一个二元运算，满足结合律、单位元和逆元。
5. 环同态：保持加法和乘法运算的映射。
6. 群同态：保持群运算的映射。
数学名词英文
数学名词英文以下是一些常见的数学名词的英文翻译：1.Addition - 加法2.Subtraction - 减法3.Multiplication - 乘法4.Division - 除法5.Fraction - 分数6.Decimal - 小数7.Percentage - 百分比8.Algebra - 代数9.Geometry - 几何10.Trigonometry - 三角学11.Calculus - 微积分12.Probability - 概率13.Statistics - 统计学14.Set Theory - 集合论15.Number Theory - 数论16.Function - 函数17.Equation - 方程18.Inequality - 不等式19.Matrix - 矩阵20.Series - 序列21.Parabola - 抛物线22.Circle - 圆23.Triangle - 三角形24.Square - 正方形25.Polygon - 多边形26.Perimeter - 周长27.Area - 面积28.Diameter - 直径29.Radius - 半径30.Circumference - 圆周长31.Hypotenuse - 斜边32.Asymptote - 渐近线33.Tangent - 切线34.Binomial Coefficient - 二项式系数35.Fibonacci Sequence - 斐波那契数列36.Prime Number - 质数posite Number - 合数38.Natural Number - 自然数39.Integer - 整数40.Rational Number - 有理数41.Irrational Number - 无理数42.Real Number - 实数43.Imaginary Number - 虚数44.Exponent - 指数45.Logarithm - 对数46.Pythagorean Theorem - 勾股定理47.Quadratic Formula - 二次公式48.Discriminant - 判别式49.Coordinate Plane - 坐标平面50.Cartesian Coordinate System - 笛卡尔坐标系这些只是数学中一部分基础术语的英文翻译，数学领域非常广泛，包含许多子领域和特定术语。
数学名词表格
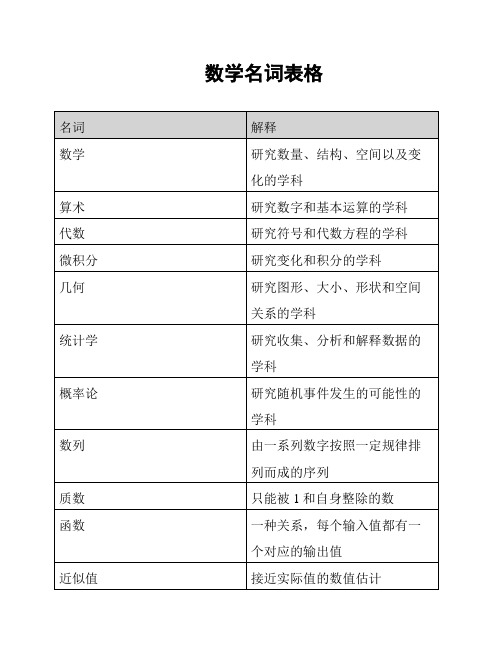
名词
解释
数学
研究数量、结构、空间以及变化的学科
算术
研究数字和基本运算的学科
代数
研究符号和代数方程的学科
微积分
研究变化和积分的学科
几何
研究图形、大小、形状和空间关系的学科
统计学
研究收集、分析和解释数据的学科
概率论
研究随机事件发生的可能性的学科
数列
由一系列数字按照一定规律排列而成的序列
质数
只能被1和自身整除的数
函数
一种关系，每个输入值都有一个对应的输出值
近似值
接近实际值的数值估计
平方根
一个数的平方等于该数的正平方根
对数
表示某个数需要被另一个数的多少次幂才能得到的指数
三角函数
以角度为自变量的函数
复数
由实数和虚数部分组成的数
矩阵
由元素排列成矩形阵列的数学对象
向量
具有大小和方向的量
导数
表示函数变化率的概念
积分
求定积分是一个函数的反导数的过程
数论
研究整数性质和整数关系的学科
以上是一些常见的数学名词及其解释，这些名词在数学中起着重要的作用，对于理解和应用数学知识都非常重要。
谜材-数学名词
谜材-数学名词【数学名词】一字：边、差、长、乘、除、底、点、度、分、高、勾、股、行、和、弧环、集、加、减、积、角、解、宽、棱、列、面、秒、幂、模、球式、势、商、体、项、象、线、弦、腰、圆二字：十位、个位、几何、子集、大圆、小圆、元素、下标、下凸、下凹百位、千位、万位、分子、分母、中点、约分、加数、减数、数位通分、除数、商数、奇数、偶数、质数、合数、乘数、算式、进率因式、因数、单价、数量、约数、正数、负数、整数、分数、倒数乘方、开方、底数、指数、平方、立方、数轴、原点、同号、异号余数、除式、商式、余式、整式、系数、次数、速度、距离、时间方程、等式、左边、右边、变号、相等、解集、分式、实数、根式对数、真数、底数、首数、尾数、坐标、横轴、纵轴、函数、常显变量、截距、正弦、余弦、正切、余切、正割、余割、坡度、坡比频数、频率、集合、数集、点集、空集、原象、交集、并集、差映射、对角、数列、等式、基数、正角、负角、零角、弧度、密位函数、端点、全集、补集、值域、周期、相位、初相、首项、通项公比、公差、复数、虚数、实数、实部、虚部、实轴、虚轴、向量辐角、排列、组合、通项、概率、直线、公理、定义、概念、射线线段、顶点、始边、终边、圆角、平角、锐角、纯角、直角、余角补角、垂线、垂足、斜线、斜足、命题、定理、条件、题设、结论证明、内角、外角、推论、斜边、曲线、弧线、周长、对边、距离矩形、菱形、邻边、梯形、面积、比例、合比、等比、分比、垂心重心、内心、外心、旁心、射影、圆心、半径、直径、定点、定长圆弧、优弧、劣弧、等圆、等弧、弓形、相离、相切、切点、切线相交、割线、外离、外切、内切、内径、外径、中心、弧长、扇形轨迹、误差、视图、交点、椭圆、焦点、焦距、长袖、短轴、准线法线、移轴、转轴、斜率、夹角、曲线、参数、摆线、基圆、极轴极角、平面、棱柱、底面、侧面、侧棱、楔体、球缺、棱锥、斜高棱台、圆柱、圆锥、圆台、母线、球面、球体、体积、环体、环球冠、极限、导数、微分、微商、驻点、拐点、积分、切面、面角极值、三字：被减数、被乘数、被除数、假分数、代分数、质因数、小数点多位数、百分数、单名数、复名数、统计表、统计图、比例尺循环节、近似数、准确数、圆周率、百分位、十分位、千分位万分位、自然数、正整数、负整数、相反数、绝对值、正分数负分数、有理数、正方向、负方向、正因数、负因数、正约数运算律、交换律、结合律、分配律、最大数、最小数、逆运算奇次幂、偶次幂、平方表、立方表、平方数、立方数、被除式代数式、平方和、平方差、立方和、立方差、单项式、多项式二项式、三项式、常数项、一次项、二次项、同类项、填空题选择题、判断题、证明题、未知数、大于号、小于号、等于号恒等号、不等号、公分母、不等式、方程组、代入法、加减法公因式、有理式、繁分式、换元法、平方根、立方式、根指数小数点、无理数、公式法、判别式、零指数、对数式、幂指数对数表、横坐标、纵坐标、自变量、因变量、函数值、解析法解析式、列表法、图象法、指点法、截距式、正弦表、余弦表正切表、余切表、平均数、有限集、描述法、列举法、图示法真子集、欧拉图、非空集、逆映射、自反性、对称性、传递性可数集、可数势、维恩图、反函数、幂函数、角度制、弧度制密位制、定义城、函数值、开区间、闭区间、增函数、减函数单调性、奇函数、偶函数、奇偶性、五点法、公因子、对逆性比较法、综合法、分析法、最大值、最小值、递推式、归纳法复平面、纯虚数、零向量、长方体、正方体、正方形、相交线延长线、中垂线、对预角、同位角、内错角、无限极、长方形平行线、真命题、假命题、三角形、内角和、辅助线、直角边全等形、对应边、对应角、原命题、逆命解、原定理、逆定理对称点、对称轴、多边形、对角线、四边形、五边形、三角形否命题、中位线、相似形、比例尺、内分点、外分点、平面图同心圆、内切圆、外接圆、弦心距、圆心角、圆周角、弓形角内对角、连心线、公切线、公共弦、中心角、圆周长、圆面积反证法、主视图、俯视图、二视图、三视图、虚实线、左视图离心率、双曲线、渐近线、抛物线、倾斜角、点斜式、斜截式两点式、一般式、参变数、渐开线、旋轮线、极坐标、公垂线斜线段、半平面、二面角、斜棱柱、直棱柱、正梭柱、直观图正棱锥、上底面、下底面、多面体、旋转体、旋转面、旋转轴拟柱体、圆柱面、圆锥面、多面角、变化率、左极限、右极限隐函数、显函数、导函数、左导教、右导数、极大值、极小值极大点、极小点、极值点、原函数、积分号、被积式、定积分无穷小、无穷大、连分数、近似数、弦切角四字：混合运算、乘法口诀、循环小数、无限小数、有限小数、简易方程四舍五人、单位长度、加法法则、减法法则、乘法法则、除法法则数量关系、升幂排列、降幂排列、分解因式、完全平方、完全立方同解方程、连续整数、连续奇数、连续偶数、同题原理、最简方程最简分式、字母系数、公式变形、公式方程、整式方程、二次方根三次方根、被开方数、平方根表、立方根表、二次根式、几次方根求根公式、韦达定理、高次方程、分式方程、有理方程、无理方程分数指数、同次根式、异次根式、最简根式、同类根式、常用对数换底公式、反对数表、坐标平面、坐标原点、比例系数、一次函数二次函数、三角函数、正弦定理、余弦定理、样本方差、集合相交等价集合、可数集合、对应法则、指数函数、对数函数、自然对数指数方程、对数方程、单值对应、单调区间、单调函数、诱导公式周期函数、周期交换、振幅变换、相位变换、正弦曲线、余弦曲线正切曲线、余切曲线、倍角公式、半角公式、积化和差、和差化积三角方程、线性方程、主对角线、副对角钱、零多项式、余数定理因式定理、通项公式、有穷数列、无穷数列、等比数列、总和符号特殊数列、不定方程、系数矩阵、增广炬阵、初等变换、虚数单位共轭复数、共轭虚数、辐角主值、三角形式、代数形式、加法原理乘法原理、几何图形、平面图形、等量代换、度量单位、角平分线互为余角、互为补角、同旁内角、平行公理、性质定理、判定定理斜三角形、对应顶点、尺规作图、基本作图、互逆命题、互逆定理凸多边形、平行线段、逆否命题、对称中心、等腰梯形、等分线段比例线段、勾股定理、黑金分割、比例外项、比例内项、比例中项比例定理、相似系数、位似图形、位似中心、内公切线、外公切线正多边形、扇形面积、互否命题、互逆命题、等价命题、尺寸注法标准方程、平移公式、旋转公式、有向线段、定比分点、有向直线经验公式、有心曲线、无心曲线、参数方程、普通方程、极坐标系等速螺线、异面直线、直二面角、凸多面体、祖恒原理、体积单位球面距离、凸多面角、直三角面、正多面体、欧拉定理、连续函数复合函数、中间变量、瞬间速度、瞬时功率、二阶导数、近似计算辅助函数、不定积分、被积函数、积分变量、积分常数、凑微分法相对误差、绝对误差、带余除法、微分方程、初等变换、立体几何平面几何、解析几何、初等函数、等差数列五字：四舍五入法、纯循环小数、一次二项式、二次三项式、最大公约数最小公倍数、代入消元法、加减消元法、平方差公式、立方差公式立方和公式、提公因式法、分组分解法、十字相乘法、最简公分母算数平方根、完全平方数、几次算数根、因式分解法、双二次方负整数指数、科学记数法、有序实数对、两点间距离、解析表达式正比例函数、反比例函数、三角函数表、样本标准差、样本分布表总体平均数、样本平均数、集合不相交、基本恒等式、最小正周期两角和公式、两角差公式、反三角函数、反正弦函数、反余弦函数反正切函数、反余切函数、第一象限角、第二象限角、第三象限角第四象限角、线性方程组、二阶行列式、三阶行列式、四阶行列式对角钱法则、系数行列式、代数余子式、降阶展开法、绝对不等式条件不等式、矛盾不等式、克莱姆法则、算术平均数、几何平均数一元多项武、乘法单调性、加法单调性、最小正周期、零次多项式待定系数法、辗转相除法、二项式定法、二项展开式、二项式系数数学归纳法、同解不等式、垂直平分线、互为邻补角、等腰三角形等边三角形、锐角三角形、钝角三角形、直角三角形、全等三角形边角边公理、角边角公理、边边边定理、轴对称图形、第四比例项外角平分线、相似多边形、内接四边形、相似三角形、内接三角形内接多边形、内接五边形、外切三角形、外切多边形、共轭双曲斜二测画法、三垂线定理、平行六面体、直接积分法、换元积分法第二积分法、分部积分法、混循环小数、第一积分法、同类二次根六字：一元一次方程、一元二次方程、完全平方公式、最简二次根式直接开平方法、半开半闭区间、万能置换公式、绝对值不等式实系数多项式、复系数多项式、整系数多项式、不等边三角形中心对称图形、基本初等函数、基本积分公式、分部积分公式二元一次方程、三元一次方程七字：一元一次不等式、一元二次不等式、二元一次方程组三元一次方程组、二元二次方程组、平面直角坐标系等腰直角三角形、二元一次不等式、二元线性方程组三元线性方程组、四元线性方程组、多项式恒等定律八字及以上：一元一次不等式组、三元一次不定方程、三元齐次线性方程组。
数学的概念名词解释
数学的概念名词解释数学是一门抽象而精确的科学，它研究量、结构、空间以及变化的规律。
在数学的世界中，有许多重要的概念名词需要我们理解和掌握。
本文将对一些常见的数学概念名词进行解释，并探索它们在数学中的应用。
一、数字（Number）数字是用来表示数量或顺序的符号。
在数学中，我们通常使用十进制系统，其中包含了0-9这些基本数字。
基于这些基本数字，我们可以构建出无限大的数集。
数学中的数字有理数和无理数两类，有理数是可以表示为两个整数的比值，而无理数是不能表示为有理数的比值的数字。
无限小数和循环小数都是无理数的特殊情况。
数字在数学中极其重要，它们用于计算、测量、排列和描述事物。
在实际生活中，数字也扮演着重要的角色，我们在购物、统计数据、计时等方面都需要数字的帮助。
二、几何（Geometry）几何是研究空间和形状的数学分支。
它探索点、线、面和体的性质以及它们之间的关系。
几何包括平面几何和立体几何两个部分。
平面几何主要研究二维空间中的图形。
例如，直线、线段、射线、圆、多边形等。
它研究这些图形的性质，如长度、角度、面积和体积，并通过几何定理和公式来解决相关的问题。
立体几何研究三维和更高维空间中的图形。
例如，球体、立方体、圆柱体等。
它探索图形的表面积和体积，以及它们之间的关系。
几何在现实生活中的应用非常广泛，从建筑设计到地图制作，从物体测量到计算机图形学等等，都离不开几何的基本原理和方法。
三、代数（Algebra）代数是研究数量关系和结构的数学分支。
它使用符号和变量来表示数和它们之间的关系。
代数通过使用方程、不等式、函数等工具来解决关于未知量的问题。
代数中的基本概念包括变量、常数、系数、指数、对数、多项式等。
代数中有许多重要的定理和公式，如二次公式、二项式定理等，它们被广泛应用于许多领域。
代数在科学、工程、经济学等领域中有着广泛的应用，例如物理学中描述物体运动的运动方程、经济学中的供需关系等。
四、概率（Probability）概率是研究随机事件发生可能性的数学分支。
数学 名词
数学是一门研究数量、结构、空间和变化等概念的学科，涉及的名词非常广泛。
以下是一些常见的数学名词：
1. 代数：研究数字、字母和代数式的性质和运算。
2. 算术：数学中的基础部分，包括整数、分数、小数等的基本运算。
3. 几何：研究形状、大小、长度、角度等的性质和关系。
4. 函数：一个数学表达式的集合，它描述了一个变量如何依赖于另一个或多个变量。
5. 方程：表示两个数学表达式之间相等关系的式子。
6. 矩阵：一个由数字或代数式组成的矩形阵列，可以用来表示向量、线性变换等。
7. 向量：一个有方向的量，可以表示速度、加速度、力等物理量。
8. 微积分：研究函数的变化率、面积、体积等的数学分支。
9. 微分方程：描述一个或多个变量的变化率与其自身和其他变量的关系。
10. 线性代数：研究线性方程组、向量空间、矩阵等的数学分支。
数学名词大全
cxGMAT必背单词之数学名词大全20093171317985026200931713155169634200931713161016878200931713162751798200931713164351485Algebra & arithmetic terms:Absolute value 绝对值Add (addition) 加Average value 算术平均值Algebra 代数Algebraic expression 代数式Arithmetic mean 算术平均值Arithmetic progression (sequence)等差数列Approximate 近似Abscissa 横坐标Ordinate 纵坐标Binomial 二项式Common factor 公因子Common multiple 公倍数Common divisor 公约数Simple fractionCommon fraction 简分数Complex fraction 繁分数Common logarithm 常用对数Common ratio 公比Complex number 复数Complex conjugate 复共轭Composite number 合数Prime number 质数Consecutive number 连续整数Consecutive even(odd) integer 连续偶(奇)数Cross multiply 交叉相乘Coefficient 系数Complete quadratic equation 完全二次方程Complementary function 余函数Constant 常数Coordinate system 坐标系Decimal 小数Decimal point 小数点Decimal fraction 纯小数Decimal arithmetic 十进制运算Decimal system/decimal scale 十进制Denominator 分母Difference 差Direct proportion 正比Divide 除Divided evenly 被整除Differential 微分Distinct 不同的Dividend 被除数，红利Division 除法Division sign 除号Divisor 因子，除数Divisible 可被整除的Equivalent fractions 等值分数Equivalent equation 等价方程式Equivalence relation 等价关系Even integer/number 偶数Exponent 指数，幂Equation 方程Equation of the first degree 一次方程Endpoint 端点Estimation 近似Factor 因子Factorable quadratic equation 可因式分解的二次方程Incomplete quadratic equation 不完全二次方程Factorial 阶乘Factorization 因式分解Geometric mean 几何平均数Graph theory 图论Inequality 不等式Improper fraction 假分数Infinite decimal 无穷小数Inverse proportion 反比Irrational number 无理数Infinitesimal calculus 微积分Infinity 无穷大Infinitesimal 无穷小Integerable 可积分的Integral 积分Integral domain 整域Integrand 被积函数Integrating factor 积分因子Inverse function 反函数Inverse/reciprocal 倒数Least common denominator 最小公分母Least common multiple 最小公倍数Literal coefficient 字母系数Like terms 同类项Linear 线性的Minuend 被减数Subtrahend 被减数Mixed decimal 混合小数Mixed number 带分数Minor 子行列式Multiplicand 被乘数Multiplication 乘法Multiplier 乘数Monomial 单项式Mean 平均数Mode 众数Median 中数Negative (positive) number 负(正)数Numerator 分子Null set (empty set) 空集Number theory 数论Number line 数轴Numerical analysis 数值分析Natural logarithm 自然对数Natural number 自然数Nonnegative 非负数Original equation 原方程Ordinary scale 十进制Ordinal 序数Percentage 百分比Parentheses 括号Polynomial 多项式Power 乘方Product 积Proper fraction 真分数Proportion 比例Permutation 排列Proper subset 真子集Prime factor 质因子Progression 数列Quadrant 象限Quadratic equation 二次方程Quarter 四分之一Ratio 比率Real number 实数Round off 四舍五入Round to 四舍五入Root 根Radical sign 根号Root sign 根号Recurring decimal 循环小数Sequence 数列Similar terms 同类项Tens 十位Tenths 十分位Trinomial 三相式Units 个位Unit 单位Weighted average 加权平均值Union 并集Yard 码Whole number 整数Mutually exclusive 互相排斥Independent events 相互独立事件Probability 概率Combination 组合Standard deviation 标准方差Range 值域Frequency distribution 频率分布Domain 定义域Bar graph 柱图Geometry terms:Angle bisector 角平分线Adjacent angle 邻角Alternate angel 内错角Acute angle 锐角Obtuse angle 钝角Bisect 角平分线Adjacent vertices 相邻顶点Arc 弧Altitude 高Arm 直角三角形的股Complex plane 复平面Convex (concave) polygon 凸(凹)多边形Complementary angle 余角Cube 立方体Central angle 圆心角Circle 圆Clockwise 顺时钟方向Counterclockwise 逆时钟方向Chord 弦Circular cylinder 圆柱体Congruent 全等的Corresponding angle 同位角Circumference (perimeter) 周长Concentric circles 同心圆Circle graph 扇面图Cone (V =pai * r^2 * h/3) 圆锥Circumscribe 外切Inscribe 内切Diagonal 对角线Decagon 十边形Hexagon 六边形Nonagon 九边形Octagon 八边形Pentagon 五边形Quadrilateral 四边形Polygon 多边形Diameter 直径Edge 棱Equilateral triangle 等边三角形Exterior (interior) angle 外角/内角Extent 维数Exterior angles on the same side of the transversal同旁外角Hypotenuse 三角形的斜边Intercept 截距Included angle 夹角Intersect 相交Inscribed triangle 内接三角形Isosceles triangle 等腰三角形Midpoint 中点Minor axis 短轴Origin 原点Oblique 斜三角形Plane geometry 平面几何Oblateness (ellipse) 椭圆Parallelogram 平行四边形Parallel lines 平行线Perpendicular 垂直的Pythagorean theorem 勾股定理Pie chart 扇图Quadrihedron 三角锥Radius 半径Rectangle 长方形Regular polygon 正多边形Rhombus 菱形Right circular cylinder 直圆柱体Right triangle 直角三角形Right angle 直角Rectangular solid 正多面体Regular prism 正棱柱Regular pyramid 正棱锥Regular solid/polyhedron 正多面体Slope 斜率Sphere ( surface area=4 pai r^2, V=4 pai r^3 / 3)Side 边长Segment of a circle 弧形Semicircle 半圆Solid 立体Square 正方形，平方Straight angle 平角(180度) Supplementary angle 补角Scalene cylinder 斜柱体Scalene triangle 不等边三角形Trapezoid 梯形Volume 体积Width 宽Vertical angle 对顶角Word problem terms:Apiece 每人Per capita 每人Decrease to 减少到Decrease by 减少了Brace 双Cardinal 基数Cent 美分Nickel 五美分Dime 一角Penny 一美分Down payment 定金，预付金Simple interest 单利Compounded interest 复利Foot 英尺Dozen 打Gross = 12 dozen 罗Gallon = 4 quart 加仑Fahrenheit 华氏温度Depth 深度Discount 折扣Cumulative graph 累计图Interest 利息Margin 利润Profit 利润Retail price 零售价Pint 品脱Score 二十Common year 平年Intercalary year(leap year) 闰年Quarter 夸脱代数 ALGEBRA1.数论natural number 自然数 positive number 正数 negative number 负数odd integer, odd number 奇数 even integer, even number 偶数 integer, whole number 整数 positive whole number 正整数 negative whole number 负整数consecutive number 连续整数real number, rational number 实数,有理数 irrational(number)无理数 inverse 倒数composite number 合数e.g. 4,6,8,9,10,12,14,15… prime number 质数e.g. 2,3,5,7,11,13,15… reciprocal 倒数 common divisor 公约数 multiple 倍数 (minimum) common multiple (最小)公倍数 (prime) factor(质)因子common factor 公因子ordinary scale, decimal scale 十进制 nonnegative 非负的 tens 十位 units 个位mode 众数 mean平均数 median中值 common ratio 公比2. 基本数学概念arithmetic mean 算术平均值 weighted average 加权平均值 geometric mean 几何平均数 exponent 指数，幂 base 乘幂的底数,底边 cube 立方数，立方体 square root平方根cube root 立方根common logarithm 常用对数digit 数字 constant 常数variable 变量inverse function 反函数complementary function 余函数 linear 一次的，线性的 factorization 因式分解 absolute value 绝对值，e.g.｜-32｜=32 round off 四舍五入数学3. 基本运算add，plus 加 subtract 减 difference 差 multiply, times 乘product 积divide 除divisible 可被整除的 divided evenly 被整除 dividend 被除数，红利divisor 因子,除数，公约数 quotient 商remainder 余数 factorial 阶乘 power 乘方radical sign, root sign 根号 round to 四舍五入 to the nearest 四舍五入4.代数式，方程，不等式algebraic term 代数项 like terms, similar terms 同类项 numerical coefficient 数字系数literal coefficient 字母系数inequality 不等式triangle inequality 三角不等式 range 值域 original equation 原方程equivalent equation 同解方程，等价方程 linear equation 线性方程(e.g.5x+6=22)5.分数，小数proper fraction 真分数 improper fraction 假分数 mixed number 带分数 vulgar fraction，common fraction 普通分数 simple fraction 简分数 complex fraction 繁分数 numerator 分子 denominator 分母 (least)common denominator (最小)公分母quarter 四分之一 decimal fraction 纯小数 infinite decimal 无穷小数 recurring decimal 循环小数 tenths unit 十分位6. 集合union 并集 proper subset 真子集 solution set 解集7.数列arithmetic progression(sequence) 等差数列 geometric progression(sequence) 等比数列8.其它approximate 近似 (anti)clockwise (逆) 顺时针方向 cardinal 基数ordinal 序数 direct proportion 正比 distinct 不同的 estimation 估计，近似 parentheses 括号 proportion 比例 permutation 排列combination 组合 table 表格 trigonometric function 三角函数 unit 单位,位几何 GEOMETRY1.角alternate angle 内错角 corresponding angle 同位角 vertical angle 对顶角central angle 圆心角 interior angle 内角 exterior angle 外角 supplementary angles 补角complementary angle 余角 adjacent angle 邻角acute angle 锐角obtuse angle 钝角right angle 直角 round angle 周角 straight angle 平角included angle 夹角2.三角形equilateral triangle 等边三角形 scalene triangle 不等边三角形sosceles triangle 等腰三角形 right triangle 直角三角形 oblique 斜三角形 inscribed triangle 内接三角形3.收敛的平面图形，除三角形外semicircle 半圆 concentric circles 同心圆 quadrilateral 四边形pentagon 五边形hexagon 六边形 heptagon 七边形 octagon 八边形nonagon 九边形 decagon 十边形 polygon 多边形 parallelogram 平行四边形 equilateral 等边形 plane 平面square 正方形，平方 rectangle长方形 regular polygon 正多边形 rhombus 菱形trapezoid 梯形4.其它平面图形arc 弧line, straight line 直线line segment 线段 parallel lines平行线segment of a circle 弧形5.立体图形cube 立方体，立方数 rectangular solid 长方体regular olid/regularpolyhedron 正多面体circular cylinder 圆柱体 cone 圆锥 sphere 球体 solid 立体的6.图形的附属概念plane geometry 平面几何 trigonometry 三角学 bisect 平分ircumscribe 外切inscribe 内切intersect 相交 perpendicular 垂直 Pythagorean theorem 勾股定理(毕达哥拉斯定理)congruent 全等的multilateral 多边的 altitude 高 depth 深度side 边长 circumference, perimeter 周长 adian 弧度 surface area 表面积 volume 体积 arm 直角三角形的股 cross section 横截面 center of a circle 圆心chord 弦diameter 直径radius 半径 angle bisector 角平分线 diagonal 对角线 edge 棱face of a solid 立体的面 hypotenuse 斜边included side 夹边 leg 三角形的直角边median(三角形的)中线 base底边，底数(e.g. 2的5次方，2就是底数) opposite 直角三角形中的对边midpoint 中点 endpoint 端点 vertex (复数形式vertices)顶点tangent 切线的transversal 截线 intercept 截距7.坐标coordinate system 坐标系 rectangular coordinate 直角坐标系 origin 原点abscissa 横坐标 ordinate 纵坐标 number line 数轴 quadrant 象限 slope 斜率complex plane 复平面8.计量单位cent 美分 penny 一美分硬币 nickel 5美分硬币 dime 一角硬币 dozen 打(12个) score 廿(20个) Centigrade 摄氏 Fahrenheit 华氏 quart 夸脱 gallon 加仑(1 gallon = 4 quart) yard 码 meter 米 micron 微米 inch 英寸 foot 英尺 minute 分(角度的度量单位，60分=1度)square measure 平方单位制 cubic meter 立方米 pint 品脱(干量或液量的单位)基本规律2 所有的质数(2除外)都是奇数，但奇数不一定是质数2 若b>a，则b/a > (b+1)/(a+1) ；若b < a>其它1.单位类cent 美分 penny 一美分硬币 nickel 5美分硬币 dime 一角硬币 dozen 打(12个) score 廿(20个) Centigrade 摄氏 Fahrenheit 华氏 quart 夸脱 gallon 加仑(1 gallon = 4 quart) yard 码 meter 米 micron 微米 inch 英寸 foot 英尺 minute 分(角度的度量单位，60分=1度) square measure 平方单位制 cubic meter 立方米 pint 品脱(干量或液量的单位)2.有关文字叙述题，主要是有关商业intercalary year(leap year) 闰年(366天) common year 平年(365天) depreciation 折旧 down payment 直接付款 discount 打折 margin 利润 profit 利润interest 利息 simple interest 单利 compounded interest 复利 dividend 红利decrease to 减少到 decrease by 减少了 increase to 增加到 increase by 增加了denote 表示 list price 标价 markup 涨价 per capita 每人 ratio 比率 retail price 零售价 tie 打。
数学课程的名词解释
数学课程的名词解释数学作为一门严谨的学科，是人类思维和科学发展中不可缺少的一部分。
它既是一种工具，用于解决实际问题，也是一种学问，关乎数理逻辑的发展。
在数学的世界中，存在着许多重要的名词和概念，它们承载着数学知识的精华和智慧。
本文将深入解释一些数学课程中的重要名词。
1.代数（Algebra）代数是数学中的一个分支，研究数与数之间的关系，以及使用符号和方程表示这种关系。
代数将自然数扩展为整数、有理数、实数和复数，并对于其中的运算规则和变量进行推导和解决问题。
代数是解决实际问题的重要工具，通过代数学习，我们可以建立模型，预测未来，解决各种数学和现实生活中的难题。
2.几何（Geometry）几何是研究点、线、面及其之间关系的数学分支。
它揭示了空间形态和性质的规律，探究了形状、大小、相似、对称等概念。
几何让我们能够测量、计算和描述物体，从而在工程、建筑和艺术等领域中发挥重要作用。
同时，几何也是逻辑推理和证明的基础，培养了我们运用逻辑和思维能力的重要工具。
3.微积分（Calculus）微积分是数学中的一门学科，主要研究变化和运动的规律。
它由微分学和积分学两部分组成。
微分学研究函数的变化率和导数，揭示了曲线的切线和斜率等概念；积分学研究函数的累积变化和面积等问题，通过求解面积、体积等来求得变化量和变化规律。
微积分应用广泛，可用于物理学、工程学、经济学等领域，是分析和预测变化的重要工具。
4.概率论（Probability Theory）概率论是研究随机事件和可能性的数学学科。
它通过概率模型和统计方法来研究和描述随机现象的规律性。
概率论不仅用于统计学和数理统计，还应用于金融、人工智能、生物学等领域，帮助我们进行风险评估、决策分析以及模型建立。
5.数论（Number Theory）数论是关于整数性质和整数关系的研究。
它探讨数的性质、性质间的规律、数的分解以及数的基本运算等内容。
数论是纯数学中的一个分支，虽然它看似与实际应用关系不大，但它的研究结果广泛应用于密码学、网络安全和编程算法等领域。
数学名词
acronym n.首字母缩略词；字首组合词
across prep.穿过；在?对面；prep.横过，穿过；在?的对面
action n.行动，动作；作用；功能；n.战斗
action 动作
action bar 动作条
action bar pull-down 动作下拉
add vt.添加；增加；加起；做加法；v.把?相加；合计；vt.补充说
addend 加数
add-in 插件
addition n.加，加法；附加物
addition record 附加记录，追加记录
additional a.附加的?；a.附加的，额外的，另外的
additionally 另外，又；ad.此外，而且
" single quotation marks 单引号
"" double quotation marks 双引号
‖ parallel 双线号
& ampersand = and
～ swung dash 代字号
§ section; division 分节号
→ arrow 箭号；参见号
计算机英语专业词汇
A.I. 人工智能
A2A integration A2A整合
abstract 抽象的
abstract base class(ABC) 抽象基类
abstract class 抽象类
Abstract Datatype 抽象数据类型
Abstraction 抽象
abstraction 抽象、抽象物、抽象性
≤ is less than or equal to 小于或等于号
常用的数学名词术语100个
常用的数学名词术语100个数学作为一门学科，拥有丰富的术语和名词，这些术语和名词在数学研究和学习中起着重要的作用。
本文将介绍100个常用的数学名词术语，帮助读者更好地理解数学知识。
1. 数字（Number）：用来表示数量或度量的符号或字符。
2. 数量（Quantity）：表示事物的多少。
3. 数（Count）：用来表示某种事物的个数。
4. 整数（Integer）：不带小数的数字，包括正整数、负整数和零。
5. 正整数（Positive Integer）：大于零的整数。
6. 负整数（Negative Integer）：小于零的整数。
7. 零（Zero）：表示没有数量或空集的数。
8. 分数（Fraction）：表示整体被均等分割的部分。
9. 真分数（Proper Fraction）：分子小于分母的分数。
10. 假分数（Improper Fraction）：分子大于分母的分数。
11. 纯分数（Mixed Fraction）：整数和真分数的组合。
12. 百分数（Percentage）：以100为基数的分数。
13. 分数形式（Fractional Form）：以分数表示的数。
14. 小数（Decimal）：整数和小数部分组成的数。
15. 有限小数（Finite Decimal）：小数部分有限的数。
16. 无限小数（Infinite Decimal）：小数部分无限循环的数。
17. 有理数（Rational Number）：可以表示为两个整数的比值的数。
18. 无理数（Irrational Number）：不能表示为两个整数的比值的数。
19. 实数（Real Number）：包括有理数和无理数的数。
20. 虚数（Imaginary Number）：不能表示为实数的数，形如a+bi。
21. 复数（Complex Number）：实数和虚数的组合。
22. 加法（Addition）：求两个或多个数的和。
23. 减法（Subtraction）：求两个数的差。
谜材 数学名词 数学用语
边、差、长、乘、除、底、点、度、分、高、勾、股、行、和、弧环、集、加、减、积、角、解、宽、棱、列、面、秒、幂、模、球式、势、商、体、项、象、线、弦、腰、圆十位、个位、几何、子集、大圆、小圆、元素、下标、下凸、下凹百位、千位、万位、分子、分母、中点、约分、加数、减数、数位通分、除数、商数、奇数、偶数、质数、合数、乘数、算式、进率因式、因数、单价、数量、约数、正数、负数、整数、分数、倒数乘方、开方、底数、指数、平方、立方、数轴、原点、同号、异号余数、除式、商式、余式、整式、系数、次数、速度、距离、时间方程、等式、左边、右边、变号、相等、解集、分式、实数、根式对数、真数、底数、首数、尾数、坐标、横轴、纵轴、函数、常显变量、截距、正弦、余弦、正切、余切、正割、余割、坡度、坡比频数、频率、集合、数集、点集、空集、原象、交集、并集、差集映射、对角、数列、等式、基数、正角、负角、零角、弧度、密位函数、端点、全集、补集、值域、周期、相位、初相、首项、通项公比、公差、复数、虚数、实数、实部、虚部、实轴、虚轴、向量辐角、排列、组合、通项、概率、直线、公理、定义、概念、射线线段、顶点、始边、终边、圆角、平角、锐角、纯角、直角、余角补角、垂线、垂足、斜线、斜足、命题、定理、条件、题设、结论证明、内角、外角、推论、斜边、曲线、弧线、周长、对边、距离矩形、菱形、邻边、梯形、面积、比例、合比、等比、分比、垂心重心、内心、外心、旁心、射影、圆心、半径、直径、定点、定长圆弧、优弧、劣弧、等圆、等弧、弓形、相离、相切、切点、切线相交、割线、外离、外切、内切、内径、外径、中心、弧长、扇形轨迹、误差、视图、交点、椭圆、焦点、焦距、长袖、短轴、准线法线、移轴、转轴、斜率、夹角、曲线、参数、摆线、基圆、极轴极角、平面、棱柱、底面、侧面、侧棱、楔体、球缺、棱锥、斜高棱台、圆柱、圆锥、圆台、母线、球面、球体、体积、环体、环面球冠、极限、导数、微分、微商、驻点、拐点、积分、切面、面角极值被减数、被乘数、被除数、假分数、代分数、质因数、小数点多位数、百分数、单名数、复名数、统计表、统计图、比例尺循环节、近似数、准确数、圆周率、百分位、十分位、千分位万分位、自然数、正整数、负整数、相反数、绝对值、正分数负分数、有理数、正方向、负方向、正因数、负因数、正约数运算律、交换律、结合律、分配律、最大数、最小数、逆运算奇次幂、偶次幂、平方表、立方表、平方数、立方数、被除式代数式、平方和、平方差、立方和、立方差、单项式、多项式二项式、三项式、常数项、一次项、二次项、同类项、填空题选择题、判断题、证明题、未知数、大于号、小于号、等于号恒等号、不等号、公分母、不等式、方程组、代入法、加减法公因式、有理式、繁分式、换元法、平方根、立方式、根指数小数点、无理数、公式法、判别式、零指数、对数式、幂指数对数表、横坐标、纵坐标、自变量、因变量、函数值、解析法解析式、列表法、图象法、指点法、截距式、正弦表、余弦表正切表、余切表、平均数、有限集、描述法、列举法、图示法真子集、欧拉图、非空集、逆映射、自反性、对称性、传递性可数集、可数势、维恩图、反函数、幂函数、角度制、弧度制密位制、定义城、函数值、开区间、闭区间、增函数、减函数单调性、奇函数、偶函数、奇偶性、五点法、公因子、对逆性比较法、综合法、分析法、最大值、最小值、递推式、归纳法复平面、纯虚数、零向量、长方体、正方体、正方形、相交线延长线、中垂线、对预角、同位角、内错角、无限极、长方形平行线、真命题、假命题、三角形、内角和、辅助线、直角边全等形、对应边、对应角、原命题、逆命解、原定理、逆定理对称点、对称轴、多边形、对角线、四边形、五边形、三角形否命题、中位线、相似形、比例尺、内分点、外分点、平面图同心圆、内切圆、外接圆、弦心距、圆心角、圆周角、弓形角内对角、连心线、公切线、公共弦、中心角、圆周长、圆面积反证法、主视图、俯视图、二视图、三视图、虚实线、左视图离心率、双曲线、渐近线、抛物线、倾斜角、点斜式、斜截式两点式、一般式、参变数、渐开线、旋轮线、极坐标、公垂线斜线段、半平面、二面角、斜棱柱、直棱柱、正梭柱、直观图正棱锥、上底面、下底面、多面体、旋转体、旋转面、旋转轴拟柱体、圆柱面、圆锥面、多面角、变化率、左极限、右极限隐函数、显函数、导函数、左导教、右导数、极大值、极小值极大点、极小点、极值点、原函数、积分号、被积式、定积分无穷小、无穷大、连分数、近似数、弦切角混合运算、乘法口诀、循环小数、无限小数、有限小数、简易方程四舍五人、单位长度、加法法则、减法法则、乘法法则、除法法则数量关系、升幂排列、降幂排列、分解因式、完全平方、完全立方同解方程、连续整数、连续奇数、连续偶数、同题原理、最简方程最简分式、字母系数、公式变形、公式方程、整式方程、二次方根三次方根、被开方数、平方根表、立方根表、二次根式、几次方根求根公式、韦达定理、高次方程、分式方程、有理方程、无理方程分数指数、同次根式、异次根式、最简根式、同类根式、常用对数换底公式、反对数表、坐标平面、坐标原点、比例系数、一次函数二次函数、三角函数、正弦定理、余弦定理、样本方差、集合相交等价集合、可数集合、对应法则、指数函数、对数函数、自然对数指数方程、对数方程、单值对应、单调区间、单调函数、诱导公式周期函数、周期交换、振幅变换、相位变换、正弦曲线、余弦曲线正切曲线、余切曲线、倍角公式、半角公式、积化和差、和差化积三角方程、线性方程、主对角线、副对角钱、零多项式、余数定理因式定理、通项公式、有穷数列、无穷数列、等比数列、总和符号特殊数列、不定方程、系数矩阵、增广炬阵、初等变换、虚数单位共轭复数、共轭虚数、辐角主值、三角形式、代数形式、加法原理乘法原理、几何图形、平面图形、等量代换、度量单位、角平分线互为余角、互为补角、同旁内角、平行公理、性质定理、判定定理斜三角形、对应顶点、尺规作图、基本作图、互逆命题、互逆定理凸多边形、平行线段、逆否命题、对称中心、等腰梯形、等分线段比例线段、勾股定理、黑金分割、比例外项、比例内项、比例中项比例定理、相似系数、位似图形、位似中心、内公切线、外公切线正多边形、扇形面积、互否命题、互逆命题、等价命题、尺寸注法标准方程、平移公式、旋转公式、有向线段、定比分点、有向直线经验公式、有心曲线、无心曲线、参数方程、普通方程、极坐标系等速螺线、异面直线、直二面角、凸多面体、祖恒原理、体积单位球面距离、凸多面角、直三角面、正多面体、欧拉定理、连续函数复合函数、中间变量、瞬间速度、瞬时功率、二阶导数、近似计算辅助函数、不定积分、被积函数、积分变量、积分常数、凑微分法相对误差、绝对误差、带余除法、微分方程、初等变换、立体几何平面几何、解析几何、初等函数、等差数列四舍五入法、纯循环小数、一次二项式、二次三项式、最大公约数最小公倍数、代入消元法、加减消元法、平方差公式、立方差公式立方和公式、提公因式法、分组分解法、十字相乘法、最简公分母算数平方根、完全平方数、几次算数根、因式分解法、双二次方程负整数指数、科学记数法、有序实数对、两点间距离、解析表达式正比例函数、反比例函数、三角函数表、样本标准差、样本分布表总体平均数、样本平均数、集合不相交、基本恒等式、最小正周期两角和公式、两角差公式、反三角函数、反正弦函数、反余弦函数反正切函数、反余切函数、第一象限角、第二象限角、第三象限角第四象限角、线性方程组、二阶行列式、三阶行列式、四阶行列式对角钱法则、系数行列式、代数余子式、降阶展开法、绝对不等式条件不等式、矛盾不等式、克莱姆法则、算术平均数、几何平均数一元多项武、乘法单调性、加法单调性、最小正周期、零次多项式待定系数法、辗转相除法、二项式定法、二项展开式、二项式系数数学归纳法、同解不等式、垂直平分线、互为邻补角、等腰三角形等边三角形、锐角三角形、钝角三角形、直角三角形、全等三角形边角边公理、角边角公理、边边边定理、轴对称图形、第四比例项外角平分线、相似多边形、内接四边形、相似三角形、内接三角形内接多边形、内接五边形、外切三角形、外切多边形、共轭双曲线斜二测画法、三垂线定理、平行六面体、直接积分法、换元积分法第二积分法、分部积分法、混循环小数、第一积分法、同类二次根一元一次方程、一元二次方程、完全平方公式、最简二次根式直接开平方法、半开半闭区间、万能置换公式、绝对值不等式实系数多项式、复系数多项式、整系数多项式、不等边三角形中心对称图形、基本初等函数、基本积分公式、分部积分公式二元一次方程、三元一次方程一元一次不等式、一元二次不等式、二元一次方程组三元一次方程组、二元二次方程组、平面直角坐标系等腰直角三角形、二元一次不等式、二元线性方程组三元线性方程组、四元线性方程组、多项式恒等定律一元一次不等式组、三元一次不定方程、三元齐次线性方程组。
数学名词
Integer整数negative负的positive正的distinct不同的Even偶odd 奇difference 减法sum 和product 乘积Quotient 商consecutive连续的remainder 余数prime质数Factor，divisor元素因数multiple 倍数union 并集intersection交集absolute value绝对值nonnegative非负的tri-三treble 三倍的decimal小数的，十进制的parallel平行perpendicular 垂直line segment线段angle 角right angle 直角acute angle 锐角obtuse angle 钝角cube 立方体area 面积perimeter 周长volume 体积diameter 直径radius 半径radio 比例in terms of 用……来表示digit 0-9中任意一个数equation 等式one-third 1/3 median 中位数mode 众数average 平均数semi-一半的…approximation 近似值tenth十分位domain 定义域range值域fraction分数circumference圆周长square 平方，正方形origin原点quadrilateral 四边形rectangle 长方形triangle 三角形intersect 相交midpoint 中点equilateral 等边isosceles等腰diagonal 对角线inscribe内切X-axis X轴coordinate坐标parallelograms 平行四边形edge 边random 任意的，随机的denominator 分母numerator 分子subtract 减identical 一样的sphere球inverse 相反的constant 常数衡量。
[经典]数学名词
![[经典]数学名词](https://img.taocdn.com/s3/m/2680855232687e21af45b307e87101f69e31fbb4.png)
数学名词抛物线直线边、差、长、乘、除、底、点、度、分、高、勾、股、行、和、弧环、集、加、减、积、角、解、宽、棱、列、面、秒、幂、模、球式、势、商、体、项、象、线、弦、腰、圆十位、个位、几何、子集、大圆、小圆、元素、下标、下凸、下凹百位、千位、万位、分子、分母、中点、约分、加数、减数、数位通分、除数、商数、奇数、偶数、质数、合数、乘数、算式、进率因式、因数、单价、数量、约数、正数、负数、整数、分数、倒数乘方、开方、底数、指数、平方、立方、数轴、原点、同号、异号余数、除式、商式、余式、整式、系数、次数、速度、距离、时间方程、等式、左边、右边、变号、相等、解集、分式、实数、根式对数、真数、底数、首数、尾数、坐标、横轴、纵轴、函数、常显变量、截距、正弦、余弦、正切、余切、正割、余割、坡度、坡比频数、频率、集合、数集、点集、空集、原象、交集、并集、差集映射、对角、数列、等式、基数、正角、负角、零角、弧度、密位函数、端点、全集、补集、值域、周期、相位、初相、首项、通项公比、公差、复数、虚数、实数、实部、虚部、实轴、虚轴、向量辐角、排列、组合、通项、概率、直线、公理、定义、概念、射线线段、顶点、始边、终边、圆角、平角、锐角、纯角、直角、余角补角、垂线、垂足、斜线、斜足、命题、定理、条件、题设、结论证明、内角、外角、推论、斜边、曲线、弧线、周长、对边、距离矩形、菱形、邻边、梯形、面积、比例、合比、等比、分比、垂心重心、内心、外心、旁心、射影、圆心、半径、直径、定点、定长圆弧、优弧、劣弧、等圆、等弧、弓形、相离、相切、切点、切线相交、割线、外离、外切、内切、内径、外径、中心、弧长、扇形轨迹、误差、视图、交点、椭圆、焦点、焦距、长袖、短轴、准线法线、移轴、转轴、斜率、夹角、曲线、参数、摆线、基圆、极轴极角、平面、棱柱、底面、侧面、侧棱、楔体、球缺、棱锥、斜高棱台、圆柱、圆锥、圆台、母线、球面、球体、体积、环体、环面球冠、极限、导数、微分、微商、驻点、拐点、积分、切面、面角极值被减数、被乘数、被除数、假分数、代分数、质因数、小数点多位数、百分数、单名数、复名数、统计表、统计图、比例尺循环节、近似数、准确数、圆周率、百分位、十分位、千分位万分位、自然数、正整数、负整数、相反数、绝对值、正分数负分数、有理数、正方向、负方向、正因数、负因数、正约数运算律、交换律、结合律、分配律、最大数、最小数、逆运算奇次幂、偶次幂、平方表、立方表、平方数、立方数、被除式代数式、平方和、平方差、立方和、立方差、单项式、多项式二项式、三项式、常数项、一次项、二次项、同类项、填空题选择题、判断题、证明题、未知数、大于号、小于号、等于号恒等号、不等号、公分母、不等式、方程组、代入法、加减法公因式、有理式、繁分式、换元法、平方根、立方式、根指数小数点、无理数、公式法、判别式、零指数、对数式、幂指数对数表、横坐标、纵坐标、自变量、因变量、函数值、解析法解析式、列表法、图象法、指点法、截距式、正弦表、余弦表正切表、余切表、平均数、有限集、描述法、列举法、图示法真子集、欧拉图、非空集、逆映射、自反性、对称性、传递性可数集、可数势、维恩图、反函数、幂函数、角度制、弧度制密位制、定义城、函数值、开区间、闭区间、增函数、减函数单调性、奇函数、偶函数、奇偶性、五点法、公因子、对逆性比较法、综合法、分析法、最大值、最小值、递推式、归纳法复平面、纯虚数、零向量、长方体、正方体、正方形、相交线延长线、中垂线、对预角、同位角、内错角、无限极、长方形平行线、真命题、假命题、三角形、内角和、辅助线、直角边全等形、对应边、对应角、原命题、逆命解、原定理、逆定理对称点、对称轴、多边形、对角线、四边形、五边形、三角形否命题、中位线、相似形、比例尺、内分点、外分点、平面图同心圆、内切圆、外接圆、弦心距、圆心角、圆周角、弓形角内对角、连心线、公切线、公共弦、中心角、圆周长、圆面积反证法、主视图、俯视图、二视图、三视图、虚实线、左视图离心率、双曲线、渐近线、抛物线、倾斜角、点斜式、斜截式两点式、一般式、参变数、渐开线、旋轮线、极坐标、公垂线斜线段、半平面、二面角、斜棱柱、直棱柱、正梭柱、直观图正棱锥、上底面、下底面、多面体、旋转体、旋转面、旋转轴拟柱体、圆柱面、圆锥面、多面角、变化率、左极限、右极限隐函数、显函数、导函数、左导教、右导数、极大值、极小值极大点、极小点、极值点、原函数、积分号、被积式、定积分无穷小、无穷大、连分数、近似数、弦切角混合运算、乘法口诀、循环小数、无限小数、有限小数、简易方程四舍五人、单位长度、加法法则、减法法则、乘法法则、除法法则数量关系、升幂排列、降幂排列、分解因式、完全平方、完全立方同解方程、连续整数、连续奇数、连续偶数、同题原理、最简方程最简分式、字母系数、公式变形、公式方程、整式方程、二次方根三次方根、被开方数、平方根表、立方根表、二次根式、几次方根求根公式、韦达定理、高次方程、分式方程、有理方程、无理方程分数指数、同次根式、异次根式、最简根式、同类根式、常用对数换底公式、反对数表、坐标平面、坐标原点、比例系数、一次函数二次函数、三角函数、正弦定理、余弦定理、样本方差、集合相交等价集合、可数集合、对应法则、指数函数、对数函数、自然对数指数方程、对数方程、单值对应、单调区间、单调函数、诱导公式周期函数、周期交换、振幅变换、相位变换、正弦曲线、余弦曲线正切曲线、余切曲线、倍角公式、半角公式、积化和差、和差化积三角方程、线性方程、主对角线、副对角钱、零多项式、余数定理因式定理、通项公式、有穷数列、无穷数列、等比数列、总和符号特殊数列、不定方程、系数矩阵、增广炬阵、初等变换、虚数单位共轭复数、共轭虚数、辐角主值、三角形式、代数形式、加法原理乘法原理、几何图形、平面图形、等量代换、度量单位、角平分线互为余角、互为补角、同旁内角、平行公理、性质定理、判定定理斜三角形、对应顶点、尺规作图、基本作图、互逆命题、互逆定理凸多边形、平行线段、逆否命题、对称中心、等腰梯形、等分线段比例线段、勾股定理、黑金分割、比例外项、比例内项、比例中项比例定理、相似系数、位似图形、位似中心、内公切线、外公切线正多边形、扇形面积、互否命题、互逆命题、等价命题、尺寸注法标准方程、平移公式、旋转公式、有向线段、定比分点、有向直线经验公式、有心曲线、无心曲线、参数方程、普通方程、极坐标系等速螺线、异面直线、直二面角、凸多面体、祖恒原理、体积单位球面距离、凸多面角、直三角面、正多面体、欧拉定理、连续函数复合函数、中间变量、瞬间速度、瞬时功率、二阶导数、近似计算辅助函数、不定积分、被积函数、积分变量、积分常数、凑微分法相对误差、绝对误差、带余除法、微分方程、初等变换、立体几何平面几何、解析几何、初等函数、等差数列四舍五入法、纯循环小数、一次二项式、二次三项式、最大公约数最小公倍数、代入消元法、加减消元法、平方差公式、立方差公式立方和公式、提公因式法、分组分解法、十字相乘法、最简公分母算数平方根、完全平方数、几次算数根、因式分解法、双二次方程负整数指数、科学记数法、有序实数对、两点间距离、解析表达式正比例函数、反比例函数、三角函数表、样本标准差、样本分布表总体平均数、样本平均数、集合不相交、基本恒等式、最小正周期两角和公式、两角差公式、反三角函数、反正弦函数、反余弦函数反正切函数、反余切函数、第一象限角、第二象限角、第三象限角第四象限角、线性方程组、二阶行列式、三阶行列式、四阶行列式对角钱法则、系数行列式、代数余子式、降阶展开法、绝对不等式条件不等式、矛盾不等式、克莱姆法则、算术平均数、几何平均数一元多项武、乘法单调性、加法单调性、最小正周期、零次多项式待定系数法、辗转相除法、二项式定法、二项展开式、二项式系数数学归纳法、同解不等式、垂直平分线、互为邻补角、等腰三角形等边三角形、锐角三角形、钝角三角形、直角三角形、全等三角形边角边公理、角边角公理、边边边定理、轴对称图形、第四比例项外角平分线、相似多边形、内接四边形、相似三角形、内接三角形内接多边形、内接五边形、外切三角形、外切多边形、共轭双曲线斜二测画法、三垂线定理、平行六面体、直接积分法、换元积分法第二积分法、分部积分法、混循环小数、第一积分法、同类二次根一元一次方程、一元二次方程、完全平方公式、最简二次根式直接开平方法、半开半闭区间、万能置换公式、绝对值不等式实系数多项式、复系数多项式、整系数多项式、不等边三角形中心对称图形、基本初等函数、基本积分公式、分部积分公式二元一次方程、三元一次方程一元一次不等式、一元二次不等式、二元一次方程组三元一次方程组、二元二次方程组、平面直角坐标系等腰直角三角形、二元一次不等式、二元线性方程组三元线性方程组、四元线性方程组、多项式恒等定律一元一次不等式组、三元一次不定方程、三元齐次线性方程组。
数学名词汇总
1.数论natural number 自然数positive number 正数negative number 负数odd integer, odd number 奇数even integer, even number 偶数integer, whole number 整数positive whole number 正整数negative whole number 负整数consecutive number 连续整数real number, rational number 实数,有理数irrational(number)无理数inverse 倒数composite number 合数e.g. 4,6,8,9,10,12,14,15…prime number 质数e.g. 2,3,5,7,11,13,15…reciprocal 倒数common divisor 公约数multiple 倍数(minimum) common multiple (最小)公倍数(prime) factor(质)因子common factor 公因子ordinary scale, decimal scale 十进制nonnegative 非负的tens 十位units 个位mode 众数mean平均数median中值common ratio 公比2. 基本数学概念arithmetic mean 算术平均值weighted average 加权平均值geometric mean 几何平均数exponent 指数，幂base 乘幂的底数,底边cube 立方数，立方体square root 平方根cube root 立方根common logarithm 常用对数digit 数字constant 常数variable 变量inverse function 反函数complementary function 余函数linear 一次的，线性的factorization 因式分解absolute value 绝对值，e.g.｜-32｜=32 round off 四舍五入数学3. 基本运算add，plus 加subtract 减difference 差multiply, times 乘product 积divide 除divisible 可被整除的divided evenly 被整除dividend 被除数，红利divisor 因子,除数，公约数quotient 商remainder 余数factorial 阶乘power 乘方radical sign, root sign 根号round to 四舍五入to the nearest 四舍五入4.代数式，方程，不等式algebraic term 代数项like terms, similar terms 同类项numerical coefficient 数字系数literal coefficient 字母系数inequality 不等式triangle inequality 三角不等式range 值域original equation 原方程equivalent equation 同解方程，等价方程linear equation 线性方程(e.g.5x+6=22)5.分数，小数proper fraction 真分数improper fraction 假分数mixed number 带分数vulgar fraction，common fraction 普通分数simple fraction 简分数complex fraction 繁分数numerator 分子denominator 分母(least)common denominator (最小)公分母quarter 四分之一decimal fraction 纯小数infinite decimal 无穷小数recurring decimal 循环小数tenths unit 十分位6. 集合union 并集proper subset 真子集solution set 解集7.数列arithmetic progression(sequence) 等差数列geometric progression(sequence) 等比数列8.其它approximate 近似(anti)clockwise (逆) 顺时针方向cardinal 基数ordinal 序数direct proportion 正比distinct 不同的estimation 估计，近似parentheses 括号proportion 比例permutation 排列combination 组合table 表格trigonometric function 三角函数unit 单位,位几何GEOMETRY1.角alternate angle 内错角corresponding angle 同位角vertical angle 对顶角central angle 圆心角interior angle 内角exterior angle 外角supplementary angles 补角complementary angle 余角adjacent angle 邻角acute angle 锐角obtuse angle 钝角right angle 直角round angle 周角straight angle 平角included angle 夹角2.三角形equilateral triangle 等边三角形scalene triangle 不等边三角形isosceles triangle 等腰三角形right triangle 直角三角形oblique 斜三角形inscribed triangle 内接三角形3.收敛的平面图形，除三角形外semicircle 半圆concentric circles 同心圆quadrilateral 四边形pentagon 五边形hexagon 六边形heptagon 七边形octagon 八边形nonagon 九边形decagon 十边形polygon 多边形parallelogram 平行四边形equilateral 等边形plane 平面square 正方形，平方rectangle长方形regular polygon 正多边形rhombus 菱形trapezoid 梯形4.其它平面图形arc 弧line, straight line 直线line segment 线段parallel lines平行线segment of a circle 弧形5.立体图形cube 立方体，立方数rectangular solid 长方体regular olid/regularpolyhedron 正多面体circular cylinder 圆柱体cone 圆锥sphere 球体solid 立体的6.图形的附属概念plane geometry 平面几何trigonometry 三角学bisect 平分circumscribe 外切inscribe 内切intersect 相交perpendicular 垂直Pythagorean theorem 勾股定理(毕达哥拉斯定理) congruent 全等的multilateral 多边的altitude 高depth 深度side 边长circumference, perimeter 周长avian 弧度surface area 表面积volume 体积arm 直角三角形的股cross section 横截面center of a circle 圆心chord 弦diameter 直径radius 半径angle bisector 角平分线diagonal 对角线edge 棱face of a solid 立体的面hypotenuse 斜边included side 夹边leg 三角形的直角边median(三角形的)中线base底边，底数(e.g. 2的5次方，2就是底数) opposite 直角三角形中的对边midpoint 中点endpoint 端点vertex (复数形式vertices)顶点tangent 切线的transversal 截线intercept 截距7.坐标coordinate system 坐标系rectangular coordinate 直角坐标系origin 原点abscissa 横坐标ordinate 纵坐标number line 数轴quadrant 象限slope 斜率complex plane 复平面8.计量单位cent 美分penny 一美分硬币nickel 5美分硬币dime 一角硬币dozen 打(12个)score 廿(20个)Centigrade 摄氏Fahrenheit 华氏quart 夸脱gallon 加仑(1 gallon = 4 quart)yard 码meter 米micron 微米inch 英寸foot 英尺minute 分(角度的度量单位，60分=1度) square measure 平方单位制cubic meter 立方米pint 品脱(干量或液量的单位)2.有关文字叙述题，主要是有关商业intercalary year(leap year) 闰年(366天) common year 平年(365天) depreciation 折旧down payment 直接付款discount 打折margin 利润profit 利润interest 利息simple interest 单利compounded interest 复利dividend 红利decrease to 减少到decrease by 减少了increase to 增加到increase by 增加了denote 表示list price 标价markup 涨价per capita 每人ratio 比率retail price 零售价tie 打。
常用的数学名词术语100个
常用的数学名词术语100个1. 数数是数学中最基本的概念，用来表示数量和大小。
2. 数字数字是表示数的符号，包括0-9十个基本数字和无穷多个组合表示的数。
3. 自然数自然数是指从1开始的正整数，包括1、2、3、4等。
4. 整数整数是指包括正整数、负整数和0在内的数，如-3、-2、-1、0、1、2、3等。
5. 有理数有理数是指可以表示为两个整数的比值的数，包括整数和分数。
6. 无理数无理数是不能表示为两个整数的比值的数，如π和根号2等。
7. 实数实数包括有理数和无理数，可以表示数轴上的任意点。
8. 正数正数是指大于0的数，如1、2、3等。
9. 负数负数是指小于0的数，如-1、-2、-3等。
10. 零零是表示没有数量或数量为0的数。
11. 等于等于是指两个数值相同，用等号“=”表示。
12. 不等于不等于是指两个数值不同，用不等号“≠”表示。
13. 大于大于是指一个数值比另一个数值要大，用大于号“>”表示。
14. 小于小于是指一个数值比另一个数值要小，用小于号“<”表示。
15. 大于等于大于等于是指一个数值比另一个数值要大或相等，用大于等于号“≥”表示。
16. 小于等于小于等于是指一个数值比另一个数值要小或相等，用小于等于号“≤”表示。
17. 加法加法是数学中常用的运算，用加号“+”表示，表示两个数值相加的结果。
18. 减法减法是数学中常用的运算，用减号“-”表示，表示两个数值相减的结果。
19. 乘法乘法是数学中常用的运算，用乘号“×”表示，表示两个数值相乘的结果。
20. 除法除法是数学中常用的运算，用除号“÷”表示，表示一个数值被另一个数值除的结果。
21. 平方平方是指一个数值乘以自身的结果，用上标“²”表示。
22. 开方开方是指求一个数值的平方根，用符号“√”表示。
23. 比例比例是指两个量之间的相对关系，用冒号“：”表示。
24. 百分数百分数是指以100为基数的比例数，用百分号“%”表示。
高等数学——基本名词
高等数学——基本名词函数function定义域domain of definition值域range of function极限limit极限值limit value发散diverge收敛converge连续性continuity连续函数continuous funcion左连续continuity from the left开集open set闭集closed set闭区间closed interval区间interval一元函数function of one variable多元函数function of several variables 内点inner point孤立点isolated point领域neighborhood导数derivative偏导数partial derivative微分differential calculus全微分total differential偏微分partial differential积分integral重积分infinitesimal calculus二重积分double integral逆时针方向counterclockwise轴axis象限quadrant变量variable常量constant quentity坐标轴axis of coordinates横坐标abscissa纵坐标ordinate锐角acute angle钝角obtuse angle平角straight angle直角right angle圆circle半径radius直径diameter三角形triangle斜率slope无穷小infinitesimal无穷大intinite正positive负negative凸convex凹concave椭圆ellipse双曲线hyperbola曲线curve曲面surface交intersection三重积分threefold integral补集complement中值定理law of the mean投影project极值extreme values等差级数arithmetical progression定积分definite integral几何级数geometric progression不定积分indefinite integral公理axioms曲线积分curvilinear integral定义definition曲面积分surface integral定理theorem级数progression集合set数列sequence元素element微分方程differential equations空集empty常微分方程partial differential equation 子集subset偏微分方程partial differential equation 相等equal差分方程difference equation常数constant特征方程characteristic equation对数logarithm间断点discontinuity point指数exponential渐近线asymptote曲率curvature切线tangent line曲率圆circle of curvature切线方程tangential equation曲率半径radius of curvature法线normal line切平面tangent plane螺旋线helices法平面normal plane拐点point of inflexion幂级数power series绝对收敛absolutely convergence 收敛半径convergence radius条件收敛conditional convergence 收敛区间convergence interval和函数sum function收敛区域convergence region解solution通解general solution初始条件initial condition特解special solution条件极值conditional extremum 阶order。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、公理是一些显而易见、能被大家所接受的但却是无法证明的命题。
任何一门数学学科都是建立在某一个或几个公理的基础上演绎而成的。
例如平面几何是建立在三条公理的基础上的，例如“过两点可以作并且只可以作一条直线。
”、“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”这是无法证明的，只能把它作为公理。
当然作为一门学科，公理应该越少越好。
（
平面几何十大公理
1.过两点有且只有一条直线.
2.两点之间,线段最短.
3.垂线段最短.
4.过一点有且只有一条直线与已知直线垂直.
5.过直线外一点有且只有一条直线与已知直线平行.(平行公理)
6.同位角相等,两直线平行.
7.有两边及其夹角对应相等的两个三角形全等.(SAS)
8.有两角及其夹边对应相等的两个三角形全等.(ASA)
9.三边对应相等的两个三角形全等.(SSS) 10.斜边和一条直角边对应相等的两个直角三角形全等.(HL)
也有六大公理的说法只是有些合关到一起了。
1.过两点有且只有一条直线.
2.两点之间,线段最短.
3.过一点有且只有一条直线与已知直线垂直
4. 过直线外一点有且只有一条直线与已知直线平行.(平行公理)
5. 同位角相等,两直线平行
6.三角形的全等SAS ASA SSS
）
2、定义就是规定，为了说起来方便，也为了学习数学的时候大家有共同的语言，对一些概念、名词、记号等等必须作出规定，这就是定义。
在这里常常看到一些人说出非常外行的话，甚至概念混淆，这些人与学习数学的人之间还没有共同语言，所以很多问题没有办法说清楚。
数学命题(mathematical proposition)是一类重要的命题，通常指数学中的判断。
数学中的定义、公理、公式、性质、法则、定理都是数学命题.
命题这个概念是可以被定义并观察的现象.命题不是指判断（陈述）本身,而是指所表达的语义.当相异判断（陈述）具有相同语义的时候,他们表达相同的命题.即定义是人为规定的,命题是判断句式,命题有真假,定义没有。
真命题：逻辑学术语。
真值只能取两个值：真或假。
真对应判断正确，假对应判断错误。
任何命题的真值都是唯一的，称真值为真的命题为真命题。
（真命题就是正确的命题，即如果命题的题设成立，那么结论一定成立．如：
①两条平行线被第三条直线所截，内错角相等．
②如果a＞b，b＞c那么a＞c．
③对顶角相等．
公理是人们在长期实践中总结出来的、正确的命题，它不需要用其他的方法来证明，初一几何中我们过的主要公理有：
①经过两点有一条直线，并且只有一条直线．
②经过直线外一点有且只有一条直线与这条直线平行．
③同位角相等，两直线平行．
④两直线平行，同位角相等．
）
定理是根据公理或已知的定理推导出来的真命题．这些真命题都是最基本的和常用的，所以被人们选作定理．还有许多经过证明的真命题没有被选作定理．所以，定理都是真命题，而真命题不都是定理．例如：“若∠1=∠2，∠2=∠3，那么∠1=∠3”，这就是一个真命题，但不能说是定理．我们在以后数学学习和处理数学问题（例如解题时）的时候可以使用，一门数学学科学习得如何，很大程度上取决于对定理的熟悉程度。
总之，公理和定理都是真命题，但有的真命题既不是公理．也不是定理．公理和定理的区别主要在于：公理的正确性不需要用推理来证明，而定理需要证明．
3、定理就是经过证明的命题，
4、推论也是定理，如果一个结论非常容易由某个定理的结论稍作处理后得到，常常把这样的定理写作是这一个定理的推论。
公理
我们学过一些图形的性质,都是真命题.其中有些命题,如“两点确定一条直线”、“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”等,它们的正确性是人们在长期的实践中总结出来的,并作为判定其他命题真假的根据,这样的真命题称为公理.
定理和证明
还有一些命题,例如“对顶角相等”、“两直线平行,内错角相等”等,它们的正确性是用推理证实的,这样的真命题叫做定理,
叫做证明.
下面,我们以证明“”来说明什么是证明.
从这个例子可以看出,证明是由题设（已知）出发,经过一步步的
推理,最后推出结论（求证）正确的过程.
注意,证明中的每一步推理都要有根据,不能“想当然”.这些根
据,可以是已知条件,也可以是定义、公理、已经学过的定理.在初学
证明时,要求把根据写在第一步推理后面的括号内,其中象等量代换,
利用等式性质加减乘除等代数运算可不注理由。