导热基本定律
合集下载
热工基础第11章 导热
解:2）求总散热量：
tw1 tw4
15 5
97.3W
R1 R2 R3 0.0014 2 0.1
3）求玻璃表面温度：
1
A
tw1
tw2 d1
tw3同理
tw2
tw1
d 1 1A
15
97.3 0.003 1.05 2 1
14.86C
3
tw1 tw4 1 ln di1
i1 2i di
解：1）求各层的导热热阻：
R1
R 3
d1 A 1
0.003 2 11.05
0.0014K
/WR 2d2 A 20.005 2 1 0.025
0.1K
/W
R2 0.1 71.43 R1 0.0014
例题1.一双层玻璃窗，高2m，1m宽，玻璃厚3mm， =1.05W/(m·K)。空气夹层厚5mm，空气完全静止， =0.025W/(m·K) 。冬季室内外玻璃表面的温度 分别为15℃和5℃ ，求双层窗的散热量和空气夹 层两侧玻璃表面的温度，并比较玻璃与空气夹层 的导热热阻。
二、热导率
q
-grad t
—— 物质的重要热物性参数
热导率的数值：就是物体中单位温度梯度、单位 时间、通过单位面积的导热量。
热导率的数值表征物质导热能力大小。实验测定
影响热导率的因素：物质的种类、材料成分、 温度、湿度、压力、密度等。
材料的种类影响
同种物质的热导率，固态最大，气态最小； 一般金属的热导率大于非金属的热导率； 纯金属的热导率大于它的合金； 同种物质，晶体的热导率大于非晶体； 导电性能好的金属，导热性能也好； 各向异性物体，热导率大小与方向有关。
传热学2.1 导热基本定律—傅立叶定律
2.1 导热基本定律—傅立叶定律研究方法：从连续介质的假设出发、从宏观的角度来讨论导热热流 量与物体温度分布及其他影响因素之间的关系。
一般情况下，绝大多数固体、液体及气体都可以看作连 续介质。
但是当分子的平均自由行程与物体的宏观尺寸相比 不能忽略时，如压力降低到一定程度的稀薄气体，就不能认 为是连续介质。
主要内容：（1）导热的基本概念、导热基本定律 ；（2）导热现象的数学描述方法； （3）几种稳态导热的计算方法。
2.1 导热基本定律—傅立叶定律气体——导热是气体分子不规则热运动 导 电 固 体——自由电子的运动 非导电固体——过晶格结构的振动(弹性声波)液体——类似气体 or 类似非导电固体1. 温度场(温度分布)：指在各个时刻物体内各点温度分布的总称。
物体的温度分布是坐标和时间的函数 t = f (x, y, z,τ ) 稳态温度场(定常温度场) t = f (x, y, z) 非稳态温度场(非定常温度场) t = f (x, y, z,τ )2.1 导热基本定律—傅立叶定律2. 等温面与等温线 等温面：同一时刻、温度场中所有温度 相同的点连接起来所构成的面 等温线：用一个平面与各等温面相交， 在这个平面上得到一个等温线簇等温面与等温线的特点： 彼此不能相交 不会中断，它们或者是物体中完全封闭的曲面（曲线），或者就终止与物体的边界上t+Δt t t-Δt2.1 导热基本定律—傅立叶定律2. 等温面与等温线 等温线图的物理意义： 若每条等温线间 的温度间隔相等 时，等温线的疏 密可反映出不同 区域导热热流密 度的大小。
如图 所示是用等温线 图表示温度场的 实例。
2.1 导热基本定律—傅立叶定律3. 温度梯度在温度场中，温度沿x方向的 变化率(即偏导数)∂t = ∂xlimΔt ΔxΔx → 0明显, 等温面法线方向的温度变化率最大，温度变化最剧烈。
∂t < ∂t ∂x ∂n温度梯度：等温面法线方向的温度变化率矢量：gradt = ∂t n ∂n温度梯度是矢量，指向温 度增加的方向。
热量传递的三种基本方式导热(热传导)、对流(热对流)和热辐射。
一. 大空间自然对流换热的实验关联式 工程中广泛使用的是下面的关联式：
l / d 60
层流
湍流
二. 横掠管束换热实验关联式
• 外掠管束在换热器 中最为常见。 • 通常管子有叉排和 顺排两种排列方式。 顺叉排换热的比较： 叉排换热强、阻力 损失大并难于清洗。 影响管束换热的因 Pr 素除 Re 、 数外，还 有：叉排或顺排； 管间距；管束排数 等。
后排管受前排管尾流的扰动作用对平均表面传热系数的影 响直到10排以上的管子才能消失。 这种情况下，先给出不考虑排数影响的关联式，再采用管 束排数的因素作为修正系数。 气体横掠10排以上管束的实验关联式为
(5) 流体的热物理性质：
3 密度 [kg m ] 热导率 [ W (m C) ] 2 比热容 c [J (kg C) ] 动力粘度 [ N s m ] 运动粘度 [m 2 s] 体胀系数 [1 K ]
1 v 1 v T p T p
Nu c Re n Nu c Re n Pr m Nu c(Gr Pr)n
式中，c、n、m 等需由实验数据确定，通常由图解法和 最小二乘法确定
④常见准则数的定义、物理意义和表达式，及其各量的 物理意义
⑤模化试验应遵循的准则数方程 强制对流:
Nu f (Re, Pr)； Nu x f ( x ' , Re, Pr)
导热热阻：平壁，圆筒壁
q
t w1 t w 2 t w1 t w 2
t r t R
t
t w1
dt
dx
Φ
A
Q
0
tw2
R A
r
传热学(第二章)
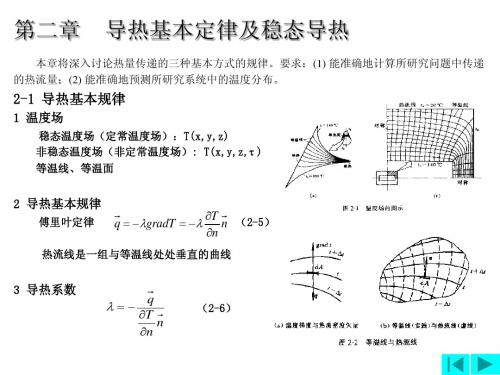
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
边界条件：r=r1时，t=t1；r=r2时，t=t2 对（2-25）式积分两次，得其通解： t = c1 ln r + c2 将边界条件代入通解，确定积分常数
t2 − t1 t −t c2 = t1 − ln r 2 1 ln( r2 / r ) ln( r2 / r ) 1 1 t −t t = t1 + 2 1 ln( r / r ) （2-26） 1 ln( r2 / r ) 1 dt λ t1 − t2 q = −λ = （2-27） dr r ln( r2 / r ) 1 c1 =
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁、圆筒壁、球壳和其他变截面物体的导热 通过平壁、圆筒壁、
• 1∂ ∂T 1 ∂ ∂T ∂ ∂T ∂T (λr + 2 (λ ) + (λ ) + Φ = ρcp ∂τ r ∂r ∂r) r ∂ϕ ∂ϕ ∂z ∂z d dt 简化变为 dr (r dr ) = 0 （2-25）
⒉ 通过圆筒壁的导热 根据热阻的定义，通过整个圆筒壁的导热热阻为 （2-29） 29） 与分析多层平壁—样，运用串联热阻叠加的原则，可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 − t4 ) Φ= （2-30） ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数，无内热源的空心球壁。内、外半径为r1、r2，其内外表面均匀 恒定温度为t1、t2，球壁内的温度仅沿半径变化，等温面是同心球面。 由傅立叶定律得： dt 各同心球面上的热流率q不相等，而热流量Φ相等。 Φ = −4πr2λ dr dr ⇒Φ 2 = −4πλdt r
东南大学传热学 第二章 导热基本定律及稳态导热
第二章 导热基本定律 及稳态导热
本章重点讨论稳态导热问题。为此首先介绍 一些相关的基本知识，如温度场、温度剃度、 导热基本定律等；然后应用这些基本知识推 导出求解导热问题的微分方程；最后应用这 些微分方程求解常见的导热问题。
第一节 导热基本定律
温度场
• 定义：某一瞬间物体内的温度分布，称为温度场。 • 分类 1.按温度是否随时间而变化可分为 稳态温度场：物体内温度不随时间的变化而变化的温度场 非稳态温度场：物体内的温度随时间变化而变化的温度场 2.按温度随空间的变化可分为 一维温度场：温度只在一个方向有变化的温度场 二维温度场：温度在两个方向有变化的温度场 三维温度场：温度在三个方向有变化的温度场 • 表示：三种表示方法
n x y z
导热基本定律
• 傅立叶定律：单位时间内通过单位截面积所传 递的热量，正比例于当地垂直于截面方向上的 温度变化率，即温度剃度，其比例系数为导热 系数。
• 表示型式： A t n
n
导热系数
•
定义：
q
t n
n
• 物理意义：单位时间单位面积当温度变化率为1时，由导
热所传递的热量
• 影响因素：主要是物质的种类和物质所处的状态
第三节 通过平壁、圆筒壁、球壳和 其他变截面物体的导热
通过 平壁导热
通过 圆筒壁导热
通过 球壳导热
通过变导热 系数物体 的导热
单层平壁 多层平壁 单层圆筒壁 多层圆筒壁 单层球壳 多层球壳
通过单层平壁的导热
通过单层 平壁的导热
物理模型
数学描写
温度分布
热流量计算
数学描写
d 2t dx2 x
数学描写
温度分布
热流量计算
物理模型
本章重点讨论稳态导热问题。为此首先介绍 一些相关的基本知识，如温度场、温度剃度、 导热基本定律等；然后应用这些基本知识推 导出求解导热问题的微分方程；最后应用这 些微分方程求解常见的导热问题。
第一节 导热基本定律
温度场
• 定义：某一瞬间物体内的温度分布，称为温度场。 • 分类 1.按温度是否随时间而变化可分为 稳态温度场：物体内温度不随时间的变化而变化的温度场 非稳态温度场：物体内的温度随时间变化而变化的温度场 2.按温度随空间的变化可分为 一维温度场：温度只在一个方向有变化的温度场 二维温度场：温度在两个方向有变化的温度场 三维温度场：温度在三个方向有变化的温度场 • 表示：三种表示方法
n x y z
导热基本定律
• 傅立叶定律：单位时间内通过单位截面积所传 递的热量，正比例于当地垂直于截面方向上的 温度变化率，即温度剃度，其比例系数为导热 系数。
• 表示型式： A t n
n
导热系数
•
定义：
q
t n
n
• 物理意义：单位时间单位面积当温度变化率为1时，由导
热所传递的热量
• 影响因素：主要是物质的种类和物质所处的状态
第三节 通过平壁、圆筒壁、球壳和 其他变截面物体的导热
通过 平壁导热
通过 圆筒壁导热
通过 球壳导热
通过变导热 系数物体 的导热
单层平壁 多层平壁 单层圆筒壁 多层圆筒壁 单层球壳 多层球壳
通过单层平壁的导热
通过单层 平壁的导热
物理模型
数学描写
温度分布
热流量计算
数学描写
d 2t dx2 x
数学描写
温度分布
热流量计算
物理模型
《传热学》第2章-导热基本定律及稳态导热
影响热导率的因素：物质的种类、材料成分、温度、 湿度、压力、密度等
λ金属 > λ非金属; λ固相 > λ液相 > λ气相
不同物质的导热机理
1、气体的热导率 λ气体 ≈ 0.006 ~ 0.6 W (mo C)
0o C : λ空气 = 0.0244 W (moC) ; 20o C : λ空气 = 0.026 W (moC)
dΦv = Φ& dxdydz
v 单位时间内，微元体热力学能的增加 dU = ρc ∂t dxdydz ∂τ
导热微分方程式
dΦλ + dΦV = dU
dΦ λ
=
∂ ∂x
λ
∂t ∂x
+
∂ ∂y
λ
∂t ∂y
+
∂ ∂z
λ
∂t ∂z
dxdydz
dΦv = Φ& dxdydz
q = − dΦ n dA
直角坐标系中： q = qxi + qy j + qz k
导热基本定律
v 1822法国数学家傅里叶（Fourier）在大量实验研究的基础 上, 提出了导热基本定律—傅里叶定律。
v 对于物性参数不随方向变化的各向同性物体, 傅里叶定律度
热流密 度矢量
导热微分方程式的求解方法
积分法、分离变量法、积分变换法、数值计算法等
导热微分方程＋单值性条件＋求解方法 è温度场
圆柱坐标系（r, Φ, z）
dz
v 感兴趣的同学
课下自己推导
练习.
v 球坐标系方程 见教材P26.
=
−λ ∂t ∂n w
=0
⇒
λ金属 > λ非金属; λ固相 > λ液相 > λ气相
不同物质的导热机理
1、气体的热导率 λ气体 ≈ 0.006 ~ 0.6 W (mo C)
0o C : λ空气 = 0.0244 W (moC) ; 20o C : λ空气 = 0.026 W (moC)
dΦv = Φ& dxdydz
v 单位时间内，微元体热力学能的增加 dU = ρc ∂t dxdydz ∂τ
导热微分方程式
dΦλ + dΦV = dU
dΦ λ
=
∂ ∂x
λ
∂t ∂x
+
∂ ∂y
λ
∂t ∂y
+
∂ ∂z
λ
∂t ∂z
dxdydz
dΦv = Φ& dxdydz
q = − dΦ n dA
直角坐标系中： q = qxi + qy j + qz k
导热基本定律
v 1822法国数学家傅里叶（Fourier）在大量实验研究的基础 上, 提出了导热基本定律—傅里叶定律。
v 对于物性参数不随方向变化的各向同性物体, 傅里叶定律度
热流密 度矢量
导热微分方程式的求解方法
积分法、分离变量法、积分变换法、数值计算法等
导热微分方程＋单值性条件＋求解方法 è温度场
圆柱坐标系（r, Φ, z）
dz
v 感兴趣的同学
课下自己推导
练习.
v 球坐标系方程 见教材P26.
=
−λ ∂t ∂n w
=0
⇒
导热基本定律
导热基本定律导热基本定律是研究物体传热过程中的一个基本原理，它描述了导热的规律和特性。
导热基本定律是热传导学中非常重要的一个定律，它对于我们理解物体的热传导行为和研究热传导过程具有重要的意义。
热传导是指热量从高温区域传递到低温区域的过程，它是由物质内部的分子热运动引起的。
导热基本定律告诉我们，热量在物体内部的传导速度与物体的温度梯度成正比，与物体的导热性能成反比。
根据导热基本定律，热量的传导速率与物体的温度梯度成正比。
温度梯度是指物体在空间上温度变化的速率。
例如，一个物体的一端温度为100℃，另一端温度为50℃，那么这个物体的温度梯度就是(100-50)/L，其中L为物体的长度。
温度梯度越大，热量的传导速率就越快。
导热基本定律还告诉我们，热量的传导速率与物体的导热性能成反比。
导热性能是指物体传导热量的能力，它与物体的导热系数有关。
导热系数越大，物体的导热性能就越好，热量的传导速率也就越快。
导热系数与物体的材料性质有关，例如金属的导热系数通常比非金属材料大。
导热基本定律的应用非常广泛。
在工程领域，我们常常需要计算物体的热传导速率，以便设计合适的散热装置。
例如，在电子设备中，为了保持设备正常工作温度，通常需要设计散热片或散热风扇来加速热量的散发。
利用导热基本定律，我们可以计算散热装置的尺寸和材料，以确保设备的热量得到有效散发。
在材料科学研究中，导热基本定律也是一个重要的工具。
通过研究不同材料的导热性能，我们可以了解材料的热传导特性，并在实际应用中选择合适的材料。
例如，在建筑材料的选用中，导热性能是一个重要的考虑因素。
对于冬季保温材料，我们希望材料导热系数较小，以减少室内热量的传导损失；而对于夏季隔热材料，我们希望材料导热系数较大，以阻止室外热量的传导入室内。
导热基本定律是研究物体传热过程中的一个基本原理，它描述了热量在物体内部的传导规律和特性。
通过了解导热基本定律，我们可以更好地理解和应用热传导学知识，为工程设计和材料选择提供科学依据。
传热学
• 通过平壁的导热 • 通过圆筒壁的导热 • 通过肋片的导热
• 肋效率 • 1、 定义：实际散热量/假设整个肋表面 处于肋基温度下的散热量。 • 2、 物理意义：表征肋片散热有效程度 的指标。
• 非稳态导热 • 定义：物体的温度随时间而变化的导热 过程称非稳态导热 • 非稳态导热过程中，在与热流量方向相 垂直的不同截面上热流量不相等，这是 非稳态导热区别于稳态导热的一个特点。
传热过程分析和换热器计算
传热过程分析
• 通过平壁的传热 • 通过圆筒壁的传热 • 临界热绝缘直径
• 在传热表面加上保温层能够起到减少传 热的作用。但是在圆筒壁面上增加保温 层却有可能导致传热量的增大。 • 传热过程的总热阻会存在一个极小值,这 就对应着一个传热量的最大值。那么， 在对应总热阻极小值的外直径被称为临 界热绝缘直径
• 、相似原理 物理量相似的性质 • （1）用相同形式且具有相同内容的微分 方程时所描述的现象为同类现象，只有 同类现象才能谈相似。 • （2）彼此相似的现象，其同名准则数必 定相等。 • （3）彼此相似的现象，其有关的物理量 场分别相似
• 努塞尔数，标志对流换热的相对强弱程 度； • 雷诺数，表征流体在强制对流时，惯 性力和粘性力的相对大小； • 普朗特数，反映流体动量扩散能力与 热扩散能力相对大小； • 格拉晓夫数，反映自然对流换热过程 中浮力与粘性力的大小。
• ⑴在一定温度下，黑体在不同波长范围 内辐射能量各不相同。 • ⑵维恩位移定律：随着温度T增高，最大 单 色 辐 射 力 Ebλ,max 所 对 应 的 峰 值 波 长 λmax 逐 渐 向 短 波 方 向 移 动 。 λmaxT=2897.6μK。 • ⑶常温下，实际物体的辐射主要是红外 辐射。
• 1、热扩散率的物理意义 • 由热扩散率的定义：ɑ=可知： • 1）是物体的导热系数，越大，在相同温度梯 度下，可以传导更多的热量。 • 2)是单位体积的物体温度升高1℃所需的热量。 越小，温度升高1℃所吸收的热量越少，可以 剩下更多的热量向物体内部传递，使物体内温 度更快的随界面温度升高而升高。由此可见ɑ 物理意义： • ① ɑ越大，表示物体受热时，其内部各点温度 扯平的能力越大。 • ② ɑ越大，表示物体中温度变化传播的越快。 所以，ɑ也是材料传播温度变化能力大小的指 标，亦称导温系数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
qxdydz
qx
qx x
dxdydz
qx dxdydz
同理在y,z方向热量差
x y
ydy
qy y
dxdydz
z
zdz
qz z
dxdydz
如单位体积内热源生成的热量为 Φ ，则微元体内产生的
热量：
Φ dxdydz
微元体内热量的增加（内能的增加）为：
c t dxdydz
代入能量平衡方程：
c t [( t )] [( t )] [( t )] Φ x x y y z z
▪ 4、定解条件的数学表达
初始条件（initial condition）--初始时刻的状态表
示为： t =0 =f (x,y,z)
边界条件（boundary condition）--边界上的温度分 布或换热条件，分为三类： 第一类边界条件：规定了边界上的温度值（变量值）
温度分布 t = 0 =f (x,y,z) 〈2〉 边界条件（boundary condition）：边界上的温
度分布或换热条件。
边界条件的分类：
第一类边界条件：规定了边界上的温度值（变量值）
0 tw f ( )
第二类边界条件： 规定了边界上的热流密度（变 量梯度）
0
(
t n
)
w
f
( )
q y dy
qy dx qz
dz qxdx
dy
微元体热平衡
导入微元体的总热量-导出微元体的总热量 + 微元微元体内产生的热量 = 体内的热量增加
X方向导入热量
x qxdydz
导出热量
xdx qxdxdydz
qxdx 用Taylor级数展开
X方向导入导出热量之差
qxdx
qx
qx x
dx
x
xdx
第二章 导热基本定律 及稳态导热
Basic Law and Steady State Conduction
§2-1 导热基本定律
1. 温度场 temperature field
定义
系统中某一时刻的温度分布
按时间 分 类
按空间
稳态温度场 Steady Temperature Field 非稳态温度场 Transient Temperature Field
第三类边界条件： 规定了温度与温度梯度在边界
任一物体，由于某种原因使温度场分布不均匀， 则就有导热发生。
二、问题的数学描述 1、导热微分方程
c t
2t x2
2t y 2
2t z 2
Φ
其中:
ρ—密度， c—比热， λ--导热系数
Φ --单位体积内热源生热，w/m3
2、定解条件
初始条件，边界条件
3、导热微分方程的推导
qx
zy
x
q z dz
3.导热系数
Thermal Conduc位负温度 梯度下的导热量。（或在单位温度梯度作 用下通过物体的热流密度。）
导热机理
•气体：分子热运动 t
•固体：自由电子和晶格振动
t 晶格振动 阻碍自由电子运动 金属 非金属
•液体机理不清
固体> 液体 > 气体 取决于物质的种类和温度
tw= f[W(x,y,z), τ]
第二类边界条件：规定了边界上的热流密度 第三类边界条件：规定了与边界换热的环境条件
三、导热微分方程的简化
1. 如 =constant 则
c t
2t x2
2t y 2
2t z 2
Φ
c t 2t Φ
令 a c
t a2t Φ
c
(称为热扩散率,导温系数 thermal diffusivity)
热绝缘（保温）材料 insulation material：
<0.2W/(mK)(50年代）
<0.14W/(mK)（GB84） <0.12W/(mK)
（GB84）
是随温度变化的
物性 工程处理： 〈1〉取平均 值 〈2〉采用线性关 系近似
0 (1 bt)
§ 2-2 导热微分方程式及定解条件
一、物理（模型）问题
2. Φ 0 , 则 t a2t
3. 稳态: a2t Φ 0
c
4.稳态且 Φ 0 , 则 2t 0
四、其它正交坐标
柱坐标: (cylinder coordinate)
x r cos y r sin z z
t
a
2 r
t
2
1 r
t r
1 r2
2t
2
2t z2
c
球坐标: (sphere coordinate)
x r sin cos y r sin sin z r cos
t
a1r
2 (rt r2
)
1
r 2 sin
s in
t
1
r 2 sin 2
2t
2
c
五、导热问题的完整数学描述
无内热源、常物性、稳态一维问题的导热微分方程：
d 2t dx2
0
dt dx c1
t c1x c2
问题不能确定，需有定解条件： 〈1〉 初始条件（ initial condition）： = 0 时的
▪ 等温面—在同一时刻，同温度各点连成 的面
▪ 二维时则成为等温线
▪ 问题—球坐标 t=f (r,)=const.
2. Fourier’s law
Φ qA A t
x
热力学第二定 律体现
q
t
n
n
gradt
t
n
t
i
t
j
t
k
n x y z
i
j
k
x y z
q gradt t
一维温度场 One Dimensional Temperature Field 二维温度场 Two Dimensional Temperature Field
三维温度场 Three Dimensional Temperature Field
等温面（isothermal surface)，等温线 (isotherm)
人头部温度示意，如 何通过理论分析得到？ （蓝、绿、红表示温度
由低到高）
电影泰坦尼克号中Jack冻 死了，为什么Rose却没死？ 用数学模型如何反映他们 传热条件的不同？
对于简单问题可以直接应用 Fourier’s law, 而 对于复杂一些的问题就需要更一般的方法, 而这一 方法的基础就是导热微分方程 (Conduction differential equation) 。
[qx dxdydz qy dxdydz qz dxdydz]
x
y
z
dxdydz c t dxdydz
以热流密度表示的导热微分方程在推 导过程中没有做任何假设，它是通用的， 即可以认为：
(x, y, z, ) c c(x, y, z, ) (x, y, z, )
q dt
dx