刚体运动的动力学方程共133页
合集下载
刚体动力学

●
刚体基本动力学量
现在取 Axyz 坐标系为一个平动参考系 , 则刚体上的 R 点相对速度为 v r R =× R
dV
【定理】刚体相对动量为 p r =× mt R C
证明:pr =∫ v r R dV =∫ × R R dV
=×∫ R R dV =×m t RC(证毕)
⇒ L'A =∫ R2 I − R R ⋅ R dV =[∫ R2 I − R R R dV ]⋅
= J A⋅
(证毕)
1 1 ' 【定理】刚体相对动能为 T r = ⋅L A= ⋅J A⋅ 2 2
证明: T r=
1 1 2 v r R dV = ∫ v r⋅v r R dV ∫ 2 2 1 1 × R ⋅ v R dV = R × v r ⋅ R dV ∫ ∫ r 2 2
【推论】匀质刚体如果有一过 A 的镜像对称面,则过 A 且 与该镜像面垂直的轴是主轴;如果过 A 有两个正交的 镜像面,则两镜像面过 A 点的法线以及镜像面的交线 构成主轴系;匀质旋转体的旋转轴和任意与之正交的 两正交轴构成主轴系 . (请自己根据定义证明) 【定理】假定角速度在主轴坐标系下表示为
d d' J A⋅ 是矢量, J A⋅ = J A⋅× J A⋅ dt dt
⇒⋯⇒ J A⋅ = J XZ X J YZ Y J ZZ Z = ˙ Z ˙
d e ⋅M A ⇒ Z⋅ J A⋅= J ZZ = ≡M Z ¨ Z dt
2
J lk = J kl
(证毕)
因为:
lk =kl , Rl R k = Rk Rl
注:一般把 Jlk 称为惯量系数,由于对称性,只有 6 个是独立的 注:如果 AXYZ 不是固连在刚体上的坐标系,则 R 相对 AXYZ 有 转动,那么在 AXYZ 上看到的质量分布一般会随时间改变, 故在这个坐标系中惯量系数依赖于时间 . 注:如果 AXYZ 不是固连在刚体上的坐标系,在少数有良好对称性 的情况下 AXYZ 上看到的质量分布可能不随时间改变,此时在 这个坐标系中惯量系数是常数 .
刚体动力学

利用上述运动微分方程组并考虑运动学方程组(5)以及初始条件,即可确定刚体在空间中的一般运动。刚体 一般运动的研究对研究各种航行器轨迹和姿态运动之间的相互关系有重要意义。
以上论及的只是单刚体动力学。由于现代科学技术的发展,多刚体系统动力学的研究也正在开展中(见多刚 体系统)。
参考文献
1、词条作者:陈滨.《中国大百科全书》74卷(第一版)力学词条:刚体动力学:中国大百科全书出版社, 1987 :168-170页.
谢谢观看
逐项类比。同质点质量m对应的量是Iz。m是质点运动时惯性的度量;Iz则是刚体定轴转动时转动惯性的度量。 这正是Iz称为“转动惯量”的来由。
应用刚体定轴转动的微分方程(2)可以对物理摆的运动规律、旋转机械输入和输出功率同平衡转速的关系进 行研究。刚体定轴转动的另一重要研究课题是支承的动载荷。动载荷是与刚体转动角速度有关的载荷。当刚体既 满足静平衡——刚体的重心在转动轴上,又满足动平衡——旋转轴是惯性主轴时,支承才不受动载荷的作用。这 个结论在工程上有重要价值(见动平衡)。
刚体平面运动是机器部件一种常见的运动形态,例如曲柄连杆、滚轮等的运动。过刚体质心作刚体平面运动 的固定平面,此平面在刚体上截得一平面图形。此图形在上述固定平面上的运动完全刻画了刚体的平面运动。由 运动学可知,刚体的平面运动可由质心C在平面上相对固定坐标系Oxy的运动和刚体绕过C并同固定平面垂直的轴 Cz的转动合成(图2)。刚体的旋转轴Cz虽然在空间中变动,但它的方向不变,相对刚体的位置也不变,因而刚 体绕Cz轴旋转的转动惯量是常值Iσ,绕Cz轴的动量矩为
刚体一般运动是对惯性坐标系而言的。设C为刚体的质心,Cxyz为同刚体固联的质心惯性主轴坐标系。因刚 体一般运动可分解为平动和绕质心的转动,故应用质心运动定理和对质心的动量矩定理,可以立即建立刚体一般 运动的微分方程组:
以上论及的只是单刚体动力学。由于现代科学技术的发展,多刚体系统动力学的研究也正在开展中(见多刚 体系统)。
参考文献
1、词条作者:陈滨.《中国大百科全书》74卷(第一版)力学词条:刚体动力学:中国大百科全书出版社, 1987 :168-170页.
谢谢观看
逐项类比。同质点质量m对应的量是Iz。m是质点运动时惯性的度量;Iz则是刚体定轴转动时转动惯性的度量。 这正是Iz称为“转动惯量”的来由。
应用刚体定轴转动的微分方程(2)可以对物理摆的运动规律、旋转机械输入和输出功率同平衡转速的关系进 行研究。刚体定轴转动的另一重要研究课题是支承的动载荷。动载荷是与刚体转动角速度有关的载荷。当刚体既 满足静平衡——刚体的重心在转动轴上,又满足动平衡——旋转轴是惯性主轴时,支承才不受动载荷的作用。这 个结论在工程上有重要价值(见动平衡)。
刚体平面运动是机器部件一种常见的运动形态,例如曲柄连杆、滚轮等的运动。过刚体质心作刚体平面运动 的固定平面,此平面在刚体上截得一平面图形。此图形在上述固定平面上的运动完全刻画了刚体的平面运动。由 运动学可知,刚体的平面运动可由质心C在平面上相对固定坐标系Oxy的运动和刚体绕过C并同固定平面垂直的轴 Cz的转动合成(图2)。刚体的旋转轴Cz虽然在空间中变动,但它的方向不变,相对刚体的位置也不变,因而刚 体绕Cz轴旋转的转动惯量是常值Iσ,绕Cz轴的动量矩为
刚体一般运动是对惯性坐标系而言的。设C为刚体的质心,Cxyz为同刚体固联的质心惯性主轴坐标系。因刚 体一般运动可分解为平动和绕质心的转动,故应用质心运动定理和对质心的动量矩定理,可以立即建立刚体一般 运动的微分方程组:
《刚体动力学 》课件

牛顿第二定律
物体的加速度与作用在物 体上的力成正比,与物体 的质量成反比。
牛顿第三定律
对于任何两个相互作用的 物体,作用力和反作用力 总是大小相等,方向相反 ,作用在同一条直线上。
刚体的平动
刚体的平动是指刚体在空间中 的位置随时间的变化而变化, 而刚体的形状和大小保持不变
的运动。
刚体的平动具有三个自由度 ,即三个方向的平动。
05
刚体的动力学方程
刚体的动力学方程
牛顿第二定律
刚体的加速度与作用力成正比,与刚体质量 成反比。
刚体的转动定律
刚体的角加速度与作用力矩成正比,与刚体 对转动轴的转动惯量成反比。
刚体的动量方程
刚体的动量变化率等于作用力对时间的积分 。
刚体的自由度与约束
自由度
描述刚体运动的独立变量,如平动自由度和转动 自由度。
约束
限制刚体运动的条件,如固定约束、滑动约束等 。
约束方程
描述刚体运动受约束的数学表达式。
刚体的动力学方程的求解方法
解析法
通过代数运算求解动力学方程,适用于简单问 题。
数值法
通过迭代逼近求解动力学方程,适用于复杂问 题。
近似法
通过近似模型求解动力学方程,适用于实际问题。
06
刚体动力学中的问题与实例 分析
人工智能和机器学习的发展将为刚体 动力学的研究提供新的思路和方法, 有助于解决复杂动力学问题。
感谢您的观看
THANKS
船舶工程
在船舶工程中,刚体动力学 用于研究船舶的航行稳定性 、推进效率以及船舶结构的 安全性等。
兵器科学与技术
在兵器科学与技术领域,刚 体动力学用于研究弹药的发 射动力学、火炮的射击精度 和稳定性等。
理论力学课件 接上,,加刚体平面运动动力学方程
rad
/θ
s/t
θ
/
rad
s/t
在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风。
s
/t rad
/θ失之毫厘、谬之千里。
竹中一滴曹溪水,涨起西江十八滩。
假如潘金莲不开窗户,就不会遇见西门庆;不遇西门,就不会出轨;不出轨,武松就不会逼上梁山。
武松不上梁山,方腊就不会被擒;方腊不被擒,就可灭大宋江山,没有了大宋江山,就不会有靖康耻;金兵就不会入关,就不会有大清朝;没有大清朝,中国就不会闭关锁国、不会有鸦片战争和八国联军入侵。
那么,中国,将是世界上唯一的超级大国!美国等其他诸侯神马的都是浮云!唉!金莲呀,没事你开什么窗户?
钉子缺,蹄铁卸;蹄铁卸,战马蹶;战马蹶,骑士绝;骑士绝,战事折;战事折,国家灭。
若
平面情况(对轴的动量矩计算)mv C d
矩。
D
3、相对质心的动量矩定理
C
C C B v m r L L v v v v ×+=由动量矩的主矩定理得(B是定点)
对时间t取导,并应用对定点的动量矩定理。
B C C C C C
B M a m r v m r L L v v v v v &v &v &=×+×+=上式第二项为零,由力矩的主矩定理
V
C C B F r M M v v v v ×+=C V a m F v v =得
C
C M L v
v &=。
理论力学:刚体平面运动的动力学

§7-2 刚体平面运动的动力学
A
Mc
mg Mk
Fx O
Fy
常系数非齐次 非线性微分方程
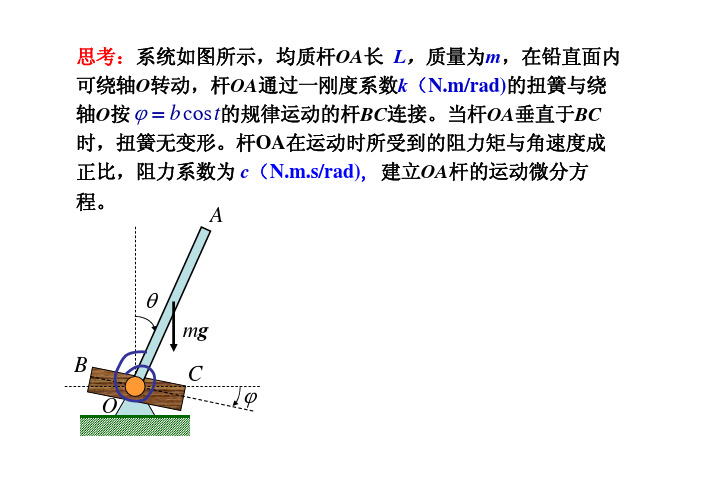
解:研究OA杆,进行受力分析
JO
d 2
dt 2
n i1
M O (Fi )
JO M mg M c M k
M mg
mg
L sin
2
M c c
Mk k( )
1 mL2 c k 1 mgLsin kbcos t
大小: a ar cos
2
2020/12/9
27
混沌(Chaos):在确定的系统中出现类似随机的运动过程
2020/12/9
9
理论力学
§7-2 刚体平面运动的动力学
1963年美国科学家洛伦兹(Edward N. Lorenz) 从简化大气对流的动力学方程中得到一组三阶 的非线性常微分方程。
即:
发现:该方程在一定参数下为周 期解,在某些参数下为混沌解。
mR2
2R 2
2020/12/9
5
理论力学
§7-2 刚体平面运动的动力学
例:系统如图所示,设均质杆OA长为 L 质量为m,其阻力系数为 c,扭簧刚 度系数为 k。当 OABC 时,扭簧无
变形,已知BC杆的转动: b cos t ,
试建立OA杆的运动微分方程。
A
mg
B
C
O
2020/12/9
6
理论力学
2020/12/9
F
B
B:滑块右侧与滑道接触
25
理论力学
§7-2 刚体平面运动的动力学
思考题:质量为m半径为R 的均质圆盘在倾角为θ 的固定
斜面上纯滚动,其上作用一主动力偶M, 试定性分析作用 在圆盘上的摩擦力的方向。
第4章刚体的运动学和动力学

P
II
M
d d 2 2 f " (t ) ቤተ መጻሕፍቲ ባይዱt dt
当 β c
0 t 1 2 ( ) t t 0 2 2 2 0 2 ( 0 )
z ω,
与质点的匀加速直线运动公式相象
二. 定轴转动刚体上各点的速度和加速度
端,试计算飞轮的角加速 解 (1) Fr J
(2) mg T ma
rO
T
Fr 98 0.2 39.2 rad/s 2 J 0.5
mgr J mr 2
两者区别
F
mg
Tr J a r
98 0.2 2 21 . 8 rad/s 0.5 10 0.22
例如 T' T
x dx
x
• 在定轴转动中,力矩可用代数值进行计算
T' T
M i TR T' R
M i TR T' r
二. 刚体对定轴的转动定律
实验证明 当 M 为零时,则刚体保持静止或匀速转动 当存在 M 时, 与 M 成正比,而与J 成反比
M J
刚体的转动定律
M kJ
例 一根长为 l ,质量为 m 的均匀细直棒,可绕轴 O 在竖直平 面内转动,初始时它在水平位置 m l x O 求 它由此下摆 角时的 解 取一质元
M xdm g g xdm
C
mg
dm
M mgxC
1 M mgl cos 2
xdm mxC
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
L x
J
1 x dx ML2 3
§7.5刚体平面运动的动力学

N mg 0, F mac m L 2
mg
2
aC
F
由转动定理:
F 0 A Io mL
1 3
A
解得:
0A 2 3 L
7.4.2 已知:质量为2.97kg,长为1.0m的匀质等截面细杆 可绕水平光滑的轴线o转动,最初杆静止于铅直方向。 一弹片质量为10g,以水平速度200m/s射入并嵌入杆 的下端,和杆一起运动,求杆的最大摆角θ。
Fi 0,
i
M
i
iz
0
R l , F f 0, 静摩擦力向后; 2 R l , F f 0, 静摩擦力向前; 2 R l , F f 0. 2
并且只有满足 mg Ff 时才能保持纯滚动。
7.3.6 已知:匀质杆可绕支点o转动,当与杆垂直的冲力 作用某点A时,支点o对杆的作用力并不因此冲力 之作用而发生变化,则A点称为打击中心。设杆长 为L,求打击中心与支点的距离。 y 解:建立图示坐标o-xyz, z轴垂直纸 N 面向外, 杆受力及运动情况如图示。 o x 由质心运动定理:
F Ff mac
F
再由圆柱对质心的转动定理
Fl Ff R Ic
l
c a c
Ff
又因纯滚动 ac R 以及 I c 1 mR 2
2
例3
解得
2F ( R l ) 3mR 2
ac R
2F ( R l ) 3mR R 2l Ff F 3R
可见,若
1 2
3 7
gl aCn
2 vC l 2
l 2 6g 2 7
7.5.2
N n 4mg 4maCn
N t 4maCt
mg
2
aC
F
由转动定理:
F 0 A Io mL
1 3
A
解得:
0A 2 3 L
7.4.2 已知:质量为2.97kg,长为1.0m的匀质等截面细杆 可绕水平光滑的轴线o转动,最初杆静止于铅直方向。 一弹片质量为10g,以水平速度200m/s射入并嵌入杆 的下端,和杆一起运动,求杆的最大摆角θ。
Fi 0,
i
M
i
iz
0
R l , F f 0, 静摩擦力向后; 2 R l , F f 0, 静摩擦力向前; 2 R l , F f 0. 2
并且只有满足 mg Ff 时才能保持纯滚动。
7.3.6 已知:匀质杆可绕支点o转动,当与杆垂直的冲力 作用某点A时,支点o对杆的作用力并不因此冲力 之作用而发生变化,则A点称为打击中心。设杆长 为L,求打击中心与支点的距离。 y 解:建立图示坐标o-xyz, z轴垂直纸 N 面向外, 杆受力及运动情况如图示。 o x 由质心运动定理:
F Ff mac
F
再由圆柱对质心的转动定理
Fl Ff R Ic
l
c a c
Ff
又因纯滚动 ac R 以及 I c 1 mR 2
2
例3
解得
2F ( R l ) 3mR 2
ac R
2F ( R l ) 3mR R 2l Ff F 3R
可见,若
1 2
3 7
gl aCn
2 vC l 2
l 2 6g 2 7
7.5.2
N n 4mg 4maCn
N t 4maCt
第八章刚体定点运动的动力学ppt课件

2 2
(ri (r
cos
i
l )2]
)2
]
mi[xi2 yi2 zi2
(xi yi zi )2]
考虑到 2 2 2 1,则上式化为
Il
I xx 2
I yy 2
I zz
2
2I xy
2I yz
2Izx
Il l I l
----------------------如已知固定点的惯量张量, 则可得过此点的任何轴的转动惯量.
沿过椭球面角速度矢量 与惯量椭球相交点P点的法线
方向上.(证明见书P303)
例题1: 一匀质薄圆盘能绕其中心O点做定点转动,其质
量面为成m,半角30径的 为轴R以,已角知速英度雄模转范动瞬,试时求圆此盘时绕圆壶盘中对心中与心盘的
角动量和圆盘的动能,以及圆盘对此轴的转动惯量.
解: 建立过O点的主轴坐标系,依题意有:
本节介绍刚体作定点运动时具有的动量、角动量、动能 的计算。
P mvc
n
及: I yz I zy mi yi zi i 1
n
I zx I xz mi zi xi
i 1
n
I xy I yx mi xi yi
i 1
惯 惯量积与转动惯量 量 合在一起统称为惯 积 性系数
则: Lx I xxx I xy y I xzz
确定z轴的位置: 和 Oxy面与O面的交线
为ON ,即节线.
, ,称为欧拉角,0 , 0 2 ,0 2
L
k0
l
k
(节线)
: :
章进动动角角,,章进动动角角速速度度为为k;0
;
:自转角,自转角速度为k.
L
k0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
刚体运动的动力学方程
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
刚体运动的动力学方程
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
