现代控制理论东北大学高立群清华大学出版社第3章

合集下载

现代控制理论（浓缩版）

现代控制理论（浓缩版）绪论1．经典控制理论与现代控制理论的比较。

经典控制理论也称为古典控制理论，多半是用来解决单输入-单输出的问题，所涉及的系统大多是线性定常系统，非线性系统中的相平面法也只含两个变量。

经典控制理论是以传递函数为基础、在频率域对单输入单输出控制系统进行分析和设计的理论。

它明显具有依靠手工进行分析和综合的特点，这个特点是与20世纪40~50年代生产发展的状况，以及电子计算机的发展水平尚处于初级阶段密切相关的。

在对精度要求不高的场合是完全可用的。

最大成果之一就是PID 控制规律的产生，PID 控制原理简单，易于实现，具有一定的自适应性与鲁棒性，对于无时间延时的单回路控制系统很有效，在工业过程控制中仍被广泛采用。

现代控制理论主要用来解决多输入多输出系统的问题，系统可以是线性或非线性的、定常或时变的。

确认了控制系统的状态方程描述法的实用性，是与状态方程有关的控制理论。

现代控制理论基于时域内的状态空间分析法，着重实现系统最优控制的研究。

从数学角度而言，是把系统描述为四个具有适当阶次的矩阵，从而将控制系统的一些问题转化为数学问题，尤其是线性代数问题。

而且，现代控制理论是以庞得亚金的极大值原理、别尔曼的动态规划和卡尔曼的滤波理论为其发展里程碑，揭示了一些极为深刻的理论结果。

面对现代控制理论的快速发展及成就，人们对这种理论应用于工业过程寄于乐期望。

但现代控制在工业实践中遇到的理论、经济和技术上的一些困难。

所以说，现代控制理论还存在许多问题，并不是“完整无缺”，这是事物存在矛盾的客观反应，并将推动现代控制理论向更深、更广方向发展。

如大系统理论和智能控制理论的出现，使控制理论发展到一个新阶段。

2．控制一个动态系统的几个基本步骤有四个基本步骤：建模，基于物理规律建立数学模型；系统辨识，基于输入输出实测数据建立数学模型；信号处理，用滤波、预报、状态估计等方法处理输出；综合控制输入，用各种控制规律综合输入。

现代控制理论课后答案

前言
本书是为了与张嗣瀛院士等编写的教材《现代控制理论》相配套而编写的习题解答。
本书对该教材中的习题给予了详细解答，可帮助同学学习和理解教材的内容。由于习题数量较多，难易程度不同，虽然主要对象是研究型大学自动化专业本科学生，但同时也可以作使用其它教材的专科、本科、以及研究生的学习参考书。
书中第5、6、8章习题由高立群教授组织编选和解答；第4、7 章由井元伟教授组织编选和解答，第1、2章由郑艳副教授组织编选和解答。
+
若取，则有
（2）解由（1）知
取，则有
若取，则有，
3.11 求下列系统在输入作用为：① 脉冲函数；② 单位阶跃函数；③ 单位斜坡函数下的状态响应。
(1)
(2)
图P2.2
解这是一个物理系统，采用机理分析法求状态空间表达式会更为方便。令为输入量，即，，的位移量，为输出量，
选择状态变量， = ， = ，。
根据牛顿定律对有：
对有：
经整理得：
状态方程为：
输出方程为：
写成矩阵形式为：
2.5 系统的结构如图P2.5所示。以图中所标记的、、作为状态变量，推导其状态空间表达式。其中，、分别为系统的输入、输出，、、均为标量。
图P2.5系统结构图
解图P2.5给出了由积分器、放大器及加法器所描述的系统结构图，且图中每个积分器的输出即为状态变量，这种图形称为系统状态变量图。状态变量图即描述了系统状态变量之间的关系，又说明了状态变量的物理意义。由状态变量图可直接求得系统的状态空间表达式。
(2) 解由已知得：
，
令：，
得：
状态变量图如下：

现代控制理论第三章课程电子教案

特点
现代控制理论强调数学建模、系统分析和优化，注重实际应用和工程实现，具有广泛的应用领域和重要的实际意义。
现代控制理论的重要性
推动自动化技术发展
促进科技创新
现代控制理论是自动化技术的重要基础，为工业自动化、智能制造等领域提供了重要的理论支持和技术手段。
现代控制理论的发展和应用，推动了科技创新和产业升级，为经济发展和社会进步做出了重要贡献。
考试
期末闭卷考试，涵盖了课程的所有重点内容，包括系统建模、稳定性分析、状态反馈和最优控制等。
学习效果评估
要点一
作业成绩
根据学生提交的作业，评估学生对控制理论知识的掌握程度和应用能力。
要点二
考试成绩
根据期末考试成绩，评估学生对整个课程内容的掌握程度。
教学改进建议
增加实践环节
为了提高学生的实际操作能力和问题解决能力，建议增加实验或实践环节，让学生亲自动手进行
课程目标
1
掌握现代控制理论的基本概念、原理和方法。
2
学会分析和设计控制系统，提高解决实际问题的能力。
3
培养学生对控制理论的兴趣和热情，为后续学习和工作打下基础。
02 现代控制理论概述
定义与特点
定义
现代控制理论是一门研究系统状态和行为变化规律的科学，通过数学模型和计算机仿真技术实现系统的分析和优化。
状态转移矩阵的求解
02
通过系统的状态方程，求解状态转移矩阵，从而得到系统状态
的转移关系。
系统的稳定性分析
03
通过分析状态转移矩阵的性质，判断系统的稳定性，为后续控
制设计提供依据。
线性系统的状态反馈与极点配置
状态反馈控制器的设计
根据系统状态和期望的输出，设计状态反馈控制器，使得系统状态能够跟踪期望的轨迹统的动态特性，实现系统性能的优化。

现代控制理论ch3资料

x1能控，x2不能控状态不完全能控
不能控系统
3.2.1 具有Jordan标准型系统能控性判别
通过以上分析，可以得出以下几点结论： 1）系统的能控性，取决于状态方程中的系统矩阵 A和控制矩阵b。系统矩阵A是由系统的结构和内部参数决定的；控制矩阵b是与控制作用的施加点有关的，因此系统的能控性完全取决于系统的结构、参数，以及控制作用的施加点。
3.1 能控性的定义
2. 线性连续时变系统的能控性
x A(t)x B(t)u
能控性的定义，与定常系统的定义相同，但是A(t)、 B(t)是时变矩阵不是而常系数矩阵，其状态矢量x(t) 的转移，与初始时刻t0的选取有关，所以在时变系统能控性定义中，应强调在t0时刻系统是能控的。
3.1 能控性的定义
(6)
x2
0
4
0
x2
4
u
x3 0 0 2 x3 0
状态不完全能控，不能控系统
3.2.1 具有Jordan标准型系统能控性判别
(7)
x1 x2
1
0
1
1
0
x1
0
0 x2 b2 u
x3
0
0
2
x3
b3
状态完全能控，能控系统
3.2.1 具有Jordan标准型系统能控性判别
1.单输入系统 x Ax bu
为简明起见，列举具有Jordan标准型的二阶系统，对能控性加以分析。例 (1)
x
1
0
0 0
2
x
b2
u
;
y c1 c2 x
3.2 线性定常系统的能控性判别
即系统模拟结构图：
x1不能控，x2能控状态不完全能控

现代控制理论-1-绪论

1.1 控制理论的发展历程
1.1.1 经典控制理论
• 1788年，英国瓦特（J.Watt）利用负反馈原理设计的用来控制蒸汽机转速的离心调速器，亦称飞球调速器/控制器-----第一个自动控制系统，首次应用于工业，拉开了控制理论发展的序幕。 • 1868年，英国麦克斯韦（J.C.Maxwell）发表了《论调速器》，指出微分方程特征根的位置（在左半面或右半面）跟稳定有关，开辟用数学方法研究控制系统中运动现象的途径。
•
1954年，钱学森的《工程控制论》在美国出版。－－－奠定了工程控制论的基础
我国自动控制界的先驱式人物、中国导弹之父、《工程控制论》作者--钱学森
“钱学森无论走到哪里，都抵得上5个师的兵力，我宁可把他击毙在美国也不能让他离开。”----美国海军高级将领金布尔
• 1934年上海交通大学毕业，次年留学美国 • 1938年在美国从事空气动力学研究 • 1939年加州理工学院获得航空、数学博士学位，曾任加州理工学院副教授，麻省理工学院教授，加州理工学院喷气推进中心主任、教授。 • 40年代末加州理工学院给研究生讲课 • 1955年一家乘克莱弗兰总统号回国 • 1964年我国第一颗原子弹爆炸成功 • 1967年我国第一颗氢弹爆炸成功 • 1970年我国第一颗人造卫星东方红一号上天 • 1989年获“小罗克韦尔奖章”（1982创立-1/16） • 2009年10月31日在北京逝世
现代控制理论 Modern Control Theory 绪论
• 教材：刘豹、唐万生主编，现代控制理论(第三版)，机械工业出版社， 2006 • 参考资料：张嗣瀛、高立群，《现代控制理论》，清华大学出版社,2006 俞立主编，《现代控制理论》，清华大学出版社，2007 袁德成等主编《现代控制理论》，清华大学出版社，2007 曲延滨、王新生主编，《现代控制理论基础》，哈尔滨工业大学出版社，2005 …… • 课时：32 考查方式：考试70% + 考勤10% + 作业20%

《现代控制理论基础》第三章(讲义)

第一和第二讲小结一、状态空间表达式的标准形式能控标准形能观测标准形对角线标准形Jordan标准形二、矩阵的特征值及对角线化矩阵是能控标准形时的变换矩阵求法（1）特征值互异（2）重根（3）一般情形三、利用MATLAB进行系统模型之间的相互转换[A, B, C, D] = tf2ss (num, den)[num,den] = ss2tf [A,B,C,D,iu]四、时域分析的基本概念状态转移矩阵及其性质，凯莱-哈密尔顿定理最小多项式五、矩阵指数计算级数法，对角线标准形与Jordan标准形法拉氏变换法凯莱-哈密尔顿定理II、分析部分第三章线性多变量系统的能控性与能观测性分析能控性(controllability)和能观测性(observability)深刻地揭示了系统的内部结构关系，由R.E.Kalman于60年代初首先提出并研究的这两个重要概念，在现代控制理论的研究与实践中，具有极其重要的意义，事实上，能控性与能观测性通常决定了最优控制问题解的存在性。

例如，在极点配置问题中，状态反馈的的存在性将由系统的能控性决定；在观测器设计和最优估计中，将涉及到系统的能观测性条件。

在本章中，我们的讨论将限于线性系统。

将首先给出能控性与能观测性的定义，然后推导出判别系统能控和能观测性的若干判据。

3.1 线性连续系统的能控性3.1.1 概述能控性和能观测性就是研究系统这个“黑箱”的内部的状态是否可由输入影响和是否可由输出反映。

例1．给定系统的描述为u x x xx⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡2150042121 []⎥⎦⎤⎢⎣⎡-=2160x x y将其表为标量方程组的形式，有：u x x+=114 u x x2522+-= 26x y -=例3－2：判断下列电路的能控和能观测性)(t u +yCR )(t uR L y23.1.2 能控性的定义考虑线性时变系统的状态方程∑:Bu x t A x+=)( ， u t D x t C t y )()()(+=，00)(x t x =，J t ∈ (3.1.1)其中，x 为n 维状态向量，u 维p 维输入向量，J 为时间定义区间，B A ,分别为n n ⨯和p n ⨯的元为t 的连续函数的矩阵。

现代控制理论3章

3.2.2 状态能观性的判据已知系统的动态方程
x’(t ) A(t ) x(t )
y C (t ) x(t )
x(0) x0
1、线性定常连续系统能观测性的格拉姆矩阵判据
线性定常连续系统{A，C} 状态完全能观测的充要条件是：存在时刻t1>t0，使如下定义的能观性格拉姆（Gram)矩阵为非奇异。
16
例：给定线性定常系统的状态方程，判断能控性。
1 x1 1 x1 0 x1 x 2.5 1.5 x 1 u y 1 0 x 2 2 2
解：
1 1 1 0 AB 1 1 2.5 1.5 1 1 rank[ B AB] rank =1 2 系统不能控 1 1 s 1.5 1 1 1 0 s 1 Cadj ( sI A) B s 2.5 1 2.5 g ( s) s 1 sI A ( s 2.5)( s 1) ( s 1) 2.5 s 1.5

0 t1 0
t1
T x0 Wc (t0 , t1 ) x0 [ BT T (t0 , ) x0 ]T BT T (t0 , ) x0 d 0
T x0 Wc
(t0 , t1 ) x0 B (t0 , ) x0 d (t0 , ) x0 0
At k 0 n 1
y (t ) k (t )CAk x(0)
k 0
n 1
y (t ) 0 (t )Cx(0) 1 (t )CAx(0) n 1 (t )CAn 1 x(0) C CA x(0) y (t ) 0 (t ) 1 (t ) ... n 1 (t ) n 1 CA C CA =n rank n 1 CA

《现代控制理论》课后习题全部答案(最完整打印版)

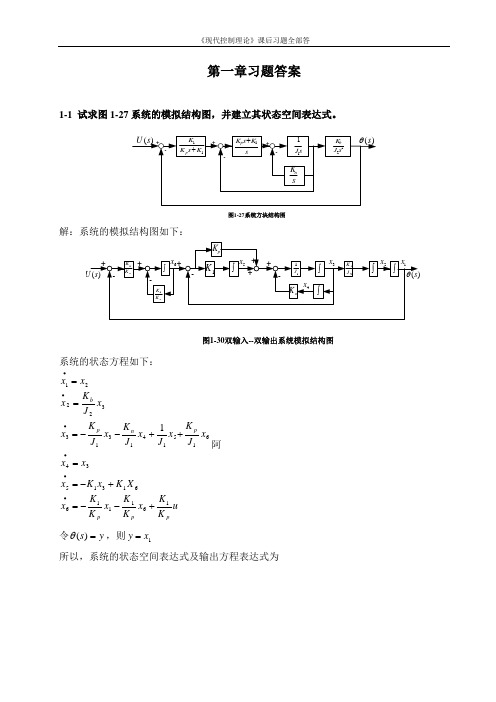
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第3章 “状态方程的解”习题解答3.1计算下列矩阵的矩阵指数te A 。

200200(1)020;(2)031002003--⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦A A0001(3) ; (4) 1040-⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A（1）解 222000000ttt t e ee e ---⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A （2）解 233300000ttt t t e e e te e ----⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A （3）解()122011001111s s s s s s s s s s -⎡⎤-=⎢⎥-⎣⎦⎡⎤⎢⎥⎡⎤-==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦I A I A ()()()11101tt e L s t t --⎡⎤⎡⎤=-=⎢⎥⎣⎦⎣⎦A I A （4）解： 14s s s ⎡⎤-=⎢⎥-⎣⎦I A()1222221144124242244s s s s ss s s s s --⎡⎤-=⎢⎥+⎣⎦⎡⎤-⋅⎢⎥++=⎢⎥⎢⎥⎢⎥++⎣⎦I A 221221242422441cos 2sin 222sin 2cos 2t ss s e L s s s t t tt -⎡⎤-⎢⎥++=⎢⎥⎢⎥⎢⎥++⎣⎦⎡⎤-⎢⎥=⎢⎥⎣⎦A3.2 已知系统状态方程和初始条件为()1001010,000121⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦x x x(1) 试用拉氏变换法求其状态转移矩阵； (2) 试用化对角标准形法求其状态转移矩阵； (3) 试用化te A 为有限项法求其状态转移矩阵； (4) 根据所给初始条件，求齐次状态方程的解。

（1）解 12100010012O O ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦A A A ，其中， 12101,12⎡⎤==⎢⎥⎣⎦A A 则有 1200tt t e e e ⎡⎤=⎢⎥⎣⎦A A A 而 1tt ee =A ， ()2112t e L s --⎡⎤=-⎣⎦A I A()112101220111(1)(2)101111212s s s s s s s s s s s ---⎡⎤-=⎢⎥--⎣⎦-⎡⎤=⎢⎥---⎣⎦⎡⎤⎢⎥-=⎢⎥⎢⎥-⎢⎥---⎣⎦I A()2112220t tt tt e eL s e e e --⎡⎤⎡⎤=-=⎢⎥⎣⎦-⎣⎦A I A 所以状态转移矩阵为()112200000tt t t tt e e L s e e e e --⎡⎤⎢⎥⎡⎤=-=⎢⎥⎣⎦⎢⎥-⎣⎦A I A （2）解21(1)(2)012I λλλλλ--==--=--A 121,2λλ==对于11λ=，100011101⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦1P P对于22λ=，2210001001⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P110101111-⎡⎤⎡⎤=⇒=⎢⎥⎢⎥-⎣⎦⎣⎦P P2122220010100111100t tt tt tt t t e ee e e e e ee -⎡⎤=⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤=⎢⎥-⎣⎦A P P2200000tt t t tt e e e e e e ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦P （3）解矩阵的特征值为1,21λ=,32λ=对于32λ=有： 2012()2()4()t e t t t ααα=++ 对于1,21λ=有： 012()()()t e t t t ααα=++ 因为是二重特征值，故需补充方程 12()2()t te t t αα=+ 从而联立求解，得：202122()2()322()t tt t t t t tt e te t te e e t e e te ααα=-=-+=-- ()()20122222222()()()20100020322010002012100100 0100100120120000 0t t t t t t t t t t t t t t t t t t e t t t e te e te te e e e te e e te e e e e e ααα=++⎡⎤-⎡⎤⎢⎥⎢⎥=-+-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥+--⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦A I A A（4）解：0)0222()()(0)001000001t t t t t t t tt t t e t e e e e e e e e -==⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A(A x x x3.3 矩阵A 是22⨯的常数矩阵，关于系统的状态方程式= xAx ，有 1(0)1⎡⎤=⎢⎥-⎣⎦x 时， 22t t e e --⎡⎤=⎢⎥-⎣⎦x2(0)1⎡⎤=⎢⎥-⎣⎦x 时， 2t t e e --⎡⎤=⎢⎥-⎣⎦x试确定这个系统的状态转移矩阵(,0)t Φ和矩阵A 。

解：因为系统的零输入响应是()(,0)(0)t t =x x Φ所以221(,0)1t t e t e --⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦Φ，22(,0)1t t e t e --⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦Φ将它们综合起来，得22122(,0)11tt t t e e t e e ----⎡⎤⎡⎤=⎢⎥⎢⎥---⎣⎦⎣⎦Φ 122222222122(,0)11122112222tt tt t t t t t t t t t t t t e e t ee e e ee e e e e e ee e -----------------⎡⎤⎡⎤=⎢⎥⎢⎥----⎣⎦⎣⎦--⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤--=⎢⎥--⎣⎦Φ 而状态转移矩阵的性质可知，状态转移矩阵0(,)t t Φ满足微分方程()()00,,dt t t t dt=A ΦΦ 和初始条件 ()00,t t =I Φ因此代入初始时间00t =可得矩阵A 为：0100022220(,)(,)2224240213t t t t t t t t t t t d t t t t dt e e e e e e e e -==--------=⎧⎫=⎨⎬⎩⎭⎡⎤-+-+=⎢⎥-+-+⎣⎦⎡⎤=⎢⎥--⎣⎦A ΦΦ3.9 已知系统= xAx 的转移矩阵0(,)t t Φ是 2202222()(,)2t tt t t tt t e e e e t t e ee e --------⎡⎤--=⎢⎥--⎣⎦Φ 时，试确定矩阵A 。

解因为 0(,)t t Φ是状态转移矩阵，所以有 00(,)(,)d t t t t dt ⎧⎫=⎨⎬⎩⎭A -1ΦΦ 将00t =，00(,)t t I =Φ代入得：0213-⎡⎤=⎢⎥-⎣⎦A 3.10 已知系统状态空间表达式为011341u ⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦x x[]11y =x(1) 求系统的单位阶跃响应； (2) 求系统的脉冲响应。

（1）解 0134⎡⎤=⎢⎥-⎣⎦A ，[]1,111⎡⎤==⎢⎥⎣⎦B C1(4)3(3)(1)034λλλλλλλ--==-+=--=-I A121,3λλ⇒==11λ=时， 1111013301-⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P23λ=时， 2231013103-⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P 1113⎡⎤=⎢⎥⎣⎦P 131311221111222-⎡⎤-⎢⎥-⎡⎤==⎢⎥⎢⎥-⎣⎦⎢⎥-⎢⎥⎣⎦P 13333333111002213110223111222233132222ttt t t t tt t t t t t e e e e e e e e e e e e e -⎡⎤-⎢⎥⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦-⎢⎥⎣⎦⎡⎤--+⎢⎥=⎢⎥⎢⎥--+⎢⎥⎣⎦A P P将()1()u t t =代入求解公式得：3313323111(0)2222()(0)33132222t tt t t t t t e e e e x t x e e e e ⎡⎤--+⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥--+⎢⎥⎣⎦x +3()3()3()3()013112333tt t t t t t t t e e e e d e e e e τττττττττ--------⎡⎤--+⎡⎤⎢⎥⎢⎥--+⎣⎦⎣⎦⎰ 331233123(0)(0)122333(0)(0)122t t ttt ttt t t e e e e x x e e e e e x x e ⎡⎤---+-⎢⎥⎢⎥=--⎢⎥-+-⎢⎥⎣⎦若取(0)0=x ，则有 1()1t t e t e ⎡⎤-=⎢⎥-⎣⎦x[][]111()11221t t t e y t e e ⎡⎤-===-⎢⎥-⎣⎦x（2）解由（1）知te =A 33333111222233132222t t t t t t t t e e e e e e e e ⎡⎤--+⎢⎥=⎢⎥⎢⎥--+⎢⎥⎣⎦取()(0)u t δ=，则有3313323()3()3()3()03312313111(0)2222()(0)33132222131(0)123333(0)(0)2233(0)2t tt t t t t t tt t t t t t t t t t ttt tte e e e x t x e e e e e e e e d e e e e e e e e x x e e e x ττττττττδτ--------⎡⎤--+⎢⎥⎡⎤=⎢⎥⎢⎥⎣⎦⎢⎥--+⎢⎥⎣⎦⎡⎤--+⎡⎤+⎢⎥⎢⎥--+⎣⎦⎣⎦---+=--⎰x 323(0)2t t t e e x e ⎡⎤⎢⎥⎢⎥-⎢⎥+⎢⎥⎣⎦若取0(0)0⎡⎤=⎢⎥⎣⎦x ，则有()t t e t e ⎡⎤=⎢⎥⎣⎦x ，[]()112t t t e y t e e ⎡⎤==⎢⎥⎣⎦3.11 求下列系统在输入作用为：① 脉冲函数；② 单位阶跃函数；③ 单位斜坡函数下的状态响应。

(1) 1001a b a u b a b ⎡⎤⎢⎥-⎡⎤-=+⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥-⎣⎦x x(2) ()0101u ab a b ⎡⎤⎡⎤=+⎢⎥⎢⎥--+⎣⎦⎣⎦ xx （1）解0000at tbt a e e b e ---⎡⎤⎡⎤=⇒=⎢⎥⎢⎥-⎣⎦⎣⎦A A ① ()()u t t δ=，()()()()()1()0212100000101(0)1(0)ata t t btb t atat bt bt x e e b a t d x e e a b e x e b a e x e b a ττδτ----------⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤-=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥-⎣⎦⎡⎤+⎢⎥-=⎢⎥⎢⎥-⎢⎥-⎣⎦⎰x取()00=x ，则()11at bt e b a t e b a --⎡⎤⎢⎥-=⎢⎥⎢⎥-⎢⎥-⎣⎦x② ()()1u t t =，()()()()()1()021201101(0)()()1(0)()()at a t t bt b t at at bt bt e x e t d e x b a e e e x a b a a b a e e x b b a b b a ττττ----------⎡⎤⎡⎤=+⋅⎢⎥⎢⎥--⎣⎦⎣⎦⎡⎤+-⎢⎥--⎢⎥=⎢⎥+-⎢⎥--⎣⎦⎰x若取()00=x ，则有 ()1()()1()()at bt e a b a a b a t e b b a b b a --⎡⎤-⎢⎥--⎢⎥=⎢⎥-⎢⎥--⎣⎦x ③ ()u t t =， ()()1()20(0)1(0)tat a t bt b t e x e t td b a e x eτττ------⎡⎤⎡⎤=+⋅⎢⎥⎢⎥--⎣⎦⎣⎦⎰x()()()()()()()()()()221222122222101011010at at bt btat at bt bt t e e x a a a e x b a t e b b b t e e x a b a a b a a b a t e e x b b a b b a b b a --------⎡⎤+-⎢⎥⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦--+⎢⎥⎣⎦⎡⎤++-⎢⎥---⎢⎥=⎢⎥--+⎢⎥---⎢⎥⎣⎦若取()00=x ，则有()()()()()()()222211at bt t e a b a a b a a b a t t e b b a b b a b b a --⎡⎤+-⎢⎥---⎢⎥=⎢⎥--+⎢⎥---⎢⎥⎣⎦x （2）解()010,1ab a b ⎡⎤⎡⎤==⎢⎥⎢⎥--+⎣⎦⎣⎦A B ()()()()1ab a b a b ab a b λλλλλλλ--=++=+++=++=⎡⎤⎣⎦I A所以12,a b λλ=-=-1a λ=-时， 111010a abb a --⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P 2b λ=-时， 221010b aba b --⎡⎤⎡⎤⎡⎤=⇒=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦P P 11a b ⎡⎤=⎢⎥--⎣⎦P 1111b a b a ---⎡⎤=⎢⎥-+⎣⎦P1111001101atat t bt bt atbtat btat bt at bt b e e e a b a a b e e be ae eea b abe abe ae be ---------------⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤-+-+=⎢⎥---⎣⎦A P P① ()()u t t δ=，()12()()()()()()()()0(0)1(0)01(0)1()1at btat bt at bt at bt ta tb t a t b t a t b t a t b t bt at x be ae e e t x a b abe abe ae be be ae e e d a b abeabe ae be ae be x a b ττττττττδτ--------------------------⎡⎤-+-+⎡⎤=⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤-+-+⎡⎤+⎢⎥⎢⎥---⎣⎦⎣⎦-=-⎰x 1212(0)()(0)()(0)()(0)at bt at btat bt at bt at bt e e x e eabe abe x ae be x ae be ----------⎡⎤+-+-+⎢⎥-+-+-⎣⎦取(0)0=x ，则有1()at bt at bt e e t a b ae be ----⎡⎤-+=⎢⎥--⎣⎦x② ()()1u t t =，()()()12()()()()()()()()01010011()1()(0)1at btat bt at btat bt a t b t a t b t t a t b t a t b t bt at x be ae e e t x a b abe abe ae be be ae e e d a b abe abe ae be ae be x a b ττττττττττ--------------------------⎡⎤⎡⎤-+-+=⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤-+-+⎡⎤+⎢⎥⎢⎥---⎣⎦⎣⎦-=-⎰x 2121111()(0)()(0)()(0)at btat bt at bt at bt at bte e x e e b a a babe abe x ae be x e e ----------⎡⎤+-++-+-⎢⎥⎢⎥-+--+⎣⎦取(0)0=x ，则有 11111()at bt at bt e e t b a a ba be e ----⎡⎤-+-⎢⎥=⎢⎥--+⎣⎦x ③()u t t =，()()()()12()()()()()()()()01010011()0(1at btat bt at btat bt ta tb t a t b t a t b t a t b t at bt x be ae e e t x a b abe abe ae be be ae e e d a b abeabe ae be be ae x e a b ττττττττττ--------------------------⎡⎤⎡⎤-+-+=⎢⎥⎢⎥---⎣⎦⎣⎦⎡⎤-+-+⎡⎤+⎢⎥⎢⎥---⎣⎦⎣⎦-++-=-⎰x ()()()2221211)011()0()0at bt at btat bt at bt at btat e bt e e x a b at e bt e abe abe x ae be x a b ----------⎡⎤-+-++-+⎢⎥⎢⎥-+-+⎢⎥-+--+⎢⎥⎣⎦取(0)0=x ，则有 ()2211111at bt at bt at e bt e a b t a b at e bt e a b ----⎡⎤-+-+-+⎢⎥⎢⎥=--+-+⎢⎥-⎢⎥⎣⎦x 3.12 线性时变系统()()()t t t = xA x 的系数矩阵如下。