常用的傅里叶变换+定理+各种变换的规律(推荐)
傅里叶变换的基本概念及基本定理

g ( x) sin( 2πnf 0 x)dx = 0
采用指数傅里叶级数展开,可以使展开系数的表达式统一而简洁。 采用指数傅里叶级数展开,可以使展开系数的表达式统一而简洁。
二维傅里叶变换
——指数傅里叶级数 可以在(-∞ 可以在 展为 满足狄氏条件的函数 g(x) 具有有限周期τ,可以在 ∞,+ ∞)展为 Байду номын сангаас数傅里叶级数: 指数傅里叶级数
第三讲 二维傅里叶变换的基本概念及基本定理
• 恩格斯(Engels) 把傅里叶 傅里叶的数学成 傅里叶 就与他所推崇的哲学家黑格尔 (Hegel) 的辩证法相提并论.
他写道:傅里叶 傅里叶是一首数学的诗, 傅里叶 黑格尔是一首辩证法的诗.
1、三角傅里叶级数展开 、
满足狄氏条件的函数 g(x) 具有有限周期τ,可以在(-∞,+ ∞)展 为三角傅里叶级数:
+∞
f (x, y) = ∫∫ F( fx , f y ) exp[ j2π ( fx x + f y y)df xdf y
−∞
记作:
f(x,y)=
-1{F(f
x,fy)}.
显然
-1
{f(x,y)}= f(x,y)
综合可写:
f(x,y)
F.T. F.T.-1
F(fx,fy)
f(x,y)和F(fx,fy)称为傅里叶变换对 x (y) 和 fx (fy )称为一对共轭变量, 它们在不同 的范畴(时空域或频域) 描述同一个物理对象.
图1-5-1 函数 ei2π(fxx+fyy) 的零位相直线族
二维傅里叶变换 2-D Fourier Transform 广义 F.T.
对于某些不符合狄氏条件的函数, 求F.T.的方法. 对某个可变换函数组成的系列取极限→不符合狄氏条件的函数, 函数系列变换式的极限→原来函数的广义F. T.
傅里叶变换常用公式大全

傅里叶变换常用公式大全傅里叶变换是一种重要的数学工具,用于将信号从时域转换到频域。
在信号处理、图像处理和通信领域广泛应用。
本文将介绍一些傅里叶变换中常用的公式,以帮助读者更好地理解和应用傅里叶变换。
1. 傅里叶变换的定义公式傅里叶变换的定义公式如下:F(ω) = ∫[f(t) * e^(-jωt)]dt其中F(ω)表示信号f(t)在频率ω处的傅里叶变换。
2. 傅里叶变换的逆变换公式傅里叶变换的逆变换公式如下:f(t) = ∫[F(ω) * e^(jωt)]dω其中f(t)表示频域信号F(ω)的逆变换。
3. 傅里叶级数展开公式傅里叶级数展开公式将一个周期信号表示为一系列正弦和余弦函数的和。
公式如下:f(t) = a₀ + Σ[aₙ * cos(nω₀t) + bₙ * sin(nω₀t)]其中a₀, aₙ, bₙ为系数,n为正整数,ω₀为基本角频率。
4. 傅里叶级数系数计算公式傅里叶级数系数的计算公式如下:a₀ = 1/T₀ * ∫[f(t)]dtaₙ = 2/T₀ * ∫[f(t) * cos(nω₀t)]dtbₙ = 2/T₀ * ∫[f(t) * sin(nω₀t)]dt其中T₀为周期。
5. 傅里叶变换的线性性质公式傅里叶变换具有线性性质,公式如下:F(a * f(t) + b * g(t)) = a * F(f(t)) + b * F(g(t))其中a和b为常数。
6. 傅里叶变换的频移性质公式傅里叶变换具有频移性质,公式如下:F(f(t - t₀)) = e^(-jωt₀) * F(f(t))其中t₀为时间偏移量。
7. 傅里叶变换的频率缩放公式傅里叶变换具有频率缩放性质,公式如下:F(f(a * t)) = (1/|a|) * F(f(t/a))其中a为常数。
8. 傅里叶变换的频域微分公式傅里叶变换的频域微分公式如下:F(d/dt[f(t)]) = jωF(f(t))其中d/dt表示对时间t的导数。
傅里叶变换常用公式

傅里叶变换常用公式1.傅里叶变换定义:F(w) = ∫[f(t)e^(-jwt)] dt2.傅里叶逆变换定义:f(t) = ∫[F(w)e^(jwt)] dw / (2π)傅里叶逆变换定义了将频域函数F(w)转换回时域函数f(t)的方式。
3.单位冲激函数的傅里叶变换:F(w) = ∫[δ(t)e^(-jwt)] dtδ(t)是单位冲激函数,其傅里叶变换结果为14.周期函数的傅里叶级数展开:f(t) = ∑[a(n)cos(nω0t) + b(n)sin(nω0t)]f(t)可以用无穷级数形式表示,其中ω0为基本角频率,a(n)和b(n)为系数。
5.周期函数的傅里叶变换:F(w)=2π∑[δ(w-nω0)]周期函数f(t)的频谱是一系列频率为nω0的冲激函数。
6.卷积定理:FT[f*g]=F(w)G(w)f*g表示函数f(t)和g(t)的卷积,FT表示傅里叶变换,*表示复数乘法。
卷积定理说明卷积在频域中的运算等于对应的傅里叶变换相乘。
7.积分定理:∫[f(t)g(t)] dt = 1/2π ∫[F(w)G(-w)] dw积分定理表明函数f(t)和g(t)的乘积在时域中的积分等于它们在频域中的乘积的逆变换。
8.平移定理:g(t) = f(t - t0) 对应的傅里叶变换 F(w) = e^(-jwt0) G(w)平移定理说明在时域中将函数f(t)右移t0单位,等价于在频域中将F(w)乘以e^(-jwt0)。
9.缩放定理:g(t) = f(at) 对应的傅里叶变换 G(w) = 1/,a, F(w/a)缩放定理说明在时域中将函数f(t)横向拉伸为af(t),等价于在频域中将F(w)纵向压缩为1/,a,F(w/a)。
除了以上列举的公式,傅里叶变换还有许多性质和定理,如频移定理、频域微分定理、频域积分定理等,这些公式和定理在信号处理中非常有用,可以加速计算和简化问题的分析。
常用的傅里叶变换 定理 各种变换的规律(推荐)

GG ( P )
sin(Sx) comb( x)
comb( P )
rect( x) tri( x)
cir (r )
sinc( P )
sinc 2 (P ) J1 ( U )
1
一、δ 函数的傅里叶变换: 设: [δ ( x )] = ∆ ( u ) ,
由卷积定理知: 等号两边作 傅里叶变换:
[g ( x )] = G ( u)
H fx
˄˅լᙗᇊ⨶˖ྲ᷌ F ^g x ` ˄㕙઼᭮৽╄ᇊ⨶˅ 1 § fx · F ^g ax ` G¨ ¸ ࡉᴹ a © a ¹ ˄অ㕍㹽ሴˈ㕍ゴ㹽ሴਈᇭ˅
G f x
˄˅ս〫ᇊ⨶˖ྲ᷌ F ^g x ` G f x ࡉᴹ F ^g x a ` G f x exp j 2Sf x a ࠭ᮠ൘オฏѝⲴᒣ〫ˈᑖᶕ仁ฏѝⲴ〫
3
二、梳状函数的傅里叶变换
F [comb( x )] = comb( u)
普遍型
x F comb = a comb( au) a
结论
comb 函数的
傅里叶变换 仍是
二维情况
x y F comb comb a b = ab comb( au) comb( bv )
结论:余弦函数的傅里叶变换是 δ 函数组合
-u0
0
u0
8
u
六、三角形函数的傅里叶变换
推导 一 维 情 况
F [Λ ( x )] = ?
已知
Λ ( x ) = rect( x ) ∗ rect( x )
= F [rect( x )] •F [rect( x )]
F [ Λ ( x )] = F [rect( x ) ∗ rect( x )] = sinc( u) • sinc( u)
常用的傅里叶变换拉普拉斯变换Z变换及其性质

Y (e jw ) = X (e jw ) H (e jw )
π
−π
X (e jθ ) H (e j ( ω−θ) )dθ
2
n=−∞
x ( n)
∞
2
=
1 2π
π
−π
X (e jω ) dω
周期信号 f (t ) 的傅里叶变换是由一些冲激函数组成的,这些冲激位于信号的谐频
f (t)为实函数, 若f (t), 则 6)能量积分 [f(t)] dt = 1 2π
F (ω)F (ω)dω =
|F(ω)| dω =
1 2π
S(ω)dω
S(ω) = |F(ω)| 称为能量密度函数(或能量密度) 7.卷积 1)定义 f (τ)f (t − τ)dτ称为f (t),f (t)的卷积,记为f (t) ∗ f (t) 2)定理 f (t) ∗ f (t) = f (t) ∗ f (t) |f (t) ∗ f (t)|≤ |f (t)| ∗ |f (t)| f (t) ∗ [f (t) + f (t) = f (t) ∗ f (t) + f (t) ∗ f (t) ℱ [F(ω)] ℱ[f (t) ∗ f (t)] = F (ω) · F (ω) ℱ[f (t) · f (t)] = 1 F (ω) ∗ F (ω) 2π ℱ[f (t) ∗ f (t) ∗···∗ f (t)] = F (ω) · F (ω) ··· F (ω) 1 2π F (ω) ∗ F (ω) ∗···∗ F (ω)
L[ f (t )dt ] =
一般形式 3 积分定理
L[ f (t )(dt ) 2 ] =
常见的傅里叶变换+定理+各种变换的规律(推荐)
= Gaus(u)
结论:
Gaus(x) F.T. Gaus(u)
7
五、余弦函数的傅里叶变换
F [cos(2πu0x) ] 其中 u0 = 1 / Τ Τ 为周期 ∞
= ∫ [cos2πu0 x ]• exp[− j2πux]dx
−∞
∫ =
∞ −∞
1 2
[exp(
j
2πu0
x)
x a
= a sin(πau) πau
= a sinc(au)
证明:根据相似性定理
6
四、高斯函数的傅里叶变换
Gaus(x) = exp[- πx2]
推导一维情况
F [Gaus(x) ]= F { exp[- πx2]}
∞
= ∫ exp[-πx2 ]• exp[− j2πux]dx −∞
−∞ 1/ 2
= ∫ exp(− j2πux)dx
rect
x a
=
1, 0,
−1/ 2
=1
1/2
exp(− j2πux)
− j2πu
-1/2
= sin(πu) πu
结论:
x ≤a 2
其它
= sinc(u) rect(x) F.T. sinc(u)
5
普遍型
F
rect
˄অ㕍㹽ሴˈ㕍ゴ㹽ሴਈᇭ˅
˄˅ս〫ᇊ⨶˖ྲ᷌ F^g x ` G fx
ࡉᴹ F^g x a ` G fx exp j2Sfxa
࠭ᮠ൘オฏѝⲴᒣ〫ˈᑖᶕ仁ฏѝⲴ〫
਼ᰦ F^g x exp j2Sfax ` G fx fa ࠭ᮠ൘オฏѝⲴ〫ˈᑖᶕ仁ฏѝⲴᒣ〫
傅里叶变换的基本概念及基本定理共39页
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
傅里叶变换的基本概念及基本定理
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进
常用傅里叶变换
时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释1 线性2 时域平移3 频域平移,变换2的频域对应4 如果值较大,则会收缩到原点附近,而会扩散并变得扁平.当|?a?|?趋向无穷时,成为狄拉克δ函数。
5 傅里叶变换的二元性性质。
通过交换时域变量和频域变量得到.6 傅里叶变换的微分性质7 变换6的频域对应8 表示和的卷积—这就是卷积定理9 变换8的频域对应。
[编辑]平方可积函数傅里叶变换傅里叶变换10 矩形脉冲和归一化的sinc函数11 变换10的频域对应。
矩形函数是理想的低通滤波器,sinc函数是这类滤波器对反因果冲击的响应。
12 tri?是三角形函数13 变换12的频域对应14 高斯函数exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。
15 光学领域应用较多161718 a>019 变换本身就是一个公式20 J0(t)?是0阶第一类贝塞尔函数。
21 上一个变换的推广形式;?T n(t)?是第一类切比雪夫多项式。
22 U n?(t)是第二类切比雪夫多项式。
[编辑]分布时域信号角频率表示的傅里叶变换弧频率表示的傅里叶变换注释23 δ(ω)代表狄拉克δ函数分布.这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换24 变换23的频域对应25 由变换3和24得到.26 由变换1和25得到,应用了欧拉公式:?cos(at) = (e iat?+?e???iat) / 2.27 由变换1和25得到28 这里,?n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。
这个变换是根据变换7和24得到的。
将此变换与1结合使用,我们可以变换所有多项式。
29 此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的.30 变换29的推广.31 变换29的频域对应.32 此处u(t)是单位阶跃函数;此变换根据变换1和31得到.33 u(t)是单位阶跃函数,且a?> 0.34 狄拉克梳状函数——有助于解释或理解从连续到离散时间的转变.[编辑]二元函数三元函数。
傅里叶变换性质及定理
(1-15)
(1-16)
• 将变量t与ω
互换 2f ( ) F (t)e jtdt
所以
2πf(-ω) ←→ F(t)
特别地, 当f(t)是t的偶函数, 那么
F(t) ←→ 2πf(-ω)=2πf(ω)
即有
f () 1 F(t) 2
(1-17)
•
例1-6 已知F1(ω)如图1-10所示, 利
仍以例1-3的f1(t)、 f(t)为例, f0(t)
的频谱F0(ω)如图1-7(b)所示。 利用一个
低通滤波器(在后面介绍), 滤除2ω0附
近的频率分量, 即可提取f1(t), 实现解
调。
(a)
f (t)
f0(t)
低 通 滤波 器
f1(t)
cos0t
F() A 2
A 4
(b) - 20
-0
0
0
A F0() 2
信号与系统
傅里叶变换性质及定理
•
1. 线性
•
若f1(t)←→F1(ω), f2(t)←→F2(ω), 则
•
af1(t)+bf2(t) ←→ aF1(ω)+bF2(ω)
• 式中, a、 b为任意常数。
(3.3-1)
•证
af1(te jtdt
b
f(-t) ←→ F(-ω)
尺度特性说明, 信号在时域中压缩, 频域中 就扩展; 反之, 信号在时域中扩展, 在频域中 就一定压缩; 即信号的脉宽与频宽成反比。
•
一般时宽有限的信号, 其频宽无限,
反之亦然。 由于信号在时域压缩(扩展)
时, 其能量成比例的减少(增加), 因
此其频谱幅度要相应乘以系数1/|a|。 也
常用傅里叶变换表
时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3
频域平移, 变换2的频域对应
4
如果
值较大,则会收缩到原
点附近,而会扩散并变得
扁平. 当 | a | 趋向无穷时,成为
Delta 函数。
5
傅里叶变换的二元性性质。
通过交换时域变量 和频域变量 得到.
6
傅里叶变换的微分性质
7
变换6的频域对应
表示和的卷积—这就是卷积定理
矩形脉冲和归一化的
变换
想的低通滤波器,
滤波器对反因果冲击的响应。
tri
变换
高斯函数
换是他本身
这是可积的。
a>0
变换本身就是一个公式δ
这个变换展示了狄拉克要性:
变换
由变换
由变换
式
由变换
这里
是狄拉克
这个变换是根据变换将此变换与
换所有多项式。
此处
换与变换
变换
变换
此处
根据变换
u
狄拉克梳状函数
理解从连续到离散时间的转变
Welcome !!! 欢迎您的下载,资料仅供参考!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
˄˅լᙗᇊ⨶˖ྲ᷌ F ^g x ` ˄㕙઼᭮৽╄ᇊ⨶˅ 1 § fx · F ^g ax ` G¨ ¸ ࡉᴹ a © a ¹ ˄অ㕍㹽ሴˈ㕍ゴ㹽ሴਈᇭ˅
G f x
˄˅ս〫ᇊ⨶˖ྲ᷌ F ^g x ` G f x ࡉᴹ F ^g x a ` G f x exp j 2Sf x a ࠭ᮠ൘オฏѝⲴᒣ〫ˈᑖᶕ仁ฏѝⲴ〫
F.T.
g( x ) ∗ δ ( x ) = g( x )
F.T. F.T.
G( u) • ∆ ( u) = G( u)
即:
∆ ( u) = 1
F [δ ( x )] = 1
(1-55)
F [1] = δ ( x )(1-56)
物理意义
一个
光脉冲
的傅氏变换
是一束 空间频率为 0 的 单位振幅平面波 反之亦然
3
二、梳状函数的傅里叶变换
F [comb( x )] = comb( u)
普遍型
x F comb = a comb( au) a
结论
comb 函数的
傅里叶变换 仍是
二维情况
x y F comb comb a b = ab comb( au) comb( bv )
√
√
τSa 2 (
ωτ
2
)
W Wt Sa 2 ( ) 2π 2
√
e − at u (t ), Re{a} > 0
e
−a t
1 a + jω
2a ω + a2
2
1
τ − jt
τ
t +τ 2
2
2πe −τω u (ω ),τ > 0
, Re{a} > 0
πe −τ ω ,τ > 0
√ √
e − at cos ω 0tu (t ), Re{a} > 0
0
]
k = −∞
∑F e
k
+∞
jkω 0t
2π
k = −∞
∑ F δ (ω − kω
)
连续傅里叶变换性质及其对偶关系
f (t ) =
1 2π
+∞ −∞
∫ F (ω )e
jωt
dω
F (ω ) =
+∞
−∞
∫ f (t )e
+∞
− jωt
dt
f (0) =
1 2π
∫
+∞
−∞
F (ω )dω
F (0) = ∫−∞ f (t )dt
GG ( P )
sin(Sx) comb( x)
comb( P )
rect( x) tri( x)
cir (r )
sinc( P )
sinc 2 (P ) J1 ( U )
1
一、δ 函数的傅里叶变换: 设: [δ ( x )] = ∆ ( u ) ,
由卷积定理知: 等号两边作 傅里叶变换:
[g ( x )] = G ( u)
㵍㬒⫇䊻㰖⳦巛㠞䄧㬒⭥䊬㰄Ⳟⳉ
㠞䄧巛㰖⳦㉚㬨ⰵ䓵⢅㑠 [ 巛 P 㡑䔘䇤᱄ 㪉
[ f ( x)] F (P ) 䋓
x0 ½ a ® f [ ( x r )]¾ a ¿ ¯ b
ax r x0 [f( )] b
x0 b b exp(r j 2S P ) F ( P ) a a a
ሩ࠭ᮠ㔗䘋㹼↓ਈᦒ઼䘶ਈᦒˈ䟽ᯠᗇ ࡠ࠭ᮠ˗㘼ሩ࠭ᮠ㔗䘋㹼є⅑↓ਈᦒ ᡆ䘶ਈᦒˈᗇࡠ࠭ᮠⲴĀۿ・قāDŽ
ު
$᷏㉎〞Ⰹ㏎ 㪉
[ f ( x)] F (P ), [ g ( x)] G( P ) ᷍
䋓䇱ᷛ [ f ( x) g ( x)] F (P )G(P ) %᷏㉎〞Ⰹ㏎
F [cos(2πu0x) ]
∞
其中 u0 = 1 / Τ
Τ 为周期
=
−∞
∫ [cos2πu
0
x ] • exp[− j 2πux ]dx
1 = ∫ [exp( j 2πu0 x ) + exp(- j 2πu0 x ) ] 2 F (u) −∞ 1/2 • exp[− j 2πux ]dx
∞
1 = [δ ( u − u0 ) + δ ( u + u0 )] 2
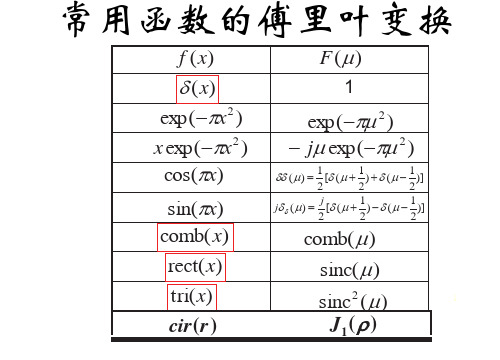
常用函数的傅里叶变换
f ( x) G ( x) F (P )
1
2
exp( Sx 2 ) x exp( Sx ) cos(Sx)
exp( SP ) 2 jP exp( SP )
2
1 1 1 [G ( P ) G ( P )] 2 2 2 1 j 1 jG G ( P ) [G ( P ) G ( P )] 2 2 2
਼ᰦ F ^g x exp j 2Sf a x ` G f x f a ࠭ᮠ൘オฏѝⲴ〫ˈᑖᶕ仁ฏѝⲴᒣ〫
㪉
[ f ( x)] F (P ) ᷍ x0 㬨⤜㸋㒄⭥㬖⧄㭞᷍䋓䇱
[ f ( x r x0 )] exp(r j 2SP x0 ) F (P ) ᷉㠞䄧㾵䐫᷊ [exp p(r j 2SP0 x) f ( x)] F (P P0 ) ᷉㼁䄧㾵䐫᷊
请自行证明 提示: 利用关系式
2step( x ) - 1 = sgn( x )
以及傅里叶变换的定理进行推导
12
ࡳሀؐওު
˄˅㓯ᙗᇊ⨶˖ྲ᷌ F^g x ` G f x , F^h x ` ˄⌒Ⲵਐ࣐⨶˅ ࡉᴹ F^Dg x Eh x ` DG f x EH f x
= sinc( u)
−1 / 2
∫ exp(− j 2πux )dx
a x ≤ 2 其它
rect(x)
F.T.
sinc(u)
5
普遍型
x F rect a
sin(πau) = a πau
= a sinc( au)
证明:根据相似性定理
6
四、高斯函数的傅里叶变换
[ f ( x) g ( x)] F (P ) G(P )
总结
表 6.3
f (t ) = 1 2π
+∞ −∞
常用的连续傅里叶变换对及其对偶关系
dω F (ω ) =
+∞ −∞
∫ F (ω )e
jωt
∫ f (t )e
− jωt
dt
重 要
连续傅里叶变换对 连续时间函数 f (t ) 傅里叶变换 F (ω )
√ √
δ T (t ) =
l = −∞
∑ δ (t − lT )
t − ( )2
+∞
2π T
k = −∞
∑ δ (ω − k
π τe
−(
+∞
2π ) T
ωτ
2
e
τ
)2
√
[u (t +
τ
2
) − u (t −
τ
)] cos ω t 0 2
τ
2
[ Sa
(ω + ω )τ 0 2
+∞ k
+ Sa
(ω − ω )τ 0 2
2
普遍型
F [δ ( x − x0 )] = ?
由位移定理: F
[δ ( x − x0 )] = F [δ ( x )]• exp(− i 2πux0 )
= exp(− i 2πux0 )
一个位于 x0 点的
经傅氏变换
物理意义
δ ( x − x0 )
F.T.
光脉冲
exp(− i 2πux0 )
一束 空间频率为 u 的 单位振幅平面波
证明请查阅有关参考书
comb 函数
4
三、矩形函数的傅里叶变换
根据定义
F [rect( x )] = ?
x 1, rect = a 0 , 1/2
-1/2
F [rect( x )] =
1/ 2
∞
−∞
∫ rect( x ) • exp(− j 2πux )dx
=
1 = exp(− j 2πux ) − j 2πu sin(πu) = 结论: πu
᷊᷉㘇〞ⰵ䇇㻖
㪉 [ f ( x)] F (P ) 䋓䇱
³
f
f
f ( x) dx
F (0)
³
f
f
F (P ) dP
f (0)
᷊᷉ I᷉[᷊㤛㼀㻣㘇〞⭩䇻 F (0) ᷍㒄㠖⭩䇻凵 㭞⭥㚽㑠䐖ᷜ ᷊᷉ F ( P ) ⭥㤛㼀㻣㘇〞䋓⭩䇻 f (0) ᱄
请自行证明
10
七、圆域函数的傅里叶变换
F [circ( x + y )] =
2 2
J 1 ( 2πρ )
ρ
一阶第一类贝塞尔函数 普遍型:
x2 + y2 J 1 ( 2πaρ ) )] = F [circ( a ρ 半径
请自行证明
11
七、step函数的傅里叶变换
1 1 F [step( x )] = + δ ( u) j 2πu 2
重 要
名称
连续傅里叶变换对 傅里叶变换 F (ω ) 连续时间函数 f (t )
䋓䇱ᷛ
³
f
f
f ( x ) g * ( x ) dx
³
f
f
F ( P ) G * ( P ) dP
˄ ˅ڵ䟼ਦ〟࠶ᇊ⨶˖൘࠭ᮠ g x,y Ⲵ њ䘎㔝⛩кᴹ
F -1 F ^g x,y ` FF
-1
^g x,y ` g x,y
