七年级下册数学几何复习题
初中七年级的数学下册的平面直角坐标系中几何综合题总结复习题

2015 年七年级下学期《平面直角坐标系中几何综合题》2015-07一.解答题(共17 小题)1.( 2015 春?玉环县期中)如图在平面直角坐标系中,A( a,0),B(b,0),(﹣ 1,2).且 |2a+b+1|+=0.(1)求 a、b 的值;(2)①在 y 轴的正半轴上存在一点 M ,使 S△COM= S△ABC,求点 M 的坐标.(注明:三角形 ABC 的面积表示为S△ABC)②在坐标轴的其他地址可否存在点M ,使 S△COM= S△ABC仍成立?若存在,请直接写出吻合条件的点M 的坐标.2.( 2015 春?汕头校级期中)如图,在下面直角坐标系中,已知 A ( 0,a),B(b,0),C( 3,c)三点,其中a、b、2c 满足关系式:|a﹣ 2|+( b﹣ 3) +=0.( 1)求 a、b、 c 的值;( 2)若是在第二象限内有一点P( m,),请用含m 的式子表示四边形ABOP 的面积;(3)在( 2)的条件下,可否存在负整数 m,使四边形 ABOP 的面积不小于△AOP 面积的两倍?若存在,求出所有满足条件的点 P 的坐标,若不存在,请说明原由.3.( 2015 春 ?鄂城区期中)如图,在平面直角坐标系中,点 A ,B 的坐标分别为 A ( a,0), B( b, 0),且 a、 b 满足 a=+﹣1,现同时将点 A , B 分别向上平移 2 个单位,再向右平移 1 个单位,分别获取点 A ,B 的对应点 C, D,连接 AC ,BD , CD .( 1)求点 C, D 的坐标及四边形ABDC 的面积 S 四边形ABDC.P 的坐标;若不( 2)在 y 轴上可否存在一点P,连接 PA, PB,使 S△PAB=S 四边形ABDC?若存在这样一点,求出点存在,试说明原由.( 3)点P 是线段BD 上的一个动点,连接PC, PO,当点P 在BD 上搬动时(不与 B ,D 重合)的值可否发生变化,并说明原由.4.(2014 春?富顺县校级期末)在平面直角坐标系中, A( a,0),B( b,0),C(﹣ 1,2)(见图 1),且 |2a+b+1|+ =0 ( 1)求 a、b 的值;( 2)①在 x 轴的正半轴上存在一点M ,使△COM 的面积 =△ABC的面积,求出点M 的坐标;② 在坐标轴的其他地址可否存在点M ,使△ COM 的面积 = △ ABC 的面积依旧成立?若存在,请直接写出吻合条件的点 M 的坐标;( 3)如图2,过点 C 作CD⊥y 轴交y 轴于点 D ,点P 为线段CD 延长线上的一动点,连接OP, OE 均分∠ AOP ,OF⊥ OE .当点P 运动时,的值可否会改变?若不变,求其值;若改变,说明原由.5.( 2014 春 ?泰兴市校级期末)已知:如图①,直线 MN ⊥直线 PQ,垂足为 O,点 A 在射线 OP 上,点 B 在射线 OQ 上( A、 B 不与 O 点重合),点 C 在射线 ON 上且 OC=2,过点 C 作直线 l∥ PQ,点 D 在点 C 的左边且 CD=3 .(1)直接写出△ BCD 的面积.(2)如图②,若 AC ⊥BC ,作∠ CBA 的均分线交 OC 于 E,交 AC 于 F,求证:∠ CEF= ∠ CFE.(3)如图③,若∠ ADC= ∠ DAC ,点 B 在射线 OQ 上运动,∠ ACB 的均分线交 DA 的延长线于点 H ,在点 B 运动过程中的值可否变化?若不变,求出其值;若变化,求出变化范围.26.( 2014 春 ?江岸区期末)如图 1,在平面直角坐标系中, A ( a ,0), B ( b , 3),C ( 4, 0),且满足( a+b ) +|a﹣ b+6|=0 ,线段 AB 交 y 轴于 F点.( 1)求点 A 、 B 的坐标.( 2)点 D 为 y 轴正半轴上一点,若 ED ∥ AB ,且 AM ,DM 分别均分∠ CAB ,∠ ODE ,如图 2,求∠ AMD 的度数.( 3)如图 3,(也可以利用图 1)① 求点 F 的坐标; ② 点 P 为坐标轴上一点,若△ABP的三角形和 △ABC 的面积相等?若存在,求出 P 点坐标.7.( 2014 春?黄陂区期末) 在直角坐标系中,已知点 A 、B 的坐标是( a ,0)( b ,0),a ,b 满足方程组,c 为 y 轴正半轴上一点,且S △ ABC =6 .( 1)求 A 、 B 、 C 三点的坐标;( 2)可否存在点 P ( t , t ),使 S △PAB =S △ABC ?若存在,央求出P 点坐标;若不存在,请说明原由;( 3)若 M 是 AC 的中点,N 是 BC 上一点,CN=2BN ,连 AN 、BM 订交于点 D ,求四边形 CMDN 的面积是.8.( 2014 春 ?海珠区期末)在平面直角坐标系中,点 A ( a , b )是第四象限内一点, AB ⊥ y 轴于 B ,且 B (0, b )是 y 轴负半轴上一点, b 2=16 , S △AOB =12.( 1)求点 A 和点 B 的坐标;( 2)如图 1,点 D 为线段 OA (端点除外)上某一点,过点∠ AFD 的均分线订交于N ,求∠ 的度数.D 作AO垂线交x 轴于E,交直线AB 于F,∠EOD、( 3)如图E,交直线2,点AB 于D 为线段 OA(端点除外)上某一点,当点F,∠ EOD,∠ AFD 的均分线订交于点D 在线段上运动时,过点 D 作直线 EF 交 xN.若记∠ ODF= α,请用α的式子表示∠ONF轴正半轴于的大小,并说明原由.9.( 2014 春 ?黄梅县校级期中)如图,在下面的直角坐标系中,已知 A ( 0, a),B( b, 0), C( b, 4)三点,其中a,b 满足关系式.( 1)求a,b 的值;( 2)若是在第二象限内有一点P( m,),请用含m 的式子表示四边形ABOP 的面积;( 3)在( 2)的条件下,可否存在点若不存在,请说明原由.P,使四边形ABOP 的面积与△ ABC 的面积相等?若存在,求出点P 的坐标;10.( 2014 春 ?通州区校级期中)在如图直角坐标系中,已知 A ( 0, a), B( b,0), C( b, c)三点,其中a、 b、 c满足关系式2 2+( b﹣ 3) =0 ,( c﹣ 4)≤0.(1)求 a、b、 c 的值;(2)若是点 P( m, n)在第二象限,四边形 CBOP 的面积为 y,请你用含 m, n 的式子表示 y;( 3)若是点P 在第二象限坐标轴的夹角均分线上,并且y=2S 四边形CBOA,求 P 点的坐标.11.(2014 春 ?鄂州校级期中)如图,A 、B 两点坐标分别为2=0,A(a,4),B( b,0),且 a,b 满足( a﹣2b+8) +E 是 y 轴正半轴上一点.(1)求 A 、 B 两点坐标;(2)若 C 为 y 轴上一点且 S△AOC= S△AOB,求 C 点的坐标;( 3)过 B 作 BD ∥ y 轴,∠ DBF=∠DBA,∠ EOF=∠ EOA,求∠ F与∠ A间的数量关系.12.( 2014 春 ?东湖区期中)如图,平面直角坐标系中 A (﹣ 1,0), B( 3, 0),现同时将 A 、B 分别向上平移 2 个单位,再向右平移 1 个单位,分别获取 A 、 B 的对应点C、D ,连接 AC 、BD( 1)直接写出C、D 的坐标: C D及四边形ABCD 的面积:( 2)在 y 轴负半轴上可否存在点 M ,连接 MA 、 MB 使得 S△MAB> S 四边形ABCD?若存在,求出 M 点纵坐标的取值范围;若不存在说明原由( 3)点 P 为线段 BD 上一动点,连PC、PO,当点 P 在 BD 上搬动(不含端点)现给出①的值不变,②的值不变,其中有且只有一个正确,请你找出这个结论并求其值.13.( 2014 春 ?台州月考)如图,在平面直角坐标系中,点 A , B 的坐标分别为 A ( 0,α), B( b,α),且α、 b 满22 个单位,再向左平移 1 个单位,分别获取点 A ,B 的对应足( a﹣ 2) +|b﹣ 4|=0,现同时将点 A ,B 分别向下平移点 C,D ,连接 AC , BD ,AB .( 1)求点 C, D 的坐标及四边形ABDC 的面积 S 四边形ABCD(2)在 y 轴上可否存在一点 M ,连接 MC , MD ,使 S△MCD =S 不存在,试说明原由.(3)点 P 是线段 BD 上的一个动点,连接 PA, PO,当点 P 在四边形ABDC?若存在这样一点,求出点M 的坐标,若BD 上搬动时(不与B, D 重合)的值可否发生变化,并说明原由.14.( 2014 春 ?海安县月考)如图,在平面直角坐标系中,点 A ,B ,C 的坐标分别为(﹣1, 0),( 3, 0),( 0, 2),图中的线段 BD 是由线段 AC 平移获取.( 1)线段 AC 经过怎样的平移可获取线段BD ,所得四边形是什么图形,并求出所得的四边形ABDC 的面积 S 四边形ABDC;( 2)在 y 轴上可否存在点 P,连接 PA, PB,使 S =S 四边形ABDC?若存在,求出点P 的坐标;若不存在,试说△ PAB明原由;( 3)点 P 是线段 BD 上的一个动点,连接PC、 PO,当点 P 在 BD 上搬动时(不与 B ,D 重合)给出以下结论:①的值不变;②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.15.( 2014 春 ?武汉月考)已知,在平面直角坐标系中,2;点 A(0,m),点 B( n,0),m、n 满足( m﹣ 3) =﹣( 1)求 A 、 B 的坐标;( 2)如图1, E 为第二象限内直线 AB 上一点,且满足S△AOE= S△AOB,求 E 的坐标.( 3)如图 2,平移线段 BA 至 OC,B 与 O 是对应点, A 与 C 对应,连 AC .E 为 BA 的延长线上一动点,连 EO.OF均分∠ COE,AF 均分∠ EAC ,OF 交 AF 于 F 点.若∠ ABO+ ∠ OEB= α,请在图 2 中将图形补充完满,并求∠F(用含α的式子表示).16.( 2013 秋 ?江岸区校级月考)如图,已知点 A (﹣ m, n), B( 0, m),且 m、 n 满足2+( n﹣5) =0,点 C在 y 轴上,将△ ABC 沿 y 轴折叠,使点 A 落在点 D 处.(1)写出 D 点坐标并求 A 、 D 两点间的距离;(2)若 EF 均分∠ AED ,若∠ ACF ﹣∠ AEF=20 °,求∠ EFB 的度数;(3)过点 C 作 QH 平行于 AB 交 x 轴于点 H,点 Q 在 HC 的延长线上, AB 交 x 轴于点 R,CP、RP 分别均分∠ BCQ和∠ ARX ,当点 C 在 y 轴上运动时,∠CPR 的度数可否发生变化?若不变,求其度数;若变化,求其变化范围.17.( 2013 春 ?武汉校级月考)如图,在平面直角坐标系中,点 A , B 的坐标分别为 A (﹣ 1, 0)、 B( 3, 0).现同时将点 A , B 分别向上平移 2 个单位,再向右平移 1 个单位,分别获取点 A , B 的对应点C、 D,连接 AC , BD .( 1)直接写出点C、 D 的坐标,求四边形ABDC 的面积S 四边形ABDC;( 2)在坐标轴上可否存在一点P,使S△PAC=S 四边形ABDC?若存在这样一点,求出点P 的坐标;若不存在,试说明原由.( 3)如图 3,在线段 CO 上取一点 G,使 OG=3CG ,在线段 OB 上取一点 F,使 OF=2BF , CF 与 BG 交于点 H,求四边形OGHF 的面积 S 四边形OGHF.。
七年级数学下册专题08 期中-几何综合大题必刷(压轴题)(原卷版)
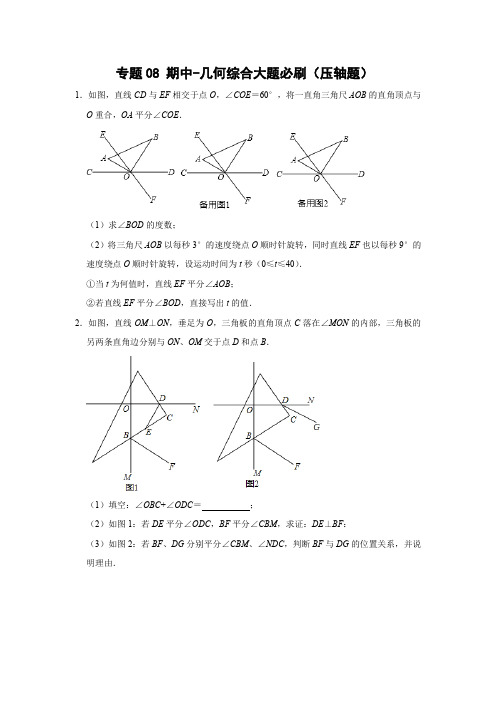
专题08 期中-几何综合大题必刷(压轴题)1.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.(1)求∠BOD的度数;(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).①当t为何值时,直线EF平分∠AOB;②若直线EF平分∠BOD,直接写出t的值.2.如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.(1)填空:∠OBC+∠ODC=;(2)如图1:若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF:(3)如图2:若BF、DG分别平分∠CBM、∠NDC,判断BF与DG的位置关系,并说明理由.3.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM 时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC 与边ON互相垂直.(直接写出答案)4.【学科融合】物理学中把经过入射点O并垂直于反射面的直线ON叫做法线,入射光线与法线的夹角i叫做入射角,反射光线与法线的夹角r叫做反射角(如图①).由此可以归纳出如下的规律:在反射现象中,反射光线、入射光线和法线都在同一平面内;反射光线、入射光线分别位于法线两侧;反射角等于入射角.这就是光的反射定律(reflection law).【数学推理】如图1,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:∠1=∠2,∠3=∠4.在这样的条件下,求证:AB∥CD.【尝试探究】两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD.(1)如图2,光线AB与CD相交于点E,则∠BEC=;(2)如图3,光线AB与CD所在的直线相交于点E,∠BED=β,则α与β之间满足的等量关系是.5.已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG =30°,求∠MGN+∠MPN的度数;(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.6.“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B 射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.7.如图,直线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF(1)求∠EOB的度数;(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.8.如图1,MN∥EF,C为两直线之间一点.(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系:.9.(1)【问题】如图1,若AB∥CD,∠BEP=25°,∠PFC=150°.求∠EPF的度数;(2)【问题迁移】如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;(3)【联想拓展】如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.10.如图,已知直线AB∥射线CD,∠CEB=100°.P是射线EB上一动点,过点P作PQ ∥EC交射线CD于点Q,连接CP.作∠PCF=∠PCQ,交直线AB于点F,CG平分∠ECF.(1)若点P,F,G都在点E的右侧.①求∠PCG的度数;②若∠EGC﹣∠ECG=40°,求∠CPQ的度数.(2)在点P的运动过程中,是否存在这样的情形,使?若存在,求出∠CPQ 的度数;若不存在,请说明理由.11.如图,AB∥CD,∠ABE=120°.(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.12.已知:AB∥CD,点E在直线AB上,点F在直线CD上.(1)如图(1),∠1=∠2,∠3=∠4.①若∠4=36°,求∠2的度数;②试判断EM与FN的位置关系,并说明理由;(2)如图(2),EG平分∠MEF,EH平分∠AEM,试探究∠GEH与∠EFD的数量关系,并说明理由.13.已知M、N分别为直线AB,直线CD上的点,且AB∥CD,E在AB,CD之间.(1)如图1,求证:∠BME+∠DNE=∠MEN;(2)如图2,P是CD上一点,连PM,作MQ∥EN,若∠QMP=∠BME.试探究∠E与∠AMP的数量关系,并说明理由;(3)在(2)的条件下,作NG⊥CD交PM于G,若MP平分∠QME,NF平分∠ENG,若∠MGN=m°,∠MFN=n°,直接写出m与n的数量关系.14.如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.(1)试说明:∠BAG=∠BGA;(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.15.已知:如图,直线PQ∥MN,点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.(1)若∠1与∠2都是锐角,如图1,请直接写出∠C与∠1,∠2之间的数量关系.(2)若小明把一块三角板(∠A=30°,∠C=90°)如图2放置,点D,E,F是三角板的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数.(3)将图2中的三角板进行适当转动,如图3,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,给出下列两个结论:①的②∠GEN﹣∠BDF的值不变.其中只有一个是正确的,你认为哪个是正确的?并求出不变的值是多少.16.已知AB∥CD,解决下列问题:(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.(2)如图②,若∠ABP=∠ABE,∠CDP=∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=∠ABE,∠CDP=∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).17.如图1,AM∥CN,点B为平面内一点,AB⊥BC于B,过B作BD⊥AM.(1)求证:∠ABD=∠C;(2)如图2,在(1)问的条件下,分别作∠ABD、∠DBC的平分线交DM于E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,①求证:∠ABF=∠AFB;②求∠CBE的度数.18.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,连接PM、PN、PQ,PQ平分∠MPN,如图①.(1)若∠PMA=α、∠PQC=β,求∠NPQ的度数(用含α,β的式子表示);(2)过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F,如图②,请你判断EF与PQ的位置关系,并说明理由;(3)在(2)的条件下,连接EN,如图③,若∠NEF=∠PMA,求证:NE平分∠PNQ.19.如图1,AB∥CD,G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2,若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.20.如图1,直线AB∥CD,直线EF交AB于点E,交CD于点F,点G和点H分别是直线AB和CD上的动点,作直线GH,EI平分∠AEF,HI平分∠CHG,EI与HI交于点I.(1)如图1,点G在点E的左侧,点H在点F的右侧,若∠AEF=70°,∠CHG=60°,求∠EIH的度数.(2)如图2,点G在点E的右侧,点H也在点F的右侧,若∠AEF=α,∠CHG=β,其他条件不变,求∠EIH的度数.(3)如图3,点G在点E的右侧,点H也在点F的右侧,∠GHC的平分线HJ交∠KEG 的平分线EJ于点J.其他条件不变,若∠AEF=α,∠CHG=β,求∠EJH的度数.21.如图1,已知直线EF分别与直线AB,CD相交于点E,F,AB∥CD,EM平分∠BEF,FM平分∠EFD(1)求证:∠EMF=90°.(2)如图2,若FN平分∠MFD交EM的延长线于点N,且∠BEN与∠EFN的比为4:3,求∠N的度数.(3)如图3,若点H是射线EA之间一动点,FG平分∠HFE,过点G作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系,并证明你的结论.22.已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.(1)如图1,点G在CH的延长线上时,①若∠GAB=36°,则∠MCD=.②猜想:∠GAB与∠MCD之间的数量关系是.(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.23.已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.(1)如图1,∠BME,∠E,∠END的数量关系为;(直接写出答案)(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数.(用含m的式子表示)(3)如图3点G为CD上一点,∠BMN=n•∠EMN,∠GEK=n•∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)24.如图1,AB∥CD,P为AB、CD之间一点(1)若AP平分∠CAB,CP平分∠ACD.求证:AP⊥CP;(2)如图(2),若∠BAP=∠BAC,∠DCP=∠ACD,且AE平分∠BAP,CF平分∠DCP,猜想∠E+∠F的结果并且证明你的结论;(3)在(1)的条件下,当∠BAQ=∠BAP,∠DCQ=∠DCP,H为AB上一动点,连HQ并延长至K,使∠QKA=∠QAK,再过点Q作∠CQH的平分线交直线AK于M,问当点H在射线AB上移动时,∠QMK的大小是否变化?若不变,求其值;若变化,求其取值范围.25.如图1,AB∥CD.G为AB、CD之间一点.(1)若GE平分∠AEF,GF平分∠EFC.求证:EG⊥FG;(2)如图2.若∠AEP=∠AEF,∠CFP=∠EFC,且FP的延长线交∠AEP的角平分线于点M,EP的延长线交∠CFP的角平分线于点N,猜想∠M+∠N的结果并且证明你的结论;(3)如图3,若点H是射线EB之间一动点,FG平分∠EFH,MF平分∠EFC,过点G 作GQ⊥FM于点Q,请猜想∠EHF与∠FGQ的关系;并证明你的结论.26.已知,BC∥OA,∠B=∠A=100°,试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,此时∠EOC的度数等于(直接写出答案即可);(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,求此时∠OCA度数.27.如图1,AB∥CD,点E、F分别在AB、CD上,点O在直线AB、CD之间,且∠EOF =80°.(1)求∠BEO+∠OFD的值;(2)如图2,直线MN分别交∠BEO、∠OFC的角平分线于点M、N,直接写出∠EMN ﹣∠FNM的值(3)如图3,EG在∠AEO内,∠AEG=m∠OEG;FH在∠DFO内,∠DFH=m∠OFH,直线MN分别交EG、FH分别于点M、N,且∠FMN﹣∠ENM=80°,直接写出m的值.28.已知,两直线AB,CD,且AB∥CD,点M,N分别在直线AB,CD上,放置一个足够大的直角三角尺,使得三角尺的两边EP,EQ分别经过点M,N,过点N作射线NF,使得∠ENF=∠ENC.(1)转动三角尺,如图①所示,当射线NF与NM重合,∠FND=45°时,求∠AME的度数;(2)转动三角尺,如图②所示,当射线NF与NM不重合,∠FND=60°时,求∠AME 的度数.(3)转动直角三角尺的过程中,请直接写出∠FND与∠AME之间的数量关系.29.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∥CD;(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.30.如图1,BC⊥AF于点C,∠A+∠1=90°.(1)求证:AB∥DE;(2)如图2,点P从点A出发,沿线段AF运动到点F停止,连接PB,PE.则∠ABP,∠DEP,∠BPE三个角之间具有怎样的数量关系(不考虑点P与点A,D,C重合的情况)?并说明理由.31.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.(1)如图1,求证:EF∥GH;(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.32.如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF 交CD于点M,且∠FEM=∠FME.(1)判断直线AB与直线CD是否平行,并说明理由;(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.①当点G在点F的右侧时,若β=56°,求α的度数;②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.33.如图1,G,E是直线AB上两点,点G在点E左侧,过点G的直线GP与过点E的直线EP交于点P.直线PE交直线CD于点H,满足点E在线段PH上,∠PGB+∠P=∠PHD.(1)求证:AB∥CD;(2)如图2,点Q在直线AB,CD之间,PH平分∠QHD,GF平分∠PGB,点F,G,Q在同一直线上,且2∠Q+∠P=120°,求∠QHD的度数;(3)在(2)的条件下,若点M是直线PG上一点,直线MH交直线AB于点N,点N 在点B左侧,请直接写出∠MNB和∠PHM的数量关系.(题中所有角都是大于0°且小于180°的角)34.已知,DE平分∠ADB交射线BC于点E,∠BDE=∠BED.(1)如图1,求证:AD∥BC;(2)如图2,点F是射线DA上一点,过点F作FG∥BD交射线BC于点G,点N是FG 上一点,连接NE,求证:∠DEN=∠ADE+∠ENG;(3)如图3,在(2)的条件下,连接DN,点P为BD延长线上一点,DM平分∠BDE 交BE于点M,若DN平分∠PDM,DE⊥EN,∠DBC﹣∠DNE=∠FDN,求∠EDN的度数.35.综合应用题:如图,有一副直角三角板如图①放置(其中∠D=45°,∠C=30°),P A、PB与直线MN重合,且三角板P AC,三角板PBD均可以绕点P逆时针旋转.(1)∠DPC=;(2)如图②,若三角板PBD保持不动,三角板∠P AC绕点P逆时针旋转,转速为10°/秒,转动一周三角板P AC就停止转动,在旋转的过程中,当旋转时间为多少时,有PC ∥DB成立;(3)如图③,在图①基础上,若三角板P AC的边P A从PN.处开始绕点P逆时针旋转,转速为3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/秒,(当PC转到与PM重合时,两三角板都停止转动),在旋转过程中,当∠CPD=∠BPM,求旋转的时间是多少?36.已知E,F分别是AB、CD上的动点,P也为一动点.(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.37.“一带一路”让中国和世界联系更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视若灯A转动的速度是每秒2°,灯B转动的速度是每秒1°.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.(1)填空:∠BAN=°;(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(3)若两灯同时开始转动,两灯射出的光束交于点C,且∠ACB=120°,则在灯B射线到达BQ之前,转动的时间为秒.38.已知AB∥CD,点E在AB上,点F在DC上,点G为射线EF上一点.(1)【基础问题】如图1,试说明:∠AGD=∠A+∠D.(完成图中的填空部分)证明:过点G作直线MN∥AB,又∵AB∥CD,∴∥CD∵MN∥AB,∴∠=∠MGA.∵MN∥CD,∴∠D=()∴∠AGD=∠AGM+∠DGM=∠A+∠D.(2)【类比探究】如图2,当点G在线段EF延长线上时,请写出∠AGD、∠A、∠D三者之间的数量关系,并说明理由.(3)【应用拓展】如图3,AH平分∠GAE,DH交AH于点H,且∠GDH=2∠HDF,∠HDF=22°,∠H=32°,直接写出∠DGA的度数为°.39.如图1,直线AB、CD被直线EF截,分别交AB于点G,交CD于点H,∠AGE与∠EHC互补.(1)求证:AB∥CD;(2)如图2,点P在直线AB、CD内部直线EF上,点M、N分别在直线AB、CD上,连接PM、PN,点K在∠PMB的角平分线上,连接KN,若∠MKN=180°∠MPN,求证:∠PNK=∠CNK;(3)如图3,在(2)的条件下,点O为AB上一点,连接ON、MN,MN平分∠PNO,若∠MNK:∠PMK=2:7,2∠MKN﹣∠PNO=180°,求∠NOM的度数.40.已知,AB∥CD,点F、G分别在AB、CD上,且点E为射线FG上一点.(1)如图1:当点E在线段FG上时,连接AE、DE,易得∠AED=∠EAF+∠EDG.小明给出的理由是:如图1,过E作EH∥AB,∵AB∥CD,∴AB∥CD∥EH,(平行于同一条直线的两条直线互相平行)∴∠EAF=∠AEH,∠EDG=∠DEH,(依据1)∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(依据2)填空:依据1:.依据2:.(2)如图2,当点E在FG延长线上时,求证:∠EAF=∠AED+∠EDG;(3)如图3,AI平分∠BAE,DI交AI于点I,交AE于点K,且∠EDI:∠CDI=2:1,∠AED=20°,∠I=30°,求∠EKD的度数.41.如图1,已知直线PQ∥MN,点A在直线PQ上,点C、D在直线MN上,连接AC、AD,∠P AC=50°,∠ADC=30°,AE平分∠P AD,CE平分∠ACD,AE与CE相交于E.(1)求∠AEC的度数;(2)若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置,此时A1E平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠P AC=50°,∠A1D1C=30°,求∠A1EC 的度数.(3)若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置,其他条件与(2)相同,求此时∠A1EC的度数.42.阅读下面材料:小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是.参考小亮思考问题的方法,解决问题:(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,作∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M=(直接用含α的式子表示).。
七年级 数学 第4章 几何图形 复习

O
所以∠AOE=∠AOC+∠COE =49.8°+18.9° = 68.7°= 68°42'
13.已知∠2是∠1的余角,∠3是∠2的补角,且∠1=40°, 分别求∠2,∠3的度数。
解:因为∠2是∠1的余角, 所以∠2=90°-∠1=90°-40°=50° 因为∠3是∠2的补角, 所以∠3=180°-∠2=180°-50°=130°
17.如图,OM,ON分别是∠BOC和∠AOC的平分线.如果 ∠AOB的大小不变,当OC在∠AOB内绕着点0转动时,∠MON的 大小是否会改变?为什么?
解:∠MON的大小不会改变. 理由:因为OM,ON分别是∠BOC和∠AOC的平分线, 所以∠MOC= ∠BOC,∠NOC= ∠AOC, 所以∠MON =∠MOC+∠NOC = ∠BOC+ ∠AOC= = (∠BOC+∠AOC)= ∠AOB. 因为∠AOB的大小不变,所以 ∠CAOB的大小也是固定的值, 因此∠MON的大小不会改变.
DB
6.如图,小强要从A点走到C点,有三条路可到达目的地. 请你帮他这选择一条最近的路径(只要求在图中标出来).
7.如图,线段AB=6cm,点C是AB的中点,点D是BC的 中点,E是 AD的中点,求线段AE的长.
A
EC
DB
解:因为点C是AB的中点,所以CB= AB= x6=3(cm) 因为点D是BC的中点,所以DB= CB= ×3= (cm) 因为AD+DB=AB所以AD=AB-DB=6- = (cm) 因为点E是AD的中点,所以AE= AD= × = (cm)
= ×180°=90°
12.如图,OD,OE分别是∠AOC和∠BOC的平分线,
∠AOD=24.9°,∠BOC=37.8°求∠AOE的度数(结果用
七年级数学下册期末几何压轴题试题(带答案) (一)解析

一、解答题1.如图,在平面直角坐标系中,()()()A 1,0,B 3,0,C 0,2-,CD//x 轴,CD=AB .(1)求点D 的坐标:(2)四边形OCDB 的面积S 四边形OCDB ;(3)在y 轴上是否存在点P ,使S △PAB =S 四边形OCDB ;若存在,求出点P 的坐标,若不存在,请说明理由.2.如图1,把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上. (1)根据图1填空:∠1= °,∠2= °;(2)现把三角板绕B 点逆时针旋转n °.①如图2,当n =25°,且点C 恰好落在DG 边上时,求∠1、∠2的度数;②当0°<n <180°时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n 的值和对应的那两条垂线;如果不存在,请说明理由.3.已知:如图,直线AB //CD ,直线EF 交AB ,CD 于P ,Q 两点,点M ,点N 分别是直线CD ,EF 上一点(不与P ,Q 重合),连接PM ,MN .(1)点M,N分别在射线QC,QF上(不与点Q重合),当∠APM+∠QMN=90°时,①试判断PM与MN的位置关系,并说明理由;②若PA平分∠EPM,∠MNQ=20°,求∠EPB的度数.(提示:过N点作AB的平行线)(2)点M,N分别在直线CD,EF上时,请你在备用图中画出满足PM⊥MN条件的图形,并直接写出此时∠APM与∠QMN的关系.(注:此题说理时不能使用没有学过的定理)4.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质,可得∠APC=∠APE+∠CPE=50°+60°=110°.问题解决:(1)如图2,AB∥CD,直线l分别与AB、CD交于点M、N,点P在直线I上运动,当点P 在线段MN上运动时(不与点M、N重合),∠PAB=α,∠PCD=β,判断∠APC、α、β之间的数量关系并说明理由;(2)在(1)的条件下,如果点P在线段MN或NM的延长线上运动时.请直接写出∠APC、α、B之间的数量关系;(3)如图3,AB∥CD,点P是AB、CD之间的一点(点P在点A、C右侧),连接PA、PC,∠BAP和∠DCP的平分线交于点Q.若∠APC=116°,请结合(2)中的规律,求∠AQC 的度数.5.如图,∠EBF=50°,点C是∠EBF的边BF上一点.动点A从点B出发在∠EBF的边BE 上,沿BE方向运动,在动点A运动的过程中,始终有过点A的射线AD∥BC.(1)在动点A运动的过程中,(填“是”或“否”)存在某一时刻,使得AD平分∠EAC?(2)假设存在AD平分∠EAC,在此情形下,你能猜想∠B和∠ACB之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.6.已知,AB ∥CD ,点E 为射线FG 上一点.(1)如图1,若∠EAF =25°,∠EDG =45°,则∠AED = .(2)如图2,当点E 在FG 延长线上时,此时CD 与AE 交于点H ,则∠AE D 、∠EAF 、∠EDG 之间满足怎样的关系,请说明你的结论;(3)如图3,当点E 在FG 延长线上时,DP 平分∠EDC ,∠AED =32°,∠P =30°,求∠EKD 的度数.7.阅读下面的文字,解答问题 22的小数部分我们不可能全部212 21,将这个数减去其整数部分,差就是小数部分. 479273,∴7272)请解答:(157整数部分是 ,小数部分是 .(211a 7b ,求|a ﹣b 11(3)已知:5x +y ,其中x 是整数,且0<y <1,求x ﹣y 的相反数.8.对任意一个三位数n ,如果n 满足各数位上的数字互不相同,且都不为零,那么称这个数为“梦幻数”,将一个“梦幻数”任意两个数位上的数字对调后可以得到三个不同的新三数,把这三个新三位数的和与111的商记为K (n ),例如123n =,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213321132666++=,6661116÷=,所以()1236K =.(1)计算:()342K 和()658K ;(2)若x 是“梦幻数”,说明:()K x 等于x 的各数位上的数字之和;(3)若x ,y 都是“梦幻数”,且1000x y +=,猜想:()()K x K y +=________,并说明你猜想的正确性.9.阅读下面的文字,解答问题:是无理数,而无理数是无限不循环小数,的小数部分我们不可能全部写出来,而121.请解答下列问题:_______,小数部分是_________;(2)的小数部分为a b ,求a b +(3)已知:100x y +=+,其中x 是整数,且01y <<,求24x y -的平方根. 10.规定:求若千个相同的有理数(均不等于0)的除法运算叫做除方,如()()()()2223333÷÷-÷-÷-÷-,等,类比有理数的乘方,我们把222÷÷记作()32,读作“2的圈3次方”,()()()()3333-÷-÷-÷-记作()()43-,读作“3-的圈4次方”,一般地,把n a a a a a↑÷÷÷⋯⋯÷记作()n a ,读作“a ”的圈n 次方.(初步探究)(1)直接写出计算结果:()()32=- ;()()42=- ;(2)关于除方,下列说法错误的是( )A .任何非零数的圈2次方都等于1B .对于任何正整数(),1=1n nC .()()433=4D .负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数 (深入思考)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(3)试一试:()()()2446113=5=35⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭,,依照前面的算式,将()93,()1012⎛⎫- ⎪⎝⎭的运算结果直接写成幂的形式是()93= ,()101=2⎛⎫- ⎪⎝⎭; (4)想一想:将一个非零有理数a 的圆n 次方写成幂的形式是:()n a = ; (5)算一算:()()()()4652311122333⎛⎫⎛⎫÷-⨯---÷ ⎪ ⎪⎝⎭⎝⎭.11.我们知道,正整数按照能否被2整除可以分成两类:正奇数和正偶数,小华受此启发,按照一个正整数被3除的余数把正整数分成了三类:如果一个正整数被3除余数为1,则这个正整数属于A 类,例如1,4,7等;如果一个正整数被3除余数为2,则这个正整数属于B 类,例如2,5,8等;如果一个正整数被3整除,则这个正整数属于C 类,例如3,6,9等.(1)2020属于 类(填A ,B 或C );(2)①从A 类数中任取两个数,则它们的和属于 类(填A ,B 或C );②从A 、B 类数中任取一数,则它们的和属于 类(填A ,B 或C );③从A 类数中任意取出8个数,从B 类数中任意取出9个数,从C 类数中任意取出10个数,把它们都加起来,则最后的结果属于 类(填A ,B 或C );(3)从A 类数中任意取出m 个数,从B 类数中任意取出n 个数,把它们都加起来,若最后的结果属于C 类,则下列关于m ,n 的叙述中正确的是 (填序号). ①2m n +属于C 类;②m n -属于A 类;③m ,n 属于同一类.12.观察下面的变形规律:;;;….解答下面的问题:(1)仿照上面的格式请写出= ; (2)若n 为正整数,请你猜想= ; (3)基础应用:计算:. (4)拓展应用1:解方程:=2016 (5)拓展应用2:计算:. 13.如图1在平面直角坐标系中,大正方形OABC 的边长为m 厘米,小正方形ODEF 的边长为n 厘米,且|m ﹣4|+2n -=0.(1)求点B 、点D 的坐标.(2)起始状态如图1所示,将大正方形固定不动,小正方形以1厘米/秒的速度沿x 轴向右平移,如图2.设平移的时间为t 秒,在平移过程中两个正方形重叠部分的面积为S 平方厘米.①当t =1.5时,S = 平方厘米;②在2≤t ≤4这段时间内,小正方形的一条对角线扫过的图形的面积为 平方厘米; ③在小正方形平移过程中,若S =2,则小正方形平移的时间t 为 秒.(3)将大正方形固定不动,小正方形从图1中起始状态沿x 轴向右平移,在平移过程中,连接AD ,过D 点作DM ⊥AD 交直线BC 于M ,∠DAx 的角平分线所在直线和∠CMD 的角平分线所在直线交于N (不考虑N 点与A 点重合的情形),求∠ANM 的大小并说明理由. 14.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.15.如图,在平面直角坐标系中,点A B 、的坐标分别为(1,0)、(-2,0),现同时将点A B 、分别向上平移2个单位,再向左平移1个单位,分别得到点AB 、的对应点CD 、,连接AC 、BD 、CD .(1)若在y 轴上存在点M ,连接MA MB 、,使S △ABM =S □ABDC ,求出点M 的坐标; (2)若点P 在线段BD 上运动,连接PC PO 、,求S =S △PCD +S △POB 的取值范围; (3)若P 在直线BD 上运动,请直接写出CPO DCP BOP ∠∠∠、、的数量关系.16.对x ,y 定义一种新的运算P ,规定:,()(,),()mx ny x y P x y nx my x y +≥⎧=⎨+<⎩(其中0mn ≠).已知(2,1)7P =,(1,1)1P -=-.(1)求m 、n 的值;(2)若0a >,解不等式组(2,1)4111,523P a a P a a -<⎧⎪⎨⎛⎫---≤- ⎪⎪⎝⎭⎩. 17.如图1,在平面直角坐标系中,点A 为x 轴负半轴上一点,点B 为x 轴正半轴上一点,()0,C a ,(),D b a ,其中a 、b 满足关系式:24(1)0a b a ++--=.()1a =______,b =______,BCD 的面积为______;()2如图2,石AC BC ⊥于点C ,点P 是线段OC 上一点,连接BP ,延长BP 交AC 于点.Q 当CPQ CQP ∠=∠时,求证:BP 平分ABC ∠;(提示:三角形三个内角和等于180) ()3如图3,若AC BC ⊥,点E 是点A 与点B 之间上一点连接CE ,且CB 平分.ECF ∠问BEC ∠与BCO ∠有什么数量关系?请写出它们之间的数量关系并请说明理由.18.如图,在下面直角坐标系中,已知()0,A a ,(),0B b ,(),C b c 三点,其中a ,b ,c 满足关系式()22340a b c ---=.(1)求a ,b ,c 的值;(2)如果在第二象限内有一点1,2P m ⎛⎫ ⎪⎝⎭,请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使四边形ABOP 的面积与三角形ABC 的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.19.先阅读下面材料,再完成任务:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x ,y 满足35x y -=,……①,237x y +=,……②,求4x y -和75x y +的值. 本题常规思路是将①②两式联立组成方程组,解得x ,y 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得42x y -=-,由①+②×2可得7519x y +=,这样的解题思想就是通常所说的“整体思想”解决问题:(1)已知二元一次方程组322233x y x y -=-⎧⎨-=-⎩,则x y -=______,x y +=______; (2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记木共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?(3)对于实数x ,y ,定义新运算:x y ax by c *=++,其中a ,b ,c 是常数,等式右边是通常的加法和乘法运算.已知3515*=,4728*=,那么11*=______.20.阅读下列材料,解答下面的问题:我们知道方程2312x y +=有无数个解,但在实际生活中我们往往只需求出其正整数解.例:由2312x y +=,得:1222433x x y -==-,(x 、y 为正整数) ∴01220x x >⎧⎨->⎩,则有06x <<.又243x y =-为正整数,则23x 为正整数.由2与3互质,可知:x 为3的倍数,从而x=3,代入2423x y =-=∴2x+3y=12的正整数解为32x y =⎧⎨=⎩ 问题:(1)请你写出方程25x y +=的一组正整数解: .(2)若62x -为自然数,则满足条件的x 值为 .(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?21.某校规划在一块长AD为18 m、宽AB为13 m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮,如图所示,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM∶AN=8∶9,问通道的宽是多少?22.某公园的门票价格如下表所示:某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如果两个班联合起来,作为一个团体购票,则需付 1078 元.(1)列方程求出两个班各有多少学生;(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮他们买票呢?请给出最省钱的方案.23.小明为班级购买信息学编程竞赛的奖品后,回学校向班主任李老师汇报说:“我买了两种书,共30本,单价分别为20元和24元,买书前我领了700元,现在还余38元.”李老师算了一下,说:“你肯定搞错了.”(1)李老师为什么说他搞错了?试用方程的知识给予解释;(2)小明连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本.但笔记本的单价已模糊不清,只能辨认出应为小于10元的整数,如果单价为20元的书多于24元的书,请问:笔记本的单价为多少元?24.对a,b定义一种新运算T,规定:T(a,b)=(a+2b)(ax+by)(其中x,y均为非零实数).例如:T(1,1)=3x+3y.(1)已知T(1,﹣1)=0,T(0,2)=8,求x,y的值;(2)已知关于x,y的方程组()()113028T aT a⎧-=-⎪⎨=⎪⎩,,,若a≥﹣2,求x+y的取值范围;(3)在(2)的条件下,已知平面直角坐标系上的点A(x,y)落在坐标轴上,将线段OA 沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.25.某校为了丰富同学们的课外活动,决定给全校20个班每班配4副乒乓球拍和若干乒乓球,两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动,甲商店买一副乒乓球拍送10个乒乓球,乙商店所有商品均打九折(按标价的90%)销售,已知2副乒乓球拍和10个乒乓球110元,3副乒乓球拍和20个乒乓球170元。
七年级数学下几何与代数练习题

七年级数学下几何与代数练习题
练一(几何)
1. 在平面直角坐标系中,A(2, 3)和B(6, 5)是两个点,求线段AB的长度。
2. 勾股定理:已知直角三角形的两个直角边长分别为3cm和4cm,求斜边的长度。
3. 一个平面上有一个正方形,已知其边长为5cm,求正方形的周长和面积。
练二(代数)
1. 已知x = 2,求下列代数式的值:
a) 2x^2 - 3x + 1
b) x^3 - 4x^2 + 5x - 2
2. 已知y = -3,求下列代数式的值:
a) 3y^2 + 2y - 1
b) y^3 - 2y^2 - 3y + 4
3. 计算下列代数式的值:
a) 2(x + 3) - 3
b) 4(x - 2)^2 + 2(x - 2) + 1
练三(几何与代数综合)
1. 已知直角三角形的斜边长度为10cm,其中一条直角边的长
度为6cm,求另一条直角边的长度。
2. 设正方形的周长为20cm,求正方形的面积。
3. 如果一个矩形的长是5cm,宽是3cm,求矩形的周长和面积。
练四(几何与代数综合)
1. 已知直角三角形的斜边长度为13cm,其中一条直角边的长
度为5cm,求另一条直角边的长度。
2. 计算下列代数式的值:
a) (x + 3)(x - 2)
b) (2x + 1)^2
3. 如果一个矩形的长是7cm,宽是4cm,求矩形的周长和面积。
(完整版)数学f1初中数学七年级(下)易错题和典型题期末复习专练二几何部分

知识决定数运 百度提高自我本文为自自己收藏 版权全部 仅供参照 本文为自自己收藏版权全部仅供参照易错题和典型题专练二 几何部分一、填空题:1、若等腰三角形的底边长为8 cm ,则腰长 x 的取值范围是 ;若等腰三角形的腰长为8 cm ,则底边长 x 的取值范围是。
2、已知一个三角形的两边的长是3 和 4,则第三边的长 x 的取值范围是 ;周长y 的取值范围是;3、三角形按角分类成:,,。
4、已知两个角的两边分别平行,且此中一个角比另一个角的3 倍少36o,则这两个角的度数是。
5、三角形三个内角的比为1:3: 5,则最大的内角是度,最大的外角是度,按角分类,它属于三角形。
6、如图:在△ ABC 中,∠ A =40°,高 BE 、 CF 交于点 O ,则∠ BOC 为=。
(第 6题) (第 10 题) (第 11 题) (第 12 题)7、已知∠ A 、∠ B 、∠ C 是 △ ABC 的三个内角, α=∠ A +∠ B , β=∠ C +∠ A ,γ=∠ B ++∠ C ,则 α、 β、 γ中,锐角最多有__________ 个。
8、将一个正六边形纸片对折,并完整重合,那么,获得的图形是________边形, ?它的内角和(按一层计算)是 _______ 度。
9、合适条件∠ A = 1 ∠B = 1∠ C 的△ ABC 的形状是。
2 3合适条件∠ A = 2∠B = 3∠ C 的△ ABC 的形状是。
10、如图:已知 BC ∥DE ,则∠ 1、∠ 2、∠ 3 之间的关系是 。
11、如图:已知 AB ∥ DE ,则∠ 1、∠ 2、∠ 3 之间的关系是。
12、如图:已知∠ A = 120o ,∠ D =150o , BE 、 CE 分别是角均分线,则∠ E = 。
13、有两角及 上的高对应相等的两个三角形全等。
14、有两边及上的中线对应相等的两个三角形全等。
第1页共11页15、△ A /B/C/是△ ABC 经过平移获得的,则AA /与 BB /的关系是,原由是。
七年级下册数学期末考试几何大题证明必考题
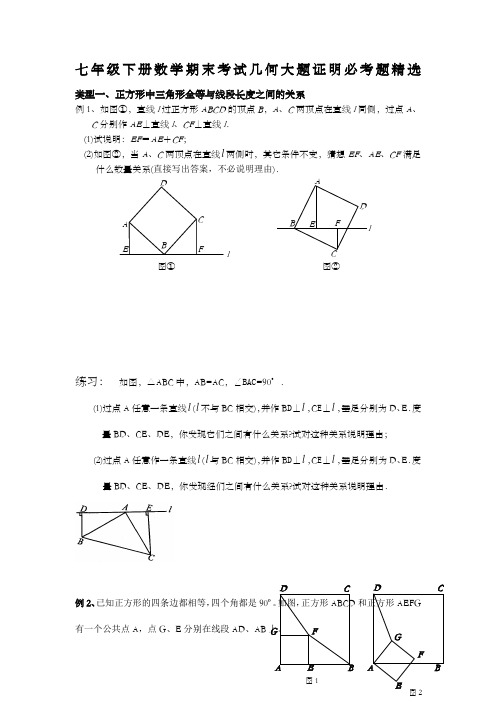
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
A E B 图1D CG FA BD CG FE图2(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE(1)BD 与CE 相等吗?请说明理由.A BCFDE GP32B(2)你能求出BD与CE的夹角∠BFC的度数吗?(3)若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连结BE、DG交点记为点M(如图).请直接写出线段BE和DGF例3、正方形四边条边都相等,四个角都是90o.如图,已知正方形ABCD在直线MN 的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明理由;②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.图 2FG DA图 1FDA类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.CBAPDE2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形,将一块含30o 角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立C图1吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
七年级下册数学期末考试几何大题证明必考题精选

l图②C七年级下册数学期末测验几何大题证实必考题精选类型一.正方形中三角形全等与线段长度之间的关系例1.如图①,直线l 过正方形ABCD 的极点B ,A .C 两极点在直线l 同侧,过点A .C 分离作AE ⊥直线l .CF ⊥直线l . (1)试解释:EF =AE +CF ;(2)如图②,当A .C 两极点在直线l 两侧时,其它前提不变,猜测EF .AE .CF 知足什么数目关系(直接写出答案,不必解释来由).演习:∠ (1)l (l BD ⊥l ,CE ;(2)过点A 随意率性作一条直线l (l 与BC 订交),并作BD ⊥l ,CE ⊥l ,垂足分离为D.E .器量BD.CE.DE,你发明经们之间有什么关系?试对这种关系解释来由.例 2.已知正方形的四条边都相等,四个角都是90º.如图,正方形ABCD 和正方形AEFG 有一个公共点A,点G.E 分离在线段AD.AB 上. (1)如图1, 贯穿连接DF.BF,解释:DF =BF; (2)若将正方形AEFG绕点A 按顺时针偏向扭转,贯穿连接DG,在扭转的进程中,你可否找到一条长度与线段DGA E B图1D C G FA BD CGFE图2的长始终相等的线段?并以图2为例解释来由.演习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B.C.G 三点在一条直线上,且边长分离为2和3,在BG 上截取GP =2,贯穿连接AP.PF.(1)不雅察猜测AP 与PF 之间的大小关系,并解释来由.(2)图中是否消失经由过程扭转.平移.反射等变换可以或许互相重合的两个三角形?若消失,请解释变换进程;若不消失,请解释来由.(3)若把这个图形沿着PA.PF 剪成三块正方形,在原图上画出示意图,附加:如图,△ABC 与△ADE 记为点F .(1)BD 与CE 相等吗?请解释来由.(2)你能求出BD 与CE 的夹角∠BFC (3)若将已知前提改为:四边形ABCD 与四边形AEFG 都是正方形, 贯穿连接BE .DG 交点记为点M 之间的关系?例 3.正方形四边条边都相等,四个角都是90ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .A B2F(1)如图1,当点E 在线段BC 上(不与点B.C 重合)时: ①断定△ADG 与△ABE 是否全等,并解释来由;②过点F 作FH ⊥MN,垂足为点H,不雅察并猜测线段BE 与线段CH 的数目关系,并解释来由;(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①断定△ADG 与△ABE 是否全等,不需解释来由;②过点F 作FH ⊥MN,垂足为点H,已知GD =4,求△CFH 的面积.是正方形,G 与的来由(2)将图1中的正方形CEFG 绕着点C 按顺时针偏向扭转随意率性角度α,得到如图2.请你猜测①BG= DE 是否仍然成立?②BG 与DE 地位关系?并拔取图2验证你的猜测. 类型二.探讨题例1.如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B .A C .B C(或其延伸线)的距离分离为h 1.h 2.h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:hh h h =++321.在图(2)--(5)中,点P 分离在线段M C 上.M C 延伸线上.△A B C 内.△A B C 外.(1)请探讨:图(2)--(5)中,h 1.h 2.h 3.h 之间的关系;图 2图 1(直接写出结论)(2)证实图(2)所得结论; (3)证实图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o o,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R .R S .S C .C B 的距离分离是h 1.h 2.h 3.h 4,桥形的高为h ,则h 1.h 2.h 3.h 4.h 之间的关系为:;图(4)与图(6)中的等式有何干系?演习:1.如图,在△ABC 中,AB=AC,P为底边上随意率性一点⊥AB,PF ⊥AC,BD ⊥AC. (1)求证:PE+PF=BD;(2)若点P 是底边BC 的延伸线上一点,其余前提不变,(1)中的,请解释来由;假如不成立,请画出图形,并探讨它们的关系.2.如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB .AC .BC (或其延伸线)的距离分离为h 1.h 2.h 3,△ABC 的高为h .在图(1)中,点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:hh h h =++321.图(2)~(5)中,点P 分离在线段MC 上.MC 延伸线上.△ABC 内.△ABC 外.ABCDE P ABCDE P M (2) ABC D E M (P ) (1)ABCDE P M(5)CB APDEF C B E(1)请探讨:图(2)~(5)中,h 1.h 2.h 3.h 之间的关系;(直接写出结论)⑵⑶⑷⑸(2)解释图(2)所得结论为什么是准确的; (3)解释图(5)所得结论为什么是准确的.例 2.已知△ABC 是等边三角形,将一块含30角的直角三角板如图1放置,当点E 与点B 重应时,点A 正好落在三角板的斜边DF 上.(1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的进程中,(如图2)是否消失与线段EB 始终相等的线段(设AB,AC 与三角板斜边的交点分离为G,H )?假如消失,实;假如不消失,请解释来由.GEF ABCD 的两条边分离重合,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针偏向扭转.(1)如图2,当EF 与AB 订交于点M ,GF 与BD 订交于点N 时,经由过程不雅察或测量BM ,FN 的长度,猜测BM ,FN 相等吗?并解释来由; (2)若三角尺GEF 扭转到如图3所示的地位时,线段FE 的延伸线(B) C F 图1ABCDE P ABCDEPM (3)ABC D EP M (2)ABCDEM (P )(1)AB C DE P M(5)与AB 的延伸线订交于点M ,线段BD 的延伸线与GF 的延伸线订交于点N ,此时,(12.,M 是BCA,且60º角的极点E 在BC 上滑动,(点E 不与点B.C 重合),斜边∠ACM 的等分线CF 交于点F(1)如图(1)当点B 在BC 边得中点地位时(6分) ○1猜测AE 与BF 知足的数目关系是.○2贯穿连接点E 与AB边得中点N,猜测BE和CF知足的数目关系是○3请证实你的上述猜测(4分)(2)如图(2)当点E在BC边得随意率性地位时: 此时AE和BF有如何的数目关系,并解释你的来由?图3图1 A ( B ( E )E图(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9.(2011·扬州)如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB =________.答案 105°解析 如图,∵(60°+∠CAB )+(45°+∠ABC )=180°,∴∠CAB +∠ABC =75°,在△ABC 中,得∠C =105°.12.如图所示,在△ABC 中,∠A =80°,∠B =30°,CD 平分∠ACB ,DE ∥AC .(1)求∠DEB 的度数; (2)求∠EDC 的度数.解 (1)在△ABC 中,∠A =80°,∠B =30°,∴∠ACB =180°-∠A -∠B =70°. ∵DE ∥AC ,∴∠DEB =∠ACB =70°. (2)∵CD 平分∠ACB , ∴∠DCE =12∠ACB =35°.∵∠DEB =∠DCE +∠EDC , ∴∠EDC =70°-35°=35°.13.已知,如图,∠1=∠2,CF ⊥AB 于F ,DE ⊥AB 于E ,求证:FG ∥BC .(请将证明补充完整)证明 ∵CF ⊥AB ,DE ⊥AB (已知),∴ED ∥FC ( ). ∴∠1=∠BCF ( ). 又∵∠1=∠2(已知), ∴∠2=∠BCF (等量代换), ∴FG ∥BC ( ).解 在同一平面内,垂直于同一直线的两条直线互相平行;两直线平行,同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法1:如图甲,延长BC到D,过C画CE∥BA.∵BA∥CE(作图所知),∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换).如图乙,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.解∵FH∥AC,∴∠BHF=∠A,∠1=∠C.∵FG∥AB,∴∠BHF=∠2,∠3=∠B,∴∠2=∠A.∵∠BFC=180°,∴∠1+∠2+∠3=180°,即∠A+∠B+∠C=180°.15.(2010·玉溪)平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,则∠BPD 、∠B 、∠D 、∠BQD 之间有何数量关系?(不需证明) (3)根据(2)的结论求图d 中∠A +∠B +∠C +∠D +∠E +∠F 的度数.解 (1)不成立,结论是∠BPD =∠B +∠D .延长BP 交CD 于点E , ∵AB ∥CD ,∴∠B =∠BED . 又∠BPD =∠BED +∠D , ∴∠BPD =∠B +∠D .(2)结论:∠BPD =∠BQD +∠B +∠D . (3)设AC 与BF 交于点G .由(2)的结论得:∠AGB =∠A +∠B +∠E .又∵∠AGB =∠CGF ,∠CGF +∠C +∠D +∠F =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°.14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE 是 度.2.如图,在△ABC 和△ABD 中,现给出如下三个论断:①AD =BC ;②∠C =∠D ;③∠1=∠2。
请选择其中两个论断为条件,一个论断为结论,另外构造一个命题. (1)写出所有的正确命题(写成“②③①⇒⎭⎬⎫”形式,用序号表示):. (2)请选择一个正确的命题加以说明.你选择的正确命题是: ⇒⎭⎬⎫ 说明:3.如图,直线AD 和BC 相交于O ,AB ∥CD ,∠AOC =95°,∠B =50°,求∠A 和∠D .AB CDE第14题4.如图,△ABC 中,角平分线AD 、BE 、CF 相交于点H ,过H 点作HG ⊥AB ,垂足为G ,那么∠AHE =∠CHG 吗?为什么?5.如图17,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是228cm ,AB=20厘米,AC=8厘米,求DE 的长.6.如图,已知AB ⊥CD ,垂足为B ,AB=DB ,AC=DE .请你判断∠D 与∠A 的关系,并说明理由.第6题7.如图,AD=BC ,DC=AB ,AE=CF ,找出图中的一对全等三角形,并说明你的理由.第5题FEDCBAC EDB A第7题8.如图,已知M 在AB 上,BC=BD ,MC=MD .请说明:AC=AD .第8题9.如图, 在△ABC 中,AB=AC ,AC 边上中线BD 把△ABC 的周长分为21厘米 12厘米两部分,求△ABC 各边的长.10.已知AE ⊥BD ,CF ⊥BD ,且AD=BC ,BE=DF ,试判断AD 和BC 的位置关系.说明你的结论.11.如图,∠ACB=∠BDA=90°,AD=BC ,AB//CD .试说明:∠1=∠2.12.如图3,AC ⊥BD ,AC=DC ,CB=CE ,试说明:DE ⊥AB .13.如图,已知AB//DE ,AB=DE ,BE=CF ,试说明△ABC ≌△DEF 的理由. 小明的说理过程如下: 因为AB//DE ,所以∠1=∠2, 在△ABC 和△DEF 中因为BE=CF ,∠1=∠2,AB=DE ,所以△ABC ≌△DEF (SAS ).MDC BADA BC小明的说理正确吗?若不正确,请你指出错误,帮助小明走出说理误区.14.如图2,AC与BD相交于点E,AD=BC,∠D=∠C,试说明AC与BD全等的理由.小华的说理过程如下:在△ABD和△BAC中,因为AD=BC,AB=BA,∠C=∠D,所以△ABD≌△BAC(SSA)所以AC=BD.3.(10分)如图15,在△ABC中,点D在AB上,BD=BE,(1)请你再添加一个条件,使得△BEA≌△BDC,并说明理由,你添加的条件是理由是:(2)根据你添加的条件,再写出图中的一对全等三角形(只要求写出一对全等三角形,不再添加其它线段,不再标注或使用其它字母,不必说明理由).4.(10分)已知:如图16,Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,试以图中标有的字母的点为端点,连接两条线段,如图你所连接的两条线段满足相等、垂直或平行关系中的一种,那么请你把它写出来并证明.1. 现有两根棍子长分别为3厘米,5厘米,若要选第三根棍子,使其与前两根拼成一个三角形,则它的长可为()A.1厘米B.2厘米C.5厘米D.10厘米图1 图22.如图1所示,AD 是△ABC 的高,延长BC 至E ,使CE =BC ,△ABC 的面积为S 1,△ACE 的面积为S 2,那么( )A.S 1>S 2B.S 1=S 2C.S 1<S 2D.不能确定 2.三角形的三边长分别为5,x ,8,则x 的取值范围是_ .3.(10分)如图16,△ABC 中,角平分线AD 、BE 、CF 相交于点H ,过H 点作HG ⊥AB ,垂足为G ,那么∠AHE =∠CHG 吗?为什么?4. (10分)如图17,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是228cm ,AB=20厘米,AC=8厘米,求DE 的长.四、拓广探索!(本大题共22分)1.(10分)如图18,在△ABC 中,点D 在AB 上,BD=BE , (1)请你再添加一个条件,使得△BEA ≌△BDC , 并说明理由,你添加的条件是 理由是:(2)根据你添加的条件,再写出图中的一对全等三角形(只要求写出一对全等三角形,不再添加其它线段,不再标注或使用其它字母,不必说明理由。
)ED CB A图17E DC BAG HF图162.(12分)(1)如图19①,有一块直角三角板XYZ 放置在△ABC 上,恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B 、C .△ABC 中,∠A =30°,则∠ABC +∠ACB =______,∠XBC +∠XCB =______.(2)如图19②,改变直角三角板XYZ 的位置,使三角板XYZ 的两条直角边XY 、XZ•仍然分别经过B 、C ,那么∠ABX +∠ACX 的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX +∠ACX 的大小.三、解答题21,先画两条已知线段a 和b (a >b ),然后再画出线段AB =a -b .22,如图,已知AE ∥BD ,∠1=3∠2,∠2=28°.求21∠C .(图22)23,如图,已知l ∥m ,求∠x ,∠y 的度数.②①24,如图,直线l 1,l 2,分别和直线l 3,l 4,相交,∠1与∠3互余,∠2与∠3的余角互补,∠4=115°.求∠3的度数.25,如图,已知∠C =∠D ,DB ∥EC .AC 与DF 平行吗?试说明你的理由.(图25)26,如图,AB 、AE 是两条射线,∠2+∠3+∠4=∠1+∠2+∠5=180°,求∠1+∠2+∠3的度数.27,如图,已知DB ∥FG ∥EC ,∠ABD =60°,∠ACE =60°,AP 是∠BAC 的平分线.求∠PAG 的度数.28,如图,CD ∥AB ,∠DCB =70°,∠CBF =20°,∠EFB =130°,问直线EF 与AB 有怎样的位置关系,为什么?CFABE D29,如图,已知:AB⊥BF,CD⊥BF,∠BAF=∠AFE.试说明∠DCE+∠E=180°的理由.7、如图,AB∥CD,直线EF分别交AB、CD于点E、F,ED平分∠BEF,若∠1=72°,则∠2=___________.8、如图,DE∥BC,∠DBE=40°,∠EBC=25°,则∠BED=___________度,∠BDE=___________度.9、已知,如图,∠1=∠2,AB∥CD,∠A=105°,∠ABD=35°,则∠BDE=___________度,∠ABC=___________度.10、如图,AB∥CD,且∠1=42°,AE⊥EC于E,则∠2=__________度.三、认真答一答(每小题10分,共60分)1、如图所示的长方形台球桌面上,如果∠1=∠2=30°,那么∠3等于多少度?∠1与∠3有什么关系?2、给下列证明过程写理由.已知:如图,AB⊥BC于B,CD⊥BC于C,∠1=∠2,求证:BE∥CF.证明:∵ AB⊥BC于B,CO⊥BC于C()∴∠1+∠3=90°,∠2+∠4=90°()∴∠1与∠3互余,∠2与∠4互余()又∵∠1=∠2(),∴__________=___________()∴BE∥CF() .3、如图,已知AF平分∠BAC,DE平分∠BDF,且∠1=∠2.(1)能判定DF∥AC吗?为什么?(2)能判定DE∥AF吗?为什么?4、如图,已知AB∥CD,AD∥BC,求证:∠A=∠C,∠B=∠D.5、如图,已知AB∥CD,∠1=∠2,求证:∠BEF=∠EFC.6、已知∠α、∠β,用尺规作一个角,使它等于2∠α-∠β.答案:三、1.∠3=60°,∠1与∠3互余.2.已知垂直定义互余定义等角的补角相等∠3∠4内错角相等,两直线平行3.(1)能判定DF∥AC,可以证明,∠BDF=∠BAC,则由同位角相等,两直线平行来判定.(2)能判定DE∥AF,可证∠1=∠BAF,则同位角相等,两直线平行.4.AB∥CD,∴ ∠B+∠C=180°,∠A+∠D=180°又AD∥BC∴ ∠A+∠B=180°,∠C+∠D=180°∴ ∠B=∠D,∠A=∠C。
