(完整版)《运算律》知识点归纳及练习
四年级下册数学【运算律】知识点+例题解析
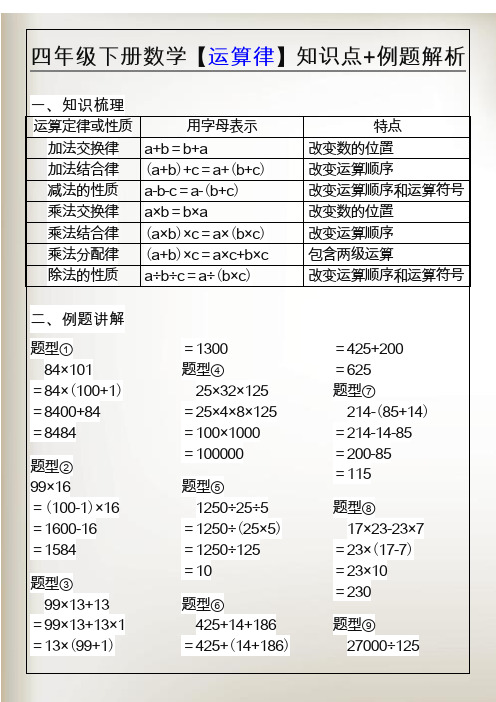
四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10＝230题型⑨27000÷125＝27×1000÷125 ＝27×8 ＝216四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10。
四年级下册数学教案-《运算律》整理与练习丨苏教版
一、教学内容
《运算律》整理与练习，选自苏教版四年级下册数学教材第六章。主要包括以下内容：加法交换律与结合律、乘法交换律与结合律、分配律以及运算律的应用。具体内容包括：
1.加法交换律与结合律：a+b=b+a；(a+b)+c=a+(b+c)。
2.乘法交换律与结合律：a×b=b×a；(a×b)×c=a×(b×c)。
举例：购物时，计算购买3件衣服和2双鞋子的总价，可引导学生运用分配律，将价格进行组合计算。
2.教学难点
（1）理解运算律的本质：学生对运算律的理解可能停留在表面，难以理解其背后的数学原理。
解决方法：通过举例、图示等方法，让学生直观感受运算律的本质，加深理解。
（2）灵活运用运算律：学生在解决问题时，可能难以灵活运用运算律简化计算。
1.理论介绍：首先，我们要了解运算律的基本概念。运算律是指在数学运算中普遍适用的规律，它能帮助我们简化计算过程，提高解题效率。它是数学中的基础知识，对于我们的学习和生活都有很大帮助。
2.案例分析：接下来，我们来看一个具体的案例。通过计算123+456，我们运用加法交换律和结合律，将复杂的加法问题转化为简单的步骤，从而快速得出结果。
同学们，今天我们将要学习的是《运算律》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要简化计算的情况？”比如购物时计算总价，或者做游戏时计算得分。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索运算律的奥秘。
（二）新课讲授（用时10分钟）
3.重点难点解析：在讲授过程中，我会特别强调加法交换律、结合律以及乘法分配律这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
运算律总结知识点
运算律总结知识点一、加法运算律1. 加法结合律：a+(b+c)=(a+b)+c这个运算律就是加法的结果不受加数的次序的影响，即改变加数的次序，其和不变。
例如：2+(3+4)=(2+3)+4=9。
2. 加法交换律：a+b=b+a这个运算律就是加法的结果不受加数次序的影响，即相加的两数次序实质上不影响其和。
例如：2+3=3+2=5。
3. 零的作用：0+a=a+0=a这个运算律就是任何数与零相加都等于原来的数。
例如：0+5=5+0=5。
二、减法运算律1. 减法的性质：a-b≠b-a减法不满足交换律与结合律。
例如：3-2≠2-3。
2. 减法的相反性：a-b=a+(-b)这个运算律就是减法可以看作是加法的一个特例，减去一个数等于加上它的相反数。
例如：3-2=3+(-2)=1。
三、乘法运算律1. 乘法结合律：a*(b*c)=(a*b)*c这个运算律就是乘法的结果不受乘数的次序的影响，即改变乘数的次序，其积不变。
例如：2*(3*4)=(2*3)*4=24。
2. 乘法交换律：a*b=b*a这个运算律就是乘法的结果不受乘数次序的影响，即相乘的两数次序实质上不影响其积。
例如：2*3=3*2=6。
3. 乘法分配律：a*(b+c)=a*b+a*c这个运算律就是乘法对加法的分配律，即一个数乘以两个数的和等于这个数乘以这两个数的和。
例如：2*(3+4)=2*3+2*4=14。
四、除法运算律1. 除法的性质：a÷b≠b÷a除法不满足交换律与结合律。
例如：3÷2≠2÷3。
2. 除法的相反性：a÷b=a*1/b这个运算律就是除法可以看作是乘法的一个特例，除以一个数等于乘以它的倒数。
例如：3÷2=3*1/2=1.5。
五、指数运算律1. 乘幂运算律：a^m*a^n=a^(m+n)这个运算律就是相同底数的幂相乘，指数相加。
例如：3^2*3^3=3^(2+3)=3^5。
2. 乘幂数乘法运算律：(a^m)^n=a^(m*n)这个运算律就是幂的幂，指数相乘。
小学运算定律知识点总结
小学运算定律知识点总结一、加法运算定律1.加法的交换律：a+b=b+a。
即加法运算中，加数的位置不同，结果不变。
2.加法的结合律：(a+b)+c=a+(b+c)。
即加法运算中，加数可以按照不同的顺序进行运算，结果不变。
3.零的作用定律：a+0=a。
即任何数与0相加，结果仍为原来的数。
二、减法运算定律1.减法的性质：a-b=a+(-b)。
即减法运算可以转化为加法运算。
2.减法的退位借位法则：当被减数的其中一位小于减数的对应位时，应向高位借1，被减数的该位加上10。
3.减法的补数定律：a-b=a+(10-b)。
即减法运算可以转化为加法运算，同时减法中的减数改为它的补数。
三、乘法运算定律1.乘法的交换律：a×b=b×a。
即乘法中，因子的位置可以交换，结果不变。
2.乘法的结合律：(a×b)×c=a×(b×c)。
即乘法中，因子可以按照不同的顺序进行运算，结果不变。
3.乘法的分配律：a×(b+c)=a×b+a×c。
即乘法可以分配到加法上。
四、除法运算定律1.除法的性质：a÷b=a×(1/b)。
即除法可以转化为乘法运算，除数改为它的倒数。
2.除法的整除性规则：如果一个数能被另一个数整除，那么这两个数的约数是一样的。
五、乘方运算定律1.乘方的基本性质：a^m×a^n=a^(m+n)。
即相同底数的乘方，指数相加。
2.乘方的性质：(a^m)^n=a^(m×n)。
即幂的幂，指数乘法。
3.乘方的分配律：(a×b)^n=a^n×b^n。
即乘方可以分配到乘法上。
六、数的整除性定律1.偶数的性质：如果一个数是偶数，那它可以被2整除，即能被2整除的数都是偶数。
2.奇数的性质：如果一个数是奇数，那它不能被2整除，即不能被2整除的数都是奇数。
3.3的整除性规则：如果一个数的各位数字之和能被3整除，那这个数也能被3整除。
四年级数学上册第四单元 《运算律》知识点归纳及练习
第四单元《运算律》知识点归纳及练习乘法结合律1、乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，它们的积不变。
用字母表示是：（a×b）×c=a×(b×c).使用时机：当几个数相乘时，如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
数字如;25和4、50和2、125和8、50和4、500和2等。
加法运算时也有结合律。
如果用a/b/c表示三个数，那么加法结合律表示为：（a+b）+c=a+（b+c）2、认识乘法交换律a、b表示两个数，那么乘法交换律用字母表示为：a×b=b×a。
1）上述规律可推广到更多个数相乘。
如：125×4×8×25=（125×8）×（25×4）=1000×100=1000002）加法运算时也有交换律，如用字母a、b表示两个数，那么加法交换律用字母表示为：a+b=b+a。
3）运用加法交换律和结合律可以使得一些运算简便。
50+7+40+9=（50+40）+（7+9）=90+16=106练习题：73×25×4 125×63×8 4×（25×93）12×125×5×8 32×125×25 48×125×5乘法分配律1、乘法分配律：两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相乘，在把两个积相加（或相减），结果不变。
用字母表示数：（a+b）×c=a×c+b×c或（a-b）×c=a×c－b×c1、式子的特点：式子的原算符号一般是×、+(-)、×的形式；在两个乘法式子中，有一个相同的因数；另为两个不同的因数之和(或之差)是能凑成整十、整百、整千的数。
运算律总结
(2) 34×25×4 =34×(25×4) =34×100 =3400 (4) 125×32×25 =125×8×(4×25) =1000×100 =100000
3. 乘法分配律：两个数的和与一个数 相乘，可以把这两个加数分别与这个 数相乘，再把积相加。 用字母表示为： (a+b)×c= a×c+b×c 4.乘法分配律的拓展：两个数的差与 另一个数相乘，可以用这个分别去乘 先前的两个数，在把积相减。 用字母表示为： (a－b)×c= a×c－b×c
(2) 45×104 (1) 125× (8+80) =45×(100+4) =125×8+125×80 =45×100+45×4 =1000+10000 =4500+180 =11000 =4680 (3) 125× (80-8) (4) 45×98 =125×80-125×8 =45×(100-2) =10000-1000 =45×100-45×2 =9000 =4500-90 =4410 (5) 38×99+38 (6) 87×101-87 =38× (99+1) =87×(101-1) =38×100 =87×100 =3800 =8700
(2) 598+104 =598+100+4 =698+4 =702
(1) 175+38+25 =175+25+38 =200+38 =238 (3) 356+97 =356+100-3 =456-3 =453
（二） 减法的性质：一个数连 续减去两个数，可以用这个减去 这两个减数的和，结果不变。 用字母表示为： a－b－c= a－(b+c) a－(b+c)= a－b－c
第四单元《运算律》知识点总结
（一）四则混合运算1.在一个算式里，如果只含有同一级运算，要从左往右依次计算。
2.在一个算式里，如果既有加、减运算，又有乘、除运算，要先算乘、除，再算加、减；如果有括号，要先算小括号里面的，要先算中括号里面的。
（二）加法交换律和乘法交换律1.加法交换律：两个数相加，交换两个加数的位置，和不变。
用字母表示：a＋b=b＋a。
2.乘法交换律：两个数相乘，交换两个乘数的位置，积不变。
用字母表示：a×b=b×a。
提醒：加法交换律或乘法交换律，结果相同，两个加数或乘数不变，只是交换了位置。
3.加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，它们的和不变。
用字母表示：(a＋b)＋c=a＋(b＋c)。
①使用时机：当几个数相加时，如果其中的两个数相加能得到一个整十、整百或整千数就可以应用加法交换律和加法结合律进行简算。
加法结合律可以改变加法运算顺序。
连减运算：a－b －c=a－(b＋c)。
注意：加减同级运算，为了改变运算顺序而加括号或去括号时：“＋”在前，不变号；“－”在前，必变号。
4.乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，它们的积不变。
用字母表示：(a×b)×c=a×(b×c)。
①使用时机：当几个数相乘时，如果其中的两个数相乘能得到一个整十、整百或整千数就可以应用乘法交换律和乘法结合律进行简算。
乘法结合律可以改变乘法运算顺序。
数字如：25和4、75和4、125和8等。
连除运算：a÷b ÷c=a÷(b×c)。
注意：乘除同级运算，为了改变运算顺序而加括号或去括号时：“×”在前，不变号；“÷”在前，必变号。
5.乘法分配律：两个数的和与一个数相乘，可以把这两个加数分别与这个数相乘，再把两个积相加，结果不变。
第三单元《运算律》整理与复习-新人教版数学四年级下册 (1)精选全文
固
(3)水果店购进苹果和梨子各40箱。苹果每箱68元， 梨子每箱53元。买苹果比梨子多花多少元？ (68－53)×40＝600(元) 答：买苹果比梨子多花600元。
固
5.李大爷家有一块菜地
（如右图），这块菜地
的面积有多少平方米？ 9×(21－9) ＋9×（19+9） =9×12＋9×28 =9×（12＋28） =9×40 =360m²
识
乘 法
乘法交换律 两个数相乘，交换两个因数的位置，积不变 a×b=b×a
运 算
三个数相乘，先乘前两个数，或者先乘后
定 乘法结合律 两个数，积不变
律
(a×b)×c=a×(b×c)
两个数的和与一个数相乘，可以先把它们 乘法分配律 与这个数分别相乘
(a+b)×c=a×c+b×c
识
除
一个数连续除以两个数，可以用这个数除以两个数
固
4．解决问题。 (1)每本集邮册都是24页，每页都可以插8张邮票。小
峰有这样的集邮册5本，一共可以插多少张邮票？
24×8×5＝960(张) 答：一共可以插960张邮票。
固
(2)彭老师准备给篮球队8名队员每人发一套球衣和一 双球鞋，每套球衣64元，每双球鞋36元。买这些 球衣和球鞋一共需要多少元？ (64＋36)×8＝800(元) 答：买这些球衣和球鞋一共需要800元。
+ 37 +a
加法的运算定律
连线。 360+270+640 62+21+38 527+(303+697)
型
21+(62+38) 697+527+303 360+640+270
《运算律》知识点
《运算律》知识点运算律知识点1、乘法结合律:三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。
用字母表示是:×c=a×.使用时机:当几个数相乘时,如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
数字如;25和4、50和2、125和8、50和4、500和2等。
加法运算时也有结合律。
如果用a/b/c表示三个数,那么加法结合律表示为:+c=a+2、认识乘法交换律两个数相乘,交换他们的位置,积不变,这叫乘法交换律。
如用字母a、b表示两个数,那么乘法交换律用字母表示为:a ×b=b×a。
1)上述规律可推广到更多个数相乘。
如:125×4×8×25=×=1000×100=1000002)加法运算时也有交换律,如用字母a、b表示两个数,那么加法交换律用字母表示为:a+b=b+a。
3)运用加法交换律和结合律可以使得一些运算简便。
50+7+40+9=+=90+16=106练习题1.用简便方法计算。
584+289+416=（）7×8×4×125=（）4×17×2536×15=（）2.选一选。
250×320的简便算法是。
A.250×300×20B.250×4×80c.25×8×4037×25×40=37×，这个算式是运用了。
A.乘法结合律B.乘法交换律c.乘法交换律和结合律3.水果市场运来23车苹果，平均每车有50箱，平均每箱有20千克，水果市场一共运来多少千克苹果?__________________________________________________________。
《运算律》整理和复习
5.乘法分配律的灵活运用：
45×102
58×99+58
=45×（100+2） =45×100+45×2 =4500+90 =4590
=58×99+58×1 =58×（99+1） =58+100 =5800
6.加减混合、乘除混合
256–58+44
＝256+44-58 ＝300-58 ＝242
250÷8×4
528–89–128 ＝528-128-89
＝100+100
＝400-89
＝200
＝311
2.（乘法）：能相乘得整十、整百或整千的数先乘
25×125×4×8 ＝(25×4)×(125×8)
熟记！！！
＝100×1000 ＝100000
25×4=100 125×8
3.在减法算式中，把减数看做接近它的整百去减，零头补齐。 需要注意的是：多减的要加上，少减的要减去。
（√ ）
256–198
=256-200+2 =56+2 =58
256–203
=256–200–3 =56–3 =53
ቤተ መጻሕፍቲ ባይዱ
4.在减法算式中，把加数看做接近它的整百去加，零头补齐。 需要注意的是：多加的要减去，少加的要加上。
256+198
=256+200-2 =456-2 =454
256+203
=256+200+3 =456+3 =459
的
相乘，再同第三个数相乘；或者
运 算 律
先把后两个数相乘，再同第一个 数相乘，它们的积不变。
字母表示：(a×b)×c=a×(b×c)
运算定律练习题(打印版)
运算定律练习题（打印版）### 运算定律练习题（打印版）#### 一、加法运算定律1. 加法交换律：两个数相加，交换加数的位置，和不变。
- 练习题：计算 \( 34 + 56 \) 和 \( 56 + 34 \)，验证加法交换律。
2. 加法结合律：三个或三个以上的数相加，可以先把任意两个数相加，再与其余的数相加，和不变。
- 练习题：计算 \( (23 + 45) + 78 \) 与 \( 23 + (45 + 78) \)，验证加法结合律。
3. 加法分配律：一个数与两个数的和相乘，等于这个数分别与这两个数相乘的和。
- 练习题：计算 \( 9 \times (7 + 8) \) 与 \( 9 \times 7 + 9 \times 8 \)，验证加法分配律。
#### 二、乘法运算定律1. 乘法交换律：两个数相乘，交换因数的位置，积不变。
- 练习题：计算 \( 12 \times 35 \) 和 \( 35 \times 12 \)，验证乘法交换律。
2. 乘法结合律：三个或三个以上的数相乘，可以先把任意两个数相乘，再与其余的数相乘，积不变。
- 练习题：计算 \( (13 \times 27) \times 4 \) 与 \( 13\times (27 \times 4) \)，验证乘法结合律。
3. 乘法分配律：一个数与两个数的和相乘，等于这个数分别与这两个数相乘的积的和。
- 练习题：计算 \( 7 \times (14 + 3) \) 与 \( 7 \times 14 + 7 \times 3 \)，验证乘法分配律。
4. 乘法分配律的逆运算：一个数分别与两个数相乘，再求和，等于这个数与这两个数的和相乘。
- 练习题：计算 \( 15 \times 4 + 15 \times 6 \) 与 \( 15\times (4 + 6) \)，验证乘法分配律的逆运算。
#### 三、混合运算定律1. 加法与乘法的结合：一个数加上另一个数的积，可以先计算积，再加上另一个数。
四年级运算定律与简便运算知识点归纳与练习(精品)
运算定律与简便运算一、加减法运算定律1、加法交换律定义：两个加数交换位置，和不变字母表示：a b b a +=+例如：16+23=23+16 546+78=78+5462、加法结合律定义：先把前两个数相加，或者先把后两个数相加，和不变。
字母表示：)()(c b a c b a ++=++注意：加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数进行调换位置，再将这两个加数结合起来先运算。
例题：（1）50+98+50 （2）488+40+60 （3）165+93+353.减法交换律、结合律注：减法交换律、结合律是由加法交换律和结合律衍生出来的。
减法交换律：如果一个数连续减去两个数，那么后面两个减数的位置可以互换。
字母表示：b c a c b a --=--例题：（1）198-75-98 （2）528—89—128 （3）226-58-26减法结合律：如果一个数连续减去两个数，那么相当于从这个数当中减去后面两个数的和。
字母表示：)(c b a c b a +-=--例题：（1）369-45-155 （2）896-580-120 （3）528—（150+128） （4）126-(26+88)4、加减法的“符号搬家”：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。
字母表示：b c a c b a +-=-+例题：（1）256－58 +44 （2）123 + 38 - 23 （3）146 -78 +54二、乘除法运算定律1、乘法交换律定义：交换两个因数的位置，积不变。
字母表示：a b b a ⨯=⨯例如：85×18=18×85 23×88=88×232、乘法结合律定义：先乘前两个数，或者先乘后两个数，积不变。
字母表示：)()(c b a c b a ⨯⨯=⨯⨯运用：①使用乘法交换律、结合律凑整（把积是整十、整百、整千的数先交换再结合在一起。
(完整版)新人教版四年级下第三单元《运算定律》知识点总结
第三单元知识点总结1.加法交换律：两个数相加，交换加数的位置，和不变。
用字母表示为：a+b=b+a。
2.加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。
用字母表示为：(a+b)+c=a+(b+c)。
3.加法交换律与加法结合律的区分方法：（1）加法交换律改变的是加数的位置，加法结合律改变的是运算顺序。
（2）加法结合律的重要标志是小括号的使用。
4.加法的简便运算：在一个连加算式中，运用加法运算定律，把能凑成整十、整百、整千……的数先相加，可以使计算简便。
5.在连减运算中，交换两个减数的位置，差不变。
用字母表示为：a－b－c＝a－c－b。
6. 一个数连续减去两个数，等于这个数减去这两个数的和。
用字母表示为：a－b－c＝a－(b＋c)。
7.乘法交换律：两个数相乘，交换两个因数的位置，积不变。
用字母表示为：a×b＝b×a。
8.乘法结合律：三个数相乘，先乘前两个数，或者先乘后两个数，积不变。
用字母表示为：（a×b）×c＝a×（b×c）。
9.乘法分配律：（1）两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。
用字母表示为：(a＋b)×c=a×c＋b×c或a×(b＋c)=a×b＋a×c（2）两个数的差与一个数相乘，可以先把被减数和减数分别与这个数相乘，再把所得的积相减。
用字母表示为：(a－b)×c=a×c －b×c。
10.乘法的简便算法：两个数相乘，如果其中一个因数是25（或125），可考虑将另一个因数分解成4×（）或8×（），再运用乘法结合律进行简便计算；如果其中一个因数接近整十数、整百数、整千数……可将其分解成10±（）、100±（）、1000±（）……再运用乘法分配律进行简便计算。
《运算律》知识点
《运算律》知识点运算律知识点1、乘法结合律:三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个数相乘,它们的积不变。
用字母表示是:×=a×使用时机:当几个数相乘时,如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
数字如;2和4、0和2、12和8、0和4、00和2等。
加法运算时也有结合律。
如果用a/b/表示三个数,那么加法结合律表示为:+=a+2、认识乘法交换律两个数相乘,交换他们的位置,积不变,这叫乘法交换律。
如用字母a、b表示两个数,那么乘法交换律用字母表示为:a ×b=b×a。
1)上述规律可推广到更多个数相乘。
如:12×4×8×2=×=1000×100=1000002)加法运算时也有交换律,如用字母a、b表示两个数,那么加法交换律用字母表示为:a+b=b+a。
3)运用加法交换律和结合律可以使得一些运算简便。
0+7+40+9=+=90+16=106练习题1用简便方法计算。
84+289+416=（）7×8×4×12=（）4×17×236×1=（）2选一选。
20×320的简便算法是。
A20×300×20B20×4×802×8×4037×2×40=37×，这个算式是运用了。
A乘法结合律B乘法交换律乘法交换律和结合律3水果市场运来23车苹果，平均每车有0箱，平均每箱有20千克，水果市场一共运来多少千克苹果?__________________________________________________________。
参考答案1用简便方法计算。
84+289+416=（1289）7×8×4×12=（28000）4×17×2=（1700）36×1=（40）2选一选。
四年级上册数学复习运算律及练习
商不变的规律
概念：被除数和除数同时乘上或除以相同的数（0 除外）它们的商不变。
字母公式：
A÷B=(AN)÷(BN)
A÷B=(A÷N)÷(B÷N) （N≠0 B≠0)
题例：80÷125
=(80×8)÷(125×8) =640÷1000 =0.64
类型一：（注意：一定要括号外的数分别乘括号里的两个数，再把积相加或相减）
像 102×88、99×15 这类题的特点：两个数相乘，把其中一个比较接近整十、整百、整千的数改写成整十、整百、 整千与一个数的和（或差），再应用乘法分配律可以使运算简便。
六、减法性质
减法性质的概念为：一个数连续减去两个数，可以先把后两个数相加，再相减。
字母公式：A-B-C=A-(B+C)
例(简算过程)：
328×15+72×15 6300÷（63×5） 125×（100+8） 480×46÷48 302×99+302 98×35 练习六 43×202 59×299 134×51—51×34 480×46÷48 302×99+302 3000÷125÷8 68×32—784÷56 3000÷125÷8 7200÷36 756+483—556 98×35 230×54+540×77 43×202 59×299 960×46÷48 练习七 35×102 887×25—87×25 8800÷（25×88） 25×（20+4） 498+（201—154） 415—176—24 487—287—139—61 3600÷50÷2 125×89×8 428×78+572×78
简便运算：
一、加法交换律：加 法 交 换 律 的 概 念 为 ： 两 个 加 数 交 换 位 置 ， 和 不 变 。
北师大版数学四年级上册章末复习 第四单元《运算律》(及答案)
第四单元运算律知识点一：买文具-四则混合运算顺序（1）四则混合运算顺序在没有括号的算式里，当只有加、减运算或乘、除运算时，按从左到右的顺序进行计算，既有加、减运算，又有乘、除运算时，要先算，再算。
（2）含有中括号的四则混合运算在一个算式里，如果既有小括号又有中括号，要先算的，再算面的，最后算。
知识点二：运算律及其应用加法交换律用字母表示为 a＋b＝加法结合律用字母表示为（a+b）+c=乘法交换律用字母表示为 a×b＝乘法结合律用字母表示为 (a×b) ×c=乘法分配律用字母表示为 (a+b) ×c=1.在连加计算中，运用可以让一些加法计算简便。
2.乘法结合律只适用于运算，不可以在乘加或乘减运算中运用。
3.乘法分配律可以正用，也可以逆用。
如果a×c和b×c计算简便时，可以先算a×c和b×c，再把两个积相加；如果a＋b的和正好是整十、整百、整千数时，可以用来计算。
4.运用乘法分配律进行计算时，两个加数要，然后再把。
【易错典例1】（2019秋•嘉陵区期末）实践探究．【思路引导】根据整数乘法的竖式计算法则解答即可．【完整解答】解：乘数14个位上的4与326相乘，表示4×326的积是1304，十位上的1与326相乘，表示10×326的积是3260；【易错注意点】此题考查了整数乘法的竖式计算方法．【易错典例2】（2019秋•洛川县期末）如图算式中的汉字各代表什么数字？我＝3；是＝9；中＝7；国＝1；人＝0．【思路引导】根据整数乘法的运算法则，第一个因数与第二个因数的个位相乘得：3438，所以第二个因数的个位为9，第一个因数的百位为3．原式为：382×29＝11078，完成竖式，并找到各汉字代表的数字．【完整解答】解：原式为：所以：我＝3；是＝9；中＝7；国＝1；人＝0．故答案为：3；9；7；1；0．【易错注意点】本题主要考查凑数谜，关键根据整数乘法及加法的运算法则，找到合适的数，完成计算．【易错典例3】点A表示的数可能是算式（）的积．A．201×51B．199×45C．199×51【思路引导】根据题意，点A介于1与10000之间，且更接近10000；根据估算的计算方法，分别求出各个算式的结果，再进一步解答．【完整解答】解：201×51≈200×50＝10000，等于10000，不符合题意；199×45≈200×45＝9000，接近10000，符合题意；199×51≈200×50＝10000，等于10000，不符合题意；故选：B．【易错注意点】考查了三位数乘两位数的估算，把两位数看作与它接近的整十整百数，然后再进一步解答．【易错典例4】（2018秋•单县期末）学校准备发练习本，发给15个班，每班144本，还要留40本作为备用．学校应买多少练习本？【思路引导】首先用发给每个班的练习本的数量乘班级的数量，求出发给15个班多少本练习本；然后用它加上备用的练习本的数量，求出学校应买多少练习本即可．【完整解答】解：144×15+40＝2160+40＝2200（本）答：学校应买2200本练习本．【易错注意点】此题主要考查了整数乘法的意义和应用，要熟练掌握，解答此题的关键是求出发给15个班多少本练习本．:考点1：带括号的混合运算（含较大数的除法）1．（2020春•江北区期末）把方框中的三个分步算式合并成综合算式是（）12+6＝1836÷18＝220+2＝22A．36÷（12+6）+20B．20+36÷（12+6）C．36÷12+6+20D．36÷（12+6）+22．（270+770÷55）﹣190÷10正确的运算顺序是（）A．②除法→①加法→③减法→④除法B．②除法→①加法→③减法→②除法C．②除法→①加法→④除法→③减法3．（2021春•浑源县期中）用计算器计算（801﹣576）÷15时，当按到“÷”的时候，显示屏上显示接着按“15”，再按“＝”，显示屏上显示的是。
运算律知识点总结
运算定律练习题练习1.2：选出正确答案，将序号填在相应的括号里。
①41+37+13=41+（37+13）②x+y=y+x ③35+(b+65)=(35+65)+b ④a+b+c=a+c+b ⑤32+45+55=32+(45+55) ⑥m+n+t=n+(m+t) 只应用加法交换律的是（）。
只应用加法结合律的是（）。
既应用加法交换律，又应用加法结合律的是（）。
知识点1：减法的运算性质1：一个数连续减去两个数等于这个数减去这两个减数的和。
用字母表示：a-b-c=a-(b+c)减法的运算性质2：一个数减去两个数的和等于这个数连续减去和里每个加数。
例3.1： 324-58-42 670-25-75 159﹣（59+37） 268﹣（35+68）加减的规律：（1）先加后减等于先减后加。
（2）先减后加等于先加后减。
练习325+41﹣25 268+45﹣68 268﹣45+32 325﹣41+75知识点2：乘法的交换律和结合律1．乘法交换律：两个数相乘，交换乘数的位置，积不变。
用字母表示为：a×b=b×a 2．乘法结合律：三个数相乘，先把前两个数相乘，再和第三个数相乘；或者先把后两个数相乘，再和第一个数相乘，积不变。
用字母表示为：(a×b) ×c=a×(b×c)练习4.2：下面的计算分别应用了什么运算律？在括号里填一填。
76 × 40 × 25 = 76 ×（40 × 25）（） 125 × 67 × 8 = 67 ×（125 × 8）（）知识点3：应用乘法运算律进行简便计算在连乘计算中，当某两个乘数的积正好是整十、整百、整千的数时，运用乘法运算律可使计算简便。
例5.1： 24×15×2 25×78×4 35×7×2 5×49×2运用分解的方法，将某个乘数拆分成几个数相乘的形式，使其中的乘数与其他乘数的乘积“凑整”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四单元《运算律》知识点归纳及练习
乘法结合律
1、乘法结合律：
三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一
个数相乘，它们的积不变。
用字母表示是：
（a×b）×c=a×(b×c).
使用时机：
当几个数相乘时，如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和
乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
数字如;25和4、50和2、125和
8、50和4、500和2等。
加法运算时也有结合律。
如果用a/b/c表示三个数，那么加法结合律表示为：（a+b）+c=a+
（b+c）
2、认识乘法交换律
两个数相乘，交换他们的位置，积不变，这叫乘法交换律。
如用字母a、b表示两个数，那
么乘法交换律用字母表示为：a×b=b×a。
1）上述规律可推广到更多个数相乘。
如：125×4×8×25=（125×8）×（25×4）=1000×
100=100000
2）加法运算时也有交换律，如用字母a、b表示两个数，那么加法交换律用字母表示为：
a+b=b+a。
3）运用加法交换律和结合律可以使得一些运算简便。
50+7+40+9=（50+40）+（7+9）
=90+16=106
练习题：
73×25×4 125×63×8 4×（25×93） 12×125×5×8 32×125×25 48×125×5
乘法分配律
1、乘法分配律：
两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相
乘，在把两个积相加（或相减），结果不变。
用字母表示数：
（a+b）×c=a×c+b×c或（a-b）×c=a×c－b×c
1、式子的特点：
式子的运算符号一般是×、+(-)、×的形式；在两个乘法式子中，有一个相同的因数；另
为两个不同的因数之和(或之差)是能凑成整十、整百、整千的数。
（逆运算）
2、102×88、99×15这类题的特点：
两个数相乘，把其中一个比较接近整十、整百、整千的数改写成整十、整百、整千与一个
数的和（或差），再应用乘法分配律可以使运算简便。
习题：
（80+4）×25 34×72+34×28 （23×99）×25+（77+71）×25 25×99 9999×2222+3333×3334 6666×3333+2222
第四单元备选练习题
一、填空。
（24）
1、两个数相加，交换加数的，结果不变，这叫做。
用字母表示为。
2、三个数相加，先把相加，再和相加；或者先把相加，再和相加，它们的结果不变，这叫做。
用字母表示为。
3、两个数相乘，交换乘数的，结果不变，这叫做。
用字母表示为。
4、三个数相乘，先把相乘，再和相乘；或者先把相乘，再和相乘，它们的结果不变，这叫做。
用字母表示为。
5、在
29＋37＋171＝37＋（。
42×5×8＝42×（。
47＋＝28 。
427＋39＋73＝（427 。
35×21×2＝21×（。
45×16＝45×。
6、计算64×26后，可以交换两个数的位置验算，是用了（）律。
7、一道减法算式的差是16，如果被减数不变，减数增加4，则差是（）。
二、用竖式计算下面各题，并验算。
（9）
618＋324 76×28 728÷18
三、简便计算。
（45）
44＋37＋56 163＋49＋261 74＋（137＋326） 5×（63×2）
249＋402 189＋35＋211＋165 483－236－64
582－157－182 65×5×2 15×23×4 540÷45÷2
36×25 25×125×32 35×22 540÷36
四、解决实际问题（22）
1、食堂买来5筐西红柿，每筐24千克，每千克2元，这些西红柿一共多少元？
2、一只熊猫体重75千克，一只小象的体重比熊猫的12倍少20千克，小象的体重多少千克？
3、每个书架有三层，每层大约放20本书。
（1）三个书架大约一共放多少本书?
(2)学校图书馆又新买来550本新书，增加几个这样的书架比较合适？
4、请算出育才小学四、五、六年级分别有多少人？并写出简便运算的过程。
5、按要求填表。