动量——爆炸反冲模型
动量守恒之爆炸与反冲(火箭)模型高三物理一轮复习专题

一.必备知识精讲 1.反冲〔1〕定义:当物体的一局部以一定的速度离开物体时,剩余局部将获得一个反向冲量,这种现象叫反冲运动.〔2〕特点:系统内各物体间的相互作用的内力远大于系统受到的外力.实例:发射炮弹、发射火箭等.(3)规律:遵从动量守恒定律.(1)火箭加速的原理设火箭飞行时在极短的时间Δt 内喷射燃气的质量是Δm ,喷出的燃气相对喷气前火箭的速度是u ,喷出燃气后火箭的质量是m ,火箭在这样一次喷气后增加的速度为Δv 。
以喷气前的火箭为参考系。
喷气前火箭的动量是0,喷气后火箭的动量是m Δv ,燃气的动量是Δmu 。
根据动量守恒定律,喷气后火箭和燃气的总动量仍然为0,所以m Δv +Δmu =0, 解出Δv =-Δmmu 。
上式说明,火箭喷出的燃气的速度u 越大、火箭喷出物质的质量与火箭本身质量之比Δmm越大,火箭获得的速度Δv 越大。
(2)现代火箭的发射原理由于现代火箭喷气的速度在~4000 m/s ,近期内难以大幅度提高;火箭的质量比(火箭起飞时的质量与火箭除燃料外的箭体质量之比)一般要小于10,故为使火箭到达发射人造地球卫星的7.9 km/s 的速度,采用多级火箭,即把火箭一级一级地接在一起,第一级燃料用完之后就把箭体抛弃,减轻负担,然后第二级开始工作,这样一级一级地连起来,不过实际应用中一般不会超过四级。
〔3〕火箭获得的最终速度设火箭发射前的总质量为M 、燃料燃尽后的质量为m ,以地面为参考系,火箭燃气的喷射速度大小为v 1,燃料燃尽后火箭的飞行速度大小为v ,在火箭发射过程中,由于内力远大于外力,所以动量守恒。
发射前的总动量为0,发射后的总动量为(M -m )v 1-mv (以火箭的速度方向为正方向),那么:(M -m )v 1-mv =0,所以v =⎝⎛⎭⎪⎫Mm-1v 1,燃料燃尽时火箭获得的最终速度由喷气速度及质量比M m决定。
3.爆炸问题 动量守恒爆炸物体间的相互作用力远远大于受到的外力,所以在爆炸过程中,系二.典型例题精讲:题型一:爆炸类例1:(·全国卷Ⅰ)一质量为m 的烟花弹获得动能E 后,从地面竖直升空。
专题动量守恒定律的应用三爆炸反冲人船模型课件-高二物理人教版(2019)选择性必修第一册

过 一推:甲推箱 程 一接:乙接箱 追 刚好避免相撞 踪 全过程追踪
味
道
感觉不错!
闯关5
独 闯 天 涯
如图所示,半径为R的光滑半圆槽质量为M,静止在光滑的 水平面上,其内表面有一小球被细线吊着恰位于槽的边缘处,如将 线烧断。重力加速度为g.求: (1)小球滑到另一边的最高点时,半圆槽的速度V1; (2)小球滑到另一边的最高点时,半圆槽的位移; (3)小球滑到半圆槽最低点时的速度V2; (4)小球滑到半圆槽最低点时对轨道的压力.
独
假设万户及其所携设备(火箭、椅子、风筝等)的总质量为 M,点燃火箭后在极短的时间内,
闯 天 涯
质量为 m 的燃气相对地面以 v0 的速度竖直向下喷出,忽略空气阻力的影响,重力加速度为
g,下列说法正确的是(B)
载 人
A.火箭的推力来源于空气对它的反作用力
航
味
B.在燃气喷出后的瞬间,火箭的速度大小为Mm-v0m
D.以上说法都不对
味 道 指点 江 迷津 湖
根据动量守恒得 v′=MMv0--mmv,mv 可能大于、小于或等于 Mv0,所以 v′可能小 于、大于或等于零。
1.系统由两个物体组成且相互作用前静止,在系统内发生相对运动的过程
中至少有一个方向的动量守恒,利用平均动量守恒求解。属于反冲模型。
人 船 mv1=Mv2
我
走 mv1=Mv2
大 MS= m(L-S)
显 身
动量守恒的应用:爆炸 反冲 高中物理课件8-5

由单方向动量守恒得 mvm=MvM=0,
设小球和凹槽移动的位移大小分别为 xm、xM,有
mvm t=MvM t,即 mxm=MxM ,
位移大小之和为 xm+xM =2R,
联立解得 xm=mM+M·2R,
xM
= m ·2R. m+M
第5节 动量守恒的应用:爆炸 反冲
一、人船模型与类人船模型 【原型题1】如图所示,质量为 M 的气球下挂着长为 L 的绳梯,一质量为 m 的人站在绳梯的下端,
第5节 动量守恒的应用:爆炸 反冲
二、爆炸与类爆炸 【原型题4】如图所示,光滑水平面上有三个滑块 A、B、C,质量关系是 mA=mC=m、mB=m2 .
开始时滑块 B、C 紧贴在一起,中间夹有少量炸药,处于静止状态,滑块 A 以速度 v0正对 B 向 右运动,在 A 未与 B 碰撞之前,引爆了 B、C 间的炸药,炸药爆炸后 B 与 A 迎面碰撞,最终 A 与 B 粘在一起,以速率 v0向左运动.g 取10m/s2,求:
由动量守恒得 mvm=MvM,由能量守恒得 E=12mvm2+12MvM2, 联立解得 vm、vM 的值. 变式:若系统有初动量,系统向右的初速度为 v0,以向右为正方向. 由动量守恒得(M+m)v0=MvM+mvm,由能量守恒得 E+12(M+m)v02=12mvm2+12MvM2, 联立解得 vm、vM 的值.
第5节 动量守恒的应用:爆炸 反冲
二、爆炸与类爆炸 3.类爆炸之“滑块+光滑弧/斜面”
笔记
如图所示,质量为 M 的弧劈静止放在光滑水平面上,弧劈上表面为光滑曲面,曲面末端与 地面相切,一质量为 m 的物块(可视为质点)自斜劈的顶端自由下滑,斜劈顶端到地面的距离 h, 重力加速度为 g,求物块滑到地面时的速度大小. 【解析】由于地面光滑,故物块和弧劈组成的系统在水平方向上动量守恒.
动量爆炸反冲模型32页PPT课件

D.两根导体棒和弹簧构成的系统动量 守恒、机械能不守恒
▲以初速度v0与水平方向成60°角斜向上抛出的手 榴弹,到达最高点时炸成质量分别为m和2m的两 块.其中质量大的一块沿着原来的方向以2v0 的速 度飞行.求
(1)喷出多少O2,宇航员才能安全返回飞船? (2)为了使总耗氧量最低,应该一次喷出多少氧气 ?返回时间是多少?
▲两位同学在公园里划船.租船时间将到,她们把小船 划向码头.当小船离码头大约2m左右时,有一位同学 心想:自己在体育课上立定跳远的成绩从未低于2m, 跳到岸上绝对没有问题.于是她纵身一跳,结果却掉到 了水里(如图).她为什么不能如她所想的那样跳到岸上 呢?(假设起跳时船已静止)
▲小车上装有一桶水,静止在光滑水平地面上,如图所 示,桶的前、后、底及侧面各装有一个阀门,分别为S1、 S2、S3、S4(图中未画出),要使小车向前运动,可采用的 方法是( ) A.打开阀门S1 B.打开阀门S2 C.打开阀门S3 D.打开阀门S4
▲运送人造地球卫星的火箭开始工作后,火箭做加速运 动的原因是( ) A.燃料燃烧推动空气,空气反作用力推动火箭 B.火箭发动机将燃料燃烧产生的气体向后推出,气体 的反作用力推动火箭
船s=45m处与飞船处于相对静止状态,他准备对太空中
的哈勃望远镜进行维修,宇航员背着装有质量为m0= 0.5kg的O2贮气筒,筒内有一个可以使O2以v=50m/s的速 度喷出的喷嘴.宇航员在维修完毕哈勃望远镜后,必须
向着返回飞船方向的反方向释放O2,才能回到飞船,同 时又必须保留一部分O2供途中宇航员呼吸之用,宇航员 的耗氧率为Q=2.5×10-4kg/s,如果不考虑喷出O2对设 备与宇航员总质量的影响,则:
动量守恒的条件 爆炸、反冲运动 人船模型(附精品解析)

动量守恒的条件爆炸、反冲运动人船模型考点一动量守恒的条件考点二爆炸、反冲运动考点三人船模型考点四连续射击问题1.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.动量守恒定律常用表达式:m1v1+m2v2=m1v1′+m2v2′.1)p=p′:相互作用前系统的总动量p等于相互作用后的总动量p′.2)m1v1+m2v2=m1v1′+m2v2′:相互作用的两个物体组成的系统,作用前动量的矢量和等于作用后动量的矢量和.3)Δp1=-Δp2:相互作用的两个物体组成的系统,一个物体的动量变化量与另一个物体的动量变化量大小相等、方向相反.4)Δp=0:系统总动量增量为零.考点一动量守恒的条件⑴系统不受外力或者所受外力之和为零;⑵系统受外力,但外力远小于内力,可以忽略不计;⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
⑷全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
附:机械能守恒的条件:只有重力、系统内弹力做功.1.下列四幅图所反映的物理过程中,说法正确的是()A.甲图中子弹射入木块过程中,子弹和木块组成系统动量守恒,能量不守恒B.乙图中M、N两木块放在光滑水平面上,剪断束缚M、N的细线,在弹簧从压缩状态恢复原长过程中,M、N与弹簧组成的系统动量不守恒,机械能守恒C.丙图中细线断裂后,木球和铁球在水中运动的过程,两球组成的系统动量不守恒,机械能守恒D.丁图中木块沿光滑固定斜面下滑,木块和斜面组成的系统动量守恒,机械能守恒2.如图所反映的物理过程中,以物体A和物体B为一个系统符合系统机械能守恒且水平方向动量守恒的是()A.甲图中,在光滑水平面上,物块B以初速度v0滑上上表面粗糙的静止长木板AB.乙图中,在光滑水平面上,物块B以初速度v0滑下靠在墙边的表面光滑的斜面AC.丙图中,在光滑水平上面有两个带正电的小球A、B相距一定的距离,从静止开始释放D.丁图中,在光滑水平面上物体A以初速度v0滑上表面光滑的圆弧轨道B3.(多选)如图所示,A、B两物体质量之比为m A∶m B=3∶2,原来静止在足够长的平板小车C上,A、B间有一根被压缩的弹簧,地面光滑.当两物体被同时释放后,则( )A.若A、B与平板车上表面间的动摩擦因数相同,则A、B组成系统的动量守恒B.若A、B与平板车上表面间的动摩擦因数相同,则A、B、C组成系统的动量守恒C.若A、B所受的摩擦力大小相等,则A、B组成系统的动量守恒D.若A、B所受的摩擦力大小相等,则A、B、C组成系统的动量守恒4. (2021·全国乙卷·T14)如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。
2022年高考物理模型专题突破-动量守恒中的“碰撞模型”和“反冲模型

真题模型——动量守恒中的“碰撞模型”和“反冲模型”来源图例考向模型核心归纳2015·新课标全国卷Ⅰ物体A、B、C位于同一直线上动量守恒、机械能守恒、“多物体作用模型”1.常考的模型(1)碰撞中的“两物体作用模型”(2)碰撞中的“多物体作用模型”(3)碰撞中的“图象类问题模型”(4)“反冲模型”(5)“爆炸模型”2.模型解法(1)牢记一个定律:动量守恒定律m1v1+m2v2=m1v1′+m2v2′。
(2)熟记两种碰撞①弹性碰撞:动量守恒和机械能守恒。
②非弹性碰撞:动量守恒、机械能不守恒。
(3)会用两个结论①“一动一静”两物体发生弹性正碰后的速度满足v1=m1-m2m1+m2v0,v2=2015·新课标全国卷Ⅱ滑块a、b沿水平面上同一条直线运动动量守恒、能量守恒(功能关系)2016·新课标全国卷Ⅱ光滑冰面上静止放置一表面光滑的斜面体,一蹲在滑板上的小孩和冰块均静止于冰面上动量守恒、机械能守恒2016·新课标全国卷Ⅲ静止的a和b相距l;b与墙也相距l 动量守恒、机械能守恒、功能关系2017·全国卷Ⅰ模型火箭点火升空动量守恒2m1m1+m2v0。
②质量相等的两物体发生弹性碰撞后交换速度;发生完全非弹性碰撞后两物体共速。
【预测1】如图14所示,在光滑的水平面上,有A、B、C三个物体,开始B、C皆静止且C在B上,A物体以v0=10 m/s的速度撞向B物体,已知碰撞时间极短,撞完后A物体静止不动,而B、C最终的共同速度为4 m/s。
已知B、C 两物体的质量分别为m B=4 kg、m C=1 kg。
图14(1)求A物体的质量;(2)A、B间的碰撞是否造成了机械能损失?如果造成了机械能损失,则损失了多少?解析(1)设B、C最终的共同速度为v,则由整个过程动量守恒可得:m A v0=(m B+m C)v代入数据解得m A=2 kg。
(2)设A与B碰撞后B的速度变为v′,在B与C相互作用的时间里,B与C组成的系统动量守恒,即m B v′=(m B+m C)v,解得v′=5 m/sA与B碰撞的过程中,碰前系统的动能为E k1=12m A v2,代入数据解得E k1=100 J碰后系统的动能为E k2=12m B v′2,代入数据解得E k2=50 J所以碰撞过程中损失了机械能,损失了50 J 。
爆炸、反冲及人船模型(解析版)
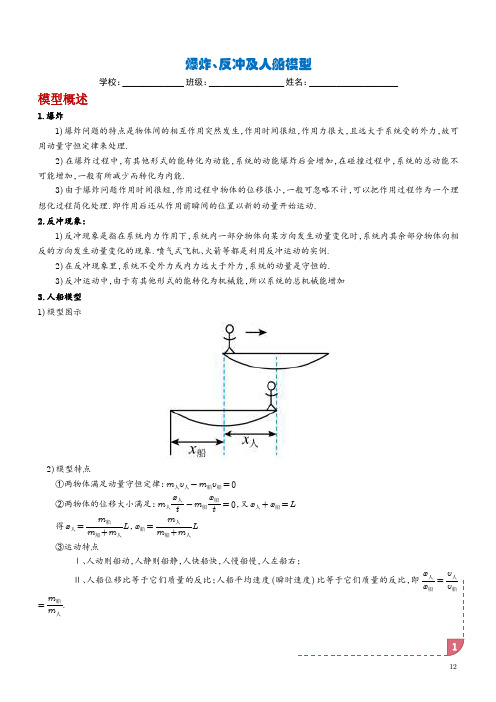
爆炸、反冲及人船模型学校:_________班级:___________姓名:_____________模型概述1.爆炸1)爆炸问题的特点是物体间的相互作用突然发生,作用时间很短,作用力很大,且远大于系统受的外力,故可用动量守恒定律来处理.2)在爆炸过程中,有其他形式的能转化为动能,系统的动能爆炸后会增加,在碰撞过程中,系统的总动能不可能增加,一般有所减少而转化为内能.3)由于爆炸问题作用时间很短,作用过程中物体的位移很小,一般可忽略不计,可以把作用过程作为一个理想化过程简化处理.即作用后还从作用前瞬间的位置以新的动量开始运动.2.反冲现象:1)反冲现象是指在系统内力作用下,系统内一部分物体向某方向发生动量变化时,系统内其余部分物体向相反的方向发生动量变化的现象.喷气式飞机、火箭等都是利用反冲运动的实例.2)在反冲现象里,系统不受外力或内力远大于外力,系统的动量是守恒的.3)反冲运动中,由于有其他形式的能转化为机械能,所以系统的总机械能增加3.人船模型1)模型图示2)模型特点①两物体满足动量守恒定律:m人v人-m船v船=0②两物体的位移大小满足:m人x人t-m船x船t=0,又x人+x船=L得x人=m船m船+m人L,x船=m人m船+m人L③运动特点Ⅰ、人动则船动,人静则船静,人快船快,人慢船慢,人左船右;Ⅱ、人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即x人x船=v人v船=m船m人.典题攻破1.爆炸1.(2024·青海海南·二模)斜向上发射的炮弹在最高点爆炸(爆炸时间极短)成质量均为m 的两块碎片,其中一块碎片沿原路返回。
已知炮弹爆炸时距地面的高度为H ,炮弹爆炸前的动能为E ,重力加速度大小为g ,不计空气阻力和火药的质量,则两块碎片落地点间的距离为()A.2EHmgB.22EH mgC.23EH mgD.42EH mg【答案】D【详解】火箭炸裂的过程水平方向动量守恒,设火箭炸裂前的速度大小为v ,则E =122mv 2得v =Em设炸裂后瞬间另一块碎片的速度大小为v 1,有2mv =-mv +mv 1解得v 1=3Em根据平抛运动规律有H =12gt 2得t =2H g两块碎片落地点之间的距离x =(v +v 1)t =42EH mg故D 。
第2讲 动量守恒定律及“两类模型”问题

第2讲动量守恒定律及“两类模型”问题一、动量守恒定律1.内容如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.表达式(1)p=p′,系统相互作用前的总动量p等于相互作用后的总动量p′。
(2)m1v1+m2v2=m1v1′+m2v2′,相互作用的两个物体组成的系统,作用前的动量和等于作用后的动量和。
(3)Δp1=-Δp2,相互作用的两个物体动量的变化量等大反向。
(4)Δp=0,系统总动量的增量为零。
3.适用条件(1)理想守恒:不受外力或所受外力的合力为零。
(2)近似守恒:系统内各物体间相互作用的内力远大于它所受到的外力。
(3)某一方向守恒:如果系统在某一方向上所受外力的合力为零,则系统在这一方向上动量守恒。
【自测(多选)如图1所示,小车与木箱紧挨着静止放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱。
关于上述过程,下列说法中正确的是()图1A.男孩和木箱组成的系统动量守恒B.小车与木箱组成的系统动量守恒C.男孩、小车与木箱三者组成的系统动量守恒D.木箱的动量增量与男孩、小车的总动量增量大小相同答案CD解析男孩和木箱组成的系统受小车的摩擦力,所以动量不守恒,A错误;小车与木箱组成的系统受男孩的力为外力,所以动量不守恒,B错误;男孩、小车与木箱三者组成的系统,所受合外力为0,所以动量守恒,C正确;木箱的动量增量与男孩、小车的总动量增量大小相同,但方向相反,D正确。
二、“两类”模型问题1.“反冲”和“爆炸”模型(1)反冲①定义:当物体的一部分以一定的速度离开物体向前运动时,剩余部分必将向后运动,这种现象叫反冲运动。
②特点:系统内各物体间的相互作用的内力远大于系统受到的外力。
实例:发射炮弹、发射火箭等。
③规律:遵从动量守恒定律。
(2)爆炸问题爆炸与碰撞类似,物体间的相互作用时间很短,作用力很大,且远大于系统所受的外力,所以系统动量守恒。
如爆竹爆炸等。
2.“人—船”模型(1)模型介绍两个原来静止的物体发生相互作用时,若整体所受外力的矢量和为零,则两物体组成的系统动量守恒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
▲质量为m=3㎏的物体在离地面高度为h=20m处,_正 以水平速度v=20m/s运动时,突然炸裂成两块,其中一 块质壁为m1=1㎏.仍沿原运动方向以v1=40m/s的速度飞行, 炸裂后的另一块的速度大小为______m/s.两块落到水平 地面上的距离为______m(小计空气阻力,g取10m/s2).
▲一个静止的质量为m的不稳定原子核,当它完成一次 α衰变.以速度v发射出一个质量为mα的α粒子后,其剩余 部分的速度等于( ).
m v (A) m
(B) -v
m v (C) m - m
m v (D) m - m
▲如图所示,两根足够长的固定平行金属光滑导轨位于同 一水平面上,导轨上横放着两根相同的导体棒ab、cd,与 导轨构成矩形回路.导体棒的两端连接着处于压缩状态的 两根轻质弹簧,两棒的中间用细线绑住,它们的电阻均为R, 回路上其余部分的电阻不计.在导轨平面内两导轨间有一 竖直向下的匀强磁场.开始时,导体棒处于静止状态,剪 断细线后,导体棒在运动过程中( ) A.回路中有感应电动势 B.两根导体棒所受安培力的方向相同 C.两根导体棒和弹簧构成的系统动量 守恒、机械能守恒 D.两根导体棒和弹簧构成的系统动量 守恒、机械能不守恒
取g=10m/s2.
▲如图所示,一艘小船静止在平静的水面上,船前舱有 一抽水机,抽水机把前舱的水均匀抽往后舱,不计水的 阻力,在船的前舱与后舱分开、不分开的两种情况下, 船的前舱运动情况分别是( ) A.不动;向前匀速动 B.向前加速动;不动 C.不动;向后匀速动 D.向后匀速动;不动
▲一火箭喷气发动机每次喷出m=200g的气体,气体离 开发动机喷出时的速度v=1000m/s,设火箭质量M= 300kg,发动机每秒喷气20次. (1)当第三次气体喷出后,火箭的速度多大? (2)运动第1s末,火箭的速度多大?
பைடு நூலகம்
▲以初速度v0与水平方向成60°角斜向上抛出 的手榴弹,到达最高点时炸成质量分别为m和2m的两 块.其中质量大的一块沿着原来的方向以2v0 的速度 飞行.求 (1)质量较小的另一块弹片速度的大小和方向. (2)爆炸过程有多少化学能转化为弹片的动能?
▲从地面竖直向上发射一炮弹,炮弹的初速度v 0 = 100m/s.经过t=6s后,此炮弹炸成质量相等的两块.从爆 炸时算起,经过t 1 =10.0s后,第一块碎片先落到发射地 点,求爆炸时另一块碎片的速度.(g取10m/s)
▲如图所示,在沙堆表面放置一长方
形木块A,其上再放一质量为mB=0.1kg 的爆竹B,木块A的质量为mA=6.0kg, 当爆竹爆炸时,因反冲作用使木块陷入 沙中,从爆竹爆炸到木块停止下陷历时 0.1s,已知木块在沙中受到的平均阻力 是90N,求爆竹能上升的最大高度,设 爆竹中火药的质量及空气阻力忽略不计,
▲小车上装有一桶水,静止在光滑水平地面上,如图所 示,桶的前、后、底及侧面各装有一个阀门,分别为S1、 S2、S3、S4(图中未画出),要使小车向前运动,可采用的 方法是( ) A.打开阀门S1 B.打开阀门S2 C.打开阀门S3 D.打开阀门S4
▲运送人造地球卫星的火箭开始工作后,火箭做加速运 动的原因是( ) A.燃料燃烧推动空气,空气反作用力推动火箭 B.火箭发动机将燃料燃烧产生的气体向后推出,气体 的反作用力推动火箭 C.火箭吸入空气,然后向后 推出,空气对火箭的反作用力 推动火箭 D.火箭燃料燃烧发热,加热 周围空气,空气膨胀推动火箭
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲
▲课外科技小组制作一只“水火箭”,用压缩空气压出 水流使火箭运动.假如喷出的水流流量保持为2×10-4m3/s, 喷出速度保持为对地10m/s.启动前火箭总质量为1.4kg,则 启动2s末火箭的速度可以达到多少?已知火箭沿水平轨道 运动阻力不计,水的密度是103kg/m3.
▲一个连同装备总质量为M=100kg的宇航员,在距离飞 船s=45m处与飞船处于相对静止状态,他准备对太空中的 哈勃望远镜进行维修,宇航员背着装有质量为m0=0.5kg的 O2贮气筒,筒内有一个可以使O2以v=50m/s的速度喷出的 喷嘴.宇航员在维修完毕哈勃望远镜后,必须向着返回飞
船方向的反方向释放O2,才能回到飞船,同时又必须保留
一部分O2供途中宇航员呼吸之用,宇航员的耗氧率为Q= 2.5×10-4kg/s,如果不考虑喷出O2对设备与宇航员总质量
的影响,则:
(1)喷出多少O2,宇航员才能安全返回飞船? (2)为了使总耗氧量最低,应该一次喷出多少氧气? 返回时间是多少?
▲两位同学在公园里划船.租船时间将到,她们把小船 划向码头.当小船离码头大约2m左右时,有一位同学 心想:自己在体育课上立定跳远的成绩从未低于2m, 跳到岸上绝对没有问题.于是她纵身一跳,结果却掉到 了水里(如图).她为什么不能如她所想的那样跳到岸上 呢?(假设起跳时船已静止)
