34.复数与逻辑推理
逻辑与推理以及复数

逻辑与推理以及复数上课时间:上课教师:上课重点:掌握四种命题的相互关系以及真假,以及复合命题的真假的判断,充分条件和必要条件的判断,简单的推理(合情推理以及演绎推理的关系),复数上课规划:解题技巧和方法一 逻辑(一)四种命题的相互关系例题:命题“若x y =,则||||x y =”,写出它的逆命题、否命题、逆否命题,并判断它们的真假注意区分:原命题的否命题与原命题的否定练习1.判断下列语句是不是命题,若是,判断出其真假,若不是,说明理由.(1)矩形难道不是平行四边形吗?(2)垂直于同一条直线的两条直线必平行吗?(3)求证:R x ∈,方程012=++x x 无实根.(4)5>x2.判断下列命题的真假.⑴空间中两条不平行的直线一定相交;⑵垂直于同一个平面的两个平面互相垂直;⑶每一个周期函数都有最小正周期;⑷两个无理数的乘积一定是无理数;(5)若1m >,则方程220x x m -+=无实数根.3.命题p :奇函数一定有(0)0f =;命题q :函数1y x x=+的单调递减区间是[10)(01],,- .则下列四个判断中正确的是( )A .p 真q 真B . p 真q 假C . p 假q 真D . p 假q 假4.如果两个三角形全等,那么它们的面积相等; ①如果两个三角形的面积相等,那么它们全等; ②如果两个三角形不全等,那么它们的面积不相等; ③如果两个三角形的面积不相等,那么它们不全等; ④命题②、③、④与命题①有何关系?5.有下列四个命题:①“若0x y += , 则,x y 互为相反数”的逆命题;②“全等三角形的面积相等”的否命题; ③“若1q ≤ ,则220x x q ++=有实根”的逆否命题;④“不等边三角形的三个内角相等”逆命题. 其中真命题()A .①②B .②③C .①③D .③④6.命题“若,x y 是奇数,则x y +是偶数”的逆否命题是 ;它是 命题.(二)判断充分,必要条件1.在空间中,“两条直线没有公共点”是“这两条直线平行”的( )A .充分不必要条件.B .必要不充分条件.C .充要条件.D .既不充分也不必要条件.2. 对任意实数a 、b 、c ,在下列命题中,真命题是( )A .“ac bc >”是“a b >”的必要条件B .“ac bc =”是“a b =”的必要条件C .“ac bc >”是“a b >”的充分条件D .“ac bc =”是“a b =”的充分条件3. 若集合2{|540}A x x x =-+<,{|||1}B x x a =-<,则“(23),a ∈”是“B A ⊆”的 A . 充分但不必要条件 B . 必要但不充分条件C . 充要条件D . 既不充分又不必要条件4.若“a b c d ⇒>≥”和“a b e f <⇒≤”都是真命题,其逆命题都是假命题,则“c d ≤”是“e f ≤”的( )A .必要非充分条件B .充分非必要条件C .充分必要条件D .既非充分也非必要条件5.已知,,,a b c d 为实数,且c d >.则“a b >”是“a c b d ->-”的( ) A . 充分而不必要条件 B . 必要而不充分条件C .充要条件D . 既不充分也不必要条件6.“12m =”是“直线(2)310m x my +++=与直线(2)(2)30m x m y -++-=相互垂直”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .非充分非必要条件(三)充分,必要条件的求解1. 设a ,b 是两条直线,α,β是两个平面,则a b ⊥的一个充分条件是( ) A .a α⊥,b β∥,αβ⊥ B .a α⊥,b β⊥,αβ∥C .a α⊂,b β⊥,αβ∥D .a α⊂,b β∥,αβ⊥2.设a b ,表示直线,αβ,表示平面,则αβ∥的充分条件是( ) A .a b a b αβ⊥⊥∥,, B .a b a b αβ⊂⊂,,∥C .a b a b αββα⊂⊂,,∥,∥ D .a b a b βα⊥⊥⊥,, 3.设m n ,是平面α内的两条不同直线,1l ,2l 是平面β内的两条相交直线,则αβ∥的一个充分而不必要条件是( )A .m β∥且1l α∥B .1m l ∥且2n l ∥C .m β∥且n β∥D .m β∥且2n l ∥4. 平面α∥平面β的一个充分条件是( )A.存在一条直线α,a α∥,a β∥B.存在一条直线a ,a α⊂,a β∥C.存在两条平行直线a ,b ,a α⊂,b β⊂,a β∥,b α∥D.存在两条异面直线a ,b ,a α⊂,a β∥,b α∥5.直线12l l ,互相平行的一个充分条件是( )A .12l l ,都平行于同一个平面B .12l l ,与同一个平面所成的角相等C .1l 平行于2l 所在的平面D .12l l ,都垂直于同一个平面6.给出以下四个条件:①0ab >;②0a >或0b >;③2a b +>;④0a >且0b >.其中可以作为“若a b ∈R ,,则0a b +>”的一个充分而不必要条件的是 .7.设集合2{|60}A x x x =+-=,{|10}B x mx =+=,则B 是A 的真子集的一个充分不必要的条件是( )A .1123m ⎧⎫∈-⎨⎬⎩⎭,B .0m ≠C .11023m ⎧⎫∈-⎨⎬⎩⎭,,D .103m ⎧⎫∈⎨⎬⎩⎭, 8.若不等式1x m -<成立的充分不必要条件是23x <<,则实数m 的取值范围是________;9.集合1|01x A x x -⎧⎫=<⎨⎬+⎩⎭,{|}B x x b a =-<,若“1a =”是“A B ≠∅ ”的充分条件,则b 的取值范围可以是( )A .20≤b -<B .02≤b <C .31b -<<-D .12≤b -<10.下列选项中,p 是q 的必要不充分条件的是( )A .:p a c b d +>+, :q a b >且c d >B .:11p a b >>, ():x q f x a b =-(0a >,且1a ≠)的图像不过第二象限C .:1p x =,2:q x x = D .:1p a >, ():log =a q f x x (0>a ,且1≠a )在()0+∞,上为增函数11.已知条件p :|1|2x +>,条件q :x a >,且p ⌝是q ⌝的充分不必要条件,则a 的取值范围可以是( )A .1a ≥B .1a ≤C .1a ≥-D .3a -≤12.已知不等式||1x m -<成立的充分不必要条件是1132x <<,则m 的取值范围是 ( ) A.41{|}32m m -≤≤ B.1{|}2m m < C. 14{|}23m m -≤≤ D. 4{|}3m m ≥(四)充要条件1. 已知,a b 是实数,则“0a >且0b >”是“0a b +>且0ab >”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件2.在ABC ∆中,条件甲:A B <,条件乙:22cos cos A B >,则甲是乙的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件3.已知a ∈R 且0a ≠,则“11a<”是 “a >1”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件4.设,a b ∈R ,则不等式a b >与11a b>都成立的充要条件是( ) A .0ab > B .00,a b >< C .0ab < D .0ab ≠ 5.已知αβ,表示两个不同的平面,m 为平面α内的一条直线,则“αβ⊥”是“m β⊥”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.若a 与b c - 都是非零向量,则“a b a c ⋅=⋅ ”是“()a b c ⊥- ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.设()322()log 1f x x x x =+++,则对任意实数a 、b ,0≥a b +是()()0≥f a f b +的A .充要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件8.对任意实数a ,b ,c ,给出下列命题:①“a b =”是“ac bc =”充要条件;②“5a +是无理数”是“a 是无理数”的充要条件;③“a b >”是“22a b >”的充分条件;④“5a <”是“3a <”的必要条件. 其中真命题的个数是( )A .1B .2C .3D .4(六)逻辑连接词(复合命题)1.写出下列命题的“p ⌝”命题:(1)正方形的四边相等;(2)平方和为0的两个实数都为0;(3)若ABC ∆是锐角三角形, 则ABC ∆的任何一个内角是锐角;(4)若0abc =,则,,a b c 中至少有一个为0;(5)若(1)(2)0x x --≠,则1x ≠且2x ≠.、2.命题“关于x 的方程(0)ax b a =≠的解是唯一的”的结论的否定是( )A .无解B .两解C .至少两解D .无解或至少两解3. 命题“2230ax ax -+>恒成立”是假命题,则实数a 的取值范围是( )A .0a <或3a ≥B .0a ≤或3a ≥C .0a <或3a >D .03a <<4.已知条件:12p x +>,条件2:56q x x ->,则p ⌝是q ⌝的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.如果命题“非p 或非q ”是假命题,给出下列四个结论:①命题“p 且q ”是真命题;②命题“p 且q ”是假命题;③命题“p 或q ”是真命题;④命题“用“充分、必要、充要”填空:①p q ∨为真命题是p q ∧为真命题的________________条件;②p ⌝为假命题是p q ∨为真命题的_____________________条件.6.结论“至少有两个解”的否定的正确说法是( )A .至少有三个解B .至多有一个解C .至多有两个解D .只有一个解二 推理(一)合情推理1.在平面几何里,有勾股定理:“设△A BC 的两边A B ,A C 互相垂直,则A B 2+A C 2=BC 2”拓展到空间,类比平面几何的勾股定理,“设三棱锥A —BC D 的三个侧面A BC 、A C D 、AD B 两两相互垂直,则可得” ( )(A)AB 2+AC 2+ AD 2=BC 2+ CD 2 + BD 2 (B)BCD ADB ACD ABC S S S S ∆∆∆∆=⨯⨯2222(C)2222BCDADB ACD ABC S S S S ∆∆∆∆=++ (D)AB 2×AC 2×AD 2=BC 2 ×CD 2 ×BD 2 2.在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,按图所标边长,由勾股定理有:.222b a c +=设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O —LMN ,如果用321,,s s s 表示三个侧面面积,4s 表示截面面积,那么你类比得到的结论是 .3.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题,可以得到命题: 。
复数的几个类比推理

下面给出了关于复数的几个类比推理:①复数的加减法运算可以类比多项式的加减法运算法则;②由向量a的性质|a|2=a2类比得到复数z的性质|z|2=z2;③由向量加法的几何意义可以类比得到复数加法的几何意义.其中类比错误的是②.考点:类比推理.专题:探究型.分析:复数的加减法运算可以类比多项式的加减法运算法则,由向量加法的几何意义可以类比得到复数加法的几何意义,但是向量的模长和复数的模长不是通过列举法得到.解答:解:复数的加减法运算可以类比多项式的加减法运算法则,①正确由向量a的性质|a|2=a2类比得到复数z的性质|z|2=z2,这两个长度的求法不是通过类比得到的.故②不正确,由向量加法的几何意义可以类比得到复数加法的几何意义.故③正确.故答案为:②点评:本题考查类比推理,是一个观察几个结论是不是通过类比得到,本题解题的关键在于对于所给的结论的理解.用类比法解决复数的三类问题从新教材的特点来看,复数高考题的难度不会大,主要以客观题的形式考察基础知识.以下结合高考题给出了用类比法解决复数的三类问题的方法,希望同学们结合数学思想方法,使知识形成网络,系统全面的掌握所学知识.一、复数的运算类比多项式的运算复数代数形式的加法、减法运算法则复数代数形式的乘法运算运算法则:显然在运算法则上类似于多项式的加减法(合并同类项),以及多项式的乘法,这就给我们对复数的运算以及记忆带来了极大的方便.二、复数的几何意义类比数轴和直角坐标里的点我们知道,实数与数轴上的点一一对应的;有序实数对与直角坐标平面内的点一一对应;类似的我们有:复数集C=与坐标系中的点集一一对应.于是:复数集=复平面内的点复数集=平面向量例1在复平面内,复数+(1+i)2对应的点位于( )(A) 第一象限(B) 第二象限(C) 第三象限(D)第四象限解析复数+(1+i)2==因为复数对应着直角坐标平面内的点故在第二象限,答案选B.分析:此题一方面考查了复数的运算能力,另一方面考察了对复数的几何意义的理解.例2非零复数分别对应复平面内向量,若=则向量与的关系必有()A .= B.C .D.共线解答:由向量的加法及减法可知:==由复数加法以及减法的几何意义可知:对应的模, 对应的模又因为= ,且非零复数分别对应复平面内向量。
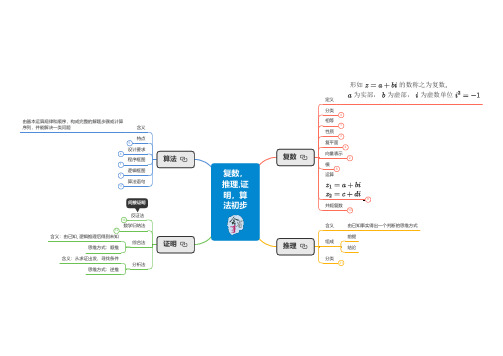
高中数学思维导图:复数,推理证明,算法初步
定理逆定理
与已知矛盾
常见矛盾
与假设矛盾 与定义,定理,公理矛盾
自相矛盾
数学归纳法
适用题型 适用范围
证明恒等式
证明整除与几何问题
证明不等式
证明数列有问题
证明立体几何问题
仅限与正整数有关的问题
:验证
时命题成立
: 假设
时,命题成立,
步骤
Байду номын сангаас
证明
时,命题也成立
:命题对从 开始的所有正整数 都成立
综合法
含义:由已知, 逻辑推理后得到未知 思维方式:顺推
由基本运算规律和顺序,构成完整的解题步骤或计算 序列,并能解决一类问题
含义
特点
5
设计要求
4
程序框图
1
逻辑框图
1
算法语句
17
间接证明
反证法
14
数学归纳法
12
含义:由已知, 逻辑推理后得到未知 思维方式:顺推
综合法
含义:从求证出发,寻找条件 思维方式:逆推
分析法
算法 证明
复数, 推理,证 明,算 法初步
含义
证明命题都使用演绎推理,合情推理不能用做证明 从一般性原理出发,推出某个特殊情况下的结论
一般 特殊
特点
三段论:
而
则
内容
一般原理:大前提,M是P
表示形式
特殊情况:小前提,S是M 结论:S是P
证明
间接证明
反证法
含义
假设求证不成立,推理,找出矛盾
反设 归谬 结论
步骤
由已知推出的结论很少
适用范围
存在性命题 结论中含有:否定,唯一,无限,至多,至少
复数算法推理证明梳理

乘方 乘 除 开方 三棱锥 正四面体
正方体 长方体 不等式
正方形 截面圆 长方形 截面圆面积 等式 大圆 大圆面积 表面积 (a b c)r
S 2
V
( S1 S2 S3 S 4 )r 3
算法知识方法清单
• 1、三种结构 • 2、赋值的形式 • 3、常见的符号:
4 2 2 4
5, i 2 1, i 3 i, i 4 1, (1 i ) 2 2i, (1 i ) 2 2i 6已知求 z i 1( z i 1), 求 z 的最值,7求7 24i的平方根
7复数的加减乘除 8复数与点、向量一一对应
推理与证明知识方法清单
归纳奠基 (1)当n = n 0时 数学归纳法: 成立 (2)假设n = k时即... 归纳递推步骤 那么 n = k 1 时 由可知对n ...都成立 用已知,用假设,推目标
2复习常见的比 加 平面 空间 减 面积 长度 三角形 体积 面积 正三角形 面 线 球 圆
复数知识方法清单
1复数的概念 实数 :b = 0 z a bi (a, b R ) 虚数 :a 0 z a bi 纯虚数a 0且b = 0 2不全为实数的两数不可比较大小 1 2i (1 2i ) 3复数的模 z a b , 4, 2 2 (3 4i ) 3 4i
, ,/, ^ ,SQR ,ABS ,\
不完全归纳法:特殊法、累加累乘法 合情推理 1概念推理 类比推理:常见的类比 演绎推理:三段论s是p,m是s,s是p 综合法:(执因索果,作差法,公式法) 推理证明 直接证明: 分析法 : 执果索因要证即证...显然成立 (有时局部用因为所以)直接平方,移项平方 证明: 假设命题结论的反面成立 间接证明:反证法:推矛盾 下结论
2023届高考复习数学专项(复数及推理与证明)好题练习(附答案)

2023届高考复习数学专项(复数及推理与证明)好题练习1.若复数:::满足(l�i)z=3+i<其中i是虚数单位),则()A.二的实部是2B.=的虚部是2iC.乞=1-2i2.已知复数z=3-4i, 则下列命题中正确的为()A.l z l= 5B.z=3+4iC. z的虚部为-4iD.z在复平而上对应点在第四象限3.下面四个命题中的真命题为()1A.若复数z满足-ER,则zERB.若复数z满足/ER,则zERC.若复数Z1,Z2满足z亿2ER,则z1=D.若复数zE R,则豆ER Z2D.lzl=✓S4.已知复数二满足i2k+1z=2+i,-(kE z), 则z在复平面内对应的点可能位于()A.第一象限B.第二象限C.第三象限D.第四象限5.设z是复数,则下列命题中的真命题是()A.若z2�o.则z是实数B.若z2<o,则z是虚数C.若z是虚数,则z2�oo.若z是纯虚数,则z2<o6.已知Z1与Z-2是共枙虚数,以下四个命题一定正确的是()2 2A. Z l <i z2B. zi z2=z Z2C.z1+z2E Rz+l.7设复数z满足——=i,则下列说法错误的是()A.z为纯虚数B.z的虚部为一-i2C.在复平而内,z对应的点位千第二象限D.z=-—ZtD .• —ERZ28.某大学进行自主招生测试,盂要对逻辑思维和阅读表达进行能力测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示,下列叙述正确的是( )A .甲同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前B .乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前C .甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前D .甲同学的总成绩排名比丙同学的总成绩排名更靠前 9.在0,0a b >>的条件下,下列四个结论正确的是( ) A .22a b aba b+≥+B .2a b +≤C .22a b a b b a+≤+D .设,,a b c 都是正数,则三个数111,,a b c b c a+++至少有一个不小于2 10.如图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论正确的是( )A.2018年3月至2019年3月全国居民消费价格同比均上涨B.2018年3月至2019年3月全国居民消费价格环比有涨有跌C.2019年3月全国居民消费价格同比涨幅最大D.2019年3月全国居民消费价格环比变化最快参考答案1.若复数:::满足(l�i)z=3+i<其中i是虚数单位),则()D.lzl=✓S A. 二的实部是2 B.=的虚部是2i C.乞=1-2i【参考答案】CD3 +i(3 +i)(l +i) 2 + 4i—= = = 1+2i,【答宋解析】z=l—1 2 2即二的实部是1,虚部是2'故A错误,B铅误,又亏=1—2i,121 =✓1三了-= Js'故C,D均正确故选CD2. 已知复数z=3-4i, 则下列命题中正确的为()A.l z l= 5B.z=3+4iC. z的虚部为-4iD. z在复平面上对应点在第四象限【参考答案】ABD【答案解析】:;=3-4i, 则仁l=F五二正=5.故A正确;�=3+4i, 故B正确;二的虚部为4,故C铅误;二在复平面上对应点的坐标为(3,-4), 在第四象限,故D正确.:.命题中正确的个数为3.故选ABD.3.下而四个命题中的真命题为()1A. 若复数z满足-E R,则zE RB.若复数z满足/E R,则zE RC. 若复数Z1,Z2满足z亿2R,则z=22D.若复数zE R,则�E R【参考答案】AD1【答案解析】若复数二满足-E R,则二E R,故命题A为真命题;复数z =i 满足z 2=﹣1∈R ,则z ∉R ,故命题B 为假命题; 若复数z 1=i ,z 2=2i 满足z 1z 2∈R ,但z 1≠,故命题C 为假命题;若复数z ∈R ,则=z ∈R ,故命题D 为真命题. 故选:AD .4.已知复数z 满足212k i z i +=+,()k z ∈,则z 在复平面内对应的点可能位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【参考答案】BD【答案解析】212k i z i +=+ ,212k iz i ++∴=15i i i === ,37i i i ===-当k 为奇数时 ()2122212k i ii i z i i i i i++++∴====-+--⨯ 在复平面上对应的点为()1,2-位于第二象限; 当k 为偶数时 ()2122212k i ii i z i i i i i++++∴====-⨯ 在复平面上对应的点为()1,2-位于第四象限;故复数z 在复平面内对应的点位于第二象限或第四象限. 故选BD5.设z 是复数,则下列命题中的真命题是( ) A .若z 2≥0,则z 是实数 B .若z 2<0,则z 是虚数C .若z 是虚数,则z 2≥0 D .若z 是纯虚数,则z 2<0 【参考答案】ABD【答案解析】设z =a +bi ,a ,b ∈R ,z 2=a 2﹣b 2+2abi , 对于A ,z 2≥0,则b =0,所以z 是实数,真命题;对于B ,z 2<0,则a =0,且b ≠0,⇒z 是虚数;所以B 为真命题; 对于C ,z 是虚数,则b ≠0,所以z 2≥0是假命题.对于D ,z 是纯虚数,则a =0,b ≠0,所以z 2<0是真命题;故选ABD.6.已知z1与z2是共轭虚数,以下四个命题一定正确的是( )A.z12<|z2|2B.z1z2=|z1z2| C.z1+z2∈R D.∈R【参考答案】BC【答案解析】解:z1与z2是共轭虚数,设z1=a+bi,z2=a﹣bi(a,b∈R).z12<|z2|2;=a2﹣b2+2abi,复数不能比较大小,因此A不正确;z1z2=|z1z2|=a2+b2,B正确;z1+z2=2a∈R,C正确;===+i不一定是实数,因此D不一定正确.故选:BC.7.设复数z满足,则下列说法错误的是( )A.z为纯虚数B.z的虚部为C.在复平面内,z对应的点位于第二象限D.|z|=【参考答案】ABC【答案解析】∵z+1=zi,设z=a+bi,则(a+1)+bi=﹣b+ai,∴,解得.∴z=.∴|z|=,复数z的虚部为,8.某大学进行自主招生测试,需要对逻辑思维和阅读表达进行能力测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示,下列叙述正确的是()A .甲同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前B .乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前C .甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前D .甲同学的总成绩排名比丙同学的总成绩排名更靠前 【参考答案】AC【答案解析】根据图示,可得甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前, 他的阅读表达成绩排名靠后.故选AC.9.在0,0a b >>的条件下,下列四个结论正确的是( )A .22a b aba b+≥+ B .2a b +≤C .22a b a b b a +≤+D .设,,a b c 都是正数,则三个数111,,a b c b c a+++至少有一个不小于2 【参考答案】ABD 【答案解析】选项A:222()4()22022()2()220,0a b ab a b ab a b a b ab a b aba b a b a b a b a b a b++--++-==∴-≥∴≥+++>+>+ ,故本选项是正确的;选项B:因为0,0a b >>,22222222()()02244a b a b a b ab a b ++++--=-=≥,所以2a b +≤,因此本选项是正确的; 选项C:222233222()()()()()a b a b ab a b a b a b a b a b b a a b b a ab ab ab +---+-+-+-+===-,因为0,0a b >>,所以22222()()()0a b b a b a a b a b a b b a ab b a+-+-+=-≤⇒+≥+,因此本选项是不正确的;选项D:根据本选项特征,用反证法来解答.假设三个数111,,a b c b c a+++至少有一个不小于2不成立,则三个数111,,a b c b c a+++都小于2,所以这三个数的和小于6,而111111()(()6a b c a b cb c a a b c+++++=+++++≥++=(当且仅当1a b c===时取等号),显然与这三个数的和小于6矛盾,故假设不成立,即三个数111,,a b cb c a+++至少有一个不小于2,故本选项是正确的.故选:ABD10.如图是国家统计局发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论正确的是()A.2018年3月至2019年3月全国居民消费价格同比均上涨B.2018年3月至2019年3月全国居民消费价格环比有涨有跌C.2019年3月全国居民消费价格同比涨幅最大D.2019年3月全国居民消费价格环比变化最快【参考答案】ABD【答案解析】对于选项A,从图可以看出同比涨跌幅均为正数,故A正确;对于选项B,从图可以看出环比涨跌幅有正数有负数,故B正确;对于选项C,从图可以看出同比涨幅最大的是2018年9月份和2018年10月份,故C错误;对于选项D,从图可以看出2019年3月全国居民消费价格环比变化最快,故D正确.故选ABD.。
高考数学艺考生总复习课件复数、推理与证明

典例变式
变式训练二
1.(2019·合肥模拟)已知 i 为虚数单位,则(2+i2)(-3i-4i) =( A )
A.5
B.5i
C.-75 − 152i
D.-75 + 152i
【解析】
1.法一:(2+i2)(-3i -4i)
=
10-5i 2-i
=5,故选
A.
法二:(2+i2)(-3i -4i)
=
(2+i)2 (3-4i ) (2+i)(2-i)
7.用反证法证明问题的一般步骤
第一步
分清命题“p⇒q”的条件和结论
第二步
作出命题结论 q 相反的假设������q
第三步
由 p 和������q 出发,应用正确的推理方法,推出矛盾结果
第四步
断定产生矛盾结果的原因在于开始所作的假设������q 不真,于是结论 q 成 立,从而间接地证明了命题 p⇒q 为真
典例变式
变式训练三
1.(2019·广州模拟)设z=1+i(i是虚数单位),则复数
2 ������
+z2在复平面内对应的点位于(
A
)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】 因为 z=1+i,所以2������+z2=12+i+(1+i)2=(12+(i1)(-1i)-i)+1+2i+i2=2(12-i)+2i=1+i,
知识梳理
(3)特点:演绎推理是由一般到特殊的推理,直接证明
内容 综合法
分析法
从要证明的结论出发,逐步寻求
《推理与证明》与《复数》
《推理与证明、数系的扩充与复数》zdj18()()()⎧⎪⎪⎨⎪⎪⎩1归纳推理:由某类事物的部分对象具有某些特征推出该类事物的全部对象具有这些特征的推理,合情 或者由个别事实概括出一般结论的推理,即归纳推理是由部分到整体,由个别到一般的推理; 2类比推理:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也推理 具有这些特征的推理,即类比推理是由特殊到特殊的推理;1定义:从一般性的原理出发,推出某个特殊情况下演绎推理推理与证明()()()⎧⎪⎧⎪⎪⎨⎨⎪⎪⎪⎩⎩ 的结论,即演绎推理是由一般到特殊的推理;大前提:已知的一般原理;2三段论模式小前提:所研究的特殊情况;结论:根据一般原理,对特殊情况作出判断;1综合法:一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最 后推导出所要证明的结论成立;2分析法:一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明 证明方法()()()()()()000,1n n n n N n k k n k N n k ++⊗∈⊗=≥∈=+ 的结论归结为判定一个明显成立的条件已知条件、定理、定义、公理等为止;3反证法:一般地,假设原命题不成立即在原命题的条件下,结论不成立,经过正确的推理, 最后得出矛盾,因此说明假设错误,从而证明了原命题成立;应用范围:证明一个与正整数有关的命题;归纳奠基:证明当取第一个值时命题成立;数学步4归纳推理:假设时命题成立,证明当归纳法骤()()02112n n i i ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎧⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎪⎨⎪⎪⎪⎪⎪⎪⎪⊗⎩⎩⎪⎪⎪⎩⎪⊕⎪⎪⎪⎩=-时命题也成立;总结:完成以上两步,就可断定命题对从开始的所有正整数都成立;由合情推理所获得的结论仅仅是一种猜想,未必可靠;演绎推理在大前提、小前提和推理形式都正确 的前提下,得出的结论一定正确;;虚数单位的性质实数可以与之进行四则运算,进复数()(,)(,),0a bi a b R z a bi a b R a b a bi b z a bi b ⎧⎪⎨⎪⎩+∈=+∈+⎫⎧⎫⎧⎪⎪⎪⎪⎨⎬⎛⎫⎪⎪⎪⎪ ⎪⎪⎪=⎩⎨⎬⎭⎝⎭⎪⎪⎫⎧⎪⎪⎨⎬=+⎪⎪⎩⎭⎩⎭行四则运算时,原有的加、乘运算律仍然成立;复数的概念:形如的数叫复数,记作,其中分别叫复数的实部与虚部;循环小数正有理数有理数零整数、有限小数、负有理数无限循环小数实数小数复数正无理数复数的分类:无理数无限不循环小数负无理数虚数()()()()()()()()()()()()00000(,,,)(,),()()a b a b a bi c di a b c d R a c b d z a bi a b R a b a bi c di a c b d i a bi c di ac bd bc ad i a b a bi c di ⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎧=≠⎪≠⎪⎨≠≠⎪⎪⎩⎩+=+∈⇔===+∈←−−−−→+±+=±+±++=-++++÷+=一一对应纯虚数且非纯虚数且复数相等的条件:且;复数的几何意义:复数复平面内的点Z ;加减法:;复数乘 法:;运算法则除 法:()()()()()()()()()441424322330111310111,256n n n n i c di c di i i ii i i i x x z z z R ωωωωωωωωω+++⎧⎪⎪⎨⎪+≠⎪+⎩⎧===-=-⎪⎪=-++====⎪⎨⎪=⇔∈⎪⎪⎩;1任意两个虚数不能比较大小; 2的周期性:;;;;结的性质:若=; ;; 4若,则或; 论; 在复数集中,实系数一元二次方程都有解;7共轭复数:两个复数的实部相等、虚部互为相反数;1题型()⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎩确定复数何时为纯虚数或实数问题:利用复数分类处理;2复数范围内方程根的问题:利用复数相等的条件处理;。
高考数学 推理与证明、数系与复数专题复习课件
2
2
1cos21cos2cos600sin2sin600 sin coscos300sinsin300
2
2
11cos211cos2 3sin2 3sin21cos2
22
24
4
4
4
3右边 4
故 s in 2 c o s 2 3 0 0 s in c o s 3 0 0 3 4
•1、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 •2、知之者不如好之者,好之者不如乐之者。 •3、反思自我时展示了勇气,自我反思是一切思想的源泉。 •4、在教师手里操着幼年人的命运,便操着民族和人类的命运。一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。 •5、诚实比一切智谋更好,而且它是智谋的基本条件。 •6、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之失败。2022年1月2022/1/302022/1/302022/1/301/30/2022 •7、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。2022/1/302022/1/30January 30, 2022 •8、教育者,非为已往,非为现在,而专为将来。2022/1/302022/1/302022/1/302022/1/30
12. 若函数 fxexex,g,x 分 别e计x 算e gx(4)-2f(2)g(2)和
2
2
g(6)-2f(3)g(3)的值,由此归纳出函数f(x)和g(x)的对于所有实数x都成立
的一个等式,并加以证明.
解析 g(4)-2f(2)g(2)=0,g(6)-2f(3)g(3)=0,
由此归纳出g(2x)-2f(x)g(x)=0.
2. 演绎推理 (1)演绎推理:从一般性的原理出发,推出某个特殊情况下的结论,我 们把这种推理称为演绎推理.简言之,演绎推理是由一般到特殊的推理. (2)“三段论”是演绎推理的一般模式,包括: ①大前提——已知的一般原理; ②小前提——所研究的特殊情况; ③结论——根据一般原理,对特殊情况做出的判断.
推理与证明、复数
答题模板
归纳—猜想—证明问题
典例 数列{an}满足Sn=2n-an(n∈N*). (1)计算a1,a2,a3,a4,并由此猜想通项公式an; (2)证明(1)中的猜想.
(1)解
(2)证明 ①当n=1时,a1=1,结论成立.
n 2 -1 3 15 7 a1=1; a2=2;a3=4; a4= 8 . 由此猜想 an= n-1 (n∈N*). 2
Pa Pb Pc + + P到相应三边的距离分别为Pa,Pb,Pc,我们可以得到结论: h a hb hc Pa Pb Pc Pd ha + hb + hc + hd =1 =1.把它类比到空间,则三棱锥中的类似结论为___________________.
解析
设ha,hb,hc,hd分别是三棱锥A-BCD四个面上的高,P为三棱锥
* n ( n + 1)( n + 2)( n + 3)( n + 4)( n ∈ N ) __________________________________. 120
1 n(n+1)(n+2)(n+3)(n+4) 5×4×3×2×1
命题点4 与图形变化有关的推理 典例 (2017· 大连调研)某种树的分枝生长规律如图所示,第1年到第5年 的分枝数分别为1,1,2,3,5,则预计第10年树的分枝数为
2k-1 即 ak= k-1 , ②假设当n=k(k≥1且k∈N*)时,结论成立, 2
k+1 2 + a 2 -1 k ∴2ak+1=2+ak. ∴ak 1= + 2 = 2k .
那么当n=k+1时,ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak=2+ak-ak+1,
∴当n=k+1时,结论成立.
n n
C. q
D. q
2021年高考数学 逻辑 推理 复数教案 苏教版
2021年高考数学 逻辑 推理 复数教案 苏教版一、考纲要求①.复数的概念(B 级)②.复数的四则运算(B 级)③.复数的几何意义(A 级)二、例题分析1.如果复数z 满足|z+i|+|z -i|=2,那么|z+i+1|的最小值是 1 .提示:充分利用数形结合,“|z+i|+|z -i|=2”表示复平面内虚轴上的一条线段,“|z+i+1|”表示复平面内点z 到点-i-1的距离。
变式:|z+i|+|z -i|=4,那么|z+3i|的最小值是 1 .2.若复数2(3)(,()z a a i a R =--+∈为纯虚数,则.提示:为纯虚数的充要条件是,故。
3.设是虚数,是实数,且.则= 1 ,的实部的取值范围.解:设,(,),0z a bi a b R b =+∈≠ 则222211a b w z a bi a b i z a bi a b a b ⎛⎫⎛⎫=+=++=++- ⎪ ⎪+++⎝⎭⎝⎭因为是实数,b ≠0,所以,即= 1 .于是,,,所以的实部的取值范围是.三、巩固练习1. -2 .2.若,则|z|的最大值是 7 .3.已知关于的方程有实根,则实数=.解:设是方程的实根,代入方程得,即()()2220m km m k i ++++=.由复数相等的充要条件得220,20m km m k ⎧++=⎨+=⎩解得或∴方程的实根为,相应的值为.常用逻辑一、考纲要求①.命题的四种形式(A 级)②.充分条件、必要条件、充分必要条件(B 级)③.简单的逻辑联结词(A 级)4.全称量词与存在量词(A 级)二、例题分析1.有下列四个命题:①“若,则互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若,则有实根”的逆否命题; ④“不等边三角形的三个内角相等”逆命题;其中真命题为 ①③ .评析:本题考查了四种命题真值关系,同时注意四种命题的等价关系。
2.若不等式成立的充分条件是,则实数的取值范围是.评析:1.数形结合思想的应用;2.注意集合与充要条件的关系;3.注意充分性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( A) 命题“若 x 2 3x 2 0 则 x 1 ”的逆否命题为:“若 x 1 , 则 x 2 3x 2 0 ”.
(B) “x=1”是“x2-3x+2=0”的充分不必要条件. (C) 若 p q 为假命题,则 p 、 q 均为假命题.
(D) 对于命题 p : x R ,使得 x2 x 1 0 . 则 p : x R ,均有 x2 x 1 0 .
12.下面给出了关于复数的四种类比推理: ①复数的加减法运算可以类比多项式的加减法运算法则; ②由向量 a 的性质|a|2=a2 类比得到复数 z 的性质|z|2=z2;
③方程 ax 2 bx c 0 (a, b, c R) 有两个不同实数根的条件是 b2 4ac 0 可以类
比得到:方程 az 2 bz c 0 (a, b, c C) 有两个不同复数根的条件是 b2 4ac 0 ;
要条件;其中真命题的个数是( ) A.1 B.2 C.3 D.4
14.命题 p:方程 x2-x+a2-6a=0 有一正根和一负根.
命题 q:函数 y=x2+(a-3)x+1 的图象与 x 轴有公共点. 若命题“ p q ”为真命题,而命题“ p q ”为假命题,则实数 a 的取值范围是____
15、观察下列的图形中小正方形的个数,则第 6 个图中有_______个小正方形,第 n 个图中
形 ,依 此 推 断 第 6 件 首饰上应有_______________颗珠宝;则前 n 件 首 饰 所 用 珠 宝 总 数 为
_____________________________颗
17 德国数学家莱布尼兹发现了下面的单位分数三角形 单位分数是分子为 1,分母为正整
数的分数 ,称为莱布尼兹三角形:
35.逻辑与推理
1.已知 a+bi=(1-I)i (a,b∈R)(i 为虚数单位), 则 a,b、的值分别是( )
A.i,-i
B.1,1
C.1,-1
D.i,-1
2..复数 (1 i)(2 i) ( )A.1 3i i
B. 3 i
C. 3 2i
D. 3 i
3.如果复数(m2+I)(1+mi)是实数,则实数 m ( )A.1 B. 1 C. 2 D. 2
10. 已 知 命 题 P : b 0, , f (x) x 2 bx c 在 0, 上 为 增 函 数 , 命 题 Q :
x0 x | x Z, 使 log 2 x0 0 ,则下列结论成立的是( )
A.﹁P∨﹁Q
B.﹁P∧﹁Q C.P∨﹁Q
11.有关命题的说法错.误.的是 (
)
D.P∧﹁Q
④由向量加法的几何意义可以类比得到复数加法的几何意义.
其中类比错误的是 A.①③
B. ②④
C. ①④
D. ②③
13..对任意实数 a,b,c,给出下列命题: ①“ a b ”是“ ac bc ”充要条件;②“ a 5 是无理数”是“a 是无理数” 的充要条件;③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必
C.第三象限
D.第四象限
6.复数 2 i ( i 是虚数单位)的实部为 1 i
7、下列命题正确的是( )(A)、①②③ (B)、①④(C)、②③④ (D)、①③④
①“若 x+y=0,则 x , y 不全为零”的否命题;②“正多边形都相似”的否命题;
③“若 a>1,则 ax2-2(a+1)x+a-3>0> 0 的解集为 R ”的逆命题;
有
________________个小正方形.
16..在一次珠宝展览会上,某商家展出一套珠
宝首饰,第一件首饰是 1 颗珠宝, 第二件首饰
是由 6 颗珠宝(图中圆圈表示珠宝)构成如图
1 所示的正六边形, 第三件首饰如图 2, 第四 图
图
件首饰如图 3, 第五件首饰如图 4, 以 后 每
图
图
件 首 饰 都 在 前 一 件 上 ,按 照 这 种 规 律 增 加 一 定 数 量 的 珠 宝 ,使 它 构 成 更 大 的 正 六 变
1
1 11
22 1111
4 12 12 4
11
1
11
5 20 30 20 5
根据前 5 行的规律,写出第 6 行的数依次是
6. 复数 (1 i )10 的值是( )A.-1 B.1 1 i
C.-32 D.32
4. 复数 z 1 的共轭复数是( 1i
)A. 1 1 i B. 1 1 i C.1 i
22
22
5.在复平面内,复数 i +(1+ 3 i )2 对应的点位于( ) 1 i
D.1 i
A.第一象限
B.第二象限
④“若 a 5 是有理数,则 a 是无理数”的逆否命题。
8.命题:“设 a 、 b 、 c R ,若 ac2 bc2 ,则 a b ”以及它的逆命题、否命题、逆否
命题中,真命题的个数为( )A.0
B.1
C.2
D.3
9. “ sin A 1 ”是“A=30º”的( ) 2
A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件
