黏滞阻尼器初始刚度的合理取值探讨
粘滞阻尼器系数取值范围

粘滞阻尼器系数取值范围全文共四篇示例,供读者参考第一篇示例:粘滞阻尼器是一种常用于减震和减振的装置,其作用是通过在振动系统中引入阻尼力,从而有效消耗振动系统的能量,减少振动的幅度和频率。
粘滞阻尼器的效果主要取决于其阻尼器系数的取值范围,而这个系数的合适取值范围是非常重要的。
粘滞阻尼器系数的取值范围可以分为三种情况:过小、适中和过大。
当阻尼器系数过小时,阻尼器的阻尼效果不明显,振动系统的振幅和频率无法有效降低,导致减振效果不明显,甚至无法达到预期的效果。
当阻尼器系数适中时,阻尼器能够较好地消耗振动系统的能量,使得振动系统的振幅和频率得以有效降低,从而达到良好的减振效果。
而当阻尼器系数过大时,虽然可以有效地减少振动的幅度和频率,但同时也会造成系统能量的过度耗散,使得系统的稳定性变差。
在实际工程中,粘滞阻尼器系数的取值范围需要根据具体的振动系统和工作条件进行合理选择。
一般来说,阻尼器系数的取值范围可以通过试验和仿真来确定。
在试验阶段,可以通过改变阻尼器系数的取值,观察系统的振动响应,并根据减振效果和系统稳定性来确定最佳的阻尼器系数。
在仿真阶段,可以利用建立的数学模型来分析系统的振动特性,结合优化算法来求解最佳的阻尼器系数。
通过以上方法的综合应用,可以得到符合实际工程需求的粘滞阻尼器系数取值范围。
需要注意的是,粘滞阻尼器系数的取值范围并非一成不变的,它受到多种因素的影响。
在不同的振动系统和工作条件下,粘滞阻尼器系数的合理取值范围可能会有所不同。
在实际工程中,需要根据具体情况对粘滞阻尼器系数进行调整,以获得最佳的减振效果。
粘滞阻尼器系数的取值范围在减振工程中起着至关重要的作用。
通过合理选择粘滞阻尼器系数的取值范围,可以有效地减少振动系统的振幅和频率,提高系统的稳定性和安全性,达到减震和减振的目的。
在工程设计和实施过程中,必须对粘滞阻尼器系数的取值范围进行充分的考虑和优化,以确保系统的正常运行和安全性。
【字数2036】第二篇示例:粘滞阻尼器是一种常用于减震和减振系统中的元件,在工程学中扮演着非常重要的角色。
粘滞阻尼器的理论研究及应用进展

粘滞阻尼器的理论研究及应用进展【摘要】本文分析总结了粘滞阻尼器的工作机理、耗能原理,以及国内粘滞阻尼器的研究与应用现状,包括粘滞阻尼材料,粘滞阻尼器的类型、性能和力学模型,粘滞阻尼减震结构的性能、分析模型和设计方法,粘滞阻尼器在工程中的应用状况等。
粘滞阻尼器作为一种被动控制装置,由于能向结构提供较大的阻尼,而且当结构变形最大时,阻尼器提供的控制力为零,从而使结构受力较为合理,因此在国内外得到了广泛的研究和一定的应用。
【关键词】粘滞阻尼器;耗能原理;应用进展一、粘滞阻尼器的工作原理粘滞阻尼器作为一种无需外部能源输入提供控制力的被动控制装置,将地震或风荷载输入结构的大部分能量加以吸收和耗散,从而保护主体结构的性能安全。
粘滞阻尼器具有:?滞回曲线呈饱满的椭圆形,具有很强的耗能能力,即使在微小变形条件下;不对主体结构附加刚度,有效解决阻尼器初始刚度难以与结构侧向刚度相匹配的问题;?采用/柔性耗能0的理念,可减少剪力墙、梁柱配筋的使用数量和构件的截面尺寸,经济性好;?不仅能用于新建土木工程结构的抗震抗风,而且能广泛应用于已有土木工程的抗震加固或震后修复工程之中;?适用性好,且维护费用低等特点,而受到越来越广泛的重视,研究和应用均取得了较快的发展,已经从作为结构附加保护系统的第二道防线发展成为结构构件的一部分,并将逐渐取代传统的结构抗震构件。
(一)粘滞阻尼器的耗能原理粘滞流体在阻尼器机构中流动,与阻尼器结构发生相互作用,使得流体动能转化为热能是粘滞阻尼器耗能的基本原理。
粘滞流体的动能向热能转化是通过摩擦耗能和孔缩效应耗能两方面进行的。
(二)粘滞摩擦耗能由于流体分子间的相互吸引力,使得流体具有内摩擦力从而产生粘度特性;流体的内摩擦力变化规律遵守牛顿内摩擦定律dzdv = (1-1)上式中:摩擦切应力;dzdv:流体的速度梯度; z :为层液厚度;:流体的动力粘度,简称流体粘度。
式(1-1)表明流体内部没有相对运动时,摩擦切应力为零,仅当出现速度梯度时才出现摩擦阻力,并且其大小取决于速度梯度。
高位转换粘滞阻尼减震结构阻尼器合理阻尼系数研究

图1
计算模型
Fig. 1 Calculation models
8]~ [ 13 ] , 将《抗规 》 中的加速度反应谱进行转换 献[ 即: 可得到位移反应谱, 1 T2 Sa ( 6) 2 S a S d = 2 ( 2 π ) ( 1 - ξ2 ) ω (1 -ξ ) 式中: S d 为位移反应谱; S a 为加速度反应谱; ω 为结 构频率; ξ 为结构阻尼。 Sd =
( 1. 广州大学 土木工程学院,广州 510006 ; 2 广州大学 建筑设计研究院,广州 510405 )
摘
《高层建筑混凝土结构技术规程 》 《建筑抗震设计规范》 要: 根据 和 对高位转换结构体系框支层的层间位移和
结构等效侧向刚度的限制要求, 采用等效侧向刚度计算方法, 将高位耗能减震结构分解成框撑剪力墙结构和纯剪力墙结 结合振型分解反应谱理论和线性粘滞阻尼减震结构等效阻尼比计算方法, 推导出高位转换粘滞阻尼减震结构合理阻 构, 尼系数的计算公式。最后, 通过算例分析得出, 采用上述方法计算高位转换粘滞阻尼减震结构粘滞阻尼系数是可行的, 该 方法计算公式简单实用, 可用于高位转换粘滞阻尼减震结构的初步设计 。 关键词: 高位转换耗能减震结构; 粘滞阻尼器; 阻尼系数 中图分类号: TU352. 1 文献标识码: A
基金项目: 国家自然科学基金项目( 50678040 ) ; 广东省自然科学基金团 队 项 目 ( 8351009101000001 ) ; 广 东 省 自 然 科 学 基 金 项 目 ( 8151009101000010 ) 收稿日期: 2009 - 08 - 31 通讯作者 周 修改稿收到日期: 2010 - 01 - 04 1981 年生 第一作者 吴从晓 男, 博士, 1965 年生 云 男, 教授, 博士生导师,
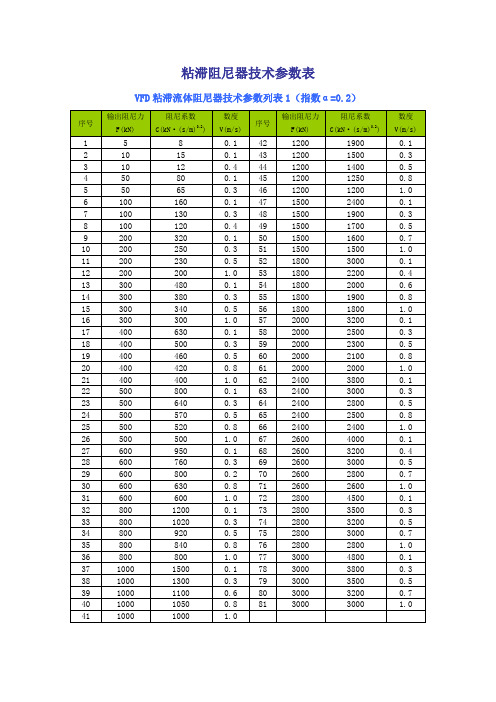
粘滞阻尼器技术参数表
1.0
41
1000
1000
1.0
VFD粘滞流体阻尼器技术参数列表4(指数α=0.35)
序号
输出阻尼力
F(kN)
阻尼系数
C(kN·(s/m)0.2)
数度
V(m/s)
序号
输出阻尼力
F(kN)
阻尼系数
C(kN·(s/m)0.2)
数度
V(m/s)
1
5
10
0.1
42
1200
2700
0.1
2
10
20
0.1
0.5
75
2800
3000
0.8
35
800
850
0.8
76
2800
2800
1.0
36
800
800
1.0
77
3000
6500
0.1
37
1000
2200
0.1
78
3000
4500
0.3
38
1000
1500
0.3
79
3000
3800
0.5
39
1000
1200
0.6
80
3000
3200
0.8
40
1000
1100
0.7
10
200
250
0.3
51
1500
1500
1.0
11
200
230
0.5
52
1800
3000
0.1
12
200
200
1.0
53
1800
粘滞阻尼器系数取值范围

粘滞阻尼器系数取值范围1. 引言1.1 粘滞阻尼器的定义粘滞阻尼器是一种用来减缓或消耗结构振动能量的装置。
它通过内部的粘滞材料或者液体阻尼剂,在结构振动时产生粘滞性阻尼力,从而减小结构的振幅和振动周期。
粘滞阻尼器在提高结构的耐震性能和减小结构疲劳损伤方面有着重要作用。
粘滞阻尼器的设计原理是基于材料内部的粘滞效应,当结构受到外力作用时,材料内部的分子会因受力而发生相对位移,从而消耗一定的能量。
通过合适选择粘滞阻尼器的材料和参数,可以达到控制结构振动的目的。
在工程实践中,粘滞阻尼器常用于桥梁、高层建筑、工业设备等结构的减震设计中。
通过结构动力学分析和优化设计,可以有效提高结构的耐震性能,减少地震带来的损害。
粘滞阻尼器的系数取值范围对结构的实际减震效果起着至关重要的作用,需要根据具体工程要求和结构特点来确定合适的系数取值。
1.2 粘滞阻尼器的作用粘滞阻尼器的作用是通过粘滞力和摩擦力的作用来消耗机械系统的振动能量,从而减小系统的振动幅度和震动频率,达到减震和减振的效果。
粘滞阻尼器能够有效地抑制结构在外力作用下的振动,提高结构的稳定性和安全性。
在工程实践中,粘滞阻尼器常被应用在桥梁、高楼、机械设备等领域,用于减小结构的振动幅度,降低对结构的疲劳损伤,延长结构的使用寿命。
粘滞阻尼器的作用还体现在其对结构的能量耗散和振动频率的抑制上。
它可以将结构振动时产生的机械能转换为热能并耗散掉,从而起到减震的效果。
粘滞阻尼器还可以通过调节其阻尼系数的大小来改变结构的振动特性,降低结构的共振频率,防止共振现象的发生,从而提高结构的抗震能力和稳定性。
粘滞阻尼器在工程实践中具有重要的作用,不仅能够减小结构振动的幅度和频率,提高结构的稳定性和安全性,还能够延长结构的使用寿命,减小结构的维护成本。
在设计工程结构时,应合理选择和配置粘滞阻尼器,以提高结构的整体性能和抗震能力。
2. 正文2.1 粘滞阻尼器系数的影响因素1. 结构参数:粘滞阻尼器的尺寸、形状、材料等结构参数会直接影响其阻尼效果以及阻尼器系数的取值范围。
粘滞阻尼框架结构动力可靠度及参数分析

粘滞阻尼框架结构动力可靠度及参数分析狄生奎;赵子斌;李凯峰【摘要】针对装有粘滞阻尼器的框架结构,建立粘滞阻尼结构的动力方程.利用虚拟激励法和Kanai-Tajimi地震动模型求解出在地震作用下的随机响应.基于随机振动的首次超越破坏理论分析装有粘滞阻尼器结构的可靠度.通过调整不同的支撑刚度和阻尼系数,得出这些参数对粘滞阻尼结构可靠度的影响.【期刊名称】《兰州理工大学学报》【年(卷),期】2014(040)002【总页数】5页(P123-127)【关键词】消能减震;粘滞阻尼器;虚拟激励法;随机地震反应;结构可靠度【作者】狄生奎;赵子斌;李凯峰【作者单位】兰州理工大学土木工程学院,甘肃兰州 730050;兰州理工大学土木工程学院,甘肃兰州 730050;兰州理工大学土木工程学院,甘肃兰州 730050【正文语种】中文【中图分类】TU311.3中国是一个多地震国家,震害严重,且存在着大量未考虑抗震设防和虽考虑抗震设防但仍不能满足现行规范的既有建筑.人们对工程安全的要求和工程抗震标准不断提高,为确保这些建筑的安全使用,就需要对建筑进行抗震加固.探寻实用而有效的抗震加固方法,越来越受到人们的重视.目前既有建筑抗震加固常用方法本质上是增强结构自身的抗震能力,依赖结构本身储存和耗散地震能量.这种“硬碰硬”式的抗震方法,不具备自我调节与自我控制的能力,将使结构产生不同程度的损坏,甚至产生严重破坏或倒塌,造成重大的人员伤亡和经济损失,是一种消极被动的抗震方法.为了满足结构功能和安全性的要求,避免过大的投资.近30多年来,国内外学者提出了结构消能减震体系这个新型的结构体系,并用来解决结构工程中的一系列问题.所谓结构消能减震体系就是通过在结构上安装耗能减震装置减轻或抑制结构由于外荷载作用引起的反应.粘滞阻尼器是为结构体系提供附加阻尼,通过粘滞介质和阻尼器结构部件的相互作用产生阻尼力,达到耗散地震输入能量的目的,保证结构构件安全[1-3].结构消能减震技术是一种积极的、主动的抗震对策,不仅改变了结构抗震的传统概念、方法和手段,而且使得结构的抗震(风)舒适度、抗震(风)能力、抗震(风)可靠性和灾害防御水平大幅度提高.郭安薪等[4]采用等价线性化建立了安装粘弹阻尼器的滞变结构体系在地震作用下的随机响应计算方法,并在此基础上探讨安装粘弹性阻尼器后的结构可靠度.谭平等[5]研究了TMD装置在容许行程范围内风荷载下的动力可靠度;陆立新等[6]提出非线性失效面的重要抽样法,应用于摩擦阻尼器减震结构的分析.杜永峰[7]基于非比例多自由度线性模型运用虚拟激励法研究了小震作用下隔震结构的失效概率.本文应用虚拟激励法计算粘滞阻尼结构的地震反应,与常用的时程分析法计算结果做比较;在此基础上从结构可靠度的角度,分析不同支撑刚度和阻尼系数对装有粘滞阻尼器结构可靠度和地震反应的影响.1 带粘滞阻尼器结构的随机地震响应1.1 粘滞阻尼结构的动力方程假定梁和楼板在平面内刚度无限大,将装有粘滞阻尼器的框架结构看成多自由度层间剪切模型,运动方程为(1)式中:M、K、C分别为质量矩阵、刚度矩阵、阻尼矩阵;F为附加的阻尼力列阵;为地面运动加速度时程;为加速度列阵;为速度列阵;x(t)为位移列阵.楼层由低向高编号,总层数为N,第j层质量为mj,第j层刚度为kj.结构阻尼采用Reyleigh阻尼,对于附加阻尼力列阵F,有式中:注:cj=njCejcos 2θj利用能量相等原理将粘滞阻尼器等效线性化[1]:得其中,1.2 虚拟激励法采用日本学者Kanai-Tajimi提出的平稳过滤白噪声模型,该模型考虑了地表土层特性对地震动频谱特征的影响[8].(2)其中,S是反映地震动强弱程度的谱参数,对于不同场地条件εj、ωg取值不同[8-9].文中利用虚拟激励法[9]将式(2)的功率谱离散化,对每个离散点构造虚拟地面加速度激励:(3)相应的结构虚拟响应量为将式(3)代入式(1),得(4)则结构响应功率谱离散数值解为由于无论在自谱还是互谱计算中,虚拟简谐激励因子eiωt、e-iωt总是成对出现并最终相乘而抵消,因此可以将结构的位移、内力等方便的求出.虚拟激励法的实质就是将平稳随机振动的计算转化为稳态简谐响应计算,将非平稳随机振动的计算转化为普通逐步积分计算,从而实现用最基本的结构动力学方法来处理一般的平稳和非平稳随机响应分析问题,使得该方法既具有功率谱法自动包含参振振型藕合项影响的特点,同时又大大降低计算量.由于对应0均值输入的结构,其响应均值也为0,由维纳-辛钦关系得:(5)2 结构可靠度分析结构受地震作用的动力可靠度分析是典型的基于首次穿越破坏的分析.该问题可转化为楼层位移反应σ(t)在给定的时段[0,T]内一次也不超过给定界限值的概率.本文采用首超变形作为粘滞阻尼结构可靠性分析的破坏准则[10],基于Poisson概率分布假定,假设结构的动力反应首次超越临界值时结构就发生破坏,并采用双侧对称安全界限,结构楼层的可靠度可以表示为(6)式中:T为地震时长;σy,j为位移方差;为速度方差;θe为层间位移限值.由虚拟激励法得到结构的各层位移均方差和速度均方差:结构楼层的失效概率:P2,j=1-P1,j(7)考虑到楼层的失效是由于该层的破坏所引起的,各楼层的失效破坏彼此无关.因此粘滞阻尼结构的失效概率为:(8)3 算例分析某8层框架结构建筑,考虑地震烈度为8度(设计基本地震加速度值为0.2g),Ⅱ类场地,设计地震分组为第三组,各层的质量均为6.17×105 kg,层间刚度分别为4.62×105、3.59×105、3.39×105、3.36×105、3.37×105、3.12×105、3.02×105、2.89×105 kN/m,层高均为3.6 m,混凝土结构阻尼比为0.05.粘滞阻尼器等效线性化后的等效阻尼为2.5×103 kN·s/m.地震动模型参数根据场地类型选取特征阻尼比εj=0.72,场地的特征周期wj=13.96 Rad/s,峰值因子S0=11.106 cm2/s3[11,12].3.1 结构随机响应分析该结构可以看成是多自由度层间剪切模型.由于各层均设置粘滞阻尼器,Ce接近比例阻尼矩阵,利用振型的正交性将其解耦为单自由度体系.首先,将0.2g的ElcentRo地震波的峰值调整为多遇地震,用时程分析法计算.然后,与虚拟激励法的计算结果进行比较,见表1.由表1可以看出:两种方法的计算结果相近,这表明利用虚拟激励法可以进行粘滞阻尼器减震结构的地震反应分析. 采用虚拟激励法,用MATLAB编程分别对非减震结构和减震结构进行随机响应分析,得到位移和速度的响应均方差.表1 时程分析法与虚拟激励法计算的楼层位移Tab.1 Time histoRy analysis and PEM to calculate the FlooR displacement 楼层虚拟激励法/mm时程分析法/mm13.199 82.722 927.147 46.101 3311.008 49.348 7414.468 312.331 7517.396 515.448 1619.914 918.405 6721.752 521.005 6822.758 422.970 3图1 楼层位移Fig.1 FlooR displacement图1为楼层位移.由表1、图1可知:设置粘滞阻尼器后,在地震作用下能有效减小结构的位移响应.其中,楼层位移比原结构减小50%~60%,层间位移比原结构减小50%~60%.这说明粘滞阻尼器支撑可以有效减小结构的地震响应,起到良好的消能减震作用.3.2 结构可靠度分析由层间位移(图2)可知,原结构第二层为薄弱层,层间位移最大,失效概率亦最大.增加粘滞阻尼器后,结构的楼层位移层间位移均明显减小,失效概率亦明显减小.减震结构与原结构的各楼层失效概率见表2,楼层可靠度见图3.地震作用下非减震结构的整体失效概率为99.998%,减震结构的整体失效概率几乎为0,可知设置粘滞阻尼器后能有效地提高结构的抗震性能.图2 层间位移Fig.2 LayeR displacement图3 楼层可靠度Fig.3 FlooR Reliability表2 各楼层与整体系统失效概率对比Tab.2 The contRast oF the FailuRe pRobability oF the FlooR and the whole system楼层非减震结构失效概率%可靠度%减震结构失效概率%可靠度%10.825 60.17440.000 30.999 720.962 80.037 20.006 10.994 030.939 80.060 20.002 30.997 640.839 30.160 70.000 20.999 850.585 40.414 601.000 060.321 60.678 401.000 070.022 80.977 201.000 0801.000 001.000 0整体系统1.000000.008 80.991 23.3 阻尼支撑参数对结构响应的影响影响减震结构随机响应的参数主要是支撑刚度与阻尼系数.粘滞阻尼器对结构不附加刚度,通常与斜撑串联布置在结构的层间.假设周期(表3)和阻尼器系数一定的结构设置粘滞阻尼器后,地震反应降低的原因有两个:1) 考虑支撑附加的刚度使结构的周期缩短;2) 通过粘滞阻尼器增大了结构原来的阻尼比从而吸收了大量的能量.为进一步了解粘滞阻尼器参数对减震结构随机反应和可靠度的影响,在调整不同支撑刚度和阻尼系数的情况下对减震结构进行随机反应和可靠度计算,其结果见图4~9.表3 非减震结构与减震结构的结构自振周期Tab.3 PeRiod oF vibRation oF the dissipation stRuctuRe and common stRuctuRe周期/s非减震结构减震结构11.407 50.717 420.486 80.420 430.300 20.282 4 图4、5为假定阻尼系数不变(C=1 500 kN·s/m)调整支撑刚度对结构楼层位移和速度响应的影响.可以看出:随着支撑刚度的提高,减震结构的楼层位移和速度均减小;当超过38 MN/m后,结构反应的变化趋于平缓.这是由于附加支撑的增加使得减震结构的刚度变大,结构整体的变形能力减小,从而导致结构楼层反应降低. 图4 支撑刚度对结构楼层位移的影响 Fig.4 The inFluence oF bRace stiFFness on the FlooR displacement图5 支撑刚度对结构楼层速度的影响Fig.5 The inFluence oF bRace stiFFness on the FlooR speed图6、7为假定支撑刚度不变(K=30 MN/m)时调整阻尼系数对结构楼层位移和速度响应的影响.可以看出:随着阻尼系数的增大,结构耗能能力增强,减震结构的楼层位移和速度均减小.图6 阻尼系数对结构楼层位移的影响Fig.6 The inFluence oF damping coeFFicient on the FlooR displacement图8、9分别为支撑刚度和阻尼系数对结构楼层失效概率的影响,可以得到以下结论.1) 支撑刚度在5~35 MN/m之间变化时,随支撑刚度的提高,减震结构的楼层失效概率显著降低;当支撑刚度大于38 MN/m时,继续增大支撑刚度,结构的失效概率趋于缓和;此时粘滞阻尼结构的能量消耗将完全由粘滞阻尼耗散.2) 随着阻尼系数的增加,结构的失效概率减小,呈指数变化形式.图7 阻尼系数对结构楼层速度的影响Fig.7 The inFluence oF damping coeFFicient on the FlooR speed图8 支撑刚度对结构失效概率的影响 Fig.8 The inFluence oF bRace stiFFness on the FailuRe pRobability图9 阻尼系数对结构失效概率的影响Fig.9 The inFluence oF damping coeFFicient on the FailuRe pRobability4 结论采用Kanai-Tajimi地震动模型,建立粘滞阻尼结构的动力方程,运用虚拟激励法求解减震结构的随机响应,以层间位移为限基于首次超越破坏理论得出减震结构与非减震结构的可靠度,并且探讨不同支撑刚度和阻尼系数对结构可靠度的影响. 1) 考虑到地震具有随机性,采用随机地震动模型比确定的时程函数能更合理地描述地震随机性;同时通过与时程分析法结果的比较,说明虚拟激励法能有效解决随机响应的问题.2) 基于层间位移首次超越破坏理论,得出装有粘滞阻尼器结构的楼层可靠度以及整体体系可靠度均明显的减小,说明粘滞阻尼减震结构的优越性.3) 探讨不同支撑刚度和阻尼系数对结构地震响应和可靠度的影响,可知在阻尼系数不变的情况下,支撑刚度对减震结构的影响很大.随着支撑刚度的增加,可以明显减小结构的楼层位移,楼层和整体体系失效概率也变小;当增加到一定程度时,结构的楼层位移趋于平缓,楼层和整体体系的失效概率也趋于平缓.在支撑刚度不变的情况下,结构的楼层位移随阻尼系数的增加一直减小,楼层和整体体系的失效概率随阻尼系数的增加而一直减小.4) 由于各层的地震响应不同,导致各层粘滞阻尼器的耗能效果不同.合理的设置支撑刚度和阻尼系数可以有利于粘滞阻尼器充分利用其特性,达到耗能减震的目的;同时各层的耗能能力得到合理的分配,使结构更趋于安全.参考文献:[1] 周云.粘滞阻尼结构减震设计 [M].武汉:武汉理工大学出版社,2006:184-190.[2] SOONG T T, DARGUSH G F.结构工程中的被动消能系统 [M].董平,译.北京:科学出版社,2005.[3] ZHANG R H,SOONG T T.Seismic design oF visco-elastic dampeRs FoR stRuctuRal application [J].JouRnal oF StRuctuRalEngineeRing,1992,18(5):1375-1392.[4] 郭安薪,吴波,徐幼麟.安装粘弹性阻尼器的滞变结构抗震可靠度分析 [J].世界地震工程,2001,17(2):8-13.[5] 谭平,卜国雄,周福霖.带限位TMD的抗风动力可靠度研究 [J].振动与冲击,2009,28(6):42-45.[6] 陆立新,吴斌,欧进萍.摩擦阻尼结构可靠度分析 [J].结构工程师,2009,25(3):80-83.[7] 杜永峰,白莉,夏亚峰,等.小震下隔震结构的随机响应及失效概率分析 [J].兰州理工大学学报,2004,30(6):101-105.[8] 欧进萍,王光远.随机振动 [M].北京:高等教育出版社,1998.[9] 林家浩,张亚辉.随机振动的虚拟激励法 [M].北京:科学出版社,2004.[10] 李桂青,曹宏,李秋胜,等.结构动力可靠性理论及其应用[M].北京:地震出版杜,1993.[11] 薛素铎,王雪生,曹资.基于新抗震规范的地震动随机模型参数研究 [J].土木工程学报,2003,6(5):5-10.[12] 欧进萍,牛荻涛,杜修力.设计用随机地震动的模型及其参数确定 [J].地震工程与工程振动,1991,1(3):45-53.。
粘土的阻尼参数

粘土的阻尼参数全文共四篇示例,供读者参考第一篇示例:粘土是一种常见的土壤类型,具有良好的阻尼特性。
阻尼是指材料吸收和耗散振动能量的能力,能够减少结构振动的幅度和频率。
在地震和风力等外部力的作用下,阻尼参数是很重要的,它影响着结构的动态响应和稳定性。
本文将探讨粘土的阻尼参数,包括影响因素、测试方法和应用。
一、影响因素粘土的阻尼参数受到多种因素的影响,主要包括以下几个方面:1. 土体的孔隙结构:孔隙结构决定了粘土的渗透性和吸水性,进而影响其阻尼性能。
孔隙结构越复杂,粘土的阻尼参数通常越高。
2. 应力水平:粘土在不同应力水平下的阻尼参数可能有所不同。
通常情况下,应力越大,阻尼参数越高。
3. 饱和度:粘土的饱和度是一个重要的影响因子,饱和度越高,阻尼参数通常越大。
4. 粘土类型:不同类型的粘土,其阻尼参数也可能存在差异。
常见的粘土类型包括黏土、壤土和淤泥等。
5. 温度和水分含量:温度和水分含量也会对粘土的阻尼参数产生影响,通常情况下,温度越高、水分含量越大,阻尼参数越高。
二、测试方法粘土的阻尼参数通常通过实验测试来确定,常用的测试方法主要有:1. 固定-自由振动法:这种方法通过给定一个固定的激振力,测量结构的振幅和频率,然后计算出阻尼比等参数。
2. 能量法:这种方法是通过对结构的能量平衡进行分析,从而确定阻尼参数,包括材料的内耗和辐射阻尼等。
3. 频率法:这种方法是通过测量结构在不同频率下的振动响应,从而确定阻尼参数。
三、应用1. 结构抗震设计:阻尼参数是结构抗震设计的重要输入参数,通过合理确定粘土的阻尼参数,可以提高结构的抗震性能。
2. 地基改良:粘土的阻尼参数直接影响地基的稳定性和承载能力,通过改良粘土的阻尼性能,可以改善地基的工程性能。
3. 地震监测:粘土的阻尼参数还可以用于地震监测和预警系统中,为地震灾害预防和减灾提供重要的依据。
粘土的阻尼参数是影响结构动态响应和稳定性的重要因素,通过合理测试和应用,可以有效提高结构的抗震性能和地基的稳定性,为工程实践提供重要的参考依据。
104-粘滞阻尼墙减震机理与参数研究-丁洁民

第二十四届全国高层建筑结构学术会议论文
2016 年
所选地震波频谱分析结果见图 8。分析软件采用 ETABS9.7.4,其中梁、柱采用杆单元模拟,楼板采用膜单 元模拟,粘滞阻尼墙采用基于 Maxwell 模型的 Damper 单元模拟。经过计算,粘滞阻尼墙提供的平均附加 阻尼比为 5.8%。
0.25 0.2 0.15 0.1 0.05 0 0 1 2 3 4 5 6 7 8 9 规范反应谱 7条地震波反应谱均值
第二十四届全国高层建筑结构学术会议论文
2016 年
粘滞阻尼墙减震机理与参数研究
丁洁民 ,陈长嘉 ,吴宏磊 ,王世玉
1,2 1 1 2
(1.同济大学建筑设计研究院(集团)有限公司,上海 200092;2.同济大学土木工程学院,上海 200092)
摘
要: 粘滞阻尼墙是一种性能良好的消能减震部件, 可适用于多层、 高层和超高层建筑结构的抗震和抗风设计。 本文从附加阻尼作用和动刚度作用两个方面阐述了粘滞阻尼墙的减震作用,并通过具体的算例进行验证。 然后分别就阻尼指数和阻尼系数对减震效果的影响进行研究,得到以下结论:当阻尼指数取 0.3~0.5 时, 结构可获得较好的减震效果;而阻尼系数越大,减震效果越好,但相应地对阻尼墙和连接部位的要求更 高。
采用粘滞阻尼墙进行减震,每层 X 向和 Y 向各布置两片阻尼墙,竖向连续布置,共计 112 片,具体 布置如图 7 所示,阻尼墙参数取 C=1000 kN·(s·m-1)0.45,α=0.45。
(a) 平面布置 图 7 粘滞阻尼墙布置示意
(b) 立面布置
选取 7 条地震波 (包括 5 条天然波和 2 条人工波) 对结构进行弹性动力时程分析, 计算结果取平均值,
地震影响系数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黏滞阻尼器初始刚度的合理取值探讨
黏滞阻尼器是一种常用的减震装置,用于减少结构在地震或其他
外部载荷作用下的振动。
其中的初始刚度是一个重要的参数,对于阻
尼器的性能和工作效果具有重要影响。
本文将探讨黏滞阻尼器初始刚
度的合理取值,并对其影响因素进行分析。
首先,需要明确初始刚度的定义。
黏滞阻尼器是一种非线性减震
装置,其初始刚度指的是在阻尼器处于初始状态时,其对结构的刚度。
初始刚度越大,阻尼器对结构的约束作用越强;初始刚度越小,则约
束作用越弱。
那么,黏滞阻尼器初始刚度的合理取值应如何确定呢?其实,初
始刚度的取值是受到多种因素的影响的。
首先,结构的特性是影响初始刚度取值的关键因素之一。
结构的
质量、刚度、自振周期等参数会影响到阻尼器的使用效果,因此在确
定阻尼器的初始刚度时,需要充分考虑结构的特性。
其次,考虑到地震等外部载荷的作用,初始刚度的取值也需要考
虑到实际的工程要求。
对于不同的结构和工程要求,其初始刚度的合
理取值也会有所不同。
另外,材料的选择也对初始刚度的取值有一定影响。
不同的材料
具有不同的刚度和耐久性,因此在选择适合的材料时,也需要考虑到
材料的特性对初始刚度的影响。
此外,还需要考虑到阻尼器的参数调节范围。
在实际工程中,由
于不同结构的要求不同,对于黏滞阻尼器的初始刚度可能有一定的调
节需求,因此需要考虑到阻尼器的参数调节范围对初始刚度取值的影响。
在确定黏滞阻尼器初始刚度的合理取值时,还需要综合考虑以上
因素,并采取合适的工程方案进行调整。
需要注意的是,初始刚度的
取值不宜过大或过小,过大会导致结构的刚度增加过快,影响结构的
柔韧性;过小则会导致阻尼器的约束作用不足,阻尼效果不佳。
在实际工程中,通常可以通过有限元分析等方法对初始刚度进行
调试和优化,以保证其能够满足结构的要求,并提高结构的减震效果。
综上所述,黏滞阻尼器初始刚度的合理取值是受多种因素的影响的,需要综合考虑结构特性、工程要求、材料选择和参数调节范围等因素。
通过科学合理的方法确定初始刚度的取值,可以保证黏滞阻尼器的减震效果和工作性能,并提高结构的抗震能力。
