多元统计分析第7章作业题选讲
多元统计分析-对应分析

03
列联表检验的零假设是两变量 X和Y 相互独立,计算一个卡方统计量,与列联表中频数取值 和零假设下期望取值之差有关,当卡方 很大时否定零假设。
BA
患慢性支 未患慢性 气管炎 支气管炎
吸烟
43
162
不吸烟
13
121
为了探讨吸烟与慢性支气管炎有无关系, 调查了339人,情况如表所示:
设想有两个随机变量A,B:A:1表示吸 烟,
对应分析
对应分析基本步骤: 建立列联表
利用对应图解释结 果。
1
2
3
一.获取对应分析 数据 确定研究目的, 选择对应分析 所需数据,应 该包括的背景 资料。
对应分析
4
5
二、对应分析 的原理
01
由于R型因子分析和 02
设原始数据矩阵为:
Q型因子分析是反映
一个整体的不同侧面,
R型因子分析是从列
来讨论(对变量),
k
特征根。
Zu k
设 1 2…
三、对应图u 1u 11u 21 A和l(0Bu <的p 1 i<非m零in特(n征,p根)),为其矩相阵应 u 2u 12u 22 的特征u p 向2量为
v 1 v 1 1v 2 1 v n 1 v 2 v 1 2 v 2 2 v n 2
我们知道因子载荷矩阵的含义是原始变量与公共因子之间的 相关系数,所以如果我们构造一个平面直角坐标系,将第一 公共因子的载荷与第二个公共因子的载荷看成平面上的点, 在坐标系中绘制散点图,则构成对应图。
Q型因子分析是从行
来讨论(对样品),
因此 在的
他们之
联 x系1。1
间
存在
x12
内
应用多元统计分析课后习题答案高惠璇第七章习题解答

7-4 设总体X=(X1,…,Xp)′~Np(μ,Σ) (Σ>0),等概率密度
椭球为
(X-μ)′Σ-1(X-μ)=C2(C为常数).
试问椭球的主轴方成分分析
7-5 设3维总体X的协差阵为
试求总体主成分.
4 0 0
0 4 0
0 0 2
解:总体主成分为
Zi Xi(i1,2,3)
1
1
(2) 求X
(3) 试问当ρ取多大时才能使第一主成分的贡献率达95%以上.
解:
5
第七章 主成分分析
6
第七章 主成分分析
7-3 设p维总体X的协差阵为
21
1
1
(01).
(1)
Z1 1p(X1X2Xp);
(2) 试求第一主成分的贡献率.
7
第七章 主成分分析
解:
1
8
第七章 主成分分析
2
12
13 14
12 2
14 13
13 14 2
12
14
13
12 2
,
其中 1 21 31,421 4 21.3
试求X的主成分.
12
第七章 主成分分析
解:
13
第七章 主成分分析
7-8
14
第七章 主成分分析
15
第七章 主成分分析
7-9
16
第七章 主成分分析
主成分向量为
Z ( X 1 ,X 2 ,X 3 ) 或 Z ( X 2 ,X 1 ,X 3 )
三个主成分的方差分别为4,4,2.
10
第七章 主成分分析
7-6
设3维总体X的协差阵为
2 2
2 2
多元统计分析第七章主成分分析习题答案

7.1 设随机变量12X(X ,X )'=的协差阵为21,12⎡⎤∑=⎢⎥⎣⎦试求X的特征根和特征向量,并写出主成分。
解:先求X的特征根λ,λ满足方程:21012-λ=-λ,即2(2)10-λ-=,因此两个特征根分别为123, 1.λ=λ=设13λ=对应的单位特征向量为()1121a ,a ',则()1121a ,a '满足:1121a 110a 110-⎛⎫⎡⎤⎛⎫= ⎪ ⎪⎢⎥-⎣⎦⎝⎭⎝⎭,故可以取1121a a ⎛⎛⎫ = ⎪ ⎝⎭ ⎝,其对应主成分为:112F X X 22=+;设21λ=对应的单位特征向量为()1222a ,a ',则()1222a ,a '满足:1222a 110a 110⎛⎫⎡⎤⎛⎫=⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭,故可以取1222a a ⎛⎫⎛⎫ ⎪= ⎪ ⎝⎭- ⎝,其对应的主成分为:212F 22=-.7.2设随机变量123X (X ,X ,X )'=的协差阵为120250,002-⎡⎤⎢⎥∑=-⎢⎥⎢⎥⎣⎦试求X的主成分及主成分对变量X的贡献率。
解:先求X的特征根λ,λ满足方程:12025002-λ---λ=-λ,即()2(2)610-λλ-λ+=,因此三个特征根分别为1235.8284,2,0.1716λ=λ=λ=设1 5.8284λ=对应的单位特征向量为()112131a ,a ,a ',则它满足:1121314.828420a 020.82840a 000 3.8284a 0--⎡⎤⎛⎫⎛⎫⎪ ⎪⎢⎥--=⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥-⎣⎦⎝⎭⎝⎭,故可以取 112131a 10.38271a 2.41420.92392.6131a 00⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,其对应主成分为: 112F 0.3827X 0.9239X =-,其贡献率为5.828472.86%5.828420.1716=++;设22λ=对应的单位特征向量为()122232a,a ,a ',则它满足:122232120a 0230a 0000a 0--⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥-= ⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭,故可以取122232a 0a 0a 1⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其对应主成分为: 23F X =,其贡献率为225%5.828420.1716=++;设30.1716λ=对应的单位特征向量为()132333a ,a ,a ',则它满足:1323330.828420a 02 4.82840a 000 1.8284a 0-⎡⎤⎛⎫⎛⎫⎪ ⎪⎢⎥-=⎪ ⎪⎢⎥ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭,故可以取132333a 10.92391a 0.41420.38271.0824a 00⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,其对应主成分为: 312F 0.9239X 0.3827X =+,其贡献率为0.17162.14%5.828420.1716=++.7.3 设随机变量12X (X ,X )'=的协差阵为14,4100⎡⎤∑=⎢⎥⎣⎦试从∑和相关阵R出发求出总体主成分,并加以比较。
应用多元统计第七章实验题答案
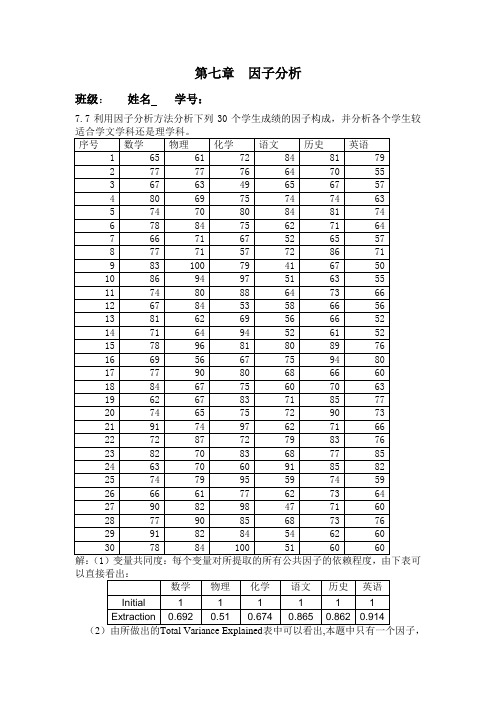
第七章因子分析班级:姓名学号:7.7利用因子分析方法分析下列30个学生成绩的因子构成,并分析各个学生较(2则由上表可写出每个原始变量的因子表达式:X1=-0.662F1+0.503F2;X2=-0.53F1+0.478F2;X6=0.816F1+0.498F2;(4)由Rotated Component Matrix表可以给出旋转后的因子载荷矩阵(见下表),第一个公共因子在指标语文、历史、英语上有较大的载荷,说明这三个指标有较强的相关性,可以归为一类,从分科情况来看,这三个指标属于学生较适合学文学科;第二个公共因子在指标为数学、物理、化学上有较大载荷,同样可以归为一类,这三个指标同属于学生较适合学理科。
(5)根据因子得分系数矩阵与原始变量的标准化值可以计算每个观测值的各F1=F2=0.439X1+0.4X2+0.484X3-0.01X4+0.073X5+0.169X6;则将学生成绩按顺序对应分别带入上面两个式子可以判定,当F1>F2时,该学生适合学文科,当F1<F2时,该学生适合学理科。
24、26的学生适合学文科;学生标号为:2、6、7、9、10、11、13、14、17、18、21、25、27、28、29、30的学生适合学理科。
7.8某汽车组织欲根据一系列指标来预测汽车的销售情况,为了避免有些指标之间的相关关系影响预测结果,须首先进行因子分析来简化系统。
下表是抽查欧洲某汽车市场7个品牌不同型号的汽车的各种指标数据,试用因子分析法找出其简X1=0.794F1;X2=0.879F1;X9=-0.893F1;(4)因为只有一个因子,因此不能被旋转。
(5)根据因子得分系数矩阵与原始变量的标准化值可以计算每个观测值的各因子的得分数,则根据下表可得出该题中的因子得分表达式即为所求的指标系统为:27X8-0.132X9。
7.10 根据习题5.11中2003年我国省会城市和计划单列城市的主要经济指标数据,利用因子分析法对其进行排序和分类,并与聚类分析的结果进行比较。
应用多元统计分析习题解答 第七章讲解学习

应用多元统计分析习题解答第七章第七章 因子分析7.1 试述因子分析与主成分分析的联系与区别。
答:因子分析与主成分分析的联系是:①两种分析方法都是一种降维、简化数据的技术。
②两种分析的求解过程是类似的,都是从一个协方差阵出发,利用特征值、特征向量求解。
因子分析可以说是主成分分析的姐妹篇,将主成分分析向前推进一步便导致因子分析。
因子分析也可以说成是主成分分析的逆问题。
如果说主成分分析是将原指标综合、归纳,那么因子分析可以说是将原指标给予分解、演绎。
因子分析与主成分分析的主要区别是:主成分分析本质上是一种线性变换,将原始坐标变换到变异程度大的方向上为止,突出数据变异的方向,归纳重要信息。
而因子分析是从显在变量去提炼潜在因子的过程。
此外,主成分分析不需要构造分析模型而因子分析要构造因子模型。
7.2 因子分析主要可应用于哪些方面?答:因子分析是一种通过显在变量测评潜在变量,通过具体指标测评抽象因子的统计分析方法。
目前因子分析在心理学、社会学、经济学等学科中都有重要的应用。
具体来说,①因子分析可以用于分类。
如用考试分数将学生的学习状况予以分类;用空气中各种成分的比例对空气的优劣予以分类等等②因子分析可以用于探索潜在因素。
即是探索未能观察的或不能观测的的潜在因素是什么,起的作用如何等。
对我们进一步研究与探讨指示方向。
在社会调查分析中十分常用。
③因子分析的另一个作用是用于时空分解。
如研究几个不同地点的不同日期的气象状况,就用因子分析将时间因素引起的变化和空间因素引起的变化分离开来从而判断各自的影响和变化规律。
7.3 简述因子模型中载荷矩阵A 的统计意义。
答:对于因子模型1122i i i ij j im m i X a F a F a F a F ε=++++++ 1,2,,i p =因子载荷阵为11121212221212(,,,)m m m p p pm a a a aa a A A A a a a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦Ai X 与j F 的协方差为:1Cov(,)Cov(,)mi j ik k i j k X F a F F ε==+∑=1Cov(,)Cov(,)mik k j i j k a F F F ε=+∑=ij a若对iX作标准化处理,=ija,因此ija一方面表示iX对jF的依赖程度;另一方面也反映了变量i X对公共因子jF的相对重要性。
最新应用多元统计分析课后习题答案高惠璇PPT课件

(2) 考虑随机变量Y= X1-X2 ,显然有
YX 1X2 0 X 1X 1,当 估计
P{Y0}P{X11或 X11} P{X11}P{X11} (X1~N(0,1)) 2(1)0.317 04
若(X1 , X2 ) 是二元正态分布,则由性质4可知,
31
第三章 多元正态总体参数的检验
证明 记rk(A)=r.
若r=n,由AB=O,知B= On×n,于是 X′AX与X′BX
若r=0时,则A=0,则两个二次型也是独 立的.
以下设0<r<n.因A为n阶对称阵,存在正 交阵Γ,使得
32
第三章 多元正态总体参数的检验
其中λi≠0为A的特征值(i=1,…,r).于是
P { X 2 x } P { X 1 x } ( x )
当x≥1时, P{X2x}
P{X2 1}P{1X2 1}P{1X2 x}
P{X11}P{1X11}P{1X1x}
P{X1x}(x) 17
第二章 多元正态分布及参数的估计
当-1≤x≤1时,
P{X2 x}P{X2 1}P{1X2 x} P{X1 1}P{xX1 1} P{X1 1}P{1X1 x} P{X1 x}(x)
它的任意线性组合必为一元正态. 但Y= X1-X2 不是正态分布,故(X1 , X2 ) 不是二元正态分布.
19
第二章 多元正态分布及参数的估计
2-17 设X~Np(μ,Σ),Σ>0,X的密度函数记为 f(x;μ,Σ).(1)任给a>0,试证明概率密度等高面
f(x;μ,Σ)= a
是一个椭球面. (2) 当p=2且
比较上下式相应的系数,可得:
1
2 2
2
1 2
应用多元统计分析习题解答_因子分析

第七章 因子分析7.1 试述因子分析与主成分分析的联系与区别。
答:因子分析与主成分分析的联系是:①两种分析方法都是一种降维、简化数据的技术。
②两种分析的求解过程是类似的,都是从一个协方差阵出发,利用特征值、特征向量求解。
因子分析可以说是主成分分析的姐妹篇,将主成分分析向前推进一步便导致因子分析。
因子分析也可以说成是主成分分析的逆问题。
如果说主成分分析是将原指标综合、归纳,那么因子分析可以说是将原指标给予分解、演绎。
因子分析与主成分分析的主要区别是:主成分分析本质上是一种线性变换,将原始坐标变换到变异程度大的方向上为止,突出数据变异的方向,归纳重要信息。
而因子分析是从显在变量去提炼潜在因子的过程。
此外,主成分分析不需要构造分析模型而因子分析要构造因子模型。
7.2 因子分析主要可应用于哪些方面?答:因子分析是一种通过显在变量测评潜在变量,通过具体指标测评抽象因子的统计分析方法。
目前因子分析在心理学、社会学、经济学等学科中都有重要的应用。
具体来说,①因子分析可以用于分类。
如用考试分数将学生的学习状况予以分类;用空气中各种成分的比例对空气的优劣予以分类等等②因子分析可以用于探索潜在因素。
即是探索未能观察的或不能观测的的潜在因素是什么,起的作用如何等。
对我们进一步研究与探讨指示方向。
在社会调查分析中十分常用。
③因子分析的另一个作用是用于时空分解。
如研究几个不同地点的不同日期的气象状况,就用因子分析将时间因素引起的变化和空间因素引起的变化分离开来从而判断各自的影响和变化规律。
7.3 简述因子模型中载荷矩阵A 的统计意义。
答:对于因子模型1122i i i ij j im m i X a F a F a F a F ε=++++++ 1,2,,i p =因子载荷阵为11121212221212(,,,)m m m p p pm a a a a a a A A A a a a ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦Ai X 与j F 的协方差为:1Cov(,)Cov(,)mi j ik k i j k X F a F F ε==+∑=1Cov(,)Cov(,)mikk j i j k aF F F ε=+∑=ij a若对i X 作标准化处理,=ij a ,因此 ij a 一方面表示i X 对j F 的依赖程度;另一方面也反映了变量iX对公共因子jF的相对重要性。
应用多元统计分析课后习题答案高惠璇第七章习题解答-20页PPT精选文档

解:
9
第七章 主成分分析
7-5 设3维总体X的协差阵为
试求总体主成分.
4 0 0
0 4 0
0 0 2
解:总体主成分为
Zi Xi(i1,2,3)
主成分向量为
Z ( X 1 ,X 2 ,X 3 ) 或 Z ( X 2 ,X 1 ,X 3 )
三个主成分的方差分别为4,4,2.
(01).
(1)
Z1 1p(X1X2Xp);
(2) 试求第一主成分的贡献率.
7
第七章 主成分分析
解:
1
8
第七章 主成分分析
7-4 设总体X=(X1,…,Xp)′~Np(μ,Σ) (Σ>0),等概率密度
椭球为
(X-μ)′Σ-1(X-μ)=C2(C为常数).
试问椭球的主轴方向是什么?
14 13
13 14 2
12
14
13
12 2
,
其中 1 21 31,421 4 21.3
试求X的主成分.
12
第七章 主成分分析
解:
13
第七章 主成分分析
7-8
14
第七章 主成分分析
15
第七章 主成分分析
7-9
16
其中ρ为X1和X2的相关系数(ρ>0). (1) 试从Σ出发求X
1
1
(2) 求X
(3) 试问当ρ取多大时才能使第一主成分的贡献率达95%以上.
解:
5
第七章 主成分分析
6
第七章 主成分分析
7-3 设p维总体X的协差阵为
21
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对应分析与因子分析的关系是: 在进行相应分析过程中, 计算出过渡矩阵后,要分别对变量和样本进行因子分析。因 此,因子分析是对应分析的基础。具体而言, 式表明Zuj为相对于特征值 的关于因素A各水平构成的协 差阵 的特征向量。从而建立了对应分析中R型因子分析 和Q型因子分析的关系。
多元统计分析
7.2 试述对应分析的基本思想。 答:对应分析,是指对两个定性变量的多种水平进行分析。 设有两组因素A和B,其中因素A包含r个水平,因素B包含c 个水平。对这两组因素作随机抽样调查,得到一个 的二维 列联表,记为 。要寻求列联表列因素A和行因素B的基本分 析特征和最优列联表示。相应分析即是通过列联表的转换, 使得因素A 和因素B具有对等性,从而用相同的因子轴同时 描述两个因素各个水平的情况。把两个因素的各个水平的状 况同时反映到具有相同坐标轴的因子平面上,从而得到因素 A、B的联系。
多元统计分析
7.3 试述对应分析的基本步骤。
答: (1)建立列联表 设受制于某个载体总体的两个因素为 A 和 B , 其中因素 A 包含 r 个水平, 因素 B 包含 c 个 水平。对这两组因素作随机抽样调查,得到一个 r c 的二维列联表,记为
K (kij )rc
。
(2)将原始的列联资料 K=(kij) r c 变换成矩阵 Z=(zij) r c,使得 zij 对因素 A 和列因素 B 具 有对等性。通过变换 (3)对因素 B 进行因子分析。 计算出 Σc Z Z 的特征向量 计算出因素 B 的因子 及其相应的特征向量 ) 。得 Σc Z Z , Σr ZZ 。
手术 处理 医院
综合征 无 有
无 有 无 有 无 有
1 23 9
23 15 20 18 9 17
3 8 9
12 8 11 8 7 11
4 12 10
15 5 14 11 13 10
A
B C D
多元统计分析
7.1 什么是对应分析?它与因子分析有何关系?
答:对应分析也叫相应分析,通常意义下,是指两个定性变 量的多种水平进行相应性研究。其特点是它所研究的变量可 以是定性的。
多元统计分析
7.4 费希尔研究头发颜色与眼睛颜色的关系,抽查了5387 人的资料如下表,试对其进行对应分析。
眼睛 颜色 蓝色 淡蓝 浅蓝 深蓝 合计 头发颜色 金黄色 326 688 343 98 1455 红色 3 116 84 48 286 褐色 241 584 909 403 2137 深红 110 188 412 681 1391 黑 3 4 26 85 118 合计 718 1580 1774 1315 5387
多元统计分析
第7章作业题:
7.1 什么是对应分析?它与因子分析有何关系? 7.2 试述对应分析的基本思想。 7.3 试述对应分析的基本步骤。 7.4 费希尔研究头发颜色与眼睛颜色的关系,抽查了5387 人的资料如下表,试对其进行对应分析(上机练习)。
眼睛 颜色
蓝色 淡蓝 浅蓝
头发颜色
金黄色 326 688 343 红色 3 116 84 褐色 241 584 909 深红 110 188 412 黑 3 4 26 合计 718 1580 1774
多元统计分析
(4)对因素 A 进行因子分析。 计算出 Σr ZZ 的特征向量 计算出因素 A 的因子 (5)选取因素 B 的第一、第二公因子 将 B 因素的 c 个水平 , , 选取因素 A 的第一、第二公因子 , , A 因素的 r 个水平 及其相应的特征向量
,同时反应到相同坐标轴的因子平面上。 (6)根据因素 A 和因素 B 各个水平在平面图上的分布,描述两因素及各个水平之间的相关 关系。
多元统计分析
输入的 SPSS数据 集如右图 所示:
多元统计分析
进行 对应 分析 输出 对应 关系 图如
右图 所示:
深蓝
合计
98
1455
48
286
403
2137
681
1391
85
118
1315
5387
多元统计分析
7.5 进行十二指肠溃疡手术,有时存在不良的综合征。下面的数据给出的 是在四个医院中进行手术,依不同的手术处理给出的统计,其中不同的手 术处理为: A. 引流和迷走神经切除;B. 25%的切除和迷走神经切除; C. 50%的切除和迷走神经切除; D. 75%的切除。 试对数据进行对应分析,研究医院和手术处理类型的关系(上机练习) 。
