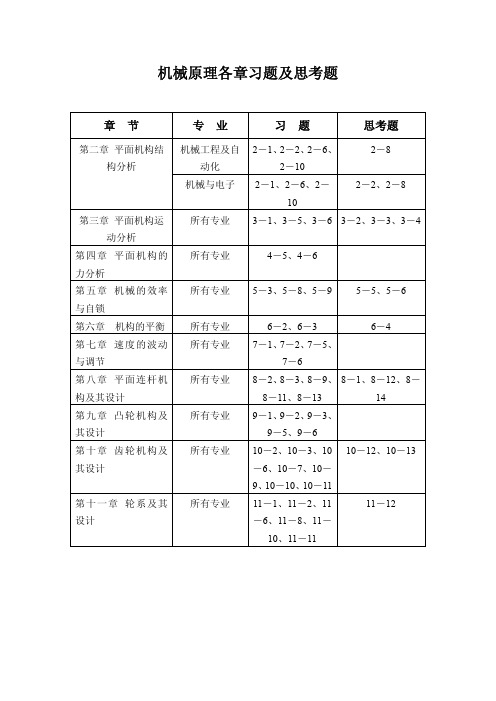
第11章齿轮系及其设计
《机械原理》课程思政的教学设计——以周转轮系的传动
要教师仔细考虑如何有效管理课堂、如何取舍课堂教学
内容、如何讲授课堂教学内容、如何有技巧地融入思政
内容。比如，需要对知识点进行深入梳理，采用合适方
法将知识点贯穿在知识创新的骨架上；需要以具体教学
内容为载体，采用合适方法引导学生发现问题、分析问
题，增强创新意识，激发探究新知识的兴趣；可以尝试结
动比。
结合以上重难点，在授课过程中要时刻观察学生掌
握程度，据此调整讲解速度；要经常设问，加强与学生互
动，必要时就所提问题要求学生分小组讨论；同时周转
轮系的运动要通过播放动画或者实物演示，加深学生的
理解。
5 “周转轮系的传动比”的思政点融入
在学习“周转轮系的传动比”之前，学生已经学会了
定轴轮系传动比的计算方法，以此为前提，
Copyright©博看网. All Rights Reserved.
· 131 ·
2023 年第 08 期
总第 315 期
《机械原理》课程具备理论性和实践性的特点。理
论性的特点要求学生在学习过程中要充分借鉴前面学
习过的《高等数学》《机械制图》《理论力学》等理论知识。
实践性的特点指本课程实验较多，要求学生独立完成以
之渗入教学内容中，对培养学生“思政”素质，实现全过
程育人具有重要意义。
2 机械原理课程简介
于课时少等原因，基本上只是知识点的讲授，很少涉及
《机械原理》课程的内容包括两部分：机构学部分和
思政内容。即便有些教师在课堂教学过程中设计了思
机械动力学部分［7］。机构学部分由机构的结构和运动
政元素，如果思政内容不能与课程内容很好的结合，由
的掌握似是而非，甚至对有些基本概念（机械学科中的
机械原理第十一十二章
周转轮系的传动比(2/2)
ω ω i =ω =ω ω ω
H m H n H m系中由m至n各从动轮齿数的乘积 在转化轮系中由m至n各主动轮齿数的乘积
式中“±”号应根据其转化轮系中m、n两轮的转向关系来确定。 而ωm、ωn、ωH均为代数值，在使用时要带有相应的“±”号。 而差动轮系的传动比就可根据已确定出的ωm、ωn、ωH大小直 接求得。 3．行星轮系的传动比 由于具有固定太阳轮的周转轮系必定为行星轮系，故行星轮 系传动比的一般表达式为
第十一章
§11-1 §11-2 §11-3 §11-4 §11-5 §11-6 §11-7 *§11-8
齿轮系及其设计
齿轮系及其分类 定轴轮系的传动比 周转轮系的传动比 复合轮系的传动比 轮系的功用 行星轮系的效率 行星轮系的类型选择及设计的基本知识 其他新型行星齿轮传动简介 返回
§11-1 齿轮系及其分类
§12-4 凸轮式间歇运动机构
1．机构的工作原理及特点 （1）工作原理 由主动轮和从动盘组成，主动凸轮作连续转动，通过其凸轮 廓线推动从动盘作预期的间歇分度运动。 （2）工作特点 动载荷小，无刚性和柔性冲击，适合高速运转，无需定位装 置，定位精度高，结构紧凑； 但加工成本高，装配与调整的要求。
凸轮式间歇运动机构(2/2)
§12-3 擒纵轮机构
1．擒纵轮机构的组成及工作原理 （1）机构的组成 由擒纵轮、擒纵叉、游丝摆轮及机 架组成。 （2）工作原理 擒纵轮受发条驱动而转动，同时受 擒纵叉上的左右卡瓦阻挡而停止，并通 过游丝摆轮系统控制动停时间，从而实 现周期性单性间歇运动。 游丝摆动系统是由游丝、摆轮及圆 销、擒纵叉及叉头钉等组成。其能量的 补充是通过擒纵轮齿顶斜面与卡瓦的短 暂接触传动来实现的。
西工大教材-机械原理各章习题及答案
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中，设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下（反行程），此斜面 机构的临界自锁条件和在此条件下正行程（在 F 力作用下）的效率。 解 1）反行程的自锁条件 在外行程（图 a），根据滑块的平衡条件：
解 1 ） 取 比 例 尺 μ 1 ＝ 1mm/mm 绘 制 机 构 运 动 简 图 （ 图 b ）
(a)
2 ）计算该机构的自由度
n=7
pι=9
ph=2（算齿轮副，因为凸轮与齿轮为一体） p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构；图 b 为凸轮一连杆组合 机构（图中在 D 处为铰连在一起的两个滑块）；图 c 为一精压机机构。并问在图 d 所示机构中， 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同？为什么？
C3 重合点继续求解。
解 1）速度分析（图 b）取重合点 B2 与 B3，有
方向 大小 ？
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B（B1、B2、B3）
ω1
A1 ϕ = 90°
§11—1轮系及分类
三、轮系的传动比(Transmission Ratio)
一对齿轮的传动比：是指两轮的角速度或转速之比，即 i12=ω1 /ω2= n1 /n2 = z2 /z1。 轮系的传动比：是指轮系中的输入轴（首构件）和输出轴 （末构件）的角速度或转速之比。
计算轮系传动比时，包括： 1）计算轮系传动比的大小； 2）确定输入轴（首构件）和输出轴（末构件）的转 向关系。 下面来介绍各种轮系的传动比的计算，这是这章的重点。
▲ 单一的定轴轮系或周转轮系称为基本轮系。
图11-3
3、复合轮系(Combined Gear Train) ： 由定轴轮系和周转轮系组成或由几个周转轮系组成的 轮系。 如图11-4的轮系：定轴轮系和周转轮系； 如图11-5的轮系：2个周转轮系（每一个行星架对应于一 个周转轮系）。
图11-4
图11-5
H2 1ຫໍສະໝຸດ Oω3 ωH ω1
2
H
3
O
1
3
齿轮2一方面绕自己的轴线O1O1回转，另一方面又随 着构件H一起绕固定轴线OO回转，就象行星的运动一样，
兼有自转和公转，故称齿轮2为行星轮；
装有行星轮2的构件H称为行星架（转臂或系杆）。 ∴ 1个周转轮系=1个行星架+1个（或几个）行星轮 +1~2个太阳轮
其中：太阳轮和行星架常作为运动的输入和输出构件，称
自由度F=1，原动件数为1，其中有一个太阳轮被固定。
H
2 1
O
3
图11-2 b）
2）周转轮系根据基本构件的不同，可分为： （太阳轮用K表示，行星架用H表示） 2K-H型（图11-2）：基本构件是2个太阳轮，1个行星架。 实际机械中用得较多。 3K型（图11-3）：基本构件是3个太阳轮，H只起支持行 星轮的作用，不是输入输出构件。
机械原理 轮系
i= 14
z2z3z4 z1z2' 3' z
传动比方向判断： 传动比方向判断：画箭头 传动比大小表示： 传动比大小表示：在传动比大小前加正负号
§11-3 周转轮系的传动比 11一、周转轮系传动比计算原理 1.反转法 1.反转法——转化轮系 反转法 转化轮系
给整个轮系加上一个假想的公共角速度(-wH)，据相对 的公共角速度( 运动原理，各构件之间的相对运动关系并不改变，但此 运动原理，各构件之间的相对运动关系并不改变， 时系杆的角速度就变成了wH-wH=0，即系杆可视为静止不 =0， 动。于是，周转轮系就转化成了一个假想的定轴轮系— 于是，周转轮系就转化成了一个假想的定轴轮系— —周转轮系的转化机构。 周转轮系的转化机构。
z5 L ⇒ω3 = − ω5 L (2) z3′
3）联立(1)、(2)求解 联立(1)、(2)求解 (1)
z ω1 z2 z3 1 + 5 + 1 ⇒ i15 = = ω5 z1 z2′ z3′
33× 78 78 = 1+ +1 = 28.24 24 × 21 18
-ω H
ωH
ω H - ω H=0
周转轮系 假想定轴轮系
转化轮系
指给整个 周转轮系加上 一个“ 的 一个“-wH”的 公共角速度， 公共角速度， 使系杆H变为 相对固定后， 相对固定后，
原轮系
所得到的假想 转化轮系 的定轴轮系。 的定轴轮系。
2. 转化轮系中各构件的角速度
3. 转化轮系的传动比
在运动简图上用箭头标明两轮的转向关 在运动简图上用箭头标明两轮的转向关 箭头标明 系。
大小： 大小：
ω 从动齿轮齿数连乘积 1 = i1k = ωk 主动齿轮齿数连乘积
河北科技大学机械原理习题
第二章机构的结构分析2-1 构件是＿＿＿＿的单元体；零件是＿＿＿＿的单元体。
2-2 使两构件＿＿＿＿又能产生＿＿＿的联接，称为运动副。
2-3 据运动副中两构件接触形式不同，运动副可分为＿＿＿副和＿＿＿副。
2-4 两构件相对运动情况，常用的低副有＿＿＿、＿＿＿。
2-5 两构件相对运动情况，常用的高副有＿＿＿、＿＿＿。
2-6 运动副是。
A．使两零件直接接触而又能产生一定相对运动的联接。
B．使两构件直接接触而又能相对固定的联接。
C．使两构件间接接触而又能相对固定的联接。
D．使两构件直接接触而又产生一定相对运动的联接。
2-7 齿轮轮齿的啮合属于。
A．移动副B．低副 C．高副D．转动副2-8 通常把机构解释为。
A．具有确定相对运动构件的组合B．具有确定相对运动元件的组合C．具有确定相对运动机件的组合 D．具有确定相对运动零件的组合2-9分析计算：(1) 如图a所示为一简易冲床的初拟设计方案。
设计的思路是：动力由１输入，使轴Ａ连续回转；而固定在轴Ａ上的凸轮２与杠杆３组成的凸轮机构将使冲头４上下运动以到达冲压的目的。
试绘出其机构运动简图，分析其是否能实现设计意图？并提出修改方案。
(2) 如图b所示为一具有急回运动的冲床。
图中绕固定轴心Ａ转动的菱形盘１为原动件，其滑块２在Ｂ点铰接，通过滑块２推动拨叉３绕固定轴心Ｃ转动，而拨叉３与圆盘４为同一构件，当圆盘４转动时，通过连杆５使冲头６实现冲压运动。
试绘制其机构运动简图。
2-10 试计算图示所示机构的自由度。
2-11 试计算图示凸轮--连杆组合机构的自由度。
图中铰接在凸轮上D处的滚子可在CE杆上的曲线槽中滚动。
2-6试计算如下图各平面高副机构的自由度。
第三章平面机构的运动分析3-1 试求图示各机构在图示位置时的全部瞬心的位置。
3-2在图示的机构中，已知各构件长度〔机构比例尺μL =实际构件长度 / 图上长度 =/mm〕，原动件以等角速度ω1 =10 rad/s逆时针转动，试用图解法求在图示位置时点E的速度和加速度，构件 2 的角速度和角加速度。
孙恒《机械原理》(第八版)学习辅导书第11章 齿轮系及其设计【圣才出品】
第11章 齿轮系及其设计11.1 复习笔记本章主要介绍了定轴轮系、周转轮系和复合轮系的传动比计算，轮系的功用，以及行星轮系的效率、齿数的确定。
学习时需要重点掌握轮系传动比的计算，尤其是复合轮系的分析计算，常以计算题的形式考查。
除此之外，轮系的类型和功用、行星轮系中各齿数的确定（需要满足4个条件）等内容，常以选择题和填空题的形式考查，复习时需要把握其具体内容，重点记忆。
一、齿轮系及其分类1．定义齿轮系是由一系列的齿轮所组成的齿轮传动系统，简称轮系。
2．分类根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定，将轮系分为三大类：（1）定轴轮系运转时各个齿轮的轴线相对于机架的位置都是固定的轮系称为定轴轮系。
（2）周转轮系（见表11-1-1）表11-1-1 周转轮系图11-1-1 周转轮系二、定轴轮系的传动比（见表11-1-2）表11-1-2 定轴轮系的传动比三、周转轮系的传动比1．周转轮系的传动比设周转轮系中的两个太阳轮分别为m 和n ，行星架为H ，则其转化轮系的传动比i mn H 可表示为H Hm m H mn H n n Hm nm nωωωi ωωω-==-=±在转化轮系中由至各从动轮齿数的乘积在转化轮系中由至各主动轮齿数的乘积2．具有固定轮的行星轮系的传动比具有固定轮的行星轮系，设固定轮为n ，即ωn ＝0，则有i mn H ＝（ωm －ωH ）/（0－ωH ）＝－i mH ＋1，即i mH ＝1－i mn H 。
四、复合轮系的传动比1．计算步骤（1）将各部分的周转轮系和定轴轮系一一分开；（2）分别列出其传动比计算式；（3）联立求解。
2．划分周转轮系（1）先要找到轮系中的行星轮和行星架（注意：轮系中行星架往往由其他功用的构件所兼任）；（2）每一行星架以及连同行星架上的行星轮和与行星轮相啮合的太阳轮组成一个基本周转轮系；（3）当将所有的基本周转轮系部分找出之后，剩下的便是定轴轮系部分。
机械原理11-本科)-轮系
ω
H 3
ω1 i1H = = 1 + 1.875= + 2.875 ωH
ω
H 1
例 ２：
在图示的周转轮系中， 在图示的周转轮系中，设已知 z1=100, z2=101, z2’=100, z3 = 99. 试求传动比 iH1。
2 2′
解： 为固定轮(即 轮3为固定轮 即n3=0) 为固定轮
n1 − nH n1 − nH i = = n3 − nH 0− nH
齿轮４对传动比没有影响， 齿轮４对传动比没有影响，但能改变从动 轮的转向，称为过轮或中介轮。 轮的转向，称为过轮或中介轮。
§11—3 周转轮系传动比的计算 一、周转轮系的分类 按周转轮系所具有的自由度数目的不同分类： 按周转轮系所具有的自由度数目的不同分类： 1) 行星轮系
F = 3× 3 − 2 × 3 − 2 = 1
i AB
从 A → B 从动轮齿数的连乘积 = 从 A → B 主动轮齿数的连乘积
二、首、末轮转向的确定 1、用“＋” “－”表示
ω1 ω1 1 ω2
1
2
ω2
p
vp
转向相反
2
转向相同
i 12
ω1 = = ω2
z2 − z1 z2 + z1
外啮合 内啮合
对于平面定轴轮系， 对于平面定轴轮系，设轮系中有 m对外啮合齿轮，则末轮转向为(-1) 对外啮合齿轮，则末轮转向为 对外啮合齿轮
关键是先要把其中的周转轮系部分划分出来 。 周转轮系的找法： 周转轮系的找法： 先找出行星轮，然后找出系杆， 先找出行星轮，然后找出系杆，以及与 行星轮相啮合的所有中心轮。 行星轮相啮合的所有中心轮。 每一系杆， 每一系杆，连同系杆上的行星轮和与行星 轮相啮合的中心轮就组成一个周转轮系 在将周转轮系一一找出之后， 在将周转轮系一一找出之后，剩下的便是 定轴轮系部分。 定轴轮系部分。
第十一章齿轮系及其设计(精)
第十一章齿轮系及其设计1图示为一手摇提高装置，此中各轮齿数均为已知，试求传动比i15，并指出当提高重物时手柄的转向。
z120z250z2 15z3 30z3 1z552z418z440题 1图2 图示轮系中，已知各轮齿数为=60，=20，=20，=20，=20，=100，试求z1 z2 z2 z3 z4 z5传动比。
i4152'231H4题 9-2图题2图322'4H1题 9-5图题 3图3 在图示的电动三爪卡盘传动轮系中，设已知各轮齿数为： z1=6，z2= z2=25，z3=57，z4=56，试求传动比 i14。
4 图示为一种大速比减速器的表示图。
动力由齿轮 1输入， H输出。
已知各轮齿数为：z1=12，z2=51，z3=76， z2=49， z4=12，z3==73。
(1)试求传动比 i1H。
(2)若将齿轮 2的齿数改为 52( 即增添一个齿 ) 则传动比i1H又为多少 ?S P3 3′ 3 61 4252 2′ⅠⅡ1 4题 4 图题 5 图5 汽车自动变速器中的预选式行星变速器如图示。
Ⅰ轴为主动轴，Ⅱ轴为从动轴，S，P 为制动带。
其传动有两种状况：(1) S 压紧齿轮3，P处于松开状态；(2) P 压紧齿轮6，S处于松开状态。
已知各轮齿数为z1=30，z2=30，z3= z6=90，z4=40，z5=25。
试求两种状况下的传动比iⅠⅡ。
机械原理习题答案新
第二章机构的结构分析2－1.计算下列各机构的自由度。
注意分析其中的虚约束、局部自由度合复合铰链等。
题图１－４c所示机构，导路ＡＤ⊥ＡＣ、ＢＣ＝ＣＤ／２＝ＡＢ。
该机构可有多种实际用途，可用于椭圆仪，准确的直线轨迹产生器，或作为压缩机或机动马达等。
题图１－４d为一大功率液压动力机。
其中ＡＢ＝Ａ｀Ｂ｀，ＢＣ＝Ｂ｀Ｃ｀，ＣＤ＝Ｃ｀Ｄ｀，ＣＥ＝Ｃ｀Ｅ｀，且Ｅ、Ｅ｀处于滑块移动轴线的对称位置。
答c)为轨迹重合虚约束，可认为ＡＢ杆或滑块之一构成虚约束。
Ｆ＝３×３－２×４＝１。
d)对称的上部分或下部分构成虚约束。
Ｆ＝３×５－２×７＝１.2－2．试计算下列机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。
e）答案：a)Ｆ＝３×７－２×１０＝１．注意其中的Ｃ、Ｇ、Ｄ、Ｈ点并不是复合铰链。
b)Ｆ＝３×５－２×７＝１C）Ｆ＝３×７－２×１０＝１其中Ｃ点为复合铰链，分别由2、３、４构件在Ｃ点构成复合铰。
d)Ｆ＝３×３－２×３－２＝１或者Ｆ＝３×５－２×５－２－２＝１其中Ｂ、Ｄ处的磙子具有局部自由度。
2-3试计算如图所示各平面高副机构的自由度,如有局部自由度、虚约束或复合铰链，请指出。
第三章平面连杆机构及其分析与设计3－1．试求题图所示各机构在图示位置时全部瞬心的位置．答案：瞬心P 12在A 点瞬心P 23、 P 24均在B 点 瞬心P 34在C 点P 14、 P 13均在垂直导路的无 瞬心P 23、 P 13均在B 点穷远处 瞬心P 14、 P 24均在D 点3-5在图示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与齿轮3的传动比31/ωω。
答案：此题关键是找到相对瞬心Ｐ13． 3-6在图示凸轮机构中，已知mm r 50=，mm l OA 22=，mm l AC 80=，οϕ901=，凸轮，凸轮以角速度s rad /101=ω逆时针方向转动。
机械原理答案第十一章 齿轮系及其设计
第十一章 齿轮系及其设计题11-1如图所示为一手摇提升装置，其中各轮齿数均已知，试求传动比i 15，并指出当提升重物时手柄的转向（在图中用箭头标出）。
解： 此轮系为空间定轴轮系78.5771811520524030504321543215=⨯⨯⨯⨯⨯⨯=='''z z z z z z z z i题11-2如图所示为一滚齿机工作台传动机构，工作台与涡轮5固联。
若已知z 1=z 1′=15，z 2=35，z 4′=1（右旋），z 5=40，滚刀z 6=1（左旋），z 7=28。
今要切制一个齿数z 5′=64的齿轮，应如何选配挂轮组的齿数z 2′、z 3和z 4。
解：由范成原理，滚刀6与轮坯5’的角速度比应为64655656==='''z z i ωω 转向如图。
这一角速度比由滚齿机工作台的传动系统来保证。
56242442175421155011528403515''''''=⨯=⨯⨯⨯⨯⨯==i z z z z z z z z z z z z i 转向如图可求得253252=z z 至于Z 3为惰轮，其齿数可根据中心距A 24的需要确定。
题11-3 如图所示为一千分表的示意图。
己知各轮齿数如图，模数mm m 11.0=（为非标准模数）。
若要测量杆1每移动mm 001.0时，指针尖端刚好移动一个刻度()mm s 5.1=。
问指针的长度?=R （图中齿轮5和游丝的作用是使各工作齿轮始终保持单侧接触，以消除齿轮间隙对测量精度的影响） 解：()4332-'-组成定轴轮系1001160120121632431224=⨯⨯===''z z z z i ϕϕ24100ϕϕ=∴再由轮2与测量杆组成齿轮与齿条传动知 测杆1每移动mm 001.0时，齿轮2的转角为：42221027.611.029001.022-⨯=⨯⨯===m Z h r h ϕ 此时要求指针刚好移动一刻度()mm s 5.1=，由4ϕR s =可得指针的长度为mm s sR 241027.61005.1100424=⨯⨯===-ϕϕ题11-4 如图所示为绕线机的计数器。
齿轮设计手册
齿轮设计手册齿轮系及其设计第11章齿轮系及其设计1齿轮系的分类及其传动比2轮系的功用和效率3行星轮系的类型选择及设计的基本知识第1讲齿轮系的分类及其传动比11.1.1 齿轮系及其分类11.1.2 轮系的传动比指南车机械式钟表1. 应用实例：例1 导弹发射快速反应装置例2 汽车后轮中的传动机构2. 轮系分类：（1）定轴轮系（普通轮系）平面定轴轮系空间定轴轮系（2）周转轮系轮系组成：由行星轮、行星架及太阳轮组成；其中作输入与输出运动的构件——基本构件：太阳轮K 和行星架H 周转轮系（2）周转轮系1）按自由度数目分差动轮系——机构自由度为2的周转轮系（F＝2）行星轮系——机构自由度为1的周转轮系（F＝1）2）按基本构件分2K-H型：由两个太阳轮、一个行星架和若干行星轮组成的周转轮系3K型：由三个太阳轮和一个行星架及一个双联行星轮组成的周转轮系（3）复合轮系混合轮系——由定轴轮系与周转轮系串联或并联而复合的轮系复合周转轮系——由两个或两个以上的基本周转轮系的串联或并联而复合的轮系轮系的传动比——轮系中的输入构件与输出构件的角速度之比包含内容：轮系传动比的大小和输入与输出两构件的转向关系分析内容：1. 定轴轮系的传动比2. 周转轮系的传动比3. 复合轮系的传动比 1. 定轴轮系的传动比定轴轮系的传动比——轮系中首、末两构件的角速度之比：大小计算和转向关系确定。
（1）传动比大小的计算方法：定轴轮系传动比的大小等于组成该轮系的各对啮合齿轮传动比的连乘积。
亦即所有从动轮齿数的连乘积所有主动轮齿数的连乘积定轴轮系的传动比＝（2）首、末轮转向关系的确定方法：一般用标注箭头的方法来确定。
当首、末两轮轴线平行时，也可用同向取+和反向取−方法来确定。
过轮（中介轮）——轮系中不影响其传动比的大小而仅起中间过渡和改变从动轮转向作用的齿轮2．周转轮系的传动比先来观察和比较一下相同结构一个周转轮系和一个定轴轮系，可知问题：周转轮系的传动比就不能直接按定轴轮系传动比的求法来计算。
孙桓《机械原理》笔记和课后习题(含考研真题)详解-第十一章至第十四章【圣才出品】
第11章齿轮系及其设计11.1复习笔记一、齿轮系及其分类1．定义由一系列的齿轮所组成的齿轮传动系统称为齿轮系，简称轮系。
2．分类根据轮系运转时各个齿轮的轴线相对于机架的位置是否固定，将轮系分为三大类：（1）定轴轮系运转时各个齿轮的轴线相对于机架的位置都是固定的轮系称为定轴轮系。
（2）周转轮系①定义如图11-1-1所示，运转时至少有一个齿轮轴线的位置不固定，而是绕着其他齿轮的固定轴线回转的轮系称为周转轮系。
图11-1-1周转轮系②基本构件在周转轮系中，一般都以太阳轮和行星架作为输入和输出构件，称为周转轮系的基本构件。
a．太阳轮轮系中绕固定轴回转的齿轮称为太阳轮。
如图11-1-1中齿轮l和内齿轮3都围绕着固定轴线OO回转，则齿轮1和内齿轮3为太阳轮；b．行星轮不仅绕自身轴线作自转，还随着行星架一起绕固定轴线做公转的齿轮称为行星轮。
如图11-1-1中齿轮2，其中构件H为行星架，又称转臂或系杆。
③分类a．根据其自由度的数目分类第一，差动轮系自由度为2的周转轮系称为差动轮系；第二，行星轮系自由度为1的周转轮系称为行星轮系。
b．根据基本构件的不同分类若轮系中的太阳轮以K表示，行星架以H表示，则如图11-1-1所示的轮系称为2K-H 型周转轮系。
（3）复合轮系既包含定轴轮系部分，又包含周转轮系部分，或者是由几部分周转轮系组成的轮系称为复合轮系。
二、定轴轮系的传动比1．轮系传动比的定义轮系的传动比是指轮系中首、末两构件的角速度之比。
2．传动比计算（1）定轴轮系的传动比等于组成该轮系的各对啮合齿轮传动比的连乘积；（2）传动比又等于各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比，即：定轴轮系的传动比＝所有从动轮齿数的连乘积/所有主动轮齿数的连乘积3．首、末轮转向关系的确定（1）转向的确定①齿轮的转向可用箭头表示，箭头方向表示齿轮可见侧的圆周速度的方向；②标志一对啮合传动的齿轮转向的箭头为同时指向节点或同时背离节点；③当首、末两轮的轴线彼此平行时，两轮的转向不是相同就是相反；当两者的转向相同时，规定其传动比为“＋”，反之为“－”；④若首、末两轮的轴线不平行，其间的转向关系只能在图上用箭头来表示。
机械原理 11-3周转轮系的传动比
（1）转化轮系传动比中的
此符号表示在转化轮系中m、n轮的转向关系，但这个符号却直接 影响周转轮系的转速 m、n、H 之间的数值关系。
另外，此符号仅代表在转化轮系中m、n轮的转向关系，并不代表 在周转轮系中m、n轮的转向关系（在转化轮系中m、n轮转向相同， 在周转轮系中m、n轮转向可能相反，也可能相同）。
机械原理
第11章 齿轮系及其设计
（3）此公式适用于周转轮系中任意两个轴线与H轴线平行的齿轮,不仅仅限于 两个太阳轮m、n，若行星轮的轴线与基本构件的轴线平行，也可用此公式求 行星轮与基本构件的角速度关系，但若行星轮的轴线与基本构件的轴线不平 行，则不能用此公式。
例如：在左图2K-H差动轮系中
i1H2
机械原理
第11章 齿轮系及其设计
定轴轮系传动比的计算 一、传动比大小的计算
定轴轮系的传动比
所有从动轮齿数的连乘积 所有主动轮齿数的连乘积
主动轮、从动轮的界定：依据首轮到末轮的传动关系
二、首、末轮转向关系的确定（传动比方向的确定）
（1）若首、末轮的轴线是平行的， 用 号表示：“+”表
示1）首若、首末、轮末转轮向轴相线同与，各“中-”间表轴示轴首线、都末是轮相转互向相i1反3 。(1)1
（2）计算公式中，m、n、H 均为代数量，需将其代数量的符 号代入公式中参加运算，计算时，可假定一个方向为正（顺时针
或逆时针），另一个方向则为负。
（3）此公式适用于周转轮系中任意两个轴线与H轴线平行的齿轮,不 仅仅限于两个太阳轮m、n，若行星轮的轴线与基本构件的轴线平行， 也可用此公式求行星轮与基本构件的角速度关系，但若行星轮的轴线 与基本构件的轴线不平行，则不能用此公式。
左图是一复合轮系，
机械原理习题集
．综合题1．根据图示机构，画出去掉了虚约束和局部自由度的等效机构运动简图，并计算机构的自由度。
设标有箭头者为原动件，试判断该机构的运动是否确定，为什么？2．计算图示机构的自由度。
如有复合铰链、局部自由度、虚约束，请指明所在之处。
DE3a）F （b）IH4．计算机构的自由度，并进行机构的结构分析，将其基本杆组拆分出来，指出各个基本杆组的级别以及机构的级别。
d)a )b )c ) e )(f )5．计算机构的自由度，并分析组成此机构的基本杆组。
如果在该机构中改选FG 为原动件，试问组成此机构的基本杆组是否发生变化。
6．试验算图示机构的运动是否确定修改方案。
b)第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置（用符号P ij 直接在图上标出）2、已知图示机构的输入角速度1,试用瞬心法求机构的输出速度3。
要求画出相应的瞬心，写出 3 的表达式，并标明方向3、在图示的齿轮 -- 连杆组合机构中，试用瞬心法求齿轮 1与 3的传动比ω 1/ ω2用瞬心法求：1）当 =165°时，点 C 的速度 v c ；2）当 =165°时，构件 3的 BC 线上速度最小的一点 E 的位置及其速度的大 小u ；uuv3）当 v c 0时，角之值（有两个解） 。
4、在图示的四杆机构中， lAB =60mm, l CD =90mm, l AD =l BC =120mm, 2 =10rad/s ，试请标出矢量v AB、v BC、v CA 及矢量 v A 、v B 、v C 的方向？5、如图为一速度多边形，6、已知图示机构各构件的尺寸，构件 1 以匀角速度ω1 转动，机构在图示位置时的速度和加速度多边形如图b）、c）所示。
（1）分别写出其速度与加速度的矢量方程，并分析每个矢量的方向与大小，（2）试在图b）、c）上分别标出各顶点的符号，以及各边所代表的速度或加速度及其指向。
9 试判断在图示的两个机构中， B 点是否存在哥氏加速度？又在何位置时其哥氏加速度为零？作出相应的机构位置图。
机械设计基础 第十一章
11.2.3 惰轮
如图11-7所示的定轴齿轮系中，运动由齿轮1经齿 轮2传给齿轮3。总的传动比为：
i13
n1 n3
z2 z3 z1z2
z3 z1
图11-7 惰轮的应用
【例11-1】如图11-2所示空间定轴轮系，蜗杆的头数 z1 2， 右旋；蜗轮的齿数z2 60，z2 20，z3 24，z3 20，z4 24， z4 30，z5 35，z5 28，z6 135 。若蜗杆为主动轮，其转速 n1 900 r / min ，试求齿轮 6 的转速n6 的大小和转向(用画箭头
14.8
r
/
min
负号表示末轮5的转向与首轮1相反，顺时针转动。
11.3 行星齿轮系的传动比计算
行星齿轮系传动比的计算方法有许多种，最常用的是转化 机构法，即设想将周转轮系转化为假想的定轴轮系，借用定 轴轮系传动比计算公式来求解周转轮系中有关构件的转速及 传动比。
如图11-8所示，现假想给行星齿轮系加一个与行星架
相同。
iH1
nH n1
600 120
5
11.4 混合齿轮系的传动比计算
既包含定轴齿轮系又包含行星齿轮系的齿轮系，称为混 合齿轮系，如图11-10所示。
图11-10 混合齿轮系
计算混合齿轮系传动比的一般步骤如下：
① 区分轮系中的定轴齿轮系部分和行星齿轮系部分。 ② 分别列出定轴齿轮系部分和行星齿轮系部分的传动比公式， 并代入已知数据。 ③ 找出定轴齿轮系部分与行星齿轮系部分之间的运动关系，并 联立求解即可求出混合轮系中两轮之间的传动比。
传动比 iGHK 也不等于绝对传动比 iGK 。
【例11-3】在图11-8(a) 所示的差动齿轮系中，已知n1 100 r / min n3 60 r / min，n1与 n3 转向相同；齿数z1 17，z2 29，z3 75
第十一章-齿轮传动思维导图
齿数z
主要参数
11-7 圆柱齿轮材料和 参数的选取与计算方法
齿宽系数及齿宽
圆周力
径向力 斜齿轮圆柱齿轮的受力分析
轴向力
圆周力、径向力与直齿圆柱齿轮的方向相同
对主动轮：用左、右手法则来判 断，从动轮方向与主动轮相反
轴向力
斜齿圆柱齿轮传动的作用力方向
11-/s，采用油池润滑
精度等级
11-4 直齿圆柱齿轮传动 的作用力及计算载荷
直齿圆柱齿轮传动的受力分析
直齿圆柱齿轮传动的作用力方向
圆周力：“主反从同” 径向力：由作用点指向各自的轮心
直齿圆柱齿轮传动的计算载荷
法向力Fn为名义载荷
齿面最大接触应力可近似用赫兹公式计算
11-5 直齿圆柱齿轮传 动的齿面接触强度计算
齿面接触强度（简化后） 齿面接触疲劳强度的校核公式 齿面接触疲劳强度的设计公式
第十一章齿轮传动
11-1 齿轮的失效形 式和设计计算准则
失效形式
轮齿折断（闭式硬齿面齿轮传动的主要失效形式） 齿面点蚀（闭式软齿面齿轮传动的主要失效形式） 齿面胶合（主要出现在高速重载的闭式齿轮传动） 齿面磨损（开式齿轮传动的主要失效形式） 齿面塑性变形（重载软软齿面齿轮传动的主要失效形式）
设计计算准则
多级传动且大齿轮直径不等时， 采用惰轮蘸油润滑
v>12m/s，采用油泵喷油润滑
减少摩擦磨损，散热和防锈蚀
开式，半闭式，低速齿轮传动采用人工定 期润滑，用润滑油或润滑脂
润滑目的 润滑方式
闭式齿轮传动的润滑方式由圆周速度v决定
查表 润滑油牌号和粘度
功率损耗 传动效率
齿轮传动的效率
11-11 齿轮传动 的润滑和效率
11-2 齿轮材料及热处理
机械原理第七版习题解答(第4、7、11章)
8
《机械原理》习题课
解 根据等效转动惯量的等效原则，有
1 2 J e 1
2
1 2
J 1 1
2
1 2
( J 2 J 2 ) 2
2
1 2
J 3 3
2
1 G 2 g
v
2
则：
J e J1 1 2 ( J 2 J 2 )(
2 1
2
) J3(
2
3 1
G rB 4 r A 1 1 2 1
10 40
2
G rB r A 1 2 i1 4
2
1 6 0 0 .9 8 0 .9 7 9
2 9 8 .1 8 ( N )
故提升10kN的重物，必须施加于链轮A上的圆周力 F为298．18N。
24
《机械原理》习题课
11-19 图示为纺织机中的差动轮系，设
20
《机械原理》习题课
解 此轮系为一个3K型行星轮系， 即有三个中心轮(1，3及4)。若 任取两个中心轮和与其相啮合的 行星轮及系杆H便组成一个2K-H 型的行星轮系。且有三种情况： 1-2-3-H行星轮系、4-2’(2)-3H行星轮系及1-2’(2)-4-H差动 轮系。而仅有两个轮系是独立的， 为了求解简单，常选两个行星轮 系进行求解。即
1
5
《机械原理》习题课
解
arctan f
总反力 F R 1 2 及 F R 3 2 的方位如图
F F
题4-14
6
机械原理习题解答
(第7章-机械的运转及其速度波动的调节)
7
《机械原理》习题课
7-7图示为一机床工作台的传动系统。设已知各齿 轮的齿数，齿轮3的分度圆半径r3，各齿轮的转动 惯量 J 1 , J 2 , J 2 , J 3 ，齿轮1直接装在电动机轴上， 故J1中包含了电动机转子的转动惯量；工作台和 被加工零件的重量之和为G。当取齿轮1为等效构 件时，试求该机械系统的等效转动惯量Je。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如果是行星轮系，则ω m、ω n中必有一个为0（不妨 设ω n＝0）,则上述通式改写如下：
i
H mn
m H
H
H
i mH 1
即
i mH 1 i mn 1 f ( z )
两者关系如何？
以上公式中的ω i 可用转速ni 代替: 30 ni=(ω i/2 π)60 =ω i π rpm 用转速表示有：
作者： 潘存云教授
2)蜗轮蜗杆
右 旋 蜗 杆
伸出左手 （画速度多边形确定）
2
1
3)交错轴斜齿轮
t O1
O2 vp1 vp2
作者：潘存云教授
左 旋 蜗 杆
O1
2
1
伸出右手
2
P
1
安徽工程科技学院专用
t O2
作者： 潘存云教授
例一：已知图示轮系中各轮 齿数，求传动比 i15 。 解：1.先确定各齿轮的转向 2. 计算传动比 过轮 i15 = ω1 /ω5
作者：潘存云教授
z1
安徽工程科技学院专用
z1
作者： 潘存云教授
例五：图示圆锥齿轮组成的轮系中，已知： z1＝33，z2＝12, z2’＝33, 求 i3H 解:判别转向: 齿轮1、3方向相反
i
H 31
r1
H
p
z2
o
3 H 1 H
3 H
0 H
z1
ω H 2 z3 δ 1 δ 2 作者：潘存云教授 ω ωH 2 r2
角速度ω H2之间的关系为： ω 2 =ω H +ω H2
如何求？
∵ P为绝对瞬心，故轮2中心速度为： V2o=r2ω H2 又 V2o=r1ω H ∴ ω H2＝ω H r1/ r2 ＝ω H tgδ 1 ＝ω H ctgδ
安徽工程科技学院专用
2
特别注意：转化轮系中两齿轮轴线不平行时，不能直接计算！
安徽工程科技学院专用
所有从动轮齿数的乘积
所有主动轮齿数的乘积
作者： 潘存云教授
2)画箭头 外啮合时： 两箭头同时指向（或远离）啮合点。 头头相对或尾尾相对。 1 1 内啮合时： 两箭头同向。
2
2
对于空间定轴轮系，只能用画箭头的方法来确定从 动轮的转向。 2 1)锥齿轮
1
作者：潘存云教授
3
安徽工程科技学院专用
∴ i1H＝1-iH13 ＝1-10/11 ＝1/11 iH1＝1/i1H=11
Z2
作者：潘存云教授
Z’2 H
Z1
Z3
模型验证
结论：系杆转11圈时，轮1同向转1圈。 若 Z1=100, z2=101, z2’=100, z3=99。
i1H＝1-iH13＝1-101×99/100×100 ＝1/10000,
iH1＝10000
结论：系杆转10000圈时，轮1同向转1圈。
安徽工程科技学院专用 作者： 潘存云教授
又若 Z1=100, z2=101, z2’=100, z3＝100，Z2 i1H＝1-iH1H＝1-101/100 ＝－1/100, iH1＝-100
H Z1
Z’2
结论：系杆转100圈时，轮1反向转1圈。
作者：潘存云教授 转化后的角速度
1 2 3 H
2 H 1
ω1 ω2 ω3 ωH
ω H1＝ω 1－ω H ω H2＝ω 2－ω H ω H3＝ω 3－ω H ω HH＝ω H－ω H＝0
2 H
作者：潘存云教授
1 3 3
安徽工程科技学院专用
转化后: 系杆=>机架， 周转轮系=>定轴轮系 可直接套用定轴轮系传动比的计算公式。
Z2
Z’3 Z1 作者：潘存云教授 Z4 Z’4 Z3 Z5
z2 z3 z4 z5 = z 1 z 2 z ’3 z ’4 z3 z4 z5
=
齿轮1、5 转向相反
z 1 z ’3 z ’4
齿轮2对传动比没有影响，但能改变从动轮的转向， 称为过轮或中介轮。
安徽工程科技学院专用 作者： 潘存云教授
§11－3 周转轮系的传动比
i3 H 1
z1 z3
=－1
i3H =2
提 H i 21 问：
系杆H转一圈，齿轮3同向2圈
Why? 因两者轴线不平行
强调：如果方向判断不对，则 会得出错误的结论：ω 3＝0。
2 H 1 H
成立否？
不成立！ ω H2 ≠ω 2－ω H
事实上，因角速度ω 2是一个向量，它与牵连角速度ω H和相对
n1 n
H H 3
n1 n H n3 n H
1 nH 1 nH
＝－3
nH 1 / 2
安徽工程科技学院专用
得： i1H = n1 / nH =－2 ,
两者转向相反。
轮1逆时针转1圈，轮3顺时针 转1圈，则系杆顺时针转半圈。
作者： 潘存云教授
3) i
H 13
n1 n
作者： 潘存云教授
i
H 13
1
H
H 3
1 H 3 H
z2 z3 z1 z 2
z3 z1
上式“－”说明在转化轮系中ω H1 与ω H3 方向相反。 右边各轮的齿数为已知，左边三个基本构件的参数中，如果已知其中任意两个， 通用表达式： 则可求得第三个参数。于是，可求得任意两个构件之间的传动比。
安徽工程科技学院专用
作者： 潘存云教授
例六：图示为龙门刨床工作台的变 速机构，J、K为电磁制动器，设已 知各轮的齿数，求J、K分别刹车时 的传动比i1B。 解 1)刹住J时 3－3’将两者连接
K
3’ 4
3 2 1
J
A
B
作者：潘存云教授
5
1－2－3为定轴轮系
定轴部分：
周转部分：
B－5－4－3’为周转轮系 i13＝ω 1/ω 3 ＝-z3/ z1
基本构件：太阳轮(中心轮)、行星架(系杆或转臂)。 其它构件：行星轮。其运动有自转和绕中心轮的公转，类似行星运动，故得名。 由于轮2既有自转又有公转,故不 类型： 3K型 能直接求传动比
2K-H型 ω3
2
H
作者：潘存云教授
－ω H
ω1
2
H
ω2
作者：潘存云教授
ωH
3
1 3
轮1、3和系杆作定 轴转动
1
施加－ω H后系杆成为机架，原轮系转化为定轴轮系
定义：由齿轮组成的传动系统－简称轮系 平面定轴轮系 定轴轮系（轴线固定） 空间定轴轮系 差动轮系（F=2） 周转轮系（轴有公转） 行星轮系（F=1） 复合轮系（两者混合） 本章要解决的问题： 1.轮系传动比 i 的计算;
轮系分类
2.从动轮转向的判断。
安徽工程科技学院专用 作者： 潘存云教授
§11－2 定轴轮系的传动比
此例说明行星轮系中输出轴的转向，不仅与输入轴的转向有关，而且与各轮的齿数有关。本例中只将 轮3增加了一个齿，轮1就反向旋转，且传动比发生巨大变化，这是行星轮系与定轴轮系不同的地方
Z3
安徽工程科技学院专用
作者： 潘存云教授
例四：马铃薯挖掘机中：z1＝z2＝z3 ，求ω 2， ω 3
i
H 21
2 H 1 H
作者：潘存云教授
2 1)用“＋” “－”表 vp 示 适用于平面定轴轮系（轴线平行，
ω1
1 2
ω2
两轮转向不是相同就是相反）。 外啮合齿轮：两轮转向相反，用“－”表示；
内啮合齿轮：两轮转向相同，用“＋”表 每一对外齿轮反向一次考 虑方向时有 示。 设轮系中有m对外啮合齿轮，则末轮转向为(-1)m i1m＝ (-1)m
i
H mn
n n
H m H n
nm nH nn nH
= f(z)
作者： 潘存云教授
安徽工程科技学院专用
例二
2K－H 轮系中， z1＝10, z2＝20, z3＝50 轮3固定, 求i1H 。
1
H
解
1 ) i13
H
H 3
1 H 3 H
1 H
0 H
2
H
1
i1 H 1
z2 z3 z1 z 2
z3 z1
50 10
3
5
模型验证
∴
i1H=6 , 小齿轮转6圈，系杆转1圈，
且两者转向相同。
安徽工程科技学院专用
作者： 潘存云教授
例三 2K－H 轮系中， z1＝z2＝20, z3＝60 1)轮3固定。求i1H 。 轮1逆转1圈，轮3顺转1圈 2)n1=1, n3=-1, 求nH 及i1H 的值。 轮1、轮3各逆转1圈 3)n1=1, n3=1, 求nH 及i1H 的值。
反转原理：给周转轮系施以附加的公共转动－ω H后，不改变轮 系中各构件之间的相对运动， 但原轮系将转化成为一新的定 轴轮系，可按定轴轮系的公式计算该新轮系的传动比。
转化后所得轮系称为原轮系的 “转化轮系”
安徽工程科技学院专用 作者： 潘存云教授
将轮系按－ω H反转后，各构件的角速度的变化如下:
构件 原角速度
i
H mn
m
H
H n
m H n H
转化轮系中由 转化轮系中由
m 至 n 各从动轮的乘积 m 至 n 各主动轮的乘积
= f(z)
特别注意： 1.齿轮m、n的轴线必须平行。 2.计算公式中的“±” 不能去掉，它不仅表明转化