不确定型决策例题
企业决策 计算题

• 降低单位变动成本Cv=13.8
• 降低固定成本F=4.8
• 提高价格p=20.2
⒈确定型决策方法——盈亏平衡分析法
运用盈亏分析法,还可通过计算经营安全率分析企业经营安全状态。 经营安全率是反映企业经营状态的一个重要指标,当销售量或销售收 入越大时,企业经营安全率L 就越接近于1,说明企业经营越安全,亏 损风险越小;若越接近于0时,企业亏损风险就越大。 经营安全率高,说明经营状态好;反之,经营安全率低,说明经营状 态差。一般根据下页表中所示来判断经营安全状态。其计算公式为:
M F S3 5 2 5 (1 0 1% 0 1) 5 10(台 1)250
T
0 .5
• 例某工厂车间生产单一产品,车间生产面积为500 ㎡,单位面积有效工作时间为每日12小时,每生 产一件产品占用时间为1小时,每件产品占用生产 面积2.5㎡,该车间的生产能力为多少?
M FB1 2500 24(件 0)0 bT 2.5 1
方案、状态数据表 单位:万元
(1)画决策树图
47万
(2)计算损益期望值
E 1 0 .6 5 0 0 .3 2 0 5 .1 ( 2 ) 5 3 万 5 元
E 2 0 .6 7 0 0 .3 3 0 0 .1 ( 4 ) 0 4 万 7 元
显然“最大收益”中最大值为70万元,其对应的方案是 “新建方案”。这种选择方案的思路是从最好的情况下寻找最 有优的方案,实际上偏于乐观。
Ⅱ定量决策方法
⒉不确定型决策方法
• ②悲观准则: 小中取大法,找出每个方案在各种自然状态下最小损益值,取 其中大者所对应的方案即为合理方案。
例3:设某企业为了增加产量而设想了三种方案,一是扩 建现有工厂,二是新建一个分厂,三是把增产部分转包给其他 工厂生产,已知未来一段时期市场对产品的要求状态有好、 中、差三种状态。而各种方案在每种状态下的预计损益值,如 下页表所示,试问如何决策?
不确定型决策试题

1.有一个市场调查公司想要预测某新产品在市场上的销售情况。
该产品
可能非常成功、一般成功、不成功,但每种情况的概率未知。
请为该公司提供一个不确定型决策的策略。
2.一家公司面临两个投资项目,每个项目都有不同的预期回报和风险。
公司没有足够的信息来确定每个项目的成功概率,但知道每个项目的预期回报和风险。
请为该公司提供一个不确定型决策的策略。
3.一家制造公司在考虑是否要扩大生产规模。
如果公司决定扩大生产规
模,可能会获得高收益,但也可能会面临高风险。
如果公司不扩大生产规模,可能会保持当前收益,但也可能失去一些机会。
请为该公司提供一个不确定型决策的策略。
4.一家航空公司面临两个航线选择,每个航线都有不同的预期利润和风
险。
公司没有足够的信息来确定每个航线的成功概率,但知道每个航线的预期利润和风险。
请为该公司提供一个不确定型决策的策略。
5.一家零售商需要考虑是否要引入一个新的产品线。
引入新产品线可能
会增加销售额,但也可能会增加运营成本。
如果不引入新产品线,销售额可能会保持稳定,但也可能失去一些机会。
请为该公司提供一个不确定型决策的策略。
不确定性决策 习题及答案

不确定性决策
康佳公司在计划年度决定开发新产品甲,根据市场调查,提出三种不同的产量方案,即40000件、45000件和50000件,在市场销路不同的情况下估计可实现的边际贡献也不同。
【解】:
按照大中取大法,应选择三个方案在市场畅销时获得最大受益者为最佳方案。
小中取大法
大中取小法:
1.先根据上述资料,就市场销售的三种不同情况分别确定其最大的收益值:
畅销情况下的最大收益值为98 000元;
一般情况下的最大收益值为58 000元;
滞销情况下的最大收益值为39 000元。
2.分别计算不同销售情况下的后悔值:
(1)畅销情况下的后悔值:
40000件产量的后悔值 =98 000-80 000 =18 000元
45000件产量的后悔值 =98 000-88 000 =10 000元
50000件产量的后悔值 =98 000-98 000 =0元
(2)一般情况下的后悔值:
40000件产量的后悔值=58 000-58 000 =0元
45000件产量的后悔值=58 000-50 000 =8 000元
50000件产量的后悔值=58 000-56 000 =2 000元
(3)滞销情况下的后悔值:
40000件产量的后悔值=39 000-34 000 =5 000元
45000件产量的后悔值=39 000-39 000 =0元
50000件产量的后悔值=39 000-31 000 = 8000元
3.将上述不同销路情况下的三种产量的后悔值列表如下。
管理学-不确定情境下的四种决策准则

该准则可以最大限度地降低决策者的后悔值。本例的 决策分析如下:
最小机会损失准则分析表:
事件 决策 0 1000 产 2000 3000 量 4000 40 30 20 10 0 40 20 30 10 20 0 10 20 0 40 20 40 (30) min 0 0 10 1000 20 0 需求量 2000 3000 40 60 20 40 4000 8现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
不确定型决策的四个准则
不确定型决策
不确定型决策:缺乏必要资料,不能测知事件发生 的规律。 设某工厂以批发方式销售它生产的产品, 例:设某工厂以批发方式销售它生产的产品,每件产品 设某工厂以批发方式销售它生产的产品 的成本为0.03 0.03元 批发价为0.05 0.05元 的成本为0.03元,批发价为0.05元。若每天生产的产品 当日销售不完,每件产品要损失0.01 0.01元 当日销售不完,每件产品要损失0.01元。该工厂每天的 产量可以是0 1000、2000、3000、4000件 产量可以是0、1000、2000、3000、4000件(可视为市 场可能的需要量), ),问 场可能的需要量),问:该工厂如何制定每天的生产计 划? 分析:市场需求量不确定,无法确切知道该作何种选择。 故此,分析在不同产量、需求量下的收益情况: 计算公式:收益 = (0.05 – 0.03) ×销量– 0.01 × 未售出量
∑0.2×aij
0 14
4、最小机会损失准则
机会损失(opportunity loss) :当某事件发生时,由于决策 的差异形成的相对损失。(未得到的收益) 决策的准则是采取使这种损失最小的决策。其计算步骤是: 1.构造一机会损失矩阵 (1) 在事件j列找一最大的收益值ajmax (2) 用该值减该列每一项的值(ajmax – aij)作为该事件发生 时的机会损失值bij 2.比较选择 min {max (bi性准则决策分析表:
管理学-不确定情境下的四种决策准则

各种决策准则下的选择结果比较:
方案 准则 悲观主义 乐观主义 等可能 机会损失 √ √ 0 √ 1000 生产量 2000 3000 4000
√
不同需求量下的收益情况
事件 决策 0 1000 产 2000 3000 量 4000 -40 -10 20 50 80 -20 -30 10 0 40 30 40 60 40 60 0 0 -10 1000 0 20 需求量 2000 0 20 3000 0 20 4000 0 20
决策准则:
由于无法预先知道每天的确切需求量,所以决策者 要根据自身的状况、承受损失的能力等去做出选择。 这时候的决策,无“最优”的标准,但同样有可以 使用的客观准则。 不确定型决策准则通常有如下几个: (1)悲观主义准则; (2)乐观主义准则; (3)等可能性准则(等概率准则); (4)最小机会损失准则(最小后悔准则)。
乐观主义准则( max--max) --max 2 、乐观主义准则( max--max)
决策依据: 决策依据:不放弃任何一个有可能达到最好结果的决 策方案,能够承受较大的风险。通常以 max {max i j (aij) } 来表示。 通常来说,决策者有较强的实力,即使出现 最坏的结果,也不会对总体产生太大的影响,决 策者往往愿意采用这种准则。 本题采取乐观主义准则决策的结果为: max {0,20,40,60,80 }=80,故选择生产 量为4000的方案。其分析如下:
i j
该准则可以最大限度地降低决策者的后悔值。本例的 决策分析如下:
最小机会损失准则分析表:
事件 决策 0 1000 产 2000 3000 量 4000 40 30 20 10 0 40 20 30 10 20 0 10 20 0 40 20 40 (30) min 0 0 10 1000 20 0 需求量 2000 3000 40 60 20 40 4000 80 60 max 80 60
不确定性决策方法

2、效用曲线决策 :
• 例题9:现有甲乙两个机会,甲概率为0.5,赢利200万 元,0.5的机会亏损100万元;乙有绝对的机会赢利25万 元。
• 甲: • 概率0.5 200万元 乙: 概率1.0 25万元
• • 概率0.5 -100万元
若用期望值决策当然选中甲,因为
E甲
2
X i Pi
200* 0.5 (100)* 0.5
不确定型决策分析法
• 由于无法预先估计或预测各种可能状态发 生的概率,只能根据决策者的经验和态度 进行的决策。
• 一)不确定型决策方法:常用的有5种:等 可能法、乐观法、悲观法、遗憾值法、系 数法。
例题:
某企业准备生产一种全新的产品,预测人员对该产品的
市场需求,只能大致估计为销路好、销路较好、销路一般和
销路较好 550 600* 200 260
销路一般 400* -100 50 100
销路差 200* -300 -100
70
1、小中取大法
小中取大法是一种保守方法,是从每一种方案中找出 最小的收益值,然后比较这些最小值,选择一个收益值最 大的方案作为决策放案。其思想是不追求市场状态好时的 收益最大,而追求市场状态差时亏损最少。
效用曲线所画的表达决策者对待某种
• 上风述三险种所类持型态决策度者的对曲风险线的。不同态度,也就是
决策者对同一货币值在不同环境下所产生的效用 大小不一。其大小的数量称为效用值,其值在0和 1之间。一般情况下,同一金额量随着风险程度的 增加,其在决策者心中的效用值不断下降,即绝 大多数决策者对风险是持厌恶态度的。效用值的 大小决定于决策者对风险的态度,反映了不同决 策者的不同的价值观以及他们对同一方案的不同 反应和评价标准。
预测与决策-不确定型决策方法

j i j
所对应的方案 d i 为最佳决策方案。如果决策 矩阵表是损失矩阵,则应采取“最小最小” 决策准则,即取 m in [ L ij ] 中的最小值
j
m in{m in [ L ij ]} ,
案。
di
所对应的方案
di
为最佳决策方
j
汽车股份公司损益矩阵表 自然 利润 (万元) 状态 方案
自然状态(市场需求状态)
若用G(di)表示(di)方案中的最大后悔值,则:
G ( d i ) m ax ( m ax L ij L ij )
j i 1,2 , , m
对每一个方案来说,都各有一个这样的最大后悔 值,故m个方案就共有m个最大后悔值。m个最大 后悔值中的最小者,即:
i 1,2 , , m
m in G ( d i )
二 “坏中求好”决策方法
概念:“坏中求好”决策准则,又叫 “小中取大”准则,或称悲观决策准则, 这种决策准则就是充分考虑可能出现的 最坏情况,从每个方案的最坏结果中选 择一个最佳值,将其对应的方案作为最 优方案。 “不求有功,但求无过”
设有一非确定型决策,备选方案为 d i ( i 1, 2 , , m ), 自然状态有n种(其出现概率未知)
“早知今日,何必当初”
设有一不确定型决策,备选方案为d1, d2, ,dm 自然状态为 1,2, ,n ,损益值为Lij (i=1,2, ,m, j=1,2, ,n )在j状态下,必有一个方案的收益值最大, 这个最大收益值可表示为:
i 1,2 , , m
m ax L ij m ax { L1 j , L 2 j , , L m j }
全面引进(A1) 全部自制(A2) 引进和改造相结合 (A3)
第1章企业战略与经营决策-第4节企业经营决策(2)
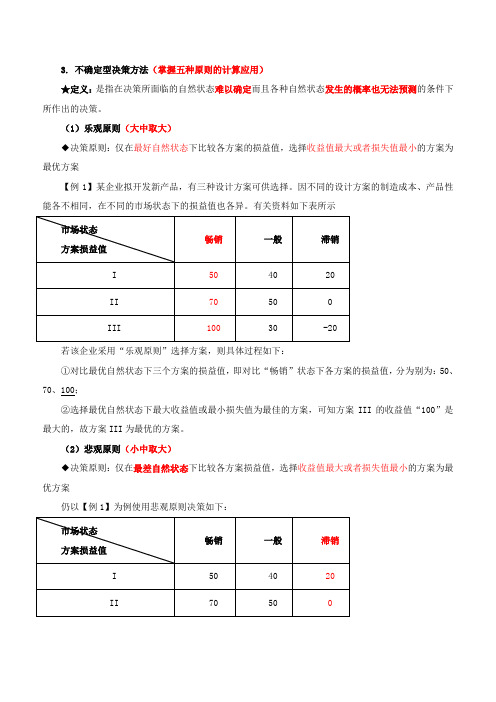
3. 不确定型决策方法(掌握五种原则的计算应用)★定义:是指在决策所面临的自然状态难以确定而且各种自然状态发生的概率也无法预测的条件下所作出的决策。
(1)乐观原则(大中取大)◆决策原则:仅在最好自然状态下比较各方案的损益值,选择收益值最大或者损失值最小的方案为最优方案【例1】某企业拟开发新产品,有三种设计方案可供选择。
因不同的设计方案的制造成本、产品性能各不相同,在不同的市场状态下的损益值也各异。
有关资料如下表所示若该企业采用“乐观原则”选择方案,则具体过程如下:①对比最优自然状态下三个方案的损益值,即对比“畅销”状态下各方案的损益值,分为别为:50、70、100;②选择最优自然状态下最大收益值或最小损失值为最佳的方案,可知方案III的收益值“100”是最大的,故方案III为最优的方案。
(2)悲观原则(小中取大)◆决策原则:仅在最差自然状态下比较各方案损益值,选择收益值最大或者损失值最小的方案为最优方案仍以【例1】为例使用悲观原则决策如下:采用“悲观原则”选择方案的过程如下:①悲观准则仅在最差自然状态下比较各方案的损益值,即“滞销”的状态下比较各方案的损益值,分别为:20,0,-20;②选择最差自然状态下最大收益值或最小损失值为最优的方案,可知方案I的收益值“20”是最大的,故选择方案I为优的方案。
(3)折中原则(只考虑最好和最差两个自然状态)◆公式:折中损益值 = ɑ×最大损益值 +(1 - ɑ)×最小损益值式中:“ɑ”表示乐观系数,即最优自然状态发生的概率,“1- ɑ”即最差自然状态发生的概率◆决策原则:选择折中损益值最大的方案【注释】当ɑ=0时,结果与悲观原则相同;当ɑ=1时,结果与乐观原则相同。
仍以【例1】为例,假设乐观系数(最大值系数)α=0.75,使用折中原则决策如下:采用“折中原则”选择方案的过程如下:①计算各方案折中损益值。
方案I:50×0.75+ 20×(1-0.75)=42.5方案II:70×0.75+0×(1-0.75)=52.5方案III:100×0.75+(-20)×(1-0.75)=70②选择折中损益值最大的方案为最优的方案,可知方案III的折中损益值“70”最大,因此选择方案III为最优的方案。
