与圆有关的角
和圆有关的角(含答案)

OFE CBAOE DCBA和圆有关的角与圆有关的角我们学习了圆心角、圆周角、弦切角以及它们的大小与它们所对(或夹)的弧的度数之间的关系.角的顶点和边与圆位置关系在运动和变化过程中也可能形成另外的两种角.•如果角的顶点在圆内,则称这样的角为圆内角,如图1中所示的∠AEB 即为圆内角.圆内角的大小究竟与弧有何关系呢?延长AE 、BE 分别交圆于C 、D 两点,再连结AD,•则∠AEB=∠A+∠D.∵∠A 的度数等于12CD ,∠D 的度数等于12AB ,∴∠AEB 的度数等于12(•AB +CD ).即圆内角的度数等于它和它的对顶角所对的两弧度数和的一半,其中圆心角是特殊的圆内角.E DCBAEDCBA(1) (2)如果角的顶点在圆外,且角的两边都与同一个圆相交,则称这样的角为圆外角,•如图2所示,∠AEB 即为圆外角,圆外角又有什么性质呢?连结AD,则∠E=∠CAD-∠D,•∵∠CAD 的度数等于12CD ,∠D 的度数等于12AB ,∴∠E 的度数等于 12(CD -AB ).即圆外角的度数等于它所夹的两弧度数的差的绝对值的一半.圆心角、圆周角、弦切角、圆内角和圆外角,弧是联系它们的中介,即“由角看弧,由弧看角”是促使它们互相转化的基本方法。
例1 已知:如图,△ABC 内接于⊙O,∠A=60°,∠B=80°,E 是BC 上一点,F•是AC 的中点,求∠BEF 的度数.解析 ∵∠C=∠AEB,∠C=180°-(∠BAC+∠ABC)=180°-(60°+80°)=40°, ∴∠AEB=40°. ∵AF FC ,∴∠ABF=12∠ABC=40°. 又∵∠AEF=∠ABF=40°. ∴∠BEF=∠AEB+∠AEF=80°.点评若所求的角是与圆有关的角,如圆心角、圆周角、弦切角、•内接四边形的内角和外角,要设法利用相关的定理进行计算,若所求的角与圆无关,要设法转化为与圆有关的角去解决。
探究与圆有关的角

探究与圆有关的角随着新课程改革的不断深入,各地中考命题都发生了很大的变化,尤其对于圆的考查,难度、内容与形式都有很大的改变,并且多数省、市都以计算或者简单探究解答题的形式来考查圆的知识,其中大多涉及到与圆有关的角:圆心角的度数等于它所对的弧的度数.圆周角的度数等于它所对的弧的度数的一半.主要考查同学们的观察、分析、推理及运用知识、发现创新能力。
现就以精选几个与圆有关的角为例进行分析与说明,希望能给同学们带来启示与帮助。
例1:如图,在等腰△ABC 中,AC =BC ,∠C =1000,点P 在△ABC 的外部,并且PC =BC ,求∠APB 的度数。
思路点拨:由题中的条件AC =BC =PC ,联想到圆的定义,画出以点C 为圆心,AC 为半径的圆,使此题得以突破与解决。
例2:.如图,BC 为半圆O 的直径,点F 是弧BC 上一动点(点F 不与B 、C 重合),A 是弧BF 上的中点,设∠FBC=α, ∠ACB=β.⑴当α=50°时,求β的度数。
⑵猜想α与β之间的关系,并给与证明。
思路点拨:解此题的关键是把握圆周角与所对弧的度数之间的关系。
例3:如图,点A 、B 、C 、D 为圆O 的四等分点,动点P 从圆心O 出发,沿O-C-D-O 的路线作匀速运动.设运动时间为t 秒, ∠APB 的度数为y 度,则下列图象中表示y 与t 之间函数关系最恰当的是().例4:如图,AB 是⊙O 的直径,BC 是弦,OD ⊥BC 于E ,交弧BC 于D .(1)请写出四个不同类型的正确结论; (2)若BC =8,ED =2,求⊙O 的半径.(3)连CD ,设∠BDC=α,∠ABC=β,探究α与β之间的关系式,并给给予适当的说明。
思路点拨:根据垂径定理及推论可得出线段相等、角相等=线段平等、三角形全等或相似等结论;同时利用构造勾股定理列出方程求出圆的半径;利用直径所对的圆周角为直角及及圆内接四边形对角互补等进行分析与探究。
第27讲:与圆有关的角

B O 4。
D. 0 7。
2 如图 5AB是o0的直径 , D是 O0的弦 , . , C 连 结 A 、 D, C A 若 ̄C B 5, A =3 ̄则 AD C的度数为
—
.
—
( 0 8, 原 ) 20 太
图9
图 1 O
数 学z G I X L E U  ̄ EK
7 如图 1, B C、 . 0A、 、 D为o0的四等分点, 动点 P从 圆心 O出发, (— L 一0路线作匀速运动. 沿 )C L 设运动 时间为 £s, () )一. 度)则下列图象中表示 Y与 t B ) , , (
‘ .
‘ E/ M/B A /O / F,
?
.
图 1 1
一、
图 1 2
M E— M F.
0
9 已知 : . 如图 1 , 是 AB 的中点 , 2M 过点 M 的弦
M N 交 AB 于点 c, ④ 0的 半 径 为 4c M N= 4 设 m, c ( ) 圆心 0 到 弦 MN 的 距 离 ; 2 求 AC 的 m+ 1求 () M 度数. (0 8 南通 ) 20 ,
1。 B O , AC=6 。则 B C一 ( 0, E
A. 5 3。
C. O 6。
1 如 图 4 在 o0 中 , . , ZAO 的 度 数 为 m , 是 B C
, 、
) .
A B上一点 , E是 AB上不 同的两 点 ( 与 A、 C D、 不 B 两点重合)则 D+ E的度数为 ( , ) .
5 ’. .
4
. 一
④E A
5如 图 8 N N  ̄ b N A , N
.
人教版-数学-九年级上册-知识归纳:圆

知识归纳:圆本章重点1.圆的定义:(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.2.判定一个点P是否在⊙O上.设⊙O的半径为R,OP=d,则有d>r点P在⊙O 外;d=r点P在⊙O 上;d<r点P在⊙O 内.3.与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数.(2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.⑤圆内接四边形的对角互补;外角等于它的内对角.(3)弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角.弦切角的性质:弦切角等于它夹的弧所对的圆周角.弦切角的度数等于它夹的弧的度数的一半.4.圆的性质:(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴.垂径定理及推论:(1)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(3)弦的垂直平分线过圆心,且平分弦对的两条弧.(4)平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.(5)平行弦夹的弧相等.5.三角形的内心、外心、重心、垂心(1)三角形的内心:是三角形三个角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“I”表示.(2)三角形的外心:是三角形三边中垂线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用O表示.(3)三角形重心:是三角形三边中线的交点,在三角形内部;它到顶点的距离是到对边中点距离的2倍,通常用G表示.(4)垂心:是三角形三边高线的交点.6.切线的判定、性质:(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线.②到圆心的距离d等于圆的半径的直线是圆的切线.(2)切线的性质:①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点.③经过切点作切线的垂线经过圆心.(3)切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.(4)切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.7.圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形,圆内接四边形对角互补,外角等于内对角.(2)各边都和圆相切的四边形叫圆外切四边形,圆外切四边形对边之和相等.8.直线和圆的位置关系:设⊙O 半径为R,点O到直线l的距离为d.(1)直线和圆没有公共点直线和圆相离d>R.(2)直线和⊙O有唯一公共点直线l和⊙O相切d=R.(3)直线l和⊙O 有两个公共点直线l和⊙O 相交d<R.9.两圆的性质:(1)两个圆是一个轴对称图形,对称轴是两圆连心线.(2)相交两圆的连心线垂直平分公共弦,相切两圆的连心线经过切点.10.圆中有关计算:圆的面积公式:,周长C=2πR.圆心角为n°、半径为R的弧长.圆心角为n°,半径为R,弧长为l的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形,底面半径为R,母线长为l的圆柱的体积为,侧面积为2πRl,全面积为.圆锥的侧面展开图为扇形,底面半径为R,母线长为l,高为h的圆锥的侧面积为πRl ,全面积为,母线长、圆锥高、底面圆的半径之间有.重点、热点垂径定理及推论;圆心角、弧、弦、弦心距之间的关系定理. 运用圆内接四边形的性质解有关计算和证明题.。
圆(全)知识点习题及答案

圆一、本章知识框架二、本章重点1.圆的定义:(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.2.判定一个点P是否在⊙O上.设⊙O的半径为R,OP=d,则有d>r点P在⊙O 外;d=r点P在⊙O 上;d<r点P在⊙O 内.3.与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角.圆心角的性质:圆心角的度数等于它所对的弧的度数.(2)圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角.圆周角的性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.⑤圆内接四边形的对角互补;外角等于它的内对角.(3)弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角.弦切角的性质:弦切角等于它夹的弧所对的圆周角.弦切角的度数等于它夹的弧的度数的一半.4.圆的性质:(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,经过圆心的任一直线都是它的对称轴.垂径定理及推论:(1)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.(3)弦的垂直平分线过圆心,且平分弦对的两条弧.(4)平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.(5)平行弦夹的弧相等.5.三角形的内心、外心、重心、垂心(1)三角形的内心:是三角形三个角平分线的交点,它是三角形内切圆的圆心,在三角形内部,它到三角形三边的距离相等,通常用“I”表示.(2)三角形的外心:是三角形三边中垂线的交点,它是三角形外接圆的圆心,锐角三角形外心在三角形内部,直角三角形的外心是斜边中点,钝角三角形外心在三角形外部,三角形外心到三角形三个顶点的距离相等,通常用O表示.(3)三角形重心:是三角形三边中线的交点,在三角形内部;它到顶点的距离是到对边中点距离的2倍,通常用G表示.(4)垂心:是三角形三边高线的交点.6.切线的判定、性质:(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线.②到圆心的距离d等于圆的半径的直线是圆的切线.(2)切线的性质:①圆的切线垂直于过切点的半径.②经过圆心作圆的切线的垂线经过切点.③经过切点作切线的垂线经过圆心.(3)切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.(4)切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.7.圆内接四边形和外切四边形(1)四个点都在圆上的四边形叫圆的内接四边形,圆内接四边形对角互补,外角等于内对角.(2)各边都和圆相切的四边形叫圆外切四边形,圆外切四边形对边之和相等.8.直线和圆的位置关系:设⊙O 半径为R,点O到直线l的距离为d.(1)直线和圆没有公共点直线和圆相离d>R.(2)直线和⊙O有唯一公共点直线l和⊙O相切d=R.(3)直线l和⊙O 有两个公共点直线l和⊙O 相交d<R.9.圆和圆的位置关系:设的半径为R、r(R>r),圆心距.(1)没有公共点,且每一个圆上的所有点在另一个圆的外部外离d>R+r.(2)没有公共点,且的每一个点都在外部内含d<R-r(3)有唯一公共点,除这个点外,每个圆上的点都在另一个圆外部外切d=R+r.(4)有唯一公共点,除这个点外,的每个点都在内部内切d=R-r.(5)有两个公共点相交R-r<d<R+r.10.两圆的性质:(1)两个圆是一个轴对称图形,对称轴是两圆连心线.(2)相交两圆的连心线垂直平分公共弦,相切两圆的连心线经过切点.11.圆中有关计算:圆的面积公式:,周长C=2πR.圆心角为n°、半径为R 的弧长.圆心角为n°,半径为R,弧长为l 的扇形的面积.弓形的面积要转化为扇形和三角形的面积和、差来计算.圆柱的侧面图是一个矩形,底面半径为R,母线长为l 的圆柱的体积为,侧面积为2πRl ,全面积为.圆锥的侧面展开图为扇形,底面半径为R,母线长为l,高为h的圆锥的侧面积为πRl ,全面积为,母线长、圆锥高、底面圆的半径之间有.一、知识点1、与圆有关的角——圆心角、圆周角(1)图中的圆心角;圆周角;(2)如图,已知∠AOB=50度,则∠ACB= 度;(3)在上图中,若AB是圆O的直径,则∠AOB= 度;OA B3、点和圆的位置关系有三种:点在圆,点在圆,点在圆;例:已知圆的半径r等于5厘米,点到圆心的距离为d,(1)当d=2厘米时,有d r,点在圆(2)当d=7厘米时,有d r,点在圆(3)当d=5厘米时,有d r,点在圆4、直线和圆的位置关系有三种:相、相、相.例:已知圆的半径r等于12厘米,圆心到直线l的距离为d,(1)当d=10厘米时,有d r,直线l与圆(2)当d=12厘米时,有d r,直线l与圆(3)当d=15厘米时,有d r,直线l与圆5、圆与圆的位置关系:例:已知⊙O1的半径为6厘米,⊙O2的半径为8厘米,圆心距为 d,则:R+r= , R-r= ;(1)当d=14厘米时,因为d R+r,则⊙O1和⊙O2位置关系是:(2)当d=2厘米时,因为d R-r,则⊙O1和⊙O2位置关系是:(3)当d=15厘米时,因为,则⊙O1和⊙O2位置关系是:(4)当d=7厘米时,因为,则⊙O1和⊙O2位置关系是:(5)当d=1厘米时,因为,则⊙O1和⊙O2位置关系是:6、切线性质:例:(1)如图,PA是⊙O的切线,点A是切点,则∠PAO= 度(2)如图,PA、PB是⊙O的切线,点A、B是切点,则 = ,∠ =∠;7、圆中的有关计算(1)弧长的计算公式:例:若扇形的圆心角为60°,半径为3,则这个扇形的弧长是多少? 解:因为扇形的弧长=()180所以l =()180= (答案保留π)(2)扇形的面积:例6:①若扇形的圆心角为60°,半径为3,则这个扇形的面积为多少? (3)圆锥:例:圆锥的母线长为5cm ,半径为4cm ,则圆锥的侧面积是多少?解:∵圆锥的侧面展开图是 形,展开图的弧长等于 ∴圆锥的侧面积=8、三角形的外接圆的圆心——三角形的外心——三角形的 交点;三角形的内切圆的圆心——三角形的内心——三角形的 交点;基础练习一。
初中数学-与圆有关的角
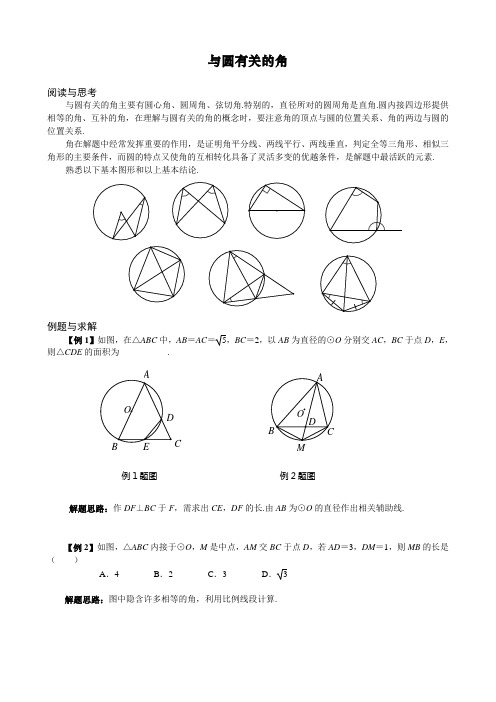
与圆有关的角阅读与思考与圆有关的角主要有圆心角、圆周角、弦切角.特别的,直径所对的圆周角是直角.圆内接四边形提供相等的角、互补的角,在理解与圆有关的角的概念时,要注意角的顶点与圆的位置关系、角的两边与圆的位置关系.角在解题中经常发挥重要的作用,是证明角平分线、两线平行、两线垂直,判定全等三角形、相似三角形的主要条件,而圆的特点又使角的互相转化具备了灵活多变的优越条件,是解题中最活跃的元素.熟悉以下基本图形和以上基本结论.例题与求解【例1】如图,在△ABC中,AB=AC=5,BC=2,以AB为直径的⊙O分别交AC,BC于点D,E,则△CDE的面积为___________.C例1题图例2题图解题思路:作DF⊥BC于F,需求出CE,DF的长.由AB为⊙O的直径作出相关辅助线.【例2】如图,△ABC内接于⊙O,M是中点,AM交BC于点D,若AD=3,DM=1,则MB的长是()A.4 B.2 C.3 D. 3解题思路:图中隐含许多相等的角,利用比例线段计算.【例3】如图1,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角三角形DCE中,∠DCE是直角,点D在线段AC上.(1) 证明:B,C,E三点共线;(2) 若M是线段BE的中点,N是线段AD的中点,证明:MN=2OM;(3) 将△DCE绕点C逆时针旋转α(0°<α<90°)后,记为△D1CE1(如图2).若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=2OM1是否成立?若是,请证明;若不是,说明理由.解题思路:对于(2),充分利用条件中的多个中点,探寻线段之间的数量关系与位置关系.【例4】如图所示,ABCD为⊙O的内接四边形,E是BD上的一点,∠BAE=∠DAC. 求证:(1)△ABE∽△ACD;(2) AB·DC+AD·BC=AC·BD.解题思路:由(1)可类比猜想,为(2)非常规问题的证明铺平道路.【例5】如图1,已知⊙M与x轴交于点A,D,与y轴正半轴交于点B,C是⊙M上一点,且A(-2,0),B(0,4),AB=BC.(1) 求圆心M的坐标;(2) 求四边形ABCD的面积;(3) 如图2,过C点作弦CF交BD于点E,当BC=BE时,求CF的长.解题思路:作出基本辅助线(如连接BM或AC),这是解(1)、(2)的基础;对于(3),由BC=BE,得∠BEC=∠BCE,连接AC,将与圆无关的∠BEC转化为与圆有关角,导出CF平分∠ACD,这是解题的关键.E1图1 图2【例6】如图,AB,AC,AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.求证:(1) ∠CAD=2∠DBE;(2) AD2-AB2=BD·DC.解题思路:对于(2),AD2-AB2=(AD+AB)(AD-AB)=(AD+AE)(AD-AE)=(AD+AE) ·DE,需证(AD+AE) ·DE=BD·DC,从构造相似三角形入手.。
2.2 与圆有关的角

2.2 与圆有关的角一个角有一个顶点和两条边,顶点和边相对于一个圆的位置关系分别有各种情况,由此可得到不同类型的与圆有关的角。
1.圆心角我们已经知道,顶点在圆心的角叫做圆心角。
圆心角的两边都与圆相交,两边所夹⌒。
的的弧是这个圆心角所对的弧。
如图2-28,∠AOB是圆心角,它所对的弧是AB在圆周上给定一条弧,由分别过弧的端点的两条半径所确定的圆心角,是这条弧所对的圆心角。
在同圆或等圆中,相等的圆心角所对的弧相等;相等的弧所对的圆心角相等。
2.圆周角操作⌒上的任意两点,试分别作出∠AMB、如图2-29,圆心角∠AOB=70°,M、N是APB∠ANB,并量出这两个角的度数。
如上所作的∠AMB和∠ANB,它们的顶点都在⊙O上,两边都与圆相交。
分别度量这两个角,所得角度都是35°,说明它们都等于∠AOB的度数的一半。
顶点在圆周上并且两边都与圆相交的角叫做圆周角。
圆周角的两边所夹的弧,是这个圆周角所对的弧;由圆周上一点分别与弧的两端点的连线确定的圆周角,是这条弧所对的圆周角。
⌒,与圆心角∠AOB 在图2-29中,∠AMB和∠ANB是圆周角;它们所对的弧都是AB所对的弧相同。
如果圆周角与圆心角所对的弧相同,那么这两个角之间的大小有以下关系:圆周角定理一条弧所对的圆周角等于这条弧所对的圆心角的一半。
试一试在⊙O上取一点A,以A为顶点画一些圆周角;在观察圆心与圆周角的位置关系,有几种可能的情况?通过画图可见,圆心与圆周角的位置关系有三种情况:圆心在圆周角的一边上,圆心在圆周角的内部,圆心在圆周角的外部。
对于圆心与圆周角位置关系的三种情况,分别画圆周角;在画出与圆周角所对的弧相同的圆心角,如图2-30所示。
下面,我们来证明圆周角定理。
已知:如图2-30,在⊙O 中,BC ⌒ 所对的圆周角是∠BAC ,所对的圆心角是∠BOC 。
求证:∠BAC=21∠BOC 。
分析:如果圆心O 在圆周角∠BAC 的一边上,入股2-30⑴,这时圆心角∠BOC 恰好为等腰三角形AOC 的外角,可推出结论;如果圆心O 在∠BAC 的内部或外部,如图2-30⑵、⑶,那么可考虑构造如图2-30⑴的图形,将问题转化。
圆中有关的角

年 级 初三 学 科 数学 编稿老师 田一鹏 课程标题 圆中有关的角一校 张琦锋二校林卉审核孙永涛一、考点突破1. 掌握和圆有关的角:圆心角、圆周角、圆内角、圆外角、弦切角的定义及其度量。
2. 掌握圆内接四边形的性质定理。
3. 了解弧、弦、圆心角、圆周角之间的关系,并能运用这些关系解决有关问题。
二、重难点提示重点:弧、弦、圆心角、圆周角之间的关系。
难点:圆周角定理的应用和分类讨论的思想在解题中的应用。
一、圆中有关的角⎧⎪⎪⎪⎨⎪⎪⎪⎩圆心角圆周角圆中有关的角圆内角圆外角弦切角1. 圆心角:顶点在圆心的角叫做圆心角。
OCB把整个圆周等分成360份,每一等份弧是1°的弧,圆心角的度数和它所对的弧的度数相等。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等。
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等,那么它们相对应的其余各组量都相等。
2. 圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角。
OBCA一条弧所对的圆周角等于它所对的圆心角的一半,同弧或等弧所对的圆周角相等;反之也成立。
直径所对的圆周角是直角。
BCAO3. 圆内角:顶点在圆内(两边自然和圆相交)的角叫圆内角。
P OBA圆内角的度数等于它所对的弧的度数与它的对顶角所对的弧的度数的和的一半。
DPB COA4. 圆外角:顶点在圆外,并且两边都和圆相交(或相切)的角叫圆外角。
DPBCAO圆外角的度数等于它所夹的两弧度数的差(较大弧的度数减去较小弧的度数)的一半。
5. 弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。
弦切角等于它所夹的弧对的圆周角。
推论①弦切角等于它所夹的弧所对的圆心角的一半。
推论②如果两个弦切角所夹的弧相等,那么这两个弦切角也相等。
二、圆的内接四边形如果一个多边形的所有顶点都在同一个圆上,那么这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.与圆有关的角知识考点:1、掌握与圆有关的角,如圆心角、圆周角、弦切角等概念;2、掌握圆心角的度数等于它所对弧的度数;3、掌握圆周角定理及其推论;4、掌握弦切角定理及其推论;5、掌握各角之间的转化及其综合运用。
精典例题:【例1】如图,在等腰△ABC 中,AC =BC ,∠C =1000,点P 在△ABC 的外部,并且PC =BC ,求∠APB 的度数。
分析:注意条件AC =BC =PC ,联想到圆的定义,画出以点C 为圆心,AC 为半径的圆,问题则得以解决。
解:∵AC =BC ,PC =BC∴A 、B 、P 三点在以C 为圆心,AC 为半径的圆上 若P 、C 在AB 的同侧,则∠APB =21∠ACB ∵∠ACB =1000,∴∠APB =500 若P 、C 在AB 的异侧,则∠APB =1800-50=1300【例2】如图,在△ABC 中,∠B =900,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于E ,与AC 切于点D ,直线ED 交BC 的延长线于F ,若AD ∶AE =2∶1,求cot ∠F 的值。
分析:由AD ∶AE =2∶1和△ADE ∽△ABD 有DE ∶DB =1∶2,而∠F =∠EBD ,则cot ∠F =cot ∠EBD =DEBD,故结论得证。
解:连结BD∵AC 为⊙O 的切线,∴∠1=∠2 ∵∠A =∠A ,∴△ADE ∽△ABD∴DE BD AE AD=,即12=AE AD ∴212==DEDB ∵BE 为⊙O 的直径,∴∠BDE =900∴∠2+∠BEF =900,∵∠F +∠BEF =900,∴∠2=∠F ∴cot ∠F =cot ∠2=DEBD=2 【例3】如图,由矩形ABCD 的顶点D 引一条直线分别交BC 及AB 的延长线于F 、G ,连结AF 并延长交△BGF 的外接圆于H ,连结GH 、BH 。
(1)求证:△DFA ∽△HBG ;(2)过A 点引圆的切线AE ,E 为切点,AE =33,CF ∶FB =1∶2,求AB 的长; (3)在(2)的条件下,又知AD =6,求tan ∠HBG 的值。
分析:(1)证∠DAF =∠AFB =∠BGH ,∠DFA =∠HFG =∠HBG 即可; P '•例1图 P C BA•例2图21OEFD CBA(2)由DC ∥AG ,得CF ∶FB =CD ∶BG =1∶2,则AB ∶AG =1∶3,由切割线定理得AB =3;(3)由(2)知AB =3,AG =9,过A 作AQ ⊥DG 于Q 。
由AB AD AQ DG ⋅=⋅2121得131318=AQ 。
所以DF =31DG =13。
由DG DQ AD ⋅=2得131312=DQ ,所以1313=QF 。
故tan ∠HBG =tan ∠HFG =tan ∠QFA =FQAQ =18。
例3图HGQEFDCBA•问题一图O PDCBA探索与创新:【问题一】如图,已知,半圆的直径AB =6cm ,CD 是半圆上长为2cm 的弦,问:当弦CD 在半圆上滑动时,AC 和BD 延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由。
分析:本题有一定难度,连结BC (或AD )可构成直角三角形,这是遇直径常用的辅助线。
解;连结BC∵CD 为定长,虽CD 滑动,但⋂CD 的度数不变,∴∠PBC 为定值 ∴∠P =∠ACP -∠PBC =900-∠PBC 为定值 ∵∠PCD =∠PBA ,∴△PCD ∽△PBA ∴3162===BA CD PB PC 在Rt △PBC 中,cos ∠P =31=PB PC ,∴sin ∠P =322)31(12=- 评注:本题是在变中寻不变,有一定的难度,但考虑到常用的辅助线――直径,问题便迎刃而解了。
变式:如图,BC 与AD 交于E ,其它条件与上题一致,问∠P 与∠DEB 的大小关系?分析:∵AB 为直径,则∠PCB =∠ADB =900,而cos ∠P =ABCDPB PC =,又∵△CED ∽△AEB ,∴EBDEAB CD ==cos ∠DEB 。
∴cos ∠P =cos ∠DEB ,故∠P 与∠DEB 的大小相等。
•问题一变式图EOPD CBAP '•问题二图OPDCBA【问题二】如图,AB 是⊙O 的直径,弦(非直径)CD ⊥AB ,P 是⊙O 上不同于C 、D 的任一点。
(1)当点P 在劣弧CD 上运动时,∠APC 与∠APD 的关系如何?请证明你的结论; (2)当点P 在优弧CD 上运动时,∠APC 与∠APD 的关系如何?并证明你的结论(不讨论P 与A 重合的情形)。
分析:(1)P 在劣弧CD 上运动时,∠APC =∠APD ,利用垂径定理及圆周角定理易证;(2)P 在优弧CD上运动时,∠APC +∠APD =1800,∠APC所对的弧是⋂ADC ,∠APD所对的弧是⋂AD ,而⋂⋂=AC AD ,⋂⋂+AD ADC 的度数和等于⋂⋂+AC ADC 的度数和,等于3600,由圆周角定理易证明得到结论。
跟踪训练:一、选择题:1、下列命题中,正确的命题个数是( )①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半; ③900的圆周角所对的弦是直径;④圆周角相等,则它们所对的弧也相等。
A 、1个B 、2个C 、3个D 、4个2、已知AB 、AC 与⊙O 相切于B 、C ,∠A =500,点P 是⊙O 上异于B 、C 的一动点,则∠BPC 的度数是( )A 、650B 、1150C 、650或1150D 、1300或5003、O 为锐角△ABC 的外心,OD ⊥BC ,OE ⊥AC ,OF ⊥AB ,垂足分别为D 、E 、F ,则OD ∶OE ∶OF 为( )A 、a ∶b ∶cB 、a 1∶b 1∶c1 C 、cosA ∶cosB ∶cosC D 、sinA ∶sinB ∶sinC4、如图,AB 是⊙O 的直径,DB 、DC 分别切⊙O 于B 、C ,若∠ACE =250,则∠D 为( ) A 、500 B 、550 C 、600 D 、650•第4题图EO CBA1O••第5题图ODCB A70x•第6题图OD CBA5、如图,⊙O 经过⊙O 1的圆心O 1,∠ADB =α,∠ACD =β,则α与β之间的关系是( ) A 、β=α B 、αβ21800-=C 、)90(210αβ-=D 、)180(210αβ-= 二、填空题:6、如图,四边形ABCD 内接于⊙O ,则x = 。
7、如图,A 、B 、C 是⊙O 上的三个点,当BC 平分∠ABO 时,能得出结论 (任写一个)。
8、如图,AB 是⊙O 的直径,C 、D 、E 都是⊙O 上的点,则∠1+∠2= 。
•第7题图 OC BA•第8题图 21DEOCB A•第9题图PDOCBA9、如图,PA 切⊙O 于点A ,PO 交⊙O 于C ,延长PO 交⊙O 于点B ,PA =AB ,PD 平分∠APB 交AB 于点D ,则∠ADP = 。
10、如图,已知直径AB ⊥CD 于E ,∠COB =α,则2sin2αBE AB = 。
11、如图,⊙O 1与⊙O 2为两个等圆,O 1在⊙O 2上,O 2在⊙O 1上,⊙O 1与⊙O 2交于A 、B两点,过B 的直线交⊙O 1于C ,交⊙O 2于D ,过C 作⊙O 1的切线CE 与过D 作⊙O 2的切线DE 交于E ,则∠E = 。
三、计算题或证明题:12、如图,已知P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,OP 与AB 相交于点M ,C 为⋂AB 上一点。
求证:∠OPC =∠OCM 。
第10题图EDOC BA2O 1O ••第11题图ED CBA•第12题图OM P C BA13、如图,⊙O 1与⊙O 2交于A 、B 两点,点O 1在⊙O 2上,⊙O 2的弦O 1C 交AB 、⊙O 1于D 、E 。
求证:(1)C O D O AO 1121⋅=; (2)E 为△ABC 的内心。
2O 1O ••第13题图D ECBA•第14题图OFGDECBA•第15题图PODCBA14、如图,已知AD 是△ABC 外角∠EAC 的平分线,交BC 的延长线于点D ,延长DA 交△ABC 的外接圆于点F ,连结FB 、FC 。
(1)求证:FB =FC ;(2)FD FA FB ⋅=2;(3)若AB 是△ABC 的外接圆的直径,∠EAC =1200,BC =6cm ,求AD 的长。
15、如图,⊙O 的直径AB =6,P 为AB 上一点,过P 作⊙O 的弦CD ,连结AC 、BC ,设∠BCD =m ∠ACD ,当347+=APBP时,是否存在正实数m ,使弦CD 最短?若存在,请求出m 的值;若不存在,请说明理由。
16、如图,在△ABC 中,AD 为∠BAC 的平分线,以C 为圆心,CD 为半径的半圆交BC 的延长线于点E ,交AD 于F ,交AE 于点M ,且∠B =∠CAE ,EF ∶FD =4∶3。
(1)求证:AF =DF ; (2)求∠AED 的余弦值;(3)如果BD =10,求△ABC 的面积。
•第16题图FMED C B A跟踪训练参考答案一、选择题:ACCAD 二、填空题:6、1400;7、OC ∥AB 等;8、900;9、450;10、1;11、1200 三、计算题或证明题:12、提示:连结OA ,22OC OP OM OA =⋅=,∴OCOPOM OC =,又∠O 是公共角,△OCM ∽△OPC 。
13、略证:(1)连结,O 1B ,由O 1A =O 1B 可得∠O 1AD =∠O 1CA ,∠AO 1D 是公共角,∴△O 1AD ∽△O 1CA ;(2)连结AE 、BE ,由∠ABE =21∠AO 1C =21∠ABC ,∠BAE =21∠BO 1E =21∠BAC 。
14、(1)(2)略;(3)34cm 。
15、解:连结OD ,设存在正实数m ,则在⊙O 中过P 点的所有弦中,只有垂直于直径的弦最短。
∴CP ⊥AB 于P 。
∵347+=APBP,设AP =k ,则BP =k )347(+,又AB =6 ∴6)1347(=++k ,解得2336-=k ∴OP =OA -AP =23363--=233 在Rt △POD 中,cos ∠POD =23=OD OP ,∴∠POD =300,∠ACD =150 ∵AB 为⊙O 的直径,∴∠ACB =900∴∠BCD =900-150=750 ∵∠BCD =m ∠ACD∴m =5,即存在正实数m ,使CD 弦最短。
16、(1)先证∠ADE =∠DAE ;(2)作AN ⊥BE 于N ,设FE =x 4,FD =x 3,可求DE =x 5,由AN DE EF AD ⋅=⋅得:AN =x 8.4,可得EN =x 4.1,cos ∠AED =257;(3)△CAE ∽△ABE ,72=∆ABC S 。
