实验四 回溯算法
算法分析与设计实验报告--回溯法

算法分析与设计实验报告--回溯法实验目的:通过本次实验,掌握回溯法的基本原理和应用,能够设计出回溯法算法解决实际问题。
实验内容:1.回溯法概述回溯法全称“试探回溯法”,又称“逐步退化法”。
它是一种通过不断试图寻找问题的解,直到找到解或者穷尽所有可能的解空间技术。
回溯法的基本思路是从问题的某一个初始状态开始,搜索可行解步骤,一旦发现不满足求解条件的解就回溯到上一步,重新进行搜索,直到找到解或者所有可能的解空间已经搜索完毕。
2.回溯法的基本应用回溯法可用于求解许多 NP 问题,如 0/1 背包问题、八皇后问题、旅行商问题等。
它通常分为两种类型:一种是通过枚举所有可能的解空间来寻找解;另一种则是通过剪枝操作将搜索空间减少到若干种情况,大大减少了搜索时间。
3.回溯法的解题思路(1)问题分析:首先需要对问题进行分析,确定可行解空间和搜索策略;(2)状态表示:将问题的每一种状况表示成一个状态;(3)搜索策略:确定解空间的搜索顺序;(4)搜索过程:通过逐步试探,不断扩大搜索范围,更新当前状态;(5)终止条件:在搜索过程中,如果找到了满足要求的解,或者所有的可行解空间都已搜索完毕,就结束搜索。
4.八皇后问题八皇后问题是指在一个 8x8 的棋盘上放置八个皇后,使得任意两个皇后都不在同一行、同一列或同一对角线上。
通过回溯法可以求解出所有的可能解。
实验过程:回溯法的实现关键在于搜索空间的剪枝,避免搜索无用的解;因此,对于八皇后问题,需要建立一个二维数组来存放棋盘状态,以及一个一维数组来存放每行放置的皇后位置。
从第一行开始搜索,按照列的顺序依次判断当前的空位是否可以放置皇后,如果可以,则在相应的位置标记皇后,并递归到下一行;如果不能,则回溯到上一行,重新搜索。
当搜索到第八行时,获取一组解并返回。
代码实现:```pythondef is_valid(board, row, col):for i in range(row):if board[i] == col or abs(board[i] - col) == abs(i - row):return Falsereturn True实验结果:当 n=4 时,求得的所有可行解如下:```[[1, 3, 0, 2],[2, 0, 3, 1]]```本次实验通过实现回溯法求解八皇后问题,掌握了回溯法的基本原理和应用,并对回溯法的核心思想进行了深入理解。
实验报告4.回溯算法

算法设计与分析实验报告实验名称_____回溯算法_____学院________数学与计算机学院____ 班级_______信科00000___________ 学号_______6666666666__________ 姓名_____000000________________ 2016年月日{if(((a+b)==24)||((a-b)==24)||((a*b)==24)||(b!=0&&a%b==0&&a/b==24)){//如果经过上面的计算得到解while(!route.empty()){node now=route.front();printf("%d%c%d=%d\n",now.a,now.oper,now.b,now.sum);//依次输出前面的计算过程route.pop();}if((a+b)==24){if(b>a) swap(a,b);printf("%d+%d=%d\n",a,b,a+b);}if((a-b)==24) printf("%d-%d=%d\n",a,b,a-b);if((a*b)==24) {if(b>a) swap(a,b);printf("%d*%d=%d\n",a,b,a*b);}if(a%b==0&&b!=0&&(a/b)==24) printf("%d/%d=%d\n",a,b,a/b);//a/b比较特殊,要求结果必须是整数flag=true;//表示找到解,一旦找到任何一个解就退出}return ;}queue <node> temp=route;node x;x.a=a,x.b=b,x.sum=a+b,x.oper='+';if(b>a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a+b,num[cur+1],temp);//(((a*b)*c)*d) 模型temp=route;x.a=a,x.b=b,x.sum=a*b,x.oper='*';if(b>a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a*b,num[cur+1],temp);temp=route;x.a=a,x.b=b,x.sum=a-b,x.oper='-';temp.push(x);dfs(cur+1,a-b,num[cur+1],temp);if(b!=0&&a%b==0){//a/b需要验证合法性temp=route;x.a=a,x.b=b,x.sum=a/b,x.oper='/';temp.push(x);dfs(cur+1,a/b,num[cur+1],temp);}temp=route;x.a=b,x.b=num[cur+1],x.sum=b+num[cur+1],x.oper='+';if(x.b>x.a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a,b+num[cur+1],temp);//a*((b*c)*d) 模型temp=route;x.a=b,x.b=num[cur+1],x.sum=b*num[cur+1],x.oper='*';if(x.b>x.a) swap(x.a,x.b);temp.push(x);dfs(cur+1,a,b*num[cur+1],temp);temp=route;x.a=b,x.b=num[cur+1],x.sum=b-num[cur+1],x.oper='-';temp.push(x);dfs(cur+1,a,b-num[cur+1],temp);if(num[cur+1]!=0&&b%num[cur+1]==0) {temp=route;x.a=b,x.b=num[cur+1],x.sum=b/num[cur+1],x.oper='/';temp.push(x);dfs(cur+1,a,b/num[cur+1],temp);}}int main(){//freopen("point24.in","r",stdin);//输入输出重定向//freopen("point24.out","w",stdout);queue <node> t;scanf("%d %d %d %d",&num[0],&num[1],&num[2],&num[3]);while(!flag){dfs(1,num[0],num[1],t);printf("%d %d %d %d\n",num[0],num[1],num[2],num[3]);if(!next_permutation(num,num+4)) break;}if(!flag) printf("No answer!\n");system("pause");return 0;}。
实验四 回溯法(图着色问题)

01 234 001 1 01 1 1 01 01 21 1 01 0 3001 01 41 1 01 0
class MGraph { public:
MGraph(int v,int s); void mColoring(int m,int *x); //一维数组x,存放1~n个顶点的颜色 ~MGraph(); private: void NextValue(int k,int m,int *x); void mColoring (int k,int m,int *x); int **a; //二维数组a,存储图的邻接矩阵 int n,e; //n表示图的顶点数,e表示边数 };
无向图G
【实验内容与要求】
图的着色问题:设G=(V,E)是一连通无向图,有3 种颜色,用这些颜色为G的各顶点着色,每个顶点着 一种颜色,且相邻顶点颜色不同。试用回溯法设计一 个算法,找出所有可能满足上述条件的着色法。
无向图G
无向图G
对应这个无向图的状态空间树应该是怎样的?
是一个完全3叉树,共6层
实验四 回溯法 — 图的着色问题
图的着色问题是由地图的着色问题引申而来的: 用m种颜色为地图着色,使得地图上的每一个 区域着一种颜色,且相邻区域颜色不同。
问题处理:如果把每一个区域收缩为一个顶点, 把相邻两个区域用一条边相连接,就可以把一
个区域图抽象为一个平面图。
地图(map)中地区的相邻关系,在图(graph )中用边表示。
//若(i, j)是图的边,且相邻结点k和j颜色相同 //发生冲突,选下一种颜色
if (j==k) return; //成功选择一种颜色返回 }while (1); //循环尝试颜色 }
运行结果:
回溯与分支限界算法设计
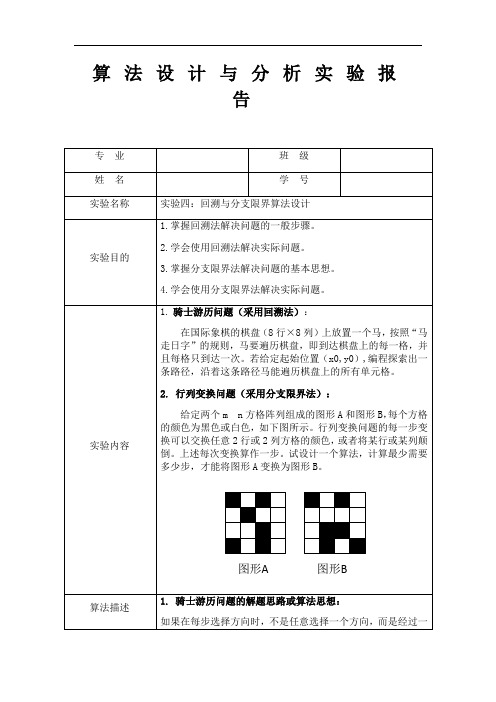
算法设计与分析实验报告1.骑士游历问题(采用回溯法):在国际象棋的棋盘(8行×8列)上放置一个马,按照“马走日字”的规则,马要遍历棋盘,即到达棋盘上的每一格,并且每格只到达一次。
若给定起始位置(x0,y0),编程探索出一条路径,沿着这条路径马能遍历棋盘上的所有单元格。
2. 行列变换问题(采用分支限界法):给定两个m n方格阵列组成的图形A和图形B,每个方格的颜色为黑色或白色,如下图所示。
行列变换问题的每一步变换可以交换任意2行或2列方格的颜色,或者将某行或某列颠倒。
上述每次变换算作一步。
试设计一个算法,计算最少需要多少步,才能将图形A变换为图形B。
图形A图形B}}实例:2. 行列变换问题的程序:package ;import graph{static int sour, dest;//sour是图形的初始整数,dest是图形的目的整数static int ans[]=new int[1<<16];//静态变量(即全局变量),用于存放图形变换的路径int m=4,n=4,x;int row[]=new int[4];int col[]=new int[4];void setx(int x){=x;}int getx(){return ;}x/=2;}}}public static void output(int N){if(N=={outb(N);return;}output[N]);//[N]存放着从初始值到目的值的遍历路径outb(N);}}实例:实验成绩:指导教师:年月日精心搜集整理,。
回溯算法实验 - 频道分配问题

} int main() { char ch[27]; while(cin>>lines&&lines)
{ int step = 1; m = 5; memset(set,0,sizeof(set)); memset(result,0,sizeof(result)); for(int i=0;i<lines;i++) { cin>>ch; for(int j=2;ch[j]!='\0';j++) set[i][ch[j]-'A']=1; } result[0] = 1; backtrack(1); if(m==1) cout<<m<<" channel needed."<<endl; else cout<<m<<" channels needed."<<endl; } return 0;
3、 分 析 出 算 法 复 杂 度 图 m 可着色问题的回溯算法的计算时间上界可以通过计算解空间树中内结 点个数来估计。图 m 可着色问题的解空间树中内结点个数是 m i 。对于每一个
i n 1
内结点,在最坏情况下,用 same 检查当前扩展结点的每一个儿子所相应的颜色 的 可 用 性 需 耗 时 O(m n) 。 因 此 , 回 溯 法 总 的 时 间 耗 费 是
四、实验内容
1 、 登 陆 POJ 系 统 , 找 到 题 号 为 1129 的 题 目 - 频 道 分 配 ; 2、 阅 读 题 目 , 分 析 出 求 解 该 问 题 的 思 路 ; 3、 使 用 回 溯 算 法 , 实 现 本 题 ; 4 、 进 行 简 单 测 试 , 完 成 之 后 提 交 到 POJ 系 统 。
回溯算法实验报告

回溯算法实验报告实验目的:回溯算法是一种递归算法,通常用于解决有限集合的组合问题。
本实验旨在通过实现回溯算法来解决一个具体的问题,并对算法的性能进行评估。
实验内容:本实验将以八皇后问题为例,展示回溯算法的应用。
八皇后问题是一个经典的问题,要求在一个8x8的棋盘上放置8个皇后,使得任意两个皇后不能在同一行、同一列或同一对角线上。
算法步骤:1. 创建一个二维数组,表示棋盘。
初始化所有元素为0,表示棋盘上无皇后。
2. 逐行进行操作,尝试在每一列放置皇后。
在每一列,从上到下逐个位置进行尝试,找到一个合适的位置放置皇后。
3. 如果找到合适的位置,则将该位置标记为1,并向下一行进行递归操作。
4. 如果当前位置无法放置皇后,则回溯到上一行,尝试放置皇后的下一个位置。
5. 当所有皇后都放置好后,得到一个解。
将该解加入结果集中。
6. 继续回溯,尝试寻找下一个解。
7. 当所有解都找到后,算法终止。
实验结果:在本实验中,我们实现了八皇后问题的回溯算法,并进行了性能测试。
根据实验结果可以看出,回溯算法在解决八皇后问题上表现出较好的性能。
实验中,我们使用的是普通的回溯算法,没有进行优化。
对于八皇后问题来说,回溯算法可以找到所有解,但是随着问题规模的增加,算法的执行时间也会大大增加。
回溯算法是一种非常灵活的算法,可以用于解决各种组合问题。
对于规模较大的问题,回溯算法的时间复杂度很高,需要考虑优化算法以提高性能。
在实际应用中,可以结合其他算法,如剪枝等技巧,来改进回溯算法的性能。
回溯算法是一种非常有价值的算法,值得进一步研究和应用。
实验4 回溯算法

《算法设计与分析》实验报告实验4 回溯算法一、实验目的:掌握回溯算法的设计思想与设计方法。
二、实验环境1、硬件环境CPU:Intel(R) Celeron(R) CPU 1007U @ 1.5GHz内存:4G硬盘:500G2、软件环境操作系统:Windows7编程环境:Visual C++ 6.0编程语言:C三、实验内容1、问题有一个背包,最大限重为C,有n个物品,重量分别为W=<w1, w2, …, w n>,要求找出一个装载方案,使得放入背包物品的重量最大。
输出装载方案和该方案下的背包所装物品总重量。
2、数据结构(1)解的结构一维数据(1)<0 1 0 1 1 1 1>(2) <0 0 1 0 1 1 0>(2)搜索空间的结构3、算法伪代码ReBack(i)1、If i>n then<x1,x2,x3,...xn>是解2、Else while Si≠∅do3、Xi Si中最小值4、SiSi-{Xi}5计算Si+16ReBack(i+1)4、算法分析时间复杂度:O(2n)空间复杂度:O(n)5、关键代码(含注释)#include<stdio.h>int n,c,bestp;//物品的个数,背包的容量,最大重量int w[10000],x[10000],bestx[10000];//w[i]物品的重量,x[i]暂存物品的选中情况,bestx[i]物品的选中情况void Backtrack(int i,int cw){ //cw当前包内物品重量int j;if(i>n)//回溯结束{if(cw>bestp){bestp=cw;for(i=0;i<=n;i++) bestx[i]=x[i];}}elsefor(j=0;j<=1;j++){x[i]=j;if(cw+x[i]*w[i]<=c){cw+=w[i]*x[i];Backtrack(i+1,cw);cw-=w[i]*x[i];}}}6、实验结果(1)输入:C=152,n=7,W=<90, 80, 40, 30, 20, 12, 10> 输出:(2)输入:C=954,n=7,W=<2, 23, 163, 241, 311, 479, 487> 输出:四、实验总结(心得体会、需要注意的问题等)回溯算法也称试探法,是一种系统的搜索问题的解的方法。
实验四 回溯法的应用------跳马算法

实验四回溯法的应用------跳马算法学号:012124345 姓名:梁文耀一、实验目的掌握使用回溯法求解问题的基本思路;理解其特点。
二、实验思想算法的基本思路是:定义结构体:struct PLACE{int x, int y}表示棋盘上的位置。
依题意,马每跳一步之后都可以从七个不同的方向选择下一步的跳马,当然,前提是跳的这一步在棋盘内且它前面的任何一步都没跳到这一格子上(限界),就可以认为这一步跳成功,否则跳马不成功。
若跳马不成功,则找下一个方向尝试跳马,若七个方向都跳马不成功,则回溯。
假设棋盘的行(列)数为n。
在本算法中设置这样一个全局数组:c[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-2,1},{-2,-1},{-1,2},{-1,-2}}; 来记录跳马的八个方向。
三、程序分析(主要算法)int map[12][12], status[12][12], kp;int start,finsh;int c[8][2]={{2,1},{2,-1},{1,2},{1,-2},{-2,1},{-2,-1},{-1,2},{-1,-2}};int flag = 0;void prt(int a[][12]) /* 打印棋盘状态*/{int i,j;printf("\n");for (i=2;i<=9;i++){for (j=2;j<=9;j++)printf("%4d",a[i][j]);printf("\n");}}void status2(void) /* 计算棋盘各点条件数*/ {int i,j,k,i2,j2,kz;for(i=0;i<12;i++)for(j=0;j<12;j++)status[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++){kz=0;for (k=0;k<=7;k++){i2=i+c[k][0];j2=j+c[k][1];if (map[i2][j2]<50) kz++;}status[i][j]=kz;}//prt(status);}void sort1(int b1[],int b2[]) /* 对8个可能的方向按条件数排序*/ {int i,j,mini,t; /*b1[]记录状态值(升序),b2[]记录排序后的下标*/ for (i=0;i<=7;i++){mini=i;for (j=i+1;j<=7;j++)if (b1[j]<b1[mini]) mini=j;t=b1[i]; b1[i]=b1[mini]; b1[mini]=t;t=b2[i]; b2[i]=b2[mini]; b2[mini]=t;}}void init1(void) /* 初始化*/{int i,j;for(i=0;i<12;i++)for(j=0;j<12;j++)map[i][j]=100;for(i=2;i<=9;i++)for(j=2;j<=9;j++)map[i][j]=0;status2();}void search(int i2,int j2) /* 利用递归回溯进行搜索*/ {if (flag == 1)return ;int b1[8],b2[8],i,i3,j3;kp++;for(i=0;i<=7;i++)//8个方向{b2[i]=i;b1[i]=status[i2+c[i][0]][j2+c[i][1]];}//forsort1(b1,b2);for(i=0;i<=7;i++)//检查是否可以走{i3=i2+c[b2[i]][0]; //按照排序中的方向查找j3=j2+c[b2[i]][1];if (map[i3][j3]==1 && kp==65){prt(map);flag = 1;}if (map[i3][j3]==0)//若有路可以走,则执行下面操作{map[i3][j3]=kp;search(i3,j3); //递归调用map[i3][j3]=0; //若还没有走完并且已经没有路走则恢复0状态}//if}//forkp--;//回朔}//searchint main(){int row, column;char ch;//int start,finsh;while (true){//打印提示信息cout<<" 1: 开始程序"<<endl;cout<<" 2: 退出程序"<<endl;cout<<"注意:"<<endl;cout<<""<<endl;cout<<"输入选择(1 或2):"<<endl;//如果输入信息不正确,继续输入do{ch = (char)_getch();}while(ch != '1' && ch != '2');system("cls");//选择3,返回if (ch == '2'){cout<<"退出!!!"<<endl;return 0;}//选择1,进入操作程序else{init1();cout<<"输入初始位置(行row)(1<=row<=8):"<<endl;cin>>row;row = row + 1;cout<<"输入初始位置(列column)(1<=column<=8):"<<endl;cin>>column;column = column + 1;map[row][column] = 1;kp = 1;start = clock();cout<<"遍历结果:"<<endl;search(row,column);flag = 0;finsh = clock();cout<<"算法运行时间:"<<finsh-start<<endl;kp = 1;}//结束cout<<endl<<"Press Any Key To Contimue:"<<endl;_getch();system("cls");}//whilereturn 0;}四、心得体会这程序和以前做的迷宫问题很相象,写起来不是很困难. 确定限界函数,在只有满足限界函数的前提下得到解,不满足限界条件时就要回溯,回到上一个节点,再从另外的方向出发。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、实验结果 通过实验编程,运行程序输入数据后,得到如下结果:
提高题一:用回溯法求解跳马问题
一、实验要求 1、 掌握回溯法的基本原理。 2、 使用回溯法编程,求解跳马问题 二、实验内容 1、 问题描述: 在 N*N 棋盘上有 N2 个格子, 马在初始位置 (X0, Y0) , 按照象棋中马走 “日” 的规则,使马走遍全部格子且每个格子仅经过一次。编程输出马的走法。 2、 给出算法描述。 编程实现,给出 N=5, (X0,Y0)=(1,1)时的运行结果。 二、实验结果 通过实验编程,运行程序输入数据后,得到如下结果:
四、实验总结与体会
教师评 价
优
良
中
及格
不及格
教师签名
日期
中国矿业大学计算机学院实验报告
课程名称 算法设计与分析 实验名称 2.实验内容 5.流程图 实验四 回溯算法 3:1.实验目的 4.运行结果
基本题一:符号三角形问题
一、实验目的 1、掌握符号三角形问题的算法; 2、初步掌握回溯算法; 二、实验内容 下面都是“-” 。 下图是由 14 个“+”和 14 个“-”组成的符号三角形。2 个同号下面都是 “+” ,2 个异号下面都是“-” 。 + + - + - + + + - - - - + - + + + - + + - + - + 在一般情况下,符号三角形的第一行有 n 个符号。符号三角形问题要求对于给定的 n,计 算有多少个不同的符号三角形,使其所含的“+”和“-”的个数相同。
三、实验结果 通过实验编程,运行程序输入数据后,得到如下结果:
基本题二:0—1 背包问题
一、实验目的 1、掌握 0—1 背包问题的回溯算法; 2、进一步掌握回溯算法; 二、实验内容 给定 n 种物品和一背包。物品 i 的重量是 wi,其价值为 vi,背包的容量为 C。问应如何选 择装入背包的物品,使得装入背包中物品的总价值最大?
