材料力学第04章杆件变形分析
合集下载
工程材料力学第四章轴向拉压杆的变形

§4-5 轴向拉(压)杆的变形·胡克定律
拉(压)杆的纵向变形 (轴向变形) 基本情况下(等直杆,两端受轴向力):
纵向总变形Δl = l1-l (反映绝对变形量)
l 纵向线应变 (反映变形程度) l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响,则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律,即
ν
亦即
- n
低碳钢(Q235):n = 0.24~0.28。
7
思考:等直杆受力如图,已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB,ΔlBC,ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系?
uB L1
22
作业:4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式: l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下,当应力不超过材料的比例极限时,
拉(压)杆的纵向变形 (轴向变形) 基本情况下(等直杆,两端受轴向力):
纵向总变形Δl = l1-l (反映绝对变形量)
l 纵向线应变 (反映变形程度) l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响,则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律,即
ν
亦即
- n
低碳钢(Q235):n = 0.24~0.28。
7
思考:等直杆受力如图,已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB,ΔlBC,ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系?
uB L1
22
作业:4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式: l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下,当应力不超过材料的比例极限时,
材料力学杆件变形分析

【解】(1)利用截面法,可以求得1、2两杆的轴力分别为
FN1 80kN (拉力) FN2 40 3kN (压力)
由胡克定律可以求得两杆的变形分别为
l1
ห้องสมุดไป่ตู้
FN1l1 E1 A1
80 103 (1/ cos30o) 200 109 960 106
4.81104 m
l2
FN2l2 E2 A2
10
40 109
通过实验发现,当材料在弹性范围内时,拉压杆的轴向正应
变ε与横向正应变ε′成正比。用μ来表示横向正应变ε′与轴向
正应变ε之比的绝对值,有
或
式中,比例常数μ称为泊松比(Poisson radio)。在比例极
限内,泊松比是一个材料的弹性常数,不同材料具有不同的 泊松比,大多数各向同性材料的泊松比
对于轴向力、横截面面积或弹性模量沿杆轴逐段变化的拉 压杆,如下图所示,其轴向变形为
l n FNili i1 Ei Ai
对于轴力和横截面面积沿轴向连续变化的情况,其轴向
变形量为
l FN (x)dx
l EA(x)
将式 l 等F号Nl两边同除以杆长,即 EA l FN l EA
得到
或 E
第一节 杆件轴向拉压变形 第二节 圆轴扭转变形 第三节 积分法求梁弯曲变形叠加法求梁弯曲变形 第四节 提高梁弯曲刚度的措施 总结与讨论
杆件在载荷作用下都将发生变形(deformation)。在 有些结构或实际工程中,杆件发生过大的变形将影响杆件或 结构的正常使用,必须对杆件的变形加以限制,如工程中使 用的传动轴、车床主轴等变形过大会造成机器不能正常工作; 而有些结构又需要杆件有较大的变形,如汽车上所使用的叠 板弹簧,只有当弹簧有较大变形时,才能起缓冲作用。在结 构的设计中,无论是限制杆件的变形,还是利用杆件的变形, 都必须掌握计算杆件变形的方法。本章将具体讨论杆件轴向 拉伸(或压缩)、圆轴扭转和弯曲三种情况下的杆件变形。 研究杆件变形的目的,一方面是为了分析杆件的刚度问题, 另一方面则是为了求解超静定问题。
杆件的四种基本变形

杆件的四种基本变形杆件变形的基本形式有四种,分别是拉伸或压缩、剪切、扭转、弯曲。
根据材料力学的内容,长度远大于截面尺寸的构件称为杆件,杆件的受力有各种情况,相应的变形就有各种形式。
1、拉伸或压缩这类变形就是由大小成正比方向恰好相反,力的促进作用线与杆件轴线重合的一对力引发的。
在变形上整体表现为杆件长度的弯曲或延长。
横截面上的内力称作轴力。
横截面上的形变原产为沿着轴线逆向的也已形变。
整个横截面形变对数成正比。
2、剪切这类变形就是由大小成正比、方向恰好相反、力的促进作用线相互平行的力引发的。
在变形上整体表现为受剪杆件的两部分沿外力作用方向出现相对错动。
横截面上的内力称作剪力。
横截面上的形变原产为沿着杆件横截面平面内的的乌形变。
整个横截面形变对数成正比。
3、扭转这类变形就是由大小成正比、方向恰好相反、促进作用面都旋转轴杆轴的两个力偶引发的。
整体表现为杆件上的任一两个横截面出现拖轴线的相对旋转。
横截面上的内力称作扭矩。
横截面上的形变原产为沿着杆件横截面平面内的的乌形变。
越紧邻横截面边缘,形变越大。
4、弯曲这类变形由旋转轴杆件轴线的纵向力,或由涵盖杆件轴线在内的横向平面内的一对大小成正比、方向恰好相反的力偶引发,整体表现为杆件轴线由直线变为曲线。
横截面上的内力称作弯矩和剪力。
在旋转轴轴线的横截面上,弯矩产生旋转轴横截面的也已形变,剪力产生平行于横截面的乌形变。
另外,受弯构件的内力有可能只有弯矩,没剪力,这时称作氢铵抠构件。
越紧邻构件横截面边缘,弯矩产生的也已形变越大。
材料力学 杆件的变形计算
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
材料力学第四章平面弯曲

得
∫ A ydA =0
M
dA
z
y z ζdA
My
横截面对中性轴 zdA 的面积矩为零, A 中性轴过形心。 E yzdA 0
A
y
Iyz =0——梁发生平面弯曲的条件
E I E 2 ∫ AσdA· z ∫ A y dA = Mz= y = ρ ρ 1 Mz = EIz —— 梁的弯曲刚度 中性层曲率公式 EI ρ z
y
m MB=-40kN· m MD=22.5kN· B M y B截面 上部受拉、下部受压 tBmax B t max 21.4MPa Iz B yt max 100mm B M y I z 186.6 106 m 4 B B c max 38.6MPa B c max yc max 180mm Iz
max
FQ S
* z max
Izd
d FQ 4 FQ 12 4 d 3 A d 64
3
d/2
z
max
四、薄壁圆环截面梁 中性轴处:
r0
z
max 2
FQ A
max
例 如图所示一T形截面。某截面上的剪力FQ=50kN,与y 轴重合。试求腹板的最大切应力,并画出腹板上的切应力分布图。
1
* FQ S z 1
I zd
4.13MPa
例 一矩形截面外伸梁,如图所示。现自梁中1、2、 3、4点处分别取四个单元体,试画出单元体上的应力,并 写出应力的表达式。
q
1 2 h/4 4 3
z l/4 b
l/4
l
解: (1)求支座反力:
FRA
FRB
1 l/4
材料力学-杆件的变形计算

EIz EIw M (x)dx C
再进行一次积分,可得到挠度方程
EIzw ( M (x)dx)dx Cx D
其中, C 和 D 是积分常数,需要经过边界条件或者连续条件来拟
定其大小。
❖ 边界条件:梁在其支承处旳挠度或转角是已知旳, 这么旳已知条件称为边界条件。
❖ 连续条件:梁旳挠曲线是一条连续、光滑、平坦旳 曲线。所以,在梁旳同一截面上不可能有两个不同 旳挠度值或转角值,这么旳已知条件称为连续条件。
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa,
= 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上旳正应力 σ (b) 螺栓旳横向变形△d
解:1) 求横截面正应力
l 0.04 7.4110-4
l 54 E 200 103 7.41104 148.2 MPa
M lBA BA GI p
180 7Ma π GI p
x
7 3
j
DB
2.33
第三节 梁旳变形
1、梁旳变形
梁必须有足够旳刚度,即在受载后不至于发生过大旳弯 曲变形,不然构件将无法正常工作。例如轧钢机旳轧辊,若 弯曲变形过大,轧出旳钢板将薄厚不均匀,产品不合格;假 如是机床旳主轴,则将严重影响机床旳加工精度。
dx
GI p
取
dj M x
dx GI p
单位长度扭转角 用来表达扭转变形旳大小
单位长度扭转角旳单位: rad/m
GI p 抗扭刚度
GI p 越大,单位长度扭转角越小
g
在一段轴上,对单位长度扭转角公式进行积分,
就可得到两端相对扭转角j 。
dj
dx
dj M x
再进行一次积分,可得到挠度方程
EIzw ( M (x)dx)dx Cx D
其中, C 和 D 是积分常数,需要经过边界条件或者连续条件来拟
定其大小。
❖ 边界条件:梁在其支承处旳挠度或转角是已知旳, 这么旳已知条件称为边界条件。
❖ 连续条件:梁旳挠曲线是一条连续、光滑、平坦旳 曲线。所以,在梁旳同一截面上不可能有两个不同 旳挠度值或转角值,这么旳已知条件称为连续条件。
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa,
= 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上旳正应力 σ (b) 螺栓旳横向变形△d
解:1) 求横截面正应力
l 0.04 7.4110-4
l 54 E 200 103 7.41104 148.2 MPa
M lBA BA GI p
180 7Ma π GI p
x
7 3
j
DB
2.33
第三节 梁旳变形
1、梁旳变形
梁必须有足够旳刚度,即在受载后不至于发生过大旳弯 曲变形,不然构件将无法正常工作。例如轧钢机旳轧辊,若 弯曲变形过大,轧出旳钢板将薄厚不均匀,产品不合格;假 如是机床旳主轴,则将严重影响机床旳加工精度。
dx
GI p
取
dj M x
dx GI p
单位长度扭转角 用来表达扭转变形旳大小
单位长度扭转角旳单位: rad/m
GI p 抗扭刚度
GI p 越大,单位长度扭转角越小
g
在一段轴上,对单位长度扭转角公式进行积分,
就可得到两端相对扭转角j 。
dj
dx
dj M x
第四章杆件的变形

ql 3 ql 3 ql 3 11ql 3 B Bi 21 24 EI 16 EI 3EI 48EI i 1
3
5ql 4 ql 4 ql 4 11ql 4 wC wCi ( ) 384 EI 48EI 16 EI 384 EI i 1
4
目录
5
目录
当拉(压)杆有两个以上的外力作用时,需要先画出轴力图,然后 分段计算各段的变形,各段变形的代数和即为杆的总伸长量。
6
目录
例题4-1 AB长2m, 面积为200mm2。AC面积为250mm2。E=200GPa。 F=10kN。试求节点A的位移。
解:1、计算轴力。(设斜杆为1杆,水平杆
若C点靠近支座B,则两者相差最大,这时,近似的有
b 0 wmax
两者相差不超过2.6%。
bFl bFl 2 wm 16EI 9 3EI
19
2
目录
第五节 用叠加法求梁的弯曲变形
设梁上有n 个载荷同时作用,任意截面上的转角为 ,挠度为w, 若梁上只有第i个载荷单独作用,同一截面上转角为
由叠加原理知:
讨论题
2数值的大小。 试比较1、2两轴扭转角 1 、
620 N· m
1400 N· m d2
780 N· m
780 N· m
620 N· m
2 1
10
目录
例题4-2 某机器传动轴AC如图所示,已知轴材料的切变模量G=80GPa, 轴直径
d 45mm , M e1 120N mm, M e2 200N m ,
d 2 w1 Fb EI M ( x ) x1 1 2 dx1 l dw Fb 2 EI 1 EI ( x1 ) x1 C1 dx1 2l Fb 3 EIw1 x1 C1 x1 D1 6l
杆件变形的基本形式 ppt课件

响! PPT课件
10
刚 度 和 稳 定 问 题
工 程 结 构 的 强 度 、
PPT课件
11
3.2、杆件及其变形形式
材料力学的研究对象是构件。 构件按几何形状分为杆、板、壳和块体。
直杆
曲杆
板
壳
块体
• 研究对象:直杆
PPT课件
12
杆件变形的基本形式
工程实际中杆件受力有各种情况, 相应的变形就有各种形式。在工程结 构中,杆件的基本变形有以下几种:
谢谢!
1、拉伸与压缩
2、剪切
3、扭转
4、弯曲
5、组合受力
PPT课件
13
杆件变形-轴向拉伸与压缩
一、概念
由大小相等、方向相反、 作用线与杆件轴线重合的 一对力所引起,表现为杆 件长度的伸长或缩短。
PPT课件
14
杆件变形-轴向拉伸与压缩
力学模型
P
P
轴向拉伸,对应的力称为拉力。
P
P
轴向压缩,对应的力称为压力。
连接件虽小,起着传递载荷的作用。 特点:可传递一般力,可拆卸。
杆件变形-剪切
2、受力特点和变形特点:
以铆钉为例:
(1)受力特点:
构件受两组大小相等、
(合力) P
n
方向相反、作用线相互很
近(差一个几何平面)的
平行力系作用。
n
(2)变形特点:
P (合力)
构件沿两组平行力系
的交界面发生相对错动。
杆件变形-剪切
单元3 : 材料力学
基础知识
PPT课件
1
材料力学-基本概念
材料力学:研究物体受力后的内在表现, 即变形规律和破坏规律特征。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解】(1)利用截面法,可以求得1、2两杆的轴力分别为
FN1 ? 80kN
(拉力)
FN2 ? 40 3kN (压力)
由胡克定律可以求得两杆的变形分别为
? l1
?
FN1l1 E1 A1
?
80 ? 103 ? (1/ cos30 o) 200 ? 109 ? 960 ? 10?6
第一节 杆件轴向拉压变形
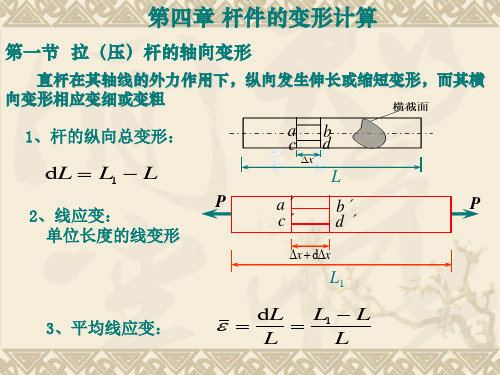
当杆件承受轴向载荷时,其轴向尺寸和横向尺寸均发生变 化,杆件沿轴线方向的变形,称为轴向变形(axial deformation);垂直于轴线方向的变形,称为横向变形 (lateral deformation)。
1.拉压杆的轴向变形与胡克定律
实验表明,杆件受拉时,轴向尺寸增大,横向尺寸缩小, 杆件受压时,轴向尺寸缩小,横向尺寸增大。设拉压杆的横 截面的面积为A,原长为l,在轴向拉力F 作用下产生变形, 如图4-1所示, 变形后杆长为l1, 则杆在轴线方向的 伸长量为
? l ? l1 ? l
Δl是杆件长度尺寸的绝对改变量,称为绝对变形,表示整
个杆件沿轴线方向总的变形量,绝对变形不能说明杆件的变
形程度。要度量杆件变形程度的大小,必须消除杆件原有尺
寸的影响,杆件均匀变形时杆件沿轴线方向的相对变形,即
轴向线应变(axial strain)为
? ? ?l
l
其中ε为杆件轴线方向的线应变,是无量纲量,拉伸时为正,压 缩时为负。
0 ? ? ? 0.5
例4-1 圆截面杆如图4-3所示,已知F =4kN, l1=l2=100mm ,弹性模量E=200GPa 。为保证杆件正常工 作,要求其总伸长不超过0.10mm ,即许用轴向变形 [Δ l]=0.10mm 。试确定杆的直径d。
【解】(1)变形分析。 AB段和BC段的轴力分别为 杆AC的总伸长为
得到
? ? ? 或 ? ? E?
E
上式为胡克定律的另一种表达式。
2.拉压杆的横向变形与泊松比
如图所示,设杆件的原宽度为b,在轴向拉力作用下,宽 度变为b1,横向变形量为Δb=b1-b,则横向应变为
??? ? b
b
显然,如果杆件是如图所示的拉伸变形,则ε′ 为负值,即轴
向拉伸时,杆沿轴向伸长,其横向尺寸减小;轴向压缩时, 杆沿轴向缩短,横向尺寸增大。也就是说,轴向的正应变与 横向的正应变的符号是相反的。
通过实验发现,当材料在弹性范围内时,拉压杆的轴向正应
变ε与横向正应变ε′成正比。用μ来表示横向正应变ε′与轴向
正应变ε之比的绝对值,有
? ? ?? 或 ??? ? ?? ?
式中,比例常数μ称为泊松比(Poisson radio )。在比例极
限内,泊松比是一个材料的弹性常数,不同材料具有不同的 泊松比,大多数各向同性材料的泊松比
(2)直径设计。
按照设计要求,总伸长Δl不得超过许用变形[Δl],即要求
由此得
12Fl1 E?d 2
?
[? l]
d?
12 Fl1
E?[? l]
?
12 ? (4 ? 103 ) ? (100? 10?3 ) ? ? (200 ? 109 ) ? (0.10 ? 10?3 )
?
8.7 ? 10?3 m
?
实验表明,对于工程中的大部分材料,当杆内应力在一定 范围(比例极限)内时,杆的变形量与外力和杆的原长成正比, 与杆的横截面面积成反比,并引入比例常数弹性模量,则可以 得到杆件变形的计算公式为
? l ? FNl EA
上述为描述弹性范围内杆件承受轴向载荷时力与变形的胡 克定律(Hooke 's law ),适用于等截面常轴力拉压杆。在 比例极限内,拉压杆的轴向变形与材料的弹性模量及杆的横 截面面积成反比,乘积EA称为拉压杆的抗拉压刚度 (tensile or compression rigidity )。显然,对于给定 长度的等截面拉压杆,在一定的轴向载荷作用下,抗拉压刚 度EA越大,杆的轴向变形就越小。
8.7mm
可以取直径为 d ? 9mm
3.桁架的节点位移
桁架的变形通常用节点的位移(displacement)表示,现 以下图所示桁架为例,说明桁架节点位移的分析方法。
例4-2 桁架是由1、2杆组成, 通过铰链连接,在节点A承受 铅垂载荷F =40kN作用。已 知杆1为钢杆,横截面面积 A1=960mm2,弹性模量 E1=200GPa,杆2为木杆, 横截面面积 A2=2.5 ×104mm 2,弹性模 量E2=10GPa,杆2的杆长为 1m。求节点A的位移。
对于轴向力、横截面面积或弹性模量沿杆轴逐段变化的拉 压杆,如下图所示,其轴向变形为
? ? l ? n FN i li
i ? 1 E i Ai
对于轴力和横截面面积沿轴向连续变化的情况,其轴向 变形量为
? ? l ? FN (x)dx
l EA(x)
将式
? l ?等F号Nl两边同除以杆长,即 EA
? l ? FN l EA
FN1=2F
F N2=FFl1 ? 12Fl1 i?1 Ei Ai E?d 2 E?d 2 E?d 2
例4-1 圆截面杆如图4-3所示,已知F =4kN, l1=l2=100mm,弹性模量E=200GPa。为保证杆件正常工 作,要求其总伸长不超过0.10mm,即许用轴向变形 [Δl]=0.10mm。试确定杆的直径d。
第四章 杆件变形分析
中北大学理学院力学系
第一节 杆件轴向拉压变形 第二节 圆轴扭转变形 第三节 积分法求梁弯曲变形叠加法求梁弯曲变形 第四节 提高梁弯曲刚度的措施 总结与讨论
杆件在载荷作用下都将发生变形(deformation)。在 有些结构或实际工程中,杆件发生过大的变形将影响杆件或 结构的正常使用,必须对杆件的变形加以限制,如工程中使 用的传动轴、车床主轴等变形过大会造成机器不能正常工作; 而有些结构又需要杆件有较大的变形,如汽车上所使用的叠 板弹簧,只有当弹簧有较大变形时,才能起缓冲作用。在结 构的设计中,无论是限制杆件的变形,还是利用杆件的变形, 都必须掌握计算杆件变形的方法。本章将具体讨论杆件轴向 拉伸(或压缩)、圆轴扭转和弯曲三种情况下的杆件变形。 研究杆件变形的目的,一方面是为了分析杆件的刚度问题, 另一方面则是为了求解超静定问题。
