中国剩余定理及应用
中国剩余定理(模板+详解)

中国剩余定理(模板+详解)问题:今有物不知其数,三三数之剩⼆,五五数之剩三,七七数之剩⼆。
问物⼏何?简单点说就是,存在⼀个数x,除以3余2,除以5余三,除以7余⼆,然后求这个数。
上⾯给出了解法。
再明⽩这个解法的原理之前,需要先知道⼀下两个定理。
定理1:⼏个数相加,如果存在⼀个加数,不能被整数a整除,那么它们的和,就不能被整数a整除。
定理2:两数不能整除,若除数扩⼤(或缩⼩)了⼏倍,⽽被除数不变,则其商和余数也同时扩⼤(或缩⼩)相同的倍数(余数必⼩于除数)。
以上两个定理随便个例⼦即可证明!现给出求解该问题的具体步骤:1、求出最⼩公倍数lcm=3*5*7=1052、求各个数所对应的基础数(1)105÷3=3535÷3=11......2 //基础数35(2)105÷5=2121÷5=4 (1)定理2把1扩⼤3倍得到3,那么被除数也扩⼤3倍,得到21*3=63//基础数633、105÷7=1515÷7=2 (1)定理2把1扩⼤2倍得到2,那么被除数也扩⼤2倍,得到15*2=30//基础数30把得到的基础数加和(注意:基础数不⼀定就是正数)35+63+30=1284、减去最⼩公倍数lcm(在⽐最⼩公倍数⼤的情况下)x=128-105=23那么满⾜题意得最⼩的数就是23了。
⼀共有四个步骤。
下⾯详细解释每⼀步的原因。
(1)最⼩公倍数就不解释了,跳过(记住,这⾥讨论的都是两两互质的情况)(2)观察求每个数对应的基础数时候的步骤,⽐如第⼀个。
105÷3=35。
显然这个35是除了当前这个数不能整除以外都能够被其他数整除,就是其他数的最⼩公倍数。
相当于找到了最⼩的起始值,⽤它去除以3发现正好余2。
那么这个基础数就是35。
记住35的特征,可以整除其他数但是不能被3整除,并且余数是2。
体现的还不够明显,再看下5对应的基础数。
21是其他数的最⼩公倍数,但是不能被5整除,⽤21除以5得到的余数是1,⽽要求的数除以5应该是余1的。
k[x]上中国剩余定理的证明及应用
![k[x]上中国剩余定理的证明及应用](https://img.taocdn.com/s3/m/b18bdc1d5f0e7cd1842536a1.png)
使得 一口( o , 关 于模 m 是 唯一 的 , 中 r dm ) 且 o 其
m m l ,m 2 … ,m k 0
其 中ห้องสมุดไป่ตู้u为展 开 式 中 提 出公 因 子 g ( 第 一 项 1之 除
外) 后所 剩 的多 项 式 。利用 上 述 引 理 可 以类 似 地 得
到在 K ] [ 上的中国剩余定理 。
q ) 唯一 的 。 ( 是
2
[ 上的中 国剩余定理 ]
引理 设 q ( , ) … , ) K[ 内互 。 ) q ( , q ( 为 ]
素且次 数 ≥1的多项 式 , 对 任一 i1 )存 在 则 ( ≤ ≤k , 多项式 h( )∈ ]使 得 K[ ,
h( 一1 m dq( ) ) ( o ) ,
1 传统 的中 国剩余定理
定理 1 … 设 ,。m:… , k 两两 互 素 的 孔, , m 是 个
且有 h 兀 ( 一u i) ( 1 j)=1+q q i u
J≠ ‘
正 整数 , 任给 k个整 数 0 , … , 必 存 在 整 数 , 口 , Ⅱ ,
1 mo 。 ( dq)
56 96
科
学
技
术
与
工
程
l O卷
( 。 ) _ )令 『 ≠ =∑ () , ()则对每 1 个 (≤
≤ , ) 有 ( h ( ( ( o ) ) ) ) r dq( 。 o ) 而 当j 时 , ( )j x -o r dq( ) 于是 #i f x h( ) ( o i j o ) , ( ^ ( ) f( ) 戈 - , )+, ( q( , ( ) ( 一 他 ) i f 戈 ) ) j
中国剩余定理的实际应用

中国剩余定理的实际应用:
有一个年级的同学,每9人一排多5人,每7人一排多1人, 每5人一排多2人,问这个年级至少有多少人?
求数学高手详细解答!剩余定理是什么意思?
5 和 9 的公倍数依次是 45、90、135、180、225 ……
这些公倍数中,被7除余1的数是 225
9 和 7 的公倍数依次是 63、126、189、252……
这其中,被5除余2的是 252
5 和 7 的公倍数是 35、70、105、140、……
其中被9除余5的数是 140
把以上 225 252 140 三个数相加,求得
225 + 252 + 140 = 617
5 7 9 三个数的最小公倍数是 5*7*9=315
617-315 = 302
因此 302 就是这个年级至少人数。
1.韩信点兵:有兵一队,若列成五行纵队,则末行一人,成六行纵队,则末行五人,成七行纵队,则末行四人,成十一行纵队,则末行十人.求兵数.
2.有一堆棋子,三个三个地数剩下2个,五个五个地数剩下4个,七个七个地数剩下6个.问这堆棋子最少有多少个?(用两种方法解)
3.某数除以7余3,除以8余4,除以9余5.从小到大求出适合条件的十个数.
4.某数除以5余2,除以7余4,除以11余8.求适合条件的最小数.
5.一猴子数一堆桃子.两个两个地数剩下1个,三个三个地数剩下1个,五个五个地数剩下3个,七个七个地数剩下3个.问这堆桃子最少是多少个?。
中国剩余定理ppt

m = n / w[i];
d = extended_euclid(w[i], m, x, y);
ret = (ret + y*m*b[i]) % n;
}
return (n + ret%n) % n;
}
模板:最大公约数
int gcd(int a,int b) {
if(0 == a )
return b;
int flag;
while (scanf ("%I64d", &n) != EOF){
scanf ("%I64d%I64d", &m1, &a1);
n--; flag = 0;
while (n--) {
scanf ("%I64d%I64d", &m2, &a2);
d = exGcd (m1, m2, x, y);
e==-1 && d==-1)){
j++;
k=(p*5544+e*14421+i*1288-d+21252)%21252;
if(k>0)
printf("Case %d: the next triple peak occurs in %d days、
\n",j,k);
else
printf("Case %d: the next triple peak occurs in 21252 days、
一些关于中国剩余定理得定理:
定理2:二数不能整除,若被除数扩大(或缩小) 了几倍,而除数不变,则其余数也同时扩大(或 缩小)相同得倍数(余数必小于除数)。
中国剩余定理内涵及其简单应用

中国剩余定理内涵及其简单应用
中国剩余定理是数论中的一个重要定理,它提供了求解一类线性同余方程组的方法。
所谓线性同余方程组,是指一组形如x ≡ a1 (mod m1), x ≡ a2 (mod m2), …, x ≡ an (mod mn)的方程,其中x是未知数,a1, a2, …, an是已知数,而m1, m2, …, mn是不同的正整数。
中国剩余定理的内涵是:当所给线性同余方程组的模m1, m2, …, mn 两两互素时,存在唯一解x ≡ X (mod M),其中X是x的一个解,而M = m1 * m2 * … * mn。
简单来说,中国剩余定理告诉我们,当模数两两互素时,我们可以通过对每个方程求解,再通过一定的运算,得到原方程组的解。
中国剩余定理的应用非常广泛,特别是在密码学和计算机科学中。
例如,当我们需要对一个数进行加密和解密时,可以使用中国剩余定理来进行模运算,从而快速计算得到加密后的结果。
此外,在计算机科学中,中国剩余定理也常用于优化算法和并行计算。
由于中国剩余定理能够将一个大问题拆分成多个小问题并行求解,因此可以显著提高计算效率。
总之,中国剩余定理作为数论中的重要定理,不仅具有深刻的理论意义,还具有广泛的实际应用。
通过它,我们可以快速求解线性同余方程组,加密和解密数据,优化算法等,从而提高计算效率和保护数据安全。
中国剩余定理及其应用

(i = 1, 2,L , n)
1 n( n − 1)(2n − 1) 6
2 2 2 2
当 f ( x) 的次数不超过 M ( x)( M ( x) = m1 ( x)m2 ( x)m3 ( x)L mn ( x)) 的次 数时, f ( x) 唯一确定 . 特 别 地, 当 mi ( x) = x − bi ∈ Q[ x]或R[ x] , bi (i = 1, 2,L , n) 是不相等的常数,从而 mi ( x)(i = 1, 2,L , n) 也就是两两互素的 多项式,由余数定理可知 mi ( x) ≡ mi (bi )(mod x − bi ), (i = 1, 2,L , n) , 从而定理可叙述为一定存在多项式 f ( x) ,使得
⎪f(x) ≡ a (x)(modm (x)) ⎪ 2 2 ⎨ ⎪LLLLLLLLLL ⎪ ⎩f(x) ≡ an (x)(modm n (x))
1 1
(n − 0)(n − 1)(n − 3) (n − 0)(n − 1)(n − 2) + 5× (2 − 0)(2 − 1)(2 − 3) (3 − 0)(3 − 1)(3 − 2)
⎧x ⎪x ⎪ ⎨ ⎪x ⎪ ⎩x ≡ 1(mod 5) ≡ 5(mod 6) ≡ 4(mod 7)
≡ 10(mod11)
按照中国属于定理的记号
M = 5 × 6 × 7 × 11 = 2310, M 1 = 6 × 7 × 11 = 462, M 2 = 5 × 7 × 11 = 385,
有正整数解 x ≡ M 1α1c1 + M 2α 2c2 + L + M nα n cn (mod M ) 且解唯一; 其中 α i 是满足 M iα i ≡ 1(mod mi ), k = 1, 2,L , n) 的一个整 数(参阅 [3]). 下面我们先给出裴蜀恒等式和一个性质,然后证明中国 剩余定理 . 裴蜀恒等式 如果两个数的最大公约数是 d ,则必定存 在两个整数 x, y 使得等式 ax + by = d 成立(参阅 [4]). 性质 同余式组 a ≡ b(mod m j ), j = 1, 2,L , n 同时成立的 充要条件是 a ≡ b(mod[m1 , m2 ,L , mn ]) (参阅 [5]). 证明: 先证存在性: M 因为 m1 , m2 ,L , mn ,两两互素, M = m , 故 ( M k , mk ) = 1, k = 1, 2,L , n , 由 裴 蜀 恒 等 式 可 知 一 定 存 在 整 数 α k , βk 使 得 M kα k + β k mk = 1 ,即 M kα k = − β k mk + 1 ,因此必定存在 α k ,使
中国剩余定理的历史价值和应用

中国剩余定理的历史价值和应用
中国剩余定理(Chinese Remainder Theorem,简称CRT)是古老的数学定理,来源于古印度人拉穆卡尼的《数书大全》,但最早由中国宋朝数学家董仲舒来提出。
CRT是一种快速求解模不互质整数方程组的方法,其历史价值和应用非常广泛。
中国剩余定理可以求解n阶不同进制的数的同余式。
由于CRT的效率高,因此,它在工业上有较多的应用,如计算机硬件中,解数论中的模运算问题时,通常都使用CRT法求解。
例如,在压缩视频时,经典加密算法RSA 就是使用CRT法进行加速计算的。
此外,CRT在许多领域中也有着广大应用,如在凸优化中有测试剩余定理的实验,在几何中的研究的有使用剩余定理的技巧,在模数几何学中也有CRT的计算和推导应用。
而且,CRT在高斯消元法、矩阵计算、主元计算中也有应用可以设计的有关计算的算法。
因此可见,中国剩余定理在古老中国宋朝就已经诞生,它的历史价值和应用十分广泛,它不仅在计算机软件、电子工程中有着重要的地位,而且在许多领域也得到了广大应用,是一种弥足珍贵的古老定理。
中国剩余定理例题讲解2
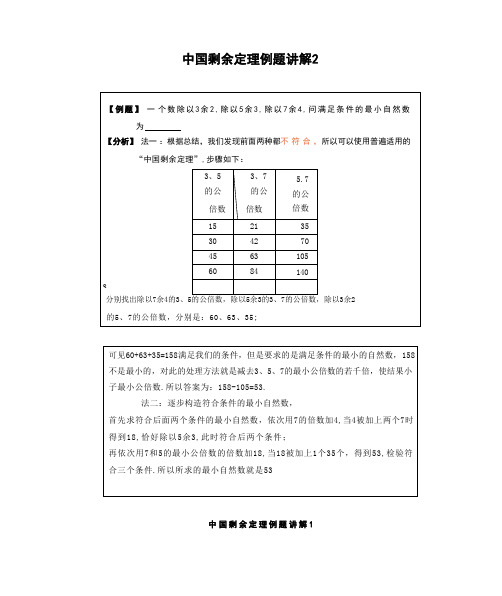
【例题】一个数除以3余2,除以5余3,除以7余4,问满足条件的最小自然数
为
【分析】法一:根据总结,我们发现前面两种都不符合,所以可以使用普遍适用的
“中国剩余定理”,步骤如下:
Q
3、5
的公
倍数
3、7
的公
倍数
5.7的公
倍数
15
21
35
30
42
70
45
63
105
60
84
140
分别找出除以7余4的3、5的公倍数,除以5余3的3、7的公倍数,除以3余2
代,数学家程大位把这个问题的算法编成了四句歌诀:
三人同行七十稀,
五树梅花廿一枝;
O
七子团圆正半月,
除百零五便得知,
用现在的话来说就是:一个数用3除,除得的余数乘70;用5除,除得的余数乘21;用7除,除得的余数乘15.最后把这些乘积加起来再减去105的倍数,算法是;
11除余7,由于[3,5,11]=165,所以这个数最小是165+7=172.
法二:事实上,如果没有“大于10”这个条件,7即可符合条件,所以只需要在7的
基础上加上3、5、11的最小公倍数,得到172即为所求的数.
什么是中国剩余定理?
“物不知数问题”一般解题步骤:
o
①凑“多”相同,即把余数处理成相同条件;余数与除数的和相同
不相互影响各自被对应除数除后所得的余数,
即70a+213+15c是被3除余a,被5除余b,被7除余c的数,
得到18,恰好除以5余3,此时符合后两个条件;
再依次用7和5的最小公倍数的倍数加18,当18被加上1个35个,得到53,检验符
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“中国剩余定理”算理及其应用
“中国剩余定理”算理及其应用:
为什么这样解呢?因为70是5和7的公倍数,且除以3余1。
21是3和7的公倍数,且除以5余1。
15是3和5的公倍数,且除以7余1。
(任何一个一次同余式组,只要根据这个规律求出那几个关键数字,那么这个一次同余式组就不难解出了。
)把70、21、15这三个数分别乘以它们的余数,再把三个积加起来是233,符合题意,但不是最小,而105又是3、5、7的最小公倍数,去掉105的倍数,剩下的差就是最小的一个答案。
用歌诀解题容易记忆,但有它的局限性,只能限于用3、5、7三个数去除,用其它的数去除就不行了。
后来我国数学家又研究了这个问题,运用了像上面分析的方法那样进行解答。
例1:一个数被3除余1,被4除余2,被5除余4,这个数最小是几?
题中3、4、5三个数两两互质。
则〔4,5〕=20;〔3,5〕=15;〔3,4〕=12;〔3,4,5〕=60。
为了使20被3除余1,用20×2=40;
使15被4除余1,用15×3=45;
使12被5除余1,用12×3=36。
然后,40×1+45×2+36×4=274,
因为,274>60,所以,274-60×4=34,就是所求的数。
例2:一个数被3除余2,被7除余4,被8除余5,这个数最小是几?
题中3、7、8三个数两两互质。
则〔7,8〕=56;〔3,8〕=24;〔3,7〕=21;〔3,7,8〕=168。
为了使56被3除余1,用56×2=112;
使24被7除余1,用24×5=120。
使21被8除余1,用21×5=105;
然后,112×2+120×4+105×5=1229,
因为,1229>168,所以,1229-168×7=53,就是所求的数。
例3:一个数除以5余4,除以8余3,除以11余2,求满足条件的最小的自然数。
题中5、8、11三个数两两互质。
则〔8,11〕=88;〔5,11〕=55;〔5,8〕=40;〔5,8,11〕=440。
为了使88被5除余1,用88×2=176;
使55被8除余1,用55×7=385;
使40被11除余1,用40×8=320。
然后,176×4+385×3+320×2=2499,
因为,2499>440,所以,2499-440×5=299,就是所求的数。
例4:有一个年级的同学,每9人一排多5人,每7人一排多1人,每5人一排多2人,问这个年级至少有多少人?(幸福123老师问的题目)
题中9、7、5三个数两两互质。
则〔7,5〕=35;〔9,5〕=45;〔9,7〕=63;〔9,7,5〕=315。
为了使35被9除余1,用35×8=280;
使45被7除余1,用45×5=225;
使63被5除余1,用63×2=126。
然后,280×5+225×1+126×2=1877,
因为,1877>315,所以,1877-315×5=302,就是所求的数。
例5:有一个年级的同学,每9人一排多6人,每7人一排多2人,每5人一排多3人,问这个年级至少有多少人?(泽林老师的题目)
题中9、7、5三个数两两互质。
则〔7,5〕=35;〔9,5〕=45;〔9,7〕=63;〔9,7,5〕=315。
为了使35被9除余1,用35×8=280;
使45被7除余1,用45×5=225;
使63被5除余1,用63×2=126。
然后,280×6+225×2+126×3=2508,
因为,2508>315,所以,2508-315×7=303,就是所求的数。
(例5与例4的除数相同,那么各个余数要乘的“数”也分别相同,所不同的就是最后两步。
)
关于“中国剩余定理”类型题目的另外解法
“中国剩余定理”解的题目其实就是“余数问题”,这种题目,也可以用倍数和余数的方法解决。
不懂论坛上有没人发过。
小学奥赛考试时学习过,也用过,现在把方法写出来,如果懂的也别笑我,呵呵。
选了一本小学奥赛的书上的题目,讲下:
例一,一个数被5除余2,被6除少2,被7除少3,这个数最小是多少?
解法:题目可以看成,被5除余2,被6除余4,被7除余4 。
看到那个“被6除余4,被7除余4”了么,有同余数的话,只要求出6和7的最小公倍数,再加上4,就是满足后面条件的数了,6X7+4=46。
下面一步试下46能不能满足第一个条件“一个数被5除余2”。
不行的话,只要再46加上6和7的最小公倍数42,一直加到能满足“一个数被5除余2”。
这步的原因是,42是6和7的最小公倍数,再怎么加都会满足
“被6除余4,被7除余4”的条件。
46+42=88
46+42+42=130
46+42+42+42=172
这是一种形式的,它的前提是条件中出现同余数的情况,如果遇到没有的,下面讲
例二,一个班学生分组做游戏,如果每组三人就多两人,每组五人就多三人,每组七人就多四人,问这个班有多少学生?
解法:题目可以看成,除3余2,除5余3,除7余4。
没有同余的情况,用的方法是“逐步约束法”,就是从“除7余4的数”中找出符合“除5余3的数”,就是再7上一直加4,直到所得的数除5余3。
得出数为18,下面只要在18上一直加7和5得最小公倍数35,直到满足“除3余2”
4+7=11
11+7=18
18+35=53
这种方法也可以解“中国剩余定理”解的题目。
比“中国剩余定理”更好理解,我觉的速度上会比那个繁琐的公式化的解题更快。
大家可以试下,。
