数学神奇的曲线美
数学中有很多寓意美好的曲线,在极坐标系中的应用

《数学曲线的美丽与应用》一、引言在数学领域中,曲线是一个引人入胜的主题。
数学中有很多寓意美好的曲线,其中在极坐标系中的应用更是令人着迷。
本文将从深度和广度的角度探讨数学曲线的美丽以及在极坐标系中的应用,带领读者一起领略和探索这一令人着迷的数学世界。
二、数学曲线的美丽1. 认识数学曲线数学曲线是描述一个或多个变量之间关系的图形。
通过数学的方法和技巧,我们可以绘制出各种各样的曲线,它们有着不同的形状和特点。
在数学曲线的世界里,有着许多美丽而又深刻的曲线,如正弦曲线、余弦曲线、阿基米德螺线等。
2. 曲线的几何美数学曲线的几何美是无法忽视的,它们的形态和轨迹往往具有令人赞叹的美感。
从螺线的旋转美到椭圆的优雅曲线,每一种曲线都展现着数学之美。
3. 曲线的数学美除了几何美,数学曲线还有着深刻的数学美。
通过对曲线的方程和性质进行分析,我们可以揭示出曲线背后的数学规律和原理,这些规律和原理是数学的精华所在。
三、极坐标系中的数学曲线应用1. 极坐标系简介极坐标系是一种描述平面上点的坐标系,它使用极径和极角来确定点的位置。
在极坐标系中,我们可以用极坐标方程来描述曲线,这为我们研究曲线的特性和应用提供了便利。
2. 极坐标系中的曲线方程在极坐标系中,一些常见的数学曲线可以用极坐标方程来描述,如圆、螺线、双曲线等。
极坐标方程的使用使得我们可以更加直观地理解和分析这些曲线的性质和特点。
3. 曲线在极坐标系中的运动和变换在极坐标系中,曲线的运动和变换也是一个重要的研究方向。
通过调整极坐标方程中的参数,我们可以观察到曲线的旋转、拉伸、平移等运动和变换,这为我们研究曲线的动态特性提供了便利。
四、总结与展望数学曲线作为数学中的经典主题,不仅具有几何美和数学美,还有着丰富的应用价值。
在极坐标系中,数学曲线的应用使得我们更加深入地理解和探索数学曲线的世界。
通过深入研究和探索数学曲线,我们可以发现更多的美和奥秘,也可以将其应用于更广泛的领域。
有趣的数学——摆线,几何中的“海伦”

有趣的数学——摆线,⼏何中的“海伦”摆线,⼏何学的“海伦” (The Helen of Geometry) ,是数学中⽐较独特⽽有趣的曲线之⼀,它被定义为:“在⼀个直线运动的圆上,某⼀固定点所经过的轨迹连成的曲线”,⼜叫做摆线。
最早介绍摆线的参考书,是1501年由査尔斯·鲍威尔(Charles Bouvelles)出版发⾏的。
但是,17世纪,许多著名的数学家(伽利略、帕司科、托⾥切利、笛卡⼉、符麦特、壬、沃利斯、惠更斯、乔恩·贝诺利、莱布尼兹、⽜顿)都致⼒于发现它的性质和特征。
17世纪,⼈们热衷于⽤数学来研究机械学和运动学,这也许可以解释为什么⼈们对摆线也产⽣了浓厚的兴趣。
同当时的许多数学发现⼀样,摆线也有着许多争论,争论谁最先发现了什么原理,相互指责对⽅剽窃,以及贬低对⽅的成果。
结果,摆线被贴上了 “祸根”这样的标签,叫做⼏何学的“海伦”,或者引起纷争的“⾦苹果” 。
17世纪期间,⼈们发现了摆线的很多特征:1) 长度为旋转圆直径的4倍。
尤其有趣的是,⼈们发现,它的长度是⼀个独⽴于π的有理数。
2) 拱形弧线下⽅区域的⾯积等于旋转圆⾯积的3倍。
3) 圆上⼀点的轨迹形成摆线,该点有着不同的速度——事实上,在其中⼀个位置,如点込上,它甚⾄是静⽌不动的。
4) ⼀个摆线形状的容器中,如果将⼤理⽯块从摆线上的不同点松开,使其降落,它们会同时到达底部。
有许多引⼈⼈胜的隽语都与摆线有关,下⾯这句关于⽕车的隽语就特别有趣:在任何时候,⾏进中的⽕车都不会完全朝着发动机牵引的⽅向前进,其本⾝总有⼀部分朝着相反的⽅向做运动。
这个似是⽽⾮的隽语就能够⽤摆线来解释。
这⾥是⼀条曲线,叫做长辐圆滚线——旋转轮外的某⼀固定点形成的轨迹。
这个图形表明,当⽕车朝前移动时,⽕车轮上有些部分在做着向后的运动。
优美的曲线

优美的曲线1.碟形弹簧圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90)) 24*t图12.葉形线.笛卡儿坐標标方程:a=10x=3*a*t/(1 (t^3))y=3*a*(t^2)/(1 (t^3))图23.螺旋线(Helical curve)圆柱坐标(cylindrical)方程:r=ttheta=10 t*(20*360)z=t*3图34.蝴蝶曲线球坐标方程:rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8图45.渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0 s*sin(ang)y=y0-s*cos(ang) z=0图56.螺旋线.笛卡儿坐标方程:x = 4 * cos ( t *(5*360)) y = 4 * sin ( t *(5*360))z = 10*t图67.对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t 0.0001)图78.球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*20图89.双弧外摆线卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360) l*cos(3*t*360) Y=3*b*sin(t*360) l*sin(3*t*360)图910.星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3图1011.心脏线圓柱坐标方程:a=10r=a*(1 cos(theta))theta=t*360图1112.圆内螺旋线采用柱座标系方程:theta=t*360r=10 10*sin(6*theta)z=2*sin(6*theta)图1213.正弦曲线笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=0图1314.太阳线(这本来是做别的曲线的,结果做错了,就变成这样了)图1415.费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做图1516.Talbot 曲线卡笛尔坐标方程:theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a f*f*c*c)*cos(theta)/ay = (a*a-2*f f*f*c*c)*sin(theta)/b图1617.4叶线(一个方程做的,没有复制)图1718.Rhodonea 曲线采用笛卡尔坐标系方程:theta=t*360*4x=25 (10-6)*cos(theta) 10*cos((10/6-1)*theta) y=25 (10-6)*sin(theta)-6*sin((10/6-1)*theta)图1819. 抛物线笛卡儿坐标方程:x =(4 * t)y =(3 * t) (5 * t ^2)z =0图1920.螺旋线圓柱坐标方程:r = 5theta = t*1800z =(cos(theta-90)) 24*t图2021.三叶线圆柱坐标方程:a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)图212.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a b)*cos(theta)-b*cos((a/b 1)*theta) y=(a b)*sin(theta)-b*sin((a/b 1)*theta) z=0图2223. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta c)y=b*sin(theta)图2324.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta) c*cos((a/b-1)*theta) y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a b)*cos(theta)-c*cos((a/b 1)*theta) y=(a b)*sin(theta)-c*sin((a/b 1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360) cos(2*t*360)) y = a*(2*sin(t*360)-sin(2*t*360))图2627.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 t*10y = 8*a^3/(x^2 4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2 a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50 solvex^3 = y^2*(2*a-x) for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x) exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图3435.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x) exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3 1图3637.八字曲线x = 2 * cos ( t *(2*180)) y = 2 * sin ( t *(5*360)) z = 0图3738.螺旋曲线r=t*(10*180) 1theta=10 t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0 图3940.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180)) y = 100*t * sin ( t *(5*180)) z = 0图4142.蛇形曲线x = 2 * cos ( (t 1) *(2*180)) y = 2 * sin ( t *(5*360))z = t*(t 1)图4243.8字形曲线柱坐标theta = t*360r=10 (8*sin(theta))^2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10 (3*sin(theta*2.5))^2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图4647.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2 z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849.甚至这种螺旋花曲线theta = t*360*4r=10 (3*sin(theta*2.5))^2 z = t*16图4950 鼓形线笛卡尔方程r=5 3.3*sin(t*180) ttheta=t*360*10z=t*10图5051 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c) y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图5253.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3 z=t^3*(t+1)图5354.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360) Y=b*sin(t*360)+a*sin(3*t*360)图5556.梅花曲线theta=t*360r=100+50*cos(5*theta) z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图5758.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图5859.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2) theta=t*360phi=log(1+t*360)*t*360图6061.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)图6162.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360) y=(50+10*sin(t*360*15))*sin(t*360) z=10*cos(t*360*5)图6263.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图6364.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图6465.柱面正弦波线柱坐标:方程theta=t*360z=5*sin(5*theta-90)图6566. ufo (漩涡线)球坐标:rho=t*20^2theta=t*log(30)*60 phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1) x=r*cos(thta0)y=r1*sin(thta1)z=068.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
数学延展出的线条美学

数学延展出的线条美学
首先,数学中的曲线和线条可以展现出优美的几何形态。
例如,圆形、椭圆、双曲线等曲线都有独特的美感,它们的数学性质和几
何特征使它们成为了艺术和设计中常用的元素。
这些曲线不仅在数
学上具有美学意义,还在艺术作品和建筑设计中被广泛运用,展现
出了数学美学的魅力。
其次,数学中的线条和曲线还可以通过函数的图像展现出丰富
的变化和对称美。
例如,正弦曲线、余弦曲线等具有周期性变化的
函数图像,展现出了优美的波动和对称美。
这些图像不仅在数学分
析中有重要的应用,还在艺术创作和设计中被广泛地运用,成为了
抽象艺术和现代设计中的灵感之源。
此外,数学中的线条美学还可以通过拓扑学和复变函数等抽象
数学理论展现出来。
拓扑学中的结点、连通性和曲面的特性,以及
复变函数中的解析性和全纯性等概念都可以被看作是线条美学的抽
象表现。
这些抽象概念的美学意义不仅体现在数学理论的深刻内涵中,也在现代艺术和设计中找到了具体的表现。
总的来说,数学延展出的线条美学是一个多维度的概念,既包
括了几何图形的美感,也包括了函数图像的变化美和抽象数学理论的深刻美。
这些美学意义不仅在数学研究中具有重要价值,也在艺术、设计和人类审美活动中产生了深远的影响。
因此,我们可以说数学延展出的线条美学是数学的一大魅力所在,也是人类文明中不可或缺的一部分。
数学的美感从形到公式的美丽之旅

数学的美感从形到公式的美丽之旅数学是一门独特而美妙的学科,它以其深邃的逻辑和精确的推理能力吸引无数学者的心灵。
从形到公式的美丽之旅,让我们一同领悟数学的美感。
一、形的美感形是数学中最基本的概念之一,它在数学中扮演着重要的角色。
让我们先来探索形的美感。
1. 几何之美几何学是研究形和空间关系的学科,从线段、角、三角形到圆、椭圆,每一种几何形状都蕴含着独特的美感。
例如,圆形代表着完美与和谐,它的对称性使得我们欣赏到了几何之美。
2. 对称的魅力对称是形美的重要特征之一。
无论是镜面对称还是轴对称,对称性都给人以美的享受。
对称性不仅仅存在于几何形状中,它也存在于许多数学问题中,如函数的对称性、方程的对称性等。
对称的魅力使我们在数学的世界中感受到了和谐与平衡。
3. 多面体的奇妙多面体是由多个平面围成的立体图形,它们的平整外表和规则的几何结构令人惊叹。
正多面体,如正方体、正六面体等,不仅在实际生活中经常出现,而且它们的对称性和完美的形状使人沉醉其中。
二、公式的美感公式是数学中用于表示关系和规律的一种形式化语言。
让我们继续我们的旅程,来领略公式的美感。
1. Euler公式的魔力欧拉公式是数学中最著名的公式之一,它连接了数学的五个最基本的数:0、1、e、π和i。
它的形式简洁而优美,具有深刻的数学内涵。
许多数学家都被这个公式的美感所吸引,把它当作最具代表性的数学公式之一。
2. 黄金分割的神奇黄金分割是指将一个线段分为两个部分,使得整体与较长部分之间的比等于较长部分与较短部分之间的比。
黄金分割具有神奇的美感,它被广泛应用于建筑、艺术和设计中,给人以和谐与美丽的感受。
3. 级数的魅力级数是数学中一个重要的概念,它是无穷个数的和。
级数的收敛与发散是数学中的重要问题之一,而级数的公式和特殊性质也展现出了独特的美感。
例如,调和级数、等比级数等都是数学中美丽的存在。
三、公式与形的结合在数学的世界中,公式和形相互交织,相互依存,共同构成了数学的美感。
奇妙的数学曲线1.碟形弹簧圆柱坐标,方程r=5,theta=t3600,z
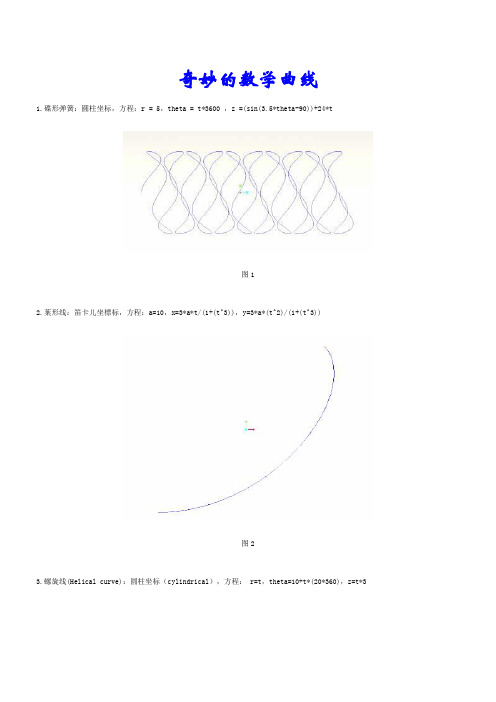
奇妙的数学曲线1.碟形弹簧:圓柱坐标,方程:r = 5,theta = t*3600 ,z =(sin(3.5*theta-90))+24*t图12.葉形线:笛卡儿坐標标,方程:a=10,x=3*a*t/(1+(t^3)),y=3*a*(t^2)/(1+(t^3))图23.螺旋线(Helical curve):圆柱坐标(cylindrical),方程: r=t,theta=10+t*(20*360),z=t*3图34.蝴蝶曲线:球坐标,方程:rho = 8 * t ,theta = 360 * t * 4 ,phi = -360 * t * 8图45.渐开线:采用笛卡尔坐标系,方程:r=1,ang=360*t,s=2*pi*r*t,x0=s*cos(ang) ,y0=s*sin(ang) ,x=x0+s*sin(ang) ,y=y0-s*cos(ang) ,z=0图56.螺旋线:笛卡儿坐标,方程:x = 4 * cos ( t *(5*360)) ,y = 4 * sin ( t *(5*360)) ,z = 10*t图67.对数曲线:笛卡尔坐标系,方程:z=0,x = 10*t ,y = log(10*t+0.0001)图78.球面螺旋线:采用球坐标系,方程:rho=4 ,theta=t*180 ,phi=t*360*20图89.双弧外摆线:卡迪尔坐标,方程: l=2.5,b=2.5,x=3*b*cos(t*360)+l*cos(3*t*360),Y=3*b*sin(t*360)+l*sin(3*t*360)图910.星行线:卡迪尔坐标,方程:a=5,x=a*(cos(t*360))^3,y=a*(sin(t*360))^3图1011.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*36012.圆内螺旋线采用柱座标系方程:theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)图1213.正弦曲线笛卡尔坐标系方程:x=50*ty=10*sin(t*360)z=014.太阳线(这本来是做别的曲线的,结果做错了,就变成这样了)图1415.费马曲线(有点像螺纹线)数学方程:r*r = a*a*theta圓柱坐标方程1: theta=360*t*5a=4r=a*sqrt(theta*180/pi)方程2: theta=360*t*5a=4r=-a*sqrt(theta*180/pi)由于Pro/e只能做连续的曲线,所以只能分两次做图1516.Talbot 曲线卡笛尔坐标方程:theta=t*360a=1.1b=0.666c=sin(theta)f=1x = (a*a+f*f*c*c)*cos(theta)/ay = (a*a-2*f+f*f*c*c)*sin(theta)/b图16 17.4叶线(一个方程做的,没有复制)图1718.Rhodonea 曲线采用笛卡尔坐标系方程:theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)图1819. 抛物线笛卡儿坐标方程:x =(4 * t)y =(3 * t) + (5 * t ^2)z =0图1920.螺旋线圓柱坐标方程:r = 5theta = t*1800z =(cos(theta-90))+24*t图2021.三叶线圆柱坐标方程:a=1theta=t*380b=sin(theta)r=a*cos(theta)*(4*b*b-1)图2122.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图2223. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图2324.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图3435.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图3637.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图3738.螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图3940.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 082 小蜜蜂笛卡尔坐标系:x=cos(t*360)+cos(3*t*360)Y=sin(t*360)+sin(5*t*360)图8283 弯月x=cos(t*360)+cos(2*t*360)Y=sin(t*360)*2+sin(t*360)*2图8384 热带鱼a=5x=(a*(cos(t*360*3))^4)*ty=(a*(sin(t*360*3))^4)*t图8485 燕尾剪x=3*cos(t*360*4)y=3*sin(t*360*3)z=t图8586 天蚕丝theta=t*3600r=(cos(360*t*20)*.5*t+1)*t图86 87 心电图圆柱坐标系:r=sin(t*360*2)+.2theta=10+t*(6*360)z=t*3图87 88 变化后的星形线迪卡尔坐标系theta=t*360x=10*cos(theta)^3y=10*sin(theta)^3z=cos(theta)89 小白兔theta=t*360-90r=cos(360*(t/(1+t^(6.5)))*6*t)*3.5+5图89 90 大家好theta=t*360+180r=cos(360*t^3*6)*2+5图9091 蛇形线笛卡尔坐标系:x=2*cos(t*360*3)*ty=2*sin(t*360*3)*tz=(sqrt(sqrt(sqrt(t))))^3*5图91 92 五环柱坐标:theta=t*360*4r=cos(t*360*5)+1图92 93 蜘蛛网柱坐标:theta=t*360*5r=t*sin(t*360*25)*5+8图93 94 次声波笛卡尔:x=t*5y=t*cos(t*360*8)图94 95 十字渐开线柱坐标:theta=t*360*4r=(cos(t*360*16)*0.5*t+1)*t图95 96 内五环笛卡尔theta=t*360*4x=2+(10-5)*cos(theta)+6*cos((10/6-1)*theta)y=2+(10-5)*sin(theta)-6*sin((10/6-1)*theta)图96 97 蜗轨线柱坐标;theta=t*360*2r=cos(t*360*30)*t*0.5+t*2。
十大最美函数曲线

十大最美函数曲线随着数学发展的不断深入,函数曲线也受到了广泛的重视。
人们发现,处理数学问题时,函数曲线会产生一种美丽的艺术效果,从而被称为函数曲线的美学。
以下就是十大最美函数曲线。
一、椭圆曲线椭圆曲线是一种非常美丽的函数曲线,它可以用来表示圆形或椭圆形。
它是一个广为人知的数学曲线,也是古希腊和罗马文化的象征。
人们发现,它的美丽和优雅也可以被用来解决复杂的数学问题。
二、牛顿-拉斯维加斯曲线牛顿-拉斯维加斯曲线是由英国数学家牛顿和瑞典数学家拉斯维加斯发现的数学曲线。
它以非常有趣的方式表示出来,可以用来描述复杂的函数行为。
它在把握事物的本质上发挥了重要作用,同时也给人们带来了艺术效果。
三、三角形曲线三角形曲线是一种把一个正三角形投影到二维空间的曲线,它可以用来描述三角形的半径,从而产生一种视觉效果。
它的美丽可以用来表示宇宙的可能性,也可以用来解决复杂的函数问题。
四、帕累托曲线帕累托曲线是由西班牙数学家帕累托发现的数学曲线,它是一个关于几何以及统计学的概念。
它表示出了一组特定的函数线,可以用来描述物体表面的形状和流动,也可以用来解决许多复杂的函数问题。
五、哈贝马尔曲线哈贝马尔曲线是由德国数学家哈贝马尔发现的一种函数曲线,它可以用来描述一个物体的运动轨迹。
它表示了宇宙中的复杂性,用来解决许多复杂的数学问题,例如三角函数,物理学,化学等。
六、弗洛伊德曲线弗洛伊德曲线是一种由德国数学家弗洛伊德发现的函数曲线,它可以用来表示一个物体的旋转轨迹。
它是一个非常精确的函数曲线,可以帮助人们理解未知的物理现象,从而有助于解决许多复杂的函数问题。
七、双曲线双曲线是一种由法国数学家德洛比发现的函数曲线,它可以用来表示一个物体的运动轨迹,同时也可以用来描述宇宙中的关系。
人们发现,它可以用来解决复杂的数学问题,例如三角函数、圆形函数以及多元函数等。
八、三次贝塞尔曲线三次贝塞尔曲线是一种由法国数学家贝塞尔发现的函数曲线,它可以用来描述一个物体的运动轨迹。
神奇的分形艺术(二):一条连续的曲线可以填满整个平面

神奇的分形艺术(二):一条连续的曲线可以填满整个平面虽然有些东西似乎是显然的,但一个完整的定义仍然很有必要。
比如,大多数人并不知道函数的连续性是怎么定义的,虽然大家一直在用。
有人可能会说,函数是不是连续的一看就知道了嘛,需要定义么。
事实上,如果没有严格的定义,你很难把下面两个问题说清楚。
你知道吗,除了常函数之外还存在其它没有最小正周期的周期函数。
考虑一个这样的函数:它的定义域为全体实数,当x为有理数时f(x)=1,当x为无理数时f(x)=0。
显然,任何有理数都是这个函数的一个周期,因为一个有理数加有理数还是有理数,而一个无理数加有理数仍然是无理数。
因此,该函数的最小正周期可以任意小。
如果非要画出它的图象,大致看上去就是两根直线。
请问这个函数是连续函数吗?如果把这个函数改一下,当x为无理数时f(x)=0,当x为有理数时f(x)=x,那新的函数是连续函数吗?Cauchy定义专门用来解决这一类问题,它严格地定义了函数的连续性。
Cauchy定义是说,函数f在x=c处连续当且仅当对于一个任意小的正数ε,你总能找到一个正数δ使得对于定义域上的所有满足c-δ< x <c+δ的x都有f(c)-ε<f(x)<f(c)+ε。
直观地说,如果函数上有一点P,对于任意小的ε,P点左右一定范围内的点与P的纵坐标之差均小于ε,那么函数在P点处连续。
这样就保证了P点两旁的点与P无限接近,也就是我们常说的“连续”。
这又被称作为Epsil on-Delta定义,可以写成“ε-δ定义”。
有了Cauc hy定义,回过头来看前面的问题,我们可以推出:第一个函数在任何一点都不连续,因为当ε< 1时,δ范围内总存在至少一个点跳出了ε的范围;第二个函数只在x=0处是连续的,因为此时不管ε是多少,只需要δ比ε小一点就可以满足ε-δ定义了。
