大学物理D类ch5流体力学2015
大学物理:第五章 流体力学 (Fluid Mechanics)

Aneurysm(动脉瘤)
若处动脉的半径增大N倍 血液流速就缩小N2倍 病灶处的压强大幅度上降 由于该处血管壁薄,使血 管容易破裂。
上海交通大学 物理系
Atherosclerosis(动脉粥样硬化)
动脉病变从内膜开始。一 般先有脂质和复合糖类积 聚、出血及血栓形成,纤 维组织增生及钙质沉着, 并有动脉中层的逐渐蜕变 和钙化,病变常累及弹性 及大中等肌性动脉,
?
? hB=0.5m
P0
?
0
1 2
v
2 c
ghc
Pc
1 2
v
2 A
ghA
PA
vc 2ghA 6 m / s
B,C点
1 2
v
2 c
ghc
Pc
1 2
v
2 B
ghB
PB
SBvB SCvC
PB P0 0.85g
PB P0 ghD
hD 0.85m
上海交通大学 物理系
一柱形容器,高1m、截面积为5x10-2 m2,储满水 ,在容器底部有一面积为2x10-4 m2 的水龙头,问 使容器中的水流尽需多少时间?
度变小,压强变大
压力
上海交通大学 物理系
马格纳斯效应
上海交通大学 物理系
机翼受到的举力
Q:用机翼上、下的流速变化,讨论其受到的升力,是否合理
上海交通大学 物理系
上海交通大学 物理系
压强的范围
太阳中心 地球中心 实验室能维持的最大压强 最深的海沟 尖鞋跟对地板 汽车轮胎 海平面的大气压 正常的血压 最好的实验室真空
四、液流连续原理(Principle of continuity of flow)
大学物理流体力学精品PPT课件

三 粘性与粘度
粘性——流体流动时,在内部产生的切应力。 流体流动时,各层流体的流速不同。快层必然带 动慢层,慢层必然阻滞快层。层与层之间的相对 滑动,产生内摩擦力。
z
F
v0
v+dv
f f v
5
四 理想流体的概念
理想流体——没有粘性并且不可压缩的流体。
五 流速场 定常流动
拉格朗日的追踪法 ——流元、流块
§2-3. 伯肃叶公式和斯托克斯公式 层流与湍流
层流: 流体运动规则,各层流动互不掺混,质 点运动轨线是光滑,而且流场稳定。
湍流: 流体运动极不规则,各部分激烈掺混, 质点运动轨线杂乱无章,而且流场极不 稳定。
21
牛顿内摩擦定律
流体流动时,各层流体的流速不同。快层必然带 动慢层,慢层必然阻滞快层。层与层之间的相对 滑动,产生内摩擦力。
1 2
v2
PA
PB
gh
v 2gh
3.飞机机翼周围的空气是如何流动的
假设在机翼右方的空气是水平方向以速度v1向左运动的,如图。 由于机翼倾斜,流经机翼的流线向 下偏移,如图中的v2。这两个矢量 之差v2- v1正是指向机翼对空气的 作用力的方向。根据牛顿第三定律, 空气对机翼施加大小相等、方向相 反的反作用,如图中的F。 这个力 的垂直分量正是飞机的升力(lift)。
公式 • §2-4. 液体的表面现象
3
§2-1. 理想流体
一 流体 液体和气体统称为流体,最鲜明的特征是
形状不定,具有流动性。
气体:易压缩 液体: 不易压缩
二 压强
dS dF
面积元 两侧流体相互作用的弹性力
dS
dF
方向为面元内法线方向
p dF 单位面积上的压力称为压强
大学物理-流体力学

五.伯努利方程的应用 1.空吸作用
由连续性原理: Sv 常量
可见:S大则v小,S小则v大。 对于水平流管,伯努利方程变为:
P 1 v2 常量
2
可见:s小则P小,s大则P大。
应用:喷雾器,水流抽气机,家俱厂的喷漆机.
喷雾器
水流抽气机
1912年,有一只大的远洋轮船和一只小的巡洋舰 几乎平行地在海上航行.当它们之间的距离只有 100m多一点时,大船好象一块巨大的磁铁,小船在 强大的吸引力作用下,径直冲向大船,结果会怎样 大家是可以想象的,这特别大的吸引力是怎样产生 的呢?
2.流线:
特点:1)流线不会相交; 2)定常流动的流线形状是稳定不变的.
3.流管:特点:内外的流体不会交换.
三.流体的连续性原理
1.推导:
在 t 时间内流过两个截面的
流体质量相等.即:
1v1s1t 2v2s2t 1v1s1 2v2s2
对于不可压缩流体,密度不变,即 1 2
v1s1 v2s2或vdS 常量 连续性方程
即单位时间内流过流管中任一截面的流体 体积都相等.
2.讨论:
(1) 理想流体稳定流动时, v 1 s
(2) 单位时间内流过某截面的流体体积和流体 质量分别称为流体的体积流量和质量流量:
体积流量: QV vS
质量流量: Qm vS
(3)对于分支管道,连续性方程变为:
v1S1 v2S2 v3S3
应用:天然气管,石油管等
例1:流体在半径为R的管内作定常流动,截面上的流速按
v v0 (1
设R=5cm,
r R)
v0
分布,r为截面上某点到轴线的距离。
1.2m s1 。求体积流量。
计算流体力学_Ch5

SIMPLE算法
5.3 定常流动的压强速度耦合算法
(1) 交错网格
高度振荡特性 的压强分布
5.3 定常流动的压强速度耦合算法 (2)动量方程的离散形式
pI , J pI 1, J Vu S Vu ai , J ui , J anbunb xu a v a v pI , J pI , J 1 V S V nb nb I, j I, j v v y v
x=0.2m F =u =2.5 D=/x=0.5 Pe =F/D =5
5.2 对流扩散问题的有限体积法 3. 用20个单元, 等距节点中心差分法: u=2.5m/s
0 0 7.25 - 0.75 - 3.25 4.0 - 0.75 0 ... ... ... ... 0 - 3.25 4.0 - 0.75 0 0 0 - 3.25 0 1 6.5 0 2 0 ... ... ... 0 19 0 0 4.75 20
题
第五章 有限体积法 5.3 定常流动的压强速度耦合算法
例:二维定常层流
u u p ( uu ) ( vu) ( ) ( ) Su x y x x y y x
v v p ( uv) ( vv) ( ) ( ) Sv x y x x y y y ( u ) ( v) 0 x y
系数矩阵必须满足的有界性条件
anb a p a a nb p
在所有节点 在至少一个节点(通常 在边界附近)
5.2 对流扩散问题的有限体积法 (2)一阶迎风格式
5.2 对流扩散问题的有限体积法 例. 用5个单元, 等距节点迎风格式解 一维对流扩散 输运方程。边界条件:(0)=1, (L)=0 L=1.0m,=1.0 kg/m3,=0.1 kg/m/s (1) u=0.1m/s;(2) u=2.5m/s。 解 x=0.2m, D=/x=0.5, (1) u=0.1m/s F =u =0.1, Pe =F/D=0.2 例 题 (2) u=2.5 m/s F =u =2.5, Pe =F/D=5
《大学物理流体力学》课件

全局旋转和局部旋转
当流体运动区域存在整体旋转时,称为全局旋转, 布尔沃姆图形是全局旋转的典型形式;反之称为局 部旋转,飞溅是一个例子。
流体的受迫旋转和自由旋转
不同的流体旋转运动分类为受迫旋转和自由旋转。 中心式受迫旋转是一个例子。
圆柱绕流和球绕流
第二章:流体的基本概念
1
流体的定义
流体是一种物质,它可以流动而不断变
流体的分类体和非牛顿流体。
3
流体的基本性质
流体具有惯性、黏性、压缩性和表面张
流体的运动状态描述
4
力等特性。
流体的流速、压强和密度等量可以用来 描述它的运动状态。
第三章:流体静力学
流体静力学基本方程
贝努利方程和庞加莱定理等方程可用于描述流体在静 止状态下的运动。
流体静压力和压强
流体静压力是由于重力导致的压强差异。底层压力更 大,顶层压力更小。
流体静压力的应用
流体静压力可用于测量液体的密度以及用在液压工 程中。
流体静压力的中心和力矩
静压力的中心称为浮心,静压力产生的力矩是力矩 的重要应用之一。
第四章:流体动力学
流体动力学的基本概念和基本方程
流体动力学研究流体在运动状态下的各种现象, 包括流速、压强和密度等参数。
连续性方程和质量守恒定律
连续性方程表示质量在流体中的守恒,质量守 恒定律表示在动力学中质量不能被破坏或创造。
动量守恒定律
动量守恒定律表示对于一个封闭系统,其初始 和最终状态的总动量是相等的。
能量守恒定律
能量守恒定律说明在封闭系统中,各种形式的 能量总是守恒且相互转化。
第五章:流体的旋转运动
实用流体力学ch5
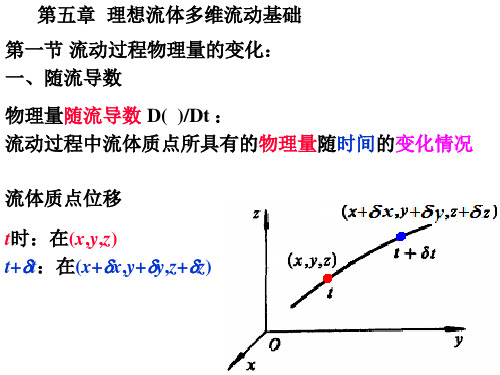
先研究二维流动
t时:正方形流体微团ABCD,边长ds
均匀流场:
各点速度大小、方向都一样
t+dt时:该流体微团移到A’B’C’D’位置
流体微团:保持原大小、形状、方向 只移动了一个位置——平移运动
不均匀流场,但速度变化连续
流体微团大小、形状、方向发生改变
除平移运动外,还要发生其它形式运动
质点A速度矢量: 质点A速度分量:(VAx, VAy)
加速度矢量形式:
质点运动加速度由两部分组成: (1) 局部加速度或当地加速度
在给定空间点上流体质点运动速度随时间变化率 由流动不定常性引起的 对定常流:
(2) 对流加速度或迁移加速度:
流体质点在空间运动时引起速度变化率 由流动不均匀性引起的。 对均匀流:
\ 加速度在三个坐标轴方向的分量:
第二节 流体微团运动分析: 流体微团基本运动形式:
涡管:在旋涡场中任取一条封闭曲线 (不是涡线) ,通过曲线上每一点作一 条涡线,所有涡线形成的管形曲面
二、速度环量: 速度环量:流场中流动速度沿给定封闭曲线的线积分
:曲线C上长度为dl的无限小弧段, 方向与曲线在该处切线方向重合
环量积分方向:逆时针方向为正 无旋或有旋运动都可用上式计算环量
第四节 无旋流动: 无旋运动:流场中各处角速度为零的流动
3)封闭控制面A3:位于远场,其上流速与压强已知
4)分速度Vx, Vy, Vz及作用力分量的正负与坐标系有关
5)控制面上法向速度Vn:以控制面外法线方向为正 动量方程变为:
二、微分形式动量方程: 微小立方体中心:x, y, z
微小立方体边长:dx, dy, dz
流体密度:r
牛顿第二运动定律:
单位时间内控制体内流体质量减少量:
大学物理_流体力学0

F1 S1
阿基米德原理
阿基米德原理:物体在流体中所受的浮力 大小等于该物体排开同体积流体的重量。 浮力作用在被物体所排开的同体积的液块 的质心(重心)上。
F Vg
阿基米德原理是帕斯卡原理的推论
§5.2 流体力学的基本概念
1. 理想流体(Ideal fluid)
不可压缩,无粘滞力(内摩擦力)的流体。
Note: 定常流动不意味匀速流动。
4. 流线(Stream line)
v1 v2
流体质点流动的轨迹线,流线上任一点的 切线方向表示流体元在该点的流速方向。
流线不会相交。
定常流动的流线形状及分布稳定不变。
5. 流管(Flow tube)
由流线所围成的管状区域。
流体质点不会穿越管壁流动。
定常流动中,流管形状稳定不变。 流线是流管的极限。 (实际流管中包含任意多由流线所 围成的流管)
c
S2
d
v2
v1S1t v2 S2 t V
所以:A P P)V ( 1 2
a b
h1 h2 P 2
能量增量(显然,能量增量为两阴影区流体能量之差) 1 1 2 2 E ( v2 V gh2 V)( v1 V gh1V) 2 2
2 2 所以得:p1 1 v1 gh1 p2 1 v2 gh2 2 2
h
1 2 1 2 PA v A PB vB 2 2
Q S Av A S B vB
SA
SB
又:
PB PA gh
A B
(范丘里流量计)
计示压强与绝对压强 以液柱高标示的压强为计示压 强。 管道中某点的实际压强为绝对 压强。 绝对压强差=计示压强差
大学物理中的流体力学流体的运动与应用

大学物理中的流体力学流体的运动与应用流体力学是研究流体在运动中的行为和性质的学科。
在大学物理课程中,流体力学是一个重要的分支,它涵盖了流体的基本概念、流体静力学、流体动力学以及流体在各种应用中的重要性。
本文将探讨大学物理中的流体力学,重点关注流体的运动和在实际应用中的应用。
一、流体的基本概念1. 流体的定义流体是指那些可以流动的物质,包括液体和气体。
与固体不同,流体具有流动性和变形性。
2. 流体的性质流体具有一些独特的性质,如压缩性、流动性、粘滞性和表面张力等,这些性质对流体的运动和应用产生重要影响。
二、流体静力学1. 流体静力学的基本原理流体静力学研究的是流体处于静止状态时的力学行为。
根据帕斯卡定律,任何外界施加在封闭流体上的压力都会均匀地传递到流体内各个部分。
2. 流体静压力流体静压力是指流体由于受到外界压力作用而产生的压力。
流体静压力与深度、密度及重力加速度相关,可以通过压力公式来计算。
三、流体动力学1. 流体的运动描述流体动力学研究的是流体在运动中的行为和特性。
流体可以分为层流和湍流两种形式,层流是指流体分层无交叉流动的情况,湍流则是流体混乱交织的流动状态。
2. 流体的连续性方程流体的连续性方程表明,在稳态流动中,流体质量的流动速率始终保持不变。
通过连续性方程,可以推导得到质量守恒定律。
3. 流体的伯努利方程伯努利方程是描述流体在不同位置之间压强、速度和高度之间关系的方程。
它说明了在理想流体中,速度增加,压强将降低,而高度会对其产生影响。
四、流体力学在实际应用中的应用1. 水压力的应用水压力广泛应用于水泵、压力表和液压机械等领域。
利用水的压力可以实现液体的输送、提供动力以及进行力的放大。
2. 空气动力学的应用空气动力学研究的是气体在空气中的行为和特性。
该领域的应用包括飞机的设计、汽车的空气动力学外形改进以及建筑物的风阻力研究等。
3. 血液循环的研究血液循环是人体内部的液体流动系统,涉及到心脏和血管等器官的运作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S1 v 1 S 2 v 2
§5.3 伯努利方程(Bernoulli’s
equation)
是理想液体作稳定流 动的基本动力学方程, 它表明理想液体作稳 定流动时,同一流管 各处的速度、高度和 压强三者之间关系的 基本规律。
伯努利方程(Bernoulli’s equation)
(功能原理,即重力和弹力之外的力对物 体做的功,等于物体机械能的增量 )
四、泊肃叶公式 研究粘滞液体在等粗水平管中的层流
r ( P 1 P 2) Q 8l
4 0
讨论:
1.
r (P Q Q 1P 2) v S r02 8l
2 0
流速与半径的平方(截面积)成正比。 泊肃叶公式中流速与截面积成正比 指不同 管子; 液流连续原理中流速与截面积成反比,指 同一管子。
二、循环系统中血流速度、血压的变化
1. S↑,v↓: S毛≈800S主, v毛≈1/800v主,
2. ∵血液是粘滞液体,
∴沿流动方向血压降低
三、血压的测量
P外↑→ 肱动脉血 流中断 → 逐渐减 小P外 →P外=P收, 血流出现 → 听到 湍流声 (K音) → 继续减小P外 → P外=P舒,血流连续 → 变音或无音
•在图(b)中,如果把圆柱 加上外围。把其轮廓造成 像机翼横截面形状的物体, 并以同样速率的水流经过 它,则设有湍流产生,每 一条都是稳定的流线。这 样的形状,就称为流线形。 •流纹形的物体,由于其 前后方都没有产生湍流, 所以前后方所受压力相近, 流体对它的压差阻力就小 很多。
•在自然界中, 很多鱼类的体 形都是流线形 的。
2、非牛顿液体——不遵循牛顿粘滞定 律的液体 。在一定温下η非常量。
三、层流、湍流、雷诺数
1、层流、湍流
速度慢
速度快
2、层流、湍流判断依据
雷诺数 (Reynold’number)R e
v d
Re 3000
Re 2000
液体作湍流
液体作层流
2000 Re 3000 液流不稳定
――忽略压缩性和粘滞性的液体 只考虑流动性
•理想流体在运动时没有和运动方向平行的 切向力作用,其内部应力与静止流体有相 同特点:任何一点的压强大小只与位置有 关,而与计算压强所选截面的方位无关。
•与静止流体不相同之处: 流体运动时,其内部任意两点之间可能存在压 强差
2、稳定流动 (steady flow)
流过各种形状障碍物的流线
流管――流线围成的管子
由于每一时刻,液流中任一
点处只可能有一个流速,所 以各流线彼此不会相交
§ 5.2 液流连续原理
(principle of continuity of flow)
(S1v1t S2v2 t )
稳定流动的 不可压缩液体 S1v1 S 2 v2 Q 恒量
Q S1 S 2
2P 1 P 2 2 S12 S 2
3、皮托管(Pitot tube)
静 压 强 动 压 强 总 压 强
小孔B在L2管 的前端,它迎 向液流,液体 在流入小孔后, 流动被阻止, 流速减为零, 这时动能就转 化为压强能而 使压强升高, 这部分由动能 转化而来的压 强叫做动压强。
v1 S2 v2 S1
流量
S1v1 S 2 v2 Q 恒量
Sv t S (v t ) Q S1v1 S 2v2 t t
(液流连续原理也可以理解为流量守恒)
原理的推广应用:
1. 同一流管内多岔道: Sv
S i vi
i
n
2. 粘滞性液体: 3. 气体
绪 论 物理学与医学 (录象,大约35分钟)
平时作业:10% 提问测验:10% 期末大考:80%
§5.1 流体运动的描述
液体: 特点是具有流动性 和粘滞性, 压缩性 流体 极小 气体
理想液体的流动
1、理想液体 (ideal liquid) 就是绝对不可压缩而又没有粘滞性的液体
1 1 2 2
3.单位和常数
流速 v
压强 P
米/秒
帕斯卡
m/s
Pa
密度 ρ
高度 h
千克/米3
米
kg/m3
m P0=105Pa
ρ水=1000 kg/m3
伯努利方程的应用
1、空吸作用 (suction)
水流抽气机
2、汾丘里管 3、皮托管
1、空吸作用
原理:SB VB PB 当PB < P0 时,产生空吸现象。
η——粘滞系数(coefficient of viscosity) 或粘度(viscosity)。
η的单位:SI制——帕· 秒(Pa· s); CGS制——泊(P)=10-1Pa· s
η与温度的关系:对液体 T 对气体 T
二、牛顿液体和非牛顿液体
1、牛顿液体——遵循牛顿粘滞定律的 液体。在一定温度下,η是常量。
S ∵ P2=P0,h2=0, v1 2 v2 5v2 S1
例题小结:
1.正确地选取截面,包含所求量 2.方程正确简化 gh P gh P 等粗管 1 2 1 2 v1 P v2 P2 1 水平管 2 2 其他隐条件:大桶小孔,大处v≈0 3. 压强选取 静压强 : P P0 gh 动压强:液面与大气接触处为P0,其他 压强计显示或计算
2、 理想液体 pA= pB = pC = p0 实际液体
由于粘滞力的作用,
pA〉 pB 〉 pC 〉 p0
r ( P P ) 1 2 3. 对于 Q 8l
4 0
令
8l R 4 r0
P P 1 P 2 则 Q R R
R——流阻
§5.5 血液的流动
一、红细胞的轴流现象
静压强和动压强
静 压 强
动 压 强
总 压 强
静压强和动压强
皮托管(Pitot tube)
ρ
ρ′
原理:
测量流体速度
1 2 v A PA PB 2
PB PA gh
测量流体速度
ρ
ρ′
vA 2 gh
§5.4 实际液体的流动
一、牛顿粘滞定理和粘滞系数
dv F A dl
(也称定常流动) ――液体质点经过空间某一定点速度 不随时间改变的流动
3、流线和流管 流线――为了形象地描述液体的流动情况, 在任一瞬时,我们在液体中作一些曲线(如 图),并使这些曲线上每一点的切线方向和 流过该点的液体质点的速度方向一致,这 样的曲线称为这一时刻的流线。 液体作稳定流动时,质点的运动轨迹
物理意义:
表明稳定流动理想液体,在同一流
管的不同截面处,流速、压强和高度的
关系(单位体积液体的动能、重力势能 和压强能三者之和是一恒量)
适用条件
1、同一流管 2、理想液体
3、作稳定流动
【例1 】 一大容器中 盛有水,其 侧壁下方开 有小孔,求: 水从小孔中 流出的速度。
【解】取a、b截面处列伯努利方程
4. 牛顿粘滞定律、牛顿液体和非牛顿液体 、 粘滞系数
dv F A dl
5. 泊肃叶公式、流阻
r ( P1 P2 ) P Q 8l R
4 0
适用范围:实际液体在等粗水平管 中作层流 6. 血液循环中血流速度和血压的 变化及测量
1kPa=7.5mmHg
思考题: 1.液体作稳定流动时,质点速度不变 是何含义? 2.液流连续原理推导前提和适用条件是什么? 3.伯努利方程的推导前提和适用条件是什么? 4.泊肃叶公式的适用条件是什么? 5.流量、压强差和流阻 之间的关系如何? 6.何谓计示压强?
由连续原理
Sb vb Sava=Sbvb ,va Sa
va≈0
因Sa>>Sb, ∴
又Pa=Pb=P0, 且hb=0 ha=h
化原方程为
1 2 gh b 2
vb 2 gh
上式表明小孔流速与自由落体的速度 具有同样的表达形式,称为托里拆利定理 (Torricelli's theorem)。
(可由层流变为湍流或相反)
交通工具设计成流线形的好处
•在A线上任一点、任何时刻, 水流经过时,其速度的大小和 方向都是不变的。这种稳定的 流动称为片流或层流。 •B线常形成飘忽不定的旋涡, 其形状在这一刻和下一刻都不 同。这样的流动,称为湍流。
•在圆柱前方。点的两旁,水流被圆柱阻挡,分为 左右两股绕圆柱流过,而对正。点的水却差不多停 顿。相反,在圆柱后方的A点.湍流的速率却很大。 根据伯努剩原理,流体速率大处压强小,速率小处 压强大.所以圆柱前方所受压力比后方大。前后方 压力之差,就是圆柱体所受的压差阻力。
A Ek E p F1v1 t F2v2 t
1 1 2 2 m2 v2 m1v1 2 2
m2 gh 2 m1 gh 1
∵
F PS
且 m1 m2
P1 S1v1t P2 S 2 v2 t 1 2 2 m(v 2 v1 ) mg(h2 h1) 2
1、空吸作用
原理:SB VB PB 当PB < P0 时,产生空吸现象。
(录象)
2、汾丘里管 (Venturi tube)
流速与流量的测量
(录象)
原理:
1 2 1 2 v1 P v2 P2 1 2 2
流速 流量
v1 S 2
2P 1 P 2 2 S12 S 2
【例2】P.19/16 水在粗细不均匀的流管中作稳定 流动,出口处较粗(2),截面积为 20cm2,流速为2m/s;另一处较细 (1),截面积为4cm2,比出口处高 20cm。(取g≈10m/s2) (1)求细处(1)的压强; (2)若在细处(1)开一小孔,将发生 什么现象?
