六自由度飞行动力学
六个自由度的四旋翼飞行控制原理
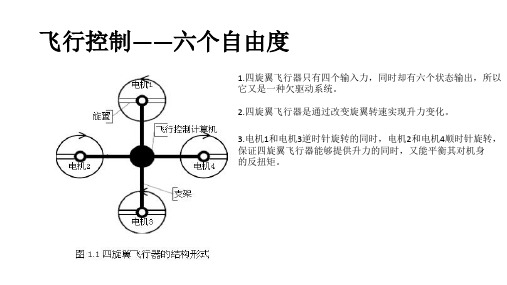
1.四旋翼飞行器只有四个输入力,同时却有六个状态输出,所以 它又是一种欠驱动系统。 2.四旋翼飞行器是通过改变旋翼转速实现升力变化。 3.电机1和电机3逆时针旋转的同时,电机2和电机4顺时针旋转, 保证四旋翼飞行器能够提供升力的同时,又能平衡其对机身 的反扭矩。
机载端控制电路版开发
• 红外接收装置——接收到发射装置的信息传递给单片机。
• 中央处理——单片机将接收到的红外信息处理,发送到PWM装置, 控制发动机的转速改变。
动力电路开发(PWM控制电流装置)
PWM电流控制电路: 每个PWM控制 器由一组电桥、及其外部一个感应电 阻(Rs)、一个内部比较器和一个单 稳多谐振荡器组成,来独立感应和控 制输出电流。
红外线接收器(接收信号)
反馈
单片机(中央处理)
PWM 步进电机(改变电流大小)
电机(转速改变) 飞行动作 轨道偏移外部扰动来自遥控电路开发(红外线装置)
• 四通道遥控器——上下、左右、前后、旋转 • 红外遥控装置——开关键,上升下降键,方向前后左右键。 (开关键:开启时,转速与飞行器重力刚好抵消,处于悬停 状态。关闭时,转速为零,处于停止状态。)
输出电流的逻辑控制:两个输入逻辑信号(l0 和 I1)用于数 字选择电机线圈电流在其最大水平的百分比,100%, 67%, 33%, or 0%。0%的输出电流值说明电桥关闭了所有驱动并且 也作为一个输出特性。
外界干扰因素
• 1.传感器噪声 • 2.外部扰动 • 3.摩擦 • 4.风速
飞行力学第六章-运动方程

ωx
ω y I x ω x I xy
0 I zx
I xy Iy I yz
I zx ω x M x I yz ω y = M y I z ω z M z
飞行器飞行力学2010
得
dω x 2 2 + ( I z I y )ω y ω z + I yz (ω z ω y ) + Ix dt dω y dω z I xy (ω x ω z ) I zx (ω x ω y + ) = Mx dt dt dω y 2 2 + ( I x I z )ω x ω z + I zx (ω x ω z ) + Iy dt dω z dω x I yz (ω x ω y ) I xy (ω y ω z + ) = M y dt dt dω z 2 2 + ( I y I x )ω x ω y + I xy (ω y ω x ) + Iz dt dω y dω x I zx (ω y ω z ) I yz (ω z ω x + ) = Mz dt dt
飞行器飞行力学2010
根据速度之间的关系
u = V cos α cos β v = V sin β w = V sin α cos β
可得
du dV dα dβ V sin α cos β V cos α sin β cos α cos β = dt dt dt dt dv dV dβ V cos β sin β + = dt dt dt dw dV dα dβ sin α cos β + V cos α cos β V sin α sin β = dt dt dt dt
dω z dω x + ( I z I y )ω y ω z I zx (ω x ω y + Ix ) = Mx dt dt 方 程 dω y 2 2 + ( I x I z )ω x ω z + I zx (ω x ω z ) = My 简 Iy dt 化 为 I d ω z + ( I I )ω ω + I (ω ω d ω x ) = M z y x x y zx y z z dt dt
六旋翼飞行器飞行原理

六旋翼飞行器飞行原理
六旋翼飞行器是一种六自由度垂直起降飞行器,相邻的两个旋翼一个顺时针转动,另一个逆时针转动,相邻两个桨一个为正桨,而另外一个为反桨。
这种设计使得飞行器自身扭矩相互抵消,从而保持飞行器的稳定。
在飞行过程中,当6个桨的升力之和等于飞行器的起飞重量时,飞行器保持悬停状态。
如果桨的升力大于飞行器本身的起飞重量,飞行器就会起飞;反之,飞行器就会下降。
通过调整飞行器6个旋翼的转速,可以实现偏航和转换飞行器姿态的目的。
以上内容仅供参考,如需更多信息,建议查阅六旋翼飞行器相关文献或咨询专业技术人员。
六自由度并联机器人运动学、动力学与主动振动控制

振动控制概述
01
02
03
振动危害
机械系统中的振动可能导 致设备损坏、工作效率降 低以及安全隐患。
振动控制方法
主动振动控制、被动振动 控制和半主动振动控制。
主动振动控制优势
能够实时监测和抑制机械 振动,提高设备性能和安 全性。
主动振动控制策略
基于模型的主动振动控制
01
利用系统模型进行预测和控制。
基于数据的主动振动控制
医疗应用
在医疗领域,六自由度并联机器人可以用于微创 手术和精确的定位,提高手术的准确性和效率。
3
农业应用
农业领域可以利用六自由度并联机器人进行自动 化采摘、分拣等作业,提高生产效率并降低人力 成本。
发展与展望
技术创新
随着机器人技术的不断发展,六自由度并联机器人的性能和稳定性 将得到进一步提升,同时将涌现出更多的应用场景。
结构设计
六自由度并联机器人的结构设计对其性能具有重要影响, 因此需要开展深入的研究以提高机器人的刚度、精度和稳 定性。
主动振动控制
在高速运动过程中,六自由度并联机器人容易产生振动, 需要进行主动振动控制研究以减小振动对机器人性能的影 响。
感谢您的观看
THANKS
六自由度并联机器人实验 平台与实验研究
实验平台介绍
硬件组成
由6个伺服电机、6个旋转关节 、1个移动关节、1个机身和1
个控制箱组成。
软件系统
采用PC+运动控制卡的模式,使用 自主开发的软件进行实时控制。
实验场地
机器人在实验台上进行实验,环境 条件稳定。
运动学实验研究
逆运动学
通过给定目标位姿,求解关节角 度。
六自由度并联机器人运动学 、动力学与主动振动控制
飞机设计的基础:六自由度非线性运动方程的建立过程

飞机设计的基础:六自由度非线性运动方程的建立过程飞机飞行,涉及到力(力矩)平衡、静稳定和静操纵性等一系列的问题。
为了保证飞机的飞行安全和良好的飞行品质,还必须在静品质基础上研究飞机的动态特性。
可以说,飞机的各个系统设计都是围绕着飞机的飞行运动这一基本概念进行的,无论是总体设计、结构设计、气动设计、控制系统设计等等。
今天我们来简单介绍一下飞机运动方程建立的基本思路。
飞行中的歼-20从动力学观点来看,动态特性是研究飞机在外力或外力矩(外界扰动或飞行员操纵)作用下,各个运动参数随时间的变化规律,也就是求解飞机的运动方程,并在此基础上,对动态特性作进一步定量分析。
对于在三维空间运动的刚体飞机,具有6个自由度。
也就是说,如果要完整地描述飞机的运动,需要6个相互独立的微分方程组。
如果再加上空间位置和姿态,完整表征飞机的各个运动参数则需要15个微分方程。
对飞机运动进行受力分析可知,飞机运动要受到重力、发动机推力、空气动力以及三个轴向的滚转力矩作用。
这些力、力矩和运动参数的定义,不在同一坐标系下,因此求解时还需要经过坐标系转换变换到同一坐标系。
六自由度微分方程组加上复杂的坐标系变换,注定了飞机运动方程是复杂的。
飞行中的无人机不过,飞机运动方程能够真实地反映运动过程每一瞬间的情况,是对飞行性能、控制律设计以及运动仿真最基本的依据。
因此,有必要明白运动方程建立的基本方法和具体表现形式。
但是,现代控制理论主要是以传递函数和矩阵形式的状态方程作为分析对象进行研究和设计的。
因此,为了分析飞机稳定性、操纵性、控制律设计的方便,有必要研究建立飞机现行矩阵运动模型的方法。
垂直起降的F-35战机飞机的运动是一个复杂的动力学问题。
如果要全面考虑地球的曲率、燃油的消耗、武器的投射,飞机内部动力系统和操纵系统等机件的相对运动及飞机本身的弹性变形,外力使飞机外形、飞行姿态和运动参数变化等因素,会使飞机运动方程的推导变得极为复杂,并且很难进行解析处理。
空气动力学基础知识

O
X
描述飞机的姿态运动
Xa 速度V
3.速度坐标系(气流轴系)S-oxayaza
Za
原点o —飞机质心
oxa — 飞机速度V的方向 oza —飞机对称平面,垂直于oxa,指向机腹 oya —垂直于oxaza平面,向右
描述飞机的速度(轨迹)运动,
气流方向—力的方向(如吹风数据)
坐标系间可以相互转换,转换矩阵
成激波,受扰区限于扰源下游的马赫锥内
六、激波
气流以超音速流经物体时,流场中的受扰区情况与物体的形 状有关,超音速—强扰动,产生激波
激波实际上就是气流各参数的不连续分界面 在激波之前,气流不受扰动,气流速度的大小和方向不变, 各状态参数也是常数; 气流通过激波,其流速突然变小,温度、压强、密度等也突 然升高
它是在流体力学的基础上,随着航空工业和喷气推 进技术的发展而成长起来的一个学科。还涉及飞行 器性能、稳定性和操纵性等问题。
包括外流、内流。
遵循基本规律:质量守恒、牛顿第二定律,能量守恒、热
力学第一、第二定律等。
发展简史:
18世纪流体力学开始创建:伯努利公式、欧拉方程 等。
19世纪流体力学全面发展;形成粘性流体动力学、 空气-气体动力学:NS方程、雷诺方程等。
钝头物体的激波是脱体波(正激波),产生大波阻 楔形物体的激波是倾斜的(附体波 ),波阻较小,用于超音
速飞机的机头
七 膨胀波
伯努利静态公式
p1V2 C(常数)
2
不适用于高速流动情况 ,由
于空气高速流动时密度不是常数
由导伯努利方程动态过程,得出考虑到空气的可压缩性的 能量守恒方程:
(M2 1)dV dA VA
鸭式导弹 鸭翼,不受气流下洗的影响,改变气动特性
民用飞机单发失效时仿真研究

民用飞机单发失效时仿真研究摘要:通过对六自由度运动方程进行仿真计算,研究了飞机非对称动力时的操稳特性,并总结了其飞行品质的验证方法。
仿真结果表明该方法的有效性,并具有一定的工程设计指导作用。
关键词:非对称动力;六自由度0 引言对于双发动机民用飞机,当其中一台发动机发生故障时,必然存在左右不平衡推力,造成不平衡力矩,飞机会产生侧滑角及滚转角并降低飞行高度。
此时需要偏转方向舵及副翼平衡不对称推力产生的横航向力矩,并保持飞机继续安全飞行。
目前,单台发动机的失效概率为1×10-5/飞行小时,相对于客机失事概率1×10-9/飞行小时要大得多。
因此,当客机发生动力的非对称损失时,要采取相应的补偿措施,保证其有效的操纵和安全飞行。
因此,有必要根据相关的飞行品质规范,对多发动机飞机的非对称动力的操稳特性进行深入研究。
本文以某典型的双发民用飞机为研究对象,依据运输类飞机适航标准,并结合空气动力学、理论力学及飞行力学等相关原理,确定仿真方法,并计算分析了单发失效时飞机相关的飞行品质,并验证该仿真方法的有效性。
1 非对称动力状态时飞行器飞行动力学模型建立非对称动力飞行指多发动机飞机一侧发动机发生故障,造成推力左右不对称时的飞行。
此时,要求飞机应能做定常直线飞行。
(1)飞行器动力学方程。
利用理论力学的动量定理可知,飞行器质心运动在任意动坐标系Oxyz上投影得质心动力学标量方程组为:m(+wq-vr)=F xm(+ur-wp)=F ym(+vp-uq=F z(1)根据理论力学中质点系的动量距定理知,dhdt=∑M(2)其中:h为质心系对所选择点的动量距;∑M 为合外力矩。
假设各坐标轴角速度的分量为ωX、ωY、ωZ,质量为d m的质心绕3个坐标轴的动量矩为:dh x=ωx(y2+z2)dm-ωyxydm-ωzzxdm dh y=ωy(z2+x2)dm-ωzzxdm-ωxxydmdh z=ωz(x2+y2)dm-ωxzxdm-ωyyzdm(3)引入惯性矩和惯性积,并对上式进行积分得,h x=ωxI x-ωyI xy-ωzI xzh y=ωyI y-ωzI yz-ωxI xyh z=ωzI z-ωxI xz-ωyI yz(4)对于飞机而言,xoz平面为对称面,因而I xy和I yz为零,所以得到转动动力学方程为:L=I x+(I z-I y)qrM=I y+(I x-I z)rpN=I z+(I y-I x)pq(5)(2)飞机运动学方程。
六自由度模型

42212312222212''22'212[()()][][()()][()()()()()()()]()sin ()[r r c c qq rr pr u vrc wq c uu c vv c ww c uw c c uvc c c rm u v v r w w q L X q X r X pr L X u X v v r X w w q L X u u X v v X w w X u u w w X u u v v W B L u u X X δδδρρρθρδ'''--+-=++'''++-+-'''+-+-+-+--+----+-+'2]s s spropT δδ+(1)○2 横向运动方程4'1||2312||2212[()()][][()()()()||][()()()c c r p pqqr r r p p v ur c vq c wp cwr c v r uu c uv c c v m v u u r w w p L Y r Y p Y p p Y pq Y qr Y r r L Y v Y u u r Y v v q Y w w p Y w w r Y r L Y u u Y u u v v Y ρρρ+---='''''+++++'''''++-+-+-+-'+'''+-+--+()||2212()()(cos sin ()w c c v v c r c r v v w w Y v v W B L Y u u δθϕρδ--'+-'+-+-(2)4221||2312||2221[()()][][()()()||][()()()()()c c q pp rr rp q q w uq c vr c vp c w q uu c vv c uv c c uwc m w u u q v v p L Z q Z p Z r Z rp Z q q L Z w Z u u q Z v v r Z v v p Z q L Z u u Z v v Z u u v v Z u u ρρρ'''''--+-=++++''''++-+-+-'+'''+-+-+--'+-()||2212()()()(()cos cos ()c c c u w ww c wwc s c s w w Z u u w w Z w w Z w w W B L Z u u δθϕρδ'-+--'+-'+-'+-+-(3)○4 横倾运动方程 51||||24123321||()[][()()()()()()][()()()(x z y p r p p qrpq r r v up c ur c vq c wpc wr c vvv c uu c uv c c v v I p I I qr L K p K r K p p K qr K pq K r r L K v K u u p K u u r K v v q K w w p K w w r K v v L K u u K u u v v K v v ρρρ+-=''''''+++++''''++-+-+-'''+-+-+-''+-+--'+-3212()()]()cos cos ()cos sin ()c vwc c G B G B r c r K v v w w y W y B z W z B L K u u δθϕθϕρδ'+--'+---+-(4)5221||2412||32212()[][()()()][()()()()()()Y X Z q pp q q rr pr w uq c vr c vp c w uu c vv c uv c c uwc c u w I q I I pr L M q M p M q q M r M pr L M w M u u q M v v r M v v p M L M u u M v v M u u v v M u u w w M ρρρ'''''+-=++++''''++-+-+-'+'''+-+-+--''+--+||321()()()(()cos cos ()sin ()c c wwc ww c G B G B s c s u u w w M w w M w w x W x B z W z B L M u u δθϕθρδ--'+-'+-'----+-(5)○6 偏航运动方程 51||||2412||3212()[][()()()()()][()()()z y X r p p p r r pq qrv upc ur c wr c wpc vq c v r uuc uv c c I r I I pq L N r N p N p p N r r N pq N qr L N v N u u p N u u r N w w r N w w p N v v q N L N u u N u u v v ρρρ''''''+-=+++++''''++-+-+-''+-+-'+''+-+--+||3212()()(()cos sin ()sin ()vw c c v v c G B G B r c rN v v w w N v v x W x B y W y B L N u u δθϕθρδ'--'+-'+-+-+-(6)○7 姿态方程: sin tan cos tan cos sin sin /cos cos /cos p q r q r q r ϕϕθϕθθϕϕψϕθϕθ=++=-=+○8 运动关系式:cos cos (cos sin sin sin cos )(cos sin cos sin sin )sin cos (sin sin sin cos cos )(sin sin cos cos sin )sin cos sin cos cos u v w u v w u v w ξψθψθϕψϕψθϕψϕηψθψθϕψϕψθϕψϕςθθϕθϕ=+-++=+++-=-++ 式中:下标为prop 的项为推进器产生的推力;)('∙X 、)('∙Y 、)('∙Z -----无因次水动力导数; )('∙K 、)('∙M 、)('∙N -----无因次水动力矩导数;u-----航速(m/s); v-----横荡速度(m/s); w-----垂荡速度(m/s); p-----横摇角速度(rad/s); q-----纵摇角速度(rad/s); r-----艏摇角速度(rad/s);r δ-----方向舵舵角(rad); s δ-----水平舵舵角(rad);m-----质量(Kg);x I -----绕x 轴的转动惯量(N.m2); y I -----绕y 轴的转动惯量(N.m2); z I -----绕z 轴的转动惯量(N.m2);,,c c c u v w 分别表示海流在,,u v w 方向的分量;,,G G G x y z :表示平台重心位置(m ); ,,B B B x y z :表示平台重心位置(m ); W 、B-----重力和浮力(N)。
