单因素随机区组设计资料的统计分析
用spss20进行可重复单因素随机区组、两因素随机区组、两因素裂区试验设计的方差分析
一、可重复单因素随机区组试验设计8个小麦品种的产比试验，采用随机区组设计，3次重复，计产面积25平米，产量结果如下，进行方差分析和多重比较。
表1 小麦品比试验产量结果（公斤）4 3 10.15 3 16.86 3 11.87 3 14.18 3 14.41、打开程序把上述数据输入进去。
2、执行：分析-一般线性模型-单变量。
3、将产量放进因变量，品种和区组放进固定因子。
4、单击模型，选择设定单选框，将品种和区组放进模型中，只分析主效应。
5、在两两比较中进行多重比较，这里只用分析品种。
可以选择多种比较方法。
6、分析结果。
主体间效应的检验因变量: 产量源III 型平方和df 均方 F Sig. 校正模型61.641a 9 6.849 4.174 .009 截距3220.167 1 3220.167 1962.448 .000 区组27.561 2 13.780 8.398 .004 品种34.080 7 4.869 2.967 .040 误差22.972 14 1.641总计3304.780 24校正的总计84.613 23a. R 方 = .729（调整 R 方 = .554）这里只须看区组和品种两行，两者均达到显著水平，说明土壤肥力和品种均影响产量结果。
下面是多重比较，只有方差分析达到显著差异才进行多重比较。
二、两因素可重复随机区组试验设计下面是水稻品种和密度对产量的影响，采用随机区组试验设计，3次重复，品种3个水平，密度3个水平，共27个观测值。
小区计产面积20平米。
表2 水稻品种与密度产比试验1、输入数据，执行：分析-一般线性模型-单变量。
注意区组作为随机因子。
2、选择模型。
注意模型中有三者的主效和品种与密度的交互。
3、分析结果。
注意自由度的分解。
使用一个误差（0.486）计算F值。
主体间效应的检验因变量: 产量源III 型平方和df 均方 F Sig. 截距假设1496.333 1 1496.333 1035.923 .0014、语句。
单因素随机区组试验设计-东北农业大学植物科学与技术试验教学中心
东北农业大学本科课程教学大纲课程名称:田间试验与统计方法英文名称：Field Experiment and Statistic-method 课程编号：01600008j适用专业：草业科学、植物生产类总学时数:40总学分：2。
5大纲主撰人:李文霞内容简介《试验设计与统计分析》是一门收集整理数据、分析数据, 并根据数据进行推断的科学。
本课程为高等农业院校农学类专业的专业基础课，主要讲授有关田间试验的基本知识和统计分析的基本方法和技能，为学习专业课程奠定基础，使学生具备承担科学试验,正确分析和评价科学试验结果及其可靠性的能力。
教学大纲一、课堂讲授部分(一）分章节列出标题、各章节要点及授课时数(务必将要点写清楚）第1章绪论一、基本内容1.1 农业科学试验的任务和要求1学时1。
1.1 农业科学试验和田间试验1.1。
2 农业科学试验的任务和来源1.1.3 农业科学试验的基本要求1。
2 试验误差及其控制2学时1.2。
1 试验误差1.2.2 试验误差的来源1。
2.3试验误差的控制1.3 生物统计学与农业科学试验1学时1.3。
1 部分生物统计学基本概念1。
3.2 生物统计学的形成与发展1。
3。
3 生物统计学在农业科学试验中的作用和注意问题二、教学目的与要求要求学生掌握农业科学试验的基本要求、试验误差的概念、来源和控制、部分生物统计学的概念，了解农业科学试验的任务和来源、生物统计学在农业科学试验中的作用和注意问题。
三、重点与难点重点：农业科学试验的基本要求、试验误差的概念、来源和控制、部分生物统计学的概念难点：试验误差的概念和生物统计学的基本概念的理解第2章试验的设计和实施一、基本内容2.1 试验方案1学时2.1。
1 试验方案的概念和类别2。
1.2 处理效应2.1。
3 试验方案的设计要点2。
2 试验设计原则1。
5学时2。
2.1 重复2.2。
2 随机排列2。
2.3 局部控制2。
3 小区技术0.5学时2。
3.1 小区2。
方差分析的应用范围单因素完全随机设计-随机化区组设计-拉丁方
方差分析(ANOVA)方差分析的应用范围单因素完全随机设计, 随机化区组设计,拉丁方设计多因素析因设计,裂区设计,交叉设计,正交设计多变量多元方差分析回归方程的假设检验第一节完全随机设计与资料分析方差分析目的：根据多个组间样本均数的差别推断总体均数是否存在差别。
一、方差分析的基本思想：1 / 162 / 16表12.2 红细胞沉降率(mm/h) 抗凝剂 红细胞沉降率 n i XS 2Σx Σx 2甲 17, 16, 16, 15 4 16.00.67 64 1026 乙 10, 11, 12, 12 4 11.3 0.92 45 509 丙 11, 9, 8, 9 4 9.3 1.58 37 347 合计1212.23.17146 1882观察值之间有变异，这变异可以用离均差平方和表示。
67.105)(112..=-=∑∑==Gi n j ij T ix x SS3 / 16进一步分析，总变异中有两类变异： 1. 组内变异，指各组内观察值的差异50.9)1()(12112.=-=-=∑∑∑===Gi ii Gi n j i ij W s n x x SS i2. 组间变异，指各组间样本均数与总均数的差异17.96)(12...=-=∑=Gi i i B x x n SS由于组内变异完全是个体间的差异，因此可以认为是随机误差。
而组间变异反映组间均数的差异，其可能仅仅包含随机误差，这时零假设成立。
也可能除随机误差外，还包含处理的效应，这时则备择假设成立。
组间变异和组内变异的自由度不同，无可比性。
计算均方，再进行比较：4 / 164 / 1637.4506.109.489/50.92/17.96)/()1/(====--=W B W B MS MS G n SS G SS F 二、方差分析的基本步骤 1. 方差分析的基本条件a. 各组观察值分别服从总体均数为μi 的正态分布。
b. 各组观察值总体方差相等。
单因素随机区组设计的方差分析
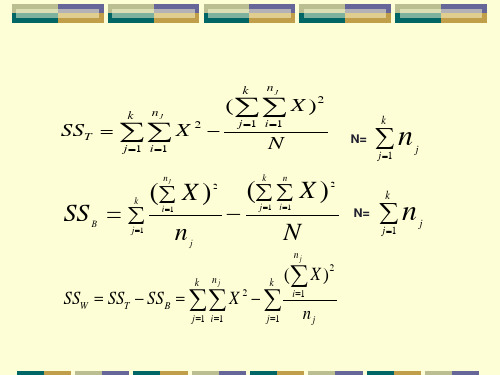
MSr Fr MSe MSb Fb MSe
变异来源 组间 区组
平方和 SSB SSR
自由度 k-1 n-1
均方 MSB MSR
F F=MSB/MSE F=MSR/MSE
p <0.05 或>0.05
误差
总变异
SSE
SST
（k-1）(n-1)
nk-1
MSE
例9-6：为研究听、触觉刺激对视觉的干扰效 果，随机抽取5名被试分别在5种不同的干扰下读
组内变异源于组内被试间的差异和实验误差，怎样
将被试间差异引起的变异从组内变异中分离出来，
从而提高F检验的精确度和灵敏度？
随机区组设计
单因素随机区组设计的方差分析
主要内容
随机区组设计（重点） 方差分析（重点）
1 随机区组设计
某研究要探讨文章的生字密度对学生阅读理解的影响， 生字密度有4个水平。由于考虑到学生的智力可能对阅读 理解测验分数产生影响，在实验实施之前，研究者首先 给32个学生做了智力测验，并按智力测验的分数将学生 分为8个区组，然后随机分配每个区组内的4个同质被试 分别阅读一种生字密度的文章，并回答阅读理解测验中 有关文章内容的问题。
k
( X ) 2
i 1
nj
nj
利用样本统计量进行方差分析（
SSB n ( X j X t )
j 1 k 2
X
k
2 ， ，n j ） S j j
SSB n j ( X j X t ) 2
j 1
SSW ( X ij X j ) n s 2 j
SST X
j 1 i 1
nj
k
nj
2
单因素随机区组实验设计
应用举例及延伸
与该设计相关的名称：随机化区组实验设计；下属的设计类型：随机 化匹配组设计，随机化配对组设计。单因素随机区组设计应用举例： 研究题目：文章的生字密度对学生阅读理解的影响。 研究假设：阅读理解随着生字密度的增加而下降。 实验变量：自变量——生字密度，含有4个水平（5：1、10：1、15： 1、20：1）； 因变量——阅读测验的分数；无关变量——被试的智 力水平 实验设计：单因素随机区组实验设计 被试及程序：首先给32个学生做智力测验，并按测验分数将被试分成 8个组，每组4人（智力水平相等），然后随机分配每个区组内的4个 被试阅读一种生字密度的文章。
结束
数据处理方法（Biblioteka PSS统计软件）包含的统计变量：实验的自变量A，区组变量X， 实验的因变量Y。 实施的统计过程：analyze—General Linear Model—Univariate… 预期的统计结果：自变量A的主效应是否显著； 无关变量即区组变量效应是否显著；若自变量主 效应显著，则进行平均数多重检验。
单因素随机区组实验设计
第二章 实验设计
单因素随机区组实验设计的基本特点
适用条件：研究中有一个自变量，自变量有两个或多于两个水平；研 究中还有一个无关变量，也有两个或多个水平，并且自变量的水平与 无关变量的水平之间无交互作用。 基本方法：首先将被试在无关变量上进行匹配，然后把各匹配组的被 试随机分配给自变量的各个水平，每个被试只接受一个水平的处理。 误差控制：区组法（无关变量纳入法）。通过统计处理，分离出由无 关变量引起的变异，使它不出现在处理效应和误差变异中，从而提高 方差分析的灵敏度。 实验设计模型 总变异组成：实验处理引起的变异；区组引起的变异；误差引起的变 异。
随机区组试验设计与分析
第一节 完全随机实验设计及分析
本试验中，水平数m＝3，重复r=5，共进行35＝15次试验。 此15次试验先做哪一个呢？ 试验的先后顺序必须随机确定。随机化方法可采用抽签的方 法，也可用随机数字表确定试验顺序。 现在采用查随机数字表确定试验顺序 （1）对所有试验编号 （2）确定读取随机数字的起始点，并读取相应数目的随机数字。 （3）根据随机数字的大小确定试验的先后顺序。
然后分别在各区组内，用随机的方法将各个处理逐个安排于各供试 单元中。
第二节 随机区组试验设计方法
由于同一区组内的各处理单元的排列顺序是随机而定的，故这 样的区组叫做随机区组。 随机区组设计是一种适用性较广泛的设计方法。既可用于单因素试 验，也适用于多因素试验。
第二节 随机区组试验设计方法
随机区组试验设计方法安排单因素试验
除杂方法（Ai） 平均值 xt
差异显著性
a=0.05
a=0.01
A4
28.4
a
A
A2
27.5
ab
A
A3
27.0
b
A
A1
25.2
c
B
A5
21.3
d
C
第二节 随机区组试验设计方法
2.1 设计方法
实验设计五原则中，其中的一条就是区组的原则。 随机区组试验设计是一种随机排列的完全区组的试验设计。 其方法是： 根据局部控制的原理，将试验的所有供试单元先按重复划分成非处 理条件相对一致的若干单元组，每一组的供试单元数与试验的处理数 相等。
雌鼠编号 1 2 3 4 5 6 7 8 … 39 40
随机数字 09 47 27 96 54 49 17 46 … 03 10
余数
1 3 3 4 2 1 1 2 …3 2
第六章 方差分析3——单因素随机区组设计
• 缺点：区组的划分难度较大，同质性不好把握。
SPSS的数据格式
“分析”——“一般线性模型”——“单变量”
SPSS结果
结果分析
• 方差分析的结果表明，不同的教学方法会 对作文成绩产生显著影响。
实验结果
实验处理
教学方法
区组
1
2
15
10
区组1：优良
9
6
12
11
3
4
20
12
18
15
25
17
10
15
区组2：中等
18
19
12
12
25
20
30
15
18
18
2
6
10
6
区组3：一般
6
3
7
8
5
7
13
11
分析
• 这是一个单因素随机区组设计。 – 因变量：作文平均数提高的成绩。 – 自变量：教学方法，它有4个水平。 – 区组变量：不同的被试组，它有3个水平。 – 控制变量：自变量的呈现顺序。
• 区组效应显著表明区组设计是合理的。 • 进一步的多重比较发现，教学方法Ⅲ条件
下的作文成绩显著高于其它3种条件下的成 绩；教学方法Ⅳ条件下作文成绩显著高于 Ⅰ和Ⅱ条件下的成绩；教学方法Ⅰ和Ⅱ之 间的作文成绩不存在显著性差异。
ቤተ መጻሕፍቲ ባይዱ方差分析——
单因素随机区组设计
举例
• 某教师为了研究四种不同的写作训练方法中， 哪种方法更有效，选择了36名高一学生。按 照前一学期历次作文成绩的平均分数将36名 学生划分为优良、中等、一般三个写作水平， 每个水平均有12名学生，而12名学生被随机 分到各实验处理。经一学期的写作训练后进 行写作能力测试，计算出每一学生的得分比 前一学期历次作文平均分提高的分数。结果 如下。
第八章单因素试验结果的统计分析[实践]
![第八章单因素试验结果的统计分析[实践]](https://img.taocdn.com/s3/m/8b715158842458fb770bf78a6529647d272834ed.png)
第八章单因素试验结果的统计分析•单因素试验指仅研究一个供试因素若干处理间的效应是否有显著差异的试验.•按试验设计的类型单因素试验可分为：•顺序排列试验•单因素完全随机试验•单因素随机区组试验•拉丁方试验第一节对比和间比试验的统计分析(自学)第二节完全随机试验设计的统计分析完全随机设计：是所有的处理和重复小区在整个试验空间完全随机排列的设计方法。
只满足试验设计三项基本原则中的重复和随机排列两项原则。
•如：k = 5，n = 3的完全随机排列示意图主要优点：对各处理的重复次数没有限制，可以相等也可以不相等不足之处：没有遵循局部控制原则，所以要求试验地较为均匀一致，不存在有明显方向性的肥力差异，一般不用于田间试验。
•根据每一处理的重复次数或重复的设计方法不同, 又分为：①组内观察值数目相等；②组内观察值数目不等的完全随机试验；③组内又可分为亚组的完全随机试验一、组内观察值数目相等的完全随机试验设计的统计分析组内观察值数目相等的完全随机试验是各处理重复次数相等的试验。
设有k个处理，每处理均有n个重复观察值，共设kn个观察值；其资料的数据结构模式类型见第7章表7.1。
其试验结果的方差分析方法列于表8.1。
表7.1 k个处理每处理n个重复观察值的完全随机试验数据符号表表7.1 nk个观察值的单向分组资料模式表8.1 组内观察值数目相等的完全随机试验的方差分析•〔例8.1〕研究6种棉花种子包衣剂对棉花生长的影响，设TW1为对照。
采用盆栽试验，各种子包衣剂处理播种5盆，完全随机设计。
出苗一定时期后测定棉花苗高（cm），其结果如下。
试检验各种子包衣剂与对照的棉花平均苗高差异显著性及各种子包衣剂棉花平均苗高间的差异显著性。
表8.2 6种棉花种子包衣剂的棉花苗高结果(cm)•解：已知：处理数k=6，重复次数n=5，共有kn=6×5=30个观察值。
•1、自由度及平方和的分解•总自由度df T = nk– 1 =6 × 5 – 1 =30 – 1 =29•处理自由度df t = k– 1 =6 – 1 =6 – 1 =5•误差自由度df e = df T–df t =29 – 5 =24或df e = n(k– 1) =6 ×( 5 – 1) =24 – 1 =23•矫正数总平方和SS T =Σx2－C=22.92+22.32+……+23.72-C=45.763处理平方和误差平方和SS e=SS T－SS t=45.763－44.463=1.3002、F 检验和列方差分析表统计假设H O：μ1= μ2=…= μ6；H A：μi不“全相等”(即至少有一个不等号)将上述计算的各项自由度、平方和、均方结果,按变异来源列出方差分析表(表8.5)。
单因素完全随机随机区组方差分析SPSS
2023.01
4
➢ 数据格式 n行2列 （指标变量、分组变量）
2023.01
5
➢ 检验环节
Analyze →Compare Means →One-Way ANOVA
2023.01
6
One-Way ANOVA 对话框
2023.01
多重比较
选项
7
Post Hoc Multiple Comparisons 对话框
单原因方差分析旳SPSS实现
2023.01
1
SPSS单原因方差分析过程名
完全随机设计方差分析： Analyze Compare Means
One－Way ANOVA
随机单位组设计方差分析： Analyze General Linear Models
Univariate
2023.01
2
1. 完全随机设计资料旳方差分析One-Way ANOVA
2023.01
3
表1 三组战士的第一秒用力肺活量(L)
对照组 锻炼组 药物组 合计 3.25 3.66 3.44 3.32 3.64 3.62 3.29 3.48 3.48 3.34 3.64 3.36 3.16 3.48 3.52 3.64 3.20 3.60 3.60 3.62 3.32 3.28 3.56 3.44 3.52 3.44 3.16 3.26 3.82 3.28
例1 某高原研究组将籍贯相同、年龄相同、身高 体重接近旳30名新战士随机分为三组，甲组为对 照组，按常规训练，乙组为锻炼组，每天除常规 训练外，接受中速长跑与健身操锻炼，丙组为药 物组，除常规训练外，服用抗疲劳药物，一月后 测定第一秒用力肺活量(L)，成果见表。试比较 三组第一秒用力肺活量有无差别。
单因素随机区组设计资料的统计分析PPT共71页
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
谢谢！
36、自己的鞋子，自己ຫໍສະໝຸດ 道紧在哪里。——西班牙37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
单因素随机区组设计资料的统计分析
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
第五章 真实验设计 34单多因素随机区组
拉丁方的标准块：当拉丁方阵的第一行或第 一列都是按字母表顺序排序的时候，叫标准 化方块。
A B B A 2×2 A B C B C A C A B 3×3 A B C D B C D C D A D B A A B C 4×4
P=4的时候标准块的个数是多少？ （4*4 为4； 5*5为56； 6*6 为9408） 拉丁方阵标准块的随机化： 当P=2 时 2*2的拉丁方阵可能的个数是2个； 当P=3 时 3*3的拉丁方阵可能的个数是12个； 当P=4 时 4*4的拉丁方阵可能的个数是576个； …… 当P=7时 7*7的拉丁方阵可能的个数是16942080个； 算法：P！*（P-1）！* 标准方块数
二、多因素随机区组设计的数据分析
• 多因素随机区组设计的数据也可通过多因素方差分 析进行处理，即将区组作为一个因素。实验处理A 和实验处理B的主效应及其交互作用是研究者关注 的中心，区组因素则作为无关变量加以控制。 • 但是研究者可以尝试分析区组因素和实验处理之间 的交互作用，如果达到统计的显著性水平，就可以 进一步修改原有的理论假设，把区组因素作为一个 实验因素加以考虑，以提高实验研究的外部效度。
实验处理平均 O.1
例.天气状况对“赛车”测试速度的影 响
年老组
好
中
差
年轻组
好
中
差
举例
一个研究者在做4种文章的生字密度对 学生阅读理解影响的研究时，在这个研究 中，自变量——生字密度有a1, a2, a3, a4 四个水平。学生智力不是研究者感兴趣 的变量，但它们对实验可能有影响，于是 将它们纳入到“自变量”中。
随机化区组设计的原则
• 随机化区组设计的原则是同一区组内的被试尽量 “同质”。 • 每一区组内被试的人数分配有3种情况： 一名被试作为一个区组。这时，每名被试(区组)均 接受全部处理，在接受处理的顺序上要采用随机化 的方法。 每个区组内被试的人数是实验处理数目的整倍数。 区组内的基本单元不是一名被试或几名被试，而是 以一个团体为单元。
随机区组设计
第十一章随机区组试验知识目标：●掌握随机区组试验田间试验设计方法；●掌握随机区组排列田间试验结果统计分析方法。
技能目标：●学会随机区组试验设计；●能够绘制随机区组设计田间布置图；●学会随机区组试验结果统计分析。
随机区组试验设计是把试验各处理随机排列在一个区组中，区组内条件基本上是一致的，区组间可以有适当的差异。
随机区组试验由于引进了局部控制原理，可以从试验的误差方差中分解出区组变异的方差（即由试验地土壤肥力、试材、操作管理等方面的非处理效应所造成的变异量），从而减少试验误差，提高F检验和多重比较的灵敏度和精确度。
随机区组试验也分为单因素和复因素两类。
本节只介绍单因素和二因素随机区组试验的方差分析方法，第一节单因素随机区组试验和统计方法一、随机区组设计随机区组设计（randomized blocks design）是根据“局部控制”和“随机排列”原理进行的，将试验地按肥力程度等性质不同划分为等于重复次数的区组，使区组内环境差异最小而区组间环境允许存在差异，每个区组即为一次完整的重复，区组内各处理都独立地随机排列。
这是随机排列设计中最常用、最基本的设计。
区组内各试验处理的排列可采用抽签法或随机数字法。
如采用随机数字法，可按照如下步骤进行：（1）当处理数为一位数时，这里以8个处理为例，首先要将处理分别给以1、2、3、4、5、6、7、8的代号，然后从随机数字表任意指定一页中的一行，去掉0和9及重复数字后，即可得8个处理的排列次序。
如在该表1页第26行数字次序为0056729559，3083877836，8444307650，7563722330，1922462930 则去掉0和9以及重复数字而得到56723841，即为8个处理在区组内的排列。
完成一个区组的排列后，再从表中查另一行随机数字按上述方法排列第二区组、第三区组……，直至完成所有区组的排列。
（2）当处理数多于9个为两位数时，同样可查随机数字表。
从随机数字表任意指定一页中的一行，去掉00和小于100且大于处理数及其最大整数倍相乘所得的数字及重复数字后，将剩余的两位数分别除以处理数，所得的各余数即为各处理在此区组内的排列。
单因素随机区组实验设计
单因素随机区组实验设计一、单因素随机区组实验设计的大体特点心理和教育科学研究中，被试的个体不同是误差变异的重要来源。
它常常会混淆实验处置的效应，因此是无关变异。
随机区组设计利用区组方式减小误差变异，即用区组方式分离出由无关变量引发的变异，使它不出此刻处置效应和误差变异中。
单因素随机区组设计适用于如此的情境：研究中有一个自变量，自变量有两个或多个水平(P ≥2)，研究中还有一个无关变量，也有两个或多个水平(n ≥2)，而且自变量的水平与无关变量的水平之间没有交互作用。
当无关变量是被试变量时，一样第一将被试在那个无关变量上进行匹配，然后将他们随机分派给不同的实验处置。
如此，区组内的被试在此无关变量上加倍同质，他们同意不同的处置水平常，可看做不受无关变量的阻碍，要紧受处置的阻碍而区组之间的变异反映了无关变量的阻碍，咱们能够利用方差分析技术区分出这一部份变异，以减少误差变异，取得对处置效应的更精准的估价。
另外，环境因素也是潜在可考虑的区组变量，例如，天天的时刻、每一年的季节、地址、仪器等方面的因素也能够进行区组，以减少误差变异，时刻是一个专门有效的区组变量，因为它常常还会带来一些附加的变量，如躯体的生理周期、疲劳等等。
单因素随机区组实验设计适合查验的假说有两个：(1)处置水平的整体平均数相等，即：0.1.2.:P H μμμ==⋅⋅⋅⋅⋅⋅⋅=或处置效应等于0，即：0:0j H a =(2)区组的整体平均数相等，即：0.1.2.:n H μμμ==⋅⋅⋅⋅⋅⋅⋅=或区组效应等于0，即：20:0i H π=图中能够看出实验中有一个自变量，自变量有4个水平。
实验中还有一个无关变量，将16个被试在无关变量上进行匹配，分为4个区组，每一个区组内4个同质被试，随机分派每一个被试同意一个处置水平。
二、单因素随机区组实验设计与计算举例(一)研究的问题与实验设计咱们仍然利用第一节中文章的生字密度对阅读明白得阻碍的研究做例子。
单因素随机化区组设计的方差分析例子
例子：研究者想考察三种背景音乐（摇滚乐、爵士乐和古典音乐）对英语单词记忆效果的影响。
从同一班级中挑选了45人参加实验，事先对他们的智商、英语基础等方面进行了评定，按照评定情况以及其他特点对被试进行了配伍，每三人一伍。
在进行实验时，每个配伍组的三个被试分别分配给一种背景音乐，在该背景音乐中学习40个陌生的英语单词。
30分钟后进行测试，要求被试根据中文意思默写出刚才学习过的单词，写对一个积一分。
被试的成绩如表12章-数据1所示。
问：不同的背景音乐对英文单词的记忆效果是否有显著影响？。
第8章-单因素试验结果分析
100
9
36.6 33.3 109.9
6
B 39.8 42.0 36.8 41.4 28.9 188.9 37.8 33.3 113.5
2
C 38.2 39.9 25.4 33.1 28.9 165.5 33.1 33.3
99.4
10
D 37.3 43.2 39.1 34.9 34.0 188.5 37.7 33.3 113.2
111.0
6
K 43.0 34.2 41.2 39.9 36.2 194.5 38.9 33.7 115.4
1
L 29.4 23.0 30.8 34.1 32.9 150.5 30.1 33.7
89.4
13
CK4 35.2 38.7 27.4 32.5 28.2 162.0 32.4
§2 随机排列设计的试验结果统计分析
1、方差分析
区组 品种
Ⅰ
A 10.9
1）求和：Tk；Tr ；T B 10.8 C 11.1
2）平方和的分解
D 9.1
E 11.8
ST S
xi2j
xij 2 F
G
n
10.1 10.0
H 9.3
计算校正系数C:
Tr 83.1
Ⅱ
Ⅲ
Tk
9.1 12.2 32.2 10.7
12.3 14.0 37.1 12.4
x2
x
n
按 SHIFT S-VAR 1 EXE 按 SHIFT S-VAR 2 EXE 按 SHIFT S-VAR 3 EXE
x
σn (大样本）
σn-1 (小样本）
品种
苗高观察值
A
18
21
单因素随机区组试验设计的方差分析
N-K法，也称q检验
q
(X X )
1
2
MS e
(
1
1
)
2nn
1
2
q值表的自由度为误差项的自由度
LSD法—最小有意义差法
H : H :
0
i
j
1
i
j
Y Y
i
j
~t
11
( df3 )
MS ( )
en n
i
j
自由度为误差项自由度
适用情况 研究中有两个试验变量，变量有两个或
多个水平 研究中还有一无关变量，也有两个或多
个水平 并且试验变量的水平和无关变量的水平
之间没有交互作用。
数据结构
A1 B1 A1 B2 A1 B3
区组一 X111… X121… …
X11r
X12r
A2 B1
A2 B2
A2 B3
X161… X16r
是不同的区组。
数据结构
A1
A2
A3
A4
区组一 x11
x12
x13
x14
区组二 x21
x22
x23
x24
区组三 x31
x32
x33
X34
区组四 x41
x42
x43
x44
研究假设H :1. 00j2. 0 为区组效应
i
i
H : , 不全为零
1
ji
x
ij
j
i
ij
双因素随机区组试验设计的方 差分析
多重比较法有许多种
几种常用多重比较方法
N-K法，也称q检验，由Newman-Keul提 出
LSD法—最小有意义差法 Bonfenomi不等式—a large number of
(仅供参考)随机区组设计
常用实验设计方法（一）一、完全随机设计（c o m p l e t e l y r a n d o m d e s i g n）属于单因素实验设计，可为两或多个水平。
将受试对象按随机化方法分配到各处理组，各处理组例数可以相等或不等。
优点：简单易行缺点：①只能分析一个因素的效应；②需要足够的样本含量，使各组基线(混杂)均衡可比。
设计要点◆完全随机设计的两组比较◆完全随机设计的多组比较1.两组比较为实验“736”对肉瘤的抑制作用，将16只长出肉瘤的小鼠随机分为两组，实验组注射“736”，对照组注射同量的生理盐水，10天后解剖称瘤重，试问：①该实验为何种设计类型？②请写出相应的设计方案？③对资料进行统计分析？组别瘤重（克）给药组1.62.22.02.02.51.03.71.5对照组2.14.92.74.32.51.74.53.4随机分配方案：①动物编号1-16②分配随机数：随机排列表第6行取0-15，弃去16-19。
③规定：随机数奇数分配至“736”组，偶数为对照组1表示给药组“736”，0表示对照组（生理盐水）备注：常用的随机分配方案：①按随机数的奇偶分配至两组；②按随机数的余数分配至各组；③将随机数排序，等分成各区段，对应将研究对象分配至各组。
统计分析①数据录入（d a t a1.x l s/s h e e t1）g r o u p瘤重11.612.2121212.51113.711.502.104.902.704.302.501.704.503.4②统计分析结果解释：两组瘤重平均水平差异有统计学意义，给药组的瘤重低于对照组。
2.完全随机设计多组比较研究某药在机体内的杀虫效果，选取20只小鼠，用幼虫感染，8d后随机取15只分为三组分别给予该药的不同药量以杀灭蠕虫，另5只为对照，用药2d后，将所有的小鼠杀死计数体内成虫数。
获得资料如下：对照低剂量中剂量高剂量381279378172346338275235340334412230470198265282318303286250试问：①该实验为何种设计类型？②请写出相应的设计方案？③对资料进行统计分析？随机分配方案：①动物编号1-20②分配随机数：随机排列表第10行。