单因素完全随机和单因素随机区组
生物统计学实验设计
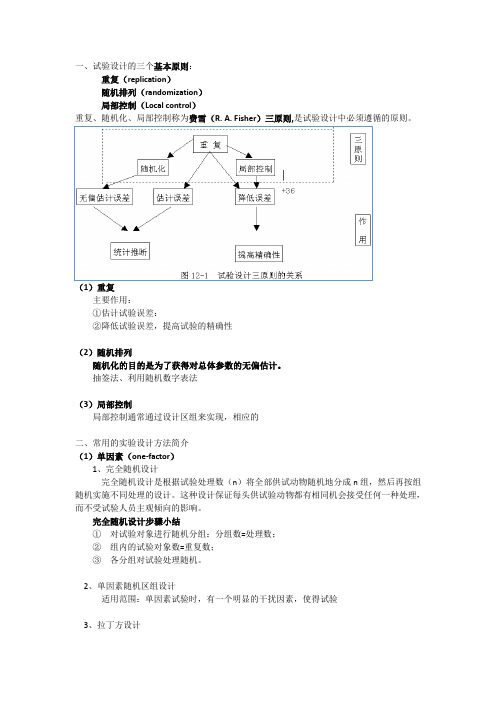
一、试验设计的三个基本原则：
重复（replication）
随机排列（randomization）
局部控制（Local control）
重复、随机化、局部控制称为费雪（R. A. Fisher）三原则,是试验设计中必须遵循的原则。
（1）重复
主要作用：
①估计试验误差：
②降低试验误差，提高试验的精确性
（2）随机排列
随机化的目的是为了获得对总体参数的无偏估计。
抽签法、利用随机数字表法
（3）局部控制
局部控制通常通过设计区组来实现，相应的
二、常用的实验设计方法简介
（1）单因素（one-factor）
1、完全随机设计
完全随机设计是根据试验处理数（n）将全部供试动物随机地分成n组，然后再按组随机实施不同处理的设计。
这种设计保证每头供试验动物都有相同机会接受任何一种处理，而不受试验人员主观倾向的影响。
完全随机设计步骤小结
①对试验对象进行随机分组：分组数=处理数；
②组内的试验对象数=重复数；
③各分组对试验处理随机。
2、单因素随机区组设计
适用范围：单因素试验时，有一个明显的干扰因素，使得试验
3、拉丁方设计
（2）两因素
1、交叉分组设
2、两因素随机区组设计
3、裂区设计
（3）多因素
正交设计。
方差分析变异分解思路剖析
方差分析变异分解思路剖析第一部分：方差分析变异分解的整体思想差分析法是一种在若干能相互比较的资料组中，把产生变异的原因加以区分开来的方法与技术，方差分析实质上是关于观测值变异原因的数量分析。
从变异性分解角度来看，主要是对观测值的总变异进行分解。
分解为两大部分：第一，来自于自变量不同处理效应的影响；第二，来自于误差因素的影响（即包括随机化选择被使过程中所产生的随机因素，也包括一些无法辨别来源的残差）。
以单因素完全随机设计为例。
某心理学家为了考察训练教程对儿童创造思维能力的影响，将20名被试随机分成四个组，每组5人，每组采用一种教程进行训练，一学期后每个被试的创造思维能力评分如下表，试检验训练教程的作用是否有显著的差异。
在这个例子中，自变量为训练教程，一共有四个水平。
因变量为创造性思维能力得分。
那么所有被试在因变量上得分的差异性（即变异）可以分解为两个来源：第一，由于自变量的四个水平所产生的四个组之间的差异性；第二，由于选择被试所导致的组内被试之间的差异性。
第二部分：不同实验设计下变异来源分解剖析一、单因素完全随机设计此主题相关图片变异分解的一般逻辑：首先，计算总变异；然后，计算处理产生的变异；最后，用总变异减去处理产生的变异即误差变异。
在单因素完全随机设计中，处理产生的变异即水平组间变异。
利用原始数据计算变异的公式规律：第一，总平方和和组间平方和的后一项记为CM，矫正数，均为总数据和的平均平方。
求多少和，即对多少平均。
第二，总平方和的前一项为所有原始数据平方的和。
第三，组间平方和的前一项为每组数据和的平方求平均，然后把几个组的计算结果相加。
PS：对我们的启示是在平方和处理变异分解过程中，我们只要搞清楚处理处理是指那几个组就差异就可以了。
以第一部分中单因素随机实验设计为例。
具体数据见下表：此主题相关图片总数据和为477，总数据和的平方为：227529，平均的总数据和的平方为：11376.45（有20个数据）。
完全随机设计说明
均小于.0001， A、B间有交互作用，从A1B1（0.8）、
A1B2(1.0)、A2B1(1.2)、A2B2(2.1)各自均值的 关系可知：A、B间有协同作用。
重复测量设计
重复测量设计
例：为研究Nm23H1基因AN：对肝癌细胞 SMMC-7721增殖和转移的影响，将4~6周龄 雌性裸鼠10只随机等分为两组。一组接种蛋 白高表达细胞克隆AN2，另一组未转染细胞 SMMC-7721作对照，测定癌细胞计数，以光 密度吸收值A595nm来反映，试分析转移基因 AN2是否对肝癌细胞有抑制作用。
配对设计(paired design)—概念
配对的特征或条件： 动物实验：常以种属、品系、性别相同，年龄、 体重相近的两只动物配成对子； 临床疗效观察常将病种、病型、族别、性别相 同，年龄相差不超过2—3岁，生活习惯、工作环 境等相似的病人配成对子；
配对设计(paired design)—注意的问题
完全随机设计
完全随机设计—概念
完全随机设计(completely random design) 亦称单因素设计。将受试对象随机分到各处理组
中进行实验观察，或分别从不同总体中随机抽 样进行对比观察。 它适用于两个或两个以上样本的比较。各组间样 本量可相等，也可不相等。样本相等时统计分 析效率较高。
全随机设计—随机分组
完全随机设计
统计假设检验方法
计量资料：t检验、方差分析或秩和检验等。
计数资料：卡方检验等
完全随机设计
优缺点： 优点：设计及统计分析简单， 缺点：试验效率不高，只能分析单因素。
配对设计
配对设计(paired design)—概念
将受试对象按某些特征或条件配成对子，然后 分别把每对中的两个受试对象随机分配到试验组 和对照组，再给予每对中的个体以不同处理，连 续试验若干对，观察对子间的差别有无意义。
心理学与教育研究中的多因素实验设计——————舒华
心理学与教育研究中的多因素实验设计——————舒华第二章 几种基本的实验设计一、 基本特点适用于：研究中有一个自变量，自变量有两个或多于两个水平。
方法：把被试随机分配给自变量的各个水平，每个水平被试只接受一个水平的处理。
二、 计算与举例（一） 检验的问题与实验设计 （二） 实验数据及其计算()()()()()22i 22j T 2j ij j ss ss X X NX X ss n nNss ss n S X ss ss X X ss X =+=-=-=∙-=-=∙=-∑∑∑∑∑∑∑∑∑∑∑∑总变异组间组内总变异组间组内总变异组间一、 基本特点适用于：研究中有一个变量，自变量有两个或多个水平（P ≥2），研究中还有一个无关变量，也有两个或多个水平（n ≥2）；并且自变量的水平与无关变量的水平之间没有交互作用。
适合检验的假说：（1）处理水平的总体平均数相等或处理效应为零；（2）区组的总体平均数相等或区组效应为零。
二、计算ss ss ss (ss SS ss =+=++总变异组间组内组间区组残差）三、优点：从实验中分离出了一个无关变量的效应，从而减少了实验误差。
一、 基本特点定义：是一个含P 行、P 列、把P 个字母分配给方格的管理方案，其中每个字母在每行中只出现一次。
适用于：（１）研究中自变量与无关变量的水平平均≥２，一个无关变量的水平被分配给Ｐ行，另一个则给Ｐ列；（２）假定处理水平与无关变量水平之间没有交互作用， （３）随即分配处理水平给2P 个方格单元，每个处理水平仅在每行，每列中出现一次。
1c 2c 3c 4c无关变量Ｃ的四个水平 无关变量Ｂ的四个水平 1b 自变量Ａ的四个水平 2b3b4bA B C SS SS SS SS SS SS SS SS =+=++++处理间总变异处理内残差单元内（）一、 基本特点：（也叫被试内设计） 基本方法：实验中每个被试接受所有的处理水平目 的：利用被试自己做控制，使被试的各方面特点在所有的处理中保持恒定，以最大限度地控制由被试的个体差异带来的变异。
完全随机设计和随机区组设计
方差分析应用条件
各样本必须是相互独立的随机样本（独立性） 各样本均来自正态总体（正态性） 相互比较的各样本的总体方差相等（方差齐性）
完全随机设计
完全随机设计属单因素研究设计，它是将随机 抽取的受试对象，随机地分配到两个或多个水 平（处理）组中，观察和比较不同处理所产生 的效应。 分组时可采用简单随机化来实现，即将随机抽 取的足够量的受试对象，按某种标识进行编号， 采用随机数字表或随机函数法等，将受试对象 分配到各组中。
编号 14 15 16 17 18 19 20 21 22 23 24 25 26
随机数 17 24 59 18 6 56 75 44 68 12 94 78 34
R
4 6 17 5 2 16 22 14 19 3 26 23 11
组别 甲 甲 丙 甲 甲 丙 丁 丙 丙 甲 丁 丁 乙
基本思想
总变异=随机变异+处理因素导致的变异 总变异=组内变异 + 组间变异
?( xij )2
? ? SS处理 ?
n（i xi ? x)2 ?
i
j
b
?C
?( xij )2
? ? SS区组 ?
n（j x j ? x)2 ?
j
i
k
?C
随机区组设计的方差分析
b：区组数 k：处理组数
F处理＝
MS处理 MS误差
＝SS处理/? SS误差/?
处理 误差
F区组＝
MS区组 MS误差
＝SS区组/? SS误差/?
随机区组设计
随机区组设计也称配伍组设计，它是将受试对象 按一定条件划分为若干个区组（配伍组），并将 各区组内的受试对象随机地分配到各个处理组中 的一种设计类型。与配对设计原理相同。 随机区组设计的多个样本均数的比较可用无重复 数据的两因素的方差分析。两个因素是指主要的 研究因素（处理因素）和区组因素。按这两个因 素纵横排列时，每个格子中仅有一个数据，故称 无重复数据。
单因素实验设计
单因素实验设计单因素实验设计是指在实验中只有一个研究因素，即研究者只分析一个因素对效应指标的作用，但单因素实验设计并不是意味着该实验中只有一个因素与效应指标有关联。
单因素实验设计的主要目标之一就是如何控制混杂因素对研究结果的影响。
常用的控制混杂因素的方法有完全随机设计、随机区组设计和拉丁方设计等。
一、完全随机设计1.概念与特点又称单因素设计或成组设计，是医学科研中最常用的一种研究设计方法，它是将同质的受试对象随机地分配到各处理组进行实验观察，或从不同总体中随机抽样进行对比研究。
该设计适用面广，不受组数的限制，且各组的样本含量可以相等，也可以不相等，但在总体样本量不变的情况下，各组样本量相同时的设计效率最高。
例如：为了研究煤矿粉尘作业环境对尘肺的影响，将18只大鼠随机分到甲、乙、丙3组，每组6只，分别在地面办公楼、煤炭仓库和矿井下染尘，12周后测量大鼠全肺湿重（g），通过评价不同环境下大鼠全肺平均湿重推断煤矿粉尘对作用尘肺的影响，具体的随机分组可以如下实施：第一步：将18只大鼠编号：1，2，3， (18)第二步：可任意设置种子数，但应作为实验档案记录保存（本例设置spss11.0软件的种子数为200）；第三步：用计算机软件一次产生18个随机数，每个随意数对应一只老鼠（本例用spss11.0软件采用均匀分布最大值为18时产成的18个随机数）；第四步：最小的6个随机数对应编号的大鼠为甲组，排序后的第7个至第12个随机数随因编号为乙组，最大的6个随机数对应编号的大鼠为丙组（结果见表1）。
表1 分配结果编号 1 2 3 4 5 6 7 8 93.75 8.75 16.29 11.12 5.49 3.98 13.64 16.71 1.69随机数组别甲乙丙乙乙甲丙丙甲编号10 11 12 13 14 15 16 17 1813.62 16.36 2.12 4.74 11.54 3.98 0.13 17.35 16.38 随机数组别丙丙甲乙乙甲甲丙丙2.随机数的产生方法（1）随机数字表：如附表13（马斌荣，医学统计学，第4版），这是一个由0～9十个数字组成60行25列的数字表。
随机区组试验设计与分析
第一节 完全随机实验设计及分析
本试验中，水平数m＝3，重复r=5，共进行35＝15次试验。 此15次试验先做哪一个呢？ 试验的先后顺序必须随机确定。随机化方法可采用抽签的方 法，也可用随机数字表确定试验顺序。 现在采用查随机数字表确定试验顺序 （1）对所有试验编号 （2）确定读取随机数字的起始点，并读取相应数目的随机数字。 （3）根据随机数字的大小确定试验的先后顺序。
然后分别在各区组内，用随机的方法将各个处理逐个安排于各供试 单元中。
第二节 随机区组试验设计方法
由于同一区组内的各处理单元的排列顺序是随机而定的，故这 样的区组叫做随机区组。 随机区组设计是一种适用性较广泛的设计方法。既可用于单因素试 验，也适用于多因素试验。
第二节 随机区组试验设计方法
随机区组试验设计方法安排单因素试验
除杂方法（Ai） 平均值 xt
差异显著性
a=0.05
a=0.01
A4
28.4
a
A
A2
27.5
ab
A
A3
27.0
b
A
A1
25.2
c
B
A5
21.3
d
C
第二节 随机区组试验设计方法
2.1 设计方法
实验设计五原则中，其中的一条就是区组的原则。 随机区组试验设计是一种随机排列的完全区组的试验设计。 其方法是： 根据局部控制的原理，将试验的所有供试单元先按重复划分成非处 理条件相对一致的若干单元组，每一组的供试单元数与试验的处理数 相等。
雌鼠编号 1 2 3 4 5 6 7 8 … 39 40
随机数字 09 47 27 96 54 49 17 46 … 03 10
余数
1 3 3 4 2 1 1 2 …3 2
第八章单因素试验结果的统计分析[实践]
![第八章单因素试验结果的统计分析[实践]](https://img.taocdn.com/s3/m/8b715158842458fb770bf78a6529647d272834ed.png)
第八章单因素试验结果的统计分析•单因素试验指仅研究一个供试因素若干处理间的效应是否有显著差异的试验.•按试验设计的类型单因素试验可分为：•顺序排列试验•单因素完全随机试验•单因素随机区组试验•拉丁方试验第一节对比和间比试验的统计分析(自学)第二节完全随机试验设计的统计分析完全随机设计：是所有的处理和重复小区在整个试验空间完全随机排列的设计方法。
只满足试验设计三项基本原则中的重复和随机排列两项原则。
•如：k = 5，n = 3的完全随机排列示意图主要优点：对各处理的重复次数没有限制，可以相等也可以不相等不足之处：没有遵循局部控制原则，所以要求试验地较为均匀一致，不存在有明显方向性的肥力差异，一般不用于田间试验。
•根据每一处理的重复次数或重复的设计方法不同, 又分为：①组内观察值数目相等；②组内观察值数目不等的完全随机试验；③组内又可分为亚组的完全随机试验一、组内观察值数目相等的完全随机试验设计的统计分析组内观察值数目相等的完全随机试验是各处理重复次数相等的试验。
设有k个处理，每处理均有n个重复观察值，共设kn个观察值；其资料的数据结构模式类型见第7章表7.1。
其试验结果的方差分析方法列于表8.1。
表7.1 k个处理每处理n个重复观察值的完全随机试验数据符号表表7.1 nk个观察值的单向分组资料模式表8.1 组内观察值数目相等的完全随机试验的方差分析•〔例8.1〕研究6种棉花种子包衣剂对棉花生长的影响，设TW1为对照。
采用盆栽试验，各种子包衣剂处理播种5盆，完全随机设计。
出苗一定时期后测定棉花苗高（cm），其结果如下。
试检验各种子包衣剂与对照的棉花平均苗高差异显著性及各种子包衣剂棉花平均苗高间的差异显著性。
表8.2 6种棉花种子包衣剂的棉花苗高结果(cm)•解：已知：处理数k=6，重复次数n=5，共有kn=6×5=30个观察值。
•1、自由度及平方和的分解•总自由度df T = nk– 1 =6 × 5 – 1 =30 – 1 =29•处理自由度df t = k– 1 =6 – 1 =6 – 1 =5•误差自由度df e = df T–df t =29 – 5 =24或df e = n(k– 1) =6 ×( 5 – 1) =24 – 1 =23•矫正数总平方和SS T =Σx2－C=22.92+22.32+……+23.72-C=45.763处理平方和误差平方和SS e=SS T－SS t=45.763－44.463=1.3002、F 检验和列方差分析表统计假设H O：μ1= μ2=…= μ6；H A：μi不“全相等”(即至少有一个不等号)将上述计算的各项自由度、平方和、均方结果,按变异来源列出方差分析表(表8.5)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
完全随机实验设计的评价： 优点：实验设计和实施简单
不需要匹配被试
统计分析及对结果的解释简单
缺点：组内变异中混杂有被试的个体差异带来的无关变 异，导致F比率的分母项加大，从而使实验准确率下降；
当有多个处理水平时，需要的被试量较大
单因素随机区组实验设计
单因素随机区组实验设计
一、基本概念
1、用区组方法分离出由无关变量引起的变异，使它不出 现在处理效应和误差变异中 2、适用情境：研究中有一个自变量(有两个或多个水平) 还有一个无关变量（有两个或多个水平） 如关于被试的无关变量，环境因素等 3、适合检验的假说 A、处理水平的总体平均数相等，即： H0：μ1 =μ2 = …… =μp
a3
8 9 8 7 5 6 7 6
a4
9 8 8 7 12 13 12 11
Σ
24 29 24 19 26 31 27 22
Σ
35
31
56
80
202
优点：比完全随机实验设计更加有效
有较好的灵活性（处理水平数和区组数不受限制）
缺点：形成同质区组、寻找同质被试的困难
限制是自变量与无关变量之间没有交互作用
或处理效应为0，即： H0： αj = 0 B、区组的总体平均数相等，即： H0：μ1 =μ2 = …… =μn 或区组效应等于0，即： H0：π j = 0 4、被试分配 a1 a2 a3
区组1 区组2 区组3 区组4 S11 S21 S31 S41 S12 S22 S32 S42 S13 S23 S33 S43
a1
S1 S5 S9 S13
a2
S2 S6 S10 S14
a3Biblioteka S3 S7 S11 S15a4
S4 S8 S12 S16
二、单因素完全随机实验设计与计算举例
（一）研究的问题与实验设计 研究假设：阅读理解随着文章中生字密度的增加而下降 （文章的生字密度对学生阅读理解的影响） 自变量： 生字密度，共四种密度，A1—A4（1/5、 1/10、 1/15、1/20） 因变量： 阅读理解测验分数 被试分配：32名被试随机分成四组，每组阅读一种生字 密度的文章，并回答阅读理解测验中有关文章 内容的问题 （二）实验数据及其计算
a4 S14 S24 S34 S44
二、单因素随机区组实验设计与计算举例
研究的问题与实验设计 文章生字密度对阅读理解的影响研究 考虑到学生的智力可能对阅读理解测验分数产生影响， 但它又不是该实验中感兴趣的因素，因此研究者决定把学 生的智力作为一个无关变量，通过实验设计将它的效应分 离出去，以更好地探讨生字密度对阅读理解的影响
在实验前，研究者首先对32位学生做了智力测验， 并按智力测验分数将学生分为8个区组，然后随机分配每 个区组内的4个同质被试分别阅读一种生字密度的文章 （二）实验数据及计算 a1
区组1 区组2 区组3 区组4 区组5 区组6 区组7 区组8 3 6 4 3 5 7 5 2
a2
4 6 4 2 4 5 3 3
单因素完全随机实验设计
单因素完全随机实验设计
一、基本概念
1、研究中只有一个自变量，但有两个或两个以上水平
2、被试随机分配给处理的各个水平，且每个被试只接受 一个水平的处理
3、用随机化的方式控制误差变异：由于被试是随机分配 的，被试之间的变异在各个处理水平之间也应是随机分布、 在统计上无差异
4、被试分配如下表：
利用基本量计算平方和
同质性检验 其基本假设是分配给不同处理水平的被试在统计上是 无差异的，只有首先证实各组被试是同质的，才能做进一 步的全方差分析。计算方法： SS1组= ( 32+62+… ) - ( 35)2/8=19.875 SS2组= (42+62+…) - (31)2/8 =10.875 SS3组= (82+92+…) - (56)2/8 =12.000 SS4组= (92+82+…) - (80)2/8 =36.00 F=SS最大/SS最小=36.000/10.875=3.31