运算律》知识点归纳及练习
四年级下册数学【运算律】知识点+例题解析
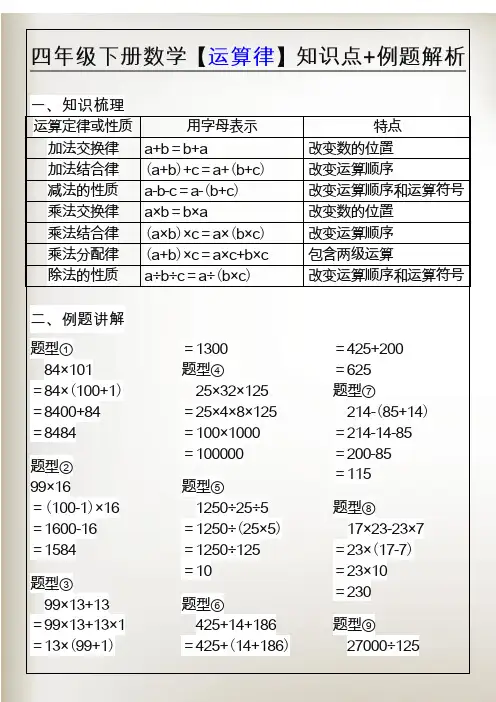
四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10＝230题型⑨27000÷125＝27×1000÷125 ＝27×8 ＝216四年级下册数学【运算律】知识点+例题解析一、知识梳理运算定律或性质用字母表示特点加法交换律a+b＝b+a 改变数的位置加法结合律(a+b)+c＝a+(b+c)改变运算顺序减法的性质a-b-c＝a-(b+c)改变运算顺序和运算符号乘法交换律a×b＝b×a 改变数的位置乘法结合律(a×b)×c＝a×(b×c)改变运算顺序乘法分配律(a+b)×c＝a×c+b×c 包含两级运算除法的性质a÷b÷c＝a÷(b×c)改变运算顺序和运算符号二、例题讲解题型①84×101＝84×(100+1)＝8400+84＝8484题型②99×16＝(100-1)×16 ＝1600-16＝1584题型③99×13+13 ＝99×13+13×1 ＝13×(99+1)＝1300题型④25×32×125＝25×4×8×125＝100×1000＝100000题型⑤1250÷25÷5＝1250÷(25×5)＝1250÷125＝10题型⑥425+14+186＝425+(14+186)＝425+200＝625题型⑦214-(85+14)＝214-14-85＝200-85＝115题型⑧17×23-23×7＝23×(17-7)＝23×10。
《运算律》整理与复习使用
这批零件共有多少个？
王师傅比他徒弟多加工多少个？
01
6
02
二‘判断
03
2、3、4
04
2、3、4
关于运算律……
《运算律》的整理与复习
PART 01
记忆大考验
单击此处添加标题
一 运算律的基本概念及表示方法
加法交换律：
加法结合律：
概念：
字母表示：
加法的运算律
两个数相加，交换加数的位置，它们的和不变。
=452+100+1 =552+1 =553
135×6+65×6 （25+11）×40
1
=（135+65）×6
2
=200×6
3
=1200
4
=25×40+11×40
5
=1000+440
6
=1440
7
乘法分配律
运算律的实际应用（三）：
258 ×8-58 ×8 （ 40-4）×25
04
认真思考做填空
159-28-72
72+120+18
25+6×4
46+78+22
35×8×2
25×17×4
540÷（18×5）
148+103
细心巧妙做计算，看谁的反应快
择优录取
15+b=b+15 这道等式应用的运算律是（ ）
01
395+77+105=77+（395+105） 运用了（ ）
02
我们用交换乘数的位置再乘一遍的方法来验算乘法，这是应用了（ ）
03
小学四年级运算定律与简便计算练习题大全
运算定律与简便计算（一）加减法运算定律1.加法交换律定义：两个加数交换位置，和不变字母表示：a b b a +=+例如：16+23=23+16 546+78=78+5462.加法结合律定义：先把前两个数相加，或者先把后两个数相加，和不变。
字母表示：)()(c b a c b a ++=++注意：加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数进行调换位置，再将这两个加数结合起来先运算。
例1.用简便方法计算下式：（1）63+16+84 （2）76+15+24 （3）140+639+860举一反三：（1）46+67+54 （2）680+485+120 （3）155+657+2453.减法交换律、结合律注：减法交换律、结合律是由加法交换律和结合律衍生出来的。
减法交换律：如果一个数连续减去两个数，那么后面两个减数的位置可以互换。
字母表示：b c a c b a --=--例2.简便计算：198-75-98减法结合律：如果一个数连续减去两个数，那么相当于从这个数当中减去后面两个数的和。
字母表示：)(c b a c b a +-=--例3.简便计算：（1）369-45-155 （2）896-580-1204.拆分、凑整法简便计算拆分法：当一个数比整百、整千稍微大一些的时候，我们可以把这个数拆分成整百、整千与一个较小数的和，然后利用加减法的交换、结合律进行简便计算。
例如：103=100+3，1006=1000+6，…凑整法：当一个数比整百、整千稍微小一些的时候，我们可以把这个数写成一个整百、整千的数减去一个较小的数的形式，然后利用加减法的运算定律进行简便计算。
例如：97=100-3，998=1000-2，…注意：拆分凑整法在加、减法中的简便不是很明显，但和乘除法的运算定律结合起来就具有很大的简便了。
例4.计算下式，能简便的进行简便计算：（1）89+106 （2）56+98 （3）658+997随堂练习：计算下式，怎么简便怎么计算（1）730+895+170 （2）820-456+280 （3）900-456-244（4）89+997 （5）103-60 （6）458+996（7）876-580+220 （8）997+840+260 （9）956—197-56（二）乘除法运算定律1.乘法交换律定义：交换两个因数的位置，积不变。
四年级下册运算律知识点归纳
四年级下册运算律知识点归纳
加法运算律。
1. 加法交换律：两个加数相加，交换加数的位置，和不变。
用字母表示为：a + b = b + a
2. 加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。
用字母表示为：(a + b) + c = a + (b + c)
乘法运算律。
1. 乘法交换律：两个因数相乘，交换因数的位置，积不变。
用字母表示为：a × b = b × a
2. 乘法结合律：三个数相乘，先乘前两个数，或者先乘后两个数，积不变。
用字母表示为：(a × b) × c = a × (b × c)
3. 乘法分配律：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。
用字母表示为：(a + b)×c = a×c + b×c
简便运算。
在进行简便运算时，要根据运算律，对算式进行变形，使计算更加简便。
例如：。
1. 25 + 36 + 75 = (25 + 75) + 36 = 100 + 36 = 136（运用了加法交换律和结合律）。
2. 25×4×8 = (25×4)×8 = 100×8 = 800（运用了乘法结合律）。
3. 102×56 = (100 + 2)×56 = 100×56 + 2×56 = 5600 + 112 = 5712（运用了乘法分配律）。
运算律总结
(2) 34×25×4 =34×(25×4) =34×100 =3400 (4) 125×32×25 =125×8×(4×25) =1000×100 =100000
3. 乘法分配律：两个数的和与一个数 相乘，可以把这两个加数分别与这个 数相乘，再把积相加。 用字母表示为： (a+b)×c= a×c+b×c 4.乘法分配律的拓展：两个数的差与 另一个数相乘，可以用这个分别去乘 先前的两个数，在把积相减。 用字母表示为： (a－b)×c= a×c－b×c
(2) 45×104 (1) 125× (8+80) =45×(100+4) =125×8+125×80 =45×100+45×4 =1000+10000 =4500+180 =11000 =4680 (3) 125× (80-8) (4) 45×98 =125×80-125×8 =45×(100-2) =10000-1000 =45×100-45×2 =9000 =4500-90 =4410 (5) 38×99+38 (6) 87×101-87 =38× (99+1) =87×(101-1) =38×100 =87×100 =3800 =8700
(2) 598+104 =598+100+4 =698+4 =702
(1) 175+38+25 =175+25+38 =200+38 =238 (3) 356+97 =356+100-3 =456-3 =453
（二） 减法的性质：一个数连 续减去两个数，可以用这个减去 这两个减数的和，结果不变。 用字母表示为： a－b－c= a－(b+c) a－(b+c)= a－b－c
第三单元《运算律》整理与复习-新人教版数学四年级下册 (1)精选全文
固
(3)水果店购进苹果和梨子各40箱。苹果每箱68元， 梨子每箱53元。买苹果比梨子多花多少元？ (68－53)×40＝600(元) 答：买苹果比梨子多花600元。
固
5.李大爷家有一块菜地
（如右图），这块菜地
的面积有多少平方米？ 9×(21－9) ＋9×（19+9） =9×12＋9×28 =9×（12＋28） =9×40 =360m²
识
乘 法
乘法交换律 两个数相乘，交换两个因数的位置，积不变 a×b=b×a
运 算
三个数相乘，先乘前两个数，或者先乘后
定 乘法结合律 两个数，积不变
律
(a×b)×c=a×(b×c)
两个数的和与一个数相乘，可以先把它们 乘法分配律 与这个数分别相乘
(a+b)×c=a×c+b×c
识
除
一个数连续除以两个数，可以用这个数除以两个数
固
4．解决问题。 (1)每本集邮册都是24页，每页都可以插8张邮票。小
峰有这样的集邮册5本，一共可以插多少张邮票？
24×8×5＝960(张) 答：一共可以插960张邮票。
固
(2)彭老师准备给篮球队8名队员每人发一套球衣和一 双球鞋，每套球衣64元，每双球鞋36元。买这些 球衣和球鞋一共需要多少元？ (64＋36)×8＝800(元) 答：买这些球衣和球鞋一共需要800元。
+ 37 +a
加法的运算定律
连线。 360+270+640 62+21+38 527+(303+697)
型
21+(62+38) 697+527+303 360+640+270
四年级数学下运算律知识点.doc
苏教版四年级数学下运算律知识点（内部资料）知识点一：加法交换律和结合律1．加法交换律：两个数相加，交换加数的位置，和不变。
用字母表示为：a+b=b+a 2．加法结合律：三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。
用字母表示为：（a+b）+c=a+（b+c）。
例1.1 ：填上适当的数。
81+（）= 62 + 81 184 + 168 + 32 = 184+ （+ 32 ）练习1.2 ：选出正确答案，将序号填在相应的括号里。
①41+37+13=41+（37+13）②x+y=y+x ③ 35+（b+65）=（35+65）+b ④ a+b+c=a+c+b ⑤32+45+55=32+（45+55）⑥m+n+t=n+（m+t）只应用加法交换律的是（）。
只应用加法结合律的是（）。
既应用加法交换律，又应用加法结合律的是（）。
知识点二：应用加法运算律进行简便计算在连加计算中，当某些加数相加可以凑成整十、整百、整千的数时，运用加法运算律可使计算简便。
口诀：连加计算仔细看，考虑加数是关键。
整十、整百与整千，结合起来更简单。
交换定律记心间，交换位置和不变。
结合定律应用广，加数凑整更简便。
例2.1 ：69+75+25 78+（47+22）387+98（多加要减）387+10（2 少加要加）387﹣98（多减要加）387﹣102（少减要减）练习2.2 ：99+124+201 380+345+120 9321+4523+972+679+5477+28苏教版四年级数学下运算律知识点（内部资料）知识点三：减法的运算性质1：一个数连续减去两个数等于这个数减去这两个减数的和。
用字母表示：a-b-c=a-（b+c）减法的运算性质2：一个数减去两个数的和等于这个数连续减去和里每个加数。
例3.1 ：324-58-42 670-25-75159﹣（59+37）268 ﹣（35+68）加减的规律：（1）先加后减等于先减后加。
第三单元运算律整理知识点
第三单元运算律整理知识点一、知识概述《运算律》①基本定义：运算律就是在进行四则运算（加、减、乘、除）的时候，一些能让计算变得简便的规律。
比如说加法交换律，就是两个数相加，交换它们的位置，和不变。
像3 + 5 = 5 + 3。
乘法分配律呢，就是一个数乘两个数的和，可以分别乘这两个数，再把积相加，比如3×（2 + 4）=3×2+3×4。
②重要程度：在数学学科里那可是非常重要的。
就像盖房子的基石一样，从简单的四则运算到复杂的代数运算，到处都有它的身影。
要是不懂运算律，做数学题的时候就会绕很多弯路，复杂的计算可能就没法做下去了。
③前置知识：得先掌握基本的四则运算，知道什么是加法、减法、乘法和除法，还有正数、负数等这些基础的数的概念。
比如说你得知道2 + 3是多少，5 - 1是多少这样的基础计算。
④应用价值：在生活中也经常能用到。
比如说去超市买东西，有促销活动的时候，你得计算不同组合的商品价格是不是划算，这就可能用到运算律。
或者计算家庭每月收支的时候，把收入和支出分类计算，其实也是在不知不觉中用运算律简化计算。
二、知识体系①知识图谱：运算律在小学数学学科里就是四则运算这个大板块中的核心规则部分。
它就像一张网中的节点，联系着各个不同运算类型之间的关系。
②关联知识：和整数、小数、分数的运算都有联系。
比如说整数的加法交换律，在小数、分数的加法里同样适用。
而且和后面要学的方程运算也密切相关，解方程很多步骤就是依据运算律来简化的。
③重难点分析：掌握难度中等偏上吧。
难点就是区分不同运算律之间的差别，像乘法结合律和乘法分配律就很容易弄混。
关键点在于理解每个运算律的本质含义，会根据具体的算式去选择合适的运算律来简化。
④考点分析：在考试中那可太重要了。
既会单独出题考查运算律的概念，像问加法交换律是什么；也会在四则混合运算的大题里考查运算律的运用，看是否能正确运用运算律简便计算。
三、详细讲解【理论概念类】①概念辨析：加法交换律：两个数相加，交换加数的位置，和不变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四单元《运算律》知识点归纳及练习
乘法结合律
1、乘法结合律：
三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，它们的积不变。
用字母表示是：
（a×b）×c=a×(b×c).
使用时机：
当几个数相乘时，如果其中两个数相乘得整十、整百、整千的数就可以应用乘法交换律和乘法结合律。
乘法结合律可以改变乘法运算中的顺序。
数字如;25和4、50和2、125和8、50和4、500和2等。
加法运算时也有结合律。
如果用a/b/c表示三个数，那么加法结合律表示为：（a+b）+c=a+（b+c）
2、认识乘法交换律
两个数相乘，交换他们的位置，积不变，这叫乘法交换律。
如用字母a、b表示两个数，那么乘法交换律用字母表示为：a×b=b×a。
1）上述规律可推广到更多个数相乘。
如：125×4×8×25=（125×8）×（25×4）=1000×100=100000
2）加法运算时也有交换律，如用字母a、b表示两个数，那么加法交换律用字母表示为：a+b=b+a。
3）运用加法交换律和结合律可以使得一些运算简便。
50+7+40+9=（50+40）+（7+9）=90+16=106
练习题：
73×25×4 125×63×8 4×（25×93） 12×125×5×8
32×125×25 48×125×5
乘法分配律
1、乘法分配律：
两个数的和（或差）与一个数相乘，可以把两个加数（或被减数、减数）分别与这个数相乘，在把两个积相加（或相减），结果不变。
用字母表示数：
（a+b）×c=a×c+b×c或（a-b）×c=a×c－b×c
1、式子的特点：
式子的运算符号一般是×、+(-)、×的形式；在两个乘法式子中，有一个相同的因数；另为两个不同的因数之和(或之差)是能凑成整十、整百、整千的数。
（逆运算）
2、102×88、99×15这类题的特点：
两个数相乘，把其中一个比较接近整十、整百、整千的数改写成整十、整百、整千与一个数的和（或差），再
应用乘法分配律可以使运算简便。
习题：
（80+4）×25 34×72+34×28 （23×99）×25+（77+71）×25 25×99 9999×2222+3333×3334 6666×3333+2222
第四单元备选练习题
一、填空。
（24）
1、两个数相加，交换加数的，结果不变，这叫做。
用字母表示
为。
2、三个数相加，先把相加，再和相加；或者先把相加，再和相加，
它们的结果不变，这叫做。
用字母表示为。
3、两个数相乘，交换乘数的，结果不变，这叫做。
用字母表示
为。
4、三个数相乘，先把相乘，再和相乘；或者先把相乘，再和相乘，
它们的结果不变，这叫做。
用字母表示为。
5、在
29＋37＋171＝37＋（。
42×5×8＝42×（。
47＋＝28 。
427＋39＋73＝（427
35×21×2＝21×（。
45×16＝45×。
6、计算64×26后，可以交换两个数的位置验算，是用了（）律。
7、一道减法算式的差是16，如果被减数不变，减数增加4，则差是（）。
二、用竖式计算下面各题，并验算。
（9）
618＋324 76×28 728÷18
三、简便计算。
（45）
44＋37＋56 163＋49＋261 74＋（137＋326） 5×（63×2）
249＋402 189＋35＋211＋165 483－236－64
582－157－182 65×5×2 15×23×4 540÷45÷2
36×25 25×125×32 35×22 540÷36
四、解决实际问题（22）
1、食堂买来5筐西红柿，每筐24千克，每千克2元，这些西红柿一共多少元？
2、一只熊猫体重75千克，一只小象的体重比熊猫的12倍少20千克，小象的体重多少千克？
3、每个书架有三层，每层大约放20本书。
（1）三个书架大约一共放多少本书?
(2)学校图书馆又新买来550本新书，增加几个这样的书架比较合适？
4、请算出育才小学四、五、六年级分别有多少人？并写出简便运算的过程。
5、按要求填表。