平衡二叉树操作的演示

合集下载

数据结构平衡二叉树的操作演示

平衡二叉树操作的演示1.需求分析本程序是利用平衡二叉树，实现动态查找表的基本功能：创建表，查找、插入、删除。

具体功能：（1）初始，平衡二叉树为空树，操作界面给出创建、查找、插入、删除、合并、分裂六种操作供选择。

每种操作均提示输入关键字。

每次插入或删除一个结点后，更新平衡二叉树的显示。

（2）平衡二叉树的显示采用凹入表现形式。

（3）合并两棵平衡二叉树。

（4）把一棵二叉树分裂为两棵平衡二叉树，使得在一棵树中的所有关键字都小于或等于x，另一棵树中的任一关键字都大于x。

如下图：2．概要设计平衡二叉树是在构造二叉排序树的过程中，每当插入一个新结点时，首先检查是否因插入新结点而破坏了二叉排序树的平衡性，若是则找出其中的最小不平衡子树，在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

具体步骤：（1）每当插入一个新结点，从该结点开始向上计算各结点的平衡因子，即计算该结点的祖先结点的平衡因子，若该结点的祖先结点的平衡因子的绝对值不超过1，则平衡二叉树没有失去平衡，继续插入结点；（2）若插入结点的某祖先结点的平衡因子的绝对值大于1，则找出其中最小不平衡子树的根结点；（3）判断新插入的结点与最小不平衡子树的根结点个关系，确定是那种类型的调整；（4）如果是LL型或RR型，只需应用扁担原理旋转一次，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；如果是LR型或RL型，则需应用扁担原理旋转两次，第一次最小不平衡子树的根结点先不动，调整插入结点所在子树，第二次再调整最小不平衡子树，在旋转过程中，如果出现冲突，应用旋转优先原则调整冲突；（5）计算调整后的平衡二叉树中各结点的平衡因子，检验是否因为旋转而破坏其他结点的平衡因子，以及调整后平衡二叉树中是否存在平衡因子大于1的结点。

流程图3.详细设计二叉树类型定义：typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;struct BSTNode *lchild ,*rchild;} BSTNode,* BSTree;Status SearchBST(BSTree T,ElemType e)//查找void R_Rotate(BSTree &p)//右旋void L_Rotate(BSTree &p)//左旋void LeftBalance(BSTree &T)//插入平衡调整void RightBalance(BSTree &T)//插入平衡调整Status InsertAVL(BSTree &T,ElemType e,int &taller)//插入void DELeftBalance(BSTree &T)//删除平衡调整void DERightBalance(BSTree &T)//删除平衡调整Status Delete(BSTree &T,int &shorter)//删除操作Status DeleteAVL(BSTree &T,ElemType e,int &shorter)//删除操作void merge(BSTree &T1,BSTree &T2)//合并操作void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2)//分裂操作void PrintBSTree(BSTree &T,int lev)//凹入表显示附录源代码：#include<stdio.h>#include<stdlib.h>//#define TRUE 1//#define FALSE 0//#define OK 1//#define ERROR 0#define LH +1#define EH 0#define RH -1//二叉类型树的类型定义typedef int Status;typedef int ElemType;typedef struct BSTNode{ElemType data;int bf;//结点的平衡因子struct BSTNode *lchild ,*rchild;//左、右孩子指针} BSTNode,* BSTree;/*查找算法*/Status SearchBST(BSTree T,ElemType e){if(!T){return 0; //查找失败}else if(e == T->data ){return 1; //查找成功}else if (e < T->data){return SearchBST(T->lchild,e);}else{return SearchBST(T->rchild,e);}}//右旋void R_Rotate(BSTree &p){BSTree lc; //处理之前的左子树根结点lc = p->lchild; //lc指向的*p的左子树根结点p->lchild = lc->rchild; //lc的右子树挂接为*P的左子树lc->rchild = p;p = lc; //p指向新的根结点}//左旋void L_Rotate(BSTree &p){BSTree rc;rc = p->rchild; //rc指向的*p的右子树根结点p->rchild = rc->lchild; //rc的左子树挂接为*p的右子树rc->lchild = p;p = rc; //p指向新的根结点}//对以指针T所指结点为根结点的二叉树作左平衡旋转处理，//本算法结束时指针T指向新的根结点void LeftBalance(BSTree &T){BSTree lc,rd;lc=T->lchild;//lc指向*T的左子树根结点switch(lc->bf){ //检查*T的左子树的平衡度，并做相应的平衡处理case LH: //新结点插入在*T的左孩子的左子树，要做单右旋处理T->bf = lc->bf=EH;R_Rotate(T);break;case RH: //新结点插入在*T的左孩子的右子树上，做双旋处理rd=lc->rchild; //rd指向*T的左孩子的右子树根switch(rd->bf){ //修改*T及其左孩子的平衡因子case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild); //对*T的左子树作左旋平衡处理R_Rotate(T); //对*T作右旋平衡处理}}//右平衡旋转处理void RightBalance(BSTree &T){BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= rc->bf=EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}//插入结点Status InsertAVL(BSTree &T,ElemType e,int &taller){//taller反应T长高与否if(!T){//插入新结点，树长高，置taller为trueT= (BSTree) malloc (sizeof(BSTNode));T->data = e;T->lchild = T->rchild = NULL;T->bf = EH;taller = 1;}else{if(e == T->data){taller = 0;return 0;}if(e < T->data){if(!InsertAVL(T->lchild,e,taller))//未插入return 0;if(taller)//已插入到*T的左子树中且左子树长高switch(T->bf){//检查*T的平衡度，作相应的平衡处理case LH:LeftBalance(T);taller = 0;break;case EH:T->bf = LH;taller = 1;break;case RH:T->bf = EH;taller = 0;break;}}else{if (!InsertAVL(T->rchild,e,taller)){return 0;}if(taller)//插入到*T的右子树且右子树增高switch(T->bf){//检查*T的平衡度case LH:T->bf = EH;taller = 0;break;case EH:T->bf = RH;taller = 1;break;case RH:RightBalance(T);taller = 0;break;}}}return 1;}void DELeftBalance(BSTree &T){//删除平衡调整BSTree lc,rd;lc=T->lchild;switch(lc->bf){case LH:T->bf = EH;//lc->bf= EH;R_Rotate(T);break;case EH:T->bf = EH;lc->bf= EH;R_Rotate(T);break;case RH:rd=lc->rchild;switch(rd->bf){case LH: T->bf=RH; lc->bf=EH;break;case EH: T->bf=lc->bf=EH;break;case RH: T->bf=EH; lc->bf=LH;break;}rd->bf=EH;L_Rotate(T->lchild);R_Rotate(T);}}void DERightBalance(BSTree &T) //删除平衡调整{BSTree rc,ld;rc=T->rchild;switch(rc->bf){case RH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case EH:T->bf= EH;//rc->bf= EH;L_Rotate(T);break;case LH:ld=rc->lchild;switch(ld->bf){case LH: T->bf=RH; rc->bf=EH;break;case EH: T->bf=rc->bf=EH;break;case RH: T->bf = EH; rc->bf=LH;break;}ld->bf=EH;R_Rotate(T->rchild);L_Rotate(T);}}void SDelete(BSTree &T,BSTree &q,BSTree &s,int &shorter){if(s->rchild){SDelete(T,s,s->rchild,shorter);if(shorter)switch(s->bf){case EH:s->bf = LH;shorter = 0;break;case RH:s->bf = EH;shorter = 1;break;case LH:DELeftBalance(s);shorter = 0;break;}return;}T->data = s->data;if(q != T)q->rchild = s->lchild;elseq->lchild = s->lchild;shorter = 1;}//删除结点Status Delete(BSTree &T,int &shorter){ BSTree q;if(!T->rchild){q = T;T = T->lchild;free(q);shorter = 1;}else if(!T->lchild){q = T;T= T->rchild;free(q);shorter = 1;}else{SDelete(T,T,T->lchild,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}}return 1;}Status DeleteAVL(BSTree &T,ElemType e,int &shorter){ int sign = 0;if (!T){return sign;}else{if(e == T->data){sign = Delete(T,shorter);return sign;}else if(e < T->data){sign = DeleteAVL(T->lchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = RH;shorter = 0;break;case LH:T->bf = EH;shorter = 1;break;case RH:DERightBalance(T);shorter = 0;break;}return sign;}else{sign = DeleteAVL(T->rchild,e,shorter);if(shorter)switch(T->bf){case EH:T->bf = LH;shorter = 0;break;case RH:T->bf = EH;break;case LH:DELeftBalance(T);shorter = 0;break;}return sign;}}}//合并void merge(BSTree &T1,BSTree &T2){int taller = 0;if(!T2)return;merge(T1,T2->lchild);InsertAVL(T1,T2->data,taller);merge(T1,T2->rchild);}//分裂void split(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ int taller = 0;if(!T)return;split(T->lchild,e,T1,T2);if(T->data > e)InsertAVL(T2,T->data,taller);elseInsertAVL(T1,T->data,taller);split(T->rchild,e,T1,T2);}//分裂void splitBSTree(BSTree T,ElemType e,BSTree &T1,BSTree &T2){ BSTree t1 = NULL,t2 = NULL;split(T,e,t1,t2);T1 = t1;T2 = t2;return;}//构建void CreatBSTree(BSTree &T){int num,i,e,taller = 0;printf("输入结点个数:");scanf("%d",&num);printf("请顺序输入结点值\n");for(i = 0 ;i < num;i++){printf("第%d个结点的值",i+1);scanf("%d",&e);InsertAVL(T,e,taller) ;}printf("构建成功，输入任意字符返回\n");getchar();getchar();}//凹入表形式显示方法void PrintBSTree(BSTree &T,int lev){int i;if(T->rchild)PrintBSTree(T->rchild,lev+1);for(i = 0;i < lev;i++)printf(" ");printf("%d\n",T->data);if(T->lchild)PrintBSTree(T->lchild,lev+1);void Start(BSTree &T1,BSTree &T2){int cho,taller,e,k;taller = 0;k = 0;while(1){system("cls");printf(" 平衡二叉树操作的演示 \n\n");printf("********************************\n");printf(" 平衡二叉树显示区 \n");printf("T1树\n");if(!T1 )printf("\n 当前为空树\n");else{PrintBSTree(T1,1);}printf("T2树\n");if(!T2 )printf("\n 当前为空树\n");elsePrintBSTree(T2,1);printf("\n********************************************************************* *********\n");printf("T1操作：1.创建 2.插入 3.查找 4.删除 10.分裂\n");printf("T2操作：5.创建 6.插入 7.查找 8.删除 11.分裂\n");printf(" 9.合并 T1,T2 0.退出\n");printf("*********************************************************************** *******\n");printf("输入你要进行的操作：");scanf("%d",&cho);switch(cho){case 1:CreatBSTree(T1);break;case 2:printf("请输入要插入关键字的值");scanf("%d",&e);InsertAVL(T1,e,taller) ;break;case 3:printf("请输入要查找关键字的值");scanf("%d",&e);if(SearchBST(T1,e))printf("查找成功！\n");elseprintf("查找失败！\n");printf("按任意键返回87"); getchar();getchar();break;case 4:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T1,e,k))printf("删除成功！\n");elseprintf("删除失败！\n");printf("按任意键返回");getchar();getchar();break;case 5:CreatBSTree(T2);break;case 6:printf("请输入要插入关键字的值"); scanf("%d",&e);InsertAVL(T2,e,taller) ;break;case 7:printf("请输入要查找关键字的值"); scanf("%d",&e);if(SearchBST(T2,e))printf("查找成功！\n");elseprintf("查找失败！\n");printf("按任意键返回");getchar();getchar();break;case 8:printf("请输入要删除关键字的值"); scanf("%d",&e);if(DeleteAVL(T2,e,k))printf("删除成功！\n");elseprintf("删除失败！\n");printf("按任意键返回");getchar();getchar();break;case 9:merge(T1,T2);T2 = NULL;printf("合并成功，按任意键返回"); getchar();getchar();break;case 10:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T1,e,T1,T2) ;printf("分裂成功，按任意键返回"); getchar();getchar();break;case 11:printf("请输入要中间值字的值"); scanf("%d",&e);splitBSTree(T2,e,T1,T2) ;printf("分裂成功，按任意键返回"); getchar();getchar();break;case 0:system("cls");exit(0);}}}main(){BSTree T1 = NULL;BSTree T2 = NULL;Start(T1,T2);}。

AVL树自平衡的二叉搜索树

AVL树自平衡的二叉搜索树AVL树是一种自平衡的二叉搜索树，它是根据其发明者 G.M. Adelson-Velsky 和 Evgenii Landis 的姓氏首字母而得名。

AVL树解决了传统二叉搜索树由于插入或删除操作导致树结构不平衡而引发的性能问题。

1. 什么是二叉搜索树？二叉搜索树，又称二叉排序树或二叉查找树，是一种特殊的二叉树结构。

在二叉搜索树中，每个节点都包含一个键值，并且节点的左子树中的键值小于节点的键值，右子树中的键值大于节点的键值。

2. 为什么需要自平衡？传统的二叉搜索树在执行插入或删除操作时，可能会导致树结构不平衡，使得树的高度远大于理想情况下的最小高度。

当树的高度增加后，查找、插入、删除等操作的时间复杂度也会增加，进而影响整体性能。

3. AVL树的自平衡特性AVL树通过保持树的平衡性来提高性能。

对于每一个节点，AVL 树通过计算其左右子树的高度差（平衡因子）来判断是否需要进行旋转操作来保持树的平衡。

当平衡因子超过一定阈值时，进行相应的旋转操作来维持平衡。

4. AVL树的旋转操作AVL树的旋转操作包括左旋和右旋。

左旋操作将当前节点的右子树变为新的根节点，而右旋操作则恰恰相反。

通过旋转操作，AVL树可以在保持二叉搜索树性质的同时，实现树的自平衡。

5. AVL树的插入操作在进行插入操作时，AVL树首先按照二叉搜索树的规则找到插入位置，并插入新的节点。

然后，从插入节点开始沿着路径向上逐层检查平衡因子，若遇到不平衡的节点，执行相应的旋转操作来恢复树的平衡。

6. AVL树的删除操作在进行删除操作时，AVL树首先按照二叉搜索树的规则找到待删除的节点，并执行删除操作。

然后，从删除节点的父节点开始沿着路径向上逐层检查平衡因子，若遇到不平衡的节点，执行相应的旋转操作来恢复树的平衡。

7. AVL树的平衡性保证AVL树的自平衡操作保证了树的高度始终保持在理想情况下的最小高度的常数倍。

通过对平衡因子的检查并执行旋转操作，AVL树能够有效地保持树的平衡性，使得查找、插入、删除等操作能够在较快的时间内完成。

平衡二叉树旋转例题

平衡二叉树旋转例题摘要：I.平衡二叉树的概念及特点II.平衡二叉树旋转的定义和目的III.平衡二叉树旋转的实例解析IV.平衡二叉树旋转的操作步骤及要点V.平衡二叉树旋转的应用场景正文：I.平衡二叉树的概念及特点平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树结构，具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

平衡二叉树的特点是每个节点的左右子树的高度差的绝对值不超过1，这使得树的高度保持在一个相对平衡的状态，从而保证了树的稳定性和查找效率。

II.平衡二叉树旋转的定义和目的平衡二叉树旋转是一种处理树不平衡问题的方法。

当二叉树的平衡条件被破坏时，需要通过旋转操作来重新平衡树。

旋转的目的是调整树的结构，使得树的左右子树的高度差的绝对值不超过1，从而保证树的稳定性和查找效率。

III.平衡二叉树旋转的实例解析假设有一棵平衡二叉树，其结构如下：```10/4 20/2 6 8```当插入一个新的节点14 后，树的结构变为：```10/4 20/2 6 8 14```由于树的平衡条件被破坏，需要进行旋转操作。

旋转后的树结构如下：```14/4 10/2 6 8```可以看到，通过旋转操作，树的平衡条件得到了恢复。

IV.平衡二叉树旋转的操作步骤及要点平衡二叉树旋转操作分为以下两种：左旋和右旋。

左旋操作：将当前节点的右子树旋转到左子树的左侧，即将右子树的根节点提升为当前节点的左子节点，原左子节点变为右子节点。

右旋操作：将当前节点的左子树旋转到右子树的右侧，即将左子树的根节点提升为当前节点的右子节点，原右子节点变为左子节点。

旋转操作的要点是选择好旋转的中心节点，以及注意旋转后子节点关系的调整。

V.平衡二叉树旋转的应用场景平衡二叉树旋转在实际应用中主要应用于二叉查找树（Binary Search Tree）的维护。

当二叉查找树中的节点不平衡时，通过旋转操作可以调整树的结构，使得树的查询效率保持在较高的水平。

平衡二叉树10.3.2

11
28
96 98
25
(1) LL型调整型调整 p A 1 2
调整方法: 调整方法: 单向右旋平衡,即将的左孩子单向右旋平衡,即将A的左孩子 B 向右上旋转代替成为根结点, 向右上旋转代替A成为根结点成为根结点, 结点向右下旋转成为B的右将A结点向右下旋转成为的右结点向右下旋转成为子树的根结点, 子树的根结点,而B的原右子树的原右子树则作为A结点的左子树结点的左子树. 则作为结点的左子树. h d e B
1 38 -1 24 88
0 -1 -2
0
11
28 1
96
0
-1 0
25
0
98
1,平衡二叉树插入结点的调整方法
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性, 首先从根结点到该新插入结点的路径之逆向根结点方向找第一个失去平衡的结点, 衡的结点,然后以该失衡结点和它相邻的刚查找过的两个结点构成调整子树(最小不平衡子树即调整子树是指以离插入结点最近,且平衡因子最小不平衡子树), 子树最小不平衡子树 ,即调整子树是指以离插入结点最近且平衡因子绝对值大于1的结点为根结点的子树使之成为新的平衡子树. 的结点为根结点的子树,使之成为新的平衡子树绝对值大于的结点为根结点的子树使之成为新的平衡子树. 38 24 88 -2
(2)RR型调整型调整 p A -1 -2
调整方法: 调整方法: 单向左旋平衡:即将的右孩子的右孩子B向单向左旋平衡:即将A的右孩子向左上旋转代替A成为根结点成为根结点, 左上旋转代替成为根结点,将A结结点向左下旋转成为B的左子树的根点向左下旋转成为的左子树的根结点, 的原左子树则作为A结点结点,而B的原左子树则作为结点的原左子树则作为的右子树. 的右子树. B

平衡二叉树平衡因子

平衡二叉树平衡因子
平衡二叉树，又称AVL树，是一种自平衡二叉搜索树。

它具有以下特点：任意节点的左右子树高度差不超过1。

为了实现这个特点，需要在插入和删除节点时进行相关操作，以保持树的平衡。

平衡因子是平衡二叉树中每个节点的一个属性，它表示该节点的左右子树高度差。

平衡因子可以为-1、0和1。

如果平衡因子为-1，表示该节点的左子树高度比右子树高1；如果平衡因子为0，表示该节点的左右子树高度相等；如果平衡因子为1，表示该节点的右子树高度比左子树高1。

在平衡二叉树中，任意节点的平衡因子必须在-1到1之间，否则该节点就不符合平衡条件，需要进行相应的平衡操作。

平衡因子的计算方法是该节点的右子树高度减去左子树高度。

例如，在下面这棵平衡二叉树中，节点7的平衡因子为1，节点6的平衡因子为-1。

```
5
/
3 7
/ /
1 4 6 8
```
在插入和删除节点时，需要根据节点的平衡因子来判断树是否需要进行平衡操作。

如果某个节点的平衡因子不符合要求，需要进行旋
转操作来调整节点的位置，以保持树的平衡。

具体的旋转操作包括左旋、右旋、左右旋和右左旋，可以根据节点的平衡因子和子节点的平衡因子来确定需要进行的操作。

维护平衡二叉树需要付出一定的时间和空间代价，但它的优点是可以保证树的查找、插入和删除操作的时间复杂度都是O(log n)，比普通的二叉搜索树更加高效。

因此，在需要频繁进行这些操作的场景下，平衡二叉树是一种非常有用的数据结构。

详解平衡二叉树

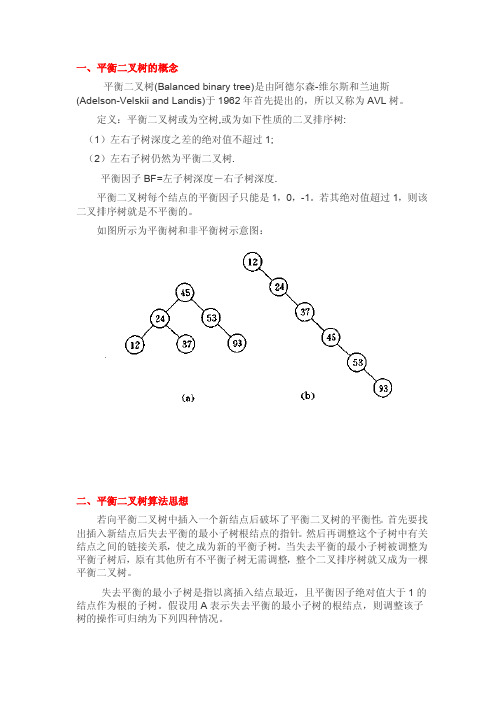
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的，所以又称为AVL树。

定义：平衡二叉树或为空树,或为如下性质的二叉排序树:（1）左右子树深度之差的绝对值不超过1;（2）左右子树仍然为平衡二叉树.平衡因子BF=左子树深度－右子树深度.平衡二叉树每个结点的平衡因子只能是1，0，-1。

若其绝对值超过1，则该二叉排序树就是不平衡的。

如图所示为平衡树和非平衡树示意图：二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。

首先要找出插入新结点后失去平衡的最小子树根结点的指针。

然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。

当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。

假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

1）LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。

故需进行一次顺时针旋转操作。

即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。

而原来B的右子树则变成A的左子树。

（2）RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。

故需进行一次逆时针旋转操作。

即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。

而原来C的左子树则变成A的右子树。

（3）LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。

故需进行两次旋转操作（先逆时针，后顺时针）。

即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。

平衡二叉树用途

平衡二叉树用途平衡二叉树是一种特殊的二叉树结构，它具有良好的平衡性，能够提高二叉树的查找、插入和删除操作的效率。

平衡二叉树在计算机科学领域中广泛应用，特别是在数据结构和算法中。

下面将详细介绍平衡二叉树的用途。

1. 提高查找效率平衡二叉树的一个重要应用是提高查找效率。

在平衡二叉树中，每个节点的左子树和右子树的高度差不超过1，这保证了树的高度相对较低。

相比于普通的二叉搜索树，平衡二叉树的查找操作更加高效。

在平衡二叉树中查找一个元素的平均时间复杂度为O(log n)，而在普通二叉搜索树中，最坏情况下的时间复杂度为O(n)。

因此，平衡二叉树适用于需要频繁进行查找操作的场景，如数据库索引、字典等。

2. 支持有序遍历平衡二叉树具有有序性的特点，可以支持有序遍历。

有序遍历是指按照节点的值从小到大或从大到小的顺序遍历二叉树。

平衡二叉树可以通过中序遍历实现有序遍历，这对于需要按照顺序获取数据的应用场景非常有用，比如按照字母顺序输出单词列表、按照时间顺序输出事件列表等。

3. 实现高效的插入和删除操作平衡二叉树对于插入和删除操作也具有很好的效率。

在普通的二叉搜索树中，如果插入或删除一个节点后导致树的不平衡，就需要通过旋转操作来重新调整树的结构，以保持平衡。

而平衡二叉树在插入和删除操作时会自动进行平衡调整，不需要额外的旋转操作。

这使得平衡二叉树在插入和删除操作上具有更好的性能表现。

4. 提供高效的范围查询平衡二叉树支持范围查询，即根据给定的范围查找满足条件的元素。

通过中序遍历平衡二叉树，可以按照节点值的顺序获取元素，然后根据范围进行筛选。

这对于需要根据范围查询数据的应用场景非常有用，比如查找某个时间段内的日程安排、查找某个价格区间内的商品等。

5. 实现高效的集合操作平衡二叉树可以用来实现高效的集合操作，如并集、交集、差集等。

通过遍历两个平衡二叉树，可以将它们的元素按照一定的规则进行合并或筛选，从而实现集合操作。

这对于需要对大量数据进行集合操作的应用场景非常有用，比如数据去重、数据合并等。

《二叉树的概念》课件

过程中进行一些特定的操作。
05
二叉树的应用
Chapter
在数据结构中的应用
二叉搜索树
二叉搜索树是一种特殊的二叉树，它的每个节点的左子树上的所有元素都小于该节点，右子树上的所有元素都大于该节点。这种数据结构可以用于快速查找、插入和删除操作。
AVL树和红黑树
这两种二叉树都是自平衡二叉搜索树，它们通过调整节点的左右子树的高度来保持树的平衡，从而在插入、删除等操作时具有较好的性能。
VS
详细描述
平衡二叉树的特点是，它的左右子树的高度差不会超过1，且左右子树都是平衡二叉树。平衡二叉树的性质还包括，它的所有叶节点的层数相等，且所有非叶节点的左右子树的高度差不超过1。平衡二叉树的查找、插入和删除操作的时间复杂度为 O(log n)，其中n为节点数。
04
二叉树的遍历
Chapter
决策树
在机器学习和人工智能领域，决策树是一种重要的分类和回归方法。其基础结构就是二叉树，通过构建决策树，可以解决分类和回归问题。
THANKS
感谢观看
代码表示法
总结词：严谨规范
详细描述：使用编程语言的语法结构来表示二叉树，每个节点用对象或结构体表示，节点间的关系通过指针或引用表示，严谨规范，易于编写和调试。
03
二叉树的性质
Chapter
深度最大的二叉树
总结词
深度最大的二叉树是指具有最大可能深度的二叉树。
详细描述
在二叉树中，深度最大的二叉树是满二叉树，即每个层级都完全填满，没有空缺的节点。满二叉树的深度等于其节点总数减一。
02
二叉树的表示方法
Chapter
图形表示法
总结词：直观明了
详细描述：通过图形的方式展示二叉树的结构，每个节点用圆圈或方框表示，节点间的关系用线段表示，直观易懂，易于理解。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

BＳTNode＊ｐ１,＊p2;
if(p->bｆ=＝0)/／原本左右子树等高,现因左子树增高而使树增高
{p-＞bf＝１;
taller=1;
}
eｌse if(p->bf==-１)//原本右子树比左子树高,现左右子树等高
{p－＞bf=0;
ｔaller=0;
｝
eｌｓe//原本左子树比右子树高，须作左子树的平衡处理
reｔｕrn０;
iｆ（tallｅr==1)//已插入到*b的左子树中且左子树长高
Le（b,taｌler);
}
else//继续在*b的右子树中进行搜索
{if（(InsｅrtAＶL(b->rcｈild,ｅ，ｔａller)）＝=0)/／未插入
return0；
iｆ(talleｒ=＝1)//已插入到*b的右子树中且右子树长高
平衡二叉树操作的演示
———————————————————————————————— 作者：
———————————————————————————————— 日期：
＃include<stdio.h＞
#include<mａlｌoc.h>
tｙpedef int KeｙＴyｐe；//定义关键字类型
ｔｙpｅdｅf structｎodｅ//记录类型
{p2=p1->lｃhild;
ｐ1->lchilｄ＝p2->rcｈild;
ｐ2->ｒcｈｉld=p1;
p->rchild=p2->ｌchilｄ;
p2->lｃｈilｄ=p;
if(p２->bf==0)//新结点插在＊ｐ２处作为叶子结点的情况
ﻩ p->bf＝p1->bｆ=0;
elseif(ｐ2->ｂｆ==-1)//新结点插在*p2的右子树上的情况
{p１=p->rｃhild;／/p指向*ｐ的右子树根结点
if(p1－>ｂf＝＝-1)／/新结点插入在*p的右孩子的左子树上,要做RR调整
{p－>rchild=p１－>ｌcｈiｌd;
p1-＞ｌｃｈiｌd＝p;
p-＞ｂf=ｐ1-＞bｆ=0;
p=p1;
｝
elｓeif（ｐ１－>bf＝＝1）//新结点插入在*p的右孩子的左子树上，要做RＬ调整
{p2=p1->rｃhild;
ｐ1－>rｃhilｄ=p2->lcｈild；
ｐ2->ｌｃhiｌd=p1；
p－>lｃhiｌｄ=p2->ｒchiｌd;
p２－>ｒchilｄ＝p;
if(ｐ２->ｂf＝=０)//新结点插入在*ｐ2处作为叶子结点的情况
ﻩp->ｂf＝p1->bf＝0;
eｌseｉｆ(ｐ２->ｂf==1)//新结点插在*ｐ2的左子树上的情况
{／/若在平衡二叉排序树b中不存在和ｅ有相同关键字的结点，则插入一个数据元素为e的新结点,
／/并返回1,否则返回０。若因插入而使二叉排序树失去平衡，则作平衡旋转处理，布尔变量talｌｅr
／/反映b长高与否
if(b==NULＬ)//原树为空,插入新结点,树长高，置taｌleｒ为１
{b=(ＢSTNｏdｅ*)malloc（sｉzｅof(BSTＮｏｄｅ）)；
{ｐ１=p－＞lcｈiｌd;／/p指向*p的左子树根节点
if（p1->ｂｆ==1)/／新结点插入在*p的左孩子的左子树上，要做LL调整
{p-＞ｌcｈｉld＝p1－＞rchilｄ；
p1-＞rchｉld＝p;
p－>bf=ｐ1->bｆ=0;
p=p1;
}
eｌse if(p１－＞ｂf＝=-1）//新结点插入在*p的左孩子的右子树上，要做LR调整
{KeyTypｅｋｅy;//关键字项
iｎt bf;//平衡因子
ｓtrｕcｔnｏｄe *lｃhild，*rｃhｉｌd;／／左右孩子指针
}BＳTNodｅ;
voidＬe(BSTNode *&ｐ,ｉnｔ＆taller）
{/／对以指针p所指结点为根的二叉树作左平衡旋转处理,本算法结束时,
//指针p指向新的根结点
ｂ-＞keｙ=ｅ;
ｂ->lchｉlｄ＝ｂ-＞rｃhｉｌd＝NULL;
b－>bf=0;
tallｅr=1；
}
ｅlse
｛if(e==b->kｅy）//树中已存在和ｅ有相同关键字的结点则不插入
{taller=０;
rｅｔurn 0;
}
ｉf(e<b-＞keｙ）//继续在＊ｂ的左子树中进行搜索
{iｆ((InsertAVL(b－>lchild，e,taｌlｅr）)==0）//未插入
iｆ（p->bf==１）
{p->ｂｆ=0;
taｌler=1;
／/指针ｐ指向新的根结点
ＢSＴＮodｅ＊p1,*p2；
if(p->bｆ==0)／/原本左右子树等高，现因右子树增高而使树增高
{ｐ->bf=-1；
ｔaller＝1;
｝
eｌse if(p－>ｂf==1)／/原本左子树比右子树高，现左右子树等高
｛p->bf=0;
tallｅr=0;
}
ｅlse／/原本右子树比左子树高，须作右子树的平衡处理
RiｇhtＰrocess(b,taｌleｒ);
}
｝
retuｒn1;
}
void DiｓpＢＳTreｅ(BSTNode *b)
｛//以括号表示法输出AVL
if(b!=NULL）
{pｒinｔf("%d",b－>keｙ);
iｆ(ｂ-＞ｌchild!=NUＬL||b-＞rｃhild！=NＵＬL）
{printｆ(＂(");
DispBSＴrｅe（b->lchｉld);
if(b->rcｈilｄ！=NULＬ)printf(",");
ＤｉspBＳTreｅ(b->ｒｃhｉld);
ｐrinｔｆ(")＂);
}
}
｝
void Lｅ（ＢSTＮｏdｅ*&p，iｎｔ&ｔalleｒ)／/在删除结点时进行左处理
{ＢSＴNoｄe *p1,*p２;
{p１->ｂｆ=０;
p->bｆ＝１；
}
elsｅ／/新结点插在＊的左子树上的情况
{p1->ｂf＝-1;
p->bf=0;
}
p＝p2;
p->bf=０;/／仍将p指向新的结点，并置其bｆ值为０
}
tａller=0;
}
}
iｎt IｎｓertAＶL（BＳTNode*&ｂ,ＫeｙTyｐe e,iｎt&tallｅr)
{p1－>ｂf=０;
ｐ－>bｆ＝-1;
}
elｓｅ／/新结点插在＊p２的右子树上的情况
{p1-＞bf=1;
p－＞ｂf＝0;
}
p=ｐ2;
p-＞bf=０；/／仍将p指向新的根结点，并置其bf值为０
}
taｌleｒ=０;
｝
}
vｏｉdRighｔProcess（ＢSTNoｄe *＆p,int &tallｅr)
{//对以指针p所指结点为根的二叉树作右平衡旋转处理,本算法结束时,