数学试题2)
高等数学试题及其参考答案(2)

高等数学试题及其参考答案一、填空题(每小题2分,共10分)________ 11.击数y=arcsin√1-x2+──────的定义域为_________√1-x2_______________。
2.击数y=x+ex上点(0,1)处的切线方程是______________。
f(Xo+2h)-f(Xo-3h)3.设f(X)在Xo可导且f'(Xo)=A,则lim───────────────h→o h=_____________。
4.设曲线过(0,1),且其上任意点(X,Y)的切线斜率为2X,则该曲线的方程是____________。
x5.∫─────dx=_____________。
1-x4二、单项选择题(在每小题的四个备选答案中,选出一个正确的答案,将其码写在题干的括号内,1~10每小题3分,共30分)(一)每小题1分,共10分11.设击数f(x)=──,g(x)=1-x,则f[g(x)]=()x111①1-──②1+──③────④xxx1-x12.x→0 时,xsin──+1是()x①无穷大量②无穷小量③有界变量④无界变量3.下列说法正确的是()①若f( X )在 X =Xo 连续, 则f( X )在X =Xo 可导②若f( X )在 X =Xo 不可导,则f( X )在X =Xo 不连续③若f( X )在 X =Xo 不可微,则f( X )在X =Xo 极限不存在④若f( X )在 X =Xo 不连续,则f( X )在X =Xo 不可导4.若在区间(a,b)内恒有f'(x)〈0,f"(x)〉0,则在(a,b)内曲线弧y=f(x)为 ( )①上升的凸弧 ②下降的凸弧 ③上升的凹弧④下降的凹弧5.设F'(x) = G'(x),则 ( )① F(X)+G(X) 为常数② F(X)-G(X) 为常数③ F(X)-G(X) =0d d④ ──∫F(x)dx = ──∫G(x)dxdx dx16.∫ │x│dx = ( )-1① 0 ② 1 ③ 2 ④ 37.方程2x+3y=1在空间表示的图形是 ( )①平行于xoy面的平面②平行于oz轴的平面③过oz轴的平面④直线x8.设f(x,y)=x3 + y3 + x2 ytg── ,则f(tx,ty)= ( )y①tf(x,y) ②t2f(x,y)1③t3f(x,y) ④ ──f(x,y)t2an +1 ∞9.设an ≥0,且lim ───── =p,则级数 ∑an ( )n→∞an=1①在p〉1时收敛,p〈1时发散②在p≥1时收敛,p〈1时发散③在p≤1时收敛,p〉1时发散④在p〈1时收敛,p〉1时发散10.方程y'+3xy=6x2y是()①一阶线性非齐次微分方程②齐次微分方程③可分离变量的微分方程④二阶微分方程(三、计算题(每小题5分,共45分)___________/x-11.设y=/──────求y' 。
2023考研数学二真题试卷+答案(超清版)

2023年全国硕士研究生入学统一考试数学(二)试题及答案考试时间:180分钟,满分:150分一、选择题:1~10小题,每小题5分,共50分,下列每题给出的四个选项中,只有一个选项符合题目要求,请将所选项前的字母填在答题纸指定位置上.(1)曲线1ln()1yx e x =+−的斜渐近线方程维( ) (A)y x e =+ (B)1y x e=+(C)y x = (D)1y x e=−【答案】B(2)设0()(1)cos ,0x f x x x x ≤=+>⎩的一个原函数为( )(A)),0()(1)cos sin ,0x x F x x x x x ⎧⎪−≤=⎨+−>⎪⎩(B))1,0()(1)cos sin ,0x x F x x x x x ⎧⎪−+≤=⎨+−>⎪⎩(C)),0()(1)sin cos ,0x x F x x x x x ⎧⎪+≤=⎨++>⎪⎩(D))1,0()(1)sin cos ,x x F x x x x x ⎧⎪++≤=⎨++>⎪⎩【答案】D (3)已知{}n x ,{}n y 满足1112x y ==,1sin n n x x +=,21(1,2,)n n y y n +== ,则当n →∞时( )(A)n x 是n y 的高阶无穷小(B)n y 是n x 的高阶无穷小(C)n x 与n y 是等价无穷小(D)n x 与n y 是同阶但不等价的无穷小【答案】B(4)若微分方程0y ay by ′′′++=的解在(,)−∞+∞上有界,则( )(A)0,0a b <>(B)0,0a b >>(C)0,0ab =>(D)0,0ab =<【答案】C(5)设函数()y f x =由2sin x t ty t t⎧=+⎪⎨=⎪⎩确定,则( )(A)()f x 连续,(0)f ′不存在(B)(0)f ′存在,()f x ′在0x =处不连续(C)()f x ′连续,(0)f ′不存在(D)(0)f ′′存在,()f x ′在0x =处不连续【答案】C (6)若函数121()(ln )f dx x x αα+∞+=⎰在0αα=处取得最小值,则0α=( ) (A)1ln(ln 2)−(B)ln(ln 2)− (C)1ln 2(D)ln 2【答案】A (7)设函数2()()x f x x a e =+,若()f x 没有极值点,但曲线()y f x =有拐点,则a 的取值范围是( )(A)[0,1)(B)[1,)+∞(C)[1,2)(D)[2,)+∞【答案】C(8)设A ,B 为n 阶可逆矩阵,*M 为矩阵M 的伴随矩阵,则*A E OB ⎛⎫= ⎪⎝⎭( ) (A)****A B B A O B A ⎛⎫−⎪⎝⎭(B)****B A A B O A B ⎛⎫−⎪⎝⎭(C)****B A B A OA B ⎛⎫−⎪⎝⎭(D)****A B A B OB A ⎛⎫−⎪⎝⎭【答案】B (9)二次型222123121323(,,)()()4()f x x x x x x x x x =+++−−的规范形为( )(A)2212y y +(B)2212y y −(C)2221234y y y +−(D)222123y y y +−【答案】B(10)已知向量1123α⎛⎫ ⎪= ⎪ ⎪⎝⎭,2211α⎛⎫ ⎪= ⎪ ⎪⎝⎭,1259β⎛⎫ ⎪= ⎪ ⎪⎝⎭,2101β⎛⎫ ⎪= ⎪⎪⎝⎭,若γ既可由12,αα线性表示,也可由12,ββ线性表示,则γ=( )(A)33,4k k R ⎛⎫ ⎪∈ ⎪ ⎪⎝⎭(B)35,10k k R ⎛⎫ ⎪∈ ⎪ ⎪⎝⎭(C)11,2k k R −⎛⎫ ⎪∈ ⎪ ⎪⎝⎭(D)15,8k k R ⎛⎫ ⎪∈ ⎪ ⎪⎝⎭【答案】D二、填空题:11~16小题,每小题5分,共30分,请将答案写在答题纸指定位置上. (11)当0x →时,函数2()ln(1)f x ax bx x =+++与2()cos x g x e x =−是等价无穷小,则ab =________【答案】2(12)曲线y =⎰的弧长为________43π(13)设函数(,)z z x y =由2ze xz x y +=−确定,则2(1,1)2zx∂=∂_________【答案】32−(14)曲线35332x y y =+在1x =对应点处的法线斜率为________【答案】119−(15)设连续函数()f x 满足:(2)()f x f x x +−=,2()0f x dx =⎰,则31()f x dx =⎰_______【答案】12(16)已知线性方程组13123123121202ax x x ax x x x ax ax bx +=⎧⎪++=⎪⎨++=⎪⎪+=⎩有解,其中,a b 为常数,若0111412a a a =,则11120a a ab =_______【答案】8三、解答题:17~22小题,共70分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(17)(本题满分10分)设曲线:()()L y y x x e =>经过点2(,0)e ,L 上任一点(,)P x y 到y 轴的距离等于该点处的切线在y 轴上的截距(1)求()y x ;(2)在L 上求一点,使得该点处的切线与两坐标轴所围三角形的面积最小。
数学期末测试题 (2).DOC

三年级数学下册期末形成性评价试卷
2、脱式计算。
(9分)
72×28+324÷6567÷7×24248+52×68六、巧手
分)
1、测量后,我知道这个长方形的长是(),宽是(),它的面积
是(),列式为()。
2、如果在它上面剪下一个最大的正方形,求它的面积,列式计算为()。
八、解决问题。
(20分)1、工人叔叔修马路,4天要修500米,第一天修了116米,后三天平均每天要修多少
米?2、商店运来5箱热水瓶,每箱12个,每个热水瓶32元,这些热水瓶可卖多
少元? 3、一只熊猫每天吃一头大象每天 18千克食物。
吃的食物是一
只熊猫的25
倍
(
1)一头大象每天吃多少千克食物?(2)一只熊猫30天吃的食物,够不够一头大象一天吃?计算说明。
4、把一块蛋糕平均分成10块,妈妈吃了2块,爸爸吃了3块,小华吃了4块。
爸爸和小华工吃了这块蛋糕的几分之几?妈妈比小华少吃了这块蛋糕
九、探索乐园。
如图:四个一样的长方形和一个小正方形,拼成一个大
正方形。
大正方形的面积是64平方分米,小正方形的面积是4平方分
米。
长方形的宽是多少?。
金卷二数学试题及答案

金卷二数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 函数y=x^2+3x-4的顶点坐标是?A. (-3, -4)B. (-1, -4)C. (-3, 2)D. (1, -4)答案:C3. 已知a=2,b=-3,计算a+b的值。
A. -1B. 1C. -5D. 5答案:C4. 以下哪个不是二次函数?A. y=x^2+2x+1B. y=2x^2-3x+4C. y=x+3D. y=-x^2+5x-65. 计算以下哪个表达式的值等于0?A. x^2 - 4x + 4B. x^2 - 2x + 1C. x^2 + 4x + 4D. x^2 + 2x + 1答案:A6. 以下哪个选项是等腰三角形?A. 三边长分别为3, 4, 5B. 三边长分别为2, 2, 3C. 三边长分别为1, 1, 2D. 三边长分别为5, 5, 10答案:B7. 已知圆的半径为5,求圆的面积。
A. 25πB. 50πC. 75πD. 100π答案:C8. 计算以下哪个表达式的值大于1?A. sin(30°)B. cos(45°)C. tan(60°)D. sin(90°)答案:C9. 以下哪个选项是不等式2x-3>5的解?B. x < 4C. x > 1D. x < 1答案:A10. 计算以下哪个表达式的值等于2?A. (√2)^2B. (√3)^2C. (√4)^2D. (√5)^2答案:C二、填空题(每题4分,共20分)11. 计算2x+3=7,x的值为________。
答案:212. 已知三角形的两边长分别为5和7,第三边长为x,根据三角形的三边关系,x的取值范围是________。
答案:2 < x < 1213. 计算以下哪个表达式的值等于-1?A. (-1)^2B. (-1)^3C. (-1)^4D. (-1)^5答案:B14. 已知函数f(x)=2x+1,求f(-2)的值。
数学试题2
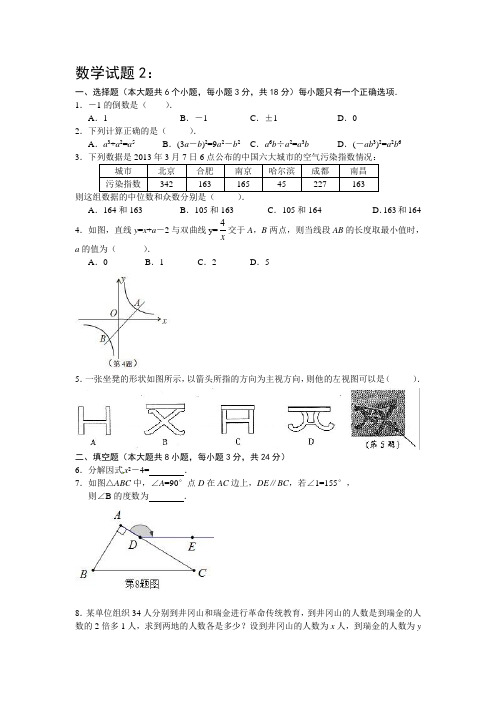
数学试题2:一、选择题(本大题共6个小题,每小题3分,共18分)每小题只有一个正确选项. 1.-1的倒数是( ). A .1 B .-1 C .±1 D .0 2.下列计算正确的是( ). A .a 3+a 2=a 5 B .(3a -b )2=9a 2-b 2 C .a 6b ÷a 2=a 3b D .(-ab 3)2=a 2b 6 3则这组数据的中位数和众数分别是( ).A .164和163B .105和163C .105和164D .163和1644.如图,直线y =x +a -2与双曲线y=x4交于A ,B 两点,则当线段AB 的长度取最小值时,a 的值为( ). A .0 B .1C .2D .55.一张坐凳的形状如图所示,以箭头所指的方向为主视方向,则他的左视图可以是( ).二、填空题(本大题共8小题,每小题3分,共24分) 6.分解因式x 2-4= .7.如图△ABC 中,∠A =90°点D 在AC 边上,DE ∥BC ,若∠1=155°, 则∠B 的度数为 .8.某单位组织34人分别到井冈山和瑞金进行革命传统教育,到井冈山的人数是到瑞金的人数的2倍多1人,求到两地的人数各是多少?设到井冈山的人数为x 人,到瑞金的人数为y人,请列出满足题意的方程组是 .9.如图,矩形ABCD 中,点E 、F 分别是AB 、CD 的中点,连接DE 和BF ,分别取DE 、BF 的中点M 、N ,连接AM ,CN ,MN ,若AB =22,BC =23,则图中阴影部分的面积为 .10.观察下列图形中点的个数,若按其规律再画下去,可以得到第n 个图形中所有的个数为 (用含n 的代数式表示).11.如图,□ABCD 与□DCFE 的周长相等,且∠BAD =60°,∠F =110°,则∠DAE 的度数为 .12.解不等式组⎩⎨⎧>-+≥+,33)3(2,12x x x 并将解集在数轴上表示出来.13.先化简,再求值:12244222+-÷+-x xx x x x ,在0,1,2,三个数中选一个合适的,代入求值.14.如图,在平面直角坐标系中,反比例函数xky(x>0)的图象和矩形ABCD 的第一象限,AD 平行于x 轴,且AB =2,AD =4,点A 的坐标为(2,6) . (1)直接写出B 、C 、D 三点的坐标;(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.15.生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查,为期半天的会议中,每人发一瓶500ml 的矿泉水,会后对所发矿泉水喝的情况进行统计,大至可分为四种:A .全部喝完;B .喝剩约31;C .喝剩约一半;D .开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:(1)参加这次会议的有多少人?在图(2)中D 所在扇形的圆心角是多少度?并补全条形统计图;(计算结果请保留整数).(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费的矿泉水约多少毫.升.? (3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500ml/瓶)约有多少瓶.?(可使用科学计算器)七、(本大题共2小题,第23题10分,第24 题12分,共22分)23.某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程: ●操作发现:在等腰△ABC 中,AB=AC ,分别以AB 和AC 为斜边,向△ABC 的外侧作等腰直角三角形,如图1所示,其中DF ⊥AB 于点F ,EG ⊥AC 于点G ,M 是BC 的中点,连接MD 和ME ,则下列结论正确的是 (填序号即可) ①AF =AG =21AB ;②MD=ME ;③整个图形是轴对称图形;④∠DAB =∠DMB . ●数学思考:在任意△ABC 中,分别以AB 和AC 为斜边,向△ABC 的外侧..作等腰直角三角形,如图2所示,M 是BC 的中点,连接MD 和ME ,则MD 和ME 具有怎样的数量和位置关系?请给出证明过程; ●类比探索:在任意△ABC 中,仍分别以AB 和AC 为斜边,向△ABC 的内侧作等腰直角三角形,如图3所示,M 是BC 的中点,连接MD 和ME ,试判断△MED 的形状. 答: .。
高等数学二试题及答案

高等数学二试题及答案一、选择题1. 函数y=2x^3-3x^2+4x-1的导数为:A. 6x^2 - 6x + 4B. 6x^2 - 4x + 4C. 6x^3 - 6x^2 + 4D. 6x^3 - 6x + 4答案:A2. 极限lim(x→0) (sin(x) - x) / x^3的值为:A. 1B. 0C. 不存在D. 无穷大答案:A3. 曲线y=x^2在点x=1处的切线方程为:A. y=2x-1B. y=x+1C. y=2xD. y=x-1答案:A4. 定积分∫(0,1) x^2 dx的值为:A. 1/3B. 1/2C. 1D. 0答案:A5. 级数Σ(n=1 to ∞) (n^2 / 2^n)收敛于:A. 1B. 2C. 3D. 4答案:B二、填空题1. 函数z=e^(x+y)在点(0,0)的偏导数∂z/∂x为_________。
答案:12. 极限lim(x→∞) (1+1/x)^x的值为_________。
答案:e3. 曲线y=2x^3在点x=-1处的法线方程为_________。
答案:y=-6x+24. 定积分∫(1,2) (2t^2 + 3t + 1) dt的值为_________。
答案:10/35. 幂级数Σ(n=0 to ∞) (x^n / 2^n)在|x|≤2时收敛于_________。
答案:1 + x三、计算题1. 求函数f(x)=ln(x^2-4)的反函数,并证明其在定义域内是单调的。
解:首先找到反函数的定义域,由于ln(x^2-4)的定义域为x^2-4>0,解得x^2>4,因此x<-2或x>2。
设y=ln(x^2-4),则x^2-4=e^y,解得x=±√(e^y+4)。
由于x<-2或x>2,我们选择x=√(e^y+4)作为反函数,定义域为y>ln(4)。
显然,当y>ln(4)时,函数√(e^y+4)是单调递增的,因此反函数也是单调的。
数学二试题及答案
数学二试题及答案一、选择题(本题共10小题,每小题3分,共30分)1. 下列哪个数是无理数?A. 0.33333B. πC. √2D. 1/3答案:C2. 已知函数f(x) = 2x - 1,求f(3)的值。
A. 3B. 4C. 5D. 6答案:C3. 以下哪个选项是二次方程x^2 + 4x + 4 = 0的解?A. x = -2B. x = 2C. x = -1D. x = 1答案:A4. 以下哪个选项是等差数列1, 3, 5, ...的第5项?A. 9C. 11D. 12答案:A5. 已知三角形ABC,其中∠A = 90°,AB = 3,AC = 4,求BC的长度。
A. 5B. 6C. 7D. 8答案:A6. 以下哪个选项是方程x^2 - 5x + 6 = 0的根?A. x = 2B. x = 3C. x = 1D. x = 4答案:B7. 已知圆的半径为5,求圆的面积。
A. 25πB. 50πC. 75πD. 100π答案:B8. 以下哪个选项是正弦函数sin(x)的周期?B. πC. 3πD. 4π答案:A9. 已知等腰三角形的底边长为6,两腰长为5,求三角形的面积。
A. 12B. 15C. 18D. 20答案:B10. 以下哪个选项是函数y = x^3 - 3x^2 + 2x的极值点?A. x = 0B. x = 1C. x = 2D. x = 3答案:C二、填空题(本题共5小题,每小题4分,共20分)11. 已知等比数列的首项为2,公比为3,求第4项的值是________。
答案:5412. 将函数f(x) = x^2 + 2x + 1转化为顶点式,结果为________。
答案:(x + 1)^213. 已知向量a = (3, 4),向量b = (-1, 2),求向量a与向量b的点积是________。
答案:1414. 已知双曲线的方程为x^2/a^2 - y^2/b^2 = 1,其中a = 2,b = 3,求双曲线的渐近线方程。
大学数学二试题及答案
大学数学二试题及答案一、选择题(每题5分,共30分)1. 下列函数中,为奇函数的是:A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = sin(x)2. 微分方程 y'' - y = 0 的通解是:A. y = C1 * cos(x) + C2 * sin(x)B. y = C1 * e^x + C2 * e^(-x)C. y = C1 * x + C2 * x^2D. y = C1 * ln(x) + C2 * x3. 矩阵 A = \[\begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix}\] 的行列式是:A. 1B. 2C. -2D. 54. 极限lim(x→0) (sin(x)/x) 的值是:A. 0B. 1C. -1D. 不存在5. 积分∫(0 to π) sin(x) dx 的值是:A. 0B. πC. -2D. 26. 函数 y = ln(x) 的反函数是:A. y = e^xB. y = e^(-x)C. y = 10^xD. y = x^e二、填空题(每题5分,共20分)1. 如果函数 f(x) 在点 x=a 处可导,则 f'(a) 表示______。
2. 函数 y = x^2 - 4x + 3 的顶点坐标是(______,______)。
3. 微分方程 y' + 2y = 0 的通解形式为 y = ______。
4. 函数 y = sin(x) 的不定积分是 ______。
三、解答题(每题10分,共50分)1. 求函数 f(x) = x^2 - 6x + 9 在区间 [2, 5] 上的最大值和最小值。
2. 证明:如果一个数列 {a_n} 收敛于 L,则其子数列 {a_{2n}} 也收敛于 L。
3. 计算定积分∫(0 to 1) (3x^2 - 2x + 1) dx。
高中数学二试题库及答案
高中数学二试题库及答案一、选择题(每题3分,共30分)1. 若函数\( f(x) = ax^2 + bx + c \)(\( a \neq 0 \))的图像与x轴有两个交点,则下列说法正确的是()。
A. \( a > 0 \)且\( b^2 - 4ac > 0 \)B. \( a < 0 \)且\( b^2 - 4ac > 0 \)C. \( a > 0 \)且\( b^2 - 4ac < 0 \)D. \( a < 0 \)且\( b^2 - 4ac < 0 \)2. 已知\( \sin \theta = \frac{3}{5} \),且\( \theta \)为锐角,则\( \cos \theta \)的值为()。
A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{3}{5} \)3. 集合\( A = \{x | x^2 - 5x + 6 = 0\} \),\( B = \{x | x^2 - 5x + 6 < 0\} \),则\( A \cap B \)为()。
A. \( \{2, 3\} \)B. \( \{2\} \)C. \( \{3\} \)D. 空集4. 若\( \log_2 8 = 3 \),则\( \log_2 32 \)等于()。
A. 3B. 5C. 6D. 95. 函数\( y = \frac{1}{x} \)的图像关于()对称。
A. y轴B. x轴C. 原点D. 直线y = x6. 已知\( \tan \alpha = 2 \),求\( \sin \alpha \)的值()。
A. \( \frac{2}{\sqrt{5}} \)B. \( \frac{1}{\sqrt{5}} \)C. \( \frac{2}{\sqrt{3}} \)D. \( \frac{1}{\sqrt{3}} \)7. 函数\( f(x) = x^3 - 3x^2 + 4 \)的极大值点是()。
高等数学试题(2)
《系 专业 班级 姓名 学号高等数学试题(2)公共模块1(80分)一.判断题(每题1分,共8分)1、若f(x)在0x 处连续,则f(x)在点0x 处左右极限存在且相等。
( √)2、函数商的导数等于函数导数的商。
( ╳ )3、在自变量的同一个变化过程中,如果f(x)为无穷大,则)(1x f 为无穷小;反之,如果f(x)为无穷小,则)(1x f 为无穷大。
( ╳ )4、函数在定义域内的最大值一定为极大值。
( ╳ )5、两个可导且相差一常数的函数是同一函数的原函数。
( √ )6、奇函数在对称区间的定积分为0。
( √ )7、连续函数在闭区间[a,b]上的定积分一定存在。
( √ )8、⎰=')())((x f dx x f ( ╳ ) 二.填空题(每题2分,共16分)1、函数)53tan(+=x y 的复合过程为: y= tanu u= 3x+52、=→xx x sin lim13、x y cos =,则()=5y-sinx4、 d 3x = 2x dx d arctanx+c =211x+ dx5、⎰=11dx x26、在直线运动中,物体的加速度a 与速度v 的关系是: v a = 三、选择题(每题2分,共16分)1、设f (sinx )=cos2x ,则f (x )= [ A ] A.2x 2-1 B. x 2-2x+1 C. 2x 2+1 D. 1- 2x 22、)(lim )(lim x f x f ax ax +-→→=处极限存在的一个是函数在点a x = [ A ]A .充要条件 B.充分条件 C.必要条件 D.无关条件3、当x →∞时,xx 1sin是 [ D ]A.无穷小量B.无穷大量C.无极限D.有极限为14、.函数x e x f =)(,则=')1(f [ A ] A.e B.e 1- C.2e D.-2e 1-5、若='⎰-dx x f x f e x )(,)(则的一个原函数是 [ C ]A.x e --B. c e x +-C. -c e x +-D. x e - 6、函数的单调增区间为x x f ln )(= [ B ]A.(+∞,e )B.( +∞,0)C.(0,e)D.(1,e)7、微分方程0sin 2=+-'''x y y 的阶数为: [ B ] A.1 B.2 C.0 D.38、下列积分等于零的是 [ B ] A.xdx x cos 211-⎰ B.xdx x sin 211-⎰ C.dx x x )1(211--⎰C.dx x e x x)(211+-⎰三.解答题一(每题5分,共30分)1、 求极限2sin limxtdt xx ⎰→解:该题用洛比塔法则=()''⎪⎭⎫ ⎝⎛⎰→200sin lim xtdt x x -----------------------------2分 =xx x 2sin lim 0→ -----------------------------2分=21 -----------------------------1分2、函数⎪⎩⎪⎨⎧<≥+=03sin 02)(x axxx x x f ,在x=0处连续,求a解:()200=+f -----------------------------2分()af 300=- -----------------------------2分所以32=a -----------------------------1分2、 求不定积分⎰+dx x x 1sin cos解: =x d x sin 1sin ⎰+-----------------------------2分 =()c x ++231sin 32-----------------------------3分3、 求反常积分dx xe x⎰+∞-02解:2lim22xdeAxA ⎰-+∞→=-----------------------------2分⎪⎭⎫ ⎝⎛--=+∞→2lim210x e AA -----------------------------2分=21-----------------------------1分四.解答题二(每题6分,共12分)1、解微分方程02=+'yxyyxdxdy 2-=-----------------------------2分cxydx x ydy +-=-=32322-----------------------------4分1、 求函数523123+-=x x y 的极大值和极小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省四年级数学上册期末质量检测及答案
班级_______姓名_______分数_______
一、知识万花筒。
1.特快列车1小时大约行160千米,12小时大约行( )千米。
2.2008年北京奥运会火炬传递行程十三万七千公里,二万一千八百八十八名火炬手参加了火炬传递。
横线上的数分别写作()、()。
3.据民政部报告,截至2008年6月13日12时,全国共接收国内外社会各界为四川灾区捐赠款物总计45502000000元,已向灾区拨付捐款物合计一百四十亿一千六百元。
(1)45502000000读作()。
(2)一百四十亿一千六百万写作(),改写成用“万”作单位的数是(),省略“亿”后面的尾数是()亿。
4.在3、7、15、20、28、60、120中,60的因数有(),7的倍数有()。
5.720÷80=()7200÷800=()
12×40=()120×40=()1200×40=()
6.每本练习本有32张纸,102本练习本大约有()张纸。
7.小明刚出生时身高58厘米,爸爸身高174厘米,爸爸的身高是小明的()倍。
8.在用计算器计算2160÷20-57时,在键盘上按下2160接着按“÷”,再按20,接着再按“-”,这时屏幕显示()。
9.用3个0和4个3组成一个所有的“0”都不读的七位数是(),组成一个只读一个“零”的七位数是()。
10.□÷21=35……△中,△最大是(),这时□是()。
二、法官判对错。
1.一条射线长5厘米。
()
2.同一平面内的两条直线,不是相交就是平行。
()
3.一个数的倍数一定比它的因数大。
()
4.5的倍数比50的倍数小。
()
5.421÷47的商是两位数。
.()
三、计算直通车。
1.直接写得数。
16×4=490÷70=200×20=910÷70=
30×200=32×5=31×30=50×50=
840÷40=96÷6=500÷50=34×2=
37×10=780-90=25×4=770÷70=
280+70=250×3=45×20=720÷90=
2.用竖式计算。
508×35 816÷48 485÷69
3.计算。
224÷16×52-270 (80+704÷44)×37 (578+358)÷(68-29)
四、快乐选择ABC。
①②③
上面几组直线中互相平行的是(),互相垂直的是()。
2.下面各数四舍五入后都是58万,其中()最接近58万。
①584500 ②580900 ③579860
3.估算601÷29,结果是()。
①2 ②20 ③30
4.把3厘米长的线段向两端各延长5米,得到的是一条()
.①直线②线段③射线
5.三条直线相交最多有()个交点。
①3 ②4 ③5
五、动手操作。
根据要求画一画。
1.过A点画出直线的垂线。
2.过B点画出直线的平行线。
3.小河边有一个药厂,要在河上修一座桥。
怎样修才能使药厂到对岸的距离最短?请你画一画并请说明原因。
六、活用知识,解决问题。
1.刘叔叔带800元买化肥,买了18袋,还剩80元。
每袋化肥的价钱是多少元?
2.南山小学四年级共有4个班,每个班48人,平均每人为四川灾区捐款25元,四年级学生一共捐了多少元钱?
3.甲乙两车同时从A地开往B地,甲车每小时行120千米,乙车每小时行100千米,当两车相距80千米时用了多少小时?
4.码头用这两种货车运货。
(如右图)
(1)一批货物用一辆大卡车来运,9次运完。
这批货物一共多少箱?
(2)如果这批货物用小货车来运,多少次可以运完?
5.体育课上把四•一班的学生按体重重新编组。
组别第一组第二组第三组第四组第五组
体重(千克)25~29 30~34 35~39 40~44 45~49
人数 4 18 10 5 3
(1)小英的体重是32千克,她编在第()组。
(2)小刚在第四组,他的体重可能是()千克。
(3)根据表中的数据,完成下面的条形统计图。
四•一班学生体重情况统计图
12月20日
参考答案
一、22分。
其中第4题3分,其余每空1分。
1. 1920
2. 137000 21888
3. (1)四百五十五亿零二百万(2)14016000000 1401600万140
4. 3 15 20 60 ; 7 28
5. 9 ; 480 4800 48000
6.3000
7. 3 8.108 9. 3333000 3003033(或其它) 10. 20 755
二、5分。
1. × 2.√ 3.× 4.× 5.×
三、38分。
1. 20分
2.9分
3.9分
四、5分。
1. ①③ 2.③ 3.② 4.② 5.①
五、8分。
1. 2分
2.2分
3. 4分。
画图占2分,说明原因占2分。
六、22分。
(下面各题只列对算式得该题的一半分,漏写或错写单位名称或答语各扣0.5分。
)
1.3分。
(800-80)÷18=40(元)
2.3分。
48×4×25=4800(元)
3.3分。
80÷(120-100)=4(小时)
4.6分。
(1)( 45+35)×9=720(箱)
(2) 720÷45=16(次)
5. 7分。
(1)2分。
二
(2) 2分。
40 (或41~44)
(3)3分。
画图略。
