焦作市2010-2011学年上学期高一期中考试--数学
河南省焦作市高一上学期期中数学试卷

河南省焦作市高一上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分)比较大小: ________ .2. (1分)已知集合U={x|﹣3≤x≤3},M={x|﹣1<x<1},∁UN={x|0<x<2},M∩N=________3. (1分)函数f(x)=xα的图象过点(2,4),则f(﹣1)=________4. (1分)关于函数,给出下列命题:①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;②若函数f(x)满足f(x+1)f(x)=2 017,则f(x)是周期函数;③若函数g(x)=是偶函数,则f(x)=x+1;④函数y=的定义域为 .其中正确的命题是________.(写出所有正确命题的序号)5. (1分)已知全集U={﹣2,﹣1,0,1,2},集合A={﹣2,﹣1,1,2},则∁UA=________.6. (1分)若x,y∈R+ ,且 + ≤a 恒成立,则a的最小值为________.7. (1分)记x2﹣x1为区间[x1 , x2]的长度.已知函数y=2|x| ,x∈[﹣2,a](a≥0),其值域为[m,n],则区间[m,n]的长度的最小值是________8. (1分)若用二分法求函数f(x)在(a,b)内的唯一零点时,精确度为0.001,则结束计算的条件是________.9. (1分)对于函数y=f(x),若在其定义域内存在x0 ,使得x0•f(x0)=1成立,则称x0为函数f(x)的“反比点”.下列函数中具有“反比点”的是________①f(x)=﹣2x+2;②f(x)=sinx,x∈[0,2π];③f(x)=x+,x∈(0,+∞);④f(x)=ex;⑤f(x)=﹣2lnx.10. (1分) (2016高三上·常州期中) 设函数f(x)= ,则f(f(﹣1))的值为________.11. (1分) (2018高一上·漳平月考) 已知函数的值域为,则实数的取值范围是________.12. (1分) (2017高二上·南京期末) 已知t>0,函数f(x)= ,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是________.13. (1分) (2017高一上·扬州期中) f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(),c=f(0.20.6),则a,b,c大小关系是________.14. (1分) (2016高三上·滨州期中) 设函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=2x﹣1 ,有以下结论:①2是函数f(x)的一个周期;②函数f(x)在(1,2)上单调递减,在(2,3)上单调递增;③函数f(x)的最大值为1,最小值为0;④当x∈(3,4)时,f(x)=23﹣x .其中,正确结论的序号是________.(请写出所有正确结论的序号)二、解答题 (共6题;共50分)15. (5分)已知集合A={1,a,b},B={a,a2 , ab},若A=B,求a+b的值.16. (5分)已知函数f(x)=logax+a﹣e(a>0且a≠1,e=2.71828…)过点(1,0).(1)求函数f(x)的解析式;(2)设函数g(x)=f2(x)﹣2f(e2x)+3,若g(x)﹣k≤0在x∈[e﹣1 , e2]上恒成立,求k的取值范围;(3)设函数h(x)=af(x+1)+mx2﹣3m+1在区间(﹣, 2]上有零点,求m的取值范围.17. (15分)(2017·崇明模拟) 设(a,b为实常数).(1)当a=b=1时,证明:f(x)不是奇函数;(2)设f(x)是奇函数,求a与b的值;(3)当f(x)是奇函数时,研究是否存在这样的实数集的子集D,对任何属于D的x、c,都有f(x)<c2﹣3c+3成立?若存在试找出所有这样的D;若不存在,请说明理由.18. (5分)(2019·浙江模拟) 已知函数f(x)=ex-ax-b(a,b∈R其中e为自然对数的底数).(Ⅰ)若f(x)≥0恒成立,求ab的最大值.(Ⅱ)设F(x)=1nx+1-f(x),若函数y=F(x)存在唯一零点,且对满足条件的a,b,不等式m(a-e+1)≥b恒成立,求实数m的取值集合.19. (10分) (2016高一上·杭州期末) 已知函数f(x)=2sin(ωx+φ)(﹣π<φ<0,ω>0)的图象关于直线对称,且两相邻对称中心之间的距离为.(1)求函数y=f(x)的单调递增区间;(2)若关于x的方程f(x)+log2k=0在区间上总有实数解,求实数k的取值范围.20. (10分) (2016高一上·金华期中) 已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2﹣2x.(1)画出偶函数f(x)的图像的草图,并求函数f(x)的单调递增区间;(2)当直线y=k(k∈R)与函数y=f(x)恰有4个交点时,求k的取值范围.参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共50分)15-1、17-1、17-2、17-3、18-1、19-1、19-2、20-1、20-2、。
河南省焦作市修武一中10-11学年高一数学上学期期中考试

焦作市2021-2021学年〔上〕必修模块〔1〕数学试卷注意本试卷总分值120分,附加题20分,答案必须写在答题卷上,在试卷上作答无效.一、 选择题〔此题共10个小题,每题4分,共40分,每个小题只有一个选项是正确的,请将正确选项移到答题卷答案栏内.〕1.集合{|22},{|13}A x x B x x =-<<=-≤<,那么A B =A.{|23}x x -<<B.{|12}x x ≤<C.{|21}x x -<≤D.{|23}x x <<(2)二次函数542+-=mx x y 的对称轴为2-=x ,那么当1=x 时,y 的值为 A.-7 B.1 C.17 D.253.以下各组函数中,表示同一个函数的是A .211x y x -=-与1y x =+B .lg y x =与21lg 2y x =C .21y x =-与1y x =-D .y x =与y=log a a x (a ﹥0且a ≠1)4.函数1()1f x x =-的定义域为 A. {x|x>1} B.{x|x<1} C. {x|-1<x<1} D. ∅5.右图给出了红豆生长时间t 〔月〕与枝数y 〔枝〕的散点图:那么“红豆生南国,春来发几枝.〞的红豆生长时间与枝数的关系用以下哪个函数模型拟合最好?A .指数函数:t y 2=B .对数函数:t y 2log =C .幂函数:3t y =D .二次函数:22t y = 6.函数y= | lg 〔x-1〕| 的图象是7.31)53(-=a ,21)53(-=b ,21)34(-=c ,那么a,b,c 三个数的大小关系是 A.b a c << B.a b c << C.c b a << D.c a b <<8.函数1])21[(l )(21-=x og x f ,那么A.函数在〔-∞,0〕上递减B.函数在〔-∞,0〕上递增C.函数在R 上递减D.函数在R 上递增9.)(x f y =在定义域〔-1,1〕上是减函数,且)12()1(-<-a f a f ,那么a 的取值范围是CA .),(321-B .),(132C . ),(320D .)(,1010.以下所给4个图象中,与所给3件事吻合最好的顺序为〔1〕我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;〔2〕我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;〔3〕我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
河南省焦作市第一中学2023-2024学年高一下学期期中考试数学试题

河南省焦作市第一中学2023-2024学年高一下学期期中考试数学试题一、单选题1.设21i (i i i z +=+为虚数单位),则z =( ) A .i B .i - C .1i + D .1i -- 2.下列命题正确的是( )A .若直线//a b ,则a 平行于经过b 的任何平面B .若直线a ,b 和平面α,β,满足a αβ⋂=,//b α,//b β,则//a bC .若直线a ,b 和平面α满足//a α,//b α,则//a bD .若直线a 和平面α满足//a α,则a 与α内任何直线平行3.如图,四边形ABCD 的斜二测画法直观图为等腰梯形A B C D ''''.已知4A B ''=,2C D ''=,则下列说法正确的是( )A .2AB = B .A D ''=C.四边形ABCD 的周长为4+D .四边形ABCD 的面积为4.已知直角ABC V 斜边BC 的中点为O ,且OA AB =u u u r u u u r ,则向量CA u u u r 在向量CB u u u r 上的投影向量为( )A .14CB u u u r B .34CB u u u rC .14CB -u u u rD .34CB -u u u r 5.已知e r 为单位向量,向量a r 满足2a e ⋅=r r ,1a e λ-=r r ,则a r 的最大值为( )A .4B .2CD .56.ABC V 中,a 、b 、c 分别是内角A 、B 、C 的对边,若222ABC a b c =+-V ,且()0||||AB AC BC AB AC +⋅=u u u r u u u r u u u r u u u r u u u r ,则ABC V 的形状是( ) A .等腰非直角三角形 B .三边均不相等的直角三角形C .等边三角形D .等腰直角三角形7.已知直三棱柱111ABC A B C -的6个顶点都在球O 的表面上,若11,4AB AC AA ===,2π3BAC ∠=,则球O 的表面积为( ) A .16πB .20πC .28πD .32π 8.在锐角ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知2cos a b B =,且b c ≠,则下列命题正确的有( )个①2A B = ②角B 的取值范围是0,4π⎛⎫ ⎪⎝⎭③cos A 的取值范围是10,2⎛⎫ ⎪⎝⎭④a b 的取值范围是 A .1 B .2 C .3 D .4二、多选题9.已知复数z 满足11z z =-=,且复数z 对应的点在第一象限,则下列结论正确的是( )A .复数z 的虚部为32B .11z 2=C .21z z =-D .复数z 的共轭复数为12- 10.下列说法中正确的有( )A .与()2,1a =-r 垂直的单位向量为⎝⎭B .已知a r 在b r 上的投影向量为12b r 且5b =r ,则252a b ⋅=r r C .若非零向量a r ,b r 满足a b a b ==-r r r r ,则a r 与a b +r r 的夹角是30︒D .已知()1,2a =r ,()1,1b =r ,且a r 与a b λ+r r 夹角为锐角,则λ的取值范围是5,3⎛⎫-+∞ ⎪⎝⎭11.如图,在棱长为2的正方体1111ABCD A B C D -中,已知M ,N ,P 分别是棱11C D ,1AA ,BC 的中点,点Q 满足1CQ CC λ=u u u r u u u u r ,[]0,1λ∈,下列说法正确的是( )A .//PQ 平面11ADD AB .若Q ,M ,N ,P 四点共面,则14λ=C .若13λ=,点F 在侧面11BB C C 内,且1//A F 平面APQ ,则点FD .若12λ=,由平面MNQ 分割该正方体所成的两个空间几何体为1Ω和2Ω,某球能够被整体放入1Ω或2Ω,则该球的表面积最大值为(12π-三、填空题12.如图,在平面五边形ABCDE 中, 1,2,AB DE BC CD AE =====90ABC BCD CDE ∠=∠=∠=︒,则五边形ABCDE 绕直线AB 旋转一周所成的几何体的体积为13.在ABC V 中,ABC ∠的平分线交AC 于点D ,2π,43ABC BD ∠==,则ABC V 周长的最小值为. 14.已知非零向量a b r r 、,满足π2,1,,3a b a b ===r r r r ,且()()0c a c b -⋅-=r r r r ,则c r 的最大值为.四、解答题15.已知,,a b c r r r 是同一平面内的三个向量,其中()1,2a =r .(1)若c =r //c a r r ,求c r 向量;(2)若b =r 2a b +r r 与2a b -r r 垂直,求a r 与b r 的夹角的余弦值. 16.记ABC V 的内角A 、B 、C 的对边分别为a 、b 、c ,且sin 2sin cos 2sin c A B A a A+=. (1)求B 的大小;(2)若b =ABC V 的面积为ABC V 的周长.17.如图,在几何体ABCDFE 中,四边形ABCD 为直角梯形,2,2DC AB GC FG ==,平面ABEF ⋂平面CDEF EF =(1)证明:AF //平面BDG(2)证明://AB EF18.在ABC V 中,已知4AB =,10AC =,60BAC ∠=︒,BC 、AC 边上的两条中线AM 、BN 相交于点G.(1)求BN u u u r 、AM u u u u r ;(2)求CN u u u r 与GM u u u u r 夹角的余弦值.19.“但有一枝堪比玉,何须九畹始征兰”,盛开的白玉兰是上海的春天最亮丽的风景线,除白玉兰外,上海还种植木兰科的其他栽培种,如黄玉兰和紫玉兰等.某种植园准备将如图扇形空地AOB 分成三部分,分别种植白玉兰、黄玉兰和紫玉兰;已知扇形的半径为70米,圆心角为2π3,动点P 在扇形的弧上,点Q 在OB 上,且//PQ OA .(1)求扇形空地AOB 的周长和面积;(2)当50OQ =米时,求PQ 的长;(3)综合考虑到成本和美观原因,要使白玉兰种植区OPQ △的面积尽可能的大.设AOP θ∠=,求OPQ △面积的最大值.。
2023-2024学年度上学期高一数学期中考试[含答案]
![2023-2024学年度上学期高一数学期中考试[含答案]](https://img.taocdn.com/s3/m/7d496179a9114431b90d6c85ec3a87c240288af8.png)
又 f (x) 是奇函数,所以 0 x 2 时, f (x) 0 , x 2 时, f (x) 0 ,且 f (0) f (2) 0 ,
不等式
xf
x
0
x
f
0
x
0
或
x
f
0 (x)
0
或
x
0
,所以 0
x
2 或 2
x
0
,
综上 2 x 2 .
故选:D.a 23 , b 45 , c 253 ,则
【解析】
【分析】根据交集含义即可得到答案.
A B 1, 0,1
【详解】根据交集含义即可得到
,
故选:B.
2. 命题: x R, x | x | 0 的否定为( )
A. x R, x | x | 0
B. x R, x | x | 0
C. x R, x | x | 0
D. x R, x | x | 0
【详解】因为
f
2x
1
x2
1 t
,令
2x
1,
x
t
1 2
,
f
(t)
t
1 2 2
1
,即
f
(x)
x 12 2
1
,
所以 f (3) 2 .
故选:B
6.
若定义在 R 的奇函数
f
x
,若
x
0
时
f
x
x 2
xf
,则满足
x 0 的 x 的取值范围是(
)
, 20, 2
A. 【答案】D 【解析】
, 2 2, , 20, 2
对于 C,
y∣y∣ x2 1, x R
2010-2011焦作市高一数学期末考试题及答案
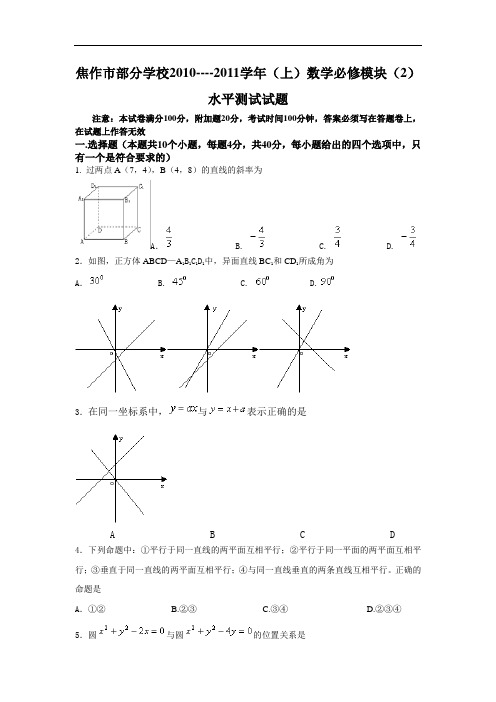
焦作市部分学校2010----2011学年(上)数学必修模块(2)水平测试试题注意:本试卷满分100分,附加题20分,考试时间100分钟,答案必须写在答题卷上,在试题上作答无效一.选择题(本题共10个小题,每题4分,共40分,每小题给出的四个选项中,只有一个是符合要求的)1. 过两点A(7,4),B(4,8)的直线的斜率为A. B. C. D.2.如图,正方体ABCD—A1B1C1D1中,异面直线BC1和CD1所成角为A. B. C. D.3.在同一坐标系中,与表示正确的是A B C D4.下列命题中:①平行于同一直线的两平面互相平行;②平行于同一平面的两平面互相平行;③垂直于同一直线的两平面互相平行;④与同一直线垂直的两条直线互相平行。
正确的命题是A.①② B.②③ C.③④ D.②③④5.圆与圆的位置关系是A.相离 B.相交 C.外切 D.内切6.用一个平面去截正方体,截面的形状不可能是A.正三角形 B.直角三角形 C.正方形 D.正六边形7..圆上的动点P到直线的最短距离为A.3 B.4 C.5 D.68.一个长方体的长、宽、高分别为2、1、1,其顶点都在一个球面上,则这个球的表面积为A.3 B.6 C.12 D. 249.光线沿直线2x-y-3=0经两坐标轴反射后所在的直线是A.2x+y+3=0 B.2x+y-3=0 C.2x-y+3=0 D.x-2y-3=010.下图2为图1所示几何体的展开图,则拼成一个棱长为6的正方体(如图3),需要这样的几何体A.2个B.3个C.4个D.5个二.填空题(本题共5个小题,每小题4分,共20分)11.与直线平行且距离为2的直线方程为 .12.在空间直角坐标系中,点A(1,1,2)关于轴对称的点的坐标为 .13.过A(,0)和B(3,0)两点的所有圆中面积最小的圆的方程为 .14.一个几何体的三视图如图所示,则这个几何体的体积为 .15.过A(0,3)的直线与圆相交且弦长为,直线方程为 .三.解答题(本题共4个小题,共40分,解答应写出文字说明、证明过程或演算步骤).16.(8分)已知直线经过直线和的交点,且与直线垂直,求直线的方程.17.(10分)如图,已知空间四边形中,。
焦作市2010-2011学年(上)数学必修模块(1)水平测试

焦作市2010-2011学年(上)必修模块(1)水平测试数学试卷命题: 修武一中 李同喜 校审: 焦作一中 王 静 市教研室 焦金安注意本试卷满分120分,附加题20分,答案必须写在答题卷上,在试卷上作答无效.一、选择题(本题共10个小题,每小题4分,共40分,每个小题只有一个选项 是正确的,请将正确选项移到答题卷答案栏内.) 1.集合{|22},{|13}A x x B x x =-<<=-≤<,那么A B =A.{|23}x x -<<B.{|12}x x ≤<C.{|21}x x -<≤D.{|23}x x <<2.二次函数542+-=mx x y 的对称轴为2-=x ,则当1=x 时,y 的值为 A.-7 B.1 C.17 D.253.下列各组函数中,表示同一个函数的是A .211x y x -=-与1y x =+B .lg y x =与21lg 2y x =C .1y =与1y x =-D .y x =与y=log a a x (a ﹥0且a ≠1) 4.函数()f x =的定义域为 A. {x|x>1} B.{x|x<1} C. {x|-1<x<1} D. ∅5.右图给出了红豆生长时间t (月)与枝数y (枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好? A .指数函数:t y 2= B .对数函数:t y 2log = C .幂函数:3t y = D .二次函数:22t y =6.函数y= | lg (x-1)| 的图象是7.已知31)53(-=a ,21)53(-=b ,21)34(-=c ,则a,b,c 三个数的大小关系是A.b a c <<B.a b c <<C.c b a <<D.c a b <<8.已知函数1])21[(l )(21-=x og x f ,则A.函数在(-∞,0)上递减B.函数在(-∞,0)上递增C.函数在R 上递减D.函数在R 上递增9.已知)(x f y =在定义域(-1,1)上是减函数,且)12()1(-<-a f a f ,则a 的取值范围是A .),(321-B .),(132C .),(320 D .)(,10 10.下列所给4个图象中,与所给3件事吻合最好的顺序为(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取 了作业本再上学;(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一 些时间;(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
2016-2017年河南省焦作市高一(上)期中数学试卷及参考答案
2016-2017学年河南省焦作市高一(上)期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)设集合A={0,1,2},B={1,2},则()A.A=B B.A∩B=∅C.A⊊B D.A⊋B2.(5分)已知函数f(x)与g(x)分别由如表给出:那么f(g(3))等于()A.3 B.4 C.2 D.13.(5分)函数f(x)=+lg(x+3)的定义域为()A.(﹣3,2]B.[﹣3,2]C.(﹣3,2)D.(﹣∞,﹣3)4.(5分)已知幂函数y=f(x)的图象过点,则log2f(2)的值为()A.B.C.1 D.﹣15.(5分)下列函数中,值域为(0,+∞)的是()A.y=2B.y=lg(x2+1)C.y= D.y=()2﹣x6.(5分)设集合M={1,9,a},集合P={1,a2},若P⊆M,则实数a的取值个数为()A.0个 B.1个 C.2个 D.3个7.(5分)设a=log23,b=log43,c=0.5,则()A.c<b<a B.b<c<a C.b<a<c D.c<a<b8.(5分)函数f(x)=的图象()A.关于原点对称B.关于直线y=x对称C.关于x轴对称D.关于y轴对称9.(5分)已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)<f(1),则()A.a>0,4a+b=0 B.a<0,4a+b=0 C.a>0,2a+b=0 D.a<0,2a+b=0 10.(5分)在用二分法求方程x3﹣2x﹣1=0的一个近似解时,现在已经将一根锁定在区间(1,2)内,则下一步可断定该根所在的区间为()A.(1.8,2)B.(,2)C.(1,)D.(1,1.2)11.(5分)已知偶函数f(x)在区间[0,+∞)上为增函数,且f(﹣1)=.若实数a满足f(log a3)+f(log a)≤1,则实数a的取值范围为()A.0<a<B.a≥3,或0<a<C.a≥3,或0<a≤D.a≥3 12.(5分)已知方程|x2﹣1|﹣x﹣a=0有两个不等的实数根,则实数a的取值范围是()A.(﹣1,1)B.[1,+∞)C.(﹣1,1)∪(,+∞)D.(﹣1,+∞)二、填空题:本大题共4小题,每小题5分,共20分).13.(5分)集合{1,2,3}的真子集的个数为.14.(5分)方程=3x﹣2的实数解为.15.(5分)已知函数f(x)=﹣3x在区间[2,4]上的最大值为.16.(5分)设f(x)=,其中[x]表示不超过x的最大整数,则方程f(x)=lgx的根的个数是.三、解答题:本大题共6小题,共48分.解答写出文字说明、证明过程或演算过程.17.(10分)(1)计算:﹣××;(2)计算:(lg2)2+lg5•lg20+1.18.(12分)函数f(x)=lg(a﹣x)+lgx(a>0)的定义域为S,函数g(x)=+的定义域为T.(1)若a=3,求S∪T和S∩T;(2)若S⊆T,求a的取值范围.19.(12分)某企业常年生产一种出口产品,根据预测可知,进入2l世纪以来,该产品的产量平稳增长.记2008年为第1年,且前4年中,第x年与年产量f (x)(万件)之间的关系如下表所示:x+a(1)找出你认为最适合的函数模型,并说明理由,然后选取08年和10年的数据求出相应的解析式;(2)因遭受某国对该产品进行反倾销的影响,2014年的年产量比预计减少30%,试根据所建立的函数模型,确定2014年的年产量.20.(12分)已知函数f(x﹣1)=lg(1<x<2),求函数f(x)的值域.21.(12分)已知函数f(x)=ax2﹣2ax+2+b,(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.(1)求a,b的值;(2)若b<1,g(x)=f(x)﹣mx在[2,4]上为单调函数,求实数m的取值范围.22.(12分)已知指数函数y=g(x)满足:g(﹣3)=,定义域为R的函数f (x)=是奇函数.(1)求函数g(x)与f(x)的解析式;(2)判断函数f(x)的单调性并证明之;(3)若关于x的方程f(x)=m在x∈[﹣1,1]上有解,求实数m的取值范围.2016-2017学年河南省焦作市高一(上)期中数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)设集合A={0,1,2},B={1,2},则()A.A=B B.A∩B=∅C.A⊊B D.A⊋B【解答】解:根据题意,集合A={0,1,2},B={1,2},则B是A的子集,即有A⊋B;故选:D.2.(5分)已知函数f(x)与g(x)分别由如表给出:那么f(g(3))等于()A.3 B.4 C.2 D.1【解答】解:由数表知g(3)=4,∴f[g(3)]=f(4)=3.故选:A.3.(5分)函数f(x)=+lg(x+3)的定义域为()A.(﹣3,2]B.[﹣3,2]C.(﹣3,2)D.(﹣∞,﹣3)【解答】解:函数f(x)=+lg(x+3),∴,解得﹣3<x<2;∴f(x)的定义域为(﹣3,2).故选:C.4.(5分)已知幂函数y=f(x)的图象过点,则log2f(2)的值为()A.B.C.1 D.﹣1【解答】解:设f(x)=xα,则f(3)=3α=,解得α=,则f(x)=,f(2)=,则log2f(2)=log2=,故选:A.5.(5分)下列函数中,值域为(0,+∞)的是()A.y=2B.y=lg(x2+1)C.y= D.y=()2﹣x【解答】解:逐一考查所给函数的值域:A中x≠0,∴,值域不是(0,+∞);B中x2+1≥1,∴y≥0,值域是[0,+∞);C中,∴y≥0,值域是[0,+∞);排除ABC选项,故选:D.6.(5分)设集合M={1,9,a},集合P={1,a2},若P⊆M,则实数a的取值个数为()A.0个 B.1个 C.2个 D.3个【解答】解:根据题意,集合M={1,9,a},集合P={1,a2},若P⊆M,则a2=9或a2=a,分2种情况讨论:①、当a2=9时,a=3或﹣3,当a=3时,M={1,9,3},集合P={1,9},符合题意;当a=﹣3时,M={1,9,﹣3},集合P={1,9},符合题意;①、当a2=a时,a=0或a=1,当a=0时,M={1,9,0},集合P={1,0},符合题意;当a=1时,M={1,9,1},集合P={1,1},不满足集合中元素的互异性,不符合题意;故a可取的值为3、﹣3、0;共3个;故选:D.7.(5分)设a=log23,b=log43,c=0.5,则()A.c<b<a B.b<c<a C.b<a<c D.c<a<b【解答】解:根据对数函数的单调性知,log 23>log22=1=log44>log43,即a>b,∵c=0.5==log42,且log43>log42,∴b>c,即a>b>c,故选:A.8.(5分)函数f(x)=的图象()A.关于原点对称B.关于直线y=x对称C.关于x轴对称D.关于y轴对称【解答】解:,∴f(x)是偶函数,图象关于y轴对称故选:D.9.(5分)已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)<f(1),则()A.a>0,4a+b=0 B.a<0,4a+b=0 C.a>0,2a+b=0 D.a<0,2a+b=0【解答】解:因为f(0)=f(4),即c=16a+4b+c,所以4a+b=0;又f(0)<f(1),即c<a+b+c,所以a+b>0,即a+(﹣4a)>0,所以﹣3a>0,故a<0.故选:B.10.(5分)在用二分法求方程x3﹣2x﹣1=0的一个近似解时,现在已经将一根锁定在区间(1,2)内,则下一步可断定该根所在的区间为()A.(1.8,2)B.(,2)C.(1,)D.(1,1.2)【解答】解:令f(x)=x3﹣2x﹣1,则f(1)=﹣2<0,f(2)=3>0,f()=﹣<0由f(2)f()<0知根所在区间为(,2)故选:B.11.(5分)已知偶函数f(x)在区间[0,+∞)上为增函数,且f(﹣1)=.若实数a满足f(log a3)+f(log a)≤1,则实数a的取值范围为()A.0<a<B.a≥3,或0<a<C.a≥3,或0<a≤D.a≥3【解答】解:由题意可得f(log a3)+f(log a)≤1,即f(log a3)+f(﹣log a3)≤1,即2f(log a3)≤1,即f(log a3)≤=f(1),∴﹣1≤log a3≤1.当a>1时,由log a3≤1,可得a≥3;当0<a<1时,由﹣1≤log a3,可得0<a ≤.综上可得,实数a满足a≥3,或0<a≤,故选:C.12.(5分)已知方程|x2﹣1|﹣x﹣a=0有两个不等的实数根,则实数a的取值范围是()A.(﹣1,1)B.[1,+∞)C.(﹣1,1)∪(,+∞)D.(﹣1,+∞)【解答】解:方程|x2﹣1|﹣x﹣a=0有两个不等的实数根,⇔函数y=|x2﹣1|的图象和直线y=x+a有2个交点,如图所示:实数a的取值范围是(﹣1,1)∪(,+∞)故选:C二、填空题:本大题共4小题,每小题5分,共20分).13.(5分)集合{1,2,3}的真子集的个数为7.【解答】解:集合的真子集为{1},{2},{3},{1,2},{1,3},{2,3},∅.共有7个.故答案为7.14.(5分)方程=3x﹣2的实数解为1.【解答】解:方程即:,令t=3x(t>0),则:,整理可得:t2﹣2t﹣3=0,∴t=3x=3,x=1.故答案为1.15.(5分)已知函数f(x)=﹣3x在区间[2,4]上的最大值为﹣4.【解答】解:∵在区间[2,4]上是减函数,﹣3x在区间[2,4]上是减函数;∴函数f(x)=﹣3x在区间[2,4]上是减函数;∴f(x)max=f(2)=﹣3×2=﹣4.故答案为:﹣4.16.(5分)设f(x)=,其中[x]表示不超过x的最大整数,则方程f(x)=lgx的根的个数是8.【解答】解:如图所示,依据题中所给函数的解析式绘制函数f(x)和函数y=lgx 的图象,观察可得,两函数图象交点的个数为8个,即方程f(x)=lgx的根的个数是8个.故答案为:8.三、解答题:本大题共6小题,共48分.解答写出文字说明、证明过程或演算过程.17.(10分)(1)计算:﹣××;(2)计算:(lg2)2+lg5•lg20+1.【解答】解:(1)原式=3﹣=3﹣2=1;(2)原式=(lg2)2+lg5•(1+lg2)+1=lg2(lg2+lg5)+lg5+1=lg2+lg5+1=2.18.(12分)函数f(x)=lg(a﹣x)+lgx(a>0)的定义域为S,函数g(x)=+的定义域为T.(1)若a=3,求S∪T和S∩T;(2)若S⊆T,求a的取值范围.【解答】解:(1)根据题意,a=3时,f(x)=lg(3﹣x)+lgx,有3﹣x>0且x>0,解可得0<x<3,其定义域S=(0,3),函数g(x)=+有x≥0且2﹣x≥0,解可得0≤x≤2,则T=[0,2];则S∪T=[0,3),S∩T=(0,2];(2)f(x)=lg(a﹣x)+lgx(a>0),有a﹣x>0且x>0,又因为a>0,所以S={x|x(x﹣a)<0}={x|0<x<a};则(0,a)⊆[0,2],所以a≤2.又a>0,所以0<a≤2.19.(12分)某企业常年生产一种出口产品,根据预测可知,进入2l世纪以来,该产品的产量平稳增长.记2008年为第1年,且前4年中,第x年与年产量f (x)(万件)之间的关系如下表所示:x+a(1)找出你认为最适合的函数模型,并说明理由,然后选取08年和10年的数据求出相应的解析式;(2)因遭受某国对该产品进行反倾销的影响,2014年的年产量比预计减少30%,试根据所建立的函数模型,确定2014年的年产量.【解答】解:(1)符合条件的是f(x)=ax+b,若模型为f(x)=2x+a,则由f(1)=2+a=4,得a=2,即f(x)=2x+2,此时f(2)=6,f(3)=10,f(4)=18,与已知相差太大,不符合.若模型为f(x)=log x+a,则f(x)是减函数,与已知不符合.由已知得,解得a=,b=,∴f(x)=x+,(x=1,2,…,6,7)经验证x=2,4,符合的比较好.(2)∵2014年预计年产量为f(7)==13,∴13×(1﹣30%)=9.1,即确定2014年的年产量约为9.1万件.20.(12分)已知函数f(x﹣1)=lg(1<x<2),求函数f(x)的值域.【解答】解:令t=x﹣1,则x=t+1 所以,结合1<x<2可得0<x﹣1=t<1,∴f(x)=(0<x<1)结合反比例函数的性质可得函数f(x)在区间(0,1)上单调递增,而:f(0)=lg1=0,当x→1时函数值为+∞,综上可得函数f(x)的值域是(0,+∞).21.(12分)已知函数f(x)=ax2﹣2ax+2+b,(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.(1)求a,b的值;(2)若b<1,g(x)=f(x)﹣mx在[2,4]上为单调函数,求实数m的取值范围.【解答】解:(1)由于函数f(x)=ax2﹣2ax+2+b=a(x﹣1)2+2+b﹣a,(a≠0),对称轴为x=1,当a>0时,函数f(x)在区间[2,3]上单调递增,由题意可得,解得.当a<0时,函数f(x)在区间[2,3]上单调递减,由题意可得,解得.综上可得,,或.(2)若b<1,则由(1)可得,g(x)=f(x)﹣mx=x2﹣(m+2)x+2,再由函数g(x)在[2,4]上为单调函数,可得≤2,或≥4,解得m≤2,或m≥6,故m的范围为(﹣∞,2]∪[6,+∞).22.(12分)已知指数函数y=g(x)满足:g(﹣3)=,定义域为R的函数f (x)=是奇函数.(1)求函数g(x)与f(x)的解析式;(2)判断函数f(x)的单调性并证明之;(3)若关于x的方程f(x)=m在x∈[﹣1,1]上有解,求实数m的取值范围.【解答】解:(1)设g(x)=a x,则解得:a=2,所以g(x)=2x所以,令f(0)=0得,所以c=1,经检验,当c=1时,为奇函数,符合题意,所以;(2)f(x)在R上单调递减,证明如下:任取x1,x2∈R,且x1<x2,则==,因为,所以而x1<x2,所以x2﹣x1>0,,,所以,即f(x1)﹣f(x2)>0,f(x1)>f(x2)所以f(x)在R上单调递减;(3)由(2)知f(x)在[﹣1,1]上单调递减,所以f(1)≤f(x)≤f(﹣1)即f(x)在[﹣1,1]上的值域为,要使得关于x的方程f(x)=m在x∈[﹣1,1]上有解,则实数m的取值范围为.。
河南省焦作市高一上学期数学期中考试试卷
河南省焦作市高一上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2018·中山模拟) 设集合,则集合等于().A .B .C .D .2. (2分) (2019高一上·大庆月考) 函数的定义域为()A .B .C .D .3. (2分)下列函数在定义域内为奇函数,且有最小值的是()A .B .C .D .4. (2分)函数y=ax﹣1+2(a>0且a≠1)图象一定过点()A . (1,1)B . (1,3)C . (2,0)D . (4,0)5. (2分)(2016高一下·抚顺期末) 若一个几何体的三视图都是三角形,则这个几何体可能是()A . 圆锥B . 四棱锥C . 三棱锥D . 三棱台6. (2分) (2018高一上·河南月考) 若函数且)的图象如图所示,则下列函数图象正确的是()A .B .C .D .7. (2分)函数,满足f(x)>1的x的取值范围()A . (-1,1)B .C . {x|x>0或x<-2}D . {x|x>1或x<-1}8. (2分) (2019高三上·珠海月考) 已知函数(),若函数有三个零点,则实数的取值范围是()A .B .C .D .9. (2分) (2018高一上·海南期中) 某厂印刷某图书总成本y(元)与图书日印量x(本)的函数解析式为y=5x+3000,而图书出厂价格为每本10元,则该厂为了不亏本,日印图书至少为()A . 200本B . 400本C . 600本D . 800本10. (2分) (2019高三上·黑龙江月考) 设,则()A .B .C .D .11. (2分) (2019高三上·东莞期末) 函数的图像大致为()A .B .C .D .12. (2分)已知函数,则的值域是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2019高一上·苍南月考) 设函数,则 ________.14. (1分)(2018·南京模拟) 设函数的值域为,若,则实数的取值范围是________.15. (1分)函数在实数集上是增函数,则k的范围是________16. (1分)现有40米长的篱笆材料,如果利用已有的一面墙(设长度够用)作为一边,围成一块面积为S 平方米的矩形菜地,则S的最大值为________平方米.三、解答题 (共6题;共40分)17. (10分) (2016高一上·杭州期中) 计算下列各式(1)求值:﹣()0+0.25 ×()﹣4;(2)求值:(lg2)2+lg5•lg20+lg100+lg +lg0.006.18. (5分) (2016高一上·安阳期中) 已知函数的定义域为集合A,B={x|x>3或x<2}.(1)求A∩B;(2)若C={x|x<2a+1},B∩C=C,求实数a的取值范围.19. (5分) (2017高一上·长春期中) 已知函数f(x)=(1)判断点(3,14)是否在f(x)的图象上.(2)当x=4时,求f(x)的值.(3)当f(x)=2时,求x的值.20. (5分) (2016高一上·西湖期中) 函数f(x)=loga(3﹣ax)(a>0,a≠1)(1)当a=3时,求函数f(x)的定义域;(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.21. (10分)平面直角坐标系xoy中,已知椭圆:的离心率为,左、右焦点分别是F1,F2 ,以F1为圆心以3为半径的圆与以F2为圆心以1为半径的圆相交,且交点在椭圆上.(1)求椭圆的方程;(2)设椭圆:为椭圆上任意一点,过点的直线y=kx=m交椭圆于,两点,射线交椭圆于点.(1)求的值;(1)求面积的最大值22. (5分) (2019高一上·宜昌期中) 屠呦呦,第一位获得诺贝尔科学奖项的中国本土科学家,在2015年获得诺贝尔生理学或医学奖,理由是她发现了青蒿素.这种药品可以有效降低疟疾患者的死亡率,从青篙中提取的青篙素抗疟性超强,几乎达到100%.据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(Ⅰ)写出服药一次后y与t之间的函数关系式;(Ⅱ)据进一步测定:每毫升血液中含药量不少于微克时,治疗有效,求服药一次后治疗有效的时间是多长?参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共40分) 17-1、答案:略17-2、答案:略18-1、答案:略18-2、答案:略19-1、19-2、19-3、20-1、答案:略20-2、答案:略20-3、答案:略21-1、21-2、22-1、。
2024-2025学年高一上学期期中模拟考试数学试题(苏教版2019,必修第一册第1-5章)含解析
2024-2025学年高一数学上学期期中模拟卷(苏教版2019)(时间:120分钟满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:苏教版2019必修第一册第1章~第5章。
5.难度系数:0.65。
第一部分(选择题共58分)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}()14,2,5A x x B =-<<=,则()R B A = ð()A .(]1,2-B .()1,2-C .()[),45,-∞⋃+∞D .()[),15,-∞-+∞ 【答案】A【解析】()2,5B =,则R (,2][5,)B =-∞+∞ ð,则()(]R 1,2B A =- ð.故选:A.2.已知集合{}{}2,,42,A xx k k B x x k k ==∈==+∈Z Z ∣∣.设:,:p x A q x B ∈∈,下列说法正确的是()A .p 是q 的充分不必要条件B .p 是q 的必要不充分条件C .p 是q 的充要条件D .p 是q 的既不充分也不必要条件【答案】B【解析】由(){}221,B xx k k ==+∈Z ∣,{}2,A x x k k ==∈Z ∣,故B 为A 的真子集,又:,:p x A q x B ∈∈,故p 是q 的必要不充分条件.故选:B.3.,,,a b c b c ∈>R ,下列不等式恒成立的是()A .22a b a c +>+B .22a b a c +>+C .22ab ac >D .22a b a c>【答案】B【解析】对于A ,若0c b <<,则22b c <,选项不成立,故A 错误;对于B ,因为b c >,故22a b a c +>+,故B 成立,对于C 、D ,若0a =,则选项不成立,故C 、D 错误;故选:B.4.已知实数a 满足14a a -+=,则22a a -+的值为()A .14B .16C .12D .18【答案】A【解析】因为()212212a a a a a a ---=+++⋅,所以()22211216214a a a a a a ---+=+-⋅=-=.故选:A.5.早在西元前6世纪,毕达哥拉斯学派已经知道算术中项,几何中项以及调和中项,毕达哥拉斯学派哲学家阿契塔在《论音乐》中定义了上述三类中项,其中算术中项,几何中项的定义与今天大致相同.若221a b +=,则()()2121a b++的最大值为()A .916B .2516C .94D .254【答案】C【解析】因为()()212122221a b a b a b++=⋅+++,又221a b +=,所以()()22292121222(224a b aba b+++=⋅+≤+=,当且仅当1222ab==,即1a b ==-时取等号,故选:C6.已知函数()25,1,1x ax x f x a x x⎧-+≤⎪=⎨>⎪⎩满足对任意实数12x x ≠,都有()()21210f x f x x x -<-成立,则a 的取值范围是()A .(]0,3B .[)2,+∞C .()0,∞+D .[]2,3【答案】D【解析】因为函数()f x 满足对任意实数12x x ≠,都有2121()()0f x f x x x -<-成立,不妨假设12x x <,则210x x ->,可得()()210f x f x -<,即()()12f x f x >,可知函数()f x 在R 上递减,则1206a a a a ⎧≥⎪⎪>⎨⎪-+≥⎪⎩,解得23a ≤≤,所以a 的取值范围是[]2,3.故选:D.7.已知函数()221x f x x x =-+,且()()1220f x f x ++<,则()A .120x x +<B .120x x +>C .1210x x -+>D .1220x x ++<【答案】A【解析】由函数单调性性质得:y x x =,21x y =+在R 上单调递增,所以()221x f x x x =-+在R 上单调递增,令函数222121()||1||||21212121x x x x x x g x x x x x x x +-=-+=-+=+++++,则2112()||||()2121x xxx g x x x x x g x -----=-+=-+=-++,所以()()0g x g x +-=,则函数()g x 为奇函数,且在R 上单调递增,故()()()()12121212200f x f x g x g x x x x x ++<⇔<-⇔<-⇔+<.故选:A .8.已知关于x 的不等式20(,,)ax bx c a b c ++>∈R 的解集为(4,1)-,则29c a b++的取值范围为()A .[)6,-+∞B .(,6)-∞C .(6,)-+∞D .(],6∞--【答案】D【解析】由不等式20(,,)ax bx c a b c ++>∈R 的解集为(4,1)-,可知1和4-是方程20ax bx c ++=的两个实数根,且0a <,由韦达定理可得4141b ac a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩,即可得3,4b a c a ==-,所以()222499169994463444a c a a a a b a a a a a -+++⎛⎫===+=--+≤-=- ⎪++-⎝⎭.当且仅当944a a -=-时,即34a =-时等号成立,即可得(]29,6c a b∞+∈--+.故选:D二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.若集合{1,1,3,5}M =-,集合{3,1,5}N =-,则正确的结论是()A .,x N x M ∀∈∈B .,x N x M ∃∈∈C .{1,5}M N ⋂=D .{1,5}M N = 【答案】BC【解析】对于A ,3N -∈,但是3M -∉,A 错误,对于B ,1N ∈,1M ∈,B 正确,对于CD ,{1,1,3,5}{3,1,5}{1,5}M N =--= ,{1,1,3,5}{3,1,5}{3,1,1,3,5}M N =--=-- ,C 正确,D 错误.故选:BC .10.已知0a >,0b >,且2a b +=,则()A .222a b +≥B .22log log 0a b +≤C .1244a b -<<D .20a b ->【答案】ABC【解析】对于A ,有()()()()2222222222111122222222a b a ab b a ab b a b a b a b ⎡⎤+=+++-+=++-≥+=⋅=⎣⎦,当且仅当a b =时取等号,故A 正确;对于B ,0a >,0b >,有()22112144ab a b ≤+=⋅=,当且仅当a b =时取等号,故1ab ≤,从而()2222log log log log 10a b ab +=≤=,故B 正确;对于C ,由,0a b >,知0ab >,所以()()()()()()222222222042224ab a ab b a ab b a b a b a b a b <=++--+=+--=--=--,故()24a b -<,从而22a b -<-<,所以22122244a b --=<<=,故C 正确;对于D ,由于当1a b ==时,有,0a b >,2a b +=,但2110a b -=-=,故D 错误.故选:ABC.11.对于任意的表示不超过x 的最大整数.十八世纪,[]y x =被“数学王子”高斯采用,因此得名为高斯函数,人们更习惯称为“取整函数”.下列说法正确的是()A .函数[]()y x x =∈R 为奇函数B .函数[]y x =的值域为ZC .对于任意的,x y +∈R ,不等式[][][]x y x y +≤+恒成立D .不等式[]2[]430x x -+<的解集为{}23x x ≤<【答案】BCD【解析】对于A ,当01x ≤<时,[]0y x ==,当10x -<<,[]1y x ==-,所以[]()y x x =∈R 不是奇函数,所以A 错误,对于B ,因为[]x 表示不超过x 的最大整数,所以当x ∈R 时,[]Z x ∈,所以函数[]y x =的值域为Z ,所以B 正确,对于C ,因为,x y +∈R 时,[][],x x y y ≤≤,所以[][][][][]x y x y x y x y ⎡⎤+=+≤+≤+⎣⎦,所以C 正确,对于D ,由[]2[]430x x -+<,得[]13x <<,因为[]x 表示不超过x 的最大整数,所以23x ≤<,所以D 正确.故选:BCD第二部分(非选择题共92分)三、填空题:本题共3小题,每小题5分,共15分。
焦作市09-10学年高一年级下学期期中考试-数学
必修模块(3)水平测试数 学 试 卷注意:本试卷满分100分,附加题20分,考试时间100分钟.答案必须写在答题卷上,在试题卷上作答无效.一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一个是符合要求的)1.算法框图中表示判断的是2.某公司现有职员160人,中级管理人员30人,高级管理人员10人,要从其中抽取20人进行体检,如果采用分层抽样的方法,则职员、中级管理人员和高级管理人员应该各抽取多少人A. 8,15,7B. 16,2,2C. 16,3,1D. 12,5,3 3.条件语句的一般形式如右图所示,其中B 表示的是 A .条件B .条件语句C .满足条件时执行的内容D .不满足条件时执行的内容4.已知样本数据12,,,n x x x的平均数为h ,样本数据12,,,m y y y 的平均数为k , 则把这两组数据合并成一组以后,这组样本的平均数为A .2h k+B .h km n ++C .nk mh m n ++D . nh mkm n ++5.样本4,2,1,0,-2的标准差是A .1B .2C .4D .6.下列说法正确的是①必然事件的概率等于1; ②某事件的概率等于1.1; ③互斥事件一定是对立事件; ④对立事件一定是互斥事件. A .①② B . ②④ C .①③ D .①④ 7.设有一个线性回归方程为3 2.5y x =-,则变量x 增加一个单位时A .y 平均增加2.5个单位B .y 平均增加1个单位C .y 平均减少2.5个单位D .y 平均减少1个单位 8.如图所示流程图中,语句1(语句1与i 无关) 将被执行的次数是A .23.B .24C .25D .26(第3题图)(第8题图)9.一枚骰子连续掷了两次,则点数之和为2或3的概率是A .112B .19C .18D .1610.某程序框图如右图所示,该程序运行后输出的k 的值是A. 3B. 4C. 5D. 6二、填空题(本大题共5小题,每小题4分,共20分) 11.阅读以下程序:输入 xIf x >0 Then y =3x +1 Else y =-2x +3 End If 输出 y End若输入x =5, 求输出的y = .12.某射手射中10环、9环、8环的概率分别为0.24,0.28,0.19,那么,在一次射击训练中, 该射手射击一次不够8环的概率是 .13.右图给出的是计算201614121++++ 的值的一个流程图, 其中判断框内应填入的条件是 .14.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后, 又从池塘内捞出50条鱼,其中有标记的有2条.根据以上数据可以 估计该池塘内共有 条鱼.15.利用如下算法框图可以用来估计π的近似值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入 1000,输出的结果为788,则由此可估计π的近似值为______________.( 保留四个有效数字)(第10题图)(第13题图)(第15题图)三 、解答题(本大题共4小题,共40分,解答应写出必要的文字说明、证明过程或演算步骤)16. (8分)根据以下算法的程序,画出其相应的流程图,并指明该算法的目的.n =1 S =0 DoS =S +n n =n +1Loop while S 2010 输出n -117. (10分)下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料(单位:厘米):(1)在这个问题中,总体是什么?并求出x 与y 的值;(2)求表中x 与y 的值,画出频率分布直方图及频率分布折线图; (3)试计算身高在147~152cm 的总人数约有多少?18.(10分)已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.(1)从中任取1个球, 求取得红球或黑球的概率; (2)列出一次任取2个球的所有基本事件; (3)从中取2个球,求至少有一个红球的概率.分组 人数 频率 [122,126 ) 5 0.042 [126,130) 8 0.067 [130,134 ) 10 0.083 [134,138) 22 0.183 [138,142) y [142,146) 20 0.167 [146,150) 11 0.092 [150,154) x 0.050 [154,158) 5 0.042 合计1201.0019.(10分)某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局和某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,程,再用被选取的2组数据进行检验.(1)求选取的2组数据恰好是相邻两个月的概率;(2)若选取的是1月与6月两组数据,请根据2至5月份的数据,用最小二乘法求出y 关于x 的线性回归方程y = a + bx ;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想? (参考公式: 1122222212,n n n x y x y nx y nx y b a y bx x x x nx+++-⋅==-+++-)附加题(本大题共2小题,每小题10分,共20分,省级示范性高中要把该题成绩记入总分, 普通高中学生选作) 20.(10分)甲、乙、丙、丁四人做相互传球练习,第一次甲传给其他三人中的一人(假设每个人得到球的概率相同),第二次由拿球者再传给其他三人中的一人,这样共传了三次. (1)用树状图列出所有不同的结果;(2)第三次球传给甲可能性和传给乙的可能性相比,哪个更大一些?为什么?.21.(10分)在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):甲:37,21,31, 20, 29, 19, 32, 23, 25, 33; 乙:10, 30, 47, 27, 46, 14, 26, 10, 44, 46.(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;(2)设抽测的10株甲种树苗高度平均值为x ,将这10 株树苗的高度依次输入,按程序框(如右图)进行运算,问输出的S 大小为多少?并说明S 的统计学意义.焦作市2009—2010学年(下)必修(3)水平测试数学参考答案一、选择题(本大题共10小题,每小题4分,共40分)题号 1 2 3 4 5 678910答案 B C C D B D C C A B二、填空题 (本大题共5小题,每小题4分,共20分)11. 16 12. 0.29 13. i >10(或i ≥11) 14. 750 15.3.152三、解答题(本大题共4小题,共40分) 16. 解:该算法的目的:求使1232010n +++⋅⋅⋅+>成立的最小自然数n . 17.解:(1)在这个问题中,总体是某校500名12岁男生身高, x 的值为6 , y 的值为0.275.(2)略. (3)47)21050.043092.0(500=⨯+⨯(人) ,∴ 身高在147~152cm 的总人数约有47人.18.解:(1)从6只球中任取1球得红球有2种取法,得黑球有3种取法,得红球或黑球的共有2+3=5种不同取法,任取一球有6种取法,所以任取1球得红球或黑球的概率得156P =.(2)将红球编号为红1,红2,黑球编号为黑1,黑2,黑3,则一次任取2个球的所有基本事件为:红1红2 红1黑1 红1黑2 红1黑3 红1白 红2白 红2黑1 红2黑2 红2黑3 黑1黑2 黑1黑3 黑1白 黑2黑3 黑2白 黑3白(3)由(2)知从6只球中任取两球一共有15种取法,其中至少有一个红球的取法共有9种,所以其中至少有一个红球概率为293155P ==. 19.解:(1)设抽到相邻两个月的数据为事件A ,因为从6组数据中选取2组数据共有15种情况,每种情况都是等可能出现的,其中,抽到相邻两个月的数据的情况有5种.所以 P (A )=31155=.(2)由数据求得24,11==y x 由公式求得718=b 再由730-=-=x b y a所以关于的线性回归方程为301877y x =-+.(3) 当2|227150|,715010<-==,y x 时 同样,当2|22778|,7786<-==,y x 时,所以,该小组所得线性回归方程是理想的. 附加题(本大题共2小题,每小题10分,共20分) 1.解:(1)(2) 由树状图可知,共有27种不同的结果.记第三次球传回到甲的手中为事件A ,有6种不同结果,故第三次球仍传回甲的概率:P (A )=92276=记第三次球传回到乙的手中为事件B ,有7种不同结果,故第三次球传给乙的概率:P (B )=277∴第三次球传给甲的可能性和传给乙的可能性不相同,传给乙的可能性要大2.解:(1)茎叶图略;统计结论:①甲种树苗的平均高度小于乙种树苗的平均高度; ②甲种树苗比乙种树苗长得整齐;③甲种树苗的中位数为27,乙种树苗的中位数为28.5;④甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布比较分散. (2)27,35x S ==,S 表示10株甲种树苗高度的方差,是描述树苗高度离散程度的量.S 值越小,表示长得越整齐,S 值越大,表示长得越参差不齐.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
焦作市2010-2011学年(上)必修模块(1)水平测试
数学试卷
注意
本试卷满分120分,附加题20分,答案必须写在答题卷上,在试卷上作答无效.
一、选择题(本题共10个小题,每小题4分,共40分,每个小题只有一个选项 是正确的,请将正确选项移到答题卷答案栏内.)
1.集合{|22},{|13}A x x B x x =-<<=-≤<,那么A B =
A.{|23}x x -<<
B.{|12}x x ≤<
C.{|21}x x -<≤
D.{|23}x x <<
2.二次函数542
+-=mx x y 的对称轴为2-=x ,则当1=x 时,y 的值为 A.-7 B.1 C.17 D.25 3.下列各组函数中,表示同一个函数的是
A .211x y x -=-与1y x =+
B .lg y x =与21lg 2y x = C
.1y =与1y x =- D .y x =与y=log a a x (a ﹥0且a ≠1)
4.
函数()f x =
A. {x|x>1}
B.{x|x<1}
C. {x|-1<x<1}
D. ∅ 5.右图给出了红豆生长时间t (月)与枝数y (枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好? A .指数函数:t y 2= B .对数函数:t y 2log = C .幂函数:3t y = D .二次函数:22t y =
6.函数y= | lg (x-1)| 的图象是
7.已知31)53(-=a ,21)53(-=b ,2
1
)3
4(-=c ,则a,b,c 三个数的大小关系是
C
A.b a c <<
B.a b c <<
C.c b a <<
D.c a b <<
8.已知函数1])21[(l )(2
1
-=x
og x f ,则 A.函数在(-∞,0)上递减 B.函数在(-∞,0)上递增 C.函数在R 上递减 D.函数在R 上递增
9.已知)(x f y =在定义域(-1,1)上是减函数,且)12()1(-<-a f a f ,则a
的取值范围是
A .),(321-
B .),(132
C .),(3
20 D .)
(,10 10.下列所给4个图象中,与所给3件事吻合最好的顺序为
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
A..(1)(2)(4) B.(4)(2)(3) C.(4)(1)(3) D.(4)(1)(2) 二、填空题(本题共5个小题,每小题4分,共20分,请将答案填写在答题卷上)
11.函数()
1,(0)()(2),0x x f x f x x +≥⎧=⎨+<⎩,则)3(-f _________.
12.指数函数(2)x
y a =-在定义域内是减函数,则a 的取值范围是 . 13.已知函数12)(+-=a x x f 在区间[],12-上存在c ,使得0)(=c f ,则实数a 的取值范围是 .
14.函数)(x f 为奇函数,且0,1)(>+=x x x f ,则当0<x 时,_____)(=x f . 15.关于下列命题:
①若函数x
y 2=的定义域是{}0|≤x x ,则它的值域是}1|{≤y y ;
② 若函数x y 1=
的定义域是}2|{>x x ,则它的值域是
}21
|{≤y y ; ③若函数2
x y =的值域是}40|{≤≤y y ,则它的定义域一定是}22|{≤≤-x x ;
④若函数x y 2log =的值域是}3|{≤y y ,则它的定义域是}80|{≤<x x . 其中不正确的命题的序号是_____________( 注:把你认为不正确的命题的序号都填上).
三、解答题(要有详细的解答或证明过程,共40分, 请将答案填写在答题卷上) 16. (本题满分10分)化简或求值:
(1)
2
;
(2)()2
81lg 500lg lg 6450lg 2lg 552
+-++.
17.(本题满分10分)
已知集合{}{}{}37,210,A x x B x x C x x a =≤≤=<<=<。
(1)求A B ⋃;(2)求()R C A B ⋂;(3)若A C ⊆,求a 的取值范围.
18. (本题满分10分)
画出函数12)(2--=x x x f 的图像,并写出该函数的单调区间与值域.
19. (本题满分10分)
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需维护费150元,未租出的车每月需维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益为多少?
附加题(本大题共两个小题,每个小题10分,满分 20分,省级示范性高中要 把该题成绩计入总分,普通高中学生选作)
20.已知x
x x f 1
)(-=,
(1)判断函数在区间(-∞,0)上的单调性,并用定义证明; (2)画出该函数在定义域上的图像.(图像体现出函数性质即可)
21.已知函数),,0()(2
R c R b a c bx ax x f ∈∈>++=,若函数)(x f 的最小值是
0)1(=-f ,且1)0(=f ,对称轴是1-=x ,⎩⎨⎧<->=0
),(0
),()(x x f x x f x g .
(1)求)(x f 的解析式; (2)求)2()2(-+g g 的值;
(3)在(1)的条件下求)(x f 在区间[])(2,R t t t ∈+上的最小值.
焦作市2010-2011学年(上)必修模块(1)水平测试
数学答题卷
一、选择题
二、
11. 12.
13. 14. 15. 三、解答题
16.
17.
18.
19.
得 分 评卷人
得 分 评卷人
附加题 20.
21.
焦作市2010-2011学年(上)必修模块(1)水平测试
数学答案
一、选择题
ADDBA CABCD 二、填空题
11. 2; 12.(1,2); 13.[],33-; 14.-x --1; 15.①②③ 三、解答题 16解:(1)1a - …………………………………………………………5分 (2)52 ……………………………………………………………………10分 17.解:(1)
{}
210A B x x ⋃=<< ……………………………………3分
(2){}37RA C x x x =<>或…………………………………………………5分
(C R A )∩B=(2,3)∪(7,10) ……………………………………………7分 (3)a ﹥7 ………………………………………………………………10分 18.解:
⎪⎩⎪⎨⎧<-+≥--=--=0
,120,1212)(2
22
x x x x x x x x x f …………………………3分
图略. ………………………………………………………………7分 单调增区间为(-1,0),(1,+∞) ,单调减区间为(-∞,-1),(0,1),
值域为[)∞+-,
2 ………………………………………………………………10分
19.解:(1)当每辆车月租金为3600元时,未租出的车辆数为12
503000
3600=-,所以这时租出了88辆. ……………………………3分 (2)设每辆车的月租金定为x 元,则公司月收益为
50
503000
)150)(503000100()(⨯-----=x x x x f ………………6分
整理得:307050
)4050(501
2100016250)(22+--=-+-=x x x x f ……8分
所以当4050=x 时,)(x f 最大,最大值为307050)4050(=f 元 ……10分
附加题
20.解:(1)函数)(x f 在(-∞,0)上递增. ………………………1分
证明略. ………………………………………………………… 8分 (2)图略. ………………………………………………………10分
21.解:(1) 2
)1()(+=x x f ……………………………4分
(2)8 …………………………………………………………7分
(3)
⎪⎩⎪
⎨⎧-≥+-<<--≤+=1,)1(13,03,)3()(22min
t t t t t x f ……………………… ……10分。
