【加速老化实验】,加速老化试验计算公式
医疗包装加速老化试验
acclerated aging testing for medical packaging
Ref. Hemmerich, Karl. “General Aging Theory and Simplified Protocol for Accelerated Aging of Medical Devices”
使用加速老化实验包含某些风险
如果对包装系统了解不多，则应该使用 保守的加速老化因子（通常取2.0）
acclerated aging testing for medical packaging
6
加速老化理论
材料总是会受外界因素影响的 按照Arrhenius理论的推断，导致材料老化的 化学反应会随着温度的增加而加剧，并且加速 规律符合一定的比例因子Q10 精确确定Q10 是个非常复杂的过程，需要材料 反应的动力学模型 所以在MDSP中，一般使用一个比较保守的 Q10 ，如2.0
acclerated aging testing for medical packaging
13
加速老化理论注意事项（一）
温度超过50oC时，反应速率与温度的 关系可能就不再是成线性比例的
含有多种成份的材料的加速老化反应 速率可能也是多种的
acclerated aging testing for medical packaging 14
由此，
AATD
acclerated aging testing for medical packaging
10
举个例子
假如产品设计的有效期是三年，而预定的 加速老化实验是55oC， 加速老化因子Q10 取 2 ，AATD 计算如下：
AAR = Q10
((55-22)/10)
热加速试验
产品寿命及平均故障间隔时间 通过提高外加应力（温度、湿度），来加快产品老化速度，使产品在短时间内完成整个寿命过程。
加速系数在试验条件下运行时间与正常使用条件下时间的比值。
一般使用Arrhenius 经验公式：AF=K *⎥⎦⎤⎢⎣⎡-1101T T k Ea e K (湿度)=B ie ie RH RH ⎥⎦⎤⎢⎣⎡1,0,其中：K 为固定值，在我们的试验中为湿度加速系数Ea 为电子激活能（单位 ev ）一般从0.3~1.2中选取。
我们选0.8ev 。
K 波尔兹曼常数 8.617*10-5ev/KT0 加速温度（单位：开尔文）T1 正常使用温度RH ie,0 为加速湿度RH ie,1 为正常使用湿度B 为常数一般为2 ，我们选择2.66根据上面公式，我们在80℃，90%RH 条件下（设定正常使用条件为：25℃，45%RH ），加速度AF=807。
MTBF,即平均无故障时间，英文全称是“Mean Time Between Failure”。
是衡量一个产品（尤其是电器产品）的可靠性指标。
单位为“小时”。
它反映了产品的时间质量，是体现产品在规定时间内保持功能的一种能力。
具体来说，是指相邻两次故障之间的平均工作时间，也称为平均故障间隔。
它仅适用于可维修产品。
同时也规定产品在总的使用阶段累计工作时间与故障次数的比值为MTBF 。
公式为：MTBF min =)22(**22+r a X AF T 其中： T 为所有器件总时间 = 试验产品个数*单个产品试验时间 （单位：小时）AF 加速系数，我们试验条件计算为807。
)22(2+r a X 为X 2 分布，和置信度有关(r 为失效个数)。
我们选取90%置信度。
左图为在90%的置信度情况，加速度807试验条件下，10片样品试验，失效个数与产品平均故障间隔时间（MTBF ）的关系。
我们保证时间为10年，但客户按20年计算。
我们按照20年换算20*365.24=175,000小时。
高温老化的时间计算
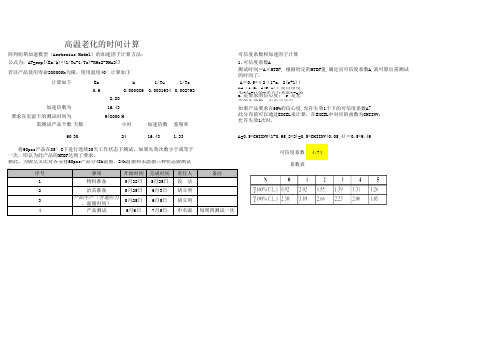
60 30
24
16.43
1.33
A=0.＝0.5*9.49
将60pcs产品在85°C下进行连续30天工作状态下测试，如果失效次数小于或等于
一次，即认为此产品的MTBF达到了要求。
据此，为做交叉比对各安排60pcs产品分48h温循、24h温循和未温循三种状态做测试
。
序号
事项
开始时间 完成时间 责任人
1
物料准备
5月22日 5月25日 段 洁
2
治具准备
5月25日 6月3日 胡立明
3
产品生产（含退应力 、温循时间）
5月25日
6月5日
胡立明
4
产品测试
高温老化的时间计算
阿列纽斯加速模型（Arrhenius Model）的加速因子计算方法： 公式为：AF=exp{(Ea/k)*(1/Tu-1/Ts)+RHs2-RHu2)}
若以产品使用寿命200000h为限，使用温度40°计算如下
计算如下 加速倍数为
Ea
k
1/Tu
1/Ts
0.6
0.000086 0.0031934 0.002792
6月6日 7月5日 申名淑
备注 每周四测试一次
可信度系数 4.74 系数表
2.80
16.43
要求在室温下的测试时间为 需测试产品个数 天数
948000 H 小时
加速倍数 鉴别率
可信度系数和加速因子计算
1.可信度系数A 测试时间＝A×MTBF, 根据给定的MTBF值,确定出可信度系数A,就可算出需测试 的时间了.
加速老化试验预测橡胶使用寿命(自己翻译过来的)
加速试验预测橡胶组件的使用寿命（翻译的）摘要：橡胶材料的性能及橡胶组件使用寿命的预测、估算在橡胶组件的设计过程中有着重要的作用。
我们通过加速老化试验和模拟相结合的办法，对橡胶材料在氧气环境中的寿命预测做了很多年的研究。
这篇论文研究了热老化对橡胶性能的影响，同时也对冷冻机用三元乙丙橡胶（EPDM），丁腈橡胶（NBR）橡胶组件的使用寿命进行了预测。
实验结果表明橡胶组分影响着橡胶的交联密度；老化时间及活化能可以很好的用以描述老化行为；通过单轴拉伸试验得到应力应变曲线。
为了预测EPDM，NBR的使用寿命，对这两种橡胶做了50℃到100℃，1天到180天的加速老化试验，并测试了一系列的物理性能试验。
通过阿伦尼乌斯方程进行了计算，并通过压缩永久变形试验，本文提出了一系列方程用以预测橡胶材料使用寿命。
关键词：加速试验，丁腈橡胶，活化能，交联，三元乙丙橡胶，热老化，寿命预测，橡胶材料。
符号缩写：C.S 压缩永久变形；d0 样品的厚度；d1压缩状态下样品厚度；d2 卸载后厚度k 交联密度变化程度；（K）T 反应速率；A，B 常数；E 反应活化能；R 气体常数；T 绝对温度I 前言橡胶是一种最为通用的材料，有着广泛的用途，甚至很难说清它到底有多少用途。
从普通的家用，商用，汽车制造等到高尖端的航天航空工业都有橡胶的身影。
许多橡胶组件在使用中需要承受一定的机械力作用，为了保证橡胶组件的安全性和可靠性，使用寿命的预测估算是一项关键技术。
如何防止橡胶组件在使用过程中损坏是一个关键问题。
橡胶组件在使用过程中承受着一定的载荷，还受到温度，辐射以及一些其它的有害物质的影响。
所有的影响因素结合在一起，导致了橡胶物理及化学结构的改变，最终表现为橡胶机械性能的降低。
橡胶在使用了一段时间后，开始老化，通常表现为挺性增加，阻尼性能下降。
老化不光光影响了性能，同时也影响了组件的使用寿命。
橡胶组件所处环境的不同，使得它们的降解方式也不一样。
橡胶组件的逐步老化降解，不仅与外部因素有关，同时与橡胶基体本身以及橡胶里面的添加剂有关。
医疗器械加速老化试验验证资料模板
×××包装加速老化试验验证方案1.0目的：通过加速老化试验来验证产品包装的储存期限为2年。
2.0适用范围：本规程适用于一次性血液净化体外循环×××产品的加速老化试验。
3.0职责：3.1研发部负责方案的制定和试验的最终报告。
3.2质量保证部人员负责验证过程的操作监控并记录。
3.3质量保证部负责验证产品的检测。
4.0工作程序：4.1概况：由于我公司产品包装的有效期要求2年，进行实时老化及留样观察时间2年太长，对产品包装的有效期2年内不能做出客观科学的评价，患者和制造商均存在一定的风险。
而ASTM F1980-02提供了一个科学的方法：加速老化试验，该试验能在较短的时间内对产品的包装在2年的有效期内做出客观科学的评价，从而将患者和制造商的风险降到最低。
4.2引用标准：4.2.1无菌医疗器械包装加速老化标准指南ASTM F1980-02，YY/T 0681.1-2009无菌医疗器械包装试验方法第1部分：加速老化试验指南；4.2.2YZB/国—2013 《一次性使用血液净化体外循环×××》；4.2.3GB/T16886.1-2011 医疗器械生物学评价第1部分：风险管理过程中的评价与试验；4.2.4 ISO11607-1，-2：2006 最终灭菌医疗器械的包装；4.2.5 YY/T 0681.1-2009 无菌医疗器械包装试验方法第1部分：加速老化试验指南；4.3试验原理与要求：4.3.1试验原理：加速老化技术以假设材料变质的化学反应遵循Arrhenius反应速率定律为基础。
4.3.2试验要求：4.3.2.1仪器：恒温箱（±1℃），无菌检测系统，温湿度计，计时器。
注：计量器具均经过法定鉴定部门的校验并取得合格证书。
4.3.2.2试验条件：环境温度25℃，相对湿度62%（资料显示该条件较严谨科学）。
4.3.2.2抽样计划：从同一批次中灭菌后抽样63套做加速老化试验，每隔30天抽18套样品作全性能检测，最后剩余27套继续作加速老化试验，到期后做全性能检测及包装完好性检测。
加速寿命试验公示计算汇总
加速寿命试验公示计算汇总一、前言新研究的医疗器械在上市前应确保在储存期( 通常 1 到5 年) 内产品的质量不应发生任何影响安全性和有效性变化，新产品一般没有实时和储存周围环境条件下确定有效期的技术资料。
如果按实际储存时间和实际环境储存条件进行检测需要很长的时间才能获得结果，为了在实时有效期结果获得以前，有必要进行加速老化实验提供确定有效期的实验数据。
医疗器械设计人员能够准确地预计聚合物性能的变化对于医疗器械产业化是非常重要的。
建立聚合物材料退行性变的动态模型是非常困难和复杂的，事实上材料短期产生的变化或变性的单速率表达形式可能不能充分反映研究的产品或材料在较长有效期的真实情况。
为了设计试验方案能准确模拟医疗器械时间相关的退行性变，有必要对材料的组成、结构、成品用途、组装和灭菌过程的影响、失效模型机制和储存条件有深入的了解。
一个给定的聚合物具有以各种方式( 晶体、玻璃、不定形等) 组成的许多化学功能基团，并含有添加剂如抗氧化剂、无机充填剂、色素和加工助剂。
所有这些变量的总和结合产品使用和储存条件变量决定了材料的化学性能的退行性变。
得庆幸的是，生产医疗器械的大部分都是采用常用的几种高分子材料，这些材料已经广泛使用并且都进行了良好的表征。
根据以碰撞理论为基础的阿列纽斯(Arrhenius) 模型建立的老化简化实验方案(Simplified Protocol for Accelerated Aging) ，也称“10 度原则”(10-degree rule) ，可在中度温度范围内适用于良好表征的聚合物，试验结果可以在要求的准确度范围内。
医疗器械或材料的老化是指随着时间的延长它们性能的变化，特别是与安全性和有效性有关的性能。
加速老化是指将产品放置在比正常储存或使用环境更严格或恶劣的条件下，在较短的时间内测定器械或材料在正常使用条件下的发生变化的方法。
采用加速老化实验合格测试的主要原因是可以将医疗器械产品尽早上市。
胶体金试纸加速老化实验
胶体金试纸加速老化实验
为了解决保质期的问题，需要将试纸放置于高温环境下烘烤的加速老化试验。
大多数文献资料里面只有"37度2个月=常温下2年"，"45度一个月=常温下2年" 的一个概念描述，没有明确的技术资料，那么这个实验的原理是什么？实验应该如何设计？结果应该如何分析？
37度或45度老化试验的原理来源于阿伦尼乌斯公式（Arrhenius equation），由瑞典的阿伦尼乌斯所创立，表示化学反应速率常数( k )对温度( T )的依赖关系的经验公式。
Ea为表观活化能（约等于19.5 Kcal/mol），R为摩尔气体常量。
变化趋势为T增大，一般k也增大。
可以计算出对应的温度与老化天数关系。
提取常用的数值，25度下保存一年，相当于37度老化91天，相当于45度老化37天。
因此在实验设计中有两个因素需要考虑，1、时间；2、温度。
另外有条件的话可以在做25度之前先模拟货物运输过程中的温度，然后再进入25度常温存储。
即要先将试纸分别放入两个条件，这样更接近真实情况。
1、放入55度烘烤2天，模拟运输过程过热；
2、3次冷冻到复融的循环，模拟冷冻运输的状态。
测试结果分析的主要方法就是灵敏度曲线的绘制。
灵敏度曲线的变化规律应该是在刚开始加烘时灵敏度上升，主要原因是外界高温为免疫反应提供了更多活化能，导致反应更容易进行。
随着加烘时间的增长，抗原抗体开始老化，灵敏度回归到正常水平，然后一直维持该正常水平到老化期将结束时。
在接近保质期极限时，灵敏度曲线呈快速下降趋势，最终归到零点。
老化 测算 模型 公式
老化测算模型公式
老化是一个复杂的生物学过程，涉及多种因素，包括基因、环境和生活方式。
在科学研究中，人们尝试使用各种模型和公式来测算老化的速度和影响因素。
其中一种常见的模型是老化速度的指数模型，该模型假设老化速度随着年龄的增长呈指数增加。
公式可以表示为A = B (C^t)，其中A代表生物体的某种老化指标，B是一个常数，C是一个大于1的常数，t代表年龄。
这种模型和公式可以用来研究老化的趋势和预测生物体的老化速度。
除了指数模型，还有其他模型和公式被用来测算老化。
例如，线性模型假设老化速度随着时间线性增加，可以用公式A = B + Ct 来表示，其中A代表老化指标，B和C是常数，t代表年龄。
此外，还有许多复杂的生物学模型，涉及到细胞衰老、基因表达和环境因素等多个方面，以更全面地理解老化过程。
在实际应用中，科学家们还会结合实验数据和统计分析来验证和改进这些模型和公式，以更准确地测算老化速度和影响因素。
总的来说，老化的测算模型和公式是一个复杂而多样化的领域，需要综合考虑生物学、数学和统计学等多个学科的知识，以全面理解和预测老化过程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【加速老化实验】,加速老化试验计算公式【加速老化实验】加速老化试验计算公式加速寿命试验寿命试验(包括截尾寿命试验)方法是基本的可靠性试验方法。
在正常工作条件下，常常采用寿命试验方法去估计产品的各种可靠性特征。
但是这种方法对寿命特别长的产品来说，就不是一种合适的方法。
因为它需要花费很长的试验时间，甚至来不及作完寿命试验，新的产品又设计出来，老产品就要被淘汰了。
所以这种方法与产品的迅速发展是不相适应的。
经过人们的不断研究，在寿命试验的基础上，找到了加大应力、缩短时间的加速寿命试验方法。
加速寿命试验是用加大试验应力(诸如热应力、电应力、机械应力等)的方法，加快产品失效，缩短试验周期。
运用加速寿命模型，估计出产品在正常工作应力下的可靠性特征。
下面就加速寿命试验的思路、分类、参数估计方法及试验组织方法做一简单介绍。
1 问题高可靠的元器件或者整机其寿命相当长，尤其是一些大规模集成电路，在长达数百万小时以上无故障。
要得到此类产品的可靠性数量特征，一般意义下的载尾寿命试验便无能为力。
解决此问题的方法，目前有以下几种：（１）故障数r=0的可靠性评定方法。
如指数分布产品的定时截尾试验θL=2S(t0)2χα(2)22S(t)χαα00为总试验时间。
为风险, =0.1时，.1(2)=4.605≈4.6；当α=0.05时，χ02.05(2)=5.991≈6。
（２）加速寿命试验方法如，半导体器件在理论上其寿命是无限长的，但由于工艺水平及生产条件的限制，其寿命不可能无限长。
在正常应力水平S0条件下，其寿命还是相当长的，有的高达几十万甚至数百万小时以上。
这样的产品在正常应力水平S0条件下，是无法进行寿命试验的，有时进行数千小时的寿命试验，只有个别半导体器件发生失效，有时还会遇到没有一只失效的情况，这样就无法估计出此种半导体器件的各种可靠性特征。
因此选一些比正常应力水平S0高的应力水平S1，S2，…，Sk，在这些应力下进行寿命试验，使产品尽快出现故障。
（３）故障机理分析方法研究产品的理、化、生微观缺陷，研究缺陷的发展规律，从而预测产品的故障及可靠性特征量。
2 加速寿命试验的思路由产品故障的应力—强度模型（见图5-5）图5-5 应力—强度模型其中：R(t)=P(强度＞应力)，F(t)=P(应力≥强度)当强度与应力均为确定型时，产品在t2故障。
实际上强度与应力是概率风险型的，当均服从正态分布时，产品则可能提前在t1，以一定概率发生故障。
由此可知：要使产品早一点出现故障，要么加大应力，要么减少强度。
因当产品一经加工形成后，其强度也就基本固定了，所以可行的办法是提高应力，以缩短寿命试验周期。
3 加速寿命试验的分类通常分为以下三种：（1）恒定应力加速寿命试验(目前常用)．它是将一定数量的样品分为几组，每组固定在一定的应力水平下进行寿命试验，要求选取各应力水平都高于正常工作条件下的应力水平。
试验做到各组样品均有一定数量的产品发生失效为止，如图5-6所示。
（2）步进应力加速寿命试验。
它是先选定一组应力水平，譬如是S1，S2，…，Sk，它们都高于正常工作条件下的应力水平S0。
试验开始是把一定数量的样品在应力水平S1下进行试验，经过一段时间，如t1小时后，把应力水平提高到S2，未失效的产品在S2应力水平继续进行试验，如此继续下去，直到一定数量的产品发生失效为止，如图5-7所示。
（3）序进应力加速寿命试验。
产品不分组，应力不分档，应力等速升高，直到一定数量的故障发生为止。
它所施加的应方水平将随时间等速上升，如图5-8所示。
这种试验需要有专门的设备。
图5-6 恒定应力图5-7 步进应力图5-8 序进应力在上述三种加速寿命试验中，以恒定应力加速寿命试验更为成熟．尽管这种试验所需时间不是最短，但比一般的寿命试验的试验时间还是缩短了不少．因此它还是经常被采用的试验方法。
目前国内外许多单位已采用恒定应力加速寿命试验方法来估计产品的各种可靠性特征，并有了一批成功的实例。
下面主要介绍如何组织恒定应力加速寿命试验及其统计分析方法，包括图估计和数值估计方法。
4 恒定应力加速寿命试验的参数估计产品不同的寿命分布应有不同的参数估计方法，下面以威布尔寿命分布的产品为例说明，其他寿命分布的估计问题可参考有关文献。
4.1 基本假定在恒定应力加速寿命试验停止后，得到了全部或部分样品的失效时间，接着就要进行统计分析。
一定的统计分析方法都是根据产品的寿命分布和产品的失效机理而制定的。
因此一个统计分析方法成为可行就必须要有几项共同的基本假定。
违反了这几项基本假定，统计分析的结果就不可靠，也得不到合理的解释。
因为这几项基本假定是从不少产品能够满足的条件中抽象出来的，所以这几项基本假定对大多数产品来说不是一种约束，只要在安排恒定应力加速寿命试验时注意到这几项基本假定，它们就可以被满足。
（１）设产品的正常应力水平为S0，加速应力水平确定为S1,S2，…，Sk，则在任何水平i下，产品的寿命都服从或近似服从威布尔分布，其间差别仅在参数上。
这一点可在威布尔概率纸上得到验证。
其分布函数为 S⎛tiFTi(ti)=1−exp⎜⎜−ηi⎝（２）在加速应力S1,S2，…，理是相同的。
⎞⎟⎟⎠，ti≥0，i=0,1,2,....,k miSk下产品的故障机理与正常应力水平S0下的产品故障机m0＝m1＝m2 因为威布尔分布的形状参数m的变化反映了产品的故障机理的变化，故有＝…＝k。
这一点可在威布尔概率纸上得到验证。
若不同档次的加速应力所得试验数据在威布尔概率纸上基本上是一族平行直线，则假定（２）就满足了。
（３）产品的特征寿命η与所加应力s有如下关系：mlnη=a+bϕ(s)a，b是待估参数，ϕ(s)是应力s的某一已知函数，上式通常称为加速寿命方程。
此假定是根据阿伦尼斯方程和逆幂律模型抽象出来的：E1Elnη=lnβ+[]KTKT ∵ η=βe，∴Eα=lnβ,b=K，则有lnη=a+bϕ(T) 令1η=dVc 又∵∴ lnη=−lnd−clnV令 a=−lnd,b=−c则lnη=a+bϕ(V)国内外大量实验数据表明，不少产品是可以满足上述三项基本假定的，也就是说对不少产品是可以进行恒定应力加速寿命试验的。
4.2 图估法(威布尔分布)步骤：① 分别绘制在不同加速应力下的寿命分布所对应的直线。
② 利用威布尔概率纸上的每条直线，估计出相应加速应力下的形状参数mi 和特征寿命ηi。
③ 由假定（２）取k个mi的加权平均，作为正常应力S0的形状参数m0的估计值，即：ˆ0=m诸ˆ1+n2mˆ2+....+nkmˆkn1mn1+n2+...+nk ni为第i个分组中投试的样品数。
④ 由假定（３），在以ϕ(s)为横坐标，以lnη为纵坐标的坐标平面上描点，根据k个点 (ϕ(s1)，lnη1),(ϕ(s2)，lnη2),…，(读出正常应力ϕ(sk)，lnηk)配置一条直线，并利用这条直线，ˆmˆηˆ0ˆS0下所对应的特征寿命的对数值lnηη，取其反对数，即得ηo 的估计值0。
⑤ 在威布尔概率纸上作一直线Lo，其参数分别为0和0。
⑥ 利用直线Lo，在威布尔概率纸上对产品的各种可靠性特征量进行估计。
5 恒定应力加速寿命试验的组织当我们随机地从一批产品中任取n个样品，分成k组，在k个应力水平下进行恒加试验时，必须事前作周密考虑，慎重仔细地做好试验设计、安排、组织工作，因为恒加试验要花费较多的人力、物力、时间，事先考虑周到才能得到预期效果。
在组织工作和实施过程中应注意以下几个方面。
5.1 加速应力S的选择因为产品的失效是由其失效机理决定的，因此就要研究什么应力会产生什么样的失效机理，什么样的应力加大时能加快产品的失效．根据这些研究来选择什么应力可以作为加速应力。
通常在加速寿命试验中所指的应力不外乎是机械应力(如压力、振动、撞击等)，热应力(温度)，电应力(如电压、电流、功率等)。
在遇到多种失效机理的情况下，就应当选择那种对产品失效机理起促进作用最大的应力作为加速应力。
如温度对电子元件的加速作用，可用“阿伦尼斯方程”描述，即寿命为t=βe式中:β――是个正常数，β＞０-4EkT k――玻尔兹曼常数，k＝0.8617×10ev/KT――绝对温度E――激活能（ev）直流电压对电容器等的加速作用，可用逆幂率描述即寿命t=d,c为正常数，d0,c0经验数据为c=5。
经验还表明：灯泡与电子管灯丝的寿命大约与电压的13次方成反比，如此等等。
值得注意的是：对于电子元器件“温度+振动”这种组合应力，更能加速其故障的出现，只是在统计处理上要困难一些。
1dVc5.2 加速应力水平S1,S2，…，Sk的确定在恒加试验中，安排多少组应力为宜呢?k取得越大，即水平数越多，则求加速方程中两个系数的估计越精确。
但水平数越多，投入试验样品数就要增加，试验设备、试验费用也要增加，这是一对矛盾。
在单应力恒加试验中一般要求应力水平数五不得少于4，在双应力恒加试验情况下，水平数应适当再增加。
确定加速应力水平S1＜S2＜…＜Sk的一个重要原则，就是在诸应力水平Si 下产品的失效机理与在正常应力水平S0下产品的失效机理是相同的。
因为进行加速寿命试验的目的就是为了在高应力水平下进行寿命试验，较快获得失效数据，估计出可靠性指标，再利用加速方程外推正常工作应力S0下产品的可靠性指标。
假如在加速应力水平S1,S2，…，Sk和正常应力水平S0下产品的失效机理有本质不同，那么外推将有困难，所以在确定应力水平S1,S2，…，Sk时，违背这条原则将会导致加速寿命试验的失败。
最低应力水平S1的选取，应尽量靠近正常工作应力S0，这样可以提高外推的精度，但是S1又不能太接近S0，否则收不到缩短试验时间的目的。
最高应力水平Sk应尽量选得大一些，但是应注意不能改变失效机理，特别不能超过产品允许的极限应力值。
如要估计晶体管常温下的储存寿命，提高储存温度是一个方法，在常温储存时，管芯表面的化学变化是导致晶体管故障的故障机理，温度升高，肯定加速其变化。
但当温度升得过高时，会引起焊锡灰化，内引线脱落开路等新的故障机理，于是温度便不能选的过高。
合理的确定S1和Sk需有丰富的工程经验与专业知识，也可以先作一些试验后再确定S1和Sk确定了S1和Sk后，中间的应力水平S2，…，Sk−1应适当分散，使得相邻应力水平的间隔比较合理。
一般有下列三种取法：（1）k个应力水平按等间隔取值；（2）温度按倒数成等间隔取值 1111−=(j−1)∆∆=(−/(k−1)TT1T1Tk ， j，j=2,3,L,k−1（3）电压V按对数等间隔取值∆=(lnVk−lnV1)/(k−1)，lnVj=lnV1+(j−1)∆，j=2,3,L,k−15.3 试验样品的选取与分组整个恒加试验由k组寿命试验组成，每个寿命试验都要有自己的试验样品，假如在应力水kn=∑ninSi=1。