加速寿命计算公式(可靠性)
产品可靠性加速试验的加速试验有关标准
产品可靠性加速试验的加速试验有关标准加速试验有关标准阿伦尼斯模型是化学家阿列尼乌斯于1880年在大量的化学反应数据基础上总结出来的，它表明在化学反应过程中反应速率与反应温度的关系kT E a Ae dtdM /-=——化学反应速率 ——常数 ——引起失效或退化过程的激活能 ——玻尔兹曼常数——热力学温度dtdMAaE k T令t=t 1-t 0阿伦尼斯斯模型的变换dtAe dM Ae dt dM kTE kT E a a //--=⇒=⎰⎰-=110/t t kT E M M dt Ae dM a 当器件在t 0时刻处于正常状态数M 0，t 1时刻处于失效状态数为M 1，如果温度与时间无关，则积分上式得：)(01/01t t Ae M M kT E a -=--kTE a e A M M t /01-=Tb a T e k E A M M t a //)lg /(lg lg 01+=+-=寿命与温度关系—阿列尼乌斯模型激活能与温度、寿命的关系T b a T e k E AM M t a //)lg /(lg lg 01+=+-=激活能越大、曲线倾斜越大、与温度的关系越密切！！加速系数加速系数的计算方法：]1exp[)()(101100T T k E F t F t a -==τ设在基准应力条件下做试验达到累积失效概率F 0所需要的时间为t 0（F 0），施加某种应力条件下进行加速寿命试验达到相同的累积失效概率所需的时间为t 1（F 0），则两者的比值即为加速系数。
激活能越大、加速系数越大、越容易被加速失效，加速试验效果越明显。
激活能与加速系数的关系]1exp[)()(101100T T k E F t F t a -==τ阿列尼乌斯模型的局限：只考虑了温度应力对物质的化学与物理性质变化的影响。
实际上，很多的物理理象和化学反应过程，除了与温度有关之外，还与此时很多非温度应力因素如电压、湿度、机械应力等密切相关。
加速寿命计算公式(可靠性)
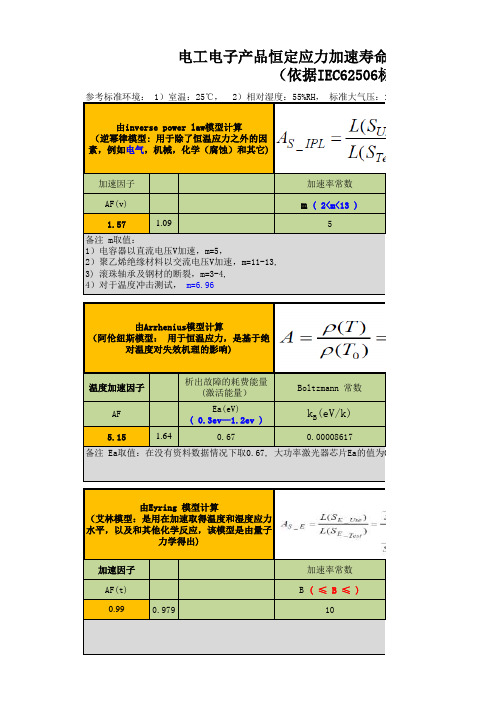
电工电子产品恒定应力加速寿命试验-加速因子计 （依据IEC62506标准）
参考标准环境： 1）室温：25℃， 2）相对湿度：55%RH， 标准大气压：101.3 kPa。
由inverse power law模型计算 （逆幂律模型: 用于除了恒温应力之外的因 素，例如电气，机械，化学（腐蚀）和其它)
加速因子
AF(v)
1.57
1.09
备注 m取值： 1）电容器以直流电压V加速，m=5， 2）聚乙烯绝缘材料以交流电压V加速，m=11-13, 3) 滚珠轴承及钢材的断裂，m=3-4, 4）对于温度冲击测试， m=6.96
加速寿命试验-加速因子计算 62506标准）
准大气压：101.3 kPa。
实际使用应力
SUse
16
加速（测试）使用应力
STest
17.5
正常工作的温度
片Ea的值为0.52.
T0(℃) 25
加速（测试）应力的温度 T(℃) 45
实际使用应力
SE-Use
298
加速（测试）使用应力
SE-Test
302
8.1
1240.2
品结构），使用应力条件，加速应力测试条件和相关的失效机理。 ）中的待测物都有自己的加速因子和测试条件（如占空比，应力水 因素。
荷（如温度，温度循环和温度变化率），化学负荷（如潮湿，腐蚀 流，功率）和机械负载（例如，准静态周期性机械 荷的组合。组合负荷的结果分析和结果到生命周期条件的外推需要定 坏的贡献。
加速寿命试验理论依据
加速寿命试验理论依据加速试验电子元器件的失效原因与器件本身所选用的材料、材料之间、器件表面或体内、金属化系统以及封装结构中存在的各种化学、物理的反应有关。
器件从出厂经过贮存、运输、使用到失效的寿命周期，无时无刻不在进行着缓慢的化学物理变化。
在各种外界环境下，器件还会承受了各种热、电、机械应力，会使原来的化学物理反应加速，而其中温度应力对失效最为敏感。
实践证明，当温度升高以后，器件劣化的物理化学反应加快，失效过程加速，而Arrhenius模型就总结了由温度应力决定的化学反应速度依赖关系的规律性，为加速寿命试验提供了理论依据。
1. 以温度应力为加速变量的加速方程由Arrhenius总结的经验公式如下（8.5）式中，dM/dt是化学反应速率，A是常数，E a是引起失效或退化过程的激活能，k是玻尔兹曼常数，T是绝对温度。
当器件在t0时刻处于正常状态数为M0，到t1时刻，器件处于失效状态数为M1。
如果温度与时间无关，则积分式（8.1）得（8.6）令DM=M1-M0，t=t1-t0，得到（8.7）取对数（8.8）可写成（8.9）其中（8.10）上式就是根据Arrhenius模型得到的以温度应力为加速度变量的加速方程。
用此方程来解释器件的高温贮存寿命试验是非常成功的。
式中，t表示器件产品达到某一F(t)的时间，它的对数与绝对温度的倒数成线性关系。
若用t～1/T单边对数坐标纸绘图，则可得到一条直线，然后用图估计法或数值法推算出器件在不同温度下的寿命值。
由式（8.1）可计算得到方程的斜率b、截距α和激活能Ea ，当T1>T2时（8.11）激活能E a与方程的斜率b与器件的失效模式与失效机理有关。
根据多年来的实践积累，有关半导体器件与微电路不同失效模式与机理的激活能数据列于表8.8。
http://Kê。
图8.3 不同激活能时温度与寿命的关系以激活能E a作为参数，可以绘出不同E a时温度与寿命的关系，如图8.3所示。
电工电子产品加速寿命试验
电工电子产品加速寿命试验之一 1概述寿命试验是基本的可靠性试验方法，在正常工作条件下，常常采用寿命试验方法去评估产品的各种可靠性特征。
但是这种方法对寿命特别长的产品来说，不是一种合适的方法。
因为它需要花费很长的试验时间，甚至来不及作完寿命试验，新的产品又设计出来，新的产品又设计出来，老产品就要被淘汰了。
老产品就要被淘汰了。
老产品就要被淘汰了。
因此，因此，因此，在寿命试验的基础上形成的在寿命试验的基础上形成的加大应力、缩短时间的加速寿命试验方法逐渐取代了常规的寿命试验方法。
加大应力、缩短时间的加速寿命试验方法逐渐取代了常规的寿命试验方法。
加速寿命试验是用加大试验应力加速寿命试验是用加大试验应力((诸如热应力、电应力、机械应力等机械应力等))的方法，激发产品在短时间内产生跟正常应力水平下相同的失效，缩短试验周期。
然后运用加速寿命模型，评估产品在正常工作应力下的可靠性特征。
加速环境试验是近年来快速发展的一项可靠性试验技术。
该技术突破了传统可靠性试验的技术思路，将激发的试验机制引入到可靠性试验，可以大大缩短试验时间，提高试验效率，降低试验耗损。
，降低试验耗损。
2 常见的物理模型元器件的寿命与应力之间的关系，通常是以一定的物理模型为依据的，下面简单介绍一下常用的几个物理模型。
2.1失效率模型失效率模型是将失效率曲线划分为早期失效、随机失效和磨损失效三个阶段，并将每个阶段的产品失效机理与其失效率相联系起来，形成浴盆曲线。
该模型的主要应用表现为通过环境应力筛选试验，剔除早期失效的产品，提高出厂产品的可靠性。
厂产品的可靠性。
2.1 失效率模型图示：O1典型的失效率曲线规定的失效率规定的失效率随机失效随机失效早期早期失效失效磨损失效磨损失效t2.2应力与强度模型该模型研究实际环境应力与产品所能承受的强度的关系。
度的关系。
应力与强度均为随机变量，因此，产品的失效与否将决定于应力分布和强度分布。
随着时间的推移，产品的强度分布将逐渐发生变化，如果应力分布与强度分布一旦发生了干预，产品就会出现失效。
加速寿命推算
注意
文中提到的110‘c/85%的加速條件在 IEC60068-2-66中有提到，以作參考 文中提到的85‘c/85%的加速條件在GR1221中有提到，以作參考 如下附檔為IEC60068-2-66:
Microsoft Word 文件
加速壽命測試時間的推算
Pinging Han April. 17 2006
Key Words
阿倫尼斯分布(Arrhenius Model) 加速因子AF(Accelerated Factor) MTBF(Mean Time To Failure) 激活能Ea(0.8eV)
引言
某種產品，客戶要求在90%的信心度下其 MTBF為20000H,其單價較貴，只能提供 1Pcs的產品作測試以判定其可靠性是否符合 要求 則1Pcs產品，在常溫下的測試時間為 20000H 此時，一般采取加速試驗(高溫高濕)。目前 有兩種加速測試方案：110c/85%和 85c/85% 問：兩種方案各需多長測試時間可判定產品 的可靠性符合要求？ 為此舉例如下：
討論
需要注意的是： 1.Ea的取值(Ea=0.8eV), 是GR-1221中 的推薦值 2.這種換算的前提是產品在兩中老化模 式中的失效機理相同. 3.這種換算的基本假設是產品在高應力 條件下與在常溫時表現的特性是一致的。 4.一般情況下，我們會考慮它們老化機 理的不同，而分別對產品采用不同的測 試方案。
舉例
Ea根據材料的不同，有不同的取值，對於 光通訊產品，在GR-1221中， Ea=0.8eV(Damp Heat的參考值)， 1.則在110‘c85%RH下作測試1h,相當於在 25’c75%RH的加速倍數為： AF=exp{(0.8*10^5/8.6) [(1/298)-(1/383)] + (0.75^2-0.85^2)} =869 若允許1次失效，則在90%的置信度下，需 要測試的時間為 Ttest=A*MTBF(A=0.5*CHIINV(10.9,2*2)=3.89)
可靠性评价中的寿命试验方法分析_段鸿杰
过相似产品的售后信息、用户调 斯曼常数（8.617×10-5 eV /K），
查 ， 可 以 很 容 易 的 得 到 相 关 的 数 T-绝对温度，E α-析出故障的激活
据 。 这 些 数 据 为 进 一 步 的 产 品 开 能。
发提供了重要的参考。通过用户试 用或试运行等形式，可以完整的检 验设计方案的合理性、生产制造的 完善性、试验室试验的覆盖性等问 题。进一步发掘在设计开发、生产 经营、用户使用等全生命周期不同 环节中对产品可靠性和质量的完美 要求。
率密度函数，则常规条件下的概率 密度函数则是
（13）
在常规条件下的可靠度函数为 （14）
常规条件下危险度函数是
（15） 表1给出了转换后的可靠度函 数的几种分布，其中加速系数为 ε。
表1 不同分布利用加速系数进行 可靠度计算的函数
分布
常规条件下的可靠度函数
威布尔
对数正态
正态
指数
五、总结
应用寿命试验，是进行产品的 可靠性评价（鉴定、认证）的必要 组成部分。通过不同形式寿命试验 的合理组合，可以在生产研发、考 核定型、生产验证、质量检验、市 场监督等多个环节对产品的可靠性 进行合理的验证。寿命试验是可靠 性评价的重要依托。
5.机械裂纹模型 Coffin-Mason模型在处理材料 开裂、疲劳和变形的一个形式如 公式11。失效前的循环周期利用 下式计算：
【加速老化实验】,加速老化试验计算公式 加速老化试验计算公式
【加速老化实验】,加速老化试验计算公式加速老化试验计算公式【加速老化实验】加速老化试验计算公式加速寿命试验寿命试验(包括截尾寿命试验)方法是基本的可靠性试验方法。
在正常工作条件下，常常采用寿命试验方法去估计产品的各种可靠性特征。
但是这种方法对寿命特别长的产品来说，就不是一种合适的方法。
因为它需要花费很长的试验时间，甚至来不及作完寿命试验，新的产品又设计出来，老产品就要被淘汰了。
所以这种方法与产品的迅速发展是不相适应的。
经过人们的不断研究，在寿命试验的基础上，找到了加大应力、缩短时间的加速寿命试验方法。
加速寿命试验是用加大试验应力(诸如热应力、电应力、机械应力等)的方法，加快产品失效，缩短试验周期。
运用加速寿命模型，估计出产品在正常工作应力下的可靠性特征。
下面就加速寿命试验的思路、分类、参数估计方法及试验组织方法做一简单介绍。
1 问题高可靠的元器件或者整机其寿命相当长，尤其是一些大规模集成电路，在长达数百万小时以上无故障。
要得到此类产品的可靠性数量特征，一般意义下的载尾寿命试验便无能为力。
解决此问题的方法，目前有以下几种：（１）故障数r=0的可靠性评定方法。
如指数分布产品的定时截尾试验θL=2S(t0) 2χα(2) 22S(t)χαα00为总试验时间。
为风险, =0.1时，.1(2)=4.605≈4.6；当α=0.05时，χ02.05(2)=5.991≈6。
（２）加速寿命试验方法如，半导体器件在理论上其寿命是无限长的，但由于工艺水平及生产条件的限制，其寿命不可能无限长。
在正常应力水平S0条件下，其寿命还是相当长的，有的高达几十万甚至数百万小时以上。
这样的产品在正常应力水平S0条件下，是无法进行寿命试验的，有时进行数千小时的寿命试验，只有个别半导体器件发生失效，有时还会遇到没有一只失效的情况，这样就无法估计出此种半导体器件的各种可靠性特征。
因此选一些比正常应力水平S0高的应力水平S1，S2，…，Sk，在这些应力下进行寿命试验，使产品尽快出现故障。
可靠性-LED加速老化寿命试验方法概论
一、可靠性理论基础1.可靠度:如果有N个LED产品从开始工作到t时刻的失效数为n（t),当N足够大时，产品在t时刻的可靠度可近似表示为:随时间的不断增长,将不断下降。
它是介于1与0之间的数，即。
2.累积失效概率:表示发光二极管在规定条件下工作到t这段时间内的失效概率，用F（t)表示,又称为失效分布函数.如果N个LED产品从开始工作到t时刻的失效数为n（t），则当N足够大时，产品在该时刻的累积失效概率可近似表示为：3.失效分布密度：表示规定条件下工作的发光二极管在t时刻的失效概率。
失效分布函数的导函数称为失效分布密度，其表达式如下:•早期失效期；•偶然失效期(或稳定使用期）；•耗损失效期。
二、寿命老化：LED发光亮度随着长时间工作而出现光强或光亮度衰减现象。
器件老化程度与外加恒流源的大小有关，可描述为：B t为t时间后的亮度，B0为初始亮度。
通常把亮度降到B t=0。
5B0所经历的时间t称为二极管的寿命. 1。
平均寿命如果已知总体的失效分布密度f(t）,则可得到总体平均寿命的表达式如下：2. 可靠寿命可靠寿命T R是指一批LED产品的可靠度下降到r时，所经历的工作时间。
T R可由R（T R）=r求解,假如该产品的失效分布属指数分布规律，则：即可求得T R如下：3. 中位寿命中位寿命T0。
5指产品的可靠度R(t）降为50％时的可靠寿命，即:对于指数分布情况，可得：二、LED寿命测试方法LED寿命加速试验的目的概括起来有：•在较短时间内用较少的LED估计高可靠LED的可靠性水平•运用外推的方法快速预测LED在正常条件下的可靠度；•在较短时间内提供试验结果，检验工艺;•在较短时间内暴露LED的失效类型及形式，便于对失效机理进行研究，找出失效原因；•淘汰早期失效产品,测定元LED的极限使用条件1. 温度加速寿命测试法由于通常LED寿命达到10万小时左右，因此要测得其常温下的寿命时间太长，因此采用加速寿命的方法。
MTBF计算
可靠性相关术语
可靠度：用概率表示的产品的可靠性程度。 故障：产品不能执行规定功能的状态。 失效：是指产品丧失完成规定功能的能力的事件。不仅指
规定功能的完全丧失，亦包括规定功能的降低。 可靠性指标：亦称可靠性参数，描述产品可靠性的量。如
：产品的“寿命”，“使用寿命”,“储存寿命”，“储 存可靠性”，MTTF，MTBF。 可靠性的三大要素：耐久性，维修性，使用性。
1980年美国颁发的MIL-STD-785B将可靠性分为任务可靠 性和基本可靠性。任务可靠性：“产品在规定的任务 剖面内完成规定功能的能力”。它反映产品的执行任 务成功的概率，它只统计危及任务成功的致命故障。 基本可靠性：“产品在规定条件下，无故障的持续时 间或概率”。它包括了全寿命单位的全部故障，它能 反映产品维修人力和后勤保障要求。
MTTR
Mean Time To Repair 平均修复时间 产品从出故障到修复的非计 划维修及计划维修时间，即 修复一个故障元件所需的平 均时间间隔，是产品维修性 的一种基本参数。
产品修复时间的长短， MTTR的估计值为产品维修 时间数据的平均值。
维修性 维修性 小时
产品可靠度指标-指数分布
对于使用大多是标准化或已经发展成熟的零组件的电子产品而言， 均以MTBF值为其可靠度指标。
MTBF 计算公式
MTBF=AF*
AF：Accelerate Factor，加速因子 T：Total Power on Time，总的开机运行时间 X2(α,2r+2)：卡方公式 C：Confidential Level，信心度水平 α：生产者的冒险率，即：1-C r：失效数，Number of Failures
根据一定时间内故障数量 的多少而做成的测量，是 指不可修复产品的一种基 本可靠性参数。
加速寿命计算公式
加速寿命计算公式加速寿命计算公式是根据寿命和应力之间的关系来推导的。
它基于一种假设，即在短时间内，产品的失效是由物理或化学损伤引起的。
这种损伤是与应力的大小成正比的。
通过增大应力，可以加速损伤的积累过程，从而预测产品在正常使用条件下的寿命。
常见的加速寿命计算公式包括：1. 温度加速因子加速寿命计算公式：L2 = L1 * exp((Ea/R) *(1/T1 - 1/T2))其中，L1是产品在温度T1下的寿命，L2是产品在温度T2下的寿命，Ea是活化能（以焦耳为单位），R是气体常数，T1和T2分别是温度T1和T2对应的绝对温度。
2. 应力加速因子加速寿命计算公式：L2 = L1 * exp((1/H1 - 1/H2) * (σ2 - σ1))其中，L1是产品在应力σ1下的寿命，L2是产品在应力σ2下的寿命，H1是应力σ1对应的材料应力导致的损伤率，H2是应力σ2对应的材料应力导致的损伤率。
3. 湿度加速因子加速寿命计算公式：L2 = L1 * exp((θ2 - θ1) / n)其中，L1是产品在相对湿度θ1下的寿命，L2是产品在相对湿度θ2下的寿命，n是湿度对于寿命的指数。
需要注意的是，加速寿命计算公式只能作为一个估计值，因为在实际的产品使用中，可能会遇到非线性应力-寿命关系或其它未知因素，这些因素不能完全被加速寿命计算公式所考虑。
此外，加速寿命计算公式的准确性也取决于对环境因素和产品失效机理的理解。
因此，在实际使用中，需要结合实验数据和经验，对公式进行验证和修正，以提高计算的准确性。
总之，加速寿命计算公式是预测产品在正常使用条件下寿命的一种方法。
通过增大应力或改变环境条件，可以加速损伤的积累，从而预测产品在特定条件下的寿命。
但需要注意的是，加速寿命计算公式只能作为估计值参考，实际结果可能会受到实际环境和失效机理等因素的影响。
【加速老化实验】 加速老化试验计算公式
【加速老化实验】加速老化试验计算公式加速寿命试验寿命试验(包括截尾寿命试验)方法是基本的可靠性试验方法。
在正常工作条件下，常常采用寿命试验方法去估计产品的各种可靠性特征。
但是这种方法对寿命特别长的产品来说，就不是一种合适的方法。
因为它需要花费很长的试验时间，甚至来不及作完寿命试验，新的产品又设计出来，老产品就要被淘汰了。
所以这种方法与产品的迅速发展是不相适应的。
经过人们的不断研究，在寿命试验的基础上，找到了加大应力、缩短时间的加速寿命试验方法。
加速寿命试验是用加大试验应力(诸如热应力、电应力、机械应力等)的方法，加快产品失效，缩短试验周期。
运用加速寿命模型，估计出产品在正常工作应力下的可靠性特征。
下面就加速寿命试验的思路、分类、参数估计方法及试验组织方法做一简单介绍。
1 问题高可靠的元器件或者整机其寿命相当长，尤其是一些大规模集成电路，在长达数百万小时以上无故障。
要得到此类产品的可靠性数量特征，一般意义下的载尾寿命试验便无能为力。
解决此问题的方法，目前有以下几种：（１）故障数r=0的可靠性评定方法。
如指数分布产品的定时截尾试验θL=2S(t0)2χα(2)22S(t)χαα00为总试验时间。
为风险, =0.1时，.1(2)=4.605≈4.6；当α=0.05时，χ02.05(2)=5.991≈6。
（２）加速寿命试验方法如，半导体器件在理论上其寿命是无限长的，但由于工艺水平及生产条件的限制，其寿命不可能无限长。
在正常应力水平S0条件下，其寿命还是相当长的，有的高达几十万甚至数百万小时以上。
这样的产品在正常应力水平S0条件下，是无法进行寿命试验的，有时进行数千小时的寿命试验，只有个别半导体器件发生失效，有时还会遇到没有一只失效的情况，这样就无法估计出此种半导体器件的各种可靠性特征。
因此选一些比正常应力水平S0高的应力水平S1，S2，…，Sk，在这些应力下进行寿命试验，使产品尽快出现故障。
（３）故障机理分析方法研究产品的理、化、生微观缺陷，研究缺陷的发展规律，从而预测产品的故障及可靠性特征量。
可靠性试验介绍
常都被用于湿度加速试验。湿度很少被用作确认防潮的唯一加速因子， 而一般应用温度和湿度应力的组合。这为了促进湿度 （水） 的反应，并 导致增加湿度寿命的加速。 湿度相关寿命的一半公式表示如下：
： 寿命 A, n：常量 一直没有关于湿度相关寿命的标准化公式，与每个制造商使用他们自己
加速寿命实验
4.3.2 温度加速 温度对半导体的寿命影响是很大的，因此使用温度加速寿命的加速试验
的最常见的方法。 温度应力基于的反应是由空气统一，空气模型被广泛用于半导体产品寿
命预测 这种空气模型公式表示如下：
：寿命 Ea：活化能 (eV) T ：绝对温度 (K) A：常量 k ：波尔兹曼 系数
注意产品试验结束后应对样品有1～2小时的恢复期。
环境试验内容
冷热冲击试验与温度循环试验的区别
冷热冲击试验
温度变化速率 循环次数 热平衡
急剧20～30℃/min 5～10个循环（多至1000循环） 正好到达（液槽式为到达）
试验时间
短
用途
1.膨胀系数不同引起的连接部剥离
2.膨胀系数不同龟裂后水分进入
湿度对产品的影响：腐蚀、离子迁移、扩散、水解、爆裂、霉菌、
环境应力与失效的关系
湿度引起塑封半导体器件腐蚀的失效： 在硅片上集成有大量电子元件的集成电路芯片及其元件通过导线连接
起来构成电路。由于铝和铝合金价格便宜，加工工艺简单，因此通常被 使用为集成电路的金属线。从进行集成电路塑封工序开始，水气便会通 过环氧树脂渗入引起铝金属导线产生腐蚀进而产生开路现象，成为品质 工程最为头痛的问题。人们虽然通过各种改善包括采用不同环氧树脂材 料、改进塑封技术和提高非活性塑封膜为提高产品质量进行了各种努力， 但是随着日新月异的半导体电子器件小型化发展，塑封铝金属导线腐蚀 问题至今仍然是电子行业非常重要的技术课题。
关于产品寿命MTBF的计算
关于产品寿命MTBF的计算
1．T/C：
条件：-55-150摄氏度
AF=（（150+55）/50）的4次方=282.6
实验的SAMPLE数：5条；
时间：168周期
试验可靠度：80%
则可以保证寿命：5*168*AF*80%(一个CYCLE=一个小时).
2．HAST：
条件：125摄氏度/85%；
加速因子：AFt=exp[0.3/（k*298）-0.3/（k*398）]
AFh=exp(0.1*(85-70))=
AF=AFt*Afh
实验的sample数：5条；
实验时间：96小时；
试验的可靠度：80%
则可以保证寿命：5*96*AF*80%
3．LIFE TEST：
条件：55摄氏度
加速因子：AF=exp(0.3/k*298-0.3/k*328)
试验的sample数：10条
实验时间：每一条直到第一次失效为止或168小时。
则寿命：实验时间累加（168*10）*AF*试验可靠度
（试验可靠度采用工业标准，80%）
经过以上计算：我公司内存的产品寿命（MTBF）在不同的试验中，试验值从10年到70年不等。
以上的试验可靠度我司采用的是比较理想的值，若需要得到实际之则必须进行大量的可靠性试验。
另外诸如4-C测试等试验都可以按照温度和湿度以及
电压的加速作用都可以用来进行计算MTBF，而且从原理上讲，直接累加每个项目的计算值都可以，这种东西，关键看我们怎么理解，因为不可能有人真的去使用20年。
失效率＝失效数量/（测试数量×时间）
单位：/H
单位：FIT=10-9/H。
橡胶加速老化时间计算公式
橡胶加速老化时间计算公式
橡胶加速老化时间的计算公式因具体情境和要求而有所不同。
以下是两种常用的计算公式：
1. t2/t1 = exp [ Q/R (1/T1 - 1/T2) ]，其中t1为实验室中模拟老化的时间（天），t2为实际使用中老化的时间（年），T1为实验室中模拟老化的温度（K），T2为实际使用中的温度（K），Q为橡胶老化时释放的能量
（J/mol），R为气体常数。
2. TimeT1=TimeRT/Q10(T1-RT)/10，其中TimeT1为加速老化时间，TimeRT室温时间（寿命），T1为加速老化温度（考虑材料极限，一般50-60℃），RT为室温（一般取20-25℃），Q10为反应速率系数（一般取2）。
以上公式仅供参考，建议查阅橡胶行业相关书籍或咨询专业人士获取更准确的信息。
产品性能可靠性评估的方法与指标
产品性能可靠性评估的方法与指标产品性能可靠性评估是在产品开发和设计过程中非常重要的一环，它旨在确保产品在正常使用条件下能够持久稳定地运行，减少故障和损坏。
本文将介绍一些常用的方法和指标，用于评估产品的可靠性。
1. 可靠性指标可靠性是评估产品正常运行的能力，常用的可靠性指标有MTBF（Mean Time Between Failures），MTTF（Mean Time To Failure），以及FIT（Failure In Time）。
- MTBF是指产品平均故障发生之间的时间。
它的计算方法是将产品的总运行时间除以发生故障的次数。
- MTTF是指产品从开始使用到发生第一次故障之间的平均时间。
它的计算方法是将产品正常运行的总时间除以发生故障的次数。
- FIT是指每一亿小时内产品发生故障的次数。
这个指标通常用于评估高可靠性产品，其计算方法是将每小时故障率乘以1亿。
这些指标可以帮助制造商评估产品的可靠性水平，并对产品的设计和制造进行改进。
2. 故障模式与影响分析（FMEA）故障模式与影响分析是一种系统化的方法，用于识别产品设计和制造过程中可能发生的故障和其潜在影响。
这种方法通过对产品的各个组成部分进行分析，确定可能发生故障的原因和影响，并制定相应的预防措施。
FMEA通常包括三个主要步骤：识别故障模式、评估故障后果和确定预防措施。
通过进行FMEA分析，可以减少故障发生的概率，提高产品的可靠性。
3. 加速寿命试验（ALT）加速寿命试验是一种通过模拟产品在实际使用条件下的使用寿命，来评估产品可靠性的方法。
它通过在短时间内加速模拟产品的使用过程，例如高温、高湿度、高压力等，来观察产品在这些极端条件下的性能表现和故障率。
ALT试验能够较早地发现产品可能存在的问题，并采取相应的改进措施，提高产品的可靠性。
4. 持续改进产品的可靠性评估是一个持续的过程，制造商应该不断改进产品的设计和制造过程，以提高产品的可靠性。
这需要收集并分析产品的使用数据和故障数据，了解产品的弱点和潜在问题。
可靠性测试之寿命计算
2.可靠性试验指的是为提高产品的可靠性而进行的有关产品的失效及其效应的试验的 总称。它贯穿于产品的研制、设计、制造和使用的各个阶段，只是试验条件会随着 各阶段的试验目的的改变而改变。
常见的加速寿命测试条件： 1）125℃，1000H，3Lots/77units 2）125℃，500H，3Lots/30units（291年） 3）125℃，500H，3Lots/77units（374年） 4）150℃，300H，3Lots/40units 5）150℃，168H，3Lots/77units（420年） 6）150℃，2000H，3Lots/77units
7.加速寿命试验的方案确定： 1）试验样品的抽取方法和数量的确定。
>抽取的样品必须具有代表性且经过可靠性筛选，且是随机抽取； >样品数量的多少，将影响可靠性寿命估计的精确度，样品数量大，试验时间短， 试验结果精确。但工作量大，成本高。
2）试验应力的选择和应力水平的确定。 >试验应力大小通常以不改变元器件在正常使用条件下的失效机理为原则。
可靠性测试之寿命试验
JESD47
5年 11年
4年 10年
大纲
1.可靠性定义 2.可靠性试验分类 3.加速寿命试验 4.小结 5.附录
1.可靠性定义
1.日本工业标准(JIS)对此的定义： The probability that an item will perform a required function under specified conditions for a specified period of time.
【加速老化实验】,加速老化试验计算公式
【加速老化实验】,加速老化试验计算公式【加速老化实验】加速老化试验计算公式加速寿命试验寿命试验(包括截尾寿命试验)方法是基本的可靠性试验方法。
在正常工作条件下，常常采用寿命试验方法去估计产品的各种可靠性特征。
但是这种方法对寿命特别长的产品来说，就不是一种合适的方法。
因为它需要花费很长的试验时间，甚至来不及作完寿命试验，新的产品又设计出来，老产品就要被淘汰了。
所以这种方法与产品的迅速发展是不相适应的。
经过人们的不断研究，在寿命试验的基础上，找到了加大应力、缩短时间的加速寿命试验方法。
加速寿命试验是用加大试验应力(诸如热应力、电应力、机械应力等)的方法，加快产品失效，缩短试验周期。
运用加速寿命模型，估计出产品在正常工作应力下的可靠性特征。
下面就加速寿命试验的思路、分类、参数估计方法及试验组织方法做一简单介绍。
1 问题高可靠的元器件或者整机其寿命相当长，尤其是一些大规模集成电路，在长达数百万小时以上无故障。
要得到此类产品的可靠性数量特征，一般意义下的载尾寿命试验便无能为力。
解决此问题的方法，目前有以下几种：（１）故障数r=0的可靠性评定方法。
如指数分布产品的定时截尾试验θL=2S(t0)2χα(2)22S(t)χαα00为总试验时间。
为风险, =0.1时，.1(2)=4.605≈4.6；当α=0.05时，χ02.05(2)=5.991≈6。
（２）加速寿命试验方法如，半导体器件在理论上其寿命是无限长的，但由于工艺水平及生产条件的限制，其寿命不可能无限长。
在正常应力水平S0条件下，其寿命还是相当长的，有的高达几十万甚至数百万小时以上。
这样的产品在正常应力水平S0条件下，是无法进行寿命试验的，有时进行数千小时的寿命试验，只有个别半导体器件发生失效，有时还会遇到没有一只失效的情况，这样就无法估计出此种半导体器件的各种可靠性特征。
因此选一些比正常应力水平S0高的应力水平S1，S2，…，Sk，在这些应力下进行寿命试验，使产品尽快出现故障。
加速寿命试验公示计算汇总
加速寿命试验公示计算汇总一、前言新研究的医疗器械在上市前应确保在储存期( 通常 1 到5 年) 内产品的质量不应发生任何影响安全性和有效性变化，新产品一般没有实时和储存周围环境条件下确定有效期的技术资料。
如果按实际储存时间和实际环境储存条件进行检测需要很长的时间才能获得结果，为了在实时有效期结果获得以前，有必要进行加速老化实验提供确定有效期的实验数据。
医疗器械设计人员能够准确地预计聚合物性能的变化对于医疗器械产业化是非常重要的。
建立聚合物材料退行性变的动态模型是非常困难和复杂的，事实上材料短期产生的变化或变性的单速率表达形式可能不能充分反映研究的产品或材料在较长有效期的真实情况。
为了设计试验方案能准确模拟医疗器械时间相关的退行性变，有必要对材料的组成、结构、成品用途、组装和灭菌过程的影响、失效模型机制和储存条件有深入的了解。
一个给定的聚合物具有以各种方式( 晶体、玻璃、不定形等) 组成的许多化学功能基团，并含有添加剂如抗氧化剂、无机充填剂、色素和加工助剂。
所有这些变量的总和结合产品使用和储存条件变量决定了材料的化学性能的退行性变。
得庆幸的是，生产医疗器械的大部分都是采用常用的几种高分子材料，这些材料已经广泛使用并且都进行了良好的表征。
根据以碰撞理论为基础的阿列纽斯(Arrhenius) 模型建立的老化简化实验方案(Simplified Protocol for Accelerated Aging) ，也称“10 度原则”(10-degree rule) ，可在中度温度范围内适用于良好表征的聚合物，试验结果可以在要求的准确度范围内。
医疗器械或材料的老化是指随着时间的延长它们性能的变化，特别是与安全性和有效性有关的性能。
加速老化是指将产品放置在比正常储存或使用环境更严格或恶劣的条件下，在较短的时间内测定器械或材料在正常使用条件下的发生变化的方法。
采用加速老化实验合格测试的主要原因是可以将医疗器械产品尽早上市。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1240.2
品结构），使用应力条件，加速应力测试条件和相关的失效机理。 ）中的待测物都有自己的加速因子和测试条件（如占空比，应力水 因素。
荷（如温度，温度循环和温度变化率），化学负荷（如潮湿，腐蚀 流，功率）和机械负载（例如，准静态周期性机械 荷的组合。组合负荷的结果分析和结果到生命周期条件的外推需要定 坏的贡献。
力学得出)
加速因子 AF(t) 0.99
0.979
加速率常数 B(≤B≤)
10
综合加速因子
8.00
* 注1： 加速因子取决于待测物的硬件参数（如材料性能，产品结构），使用应力条件，加速应力测试 因此，每一个相关的故障模式（假设它是一个失效机理的结果）中的待测物都有自己的加速因子和测试 平，应力历史，试验持续时间）应根据这些量身定制的加速度因素。
电工电子产品恒定应力加速寿命试验-加速因子计 （依据IEC62506标准）
参考标准环境： 1）室温：25℃， 2）相对湿度：55%RH， 标准大气压：101.3 kPa。
由inverse power law模型计算 （逆幂律模型: 用于除了恒温应力之外的因 素，例如电气，机械，化学（腐蚀）和其它)
加速因子
AF(v)
1.57
1.09
备注 m取值： 1）电容器以直流电压V加速，m=5， 2）聚乙烯绝缘材料以交流电压V加速，m=11-13, 3) 滚珠轴承及钢材的断裂，m=3-4, 4）对于温度冲击测试， m=6.96
加速率常数
m ( 2<m<13 )
5
由Arrhenius模型计算 （阿伦纽斯模型： 用于恒温应力，是基于绝
* 注2：当规划一个测试项目时潜在故障模式应该被列出。
* 注3：定量加速测试可以通过增加各种负载水平运行，如热负荷（如温度，温度循环和温度变化率）， 性化学物质，如酸和盐），电气负载（如稳态或瞬态电压，电流，功率）和机械负载（例如，准静态周 变形，振动和冲击/冲击/碰撞）。加速试验环境可包括这些载荷的组合。组合负荷的结果分析和结果到 量理解不同测试应力的相关交互作用和每个应力类型对整体损坏的贡献。
对温度对失效机理的影响)
温度加速因子
析出故障的耗费能量 (激活能量）
Boltzmann 常数
AF
Ea(eV) ( 0.3ev—1.2ev )
kB(eV/k)
5.15
1.64
0.67
0.00008617
备注 Ea取值：在没有资料数据情况下取0.67, 大功率激光器芯片Ea的值为0.52.
由Eyring 模型计算 （艾林模型：是用在加速取得温度和湿度应力 水平，以及和其他化学反应，该模型是由量子
加速寿命试验-加速因子计算 62506标准）
准大气压：101.3 kPa。
实际使用应力
SUse
16
加速（测试）使用应力
STest
17.5
正常工作的温度
片Ea的值为0.52.
T0(℃) 25
加速（测试）应力的温度 T(℃) 45
实际使用应力
SE-Use
298
加速（测试）使用应力
SE-Test
302
8.1