由平行线截得的比例线段
《由平行线截得的比例线段》教学设计

《4.2 由平行线截得的比率线段》教课方案一、教课内容剖析《由平行线截得的比率线段》是浙教版九年级上册第四章的第二节课。
本节课要求掌握一个基本领实:“两条直线被一组平行线所截,所得的对应线段成比率” 。
这个基本领实又被称为“平行线截割定理” 。
它属于客观存在的事实性知识,因为其证明过程比较复杂,在教课中对学生不作要求。
所以教材中是以基本领实的形式进行表现的,经过实验让学生感觉,并无给出严格的证明过程。
而后教材经过两个例题的应用帮助学生稳固对定理使用条件和结论的认识,特别是例 2 要经过增添协助线来知足定理使用的条件,表现了数学转变思想。
二、教课目的1、知识与技术:能应用平行线截割定理找出比率线段并解决有关计算问题,能利用定理将线段随意平分。
2、过程与方法:经历平行线截割定理的发现过程,能利用转变思想联合定理解决相应问题。
3、感情态度、价值观:培育学生独立思虑能力及团结协作意识,加强研究数学识题的信心。
三、学情剖析学生在学习本节课前已经学习了比率的基天性质、比率线段的观点,能依据线段的长度计算比率和利用比率计算有关线段的长度,拥有益用转变思想解决问题的经验。
要完成本节课的教课目的,学生需要具备从教课活动中发现并概括出数学规律的能力;能依据比率线段计算有关线段的长度;在不知足定理使用条件的问题中,能先合理的创建定理使用条件,再利用定理解决问题。
四、要点难点要点:学生在经历数学活动后发现和概括出平行线截割定理。
难点:例 2 的作法思路不易形成,是本节的难点。
关于要点,教师能够设计合理的问题串来指引学生一步步发现平行线截割定理,经过相互议论增补的形式帮助学生概括出定理。
关于难点,依据支架式教课策略,教师能够设计出更为特别简单的支架型问题,帮助学生利用特别到一般的思想过程形成例 2 的解题思路,以此来打破难点。
五、教课策略依据以上剖析,本节课将采纳支架式教课策略和小组合作学习策略。
本节课的定理需要学生去概括发现,但学生发现问题与概括小结的能力有差距,所以经过小组合作学习策略,让能力强的学生有更多的表现时机,经过生生互动让能力衰的学生也能获取成长。
九年级数学上册《由平行线截得的比例线段》教案、教学设计

(四)课堂练习
课堂练习环节旨在巩固学生对比例线段知识的应用。我会设计以下几类题目:
1.基础题:让学生运用比例线段的概念和性质,解决简单的几何问题。
2.提高题:设计一些综合性的题目,让学生运用所学知识解决实际问题。
3.挑战题:针对学有余力的学生,设计一些具有挑战性的题目,激发学生的求知欲。
在练习过程中,我会巡回指导,关注学生的解题思路和方法,及时纠正错误,鼓励学生相互讨论,共同解决问题。
(五)总结归纳
在总结归纳环节,我会让学生回顾本节课所学的内容,总结比例线段的知识点和解题方法。然后,我进行点评,强调以下几点:
1.比例线段的定义和性质。
2.比例线段在实际问题中的应用。
3.解题过程中要注意的问题,如识别比例线段、避免计算错误等。
4.学生在课堂讨论和练习中的优点和不足,以及如何改进。
总字数:2533字
4.培养学生运用数学知识解决实际问题的意识,使学生认识到数学在现实生活中的重要性,增强学生的社会责任感。
总字数:1015字
二、学情分析
九年级的学生已经具备了一定的几何基础,掌握了平行线的性质和判定方法,但在解决实际问题时,可能还未能熟练运用比例线段的概念。此外,学生在空间想象力、逻辑思维能力和问题解决能力方面存在一定的差异。因此,在本章节的教学中,要注意以下几点:
-采用总结性评价,通过单元测试、期中考试等形式,评估学生对比例线段知识的掌握程度。
4.教学资源:
-利用学校图书馆、网络资源等,为学生提供丰富的学习资料,拓展学生的知识视野。
-结合实际生活,设计富有情境的教学活动,让学生在实践中学习,增强知识的现实意义。
5.教学关注点:
平行线截得比例线段定理

平行线截得比例线段定理简介平行线截得比例线段定理是数学中的一条重要定理,它描述了平行线所截线段的比例关系。
这个定理可以帮助我们解决许多几何问题,特别是与平行线和线段相关的问题。
下面将详细介绍这个定理及其应用。
定理表述平行线截得比例线段定理,又称为Thales定理,它表述如下:定理:如果在两条平行直线上有一组交叉线段,那么这些交叉线段的长度比是相等的。
按照数学表达式来表示,设有两条平行线l和m,它们被一组交叉线段AB和CD分别截取,AB与CD之间的交叉线段分别为AE和CF。
那么,根据平行线截得比例线段定理,我们有以下等式成立:$\\frac{AB}{CD} = \\frac{AE}{CF}$其中,AB和CD为已知线段,AE和CF为待求线段。
证明平行线截得比例线段定理的证明可以基于数学的初等几何和比例关系。
这里简要概述一下该定理的证明过程。
首先,我们可以利用平行线之间的性质证明交叉线段的比例相等性质。
可以通过使用平行线上的内错角定理来证明同位角相等。
然后,我们可以利用对应角相等以及相似三角形的性质来证明线段的比例关系。
具体证明过程可能会涉及到对角线进行延长、三角形的相似性质以及比例的性质等。
不过,由于本篇文档的限制,无法将具体的证明过程呈现给读者。
如果你对该定理的证明感兴趣,可以通过查阅相关数学教材或资料进行深入学习。
应用示例平行线截得比例线段定理在几何问题中的应用非常广泛。
下面我们通过一个应用示例来进一步说明它的用途。
假设我们有三条平行线l,m和n,它们分别被交叉线段AB和CD截取。
已知AB与CD的比例为2:3,我们可以利用平行线截得比例线段定理来求解其他线段的长度。
假设平行线l与m之间截取的线段为AE,平行线m与n之间截取的线段为CF。
根据平行线截得比例线段定理,我们可以设立如下比例等式:$\\frac{AB}{CD} = \\frac{AE}{CF}$代入已知比例和线段长度,我们可以得到:$\\frac{2}{3} = \\frac{AE}{CF}$根据上述等式,我们可以解出AE和CF的比例关系,从而求解出AE和CF的具体长度。
第31讲 由平行线截得的比例线段(原卷版)
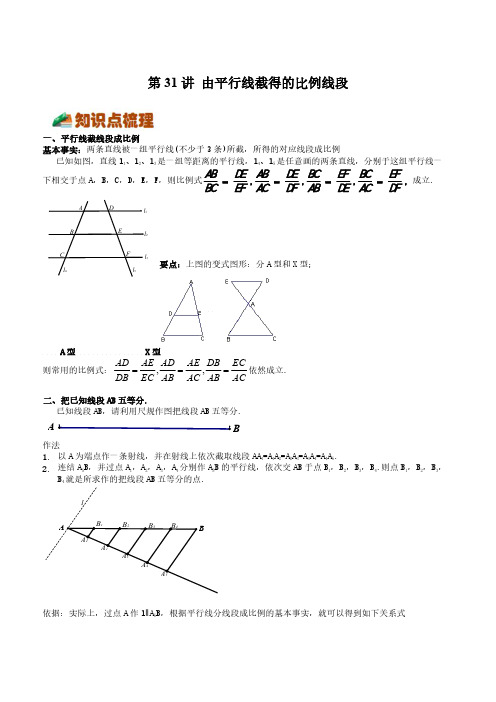
32第31讲 由平行线截得的比例线段一、平行线截线段成比例基本事实:两条直线被一组平行线(不少于3条)所截,所得的对应线段成比例已知如图,直线l 1、l 2、l 3是一组等距离的平行线,l 4、l 5是任意画的两条直线,分别于这组平行线一下相交于点A ,B ,C ,D ,E ,F ,则比例式,,,,A B D E A B D E B C E F B C E FB C E F A C D F A B D E A C D F==== 成立.要点:上图的变式图形:分A 型和X 型;A 型 X 型则常用的比例式:依然成立.二、把已知线段AB 五等分.已知线段AB ,请利用尺规作图把线段AB 五等分.作法1.以A 为端点作一条射线,并在射线上依次截取线段AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5.2.连结A 5B ,并过点A 1,A 2,A 3,A 4分别作A 5B 的平行线,依次交AB 于点B 1,B 2,B 3,B 4.则点B 1,B 2,B 3,B 4就是所求作的把线段AB 五等分的点.依据:实际上,过点A 作l ∥A 5B ,根据平行线分线段成比例的基本事实,就可以得到如下关系式,,AD AE AD AE DB ECDB EC AB AC AB AC===11223344112233445.A B B B B B B B B BA A AA A A A A A A ====∵ AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5,∴ AB 1=B 1B 2=B 2B 3=B 3B 4=B 4B,∴点B 1,B 2,B 3,B 4把线段AB 五等分.要点:在射线上截取等长的线段时使用的作图工具是圆规,不能使用直尺进行量取,尺规作图中的直尺是没有刻度的,它的用途是画线或者连线.例1.如图,已知//,2,3,6AB CD AO BO CO ===,那么DO =( )A .3B .4C .5D .6例2.如图,在△ABC 中,DE ∥BC ,若23AD DB =,则AE EC等于( )A .13B .25C .23D .35例3.已知线段a 、b 、c ,求作线段ab x c=,下列作法中正确的是( )A .B .C .D .例4.如图,点D 、E 分别在AB 、AC 上,以下能推得DE BC ∥的条件是( ).A .::AD AB DE BC=B .::AD DB DE BC=C .::AD DB AE EC =D .::AE AC AE DB=例5.如图,若l 1∥l 2∥l 3,则下列各式错误的是( )A .BC EFAC DF=B .AB DEAC DF=C .AB ACDE DF=D .AB DEAC EF=例6.如图,在△ABC 中,DE ∥BC ,EF ∥AB ,AD :BD=5:3,CF=6,则DE 的长为( )A .6B .8C .10D .12例7.如图,直线l1∥l2∥l3,直线AC 分别交l1,l2,l3于点A ,B ,C ;直线DF 分别交l1,l2,l3于点D 、E 、F ,AC 与DF 相交于点H ,且AH=2,HB=1,BC=5,则DEEF=( )A .35B .2C .25D .12例8.如图,点G 、F 分别是BCD △的边BC 、CD 上的点,BD 的延长线与GF 的延长线相交于点A ,//DE BC 交GA 于点E ,则下列结论错误的是( )A .AD AEBD EG =B .DE DF CG CF=C .AE DEAG BC=D .AD DEAB BG=例9.如图,DE 、NM 分别是V ABC 、V ADE 的中位线,NM 的延长线交BC 于点F ,则DMN S V :S 四边形MFCE等于( )A .1:5B .1:4C .2:5D .2:7例10.如图,四条平行直线1l 、2l 、3l 、4l 被直线5l 、6l 所截,::1:2:3AB BC CD =,若3FG =,则线段EF 和线段GH 的长度之和是( )A .5B .6C .7D .8例11.如图,直线123////l l l ,直线AC 分别交1l 、2l 、3l 于点A 、B 、C ,直线DF 分别交1l 、2l 、3l 于点D 、E 、F ,AC 与DF 相交于点H ,如果5,1,2AB BH CH ===,那么EFDE的值等于( )A .15B .13C .25D .35例12.如图,AB ∥CD ∥EF ,AC 与BD 相交于点E ,若CE =5,CF =4,AE =BC ,则CD AB的值是( )A .23B .12C .13D .14例13.如图,////AB GH CD ,点H 在BC 上,AC 与BD 交于点G ,2AB =,3CD =,则GH 的长为 .例14.如图,AD 是△ABC 的中线,AE =EF =FC ,BE 交AD 于点G ,则AG AD=_________.例15.如图,在ABC V 中,D 为AC 上一点,且12CD AD =,过点D 作//DE BC 交AB 于点E ,连接CE ,过点D 作//DF CE 交AB 于点F .若15AB =,则EF =______.例16.如图ABC V 中,E 、F 为BC 的三等份点,M 为AC 的中点,BM 与AE 、AF 分别交于G 、H ,则::BG GH HM =________.一、单选题1.如图,△ABC 中,点D ,E 分别在边AB ,AC 的反向延长线上,且DE ∥BC .若AE =2,AC =4,AD =3,则AB 为( )A .9B .6C .3D .322.如图,在ABC V 中,点D ,E 分别在AB ,AC 边上,DE BC ∥.若:3:1AD DB =,则:AE EC 等于( )A .3:1B .3:4C .3:5D .2:33.如图,1l ∥2l ∥3l .若23=AB BC ,DE =4,则EF 的长为( )A .6B .7C .8D .94.如图,点A ,E ,F ,C 在同一条直线上,AD BC ∥,BE 的延长线交AD 于点G ,且BG DF ∥,则下列结论中错误的是( )A .AG AD =AE AFB .AG GD=AEEF C .AE AC=AGAD D .AFFC =DF FH5.如图,l 1∥l 2∥l 3,且ADDF =32,则错误的是( )A .35AD AF =B .32BC CE =C .23AB EF =D .35BC BE =6.如图,在ABC V 中,AC ,AB 两边上的中线BE ,CD 相交于点O ,则DOEEOCS S =△△( )A .23B .14C .13D .127.如图是一架梯子的示意图,其中1111∥∥∥AA BB CC DD ,且AB BC CD ==.为使其更稳固,将A ,1D 间加一条安全绳(线段1AD ),1AD 分别交1BB ,1CC 于点E ,F ,量得0.4m =AE .则1AD 的长为( )A .0.8mB .1mC .1.2mD .1.4m8.如图,在ABC V 中,AD DE EF FB ===,AG GH HI IC ===,已知2BC =,则DG EH FI ++的长是( )A .52B .3C .32D .49.如图,在ABC D 中,点D ,点E 为边AB 的三等分点,////EF DG AC AF ,与DG 交于点H ,则下列比例式正确的是()A .AD HGDE AC=B .BF FGBE FH=C .DH BFEF BG=D .AH EFHF DG=10.如图,正方形ABCD 的边AB ,CD 上各有一个点I ,E ,连结EI ,且//EI BC ,点F ,G ,H 分别在AD ,AB ,BC 边上,连结GF ,FE ,EH ,H G ,其中EI 与GF 相交于点J ,IJ AI =,为求出平行四边形EFGH 的面积,只需知道下列哪条边的长度( )A .IGB .AFC .BGD .AG二、填空题11.如图,已知AE BC ∥,AC 、BE 交于点D ,若23AD DC =,则DEBE=______.12.如图,////,::2:3:4DE FG BC AD DF FB =,如果4EG =,那么AC =________.13.如图,AB ∥CD ∥EF ,若12=AC CE ,则BD DF_____.14.如图,已知//DE BC ,:3:2BF EF =,则:AC AE =______,:AD DB =______.15.如图,已知//a b ,35AF BF =,3BC CD=,则:AE EC =______.16.如图,在ABC V 中,AD 是中线,G 是重心,过点G 作//EF BC ,分别交AB 、AC 于点E 、F ,若18AC =,则AF =____________.17.如图,在ABC V 中,90,8,6,ACB AC BC AD Ð=°==为边BC 上的中线,BE 是ABC V 的角平分线,,AD BE 交于点F .则EF 的长为______.18.如图,在ABC V 中,点D 是边BC 的中点,直线DF 交边AC 于点F ,交AB 的延长线于点E ,如果::CF CA a b =,那么:BE AE 的值为____.(用含a 、b 的式子表示)三、解答题19.如图,在△ABC中,DE∥BC,分别与AB、AC交于点D、E,若AE:EC=2:3,DB-AD=3,求AD 和DB的长.20.如图,已知AD∥EB∥FC,AC=12,DB=3,BF=7,求EC的长.21.如图,已知AD//BE//CF,它们依次交直线1l、2l于点A、B、C和点D、E、F,且AB=6,BC=8.(1)求DEDF的值;(2)当AD=5,CF=19时,求BE的长.22.如图,B、C、D、N分别是⊿AMO边AO、MO上的点,MC∥ND,OB ODAB CD=,求证:NB∥MA23.如图,在△ABC中,点D、F是在边AB 上,点E在边AC上,且FE∥CD,线段AD是线段AF与AB 的比例中项.求证:DE∥BC24.已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.求证:2CF GF EF=×.25.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.(1)求EC的值;(2)求证:AD•AG=AF•AB.26.已知,如图,在平行四边形ABCD中,E、F分别是边BC、CD上的点,且EF∥BD,AE、AF分别交BD于点G和点H,BD=12,EF=8.求:(1)DFAB的值;(2)线段GH的长.27.如图,MN 经过D ABC 的顶点A ,MN ∥BC ,AM=AN ,MC 交AB 于D ,NB 交AC 于E .(1)求证:DE ∥BC ;(2)联结DE ,如果DE=1,BC=3,求MN 的长.28.如图,在Rt ABC △中,90ABC Ð=°,BA BC =,点D 为BC 边上的中点,连接AD ,过点B 作BE AD ^于点E ,延长BE 交AC 于点F ,求AF FC的值.29.如图,已知在正方形ABCD 中,对角线AC 与BD 交于点O ,点M 在线段OD 上,联结AM 并延长交边DC 于点E ,点N 在线段OC 上,且ON =OM ,联结DN 与线段AE 交于点H ,联结EN 、MN .(1)如果EN ∥BD ,求证:四边形DMNE 是菱形;(2)如果EN ⊥DC ,求证:AN 2=NC •AC .。
浙教版数学九年级上册《4.2 由平行线截得的比例线段》教学设计1

浙教版数学九年级上册《4.2 由平行线截得的比例线段》教学设计1一. 教材分析《4.2 由平行线截得的比例线段》这一节主要让学生掌握利用平行线截得的线段之间的比例关系,通过几何图形和线段的组合,引导学生发现和证明线段之间的比例关系,为后面进一步学习相似三角形和相似多边形打下基础。
二. 学情分析九年级的学生已经掌握了平行线的性质,同时也具备了一定的逻辑思维能力和空间想象能力。
但是,对于证明两个线段之间的比例关系,可能还存在一定的困难,因此,在教学过程中,需要通过具体例题,引导学生发现规律,再进行证明。
三. 教学目标1.理解平行线截得线段之间的比例关系。
2.学会利用平行线截得的线段之间的比例关系解决实际问题。
3.培养学生的逻辑思维能力和空间想象能力。
四. 教学重难点1.重点:平行线截得线段之间的比例关系的发现和证明。
2.难点:如何引导学生发现并证明平行线截得线段之间的比例关系。
五. 教学方法1.采用问题驱动法,引导学生发现和证明平行线截得线段之间的比例关系。
2.利用几何画板软件,动态展示平行线截得的线段之间的比例关系,帮助学生直观理解。
3.通过小组合作交流,培养学生的团队协作能力。
六. 教学准备1.教学课件。
2.几何画板软件。
3.练习题。
七. 教学过程1.导入(5分钟)利用几何画板软件,动态展示平行线截得的线段,引导学生关注线段之间的比例关系。
2.呈现(10分钟)呈现一组平行线截得的线段,请学生观察并发现其中的比例关系。
学生可能发现同位角相等,内错角相等等性质。
3.操练(10分钟)请学生利用平行线的性质,证明同位角相等,内错角相等。
通过几何画板软件,引导学生直观理解。
4.巩固(10分钟)请学生利用平行线截得的线段之间的比例关系,解决实际问题。
如:在一条直线上,距离某一点A相等的两条线段AB和AC,求证AB和AC平行。
5.拓展(10分钟)引导学生思考:在空间中,平行线截得的线段之间是否也存在比例关系?请学生举例说明。
平行线分线段成比例定理

平行线分线段成比例定理平行线分线段成比例定理:两条直线被一组平行线所截,截得的对应线段的长度成比例。
推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
定理定义三条平行线截两条直线,所得对应线段成比例。
这一定理被称为"平行线分线段成比例定理"。
如图,因为AD∥BE∥CF,所以AB:BC=DE:EF;AB:AC=DE:DF;BC:AC=EF:DF。
也可以说AB:DE=BC:EF;AB:DE=AC:DF;BC:EF=AC:DF。
上述图样只是平行线分线段的一种特殊情况。
事实上,直线AC和直线DF可以在平行线之间相交,同样有定理成立。
定理证明设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点。
连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE,S△BCE=S△BEF∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF定理推论过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
•平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
推广:过一点的一线束被平行线截得的对应线段成比例。
定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
•证明思路:该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的知识,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它(用相似三角形可以证明它,在这里要用到平移和设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点法1:过A作平行线的垂线交另两条平行线于M、N,过D作平行线的垂线交另两条平行线于P、Q,则四边形AMPD、ANQD均为矩形。
平行线分线段成比例定理

左 左 = 右 右
L5 L4 A D B E C
L5
L4 D
L1
L2
E A
L1
L2
B C 数学符号语言 L3 数学符号语言 ∵ DE∥BC ∵ DE∥BC
L3
AD AE AB AC
AD AE AB AC
平行于三角形一边的直线截其他两边(或两边的 延长线),所得的对应线段的比相等.
例1 如图: l1∥l2∥l3 ,
A1 A 要把表示对应角顶点的 字母写在对应的位置上。 注意 B1 C
B
C1
当 ∠A =∠A1,∠B =∠B1, ∠C =∠C1, AB : A1B1 = BC : B1C1 = CD : C1D1 = k 时, 则△ABC 与△A1B1C1 相似,
记作△ABC ∽ △A1B1C1。
平行线分线段成比例定理:
(1)若AB=3 , DE=2, EF=4,求 BC. 解: l ∥l ∥l A
一般把所求线段 BC EF AB DE 写成比例第一项.
即:
BC EF BCDE 4 AB
1
2
3
B C
D E
F
l1 l2 l3
3
2
BC=6
(2)若AC=8,DE=2,EF=3,求AB.
AB DE DE AB 2 16 AB AC DF DE EF 8 2 3 5
过点E作EF∥AB,EF交BC于点F. ∵DE∥BC,EF∥AB,
AD AE BF AE , . AB AC BC AC DE . BC
E
C
∵四边形DEFB是平行四边形, DE AE AD AE , ∴DE=BF,
BC AC AB AC
平行线分线段成比例定理及证明

平行线分线段成比例定理证明简介平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。
如图,因为AD∥BE∥CF,所以AB:BC=DE:EF;AB:AC=DE:DF;BC:AC=EF:DF。
也可以说AB:DE=BC:EF;AB:DE=AC:DF;BC:EF=AC:DF。
说明上述图样只是平行线分线段的一种特殊情况。
事实上,直线AC和直线DF 可以在平行线之间相交,同样有定理成立。
推广:过一点的一线束被平行线截得的对应线段成比例。
证明思路该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的知识,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它(用相似三角形可以证明它,在这里要用到平移和设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点法1:过A作平行线的垂线交另两条平行线于M、N过D作平行线的垂线交另两条平行线于P、Q则四边形AMPD、ANQD均为矩形AM=DP,AN=DQAB=AM/cosA,AC=AN/cosA,∴AB/AC=AM/ANDE=DP/cosD,DF=DQ/cosD,∴DE/DF=DP/DQ又∵AM=DP,AN=DQ,∴AB/AC=DE/DF根据比例的性质:AB/(AC-AB)=DE/(DF-DE)∴AB/BC=DE/EF法2:过A点作AN∥DF交BE于M点,交CF于N点,则AM=DE,MN=EF.∵ BE∥CF∴△ABM∽△ACN.∴AB/AC=AM/AN∴AB/(AC-AB)=AM/(AN-AM)∴AB/BC=DE/EF法3:连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE,S△BCE=S△BEF∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF定理推论平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A 型 X 型 则常用的比例式:
依然成立. 要点二、把已知线段AB 五等分.
已知线段AB ,请利用尺规作图把线段AB 五等分.
作法
1. 以A 为端点作一条射线,并在射线上依次截取线段AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5.
2. 连结A 5B ,并过点A 1,A 2,A 3,A 4分别作A 5B 的平行线,依次交AB 于点B 1,B 2,B 3,B 4.则点B 1,
B 2,B 3,B 4就是所求作的把线段AB 五等分的点.
依据:实际上,过点A 作l ∥A 5B ,根据平行线分线段成比例的基本事实,就可以得到如下关系式
11223344112233445
.AB B B B B B B B B
AA A A A A A A A A ==== ∵ AA 1=A 1A 2=A 2A 3=A 3A 4=A 4A 5, ∴ AB 1=B 1B 2=B 2B 3=B 3B 4=B 4B,
∴点B 1,B 2,B 3,B 4把线段AB 五等分.
,,AD AE AD AE DB EC
DB EC AB AC AB AC
===A B B 4
B 3
B 2
B 1
A 5
A 4
A 3
A 2
A 1
l A
B
要点诠释:
在射线上截取等长的线段时使用的作图工具是圆规,不能使用直尺进行量取,尺规作图中的直尺是没有刻度的,它的用途是画线或者连线.
1.如图,在△ABC 中,DE ∥BC ,若=,则=( )
A .
B .
C .
D .
【变式】如图,在⊿ABC, DG ∥EC, EG ∥BC,求证:
2.如图,在矩形ABCD 中,AB=2,BC=3,点E 、F 、G 、H 分别在矩形ABCD 的各边上,EF ∥AC ∥HG ,EH ∥BD ∥FG ,则四边形EFGH 的周长是( ). A. 10 B.13 C.210 D.213
3. 如图,AM 是△ABC 的中线,P 是AM 上任意一点,BP 、CP 的延长线分别交AC 、AB 于E 、D 两点.求证:DE ∥BC.
2AE AB AD =⋅A B
C
D E G
【变式】如图,在△ABC(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P,求证:.
4. 如图已知△ABC中AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CP交AB于N,若AB=6cm,求AP的值.
【变式】如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则
DE
EF
的值为()
A.
1
2
B. 2
C.
2
5
D.
3
5
5把已知线段a(如图)三等分.
BP BD
CP CE
a
【巩固练习】
一.选择题
1. 如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若=,则=()
A.B.C.D.1
2. 如图,在△ABC中,DE∥BC,则下列比例式成立的是( ).
A.B.C.D.
3. 在△ABC中,点D在AB上,点E在AC上,且DE∥BC,,则等于( ).
A.B.C.D.
4.如图,△ABC中,DE∥AC交AB、BC于D、E,如果AB=7cm,AC=5cm,AD=3cm,则DE=( ).
A.B.C.D.
5.如图,在△ABC中,如果DE∥BC,DF∥AC,则下列比例式中不正确的是( ).
A.B.C.D.
6. 如图,△ABC中,G是BC中点,E是AG中点,CE的延长线交AB于D,则EC:DE的值为( ).
A.2 B.3C.D.
二. 填空题
7. 如图,直线AD∥BE∥CF,BC=AC,DE=4,那么EF的值是.
8. 如图,DE∥BC,BF:EF=4:3,则AC:AE=____________.
9.如图,AB ∥GH ∥CD ,点H 在BC 上,AC 与BD 交于点G ,AB=2,CD=3,则GH 的长为______.
10. 如图,△PMN,点A,B 分别在MP,NP 的延长线上,
,则________.
11.如图,△ABC 中,D 、F 在AB 边上,E 、G 在AC 边上,DE △FG △BC ,且AD :DF :FB=3:2:1,若AG=15,则CE 的长为 .
12. 如图,AD ∥EF ∥BC,且AE=2EB,AD=5.BC=8,则EF=_____________.
H
G B
C
A
D
25AP BP AM BN ==MN
BA
=
三.综合题
13. 作图,已知线段AB,把它分成2:3的两条线段.
A B
14.已知:如图,△ABC为等边三角形,边长为2,DE∥BC,△BCD的面积是△ABC的面积的,
求EC的长.
15.如图,DE△BC,EF△CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD•AG=AF•AB.。
