建立坐标系
如何建立坐标系

如何建立坐标系?恰当地建立坐标系,可以使解题简便.通常以加速度a 的方向为x 轴的正方向,与此垂直的方向为y 轴,建立直角坐标系.将物体所受到的力按x 轴、y 轴方向分解,分别求得x 轴和y 轴上的合力F x 和F y ,根据力的独立作用原理得方程组F x =ma ,F y =0.但有时用这种方法得到的方程组求解较为烦琐,因此在建立直角坐标系时,也可根据物体的受力情况,使尽可能多的力位于两坐标轴上而分解加速度a 得a x 和a y ,根据牛顿第二定律得方程组F x =ma x ,F y =ma y 求解.究竟采用哪种方法,要视具体情况灵活使用.例1 质量为10kg 的物体放在水平面上,物体与水平面间的动摩擦因数为0.2,如果用大小为40 N ,方向斜向上与水平方向的夹角为37°的恒力作用,使物体沿水平面向右运动,(g 取10 m/s 2, sin370=0.6,cos370=0.8),求:(1)物体运动的加速度大小;(2)若物体由静止开始运动,需要多长时间速度达到8.4m/s?物体的位移多大?答案:(1)a =1.68m/s 2 (2)5 s 21m【解析】(1)以物体为研究对象,首先对物体进行受力分析,如图4-6-1所示.建立平面直角坐标系把外力沿两坐标轴方向分解.设向右为正方向,依据牛顿第二定律列方程:F ·cos θ-f =m aF ·sin θ+F N =mgf =μF N整理后得到:a =m F mg F )sin (cos θμθ⋅--⋅ 代入相关数据,解得物体运动加速度大小a =1.68m/s 2.(2)因为物体做匀加速直线运动,所以根据运动学公式可知:v t =v 0+a t物体运动时间为:t =a v t =68.14.8s =5 s s =v 0t +21a t 2 物体的位移大小为:s =21a t 2=21×1.68×52m =21m . 说明:(1)这是一道已知物体的受力情况,确定物体的运动情况的习题;(2)本题中物体受4个力作用(大于3个力作用),一般在处理力的关系时用正交分解法;(3)支持力不是外力在竖直方向上的分力;重力大小不等于地面给予的支持力.【点评】本题是已知物体的受力求物体的运动情况,关键在于对物体的受力分析要正确,应用牛顿第二定律求出加速度,再由运动学公式求解.图4-6-1例2 如图4-6-2所示,某商场内电梯与水平面夹角为300,当电梯加速向上运动时,人对梯面压力为其重力的56,则人与梯面间的摩擦力是其重力的多少倍? 答案:mg F f 53= 【解析】选梯面上的人为研究对象,对其进行受力分析,重力和支持力都不难分析,至于人与梯面间的摩擦力是本题分析的难点,由于人与电梯具有相同的加速度,故人所受合外力沿斜面向上,因而人所受摩擦力一定沿梯面水平向右;如图4-6-3所示,水平、竖直建立直角坐标系,将加速度在两个坐标轴上分解,设电梯倾角为θ,加速度为a ,在x 轴和y 轴分别列方程,得θcos ⋅=ma F f ①θsin ⋅=-ma mg F N ②由题意,知 mg F N 56= ③ ①②③三式联立,代入数据,得 mg F f 53=【点评】本题是已知物体的运动情况求物体的受力,关键在于对物体的受力分析要正确,能够建立合适的坐标系(本题也可以沿斜面和垂直斜面建坐标系,同学们可以试一试),使方程和求解都更加简洁.在用牛顿定律解决问题时,有时可以分解力,有时可以分解加速度,看哪一种更为简单.图4-6-2。
建立工程坐标系的方案

建立工程坐标系的方案一、引言工程坐标系是工程测量中的重要组成部分,它是确保工程测量准确和可靠的基础。
建立工程坐标系最终目的是为了实现工程测量和工程施工的精准定位和方位的控制。
在现代工程中,常见的工程坐标系统有地理坐标系、平面坐标系和高程坐标系等。
建立工程坐标系的方案需要考虑到工程地质特征、地理环境以及测量技术等多方面因素,才能确保建立的工程坐标系满足实际工程需求。
二、确定建立工程坐标系的目标1. 确定工程测量的需要:首先需要明确工程测量的具体需要,比如工程地质调查、施工测量、工程监测等。
不同的测量需要可能对工程坐标系的要求不同,因此需要根据具体需求来确定建立工程坐标系的目标。
2. 确定测量精度要求:根据工程的实际情况和测量的精度要求,确定建立工程坐标系的精度标准。
比如,对于高精度测量,需要建立高精度的工程坐标系,而对于一般工程测量,可能只需要建立一般精度的工程坐标系。
3. 考虑工程地质和地理环境:工程坐标系的建立还需要考虑工程地质特征和地理环境因素,比如地表形态、地形地貌、地质构造等因素。
这些因素对工程坐标系的建立会产生一定的影响,需要进行综合分析和考虑。
三、工程坐标系的建立方案1. 工程坐标系的选取根据工程测量的需要和测量精度的要求,选取合适的工程坐标系。
常见的工程坐标系有直角坐标系、极坐标系等,需要根据具体情况选取合适的坐标系。
2. 坐标系原点的确定确定坐标系原点是建立工程坐标系的关键步骤。
原点的确定需要考虑到工程实际需求、测量精度和方便性等因素。
原点的选取应尽量符合工程测量和施工的实际需求,并且易于控制和使用。
3. 坐标系的坐标轴方向确定坐标系的坐标轴方向是建立工程坐标系的重要环节。
坐标轴方向的确定应符合工程测量的需要,比如工程方向、施工方位等。
同时,还需要考虑实际控制的便利性和测量的准确性等因素。
4. 坐标系统的缩放比例确定坐标系统的缩放比例是工程坐标系建立的重要步骤。
根据实际工程测量的需求和精度要求,确定合适的缩放比例。
建立空间直角坐标系的几种方法

建立空间直角坐标系的几种方法坐标法是利用空间向量的坐标运算解答立体几何问题的重要方法,运用坐标法解题往往需要建立空间直角坐标系.依据空间几何图形的结构特征,充分利用图形中的垂直关系或构造垂直关系来建立空间直角坐标系,是运用坐标法解题的关键.下面举例说明几种常见的空间直角坐标系的构建策略.一、利用共顶点的互相垂直的三条棱构建直角坐标系例1 已知直四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,底面ABCD 是直角梯形,∠A 为直角,AB ∥CD ,AB =4,AD =2,DC =1,求异面直线BC 1与DC 所成角的余弦值.解析:如图1,以D 为坐标原点,分别以DA 、DC 、DD 1所在直线为x 、y 、z 轴建立空间直角坐标系,则C 1(0,1,2)、B (2,4,0),∴1(232)BC =--,,,(010)CD =-,,. 设1BC 与CD 所成的角为θ,则11317cos 17BC CD BC CD θ==. 二、利用线面垂直关系构建直角坐标系例2 如图2,在三棱柱ABC -A 1B 1C 1中,AB ⊥侧面BB 1C 1C ,E 为棱CC 1上异于C 、C 1的一点,EA ⊥EB 1.已知2AB =,BB 1=2,BC =1,∠BCC 1=3π.求二面角A -EB 1-A 1的平面角的正切值.解析:如图2,以B 为原点,分别以BB 1、BA 所在直线为y 轴、z 轴,过B 点垂直于平面AB 1的直线为x 轴建立空间直角坐标系.由于BC =1,BB 1=2,AB =2,∠BCC 1=3π, ∴在三棱柱ABC -A 1B 1C 1中,有B (0,0,0)、A (0,0,2)、B 1(0,2,0)、31022c ⎛⎫- ⎪ ⎪⎝⎭,,、133022C ⎛⎫ ⎪ ⎪⎝⎭,,. 设302E a ⎛⎫ ⎪ ⎪⎝⎭,,且1322a -<<, 由EA ⊥EB 1,得10EA EB =,即3322022a a ⎛⎫⎛⎫---- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,,,,233(2)2044a a a a =+-=-+=,∴13022a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭, 即12a =或32a =(舍去).故31022E ⎛⎫ ⎪ ⎪⎝⎭,,. 由已知有1EA EB ⊥,111B A EB ⊥,故二面角A -EB 1-A 1的平面角θ的大小为向量11B A 与EA 的夹角.因11(002)B A BA ==,,,31222EA ⎛⎫=-- ⎪ ⎪⎝⎭,, 故11112cos 3EA B A EA B A θ==,即2tan 2θ=三、利用面面垂直关系构建直角坐标系例3 如图3,在四棱锥V -ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .(1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的余弦值.解析:(1)取AD 的中点O 为原点,建立如图3所示的空间直角坐标系.设AD =2,则A (1,0,0)、D (-1,0,0)、B (1,2,0)、V (0,0,3),∴AB =(0,2,0),VA =(1,0,-3).由(020)(103)0AB VA =-=,,,,,得 AB ⊥VA .又AB ⊥AD ,从而AB 与平面VAD 内两条相交直线VA 、AD 都垂直,∴ AB ⊥平面VAD ;(2)设E 为DV 的中点,则13022E ⎛⎫- ⎪ ⎪⎝⎭,, ∴33022EA ⎛⎫=- ⎪ ⎪⎝⎭,,,33222EB ⎛⎫=- ⎪ ⎪⎝⎭,,,(103)DV =,,.∴332(103)022EB DV ⎛⎫=-= ⎪ ⎪⎝⎭,,,,, ∴EB ⊥DV .又EA ⊥DV ,因此∠AEB 是所求二面角的平面角.∴21cos 7EA EBEA EB EA EB ==,. 故所求二面角的余弦值为217. 四、利用正棱锥的中心与高所在直线构建直角坐标系例4 已知正四棱锥V -ABCD 中,E 为VC 中点,正四棱锥底面边长为2a ,高为h .(1)求∠DEB 的余弦值;(2)若BE ⊥VC ,求∠DEB 的余弦值.解析:(1)如图4,以V 在平面AC 的射影O 为坐标原点建立空间直角坐标系,其中O x ∥BC ,O y ∥AB ,则由AB =2a ,OV =h ,有B (a ,a ,0)、C (-a ,a ,0)、D (-a ,-a ,0)、V (0,0,h )、222a a h E ⎛⎫- ⎪⎝⎭,, ∴3222a h BE a ⎛⎫=-- ⎪⎝⎭,,,3222a h DE a ⎛⎫= ⎪⎝⎭,,. ∴22226cos 10BE DEa h BE DE a h BE DE -+==+,, 即22226cos 10a h DEB a h -+=+∠; (2)因为E 是VC 的中点,又BE ⊥VC ,所以0BE VC =,即3()0222a h a a a h ⎛⎫----= ⎪⎝⎭,,,,, ∴22230222a h a --=,∴2h a =. 这时222261cos 103a h BE DE a h -+==-+,,即1cos 3DEB =-∠. 引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.下面以高考考题为例,剖析建立空间直角坐标系的三条途径.五、利用图形中的对称关系建立坐标系图形中虽没有明显交于一点的三条直线,但有一定对称关系(如正三棱柱、正四棱柱等),利用自身对称性可建立空间直角坐标系.例5已知两个正四棱锥P -ABCD 与Q -ABCD 的高都为2,AB =4.(1)证明:PQ ⊥平面ABCD ;(2)求异面直线AQ 与PB 所成的角;(3)求点P 到平面QAD 的距离.简解:(1)略;(2)由题设知,ABCD 是正方形,且AC ⊥BD .由(1),PQ ⊥平面ABCD ,故可分别以直线CA DB QP ,,为x ,y ,z 轴建立空间直角坐标系(如图1),易得(2202)(0222)AQ PB =--=-,,,,,,1cos 3AQ PB AQ PB AQ PB <>==,. 所求异面直线所成的角是1arccos 3. (3)由(2)知,点(0220)(22220)(004)D AD PQ -=--=-,,,,,,,,. 设n =(x ,y ,z )是平面QAD 的一个法向量,则00AQ AD ⎧=⎪⎨=⎪⎩,,n n 得200x z x y ⎧+=⎪⎨+=⎪⎩,,取x =1,得(112)--,,n =.点P 到平面QAD 的距离22PQ d ==nn .点评:利用图形所具备的对称性,建立空间直角坐标系后,相关点与向量的坐标应容易得出.第(3)问也可用“等体积法”求距离.。
建立空间直角坐标系的几种方法

建立空间直角坐标系的几种方法1.给定坐标轴方向及原点位置:最直接的方法是给定三个坐标轴的方向及原点位置。
通常,我们选择三个相互垂直的轴,并确定它们的正方向。
例如,我们可以选择X轴向右,Y轴向上,Z轴垂直于XOY平面向外,然后选择原点为坐标轴的交点。
通过这种方法,我们就可以建立一个三维直角坐标系。
2.使用原点和两个已知点:在给定两个已知点和原点的情况下,我们可以建立一个空间直角坐标系。
首先,我们将其中一个已知点作为坐标轴上的一个点,然后确定一个与此轴垂直的第二个轴。
接下来,我们确定第三个轴的方向,使其与前两个轴正交,并选择原点位置。
通过这种方法,我们可以构建一个三维直角坐标系。
3.使用平面和轴的交点:另一种建立空间直角坐标系的方法是确定两个平面及其在坐标轴上的交点。
首先,我们选择平面XY作为参考平面,并将其与X轴和Y轴在原点处的交点作为坐标轴上的两个点。
然后,选择两个非共线的轴分别与平面XZ和平面YZ正交,并确定它们的正方向。
通过这种方法,我们可以建立一个三维直角坐标系。
4.使用向量运算:通过向量运算的方法可以建立空间直角坐标系。
首先,选择一个已知向量为其中一个坐标轴的向量。
然后,选择另一个与已知向量相互垂直的向量,并进行正规化。
接下来,使用向量叉积运算确定第三个轴的方向,并对其进行正规化。
最后,选择原点位置。
通过这种方法,我们可以建立一个三维直角坐标系。
这些方法都是建立空间直角坐标系的常见方法,可以根据具体情况选择合适的方法进行建立。
建立坐标系的必要性

建立坐标系的必要性要想正确的检测零件,有效报告测量数据,就必须建立一个正确工件坐标系, 以便在3D的空间内定义工件在测量机上的相对位置。
建立工件坐标系的三个步骤建立工件坐标系,是指根据工件来设置投影面、轴的方向、原点的位置。
坐标系可以通过以下 3 个步骤进行设置。
1. 零件找正---基准面补正测量平面:是指选择垂直于零件轴线的平面而不是垂直于CMM坐标轴的平面,找正零件:即确定第一轴线(工件的空间倾斜的设置 ),使Z 轴与平面垂直;2. 旋转轴---基准轴补正设置平面内的轴(例:XY面内的X轴/Y轴)的方向,使CMM的一轴与零件一轴线相互关联起来。
3. 原点设置原点位置的确定(例:X=0、Y=0、Z=0)在测量了所需的特征后,即可创建坐标系。
定义基准元素时的注意事项用于创建工件坐标系以及测量工件时的元素,在测量时应尽可能的大。
以下是应遵循的基本原则:–选择至少三个不同的测量元素,可以全是面,但一定不是相同的面。
–不要选择平行平面做为不同的基准(如立方体及圆柱的端面)。
–对于每个元素,测量时的点尽可能分散(测量圆柱时,两个截面距离尽可能远)–第一基准必须是一个三维元素(如:平面、圆柱、圆锥、或一个球——如果其它球定义了三个零点)–第二基准一定是个二维元素(如线),也可以是三维元素(或圆、椭圆,如果其它元素在第一基准面上定义了坐标系原点中的两个位置。
)–第三基准是一个典型的三维元素(点),但也可以选两维或三维的参考元素。
迭代法建坐标系规则当执行迭代法建坐标系时,应遵守以下一般规则:对于特征组中的每个元素,PC-DMIS 都需要测定值和理论值第一组元素的法线矢量必须大致平行。
此规则的一项例外是特征组中只使用三个特征的情况如果使用测定点(矢量、棱或曲面),则需要用所有三组元素(三个用于找平的特征、两个用于旋转的特征和一个用于设置原点的特征)来定义坐标系您可以使用任何特征类型,但三维元素是定义更完善的元素,因此可以提高精确度可能的3D 元素包括薄壁件圆、槽、柱体、球体或隅角点。
321法则建立坐标系

方法四:平面-圆-圆建立坐标系
图三:平面、圆、圆建立坐标系
步骤一:采集平面1; 步骤二:Ctrl+Alt+A,找正平面1;(作为圆1和圆2的投影 平面) 步骤三:采集圆1,采集圆2; 步骤四:Ctrl+Alt+A,同时选择两圆旋转;平面1=第一轴 =0;圆1=第二轴=第三轴=0或者圆2=第二轴=第三轴=0)
321法则建立坐标系
一.什么是321法则建立坐标系? 321建坐标就是一个定位的过程,也就是机械加工工艺里面所谓的6点定位法则, XYZ方向的移动,以及XYZ方向的旋转。 二.321原则建立坐标系的步骤: 步骤一:找正(确定坐标系的第一轴) 步骤二:旋转(确定坐标系的第二轴) 步骤三:平移(确定坐标系的原点,X=0,Y=0,Z=0) 注意事项: 1.可以用来找正的元素:平面、圆柱、圆锥; 2.可以用来旋转的元素:直线、圆柱、圆锥、两圆; 3.平移元素:任意(默认元素质心点)
注意事项:1.旋转方向由先选择的圆指向后选择的圆。
方法五:圆柱-直线-点建立坐标系
图四:圆柱、直线、点建立坐标系
• 步骤一:采集圆柱1; • 步骤二:Ctrl+Alt+A,找正圆柱1;(作为直线1的工 作平面) • 步骤三:采集直线1,采集点1; • 步骤四:Ctrl+Alt+A,旋转直线1;圆柱1=第二轴= 第三轴=0;点1=第一轴=0) • 注意事项:1.圆柱矢量方向由起始层指向终止层; • 2.注意点所在的平面应该在限制第一轴的方 向上。
下面介绍常用的5种建立坐标系的方法:
方法一:平面-线-线建立坐标系
图一:平面、线、线建立坐标系
坐标系建立
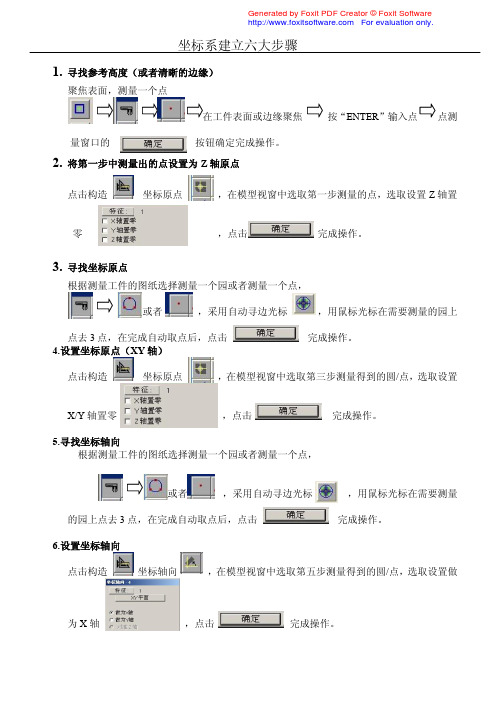
坐标系建立六大步骤
1. 寻找参考高度(或者清晰的边缘)
聚焦表面,测量一个点
按“ENTER ”输入点点测
量窗口的 按钮确定完成操作。
2. 将第一步中测量出的点设置为Z 轴原点
点击构造 坐标原点 ,在模型视窗中选取第一步测量的点,选取设置Z 轴置
零 ,点击 完成操作。
3. 寻找坐标原点
根据测量工件的图纸选择测量一个园或者测量一个点,
或者 ,采用自动寻边光标 ,用鼠标光标在需要测量的园上
点去3点,在完成自动取点后,点击 完成操作。
4.设置坐标原点(XY 轴)
点击构造 坐标原点 ,在模型视窗中选取第三步测量得到的圆/点,选取设置
X/Y 轴置零 ,点击 完成操作。
5.寻找坐标轴向
根据测量工件的图纸选择测量一个园或者测量一个点,
或者 ,采用自动寻边光标 ,用鼠标光标在需要测量
的园上点去3点,在完成自动取点后,点击 完成操作。
6.设置坐标轴向
点击构造 坐标轴向 ,在模型视窗中选取第五步测量得到的圆/点,选取设置做
为X 轴 ,点击 完成操作。
Generated by Foxit PDF Creator © Foxit Software For evaluation only.。
大地坐标系的建立

③通过 K、K、NK
和 X、Y、 Z
得到 LK、BK、H K、AK
④完成参考椭球定位与定向
3.2 广义垂线偏差和拉普拉斯方程式
B sin
L
sec
cos
tan
A tan cos sec
X
c os Y
cos X cosY
cos X cosY cos Z 1
sin X X ,
sin Y Y ,
sin Z
Z
sin X sin Y sin X sin Z sin Y sin Z 0
os H
cosB cosL
L
"
0
(M
N H )a
e2
sin
B cosB"
N a
(1
e2
sin 2
B)
cosL "
(N H ) cosB
sin B sin L "
M H cosB sin L
0
c os B M H
"
sin B
X 0
3.7 1954年北京坐标系
1954年北京坐标系可以认为是前苏联1942年坐标系的延 伸。它的原点不在北京,而在前苏联的普尔科沃。相 应的椭球为克拉索夫斯基椭球。
椭球参数有较大误差。 参考椭球面与我国大地水准面存在着自西向东明显的
系统性的倾斜,在东部地区大地水准面差距最大达 +68m。 几何大地测量和物理大地测量应用的参考面不一致。 定向不明确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
零件坐标系在精确的测量中,正确地建坐标系,与具有精确的测量机,校验好的测头一样重要。
由于我们的工件图纸都是有设计基准的,所有尺寸都是与设计基准相关的,要得到一个正确的检测报告,就必须建立零件坐标系,同时,在批量工件的检测过程中,只需建立好零件坐标系即可运行程序,从而更快捷有效。
机器坐标系MCS与零件坐标系PCS:在未建立零件坐标系前,所采集的每一个特征元素的坐标值都是在机器坐标系下。
通过一系列计算,将机器坐标系下的数值转化为相对于工件检测基准的过程称为建立零件坐标系。
PCDMIS建立零件坐标系提供了两种方法:“3-2-1”法、迭代法。
一、坐标系的分类:1、第一种分类:机器坐标系:表示符号STARTIUP(启动)零件坐标系:表示符号A0、A1…2、第二种分类:直角坐标系:应用坐标符号X、Y、Z极坐标系:应用坐标符号A(极角)R(极径)H(深度值即Z值)二、建立坐标系的原则:1、遵循原则:右手螺旋法则右手螺旋法则:拇指指向绕着的轴的正方向,顺着四指旋转的方向角度为正,反之为负。
2、采集特征元素时,要注意保证最大范围包容所测元素并均匀分布;三、建立坐标系的方法:(一)、常规建立坐标系(3-2-1法)应用场合:主要应用于PCS的原点在工件本身、机器的行程范围内能找到的工件,是一种通用方法。
又称之为“面、线、点”法。
建立坐标系有三步:1、找正,确定第一轴向,使用平面的法相矢量方向2、旋转到轴线,确定第二轴向3、平移,确定三个轴向的零点。
适用范围:①没有CAD模型,根据图纸设计基准建立零件坐标系②有CAD模型,建立和CAD模型完全相同的坐标系,需点击CAD=PART,使模型和零件实际摆放位置重合第一步:在零件上建立和CAD模型完全相同的坐标系第二步:点击CAD=PART,使模型和零件实际摆放位置重合建立步骤:●首先应用手动方式测量建立坐标系所需的元素●选择“插入”主菜单---选择“坐标系”---进入“新建坐标系”对话框●选择特征元素如:平面PLN1用面的法矢方向作为第一轴的方向如Z正,点击“找平”。
●选择特征元素如:线LIN1用线的方向作为坐标系的第二个轴向如X正,点击“旋转”。
●选择特征元素如:点PNT6,用点的X坐标分量作为坐标系的X方向的零点,然后点击原点。
线LIN1,用线的Y坐标分量作为坐标系的Y方向的零点,然后点击原点。
平面PLN1,用面的Z坐标分量作为坐标系的Z方向的零点,然后点击原点。
上述步骤完成后,如果有CAD模型,需要执行CAD=工件,使模型和零件实际摆放位置重合●最后,按“确定”按钮,即完成零件坐标系的建立。
●验证坐标系原点-------将测头移动到PCS的原点处,查看PCDMIS界面右下角“X、Y、Z”(或者打开侧头读出窗口:CTRL+W)三轴坐标值,若三轴坐标值近似为零,则证明原点正确;轴向--------将其中两个坐标轴锁定,只移动未锁定的坐标轴,查看坐标值的变化,验证轴向是否正确。
此方法还可引申为一个平面、两个圆;一个圆柱、两个圆(球)等。
注意:在手动测量特征元素时,必须考虑元素的工作平面(投影面),因此在手动测量完面后可以先建立一个坐标系,给以后手动测量特征一个正确的投影面。
(eg.装夹倾斜,线的投影面不再是Z+,而是工件的上平面)(二)、坐标系的平移与旋转坐标系的平移:即坐标系的方向不变,坐标原点移动到一个新的位置。
操作步骤:A:选择平移的坐标轴如:B:在偏置距离的方框里输入偏移的距离C:点击原点:坐标系的旋转:即围绕着某个坐标轴旋转一定的角度,从而得到一个新的坐标系。
旋转角度正负的确定:由右手螺旋法则判定。
操作步骤:A:选择旋转的坐标轴:B:输入旋转的角度:C:点击旋转:(三)、迭代法建立零件坐标系1、应用场合:主要应用于PCS的原点不在工件本身、或无法找到相应的基准元素(如面、孔、线等)来确定轴向或原点,多为曲面类零件(汽车、飞机的配件,这类零件的坐标系多在车身或机身上)。
2、用于建坐标系的元素及相关要求:A:圆、球、柱、槽①需要的特征数:3②需具备的条件:有理论值或CAD模型③迭代次数:1④原理:此类元素为三维元素,1次即可达到精确测量注:薄壁件圆、槽和柱体至少需要三个样例测点(指定特征所在的平面)。
B:矢量点、曲面点、边界点①需要的特征数:6②需具备的条件:有理论值及矢量方向或CAD模型1、第1、2、3点的法矢方向尽量一致2、第4、5点的法矢方向尽量一致,且与前三点矢量方向垂直。
3、第6点法矢方向与前5点法矢方向尽量垂直。
③迭代次数:1次或多次或无法迭代成功。
④原理:首先,PC-DMIS 将测定数据“最佳拟合”到标称数据。
接着,PC-DMIS检查每个测定点与标称位置的距离。
如果距离大于在点目标半径框中指定的量,PC-DMIS 将要求重新测量该点,直至所有测定点都处于“公差”范围内。
使用测定点的困难在于只有在建坐标系后,才能知道在何处进行测量。
这样就存在一个问题:必须在建坐标系之前测量点。
而三维元素在用途方面的定义就是第一次即可精确测量的元素。
注:1、尽量使用三维元素如:圆、槽、柱体、球体或隅角点,可提高测量精度。
2、PC-DMIS 的一项特殊功能是允许槽的中心点根据需要在轴上上下滑动。
因此,如果将槽用作原点特征组的一部分,迭代法建坐标系就无法会聚。
要将槽用作原点特征组的一部分,一种可能的方法是首先用槽构造一个点,然后将原点特征组中使用该构造点。
建议不要将槽用作迭代法建坐标系的原点特征组的一部分。
(槽的加工误差和定位误差比较大,即使使用它们,也不要在最后找正圆点的时候使用,使用槽建立的坐标系,但轴方向的误差不一定为零)3、建立迭代法坐标系步骤:(以矢量点建坐标系为例)●(1)导入数模,观察方向●(2)手动模式下取得基准的理论值,在手动模式下用自动测量命令测元素●(3)选定执行这些元素,按提示手动测量这些元素,取得在机床坐标系下的实测值●(4)迭代,找正、旋转、原点。
●(5)按提示自动迭代●自动测量矢量点没有CAD模型,而有理论点的话,在点坐标位置输入区输入理论点坐标,在法线矢量输入区输入点坐标的矢量方向,点击创建。
(注意:测量不要勾选)如果有CAD模型,可直接在CAD模型上选取特征点,PC-DMIS会自动在点坐标显示区和法线矢量显示区计算出特征点的坐标及矢量。
并将点的性质设为“标称值”点击创建。
●重复上述步骤,共得到6个点的测量程序。
●在第一个测点之前,将测量方式改为手动模式(注意:新建一个程序,模式就为手动模式),标记所有的测点程序,并运行程序。
●所有点测量完毕,此时PC-DMIS已得到两组数据,即一套理论点数据,一套实测点数据。
●进入“插入”主菜单---“坐标系”---“新建坐标系”---进入“迭代法”建坐标系迭代法建坐标系对话框●选择矢量方向一致的前三个点,点击“选择”按钮,用于找平。
●选择第4、5点,点击“选择”按钮,用于旋转。
●选择最后1点,点击“选择”按钮,用于确定原点。
●选择“一次全部测量”●设定点目标半径:不小于0.5mm●选择“确定”按钮,PC-DMIS 将测定数据“最佳拟合”到标称数据,并提示“是否立即测量所有迭代法建坐标系的特征”回答“是”PC-DMIS将每测一点,提示一次,接着,PC-DMIS 检查每个测定点与标称位置的距离。
如果距离大于在点目标半径框中指定的量,PC-DMIS 将要求重新测量该点,直至所有测定点都处于“公差”范围内。
对于,第一次进行自动迭代,通常选择“一次全部测量”。
4、迭代法坐标系参数设置说明:找平- 3:至少三个选定特征。
此组特征将使平面拟合特征的质心,以建立当前工作平面法线轴的方位。
旋转-2:至少两个选定特征。
该组特征将使拟合直线特征,从而将第二个轴向旋转到该方向。
注:如果未标记任何特征,坐标系将使用“找平”部分中的倒数第二和第三个特征。
原点-1:设置原点时必须使用一个特征。
此特征组用于将零件原点平移(或移动)到指定位置。
注:如果未标记任何特征,坐标系将使用“找平”部分中的最后一个特征。
全部测量至少一次:●PC-DMIS 将以DCC 模式对所有输入特征至少重新测量一次。
●它们将按照“编辑”窗口中迭代法建坐标系命令所指定的顺序来进行测量。
●PC-DMIS 将在测量特征前给出一个消息框,显示将要测量的特征。
●在接受移动之前,请确保测头能够接触指定特征而不会与零件发生碰撞。
●将不会执行在每个特征之前或之后找到的存储移动,但会执行侧头转角。
●在对所有特征测量至少一次后,对于未命中其点目标半径目标的点,将继续对特征进行重新测量。
●对于第一次用迭代法建立坐标系通常使用全部测量至少一次注:在此模式下,由于圆的位置从不改变,PC-DMIS 测量圆的次数不会多于一次。
指定元素测量:PC-DMIS 将以DCC 模式从起始标号处至少重新执行一次。
如果提供起始标号●PC-DMIS 将从该定义标号重新执行如果未提供起始标号●PC-DMIS 将从程序中迭代法建坐标系命令所使用的第一个测定特征开始重新执行。
●如果第一个特征之前有存储移动点,PC-DMIS 还将执行这些移动点。
●重新执行过程将持续到迭代法建坐标系命令所使用的最后一个测定特征为止。
●如果最后一个测定特征之后有存储移动,将不会执行这些移动。
重新执行一旦完成,PC-DMIS 将重新计算坐标系,并测试所有测定输入点,检查它们是否都处于点目标半径值所指定的目标半径内。
●如果它们都处于目标半径内,则无需继续重新执行,PC-DMIS 将认为迭代法建坐标系命令已完成。
●如果有任何点未命中目标区域,则将按上述方法重新执行程序的相同部分。
如果未定义起始标号:●PC-DMIS 将转到组成迭代法建坐标系的第一个特征,从此处开始进行DCC 测量点目标半径:用于指定在坐标系中用作输入的测定点特征的目标半径公差。
测定输入点包括以下类型:●测定/点●自动/矢量点●自动/棱点●自动/曲面点●自动/角度点注:切勿将矢量点目标半径的值设置得太小(如 50 微米)。
许多 CMM 无法准确定位测头,使其接触极小目标上的每个测定点。
所以最好将公差设置在 0.5 毫米左右。
如果重新测量无休止地继续,则将增加该值。
实际上,PC-DMIS 会在每个矢量点、曲面点或棱点的理论位置周围设置一个柱形公差区。
此公差区的半径就是在对话框中指定的点目标半径。
点目标半径只影响测定点。
夹具公差:用于键入一个拟合公差值,PC-DMIS 将根据该值对组成迭代法坐标系的元素与其理论值进行比较,如果有一个或多个输入特征在其指定基准轴上的误差超过此公差值,PC-DMIS 将自动转到误差标号(如果有)。
如果未提供误差标号,PC-DMIS 将显示一条错误消息,指出每个基准方向上的误差。
然后,您将可以选择接受基准并继续执行零件程序的其余部分,或取消零件程序的执行。
