坐标系建立
如何建立坐标系

如何建立坐标系?恰当地建立坐标系,可以使解题简便.通常以加速度a 的方向为x 轴的正方向,与此垂直的方向为y 轴,建立直角坐标系.将物体所受到的力按x 轴、y 轴方向分解,分别求得x 轴和y 轴上的合力F x 和F y ,根据力的独立作用原理得方程组F x =ma ,F y =0.但有时用这种方法得到的方程组求解较为烦琐,因此在建立直角坐标系时,也可根据物体的受力情况,使尽可能多的力位于两坐标轴上而分解加速度a 得a x 和a y ,根据牛顿第二定律得方程组F x =ma x ,F y =ma y 求解.究竟采用哪种方法,要视具体情况灵活使用.例1 质量为10kg 的物体放在水平面上,物体与水平面间的动摩擦因数为0.2,如果用大小为40 N ,方向斜向上与水平方向的夹角为37°的恒力作用,使物体沿水平面向右运动,(g 取10 m/s 2, sin370=0.6,cos370=0.8),求:(1)物体运动的加速度大小;(2)若物体由静止开始运动,需要多长时间速度达到8.4m/s?物体的位移多大?答案:(1)a =1.68m/s 2 (2)5 s 21m【解析】(1)以物体为研究对象,首先对物体进行受力分析,如图4-6-1所示.建立平面直角坐标系把外力沿两坐标轴方向分解.设向右为正方向,依据牛顿第二定律列方程:F ·cos θ-f =m aF ·sin θ+F N =mgf =μF N整理后得到:a =m F mg F )sin (cos θμθ⋅--⋅ 代入相关数据,解得物体运动加速度大小a =1.68m/s 2.(2)因为物体做匀加速直线运动,所以根据运动学公式可知:v t =v 0+a t物体运动时间为:t =a v t =68.14.8s =5 s s =v 0t +21a t 2 物体的位移大小为:s =21a t 2=21×1.68×52m =21m . 说明:(1)这是一道已知物体的受力情况,确定物体的运动情况的习题;(2)本题中物体受4个力作用(大于3个力作用),一般在处理力的关系时用正交分解法;(3)支持力不是外力在竖直方向上的分力;重力大小不等于地面给予的支持力.【点评】本题是已知物体的受力求物体的运动情况,关键在于对物体的受力分析要正确,应用牛顿第二定律求出加速度,再由运动学公式求解.图4-6-1例2 如图4-6-2所示,某商场内电梯与水平面夹角为300,当电梯加速向上运动时,人对梯面压力为其重力的56,则人与梯面间的摩擦力是其重力的多少倍? 答案:mg F f 53= 【解析】选梯面上的人为研究对象,对其进行受力分析,重力和支持力都不难分析,至于人与梯面间的摩擦力是本题分析的难点,由于人与电梯具有相同的加速度,故人所受合外力沿斜面向上,因而人所受摩擦力一定沿梯面水平向右;如图4-6-3所示,水平、竖直建立直角坐标系,将加速度在两个坐标轴上分解,设电梯倾角为θ,加速度为a ,在x 轴和y 轴分别列方程,得θcos ⋅=ma F f ①θsin ⋅=-ma mg F N ②由题意,知 mg F N 56= ③ ①②③三式联立,代入数据,得 mg F f 53=【点评】本题是已知物体的运动情况求物体的受力,关键在于对物体的受力分析要正确,能够建立合适的坐标系(本题也可以沿斜面和垂直斜面建坐标系,同学们可以试一试),使方程和求解都更加简洁.在用牛顿定律解决问题时,有时可以分解力,有时可以分解加速度,看哪一种更为简单.图4-6-2。
空间直角坐标系的建立

空间直角坐标系的建立空间直角坐标系是用于表示空间中一个点位置的一种系。
建立空间直角坐标系需要确定三个互相垂直的坐标轴,分别沿着三个方向选取单位长度,用来表示空间中的位置。
在这个坐标系中,根据对应的坐标值可以唯一地确定一个点的位置。
建立空间直角坐标系的方法和建立平面直角坐标系非常类似。
下面我们来介绍一下建立空间直角坐标系的步骤。
步骤一:确定原点建立空间直角坐标系需要确定一个起点,称为原点。
原点通常位于三个坐标轴的交点处。
可以任选一个位置作为原点。
步骤二:确定坐标轴方向建立空间直角坐标系需要确定三个互相垂直的坐标轴,它们固定的方向通常为正方向。
我们可以先确定一个坐标轴方向,比如说选择x轴(也可以选择y轴或z轴作为起点)。
确定x轴的正方向后,可以确定y轴的正方向与z轴的正方向。
y轴的正方向可以沿着x 轴与z轴之间垂直的方向上,z轴的正方向可以沿着x轴与y轴之间垂直的方向上。
步骤三:选取单位长度建立空间直角坐标系需要确定沿着坐标轴的单位长度。
我们需要选择一个单位长度用来表示空间中的位置。
通常情况下,我们可以选择1个单位长度。
空间直角坐标系的表示方法比较灵活。
通常情况下,我们可以用一个有序数对表示二维平面上的点,例如(1, 2),用一个有序三元组表示三维空间中的点,例如(1, 2, 3)。
其中,第一个元素对应x轴的坐标值,第二个元素对应y轴的坐标值,第三个元素对应z轴的坐标值。
在空间直角坐标系中,一个点的坐标可以表示为(x,y,z)。
其中x、y、z的取值范围是实数集合。
点的坐标是有序三元组(x,y,z)。
空间直角坐标系在数学中扮演了非常重要的角色,可用于描述空间中的物理现象,建立三维模型等等。
掌握建立空间直角坐标系的方法,对深入理解空间的坐标系,解决三维空间中的几何问题非常关键。
建立直角坐标系的原则

建立直角坐标系的原则建立直角坐标系是一项日常使用的有用工具,它有助于确定两个点之间的距离和方向。
它还可以帮助我们描绘出空间的几何形状。
鉴于其重要性,建立直角坐标系的原则也变得特别重要。
首先,建立直角坐标系的原则之一是建立一个第一坐标轴,也称作x轴,它是建立坐标系的基础。
它是把坐标系分成两条线,线的两端称为原点和端点。
原点是坐标系中的起点,代表x轴的数值为0,而端点则代表x轴的数值为最大或最小,这取决于给定的参数。
第二,建立第二个坐标轴,也称作y轴,它是建立坐标系的支柱。
它的原点和端点的位置是垂直于x轴的,并且在建立y轴的过程中,应该确保轴的原点和x轴的原点完全重合,而y轴的端点则在x轴和y轴上都有一个数值,这取决于给定的参数,同样也可以为最大或最小。
然后,基于以上两条轴建立第三条坐标轴,即z轴,它垂直于x 轴和y轴,并以原点为起点,端点也有一个数值,这取决于给定的参数,可以为最大或最小。
最后,建立三条轴后,就可以创建更多坐标点,使三个轴全部被描述出来,并有一个坐标系作为确定两个点之间的距离和方向的工具。
建立直角坐标系的基础设置会关系到空间的几何形状,因此,建立直角坐标系的原则是经过精心研究的,必须精确的确定每条轴的原点和端点的位置,并确保它们的相对位置适当。
此外,在建立坐标系的过程中,我们还需要注意每个分量,确保它们满足原则。
至此,建立直角坐标系的原则可以分为四个部分:第一,建立一个第一坐标轴,也称作x轴,并确定原点和端点的位置;第二,建立一个第二坐标轴,也称作y轴,并确定原点和端点的位置;第三,建立一个第三坐标轴,也称作z轴,并确定原点和端点的位置;第四,在构建坐标系的过程中,我们还需要注意每个分量,以确保坐标系满足原则。
建立直角坐标系是一种重要的工具,能够用在许多不同的场合,尤其是在科学、技术和工程等领域中。
理解和遵循建立直角坐标系的原则,是有效利用坐标系的基础。
三坐标建立坐标系321方法

三坐标建立坐标系321方法在几何学中,坐标系是一种用于描述点的位置的体系。
三坐标建立坐标系321方法是一种常见的坐标系建立方式,它使用三个轴来表示三维空间中的点的位置。
本文将介绍三坐标建立坐标系321方法的原理和应用。
一、三坐标建立坐标系321方法的原理三坐标建立坐标系321方法是基于数学的向量理论和坐标转换原理。
它使用三个轴来定义一个三维空间中的点的位置。
这三个轴分别称为X轴、Y轴和Z轴。
X轴与Y轴的交点称为原点,Z轴垂直于X 轴和Y轴。
在三坐标建立坐标系321方法中,我们需要先确定X轴、Y轴和Z 轴的方向。
通常情况下,X轴沿着东西方向,Y轴沿着南北方向,Z 轴沿着垂直于地面的方向。
然后,我们需要确定X轴、Y轴和Z轴的单位长度,通常以米为单位。
二、三坐标建立坐标系321方法的应用三坐标建立坐标系321方法在航空航天、工程测量、地理信息系统等领域有着广泛的应用。
下面将介绍三坐标建立坐标系321方法在航空航天和工程测量中的应用。
1. 航空航天在航空航天领域,三坐标建立坐标系321方法被用来确定飞行器在空间中的位置和姿态。
通过测量飞行器在X轴、Y轴和Z轴上的位移和旋转角度,可以确定飞行器的位置和姿态,从而实现飞行器的控制和导航。
2. 工程测量在工程测量领域,三坐标建立坐标系321方法被用来确定建筑物和工程设施的位置和形状。
通过测量建筑物和工程设施在X轴、Y轴和Z轴上的坐标和尺寸,可以确定它们的位置和形状,从而实现工程施工和设计。
三、三坐标建立坐标系321方法的优势三坐标建立坐标系321方法具有以下优势:1. 简单易用:三坐标建立坐标系321方法只需确定轴的方向和单位长度,不需要复杂的计算和转换。
2. 精确度高:三坐标建立坐标系321方法可以实现对点的位置和姿态的精确测量和控制。
3. 应用广泛:三坐标建立坐标系321方法在航空航天、工程测量等领域有着广泛的应用,可以满足不同领域的需求。
四、总结三坐标建立坐标系321方法是一种常见的坐标系建立方式,它使用三个轴来表示三维空间中的点的位置。
大地坐标系的建立

③通过 K、K、NK
和 X、Y、 Z
得到 LK、BK、H K、AK
④完成参考椭球定位与定向
3.2 广义垂线偏差和拉普拉斯方程式
B sin
L
sec
cos
tan
A tan cos sec
X
c os Y
cos X cosY
cos X cosY cos Z 1
sin X X ,
sin Y Y ,
sin Z
Z
sin X sin Y sin X sin Z sin Y sin Z 0
os H
cosB cosL
L
"
0
(M
N H )a
e2
sin
B cosB"
N a
(1
e2
sin 2
B)
cosL "
(N H ) cosB
sin B sin L "
M H cosB sin L
0
c os B M H
"
sin B
X 0
3.7 1954年北京坐标系
1954年北京坐标系可以认为是前苏联1942年坐标系的延 伸。它的原点不在北京,而在前苏联的普尔科沃。相 应的椭球为克拉索夫斯基椭球。
椭球参数有较大误差。 参考椭球面与我国大地水准面存在着自西向东明显的
系统性的倾斜,在东部地区大地水准面差距最大达 +68m。 几何大地测量和物理大地测量应用的参考面不一致。 定向不明确
建立坐标系

零件坐标系在精确的测量中,正确地建坐标系,与具有精确的测量机,校验好的测头一样重要。
由于我们的工件图纸都是有设计基准的,所有尺寸都是与设计基准相关的,要得到一个正确的检测报告,就必须建立零件坐标系,同时,在批量工件的检测过程中,只需建立好零件坐标系即可运行程序,从而更快捷有效。
机器坐标系MCS与零件坐标系PCS:在未建立零件坐标系前,所采集的每一个特征元素的坐标值都是在机器坐标系下。
通过一系列计算,将机器坐标系下的数值转化为相对于工件检测基准的过程称为建立零件坐标系。
PCDMIS建立零件坐标系提供了两种方法:“3-2-1”法、迭代法。
一、坐标系的分类:1、第一种分类:机器坐标系:表示符号STARTIUP(启动)零件坐标系:表示符号A0、A1…2、第二种分类:直角坐标系:应用坐标符号X、Y、Z极坐标系:应用坐标符号A(极角)R(极径)H(深度值即Z值)二、建立坐标系的原则:1、遵循原则:右手螺旋法则右手螺旋法则:拇指指向绕着的轴的正方向,顺着四指旋转的方向角度为正,反之为负。
2、采集特征元素时,要注意保证最大范围包容所测元素并均匀分布;三、建立坐标系的方法:(一)、常规建立坐标系(3-2-1法)应用场合:主要应用于PCS的原点在工件本身、机器的行程范围内能找到的工件,是一种通用方法。
又称之为“面、线、点”法。
建立坐标系有三步:1、找正,确定第一轴向,使用平面的法相矢量方向2、旋转到轴线,确定第二轴向3、平移,确定三个轴向的零点。
适用范围:①没有CAD模型,根据图纸设计基准建立零件坐标系②有CAD模型,建立和CAD模型完全相同的坐标系,需点击CAD=PART,使模型和零件实际摆放位置重合第一步:在零件上建立和CAD模型完全相同的坐标系第二步:点击CAD=PART,使模型和零件实际摆放位置重合建立步骤:●首先应用手动方式测量建立坐标系所需的元素●选择“插入”主菜单---选择“坐标系”---进入“新建坐标系”对话框●选择特征元素如:平面PLN1用面的法矢方向作为第一轴的方向如Z正,点击“找平”。
工程测量坐标系有哪几种方法

工程测量坐标系有哪几种方法在工程测量中,建立合适的坐标系是非常重要的,因为它能够准确地描述和记录测量数据。
工程测量坐标系的建立方法有多种,下面将介绍其中几种常用的方法。
1. 绝对坐标系绝对坐标系是一种最基本的坐标系,它以一个固定的参考点作为原点,通过坐标轴来描述空间中的点位置。
在工程测量中,通常使用全球定位系统(GPS)来确定参考点,并根据参考点的经纬度或地理坐标来建立绝对坐标系。
绝对坐标系具有较高的精度和准确性,适用于大型的工程测量项目。
2. 相对坐标系相对坐标系是以一个已知的基点为原点,以基点与其他点之间的相对位置来描述点的位置。
在工程测量中,常常使用基线测量的方法来建立相对坐标系。
基线测量即通过测量一条或多条基线的长度和方向来确定其他点的空间位置。
相对坐标系相对于绝对坐标系来说,精度和准确性稍低一些,但在小范围内的工程测量中仍然具有较高的可靠性。
3. 工程坐标系工程坐标系是一种将三维空间转化为二维平面的坐标系。
在工程测量中,由于实际工程项目往往是在平面上进行的,所以建立工程坐标系可以简化计算和描述。
常见的工程坐标系包括直角坐标系和极坐标系。
直角坐标系通过水平和竖直方向的坐标轴来描述点的位置,而极坐标系则通过点到一个固定点的距离和点与固定点连线的夹角来描述点的位置。
根据实际需要,可以选择适合的工程坐标系进行测量。
4. 局部坐标系局部坐标系是一种以任意点为基点建立的坐标系,在该点可以任意选择坐标轴的方向。
局部坐标系常常用于小范围的工程测量,例如建筑物内部或局部工程项目的测量。
由于局部坐标系的建立是相对灵活的,因此可以根据实际需要选择合适的坐标轴方向,以便更好地描述和计算。
总的来说,工程测量中建立坐标系的方法有多种选择,包括绝对坐标系、相对坐标系、工程坐标系和局部坐标系。
在实际工程项目中,可以根据项目的要求和实际情况选择适合的坐标系,以保证测量数据的准确性和可靠性。
高中物理:坐标系的分类及建立原则
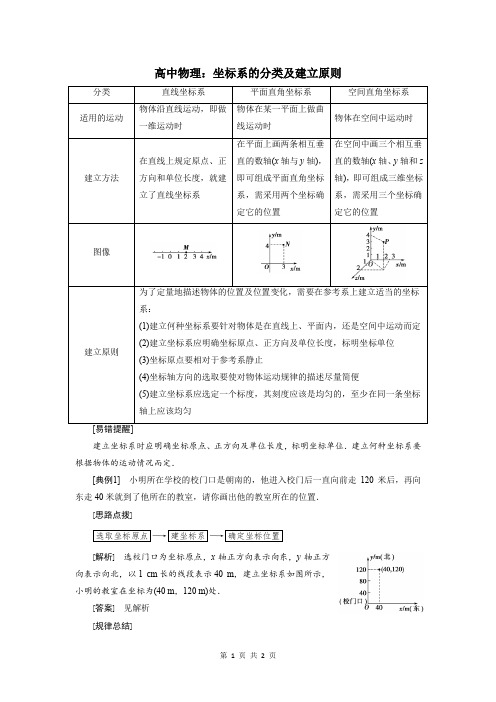
高中物理:坐标系的分类及建立原则
为了定量地描述物体的位置及位置变化,需要在参考系上建立适当的坐标建立坐标系时应明确坐标原点、正方向及单位长度,标明坐标单位.建立何种坐标系要根据物体的运动情况而定.
[典例1] 小明所在学校的校门口是朝南的,他进入校门后一直向前走120米后,再向东走40米就到了他所在的教室,请你画出他的教室所在的位置.
[思路点拨]
选取坐标原点―→建坐标系―→确定坐标位置
[解析] 选校门口为坐标原点,x 轴正方向表示向东,y 轴正方
向表示向北,以1 cm 长的线段表示40 m ,建立坐标系如图所示,
小明的教室在坐标为(40 m ,120 m)处.
[答案] 见解析
[规律总结]
坐标系的建立及坐标值的正负判断
(1)建立何种坐标系由物体的运动特点确定,建立坐标系的原则是能够方便、准确地描述物体的位置及位置变化.
(2)物体在坐标系中的坐标值是正值还是负值,与正方向的规定和原点的位置有关.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
坐标系及其相关参数确定: 一、坐标系确定 (1) Zn-1的确定(转轴轴线) (2) Xn-1:垂直两连杆公垂线xn -1=zn-1 → zn (3) Yn-1 :根据右手定则确定 二、参数确定 (1) 连杆长度ln:zn-1→ zn沿xn-1的距离; (2) 两关节轴扭角n: zn-1 → zn绕xn的转角; (3) dn:两连杆间偏置:xn-1→ xn沿zn-1距离,0; (4) n:两连杆间角度,Xn-1→ Xn绕zn-1的转角,
坐标系及其相关参数确定:
一、坐标系确定
(1) Zn-1的确定(转轴轴线、柱轴方向线) (2) Xn-1、:xn -1=zn-1× zn (3) Yn-1 :根据右手定则确定 二、参数确定
(1) 连杆长度ln:zn-1 → zn沿xn-1的距离,两轴相交0; (2) 两关节轴扭角 n: zn-1 → zn绕xn的转角,-90 ° ; (3) dn :移动关节移动变量; (4) n:移动关节转角为0。
变量。
2) 两个转动关节在空间形成 两轴间90°的扭转;连杆参数 ln—连杆的长度;如果连杆的中 心线被认作x方向并且从关节n-1 到关节n沿xn-1方向有一定距离, 整个杆件可以绕关节n-1转动n 角,该角认为是两连杆夹角,这 个角就是一般转动关节的变量; 同时关节轴被认为是z方向并且 绕zn-1转动;y轴由右手定则确定。
90°; (3) dn :两连杆间偏置:xn-1 → xn沿zn-1距离,
0; (4) n:两连杆间角度,Xn-1→ Xn绕Zn-1的转
角,变量。
3) 两个转动关节相互交 叉垂直轴;两个关节转动轴 相交,连杆参数ln=0;关节 轴被认为是z方向;x方向由 两个z轴确定,y方向由右手 定则确定;dn为偏移值。
坐标系及其相关参数确定:
一、坐标系确定
(1) Zn-1的确定(转轴轴线、柱轴方向线) (2) Xn-1:xn -1=zn-1× zn (3) Yn-1 :根据右手定则确定 二、参数确定
(1) 连杆长度ln:zn-1→ zn沿xn-1的距离,两轴相交为0; (2) 两关节轴扭角 n: zn-1→ zn绕xn的转角,-90 ° ; (3) dn :两连杆间偏置:xn-1→ xn沿zn-1距离,dn; (4) n:连杆绕zn-1的转角,变量。
(1) 连杆长度ln:zn-1 → zn沿xn-1的距离,两轴相交0; (2) 两关节轴扭角 n: zn-1 → zn绕xn的转角,-90 ° ; (3) dn+1 :移动关节移动变量,dn=偏置量; (4) n:转动关节变量。
7) 一个移动柱关节和一
个转动关节相互平行;连杆 参数ln=偏置量;关节轴线方 向是z向;x方向由z轴确定, y方向由右手定则;转动和 移动关节变量为 n和dn+1。
关节
在机器人中,通常有两类 关节:转动关节和移动关节。 不同于人类的关节,一般机器 人关节为一个自由度的关节, 其目的是为了简化力学、运动 学和机器人的控制。转动关节 提供了一个转动自由度,移动 关节提供一个移动自由度,各 关节间是以固定杆件相连接的。
旋转关节有两种基本形式: 铰链和两杆的相对转动。
坐标系及其相关参数确定: 一、坐标系确定 (1) Zn-1的确定(转轴轴线) (2) Xn-1:xn -1=zn-1 → zn (3) Yn-1 :根据右手定则确定 二、参数确定 (1) 连杆长度ln:zn-1 → zn沿xn-1的距离;
(2) 两关节轴扭角 n: zn-1 → zn绕xn的转角,
坐标系及其相关参数确定:
一、坐标系确定
(1) Zn-1的确定(转轴轴线、柱轴方向线) (2) Xn-1、:xn -1=zn-1× zn (3) Yn-1 :根据右手定则确定 二、参数确定
(1) 连杆长度ln:zn-1 → zn沿xn-1的距离,两轴相交0; (2) 两关节轴扭角 n: zn-1 → zn绕xn的转角,90 ° ; (3) dn :两连杆间距离:xn-1 → xn沿zn-1移动距离,0; (4) n:连杆绕zn-1的转角,变量。
5) 两个移动柱关节相互 垂 直 并 相 交 ; 连 杆 参 数 ln=0 ; 关节轴线方向是z向;x向由z 轴确定, y方向由右手定则 确定;dn 与dn+1为柱关节变量。
Hale Waihona Puke 杆件机器人杆件是连接两个关节的固定物体(机 械)。机器人杆件的主要目的是用来保持该关节 与各相关末端关节一个固定的关系。机器人末端 杆件只有一个关节,位于最接近末端(或机座) 的位置。在最远离机座的末端,通常是附加一个 手爪。为了更容易、清楚地解释一个机器人的末 端和其各关节点的关系,课程中只以有限的杆件 数作为研究讨论对象。实际上,为了使得机器人 更容易制造,类似的限制在机器人制造中也使用。
下面给出了八种类型的常见杆件构形:
1) 两个平行的转动关节且在 两轴间没有扭转;连杆参数ln— 连杆的长度;如果连杆的中心线 被认作x方向并且从关节n-1到关 节n沿xn-1方向有一定距离,整个 杆件可以绕关节n-1转动n角, 该角认为是两连杆夹角并且这个 角就是一般转动关节的变量;同 时关节轴被认为是z方向并且绕 zn-1转动;y轴由右手定则确定。
6) 一个转动关节和一个
移动柱关节相互垂直并相交; 连 杆 参 数 ln=0 ; 转 动 关 节 轴 线方向和移动关节移动方向 是z向;x方向由z轴确定,y
方向由右手定则确定;n为转 动 关 节 变 量 、 dn+1 为 移 动 关 节变量。
坐标系及其相关参数确定:
一、坐标系确定
(1) Zn-1的确定(转轴轴线、柱轴方向线) (2) Xn-1、:xn -1=zn-1× zn (3) Yn-1 :根据右手定则确定 二、参数确定
4) 两个转动关节相互垂 直并且重合;连杆参数ln=0; 关节轴被认为是z方向;x方 向由两个z轴确定, y方向由 右手定则;dn为偏移值。原 点由n-1坐标系决定
坐标系及其相关参数确定:
一、坐标系确定
(1) Zn-1的确定(转轴轴线、柱轴方向线) (2) Xn-1、:xn -1=zn-1× zn (3) Yn-1 :根据右手定则确定 二、参数确定
