理论力学例题
理论力学试题库及答案(通用篇)

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。
理论力学大一试题及答案

理论力学大一试题及答案一、选择题(每题5分,共20分)1. 牛顿第一定律描述的是:A. 物体在没有外力作用下将保持静止或匀速直线运动B. 物体在受到外力作用下将改变其运动状态C. 物体在受到外力作用下将保持匀速直线运动D. 物体在受到外力作用下将保持静止答案:A2. 根据动量守恒定律,以下说法正确的是:A. 系统内所有物体的动量之和在没有外力作用下保持不变B. 系统内所有物体的动量之和在有外力作用下保持不变C. 系统内所有物体的动量之和在有外力作用下将增加D. 系统内所有物体的动量之和在有外力作用下将减少答案:A3. 角动量守恒的条件是:A. 系统不受外力矩B. 系统受外力矩C. 系统内力矩之和为零D. 系统内力矩之和不为零答案:A4. 以下哪项不是能量守恒定律的表述:A. 能量既不能被创造,也不能被消灭B. 能量可以以多种形式存在C. 能量可以以多种形式相互转化D. 能量在转化过程中总量会增加答案:D二、填空题(每题5分,共20分)1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成________。
答案:反比2. 一个物体在水平面上以初速度v0运动,受到大小为F的恒定摩擦力作用,其加速度为a=________。
答案:-F/m3. 一个质量为m的物体从高度h自由下落,其下落过程中的重力势能变化量为________。
答案:-mgh4. 根据动能定理,一个物体的动能变化量等于外力对物体做的功,即ΔK=________。
答案:W三、计算题(每题15分,共30分)1. 一个质量为2kg的物体从静止开始,受到一个大小为10N的水平拉力作用,求物体在5秒内的位移。
解:根据牛顿第二定律,F=ma,得a=F/m=10/2=5m/s²。
根据位移公式s=1/2at²,得s=1/2*5*5²=62.5m。
答案:62.5m2. 一个质量为5kg的物体从高度10m自由下落,求物体落地时的速度。
理论力学例题
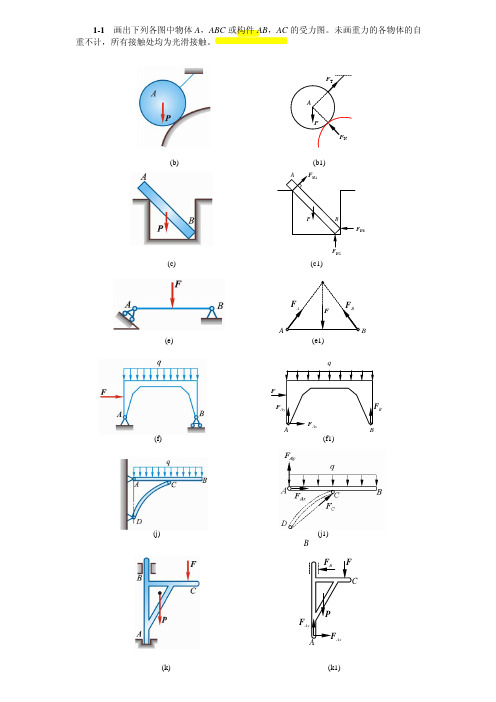
1-1画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
(b)(b1)2N 3N(c) (c1)B(e)(e1)Bq(f) (f1)(j) (j1)BF (k) (k1)1-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a) (a1)2AxFAx(a2) (a3)3N(b) (b1)N3F ′ (b2) (b3)(h) (h1)2-3F F AxC(i) (i1) (i2)F (i3)(i4)如图2-5a 所示,刚架的点B 作用1水平力F ,刚架重量不计。
求支座A ,D 的约束力。
(a)(b)图2-5解 研究对象:刚架。
由三力平衡汇交定理,支座A 的约束力F A 必通过点C ,方向如图2-5b 所示。
取坐标系Cxy ,由平衡理论得052,0=×−=∑A x F F F(1)051,0=×−=∑A D y F F F(2)式(1)、(2)联立,解得F F F A 12.125==,FF D 5.0=2-6 在图示结构中,各构件的自重略去不计,在构件BC 上作用一力偶矩为M 的力偶,各尺寸如图。
求支座A 的约束力。
解一、研究对象:BC ,受力如图(b)二、列平衡方程,求F B 、F C为构成约束力偶,有解2-8已知梁AB 上作用1力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图2-12a ,2-12b ,2-12c 三种情况下支座A 和B 的约束力。
BAF(a)BF(b)B(c)(c1)图2-12解(a )梁AB ,受力如图2-12a1所示。
B A F F ,组成力偶,故 BA F F =0=∑A M ,0=−M l F B , l M F B =,l M F A = (b )梁AB ,受力如图2-12b1所示。
0=∑A M , 0=−M l F B , l M F F A B ==(c )梁AB ,受力如图2-12c1所示。
理论力学

1、运动分析。----说明机构中主要构件的运动形式。 2、作速度分析,需要画出相关速度,求一点速度或图形角
速度。(若要分析加速度,一般需要求图形的角速度)
画速度 (1)沿点的运动轨迹切线,与相关的角速度方向协调。
(2)要符合速度投影定理。
3、作加速度分析,需要画出相关加速度,求一点加速度 或图形角加速度。 画加速度
例8-10
如图所示,在椭圆规的机构中,曲柄OD以匀角速度ω绕O 轴转动。
OD=AD=BD=l。求:当 60 时,尺AB的角加速度和点A的加速度。
B ABC AB D
O O
O
A A
vD
O
aA
n a BA
a A B
aD
v A
aD
n a AD y’ a AD
n a AD l 2
n x’ a A cos aD cos 2 a AD
y’ n a A 0 aD sin aAD cos a AD sin
x’
若OD变速转动,有什么变化?
a A l
2
a 0 AD AD
a AD 0 AD
解:
(1)动点:OA上的A点
动系:摇杆O1B
(2)运动分析: 绝对运动: 圆周运动。 相对运动: 直线运动。 牵连运动: 摇杆转动。
(3)速度分析与计算
v a r
ve
O ω
va
B vr
A ω1
vr va cos
ve va sin
r 2 O1 1 2 2 O1 A l r ve
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
(完整版)理论力学计算题及答案

1. 图示圆盘受一平面力系作用,已知圆盘半径R =0.1m ,F 1=100N ,F 2=200N ,M 0=400Nm 。
求该平面任意力系的合力及其作用线与AC 或其延长线的交点位置。
平面任意力系简化191.42,54.82,199.12391.347.16R xyF N F N F NM NmOE m==-==-=∑∑∑2. 求图示桁架中各杆的内力。
桁架内力计算,截面法与节点法:13F F =3. 已知图示结构中2m a =,在外力5kN F =和力偶矩=10kN m M ⋅作用下,求A 、B 和D处的约束反力。
力系的平衡条件的应用,隔离体与整体分析:()()()1010D Ax Ay Bx By A F F F F F kN M kNm↑=→=↓====4. 已知图示结构中1m =60,a οθ=,在外力10kN F =和力偶矩0=20kN m M ⋅作用下,求A 、C 处的约束反力。
同上()20,0,20,17.32Ax Ay A c F kN F M kNm F kN =→===5. 图示构件截面均一,图中小方形边长为b ,圆形半径均为R ,若右图中大方形和半圆形材料密度分别为12,ρρ,试计算确定两种情况下平面图形的质心位置。
以圆心为原点:()()3222c b x =-R b π→-左以方形下缘中点为原点:()()()12212123238c 2x =ρπρρρπρ++↑+右6. 斜坡上放置一矩形匀质物体,质量m=10kg ,其角点A 上作用一水平力F ,已知斜坡角度θ=30°,物体的宽高比b/h=0.3,物体与斜坡间的静摩擦系数s f =0.4。
试确定不致破坏平衡时F 的取值范围。
计算滑动和翻倒两种情况得到(1)滑动平衡范围14.12124.54N F N -≤≤,(2)翻倒平衡范围:8.6962.27N F N ≤≤7. 如图机构,折杆OBC 绕着O 轴作顺时针的匀速定轴转动,角速度为ω,试求此时扣环M 的速度和加速度。
理论力学试题及答案

理论力学试题及答案一、选择题(每题2分,共20分)1. 牛顿第一定律描述的是:A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案:B2. 根据牛顿第二定律,物体的加速度与作用力和物体质量的关系是:A. 加速度与作用力成正比,与质量成反比B. 加速度与作用力成反比,与质量成正比C. 加速度与作用力成正比,与质量成正比D. 加速度与作用力成反比,与质量成反比答案:A3. 以下哪个不是刚体的运动特性?A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案:C4. 角动量守恒定律适用于:A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案:C5. 以下哪个是能量守恒定律的表述?A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案:C二、简答题(每题10分,共20分)6. 简述牛顿第三定律的内容及其在实际中的应用。
答案:牛顿第三定律,又称作用与反作用定律,表述为:对于两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
在实际应用中,例如在推门时,门对人的作用力和人对门的作用力大小相等,方向相反。
7. 描述什么是简谐振动,并给出一个生活中的例子。
答案:简谐振动是一种周期性振动,其回复力与位移成正比,且总是指向平衡位置。
生活中的例子包括弹簧振子,当弹簧被拉伸或压缩后释放,它会在原始平衡位置附近做周期性的往复运动。
三、计算题(每题15分,共30分)8. 一个质量为m的物体,从静止开始,沿着一个斜面下滑,斜面的倾角为θ。
如果斜面的摩擦系数为μ,求物体下滑的加速度。
答案:首先,物体受到重力mg的作用,分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。
理论力学试题及答案

理论力学试题及答案一、选择题(每题2分,共10分)1. 一个物体在水平面上以速度v匀速直线运动,其动摩擦因数为μ,若物体所受的摩擦力为F,则F等于:A. μvB. μmgC. μND. μ(v^2)答案:B2. 根据牛顿第二定律,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比。
这一定律的数学表达式为:A. F = maB. F = m/aC. a = F/mD. a = mF答案:A3. 一个物体从静止开始自由下落,其下落的高度h与时间t的关系为:A. h = gt^2B. h = 1/2gt^2C. h = 2gtD. h = gt答案:B4. 两个物体A和B用轻杆连接,A的质量为mA,B的质量为mB,系统在水平面上以共同速度v向右做匀速直线运动。
若杆的力为F,则F的方向是:A. 向左B. 向右C. 不确定D. 无法判断答案:B5. 一个物体在竖直平面内做圆周运动,当物体通过最高点时,其向心力的来源是:A. 重力B. 杆的支持力C. 绳子的张力D. 重力和杆的支持力的合力答案:D二、填空题(每空2分,共10分)1. 一个物体的质量为2kg,受到的合外力为10N,根据牛顿第二定律,其加速度为______ m/s²。
答案:52. 一个物体做匀加速直线运动,初速度为3m/s,加速度为2m/s²,经过4秒后的速度为______ m/s。
答案:153. 在光滑水平面上,一个物体受到一个大小为5N,方向向右的恒定力作用,物体的质量为1kg,其加速度为______ m/s²。
答案:54. 一个物体在竖直上抛运动中,当其上升的最大高度为20m时,其初速度为______ m/s。
答案:205. 根据动能定理,物体的动能变化等于合外力做的功,若一个物体的动能增加了30J,合外力做的功为______ J。
答案:30三、简答题(共20分)1. 解释什么是科里奥利力,并给出其表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
21 4 21 4
mv
2
m 2 va a 2a
D
g (1 sin )
8 21
g (1 sin )
(2)取轮D如图:
3 2 F
T
FDE aD
D
mR 3 2
2
a
D
( F mg sin ) R
T
R
mg
ma mg sin
D
mg 7
( 4 3 sin )
2
2ma F P 2a
mg
(3):
Fx 0
MK
FKy K FKx
2
1 2mR 2
2
FKx 0
F K y 3 mg 2 ma F EH 0
C
E
2
Fy 0
MK 0
2a
A
2mg F EH mg
2ma
2 mR 2 3R 2 mg F EH 4 R m ( g 2 a ) 2 R 0
2 AB
v
A
y:
x:
a
t BA
v
2
B
0.1
2
0.2m / s
2
0.05 0.2 3 a a sin30 a tan 30 3
B BA B
BC
AB
0.2 3 2 0.1
4 3 3
rad / s
2
AB
a a
B
t
BA
0.2 3 2
0.4 3 3
[例3] :图示机构中,OA=20cm,O1B=100cm, AB=BC=120cm,0=10rad/s,=5rad/s2,求当 OA与O1B竖直,B点和C点的速度和加速度。
FEH
H
F
D
1 6 g
得: F
EH
4 3
mg
a
1 12
g
aA 2a
FD
2mg
FD
F Cx 0
F C y 4.5 mg
mg
a
B
mg
(1): M
1 2
(2): M
P
0
2
2 FEH m( 4a 3g ) 0
K
C E
2 mR F EH 2 R 3 maR 3 mgR 0
2 2 2 2 2
1
2
21 4
mv
2
W T T
12 2
1
2 mg (1 sin ) h
21 4
mv
2
得: v
8 21
g (1 sin ) h
v 2v
D
32 21
g (1 sin ) h
2 mg (1 sin ) h 2 mg (1 sin ) v a 4 21
r
2 3 3
v
v
v
30°
ve
v v sin 30
a
3 3
a a a
a e
r
a
v
2 a
n a
a 0
e
a
n a
2
v
2
30°
l
2 3v 9l
3l
a
t a
ar
a
r
a
a
cos 30
例2:半径为R的半圆形凸轮沿水平面向右运动,使杆 OA绕定轴转动。OA=R,在图示瞬时杆OA与铅垂线夹 角=30°,杆端A与凸轮相接触,点O与O1在同一铅直 线上,凸轮的速度为v,加速度为a。求该瞬时杆OA的 角速度和角加速度。
e CD
r
v
r
3 2
r
A ve
B
vr va60° ar
CD
a a a a
a e r
C
c
a r
a
2
a 2 v
c CD r
3 2
r
2
a cos 30 a a
t a e
aa
a
2
60°
t e
a
a
n e
c
c
a
t e
3r
2
CD
a
t
e
3
BC
例4:平面机构中,半径为R的半圆环OC与固定直杆AB 交点处套有小环M。半圆环OC绕垂直于图面的水平轴O 匀角速度转动,从而带动小环M运动。图示瞬时,OC 连线垂直于AB杆,求该瞬时小环M的绝对速度和加速度。
n n a c r e
2 R
R
2
2
2R
2
2 2
0
45°
a
n r
t r
R
a
n e
a
[例1] :已知OA= r , OA杆以匀角速度0转动, AB=6 r , 求该瞬时滑块B的速度和加速度
B 60° 0 O
A 60°
解: OA定轴转动 ; AB平面运动,滑块B平移 AB平面运动,P为速度瞬心
A M O B C
解: 取小环M为动点,动系固定在杆OC。
va ve vr
v
e
a r
ve
A va
45°
M
2R
2 2
r c
vr
C
v v
v R
e
O B
a a a a a a a a
n t a e e r r
c
aa
a
c
a a a a cos 45
B
30
AB
v
A
r 3r
0
0
3
0
PA
AB
6r
3 3r
AB
v
A
A 60°
v PB
B
3
3 3r
3r
0
v
B
60°
0 O
取点A为基点,则
a
60
t BA
P
a a a a 大小? r ? l 方向
t B A BA 2 0
A
n
BA 2 AB
B
a
E C
D B A
§13-6
普遍定理的综合应用举例
2
C E
解(1)取整体为研究对象。
W 2 mgh mg sin 2 h
12
2V
D
2
T 0
1
B
2 2 2
1 3 v T m v mR ( ) A V 2 2 2 R 1 3 2v 1 1 2v 1 3 mR ( ) mR ( ) ( 3 1) mv 2 2 R 2 2 R 2 4
§13-6
普遍定理的综合应用举例
2
K C
2
解(1)取整体为研究对象。
1 1 2 2 2 T m ( 2v ) 2 mR (2 ) 2 2 2 1 3 1 2 2 2 2 mR m v 6 mv 2 2 2
P 3 mgv mg 2 v m gv
C B
A
30°
y
C
解: AB瞬时平移
n B
a a
A
t B
t BA
30
a
v v 0.1m/s
B A
AB
0
取点A为基点,则
B
B
v
x
A
a a a a a
n t t B B A BA
n BA
a
30°
n BA
a 0
a a cos 30
n t B BA
t t n
a
n
BA
AB 0
a
B
a
A
n BA
x
A
a cos 60 a cos 60 a
B
n
BA
a r
B
2 0
a
2 0
n
BA
AB
2 AB
2 3
r
2 0
a r 3
1
[例2] :图示机构中,BC=0.05m,AB=0.1m, AB杆A端以匀速vA=0.1m/s沿水平面向右运动, 图示瞬时CB杆处于竖直状态。求该瞬时B点的 加速度和AB杆的角加速度
a a ( a a ) tan θ 1 16tanθ 3.71m/s
B
a a 3.71m/s
t C B
2
O A
R O1
v a
解: 取OA杆上A为动点,动系凸轮。
va ve vr
v v
a r
v v
e
O
v
e
2cos30
3v 3R
v 2 3 2
3 3
vr
v
R O1
t
2
va
A v a
ve
n
v
a
t
R
a a
a a a a a a a
n e r e r
r
a a
EH
d
1
2mg
A
由动量定理,得
0 F Cx
ma A F C y 2 mg mg F EH
得:
