轮船与船速优化问题
四年级数学培优第25讲 巧解行船问题

第25讲巧解行船问题巧点晴——方法和技巧行船问题中常用的概念:船在静水中航行的速度叫船速,江河水流动的速度叫水流,船从上游向下游顺水而行的速度叫顺水,船从下游向上游逆水而行的速度叫逆水速度。
各种速度之间的关系如下:顺水速度=船速+水速逆水速度=船速-水速(顺水速度+逆水速度)÷2=船速(顺水速度-逆水速度)÷2=水速巧指导——例题精讲A级冲刺名校·基础点晴【例1】一只船从甲地出发顺水般行7小时到达乙地,路程为182千米。
这只船从乙地返回甲地用了13小时。
求船在静水中的速度(即船速)和水速。
分析根据船顺水、逆水航行的时间、路程,可以先求出顺水速度、逆水速度,从而可求出船速和水速。
解顺水速度:182÷7=26(千米/小时)逆水速度:182÷13=14(千米/小时)船速:(26+14)÷2=20(千米/小时)水速:(26-14)÷2=6(千米/小时)或26-20=6(千米/小时),20-14=6(千米/小时)答:船在静水中每小时行20千米,水速为每小时6千米。
做一做1 一只渔船顺水航行每小时行20千米,逆水航行每小时行14千米。
求船速和水速。
【例2】轮船在静水中的速度是每小时21千米,轮船自甲港逆水航行7小时,到达相距126千米的乙港,再从乙港返回甲港需要多少小时?分析想求轮船从乙港返回甲港所需时间,即轮船顺水航行126千米所需的时间,就要求出顺水航行的速度,现在已经知道轮船在静水中的速度,则只需求出水流速度。
根据已知条件,可先求逆水速度,再根据逆水速度与船速、水速的关系即可求出水速。
解水流速度为:21-126÷7=3(千米/小时)顺水速度为:21+3=24(千米/小时)所求时间为:126÷24=5.25(小时)答:轮船从乙港返回甲港需5.25小时。
做一做2 一艘船在静水中的速度为每小时15千米,它逆水航行11小时走了88千米。
轮船与船速优化问题

轮船与船速优化问题一、实验目的1.熟悉MATLAB 的运行环境.2.学会使用MATLAB 作图.3.学会使用MATLAB 编程.二、实验内容实验一:油价与船速优化问题油价上涨,将影响大型海船确定合理的航行速度,以优化航行收入。
直观地,油耗的把多少直接影响船速的快慢,因而直接影响航行时间的长短,进而影响支付船员人工费用数量:过去一些经验表明:(1)油耗正比于船速的立方(2)在最省油航速的基础上改变20%的速度,则引起50%的油耗的变化。
作为一个例子:某中型海船,每天油耗40吨,减少20%的航速,省油50%即20吨。
每吨油价250美元,因此每天减少耗油费用5000美元,而航行时间的增加将增加对船员支付的费用,如何最优化?算例:航程L=1536海里,标准最省油航速20节,油耗每天50吨,航行时间8天。
最低航速10节,本次航行总收入84600美元。
油价250美元/吨,日固定开支1000美元。
试确定最佳航速。
三、实验环境Windows 操作系统;MATLAB 7.0.四、实验过程1)由资料知,最低航速为相对于静水的速度为10节,即可理解为船速。
因航速与船速不同,通过分析得知不可忽略水速并假设水速为v1,最佳船速为v ,航速v2=v-v1,每日油耗为s ,航行天数为t ,航行的收益为y 。
2)根据已知可计算出水速,计算过程如下:已知时间t=8d,航程L=1536海里,以标准省油船速20节行驶,假设航行时船匀速行驶,则实际航速v*=1536/(8*24)=8节,则水速v1=20-v*=12节。
3)又由条件(1)得出油耗与船速的比值k=1603/节吨。
4)期中总收入为该航程的总收益与航行天数无关。
但员工工资与航行天数有关。
航行天数t=L/v2,每日油耗s=3v /k 。
5)在假设航船匀速航行的条件下建立方程为()()315361536846001000*250**1212160v y v v --=--。
6)求解当12v ≥节是时的船速。
船舶推进效率优化的策略与方法

船舶推进效率优化的策略与方法在现代航运业中,船舶推进效率的优化是一个至关重要的课题。
提高船舶推进效率不仅能够降低运营成本,减少能源消耗,还能降低对环境的影响,增强船舶的竞争力。
那么,如何实现船舶推进效率的优化呢?这需要从多个方面入手,综合运用各种策略和方法。
首先,船舶的设计阶段是决定推进效率的基础。
在船舶的初步设计中,船体的线型优化是关键之一。
一个合理的船体线型能够减少水流的阻力,从而提高船舶在水中的行进效率。
这需要借助先进的流体动力学计算软件和模型试验,对不同的线型方案进行模拟和评估,以找到阻力最小的设计。
例如,采用细长的船体、优化船首和船尾的形状,可以有效地降低兴波阻力和粘滞阻力。
螺旋桨的设计也对推进效率有着重要影响。
螺旋桨的叶片数量、直径、螺距等参数需要根据船舶的主机功率、转速、航行速度等因素进行精心计算和选择。
现代螺旋桨设计通常采用计算机辅助设计(CAD)和计算流体动力学(CFD)技术,以精确模拟螺旋桨在水中的工作状态,优化其水动力性能。
此外,新型的螺旋桨设计,如可调螺距螺旋桨和导管螺旋桨,能够根据不同的航行条件调整工作状态,进一步提高推进效率。
船舶的动力系统选择也是影响推进效率的重要因素。
传统的内燃机作为船舶的主要动力源,其燃烧效率和排放性能对能源利用和环境影响有着直接的关系。
近年来,随着技术的发展,燃气轮机、电力推进系统和混合动力系统等新型动力方案逐渐受到关注。
燃气轮机具有功率密度高、启动迅速等优点,但燃油消耗较高;电力推进系统则具有调速范围广、机动性好等特点,通过优化能量管理系统,可以提高能源利用效率;混合动力系统结合了多种动力源的优势,能够根据航行工况灵活切换,实现最佳的燃油经济性。
在船舶的运营过程中,船舶的维护和管理同样对推进效率有着不可忽视的影响。
定期对船体进行清洁和保养,去除附着在船体表面的海洋生物和污垢,可以减少船体的粗糙度,降低阻力。
同时,对螺旋桨和轴系进行定期检查和维修,确保其处于良好的工作状态,避免因磨损和变形导致的效率下降。
四年级数学专题《简单行船问题》题目及答案(1)

简单行船问题(1)姓名:_____________船速:船在静水中的速度;水速:水流速度;顺水速度:船顺水航行的实际速度;逆水速度:船逆水航行的实际速度。
行船问题中的两个基本关系式:顺水速度=船速+水速; 逆水速度=船速一水速由以上两个基本关系式还可以得到以下两个关系式:船速=(顺水速度十逆水速度)÷2; 水速=(顺水速度一逆水速度)÷21、一艘客轮在静水中的速度是每小时25千米,要在水流速度为每小时5千米的河中顺水航行180千米,需要航行多少小时?如果逆水航行180千米,需要航行多少小时?顺水速度:25+5=30(千米/时) 顺水航行的时间:180÷30=6(小时)逆水速度:25-5=20(千米/时) 逆水航行的时间:180÷20=9(小时)2、甲、乙两港相距75千米,水流速度为每小时5千米,轮船在静水中的航行速度为每小时30千米。
轮船从乙港逆水航行到甲港需要几小时?逆水航行速度:30-5=25(千米/时)逆水从乙港到甲港用时:75÷25=3(小时)3、汽艇在静水中的速度是每小时18千米,水流速度是每小时3千米。
汽艇从甲港顺水航行到乙港需5小时。
两港相距多少千米?顺水航行速度:18+3=21(千米/时)两港相距路程:21×5=105(千米)4、油轮的静水速度是35千米/时,在水流速度是5千米/时的河中顺水航行120千米,需要多长时间?如果逆水航行120千米,需要多长时间?顺水航行时间:120÷(35+5)=3(小时)逆水航行时间:120÷(35-5)=4(小时)5、一艘轮船在静水中的速度是每小时20千米,轮船自甲港逆水航行10小时,到达相距150千米的乙港,再从乙港返回甲港需要多少小时?逆水速度:150÷10=15(千米/时) 水速:20-15=5(千米/时)顺水速度:20+5=25(千米/时) 顺水时间:150÷25=6(小时)6、A、B两港相距280千米。
客船运输优化方案

客船运输优化方案概述客船运输是一种重要的海上运输方式,能够满足大量人员和物资的运输需求。
为了提高客船运输的效率和安全性,需要优化客船的航线规划、装载规划和船舶运行管理等方面。
本文将介绍几种常见的客船运输优化方案。
客船航线规划优化客船航线规划优化是指通过优化航线,使得客船航行更加高效、经济和安全。
具体的优化方法有以下几点:1. 航线优化算法给定客船的起点和终点,航线优化算法可以通过计算气象、海流、水深等条件,找到一条最优的航线。
常用的航线优化算法包括模拟退火算法、遗传算法和蚁群算法等。
2. 航速优化为了减少客船的油耗和运行成本,需要调整客船的航速。
可以根据实际需求来控制客船的航速,达到最优化的效果。
3. 船舶动力优化船舶动力优化是通过船舶设计和船舶维护来提高客船的动力性能。
这可以包括增加船体的光滑性、改善螺旋桨的设计、提高发动机的效率等。
船舶装载规划优化船舶装载规划优化是指优化客船货物的装载计划和船舱空间利用率,以提高客船货物运输的效率。
具体的优化方法包括以下几点:1. 存储空间优化为了提高船舶的货物装载效率,需要对船舱进行科学的规划和布置。
可以使用一些优化算法,比如动态规划算法、贪心算法等,使得货物的存储空间得到最佳的利用。
2. 物品集中度优化为了提高装卸货物的效率,应尽可能提高船舶的物品集中度。
这可以通过货物按照相似性进行分组,并将相同种类的货物放在同一个船舱中来实现。
3. 船舱间隔优化为了提高船舶的货物存储效率,需要在不影响船舶结构安全的前提下,尽可能增加船舱的储存空间。
这可以通过设计简单和灵活的货物支撑系统来实现。
船舶运行管理优化船舶运行管理优化是指通过管理和监督客船航运,使其更加高效和安全。
具体的优化方法包括以下几点:1. 船舶维护管理为了提高客船运营的安全和可靠性,应定期对船舶进行维护和保养。
维修计划应根据船舶的规模、航线、装备和历史维修记录等进行制定。
2. 船舶运行监控为了实时掌握客船运行情况,应通过管理软件和监控设备对船舶进行远程监管。
油价与船速的优化问题(解答)

油价与船速的优化问题作者:廖美娇摘要:油价的上涨,将对大型海船确定合理的航行速度产生影响,以优化模型,使得运营商能够再最小的投资里赢取最大的利润。
关键字:模型优化 油价上涨 利润一、 问题背景燃油价格一涨再涨,一艘超巴拿马型船的日均燃油成本竟已高达12万美元。
在这种情况下,班轮公司只得下令集装箱船“猛踩刹车”。
为节约油耗,许多班轮公司已要求其在亚欧航线上运营的船舶大幅减慢航速。
随着全球进入“高油价”时代,可以预计航速还将继续下降。
二、 问题重述油价的上涨,将对大型海船确定合理的航行速度产生影响,以优化航行收入,直观地,油耗的多少直接影响船速的快慢,因而直接影响航行时间的长短,进而影响支持船员人工费用数量。
过去有一些经验表明(1)油耗正比于船速的立方;(2)最省油航速的基础上改变20%的速度,则引起50%的油耗的变化。
作为一个例子,某中型海船,每天油耗40t.若减少20%的航速,可省油50%,即每天耗油20t 。
油价250美元/吨,由此每天减少耗油费用5000美元,而航行时间的增加将对船员支付的费用的增加,如何最优化?算例:航程L=1536n mile (海里),标准最省油航速20kn(节),油耗每天50t,航行时间8天。
最低航速10kn,本次航行总收入为84600美元.油价250美元/吨,日固定开支1000美元.试确定最佳航速(1 n mile =1852m,1 kn=1 n mile/h=(1853/3600)m/s )。
三、 问题分析1、设油耗为S ,速度为v ,比例系数为k ,则,3S kv =2、设最省油航速为0v ,油耗0S ,若045v v =,则02S S = 3、根据题中所述,1,2中应该只有一个成立,4、我分析道这了,以后应该分情况讨论5、若1,则应算k ,根据k 的取值情况,讨论总花费函数的极小值6、若2,则应考虑比例p ,取值范围(-0.5,0.4),讨论总花费函数极小值四、 符号说明v 船速0v 标准船速S 耗油量0S 标准耗油量k 比例系数L 航程t 时间m 花费费用M 盈利五、 模型的建立与求解模型一:1、若油耗正比于船速的立方时有: 3S kv =(1)、若船按照标准最省油速度航行时有: 424*20L t =≈天 则在这四天之内需要消耗费用为:*1000*250*54000m t s t m =+∴= 又由于84000840005400030000M m =-=-=元故按照最佳航速航行时除去工人的工资和耗油量,可盈利30000元。
数学建模的船队运输最优化问题
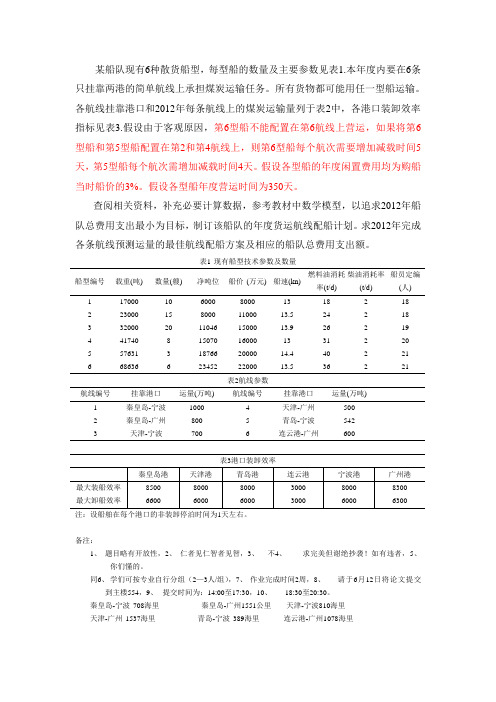
天,第5型船每个航次需增加减载时间4天。假设各型船的年度闲置费用均为购船
当时船价的3%。假设各型船年度营运时间为350天。
查阅相关资料,补充必要计算数据,参考教材中数学模型,以追求2012年船
队总费用支出最小为目标,制订该船队的年度货运航线配船计划。求2012年完成
各条航线预测运量的最佳航线配船方案及相应的船队总费用支出额。
现有船型技术参数及数量船型编号载重吨数量艘净吨位万元船速kn燃料油消耗170001060008000131823000158000110001352432000201104615000139261507016000133118766200001444023452220001353621表2航线参数航线编号挂靠港口运量万吨航线编号挂靠港口运量万吨秦皇岛宁波1000天津广州500秦皇岛广州800青岛宁波542天津宁波700连云港广州600表3港口装卸效率秦皇岛港天津港青岛港连云港宁波港广州港最大装船效率850080008000300080008300最大卸船效率660060006000300060006300注
a62 A62 a63 A63 a64 A64
a65 A65
a66 A66
小写字母代表船数 大写代表船次
各种船往返一次所用的时间
D=2+M/p+M/q+2S/V/24 M:载重量 p:装货率 q:卸货率
S:航线长度 V:船速 2:港口为停靠时间 24:一天 24 小时
1
2
3
4
5
6
秦皇岛-宁 波
11.372
船型编号 载重(吨) 数量(艘)
表1 现有船型技术参数及数量
燃料油消耗 柴油消耗率 船员定编
净吨位 船价 (万元) 船速(kn)
小学数学专题之流水行船问题 例题+练习 带答案

小学数学专题之流水行船问题例题讲解:例题1:一条轮船往返于A、B两地之间,由A地到B地是顺水航行,由B地到A地是逆水航行。
已知船在静水中的速度是每小时20千米,由A地到B地用了6小时,由B地到A地所用的时间是由A地到B地所用时间的1.5倍,求水流速度。
解答:设水流速度为每小时x千米,则船由A地到B地行驶的路程为[(20+x)×6]千米,船由B地到A地行驶的路程为[(20—x)×6×1.5]千米。
列方程为(20+x)×6=(20—x)×6×1.5x=4练习1:1、水流速度是每小时15千米。
现在有船顺水而行,8小时行320千米。
若逆水行320千米需几小时?解答:32小时2、水流速度每小时5千米。
现在有一船逆水在120千米的河中航行需6小时,顺水航行需几小时?解答:4小时3、一船从A地顺流到B地,航行速度是每小时32千米,水流速度是每小时4千米,2.5天可以到达。
次船从B地返回到A地需多少小时?解答:80小时例题2:有一船行驶于120千米长的河中,逆行需10小时,顺行要6小时,求船速和水速。
解答:逆流速:120÷10=12(千米/时)顺流速:120÷6=12(千米/时)船速:(20+12)÷2=16(千米/时)水速:(20—12)÷2=4(千米/时)答:船速是每小时行16千米,水速是每小时行4千米。
练习2:1、有只大木船在长江中航行。
逆流而上5小时行5千米,顺流而下1小时行5千米。
求这只木船每小时划船速度和河水的流速各是多少?解答:船速:3千米/小时水速:2千米/小时2、有一船完成360千米的水程运输任务。
顺流而下30小时到达,但逆流而上则需60小时。
求河水流速和静水中划行的速度?解答:船速:9千米/时水速:3千米/时3、一海轮在海中航行。
顺风每小时行45千米,逆风每小时行31千米。
求这艘海轮每小时的划速和风速各是多少?解答:轮速:38千米/时风速:7千米/时例题3:轮船以同一速度往返于两码头之间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轮船与船速优化问题
一、实验目的
1.熟悉MATLAB 的运行环境.
2.学会使用MATLAB 作图.
3.学会使用MATLAB 编程.
二、实验内容
实验一:油价与船速优化问题
油价上涨,将影响大型海船确定合理的航行速度,以优化航行收入。
直观地,油耗的把多少直接影响船速的快慢,因而直接影响航行时间的长短,进而影响支付船员人工费用数量:过去一些经验表明:(1)油耗正比于船速的立方(2)在最省油航速的基础上改变20%的速度,则引起50%的油耗的变化。
作为一个例子:某中型海船,每天油耗40吨,减少20%的航速,省油50%即20吨。
每吨油价250美元,因此每天减少耗油费用5000美元,而航行时间的增加将增加对船员支付的费用,如何最优化?
算例:航程L=1536海里,标准最省油航速20节,油耗每天50吨,航行时间8天。
最低航速10节,本次航行总收入84600美元。
油价250美元/吨,日固定开支1000美元。
试确定最佳航速。
三、实验环境
Windows 操作系统;
MATLAB 7.0.
四、实验过程
1)由资料知,最低航速为相对于静水的速度为10节,即可理解为船速。
因航速与船速不同,通过分析得知不可忽略水速并假设水速为v1,最佳船速为v ,航速v2=v-v1,每日油耗为s ,航行天数为t ,航行的收益为y 。
2)根据已知可计算出水速,计算过程如下:
已知时间t=8d,航程L=1536海里,以标准省油船速20节行驶,假设航行时船匀速行驶,则实际航速v*=1536/(8*24)=8节,则水速v1=20-v*=12节。
3)又由条件(1)得出油耗与船速的比值k=1603
/节吨。
4)期中总收入为该航程的总收益与航行天数无关。
但员工工资与航行天数有关。
航行天数t=L/v2,每日油耗s=3v /k 。
5)在假设航船匀速航行的条件下建立方程为()()3
15361536846001000*250**1212160
v y v v --=--。
6)求解当12v ≥节是时的船速。
v=linspace(0,20,100);
y=84600-1000.*1536./(v-12)-250.*(1536./(v-12)).*(v.^3./160);
plot(v,y),title(‘利润曲线’)
由图像放大法知利润最大点为当船速为12节时,但12节时方程无解,则带入大于12节的且接近12节的船速,即假设精度为0.001。
带入计算此时利润约为78915.76。
即最大利润不超过78915.76.
此模型是基于已知条件(1)做出的假设模型,但是存在一个问题就是在取最佳船速的选取时存在最佳船速的确定值不可选取的问题。
只有取值区间及方向。
经计算的v=12节,表示是航速近似为0的状态。
但是若航速近似为0,则航行天数可大致估算出为127天。
则每日固定开支总和可求出为约为127000,则该次航行已亏本。
因此根据上述分析需对模型进行优化,即提高船速,减少固定开支的总费用。
此模型是基于已知条件(1)做出的假设模型,但只有取值区间及方向。
经计算的v=12节,表示是航速近似为0的状态。
但是若航速近似为0,则航行天数可大致估算出为127天。
则每日固定开支总和可求出为约为127000,则该次航行已亏本。
因此根据上述分析需对模型进行优化,即提高船速,减少固定开支的总费用。
由条件(2)知,在最省油航速的基础上改变20%的速度,则引起50%的油耗的变化。
则重新改进模型。
即求出最少油耗的最大船速。
则此时的最佳航速v3表示为(v-12),且假设改变了k个20%,则此时油耗就改变了k个50%。
又因为标准最省油航速为20节,则低于20节大于12节的航速都为最省油航速。
在这个范围内都满足条件(2)。
则改进模型建立如下:
则可计算出k最多为40次。
则现在可从最小利润入手,求出何时是最小利润。
则可结合已知模型进行模型改进:如下假设油耗之前的油耗为s,之后的油耗为s1,成本为y。
可由下c语言程序
void main()
{float v1,v=12.0,y=84600.0,s,s1;
int k;
for(k=1;k<=40;k++)
{while(84600.0-y<=0.0)
{v1=v*(1+k*0.2);
s=v*(1+k*0.2)/(k*0.5);
s1=s*(k*0.5);
y=1000*1536/(v*(1+k*0.2))+250*1536/(v*(1+k*0.2))*s1;}
printf("%f",v1);}}
求出最佳船速为:14.4节(当k=1时)
最佳航速为:2.4节时为最少耗油的最大航速。
此时可计算出该次航行的利润约为-790067。
即大于14.4节接近20节的船速都为可盈利船速,越接近20节盈利越多。
则可确定函数取值范围,再次做出利润曲线为
则综上知当船速v=18节时可得最大利润。
此时利润y为:-307933美元。
五、实验总结
1.遇到的问题及解决过程
在分析问题时,对于已知的船速和航速没有分析清楚则做题时出现了问题。
最后经过分析可求出所需答案。
另外题目分析时可知条件矛盾,该次航行计算结果总为亏本的。
而因此需要求出最少亏损。
则通过分析要求出最小耗油最大船速最大利润点。
2.产生的错误及原因分析
对问题的一些知识理解不到位,导致分析出现了问题。
另外分析时,忽略了一些因素的影响,在考虑时不断改进才能完善问题的回答。
3.体会和收获
了解了相关的知识,对该问题进行了多方位思考,了解到该如何思考问题。
使思考问题的过程科学化,以及思考的角度和思考的方向。
可以分步骤的完成思考。
六、参考文献
[1]数学实验,重庆大学数学系傅鹂、龚劬、刘琼荪、何中市编著,科学出版社,2000年9月.
七、教师评语。
