(二端口网络)习题解答
第十六章二端口网络习题

例25 求Z参数等效电路(题解) 求图(a)所示二端口电路的Z参数等效电路
(a) (b)
解:如图(a),由KVL得
U1 3I1 2I3
(1)
U2 3I3 2I3 5I3 (2)
将 I3 I2 2代入得
U1 3I1 2I2 4
U2
5I2 10
则Z参数等效电路如图(b)
题16-4a题解
10I1 U1 530 (3)
U2 4I2
(4)
将式(1)代入式(3)得
将式(2)代入式(4)得
3I1 6I2 4I2 (6)
I2 0.0961530 96.15 150 mA
I1
10 3
I2
0.3230
A
15I1 2I2 530 (5)
将 I1 代入式(3)得
U1 530 10 0.3230 1.830 V
1 2
U1
1 2
U2
I1
(1)
解:参考方向如图(b)
1 1
1 2
U
2
1 2
U1
I2
3I1
(2)
由(1)式整理得
I1
3 2 U1
1 2 U2
(3)
由(1)式代入(2)式整理得
I2 5U1 3U2 (4)
(b)
3 Y 25
1 2 3
S
16-6题解(Z参数)
解:电流和电压及参考 方向如图所示.
5 25
因 H12 H21 电路互易
所以电路不含受控源
将(3)式代入(2)式得
作业16-16 求Z参数
16-16(e)题解 求图示二端口的Z参数矩阵
i1
i2
(3)式代入(2)式得
二端口网络2

U1b I1b U Zb I 2b 2b
U1 U1a U1b U1a U1b U U U U U 2 2a 2b 2a 2b
I1 I1a I1b I I I 2 2 a 2b
T
U1a U 2a Ta I I 1a 2a
U1b U 2b Tb I I 1b 2b U 2a U1b I 2a I1b
U 2b U1 U 2 T TaTb I I I 1 2 2b
在输入端口 U 5I U S 1 1 在输出端口
U 2 16 I 2
联立可解得
US 3.297U 2
所以
U2 1 0.3033 U S 3.297
并联
两个或两个以上二端口网络的对应端口分别 作并联连接称为二端口网络的并联,如图所示。
6 RC
在该频率下: U2 1 1 2 2 2 U1 1 5 C R 29
串联
两个或两个以上二端口网络的对应端口分别 作串联连接称为二端口网络的串联,如图所示。
串联时,二端口网络参数的计算,采用Z参数方便。
U1a I1a U Z a I 2a 2a
T TaTb
即两个二端口网络级联的等效T参数矩阵等于 各二端口网络的矩阵Ta和Tb之积。 同理,当n个二端口网络级联时,则复合后的 二端网络T参数矩阵为:
T T1 T2 T3
Tn
注意
(1) 级联时T 参数是矩阵相乘的关系,不是对应元素 相乘。
A B A B A B C D C D C D A A BC A B BD C A D C C B D D
二端口网络习题课

1
2
Na
2S
1
2
N
典型题(4/6)
4 解(1) 方法1
双口网络 Na 的传输参数方程为
1 I1
I2
I2 2
U1 U2 4I2
U1
Na
2S
U2
I1
3U 2
2I2
I2 I2 2U2
1
2
N
U1 U2 4I2 U2 4 I2 2U2 9U2 4I2
I1
3U 2
2I2
3 解(3)用等效电路求解。
R22 R11 9 R12 R21 6
I1 3
3 I2
18V
6
3
I1
3
18 6 //(3 3)
3A
I2
1 2
I1
1.5A
典型题(4/6)
4 图示网络中,双口网络Na 的传输参数矩阵为
1 4 Ta 3 2
求:(1)整个双口网络的传输参数;
(2)当输出端口接1电阻时,输入端口的
gr
i2 u2
i1 i2
gu2 gu1
i1 i2
0 g
g u1
0
u2
i1
g
i2
L r2C
L
u1
u2
C
1 主要内容(续)
二端口元件
(2)负阻抗变换器(NIC) 可将正阻抗变换为负阻抗
负阻抗变换器的方程
i1
i2
u1
NIC
u2
电压反向型
电流反向型
u1 i1
ku2 i2
u1 u2 i1 ki2
u1
i1
k
0
0 u2
二端口网络

二端口网络练习题1. 在图示电路中,已知 R 1=1Ω, R 2=2Ω,α=2,试计算二端口网络的开路阻抗参数矩阵Z 和短路导纳参数矩阵Y ,并说明该网络是否互易网络。
2. 求图示二端口网络的短路导纳矩阵Y 。
3. 已知线性无源二端口网络N 的传输参数矩阵⎥⎦⎤⎢⎣⎡=21.0302T ,今有一电阻R 并联于输出端(如图(a )),则输入电阻等于将R 并联于输入端(如图(b ))时的输入电阻的6倍,求该电阻R 之值。
4. 图示电路中N 为由线性电阻元件构成的二端口网络,当在a 、b 端加100V 电压时,流入网络的电流为2.5A ,同时测得c 、d 端电压u cd =60V ,若将100V 电压加于c 、d 端,则流入网络的电流为2A ,这时测得a 、b 端电压u ab =48V ,求该二端口电阻网络的传输参数。
(a)(b)R 1 ② ②/ ① ①/R 2I 题5图5.在图5所示含二端口网络N 的电路中,已知R 1=2Ω, R 2=1Ω。
开关S 断开时,测得U S =12V, U 1=6V, U 2=2V, 开关S 闭合时,测得U S =12V, U 1=4V, U 2=1V ,求网络N的传输参数矩阵T 。
6 已知如图所示二端口网络N 的短路导纳参数矩阵S ⎥⎦⎤⎢⎣⎡=1223/2Y ,求二端口网络的输入功率P 1和输出功率P 2。
7在图7所示电路中,N 为二端电阻元件构成的双口网络,已知N 的开路阻抗参数矩阵Ω⎥⎦⎤⎢⎣⎡=6/76/16/16/7Z ,试求负载电阻R f =2Ω所吸收的功率。
8. 已知图8 所示二端口网络N 的Z 参数是Z 11=10Ω,Z 1 2=15Ω,Z 21=5Ω,Z 22=20Ω。
试求转移电压比U 2 (S) / U S (S) 之值。
4Ω图7R f =2Ω图8U S 25Ω。
第十六章(二端口网络)习题答案

第十六章(二端口网络)习题答案选择题1、ffi示n 掃口的2参数£B 、C 、3G 答案:AC 1.5S0.5S 0.5S 1.5SD0.5S1.5S 0.5S答案:B3.图示二端口网络的F 参数矩阵中r 叛(答案:C5、设两个无源二端口 P,P 的传输参数分别为匚八则当两个无源二端口级联时,•其复合二端口的传输鉢r 为:()B. T-TC 、T +T答案:D答案:A7x 对线性无源二制口而言,以下关系式正确的是(答案:B2.图示二端口的F 参数为:<A -0.5S 1.5S0.5S-1.5SB 0.5S -1.5S -0.5S 1.5S A.1 r B. C 、 1D 、~T答案:BZ2D,1.5S4>图示二端口网络的N 参魏e 阵中右区 为:(lo<■3A 、2 +Z ,ZBs 2 ,2 C> Z ,2 +ZD 、Q2D 、 丁丁6,在对称二端口网络的F 参数矩阵中,只有()个参数是独立的。
Ax 2个CxD 、4个C>A^HD 、H =F答案:B10.将两个无源二端口 £严串联时,其复合二端口的参数为:(AvD 、7 + r答案: 二、填空题8.若两个传输参数都为 ■3 42'3 的二端口级联,则级联后复合二端口传输参数矩阵为( A. 飞 4-B, 9 4'£ 16 9JG 17 12'D 、 12 IJ 1 ™24 1717 24答案: C49B.亠身胡G3Ci3 F12 D\ 2^^— 79、若e 知二4崗口传输参数矩阵T ・ A 、严 £ 1c 、-mQ;,则图示T 型等效电路参数2忆忆依次分别为C 、 1.图 16 — 3 (a )所示二端口电路的 Y 参数矩阵为丫=〔丫丫I 图16—3 ( b )所示二端口的 Z 参数矩阵为k 丫」Z=E Z图1A32 •图16—4所示二端口网络的 丫参数矩阵是丫 =「1 3 7L 6_11 6 2 3」 602Qk L 51 节。
资料:二端口(答案)

第15章 二端口网络1、网络按图示方式连接时,下列结论中错误的是: ( A )A .网络N 1和N 2都是双口(二端口)网络B .若网络N 1为双口网络时,网络N 2不是双口网络C .若网络N 2为双口网络时,网络N 1不是双口网络D .网络N 1和N 2都可能不为双口网络︒︒︒︒网络N 1网络N 2RN 1N 2R2、 图示二端口网络H 参数中h 21等于: A 。
N N 12 B 。
N N 21C 。
-N N 12D。
-N N 21答( A )︒︒︒︒N N 1211'22'3、下列传输参数矩阵中,哪一个是互易、对称二端口网络?A.6486⎡⎣⎢⎤⎦⎥B.3553⎡⎣⎢⎤⎦⎥C.91659⎡⎣⎢⎤⎦⎥D.10775⎡⎣⎢⎤⎦⎥答( C )4、图示级联二端口网络的传输参数矩阵为:︒︒︒Z 1Z 2︒A. 10112Z Z ⎡⎣⎢⎤⎦⎥ B. 20212Z Z +⎡⎣⎢⎤⎦⎥ C. 10112Z Z +⎡⎣⎢⎤⎦⎥ C. 以上皆非 答( C ) 5、若某二端口网络的传输参数为2714⎡⎣⎢⎤⎦⎥,则根据 24711⨯-⨯= 可知该网络具有互易性。
6、在二端口网络的Z 、 Y 、 H 、T 四种参数矩阵的各元素中,称为转移阻抗的参数是____ z 12 z 21 a 12 _________________________。
7、试求图示二端口网络的Z 参数。
︒︒︒︒22'11'R 1R 2I 12I⋅U 2⋅U 1⋅r 1I +-++--解:U z I z I U z I z I 11111222211222=+=+⎧⎨⎩ 2 U R I R I 11211=+ , z R R 1112=+ 4 U R I 122= , z R 122= 6 I rI R I 2121=-+ , z R r 212=- 8 U R I 222= , z R 222= 108、已知二端口网络的Y 参数为3212--⎡⎣⎢⎤⎦⎥S ,试用线性电阻及受控源画出该网络的一种等效电路。
第10章 习题解答
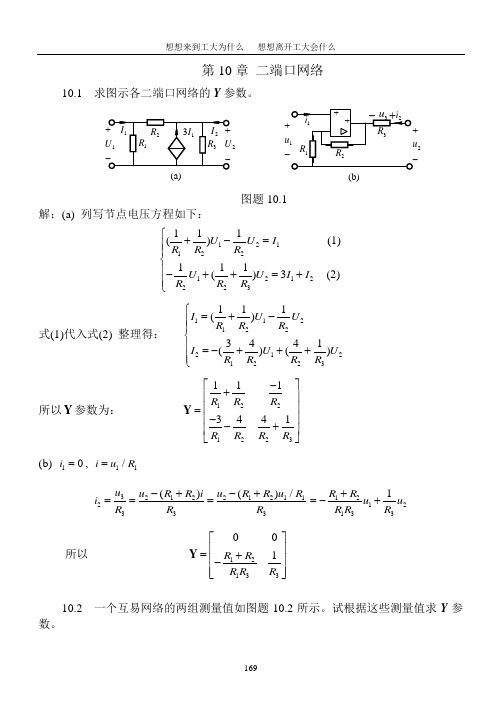
第10章 二端口网络10.1 求图示各二端口网络的Y 参数。
22u (b)图题10.1解:(a) 列写节点电压方程如下:1211221212223111() (1)111()3 (2)U U I R R R U U I I R R R ⎧+-=⎪⎪⎨⎪-++=+⎪⎩ 式(1)代入式(2) 整理得: 1121222121223111()3441()()I U U R R R I U U R R R R ⎧=+-⎪⎪⎨⎪=-+++⎪⎩所以Y 参数为:12212231113441R R R R RR R -⎡⎤+⎢⎥⎢⎥=-⎢⎥-+⎢⎥⎣⎦Y (b) 10i =, 11/i u R =3212212112333()()/u u R R i u R R u R i R R R -+-+===12121331R R u u R R R +=-+ 所以12133001R R R R R ⎡⎤⎢⎥=+⎢⎥-⎢⎥⎣⎦Y10.2 一个互易网络的两组测量值如图题10.2所示。
试根据这些测量值求Y 参数。
(a)(b)22-+U图题10.2解:图(a)中11222A,j2V 2j5j 10V j5A I U U I ===⨯==-,,由Y 参数方程得:11112221222j2j 10 (1)j5j2j 10 (2)I Y Y I Y Y ⎧==⨯+⨯⎨=-=⨯+⨯⎩ 由图(b)得 222jA 1V I Y ==⨯ (3) 对互易网络有:1221Y Y = (4)由式(3) 得: 22j 1S Y =,代入式(2) 得:2112( 2.5j5)S Y Y ==-- 再代入式(1)得:11(12.5j24)S Y =+ 所以12.5j2425j52.5j5j1.+--⎡⎤=⎢⎥--⎣⎦Y S 10.3 求图示各二端口网络的Z 参数。
(b)图题10.3解 (a):按网孔列写KVL 方程得1211221(2)2 (1)2(2)3 (2)R R I RI U RI R R I U U ++=⎧⎨++=+⎩ 将式(1)代入式(2)整理得1122123273U RI RI U RI RI =+⎧⎨=--⎩ 所以 3273RR R R ⎡⎤=⎢⎥--⎣⎦Z(b) 将∆联接的三个阻抗转换成Y 形联接,如图(c)所示,由此电路可直接写出Z 参数1j j j 0+⎡⎤=⎢⎥⎣⎦Z Ω10.4求图示各二端口网络的A 参数。
邱关源《电路》配套题库-课后习题(二端口网络)【圣才出品】

第16章二端口网络1.求图16-1所示二端口的Y参数、Z参数和T参数矩阵。
图16-1解:(1)图16-1(a),两端口电压和电流参考方向,如图16-2(a)所示。
根据各元件的特性及电路的KVL和KCL定理,可得:将式②代入式①得:综上可得:图16-2(2)图16-1(b),两端口电压和电流参考方向,如图16-2(b)所示。
根据各元件的特性及电路的KVL和KCL定理,可得:将式②代入式①得:综上可得:2.求图16-3所示二端口的Y参数和Z参数矩阵。
图16-3解:图16-3所示电路为纯电阻电路,所以只求Z即可。
(1)图16-3(a),将三个电阻为1Ω的三角形电路转换为星形电路,如图16-4(a)所示,可得:所以(a)(b)图16-4(2)图16-3(b),电流电压方向如图16-4(b)所示,则有:又根据电路的对称特点可得:所以3.求图16-5所示二端口的T参数矩阵。
图16-5解:图16-6是五个二端口电路,分别标出了端口电压、,电流、及其参考方向。
图16-6(1)图16-6(a),,所以T参数矩阵为(2)图16-6(b),,所以T参数矩阵为(3)图16-6(c),建立KVL方程:整理得:所以T参数矩阵为:(4)图16-6(d),,所以T参数矩阵为(5)图16-6(e),,所以T参数矩阵为。
4.求图16-7所示二端口的Y参数矩阵。
图16-7解:图16-8是两个二端口电路,分别标出了端口电压、,电流、及其参考方向。
图16-8(1)图16-8(a),网孔电流方程为:所以Y参数矩阵为:(2)图16-8(b),结点电压方程为:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六章(二端口网络)习题解答一、选择题1.二端口电路的H参数方程是 a 。
a .⎩⎨⎧+=+=22212122121111U H I H I U H I H U &&&&&&b . ⎩⎨⎧+=+=22212122121111I H U H U I H U H I &&&&&&c .⎩⎨⎧+=+=22222112122111U H I H U U H I H I &&&&&&d . ⎩⎨⎧+=+=22212112121112I H U H I I H U H U &&&&&&2.图16—1所示二端口网络的Z 参数方程为 b 。
a .⎥⎦⎤⎢⎣⎡---+j1j4j4j43;b .⎥⎦⎤⎢⎣⎡----j1j4j4j43;c .⎥⎦⎤⎢⎣⎡--j1j4j4j43;d .⎥⎦⎤⎢⎣⎡--+j1j4j4j433.无任何电源的线性二端口电路的T 参数应满足 d 。
a .D A =b .C B =c .1=-AD BCd .1=-BC AD 4.两个二端口 c 联接,其端口条件总是满足的。
a .串联b .并联c .级联d .a 、b 、c 三种 5.图16—2所示理想变压器的各电压、电流之间满足的关系为 d 。
a .n u u 121=,n i i =21;b .n u u =21,ni i121-=;c .n u u 121-=,n i i=21;d .n u u =21,ni i121=; 二、填空题1.图16—3(a )所示二端口电路的Y 参数矩阵为Y =⎥⎦⎤⎢⎣⎡--Y Y Y Y,图16—3(b )所示二端口的Z 参数矩阵为Z =⎥⎦⎤⎢⎣⎡Z Z Z Z。
2.图16—4所示二端口网络的Y参数矩阵是Y=⎥⎦⎤⎢⎣⎡-32676131。
解:将图16—4中三个Ω2星形连接的电阻等效为三个Ω6三角形连接的电阻,则电路如图16—4(a)所示。
由图16—4(a)得:212111613166UUUUUI-=-+=⎪⎭⎫⎝⎛-++-=-+++=21211221226131434616641UUUUUUUIUI=213267UU+于是Y =⎥⎦⎤⎢⎣⎡-326761313.图16—5所示回转器的T参数矩阵为⎥⎦⎤⎢⎣⎡1gg。
解:由回转器两个端口电压、电流的关系,得211igu-=,121igu=即211igu-=,21gui=由此可见T=⎥⎦⎤⎢⎣⎡1gg4.图16—6所示的二端口网络中,设子二端口网络1N 的传输参数矩阵为⎥⎦⎤⎢⎣⎡D C B A ,则复合二端口网络的传输参数矩阵为⎥⎦⎤⎢⎣⎡++D BY CAY BA。
解:图16—6所示的二端口网络可看成由1N 和虚线框中的二端口级连而成。
虚线框中的二端口的传输参数矩阵为⎥⎦⎤⎢⎣⎡101Y 。
设图16—6所示二端口网络的传输参数矩阵为T ,则 T = ⎥⎦⎤⎢⎣⎡101Y ⎥⎦⎤⎢⎣⎡⋅D C B A =⎥⎦⎤⎢⎣⎡++D BY C AY B A5.图16—7所示二端口网络的Y 参数矩阵为 ⎥⎦⎤⎢⎣⎡∆∆-∆-∆12n n n ,式中212R R n +=∆ 。
解:由图16—7得:3111U I R U &&&+= …… ① 4222U I R U&&&+= …… ② 34U n U &&= …… ③ 21I n I&&-= …… ④ 从以上四式中消去3U &,4U &和2I &得 2212121221U R R n n U R R n n I &&&+-+= 消去3U &,4U &和1I &得 2212121221U R R n U R R n n I &&&+++-= 因此 Y =⎥⎦⎤⎢⎣⎡∆∆-∆-∆12n n n ,式中 212R R n +=∆三、计算题1.图16—8所示二端口网络的Z 参数是Ω=1011Z 、Ω=1512Z 、Ω=521Z ,Ω=2022Z 。
试求sU U2。
解:由给定的Z 参数得2111510I I U += …… ①212205I I U += …… ②由输入、输出端口得11100U I U s += …… ③2225I U -= …… ④由①、③得 2115110I I U s +=由②、④得 219I I -=于是 2222239)25(3997515)9(110U I I I I U s =-⨯=-=+-⨯= 即3912=s U U 2.已知某二端口的Y 参数矩阵为Y ⎥⎦⎤⎢⎣⎡--=3225S ,求其π形等效电路(如图16—9所示)中的1Y 、2Y 、3Y 。
解:由题目给出的Y 参数矩阵得⎩⎨⎧+-=-=2122113225U U I U U I &&&&&& 而图16—9的Y 参数方程为⎩⎨⎧++-=-+=232122221211)()(U Y Y U Y I U Y U Y Y I &&&&&& 对照上述两组方程得521=+Y Y ,332=+Y Y ,22-=-Y 故 S 22=Y ,S 31=Y ,S 13=Y3.已知图16—10所示二端口S N 的Z 参数为Ω=10011Z ,Ω-=50012Z ,Ω=32110Z ,Ω=1022Z ,求:L Z 等于多少时其吸收功率最大。
解:将L Z 以左的部分视为一端口电路,那么当L Z 和此一端口电路匹配时L Z 可获得最大功率,计算此一端口电路戴维南阻抗的等效电路如图16—10(a )。
由给定的条件可得211500100I I U &&&-=,212101000I I U &&&+=,11500I U &&-= 从以上三式中消去1U &和1I &,得3253022=IU &&,因此Ω=32530L Z 4.求图16—11所示二端口网络的T 参数。
解:图16—11所示的二端口网络可视为三个子二端口网络级连而成。
设左、中、右三个子二端口网络的传输参数矩阵分别为T 1 ,T 2 ,T 3 则T 1 ⎥⎦⎤⎢⎣⎡=010g g , T 2 ⎥⎦⎤⎢⎣⎡=n n 100, T 3 ⎥⎦⎤⎢⎣⎡=1101R而 T = T 1 T 2 T 3 ⎥⎦⎤⎢⎣⎡=010g g ⎥⎦⎤⎢⎣⎡n n 100⎥⎦⎤⎢⎣⎡1101R ⎥⎦⎤⎢⎣⎡=0)(1)(1ng ng ngR 5.电路如图16—12所示,试求用H 参数表示的双端接二端口电压转移函数sU U&&2。
解:由H 参数方程及端口外电路的伏安关系 ⎪⎩⎪⎨⎧-=+=-=+=z s s RU U H I H I I Z U U H I H U 2222121212121111&&&&&&&&&从上两式中消去1I &得 s s zU U H Z H R H H &&=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛+-211222112)(11 ∴ )(111222112212H Z H R H H H U Us z s+⎪⎭⎫⎝⎛+-=&&。
